5.5: Рух

Якщо частинка рухається з рівномірним або постійним прискоренням, то вона повинна вести себе за певними стандартними законами кінематики. У цьому розділі ми розробимо ці закони руху і застосуємо їх до ряду цікавих додатків.

Рівномірна швидкість

Якщо об'єкт рухається з рівномірною (постійною) швидкістю v, то відстань d, пройдена за часом t, задається за формулою

\[d=v t\]

або словами, «відстань дорівнює швидкості раз часу». Це поняття, напевно, знайоме тим з нас, хто їздить на наших автомобілей по шосе. Наприклад, якщо я їду на своєму автомобілі з постійною швидкістю 50 миль на годину, за 3 години я проїду 150 миль. Тобто,

\[150 \mathrm{mi}=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 3 \mathrm{h}\]

Зауважте, що це обчислення має вигляд «відстань дорівнює швидкості раз часу». Важливо відзначити, як одиниці балансують з кожного боку цього результату. Це легко побачити, скасуючи одиниці так само, як ви скасуєте числа зі звичайними дробами.

\[150 \mathrm{mi}=50 \frac{\mathrm{mi}}{\not{h}} \times 3 \not{h}\]

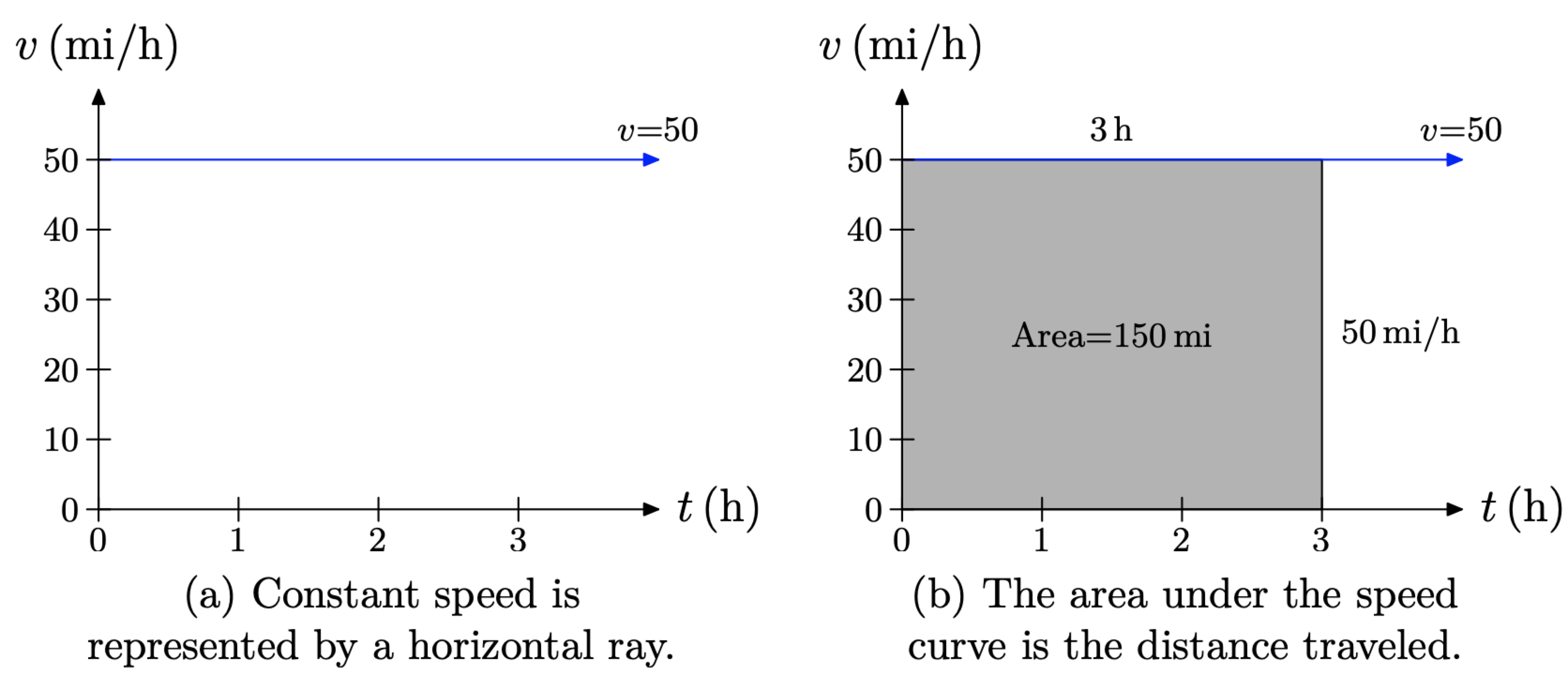
На малюнку\(\PageIndex{1}\) (a) ми побудували швидкість v автомобіля проти часу t Оскільки швидкість рівномірна (постійна), графік є горизонтальним променем, починаючи з часу t = 0 і рухаючись вправо. На малюнку\(\PageIndex{1}\) (b) ми затінювали область під променем постійної швидкості протягом часового інтервалу [0, 3] годин. Зверніть увагу, що площа затіненої прямокутної області має висоту рівну 50 миль на годину (50 миль/год) і ширину рівну 3 годинам (3 год), тому площа цього прямокутника дорівнює

\[\text { Area }=\text { height } \times \text { width }=50 \frac{\mathrm{mi}}{\mathrm{h}} \times 3 \mathrm{h}=150 \mathrm{mi}\]

Зверніть увагу на одиниці на відповідь. Площа під променем постійної швидкості становить 150 миль. Тобто площа під кривою швидкості - це пройдена відстань!

Наша робота привела нас до наступного результату.

Рівномірна швидкість

Припустимо, що об'єкт рухається з рівномірною (постійною) швидкістю v.

• Пройдена відстань d задається формулою d = vt, де t - час подорожі.
• Графік швидкості v проти часу t буде горизонтальним променем, що починається з часу t = 0 і рухається вправо.
• Площа прямокутної області під графіком v за часовий проміжок [0, t] дає відстань, пройдену за цей період часу.

Малюнок\(\PageIndex{1}\)

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{1}\)

Об'єкт рухається з рівномірною швидкістю v. Графік v проти t показаний на наступному графіку.

Малюнок\(\PageIndex{2}\). Графік швидкості об'єкта в порівнянні з часом.

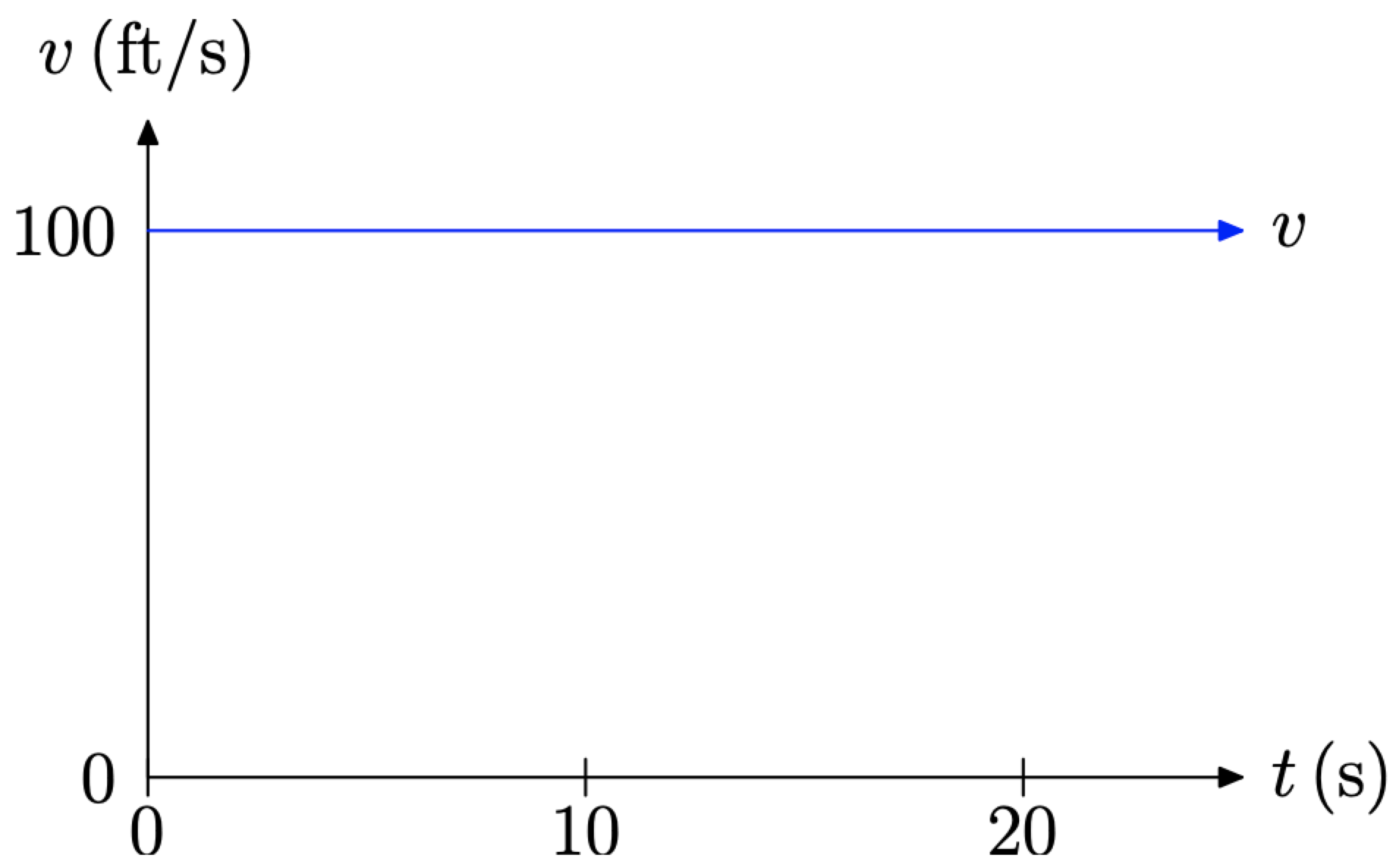
Яка швидкість руху об'єкта в будь-який момент t? Як далеко проїде об'єкт за 20 секунд?

Рішення

Швидкість зчитуємо з графіка. Зверніть увагу, що промінь, що представляє швидкість, є рівним (постійним) зі швидкістю 100 футів в секунду (100 футів/с). Тому швидкість в будь-який момент t дорівнює v = 100. У позначенні функції ми б написали v (t) = 100, пам'ятаючи, що одиниці є футами в секунду (ft/s).

Щоб знайти пройдену відстань за 20 секунд, у нас є два варіанти:

1. Якщо використовувати формулу d = vt, то

\[\begin{aligned} d &=v t \\ d &=100 \frac{\mathrm{ft}}{\not{s}} \times 20 \not{s} \\ d &=2000 \mathrm{ft} \end{aligned}\]

Тобто об'єкт подорожує 2000 футів за 20 секунд.

2. Ми також можемо знайти пройдену відстань, затінюючи область під рівномірною кривою швидкості протягом 20-секундного інтервалу часу.

Малюнок\(\PageIndex{3}\). Площа під рівномірною кривою швидкості представляє пройдену відстань.

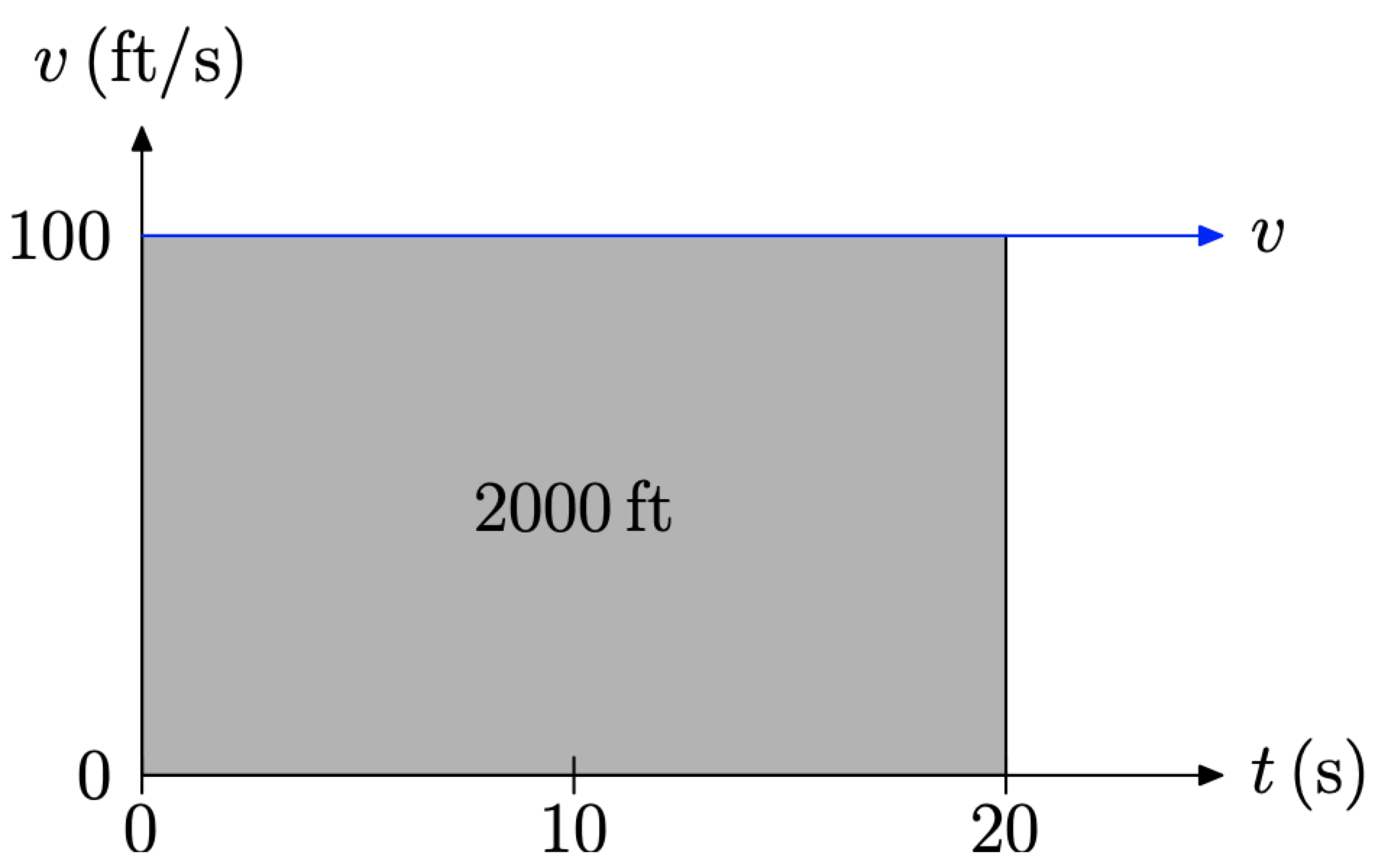
Зверніть увагу, що висота затіненої прямокутної області на малюнку\(\PageIndex{3}\) становить 100 футів в секунду (100 футів/с), а ширина 20 секунд (20 с). Значить, площа затіненої прямокутної області

\[\text { Area }=100 \frac{\mathrm{ft}}{\not{s}} \times 20 \not{s}=2000 \mathrm{ft}\]

який ідентичний знайденому результату з формулою d = vt.

рівномірне прискорення

Давайте знову повернемося в машину і їдемо по шосе зі стійкою (постійною) швидкістю v = 30 миль на годину. Ми вирішуємо обігнати перед нами вантажівку, тому наступаємо на прискорювач автомобіля, який збільшує швидкість автомобіля, дозволяючи нам проїхати вантажівку.

Визначення

Прискорення - це швидкість, з якою швидкість об'єкта змінюється по відношенню до часу.

Наприклад, припустимо, що коли ми наступаємо на прискорювач автомобіля, швидкість автомобіля змінюється на постійних 20 миль на годину на годину. Тоді ми б сказали, що прискорення рівномірне (постійне) і пише

\[\text { Acceleration }=20 \frac{\mathrm{mi} / \mathrm{h}}{\mathrm{h}}\]

або, більш лаконічно, як

\[\text { Acceleration }=20 \frac{\mathrm{mi}}{\mathrm{h}^{2}}\]

Останнє позначення воліють вчені, але позначення a = 20 (mi/h) /h зрозуміти набагато простіше. Тобто швидкість збільшується з постійною швидкістю 20 миль на годину щогодини.

• На даний момент ми наступаємо на акселератор, щоб проїхати вантажівку, початкова швидкість автомобіля v = 30 миль на годину. Якщо підтримувати постійне розгін 20 миль на годину на годину, то через 1 годину швидкість збільшується на 20 миль на годину, тому швидкість автомобіля в кінці 1 години дорівнює\[v=30+20(1)\] або v = 50 миль на годину.
• Після закінчення двох годин швидкість автомобіля дорівнює\[v=30+20(2)\] або v = 70 миль на годину.
• Після закінчення трьох годин швидкість автомобіля дорівнює\[v = 30 + 20(3)\], або v = 90 миль на годину.

Продовжуючи таким чином, нескладно помітити, що швидкість автомобіля в кінці t годин буде задаватися за формулою\[v=30+20 t\]

Важливо зазначити, що ми робимо припущення, що ми тримаємо ногу на цьому прискорювачі, щоб підтримувати рівномірне (постійне) прискорення 20 миль на годину на годину. Звичайно, це досить дурний приклад з дуже низьким прискоренням (це автомобіль Фреда Флінтстоуна?) , але це дозволяє нам зосередитися на концепції без необхідності мати справу з брудними одиницями.

Якщо слідувати аргументу вище, не важко розробити перше рівняння руху.

Перше рівняння руху

Якщо об'єкт, що має початкову швидкість,\(v_{0}\) відчуває постійне прискорення a, то його швидкість в час t задається формулою\[v=v_{0}+a t\].

Слідуємо науковій практиці позначення початкової швидкості v0, швидкості в момент t = 0. Ось чому ми підписали v з нулем.

Звичайно, перше рівняння руху дійсне лише в тому випадку, якщо кожна величина має відповідні одиниці.

Приклад\(\PageIndex{2}\)

Припустимо, що частка має початкову швидкість 20 футів в секунду (20 футів/с) і отримує постійне прискорення 4 фути в секунду в секунду\(\left(4 f t / s^{2}\right)\). Якою буде швидкість частки через 3 хвилини (3 хв)?

Рішення

Заманливо почати з формули\[v=v_{0}+a t\]

і замінюють\(v_{0}=20 \mathrm{ft} / \mathrm{s}, a=4 \mathrm{ft} / \mathrm{s}^{2},\) і\(t=3 \mathrm{min}\)

\[v=20 \frac{\mathrm{ft}}{\mathrm{s}}+4 \frac{\mathrm{ft}}{\mathrm{s}^{2}} \times 3 \mathrm{min}\]

Однак зауважте, що одиниці не скасовуватимуться, оскільки час вимірюється в хвилинах. Що нам потрібно зробити, це змінити час на секунди з перетворенням

\[t=3 \not{min} \times 60 \frac{\mathrm{s}}{\not{min}}=180 \mathrm{s}\]

Тепер одиниці повинні бути правильними. Підставляємо час в секундах в формулу\(v = v_{0} + at\) і отримуємо

\[\begin{aligned} v &=20 \frac{\mathrm{ft}}{\mathrm{s}}+4 \frac{\mathrm{ft} / \mathrm{s}}{\not{s}} \times 180 \not{\mathrm{s}} \\ &=20 \frac{\mathrm{ft}}{\mathrm{s}}+720 \frac{\mathrm{ft}}{\mathrm{s}} \\ &=740 \frac{\mathrm{ft}}{\mathrm{s}} \end{aligned}\]

Значить, швидкість частки в три хвилини дорівнює v = 740 ft/s.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{3}\)

М'яч кидається в повітря з початковою швидкістю 180 футів в секунду (180 футів/с). Він відразу починає сповільнюватися з постійною швидкістю 32 футів в секунду в секунду\((32 ft/s^2 )\). В який час м'яч досягне максимальної висоти?

Рішення

Коли кулька досягне максимальної висоти, його швидкість дорівнюватиме нулю. Тобто в той момент, коли м'яч виявиться на максимальній висоті, він зупиниться до того, як повернеться на землю. Таким чином, щоб знайти час, коли куля знаходиться на максимальній висоті, підставляємо в формулу v = 0\(v = v_{0} + at\) і вирішуємо для t.

\[\begin{aligned} 0 &=v_{0}+a t \\ a t &=-v_{0} \\ t &=-\frac{v_{0}}{a} \end{aligned}\]

Коли ми говоримо, що м'яч сповільнюється з постійною швидкістю 32 футів/с кожну секунду, ми маємо на увазі, що м'яч втрачає швидкість зі швидкістю 32 футів/с кожну секунду. Таким чином, прискорення негативне в даному випадку і пишемо\(a = −32 ft/s^2\).

Нарешті, нам потрібно лише підставити початкову швидкість (v0 = 180 ft/s) і прискорення\((a = −32 ft/s^2)\) в рівняння (6) і спростити.

\[t=-\frac{180 \mathrm{ft} / \mathrm{s}}{-32 \mathrm{ft} / \mathrm{s}^{2}}\]

Аналіз одиниць - це хороша перевірка того, що ми робимо речі правильно. Зауважте, що\[\frac{\mathrm{ft} / \mathrm{s}}{\mathrm{ft} / \mathrm{s}^{2}}=\frac{\mathrm{ft}}{\mathrm{s}} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}=\mathrm{s}\]

Таким чином, час досягнення м'ячем своєї максимальної висоти становить\[t = 5 s\].

Площа - це пройдена відстань

Якщо ми будуємо графік швидкості v проти часу t, зверніть увагу, що рівняння\(v = v_{0} +at\) має вигляд y = mx+b, особливо якщо ми розташуємо рівняння в порядку\(v = at+v_{0}\). Потім легко помітити, що графік буде лінією з перехопленням, що дорівнює початковій швидкості\(v_{0}\) і нахилу, що дорівнює прискоренню a Графік\(v = v_{0} + at\) показаний на малюнку\(\PageIndex{4}\) (а).

На малюнку\(\PageIndex{4}\) (b) ми затінювали область під графіком\(v = v_{0} + at\) протягом часового інтервалу [0, t]. Є природне питання, яке потрібно задати. Чи буде площа під графіком на\(v = v_{0} + at\) малюнку\(\PageIndex{4}\) (b) відображати відстань, пройдену за проміжок часу [0, t]?

Малюнок\(\PageIndex{4}\). Графік\(v = v_{0} + at\) - це лінія з перехопленням v0 і нахилом a.

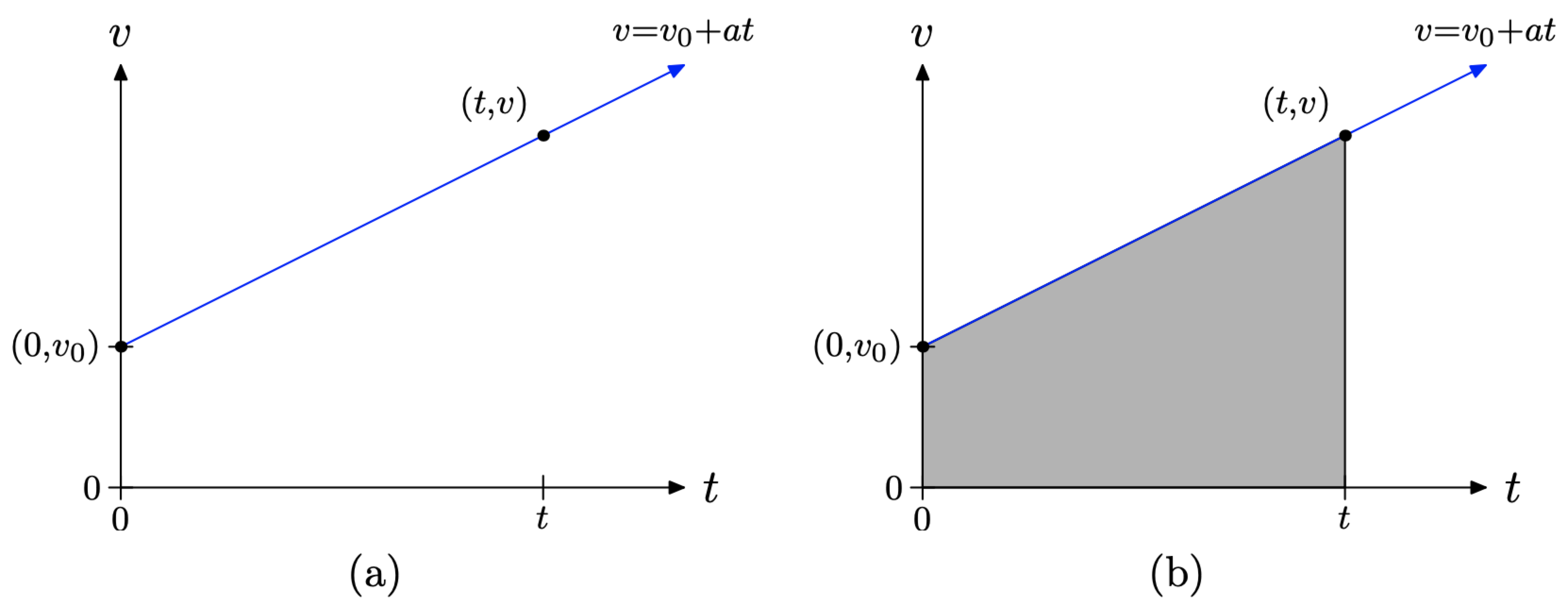
Ми знаємо, що площа під рівномірною (постійною) швидкістю променя буде дорівнювати пройденій відстані. Чи можемо ми використовувати цей факт, щоб відповісти на наше запитання щодо затіненої трикутної області на малюнку\(\PageIndex{4}\) (b)?

Візьмемо часовий інтервал [0, t] на малюнку\(\PageIndex{4}\) (b) і розділимо його на 4 рівні підпроміжки часу, як показано на малюнку\(\PageIndex{5}\) (а).

Малюнок\(\PageIndex{5}\). Поділ площі на прямокутники.

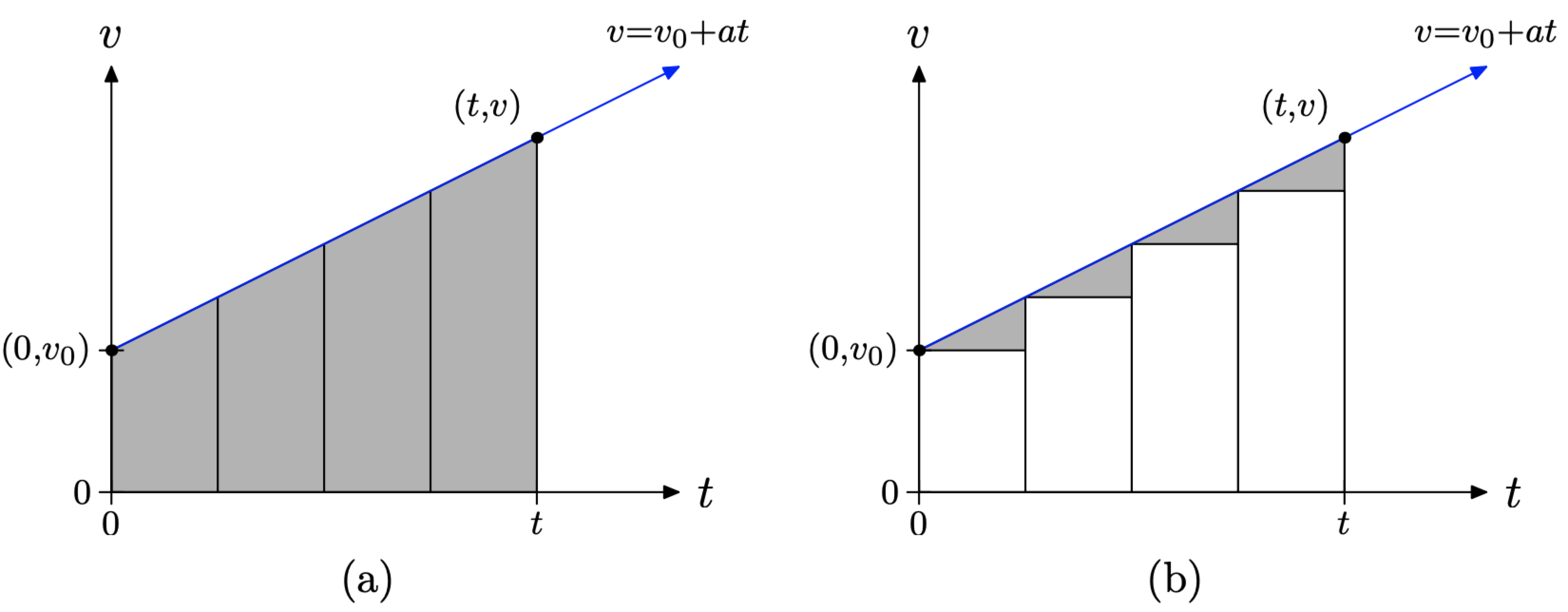
Далі за допомогою лівої кінцевої точки кожного підінтервалу часу намалюйте чотири прямокутники і залийте їх білим кольором, як показано на малюнку\(\PageIndex{5}\) (b). Вершина кожного прямокутника горизонтальна, тому ми знаємо, що це являє собою рівномірну (постійну) швидкість. Тому площа кожного білого прямокутника представляє відстань, пройдену протягом цього підінтервалу часу. Якщо підсумувати площі всіх чотирьох прямокутників, то отримаємо загальну відстань, пройдену за часовий проміжок [0, t], з, звичайно, припущенням, що швидкість постійна протягом кожного з підінтервалів часу.

Однак швидкість не є постійною протягом кожного підінтервалу часу, тому сума площ прямокутників лише наближає загальну відстань, пройдену на часовому інтервалі [0, t].

Ключова ідея полягає в тому, щоб намалювати більше прямокутників. На малюнку\(\PageIndex{6}\) (a) ми розділили часовий інтервал [0, t] на 8 рівних підінтервалів часу. На малюнку\(\PageIndex{6}\) (b) ми знову використовуємо ліві кінцеві точки кожного підінтервалу часу, щоб намалювати прямокутники і заливаємо їх кольором білим.

Знову ж таки, вершина кожного білого прямокутника горизонтальна, що представляє рівномірну (постійну) швидкість на цьому підінтервалі часу. Тому площа кожного білого прямокутника знову представляє відстань, пройдену протягом цього підінтервалу часу. Сума всіх 8 прямокутників представляє відстань, пройдену за проміжок часу [0, t], припускаючи, що швидкість постійна протягом кожного з підінтервалів часу.

Однак швидкість не є постійною на часовому інтервалі [0, t], тому сума восьми прямокутників пропонує лише наближення відстані, пройденої протягом часового інтервалу [0, t], хоча і краще наближення, ніж та, яку пропонує сума площ лише чотирьох прямокутників на малюнку\(\PageIndex{5}\) (b).

Коли ми розділимо часовий інтервал [0, t] далі, відбудеться дві речі

Малюнок\(\PageIndex{6}\). Поділ площі на прямокутники.

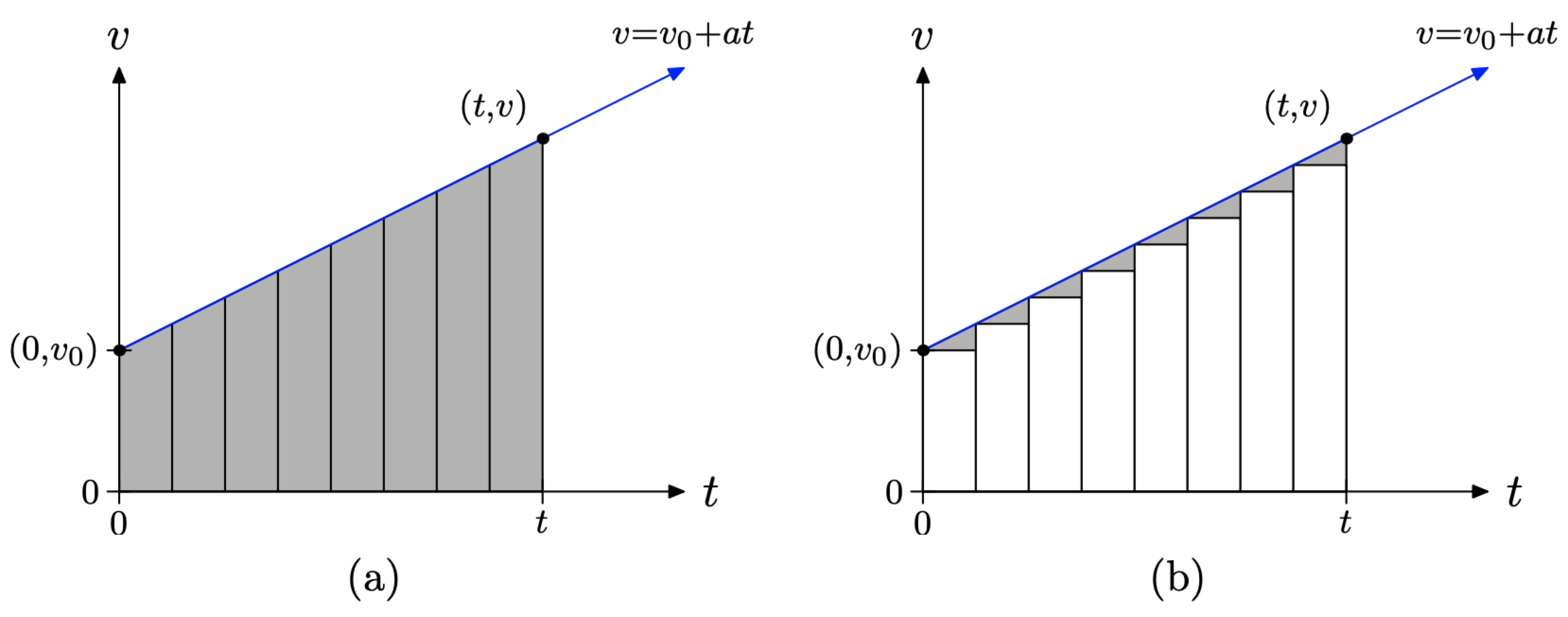
1. Субінтервалів часу стануть менше (насправді, нескінченно малі). Коли це трапляється, стає все більш розумним припустити, що швидкість постійна протягом цього субінтервалу часу. Тому в межі сума площ прямокутників буде представляти загальну відстань, пройдену за проміжок часу [0, t].
2. Сума площ прямокутників сходиться до площі затіненої області під кривою швидкості на малюнку\(\PageIndex{4}\) (а).

Цей аргумент призводить до одного переконливого висновку.

Площа дорівнює пройденій відстані

Площа під кривою швидкості\(v = v_{0} + at\) за часовий інтервал [0, t] представляє відстань, пройдену за часовий інтервал [0, t].

На\(\PageIndex{7}\) малюнку затінена область під\(v = v_{0} + at\) є трапецією. Щоб знайти площу цієї трапеції, складаємо підстави (паралельні сторони) разом, множимо на висоту, потім беремо половину результату.

Малюнок\(\PageIndex{7}\). Площа затіненої трапецієподібної області представляє пройдену відстань.

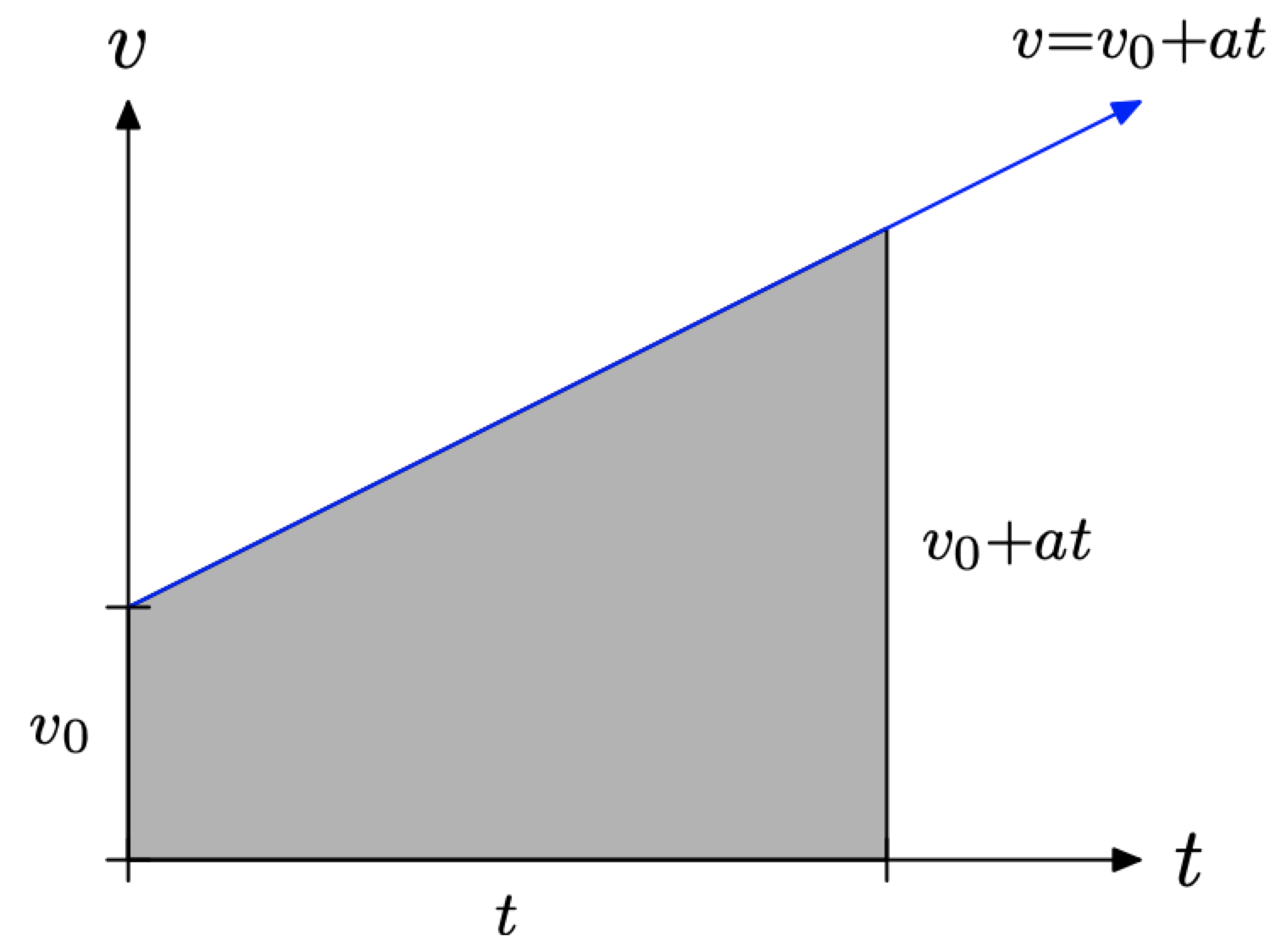
Таким чином, площа затіненої області на малюнку\(\PageIndex{7}\) задається за формулою

\[\text { Area }=\frac{1}{2}\left[v_{0}+\left(v_{0}+a t\right)\right] t\]

Підсумуйте кількість всередині дужок, потім розподіліть 1/2 і t для отримання

\[\text { Area }=v_{0} t+\frac{1}{2} a t^{2}\]

Рух в одному вимірі

Припустимо, що частка обмежена рухатися по реальній лінії. Крім того, припустимо, що в момент t = 0 початкове положення частинки знаходиться в,\(x_{0}\) а частка має початкову швидкість\(v_{0}\) і рухається вправо (як показано на малюнку\(\PageIndex{8}\)). Припустимо, що частинка відчуває рівномірне прискорення a, яке є позитивним, так що частинка продовжує рухатися вправо зі збільшенням швидкості. У момент t нехай положення частки позначається x, а її швидкість - v (також показано на малюнку\(\PageIndex{8}\)).

Малюнок\(\PageIndex{8}\). Частка рухається по лінії з рівномірним прискоренням.

Оскільки ми припустили, що частинка рухається вправо зі збільшенням швидкості, відстань, пройдена частинкою, задається виразом\(x − x_{0}\). Однак ми також дізналися, що пройдена відстань - це площа під графіком швидкості (показано на малюнку\(\PageIndex{7}\)), яку ми обчислили в рівнянні (7) бути\(v_{0} t+ (1/2)at^2\). Ми робимо висновок, що\[x-x_{0}=v_{0} t+\frac{1}{2} a t^{2}\]

що призводить до другого рівняння руху.

Друге рівняння руху

Припустимо, що частинка рухається по дійсній лінії з рівномірним прискоренням a Причому припустимо, що положення і швидкість частинки в момент t = 0 задаються x0 і v0 відповідно. Нехай x представляє позицію частинки в момент t Потім положення частинки в момент t задається за формулою

\[x=x_{0}+v_{0} t+\frac{1}{2} a t^{2}\]

Розробляючи рівняння руху (9), ми уникали поняття швидкості. Однак, якщо частка обмежена рухатися вздовж реальної лінії, вона може рухатися вправо або вона може рухатися вліво. Це додає ще один вимір швидкості.

Давайте проведемо числову лінію (як показано на малюнку\(\PageIndex{9}\)), знайдемо початок і домовимося, що позитивні зсуви - вправо, а негативні - вліво.

Малюнок\(\PageIndex{9}\). Орієнтування реальної лінії

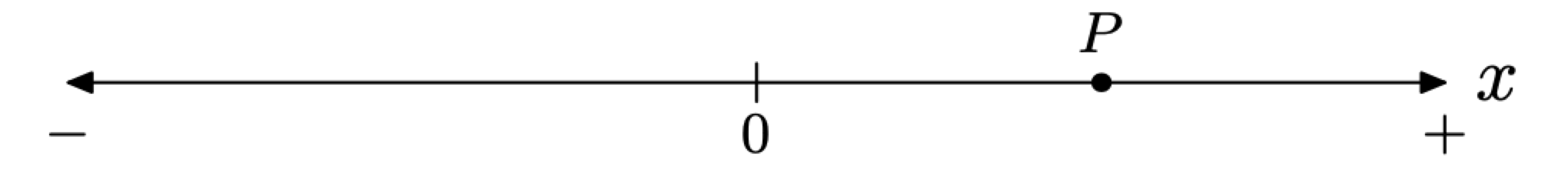
Далі визначаємо, що мається на увазі під швидкістю

Визначення

Швидкість - це швидкість, з якою положення об'єкта змінюється щодо часу.

Наприклад, припустимо, що зміщення на орієнтованій лінії на малюнку\(\PageIndex{9}\) вимірюються в метрах. Крім того, припустимо, що частка в точці P на малюнку\(\PageIndex{9}\) має швидкість v = 20 метрів в секунду. Це означало б, що положення частинки змінюється на позитивні 20 метрів кожну секунду. Через те, як ми орієнтували лінію Figure\(\PageIndex{9}\), це означає, що частинка рухається вправо зі швидкістю 20 метрів в секунду.

З іншого боку, якби швидкість частинки в точці P становила v = −20 метрів в секунду, це означало б, що положення частинки змінюється на від'ємні 20 метрів кожну секунду. Через орієнтацію, яку ми вибрали на малюнку\(\PageIndex{9}\), це означало б, що частинка рухається вліво зі швидкістю 20 метрів в секунду.

Зверніть увагу, що в кожному випадку (позитивна або негативна швидкість) швидкість становить 20 метрів в секунду. Те, що швидкість приносить таблиці, є додатковим атрибутом орієнтації. Знак швидкості вказує напрямок, тоді як величина швидкості вказує на швидкість.

Нам важливо констатувати, що рівняння руху однаково добре застосовуються, коли ми вводимо поняття швидкості. Таким чином, ми можемо підсумувати наступним чином.

Рівняння руху

Припустимо, що частинка рухається по орієнтованій дійсній лінії з рівномірним прискоренням а. далі, нехай\(x_{0}\) і\(v_{0}\) представляють початкове положення і швидкість частинки в момент t = 0.

• Швидкість v частинки в момент t задається за формулою\(v = v_{0} + at\).
• Положення x частинки в момент t задається за формулою\(x = x_{0} + v_{0} t + \frac{1}{2} at^2\).

Давайте розглянемо деякі програми цих рівнянь руху.

Приклад\(\PageIndex{4}\)

Орієнтуйте реальну лінію, як на малюнку\(\PageIndex{9}\). Припустимо, що в момент t = 0 частка розташована на 2 метри праворуч від початку і рухається зі швидкістю 3 метри в секунду. Далі припустимо, що частка рухається з рівномірним прискоренням\(1.5 m/s^2\). Знайти швидкість і положення частинки в кінці 10 секунд.

Рішення

Нам дано, що\(v_{0} = 3\) м/с і\(a = 1.5 m/s^2\). Таким чином, після t = 10 секунд,

\[\begin{array}{l}{v=v_{0}+a t} \\ {v=3 \frac{\mathrm{m}}{\mathrm{s}}+1.5 \frac{\mathrm{m} / \mathrm{s}}{\not{s}} \times 10 \not{\mathrm{s}}} \\ {v=3 \frac{\mathrm{m}}{\mathrm{s}}+15 \frac{\mathrm{m}}{\mathrm{s}}} \\ {v=18 \frac{\mathrm{m}}{\mathrm{s}}}\end{array}\]

Ми також дали, що\(x_{0} = 2\) м Таким чином, після t = 10 секунд

\[\begin{aligned} x &=x_{0}+v_{0} t+\frac{1}{2} a t^{2} \\ x &=2 \mathrm{m}+\left(3 \frac{\mathrm{m}}{\mathrm{s}}\right)(10 \mathrm{s})+\frac{1}{2}\left(1.5 \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)(10 \mathrm{s})^{2} \\ x &=2 \mathrm{m}+\left(3 \frac{\mathrm{m}}{\not{s}}\right)(10 \mathrm{s})+\frac{1}{2}\left(1.5 \frac{\mathrm{m}}{\not{\mathrm{s}^{2}}}\right)\left(100 \not{\mathrm{s}^{2}}\right) \\ x &=2 \mathrm{m}+30 \mathrm{m}+75 \mathrm{m} \\ x &=107 \mathrm{m} \end{aligned}\]

Таким чином, в кінці t = 10 секунд частка розташовується на 107 метрів праворуч від початку і має швидкість 18 метрів в секунду (рухається вправо зі швидкістю 18 метрів в секунду)

Давайте розглянемо ще одне застосування Рівняння руху.

Приклад\(\PageIndex{5}\)

Автомобіль їде по шосе зі швидкістю 60 миль на годину. Раптом на дорозі попереду з'являється олень і водій застосовує гальма, сповільнюючи машину з постійною швидкістю 12,9 футів в секунду кожну секунду. Скільки часу займає зупинка автомобіля і як далеко він проїжджає за цей час?

Рішення

Швидкість руху автомобіля задається за формулою v = v0 + at. Автомобіль зупиниться, коли v = 0. Тому підставляємо в формулу v = 0 і вирішуємо для t

\[\begin{array}{l}{v=v_{0}+a t} \\ {0=v_{0}+a t} \\ {t=-\frac{v_{0}}{a}}\end{array}\]

Під час t = 0 початкова швидкість автомобіля дорівнює v0 = 60 mi/h. автомобіль сповільнюється, тому він втрачає швидкість з заданою швидкістю 12,9 футів в секунду кожну секунду; тобто\(a = −12.9 ft/s^2\). Ми могли б спробувати замінити ці числа в наш останній результат.

\[t=-\frac{60 \mathrm{mi} / \mathrm{h}}{-12.9 \mathrm{ft} / \mathrm{s}^{2}}\]

Проблема відразу очевидна: одиниці не скасують. У нас є два варіанти; ми можемо або (1) змінити початкову швидкість на фути в секунду, або (2) змінити прискорення на милі на годину на годину. Перші ми зробимо з наступним розрахунком.

\[v_{0} = \frac{60\not{\text{mi}}}{\not{\text{h}}} \times \frac{5280\text{ft}}{\not{\text{mi}}} \times \frac{1\not{\text{h}}}{60\not{\text{min}}} \times \frac{1\not{\text{min}}}{60\not{\text{s}}} = 88\text{ft/s}\]

Ми підставимо це число в рівняння (13).

\[\begin{aligned} t &=-\frac{v_{0}}{a} \\ t &=-\frac{88 \mathrm{ft} / \mathrm{s}}{-12.9 \mathrm{ft} / \mathrm{s}^{2}} \\ t & \approx 6.8 \mathrm{s} \end{aligned}\]

Знову ж таки, важливо перевірити агрегати. Зверніть увагу, що

\[\frac{\mathrm{ft} / \mathrm{s}}{\mathrm{ft} / \mathrm{s}^{2}}=\frac{\mathrm{ft}}{\mathrm{s}} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}=\mathrm{s}\]

яка є правильною одиницею часу.

Тепер ми знайдемо гальмівний шлях, дозволивши початковому положенні автомобіля бути\(x_{0} = 0\) ногами. Таким чином,\(x = x_{0} + v_{0} t + (1/2)at^2\) стає

\[x=v_{0} t+\frac{1}{2} a t^{2}\]

а x буде представляти гальмівний шлях.

Тепер підставляємо початкову швидкість v0 = 88 футів в секунду, прискорення a = −12,9 футів в секунду кожну секунду, а час зупинки t = 6,8 секунди. Таким чином,

\[\begin{aligned} x &=v_{0} t+\frac{1}{2} a t^{2} \\ x &=\left(\frac{88 \mathrm{ft}}{\mathrm{s}}\right)(6.8 \mathrm{s})+\frac{1}{2}\left(\frac{-12.9 \mathrm{ft} / \mathrm{s}}{\mathrm{s}}\right)(6.8 \mathrm{s})^{2} \\ x &=\left(\frac{88 \mathrm{ft}}{\not{s}}\right)(6.8 \not{\mathrm{s}})+\frac{1}{2}\left(\frac{-12.9 \mathrm{ft}}{\not{\mathrm{s}^{2}}}\right)\left(46.24 \not{\mathrm{s}^{2}}\right) \\ x &=598.4 \mathrm{ft}-298.248 \mathrm{ft} \\ x & \approx 300 \mathrm{ft} \end{aligned}\]

де ми округлили гальмівний шлях до найближчої ноги.

Прискорення за рахунок гравітації

Якщо знехтувати опором повітря, то тіло впаде на поверхню землі з рівномірним прискоренням. Фізики використовують букву g для представлення прискорення, обумовленого гравітацією. Біля поверхні землі це прискорення задається\(g=32 \mathrm{ft} / \mathrm{s}^{2}\) або, в метричній системі,\(g=9.8 \mathrm{m} / \mathrm{s}^{2}\).

Пам'ятайте, прискорення - це швидкість, з якою швидкість тіла змінюється щодо часу. Отже, якщо ми скинемо тіло з відпочинку на дуже великій висоті, через 1 секунду його швидкість складе 32 фути в секунду. Через 2 секунди його швидкість складе 64 фути в секунду. Через 3 секунди його швидкість складе 96 футів в секунду. Зверніть увагу, як швидкість змінюється зі швидкістю 32 футів в секунду кожну секунду.

Гравітація завжди притягує об'єкт до центру землі, тому ми повинні пам'ятати про це, використовуючи Рівняння руху.

Давайте розглянемо приклад.

Приклад\(\PageIndex{6}\)

Куля звільняється від спокою з повітряної кулі, яка ширяє на відстані 2000 футів над поверхнею землі. Скільки часу пройде, поки м'яч не вдарить об землю?

Рішення

У цій вправі ми повернемо реальну лінію так, щоб вона була вертикальною, як показано на малюнку\(\PageIndex{10}\) (а). Ми встановимо початок на рівні землі і дозволимо позитивному напрямку y вгору (позначається знаком + у верхній частині лінії на малюнку\(\PageIndex{10}\) (а).

Малюнок\(\PageIndex{10}\).

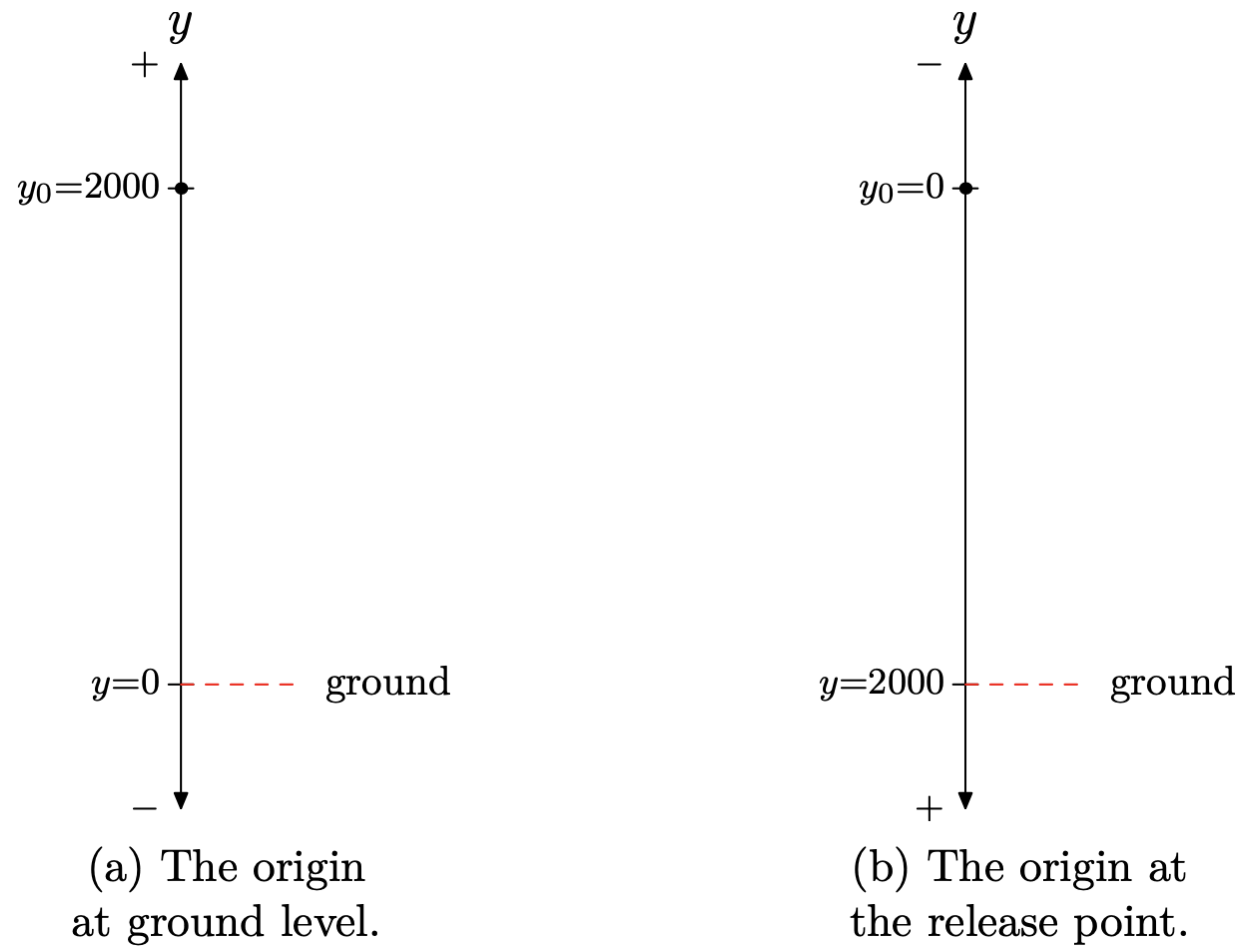
Ми почнемо з рівняння\(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\), а потім зауважимо, що початкова швидкість -\(v_{0} = 0\) фути в секунду (м'яч звільняється від відпочинку), тому рівняння стає\[y=y_{0}+\frac{1}{2} a t^{2}\]

Нас просять знайти, коли м'яч потрапляє на землю, так що це означає, що нас просять знайти, коли y = 0\(\PageIndex{10}\) (див. Рис. Встановіть y = 0 в останньому рівнянні і вирішіть для t.

\[\begin{aligned} 0 &=y_{0}+\frac{1}{2} a t^{2} \\ t^{2} &=-\frac{2 y_{0}}{a} \\ t &=\sqrt{-\frac{2 y_{0}}{a}} \end{aligned}\]

Зверніть увагу, що позитивні зсуви - вгору (див. Рис. 10 (а)). Якщо швидкість позитивна, м'яч рухається вгору. У нашому випадку кулька рухається вниз, тому швидкість негативна. У міру руху м'яча вниз його швидкість стає більшою, тому швидкість стає все більш негативною. Значить, прискорення має бути негативним; т\(a = −32 ft/s^2\). Е. Підставляємо це прискорення і початкове положення y0 = 2000 ft в останній результат і спрощуємо

\[\begin{aligned} t &=\sqrt{-\frac{2(2000 \mathrm{ft})}{-32 \mathrm{ft} / \mathrm{s}^{2}}} \\ t & \approx 11.2 \mathrm{s} \end{aligned}\]
Ми округлили результат до найближчої десятої частки секунди. Знову ж таки, важлива перевірка агрегатів. У цьому випадку

\[\sqrt{\frac{\mathrm{ft}}{\mathrm{ft} / \mathrm{s}^{2}}}=\sqrt{\mathrm{ft} \times \frac{\mathrm{s}^{2}}{\mathrm{ft}}}=\sqrt{\mathrm{s}^{2}}=\mathrm{s}\]

Крім того, ми могли б встановити реальну лінію, як показано на малюнку 10 (b), де ми розмістили початок у точці випуску та змінили орієнтацію (позитивний напрямок тепер вниз). Таким чином, вихідне положення -\(y_{0} = 0\) ноги, а початкова швидкість -\(v_{0} = 0\) фути в секунду (м'яч звільняється від спокою). Встановіть ці значення в рівнянні\(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\) і вирішіть для t.

\[\begin{aligned} y &=\frac{1}{2} a t^{2} \\ t^{2} &=\frac{2 y}{a} \\ t &=\sqrt{\frac{2 y}{a}} \end{aligned}\]

Позитивні зсуви знаходяться в напрямку вниз (зверніть увагу на розворот орієнтації на малюнку\(\PageIndex{10}\) (b)). Це означає, що коли швидкість позитивна, м'яч рухається вниз. Коли ми відпускаємо м'яч, він збирається набирати більше швидкості, тому швидкість стає все більш позитивною. Отже, прискорення є позитивним в цій орієнтації; т\(a = 32 ft/s^2\). Е.

Коли м'яч потрапляє на рівень землі, позиція y = 2000 футів. Підставляємо це значення y і прискорення в останній результат і спрощуємо (перевіряємо одиниці виміру).

\[t=\sqrt{\frac{2(2000 \mathrm{ft})}{32 \mathrm{ft} / \mathrm{s}^{2}}}\]

Зверніть увагу, що це дасть той самий результат, що і раніше; тобто\(t \approx 11.2\) секунди.

Приклад\(\PageIndex{7}\)

М'яч кидається в повітря з висоти плеча (близько 5 футів) з початковою швидкістю вгору 100 футів в секунду. Знайдіть час, який потрібно м'ячу, щоб повернутися на землю.

Рішення

Давайте знайдемо рішення за допомогою графічного калькулятора. Використовуючи орієнтацію рисунка\(\PageIndex{10}\) (а), почніть з рівняння

\[y=y_{0}+v_{0} t+\frac{1}{2} a t^{2}\]

і зауважте, що початкове положення -\(y_{0}=5\) фути, початкова швидкість -\(v_{0} = 100\) фути в секунду, а прискорення - a = −32 фути в секунду. Підставте ці числа в попереднє рівняння, щоб отримати

\[\begin{array}{l}{y=5+100 t+\frac{1}{2}(-32) t^{2}} \\ {y=5+100 t-16 t^{2}}\end{array}\]

Введіть це рівняння в меню Y =, як показано на малюнку\(\PageIndex{11}\) (а). Налаштуйте параметри вікна, як показано на малюнку\(\PageIndex{11}\) (b), щоб отримати зображення, показане на малюнку\(\PageIndex{11}\) (c).

Малюнок\(\PageIndex{11}\) За допомогою графічного калькулятора визначити час повернення на землю.

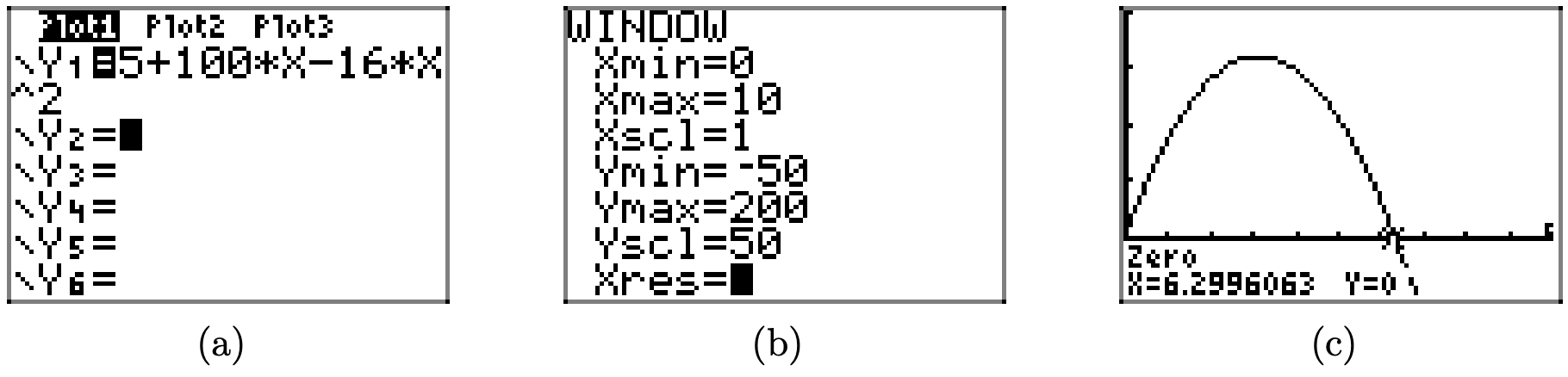
Щоб визначити час, який потрібно м'ячу, щоб повернутися на землю, ми повинні знайти, де висота м'яча y = 0 футів. Оскільки графік на малюнку\(\PageIndex{11}\) (c) - це графік висоти або положення (на вертикальній осі) проти часу (на горизонтальній осі), це відбувається, коли графік на малюнку\(\PageIndex{11}\) (c) перетинає горизонтальну вісь; тобто при нулі функції, визначеної\(y=5+100 t-16 t^{2}\). Щоб визначити цей час, скористайтеся утилітою 2:нуль в меню CALC для визначення нуля. Результат показаний на малюнку\(\PageIndex{11}\) (в), де ми визначаємо, що потрібно приблизно\(t \approx 6.29\) секунд, щоб м'яч повернувся на землю.

Крім того, ми можемо встановити y = 0 у рівнянні\(y=y_{0}+v_{0} t+(1 / 2) a t^{2}\) і використовувати квадратичну формулу для вирішення часу t.

\[\begin{aligned} 0 &=y_{0}+v_{0} t+\frac{1}{2} a t^{2} \\ t &=\frac{-v_{0} \pm \sqrt{v_{0}^{2}-4\left(\frac{1}{2} a\right)\left(y_{0}\right)}}{2\left(\frac{1}{2} a\right)} \\ t &=\frac{-v_{0} \pm \sqrt{v_{0}^{2}-2 a y_{0}}}{a} \end{aligned}\]

Тепер ми можемо вставити\(y_{0}=5 \mathrm{ft}, v_{0}=100 \mathrm{ft} / \mathrm{s},\) і\(a=-32 \mathrm{ft} / \mathrm{s}^{2}\), а потім використовувати калькулятор для отримання

\[\begin{aligned} t &=\frac{-100 \mathrm{ft} / \mathrm{s} \pm \sqrt{(100 \mathrm{ft} / \mathrm{s})^{2}-2\left(-32 \mathrm{ft} / \mathrm{s}^{2}\right)(5 \mathrm{ft})}}{-32 \mathrm{ft} / \mathrm{s}^{2}} \\ t & \approx-0.05,6.29 \mathrm{s} \end{aligned}\]

Негативна відповідь в даній ситуації не застосовується, тому тримаємо рішення\(t \approx 6.29\) секунди. Зверніть увагу, як це узгоджується з рішенням, знайденим на графічному калькуляторі.

Знову ж таки, важливо переконатися, що агрегати перевіряють. Під радикалом обидва терміни мають одиниці\(\mathrm{ft}^{2} / \mathrm{s}^{2}\). Коли береться квадратний корінь, ці одиниці стають ft/s. таким чином, обидва члени в чисельнику знаходяться в ft/s, але знаменник має одиниці\(\mathrm{ft} / \mathrm{s}^{2}\). Коли ви інвертуєте і множите, як ми бачили в прикладі\(\PageIndex{5}\), одиниці спрощуються до секунд.

Вправа

У вправах 1 - 12 запишіть формулу d = vt і розв'яжіть для невідомої величини в задачі. Як тільки це буде завершено, підставити відомі величини в результат і спростити. Переконайтеся, що ваші підрозділи скасовують і надайте відповідні одиниці для вашого рішення.

Вправа\(\PageIndex{1}\)

Якщо Марта підтримує постійну швидкість 30 миль на годину, як далеко вона проїде за 5 годин?

Відповідь

150 миль

Вправа\(\PageIndex{2}\)

Якщо Джамал підтримує постійну швидкість 25 миль на годину, як далеко він проїде за 5 годин?

Вправа\(\PageIndex{3}\)

Якщо Артуро підтримує постійну швидкість 30 миль на годину, скільки часу йому знадобиться, щоб проїхати 120 миль?

Відповідь

4 години

Вправа\(\PageIndex{4}\)

Якщо Мей підтримує постійну швидкість 25 миль на годину, скільки часу їй знадобиться, щоб проїхати 150 миль?

Вправа\(\PageIndex{5}\)

Якщо Аллен підтримує постійну швидкість і проїжджає 250 миль за 5 годин, яка його постійна швидкість?

Відповідь

50 миль на годину

Вправа\(\PageIndex{6}\)

Якщо Джейн підтримує постійну швидкість і проїжджає 300 миль за 6 годин, яка її постійна швидкість?

Вправа\(\PageIndex{7}\)

Якщо Хосе підтримує постійну швидкість 15 футів в секунду, як далеко він проїде за 5 хвилин?

Відповідь

4500 футів

Вправа\(\PageIndex{8}\)

Якщо Тамі підтримує постійну швидкість 1,5 футів в секунду, як далеко вона проїде за 4 хвилини?

Вправа\(\PageIndex{9}\)

Якщо Кармен підтримує постійну швидкість 80 метрів на хвилину, як далеко вона проїде за 600 секунд?

Відповідь

800 метрів

Вправа\(\PageIndex{10}\)

Якщо Альфонсо підтримує постійну швидкість 15 футів в секунду, скільки часу йому знадобиться, щоб проїхати 1 милю? Примітка: 1 миля дорівнює 5280 футів.

Вправа\(\PageIndex{11}\)

Якщо Хоші підтримує постійну швидкість 200 сантиметрів в секунду, скільки часу їй знадобиться, щоб проїхати 20 метрів? Примітка: 100 сантиметрів дорівнює 1 метру.

Відповідь

10 секунд

Вправа\(\PageIndex{12}\)

Якщо Maeko підтримує постійну швидкість і проїжджає 5 миль за 12 хвилин, яка її швидкість у милі на годину?

У Вправах 13 - 18 представлений сюжет швидкості v проти часу t.

1. Зробіть точне дублювання сюжету на графічному папері. Позначте та масштабуйте кожну вісь. Відзначте одиниці на кожній осі.
2. Використовуйте графік для визначення відстані, пройденої за період часу [0, 5], використовуючи одиниці часу, наведені на графіку.

Вправа\(\PageIndex{13}\)

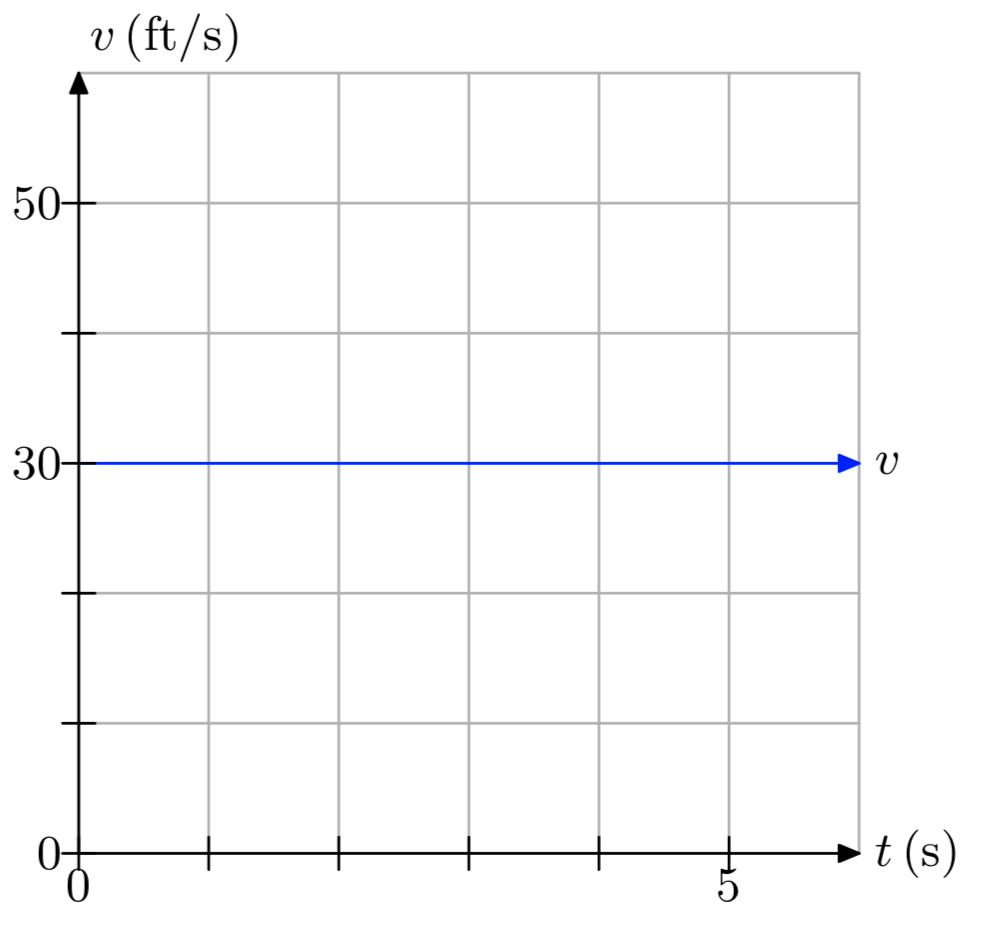
Відповідь

Пройдена відстань становить 150 футів.

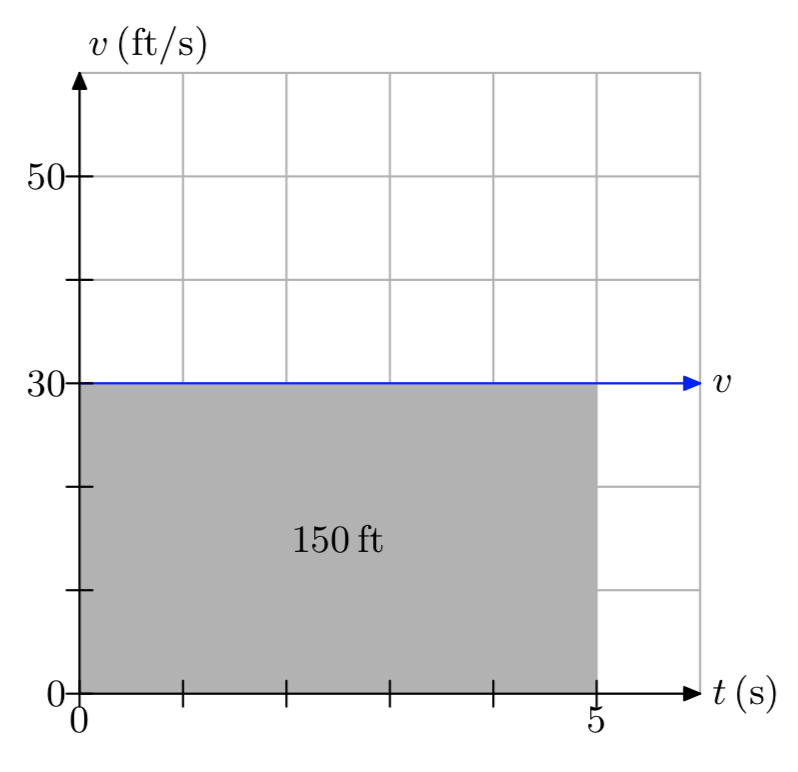
Вправа\(\PageIndex{14}\)

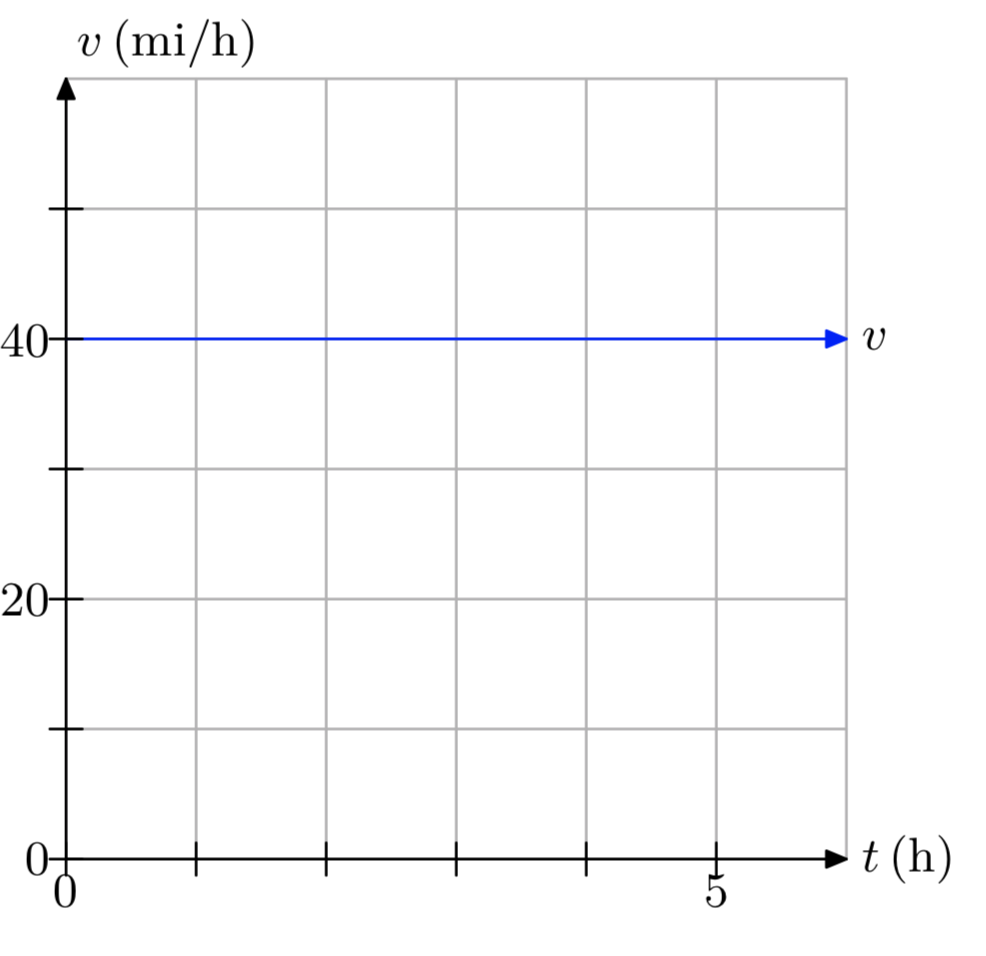
Вправа\(\PageIndex{15}\)

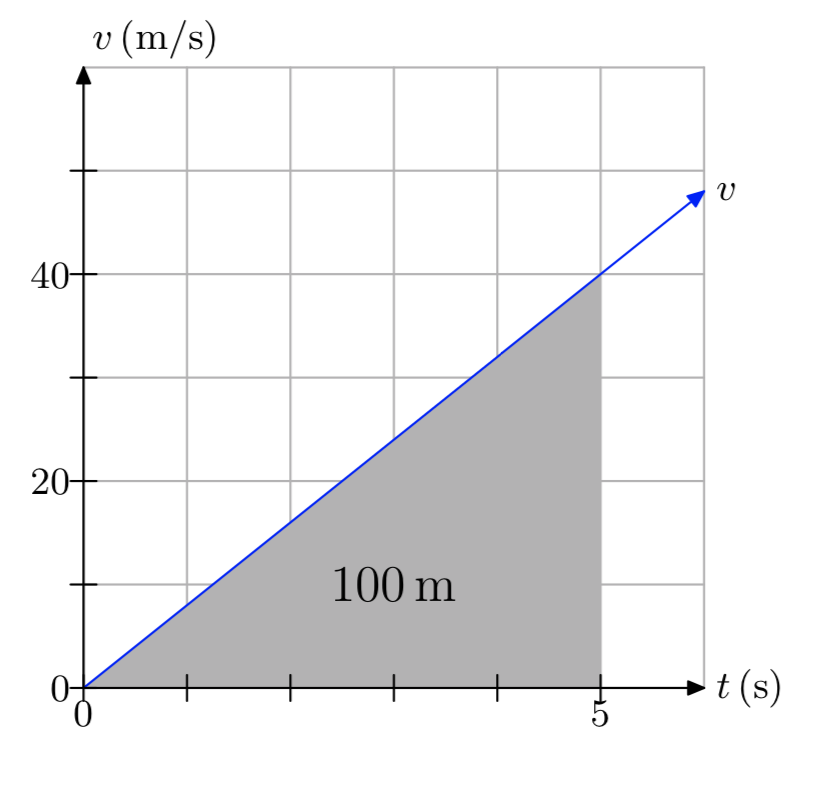
Відповідь

Пройдена відстань становить 100 метрів.

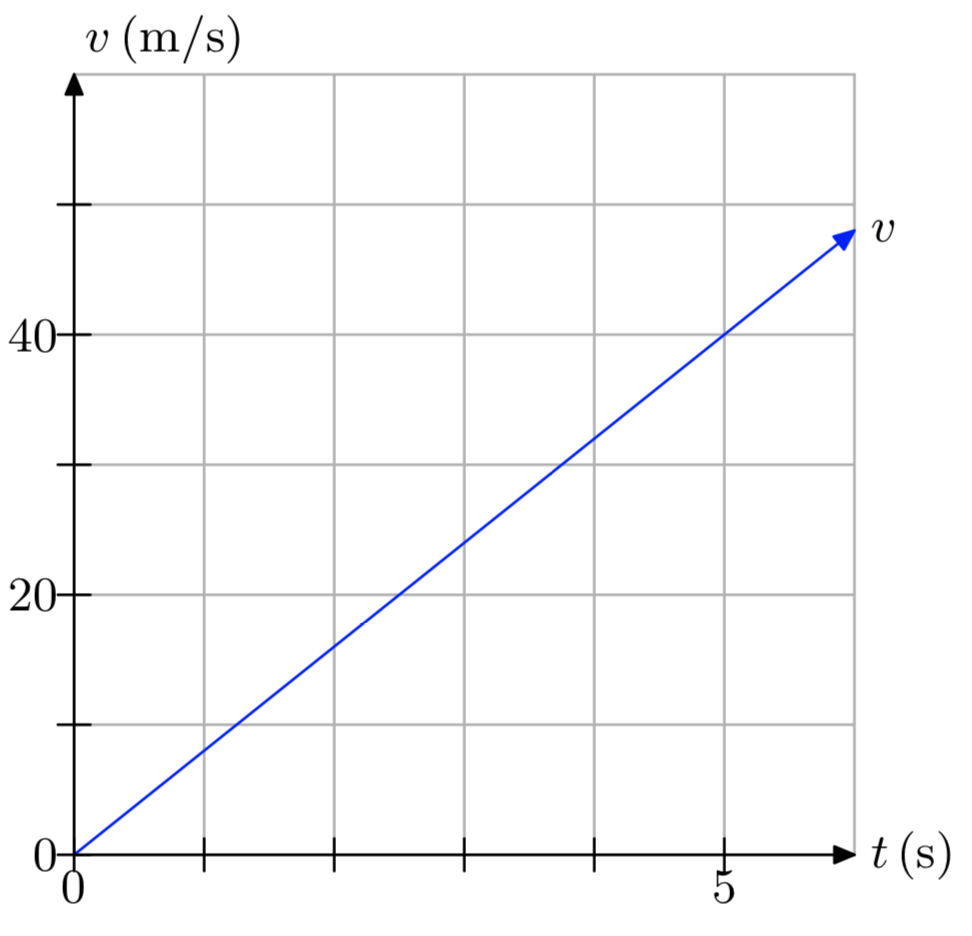
Вправа\(\PageIndex{16}\)

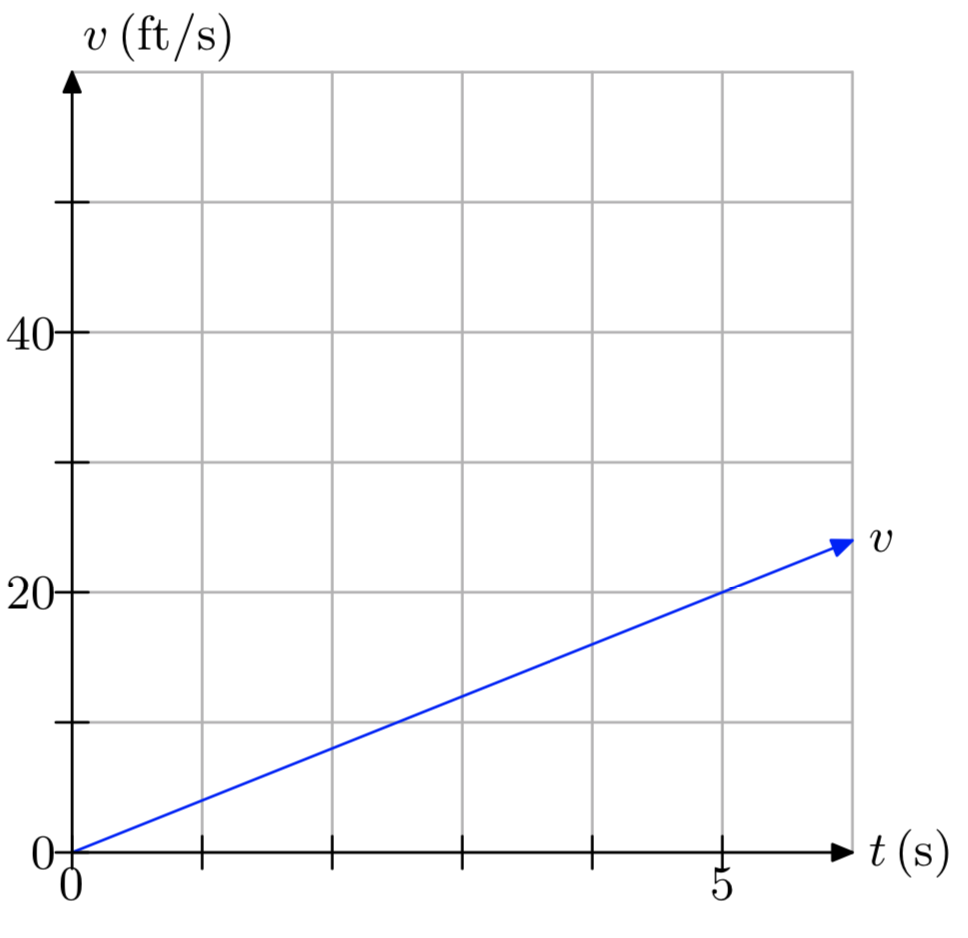
Вправа\(\PageIndex{17}\)

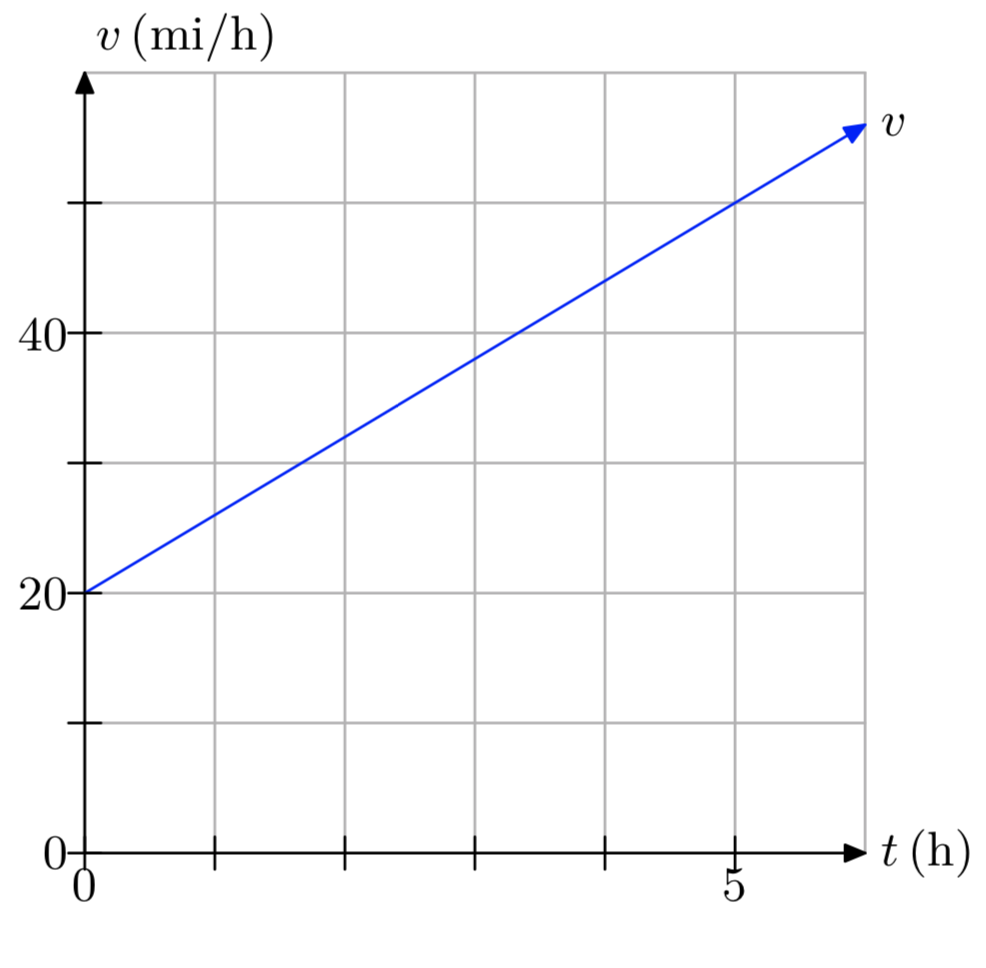
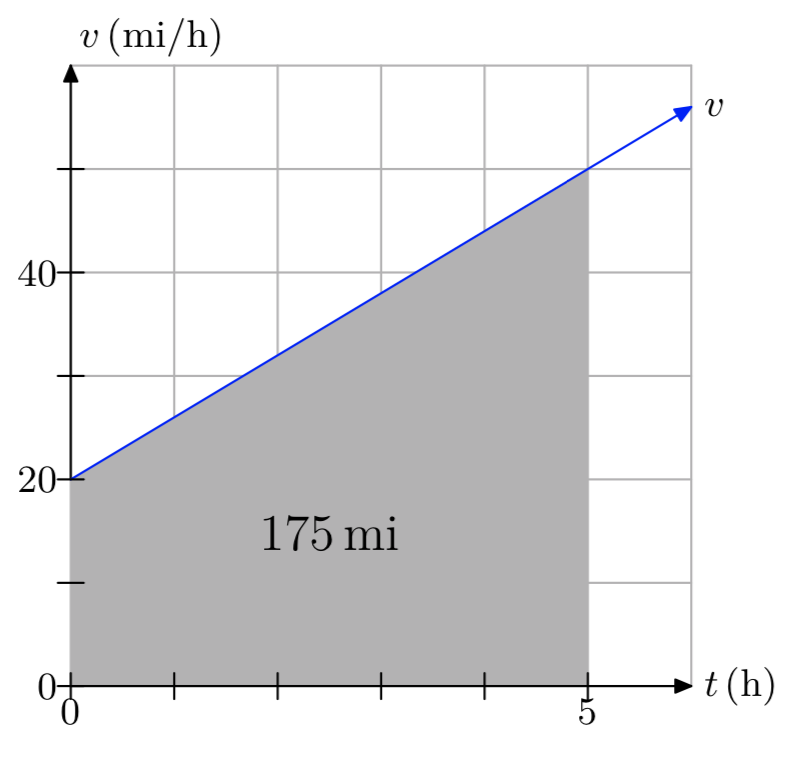
Відповідь

Пройдена відстань становить 175 миль.

Вправа\(\PageIndex{18}\)

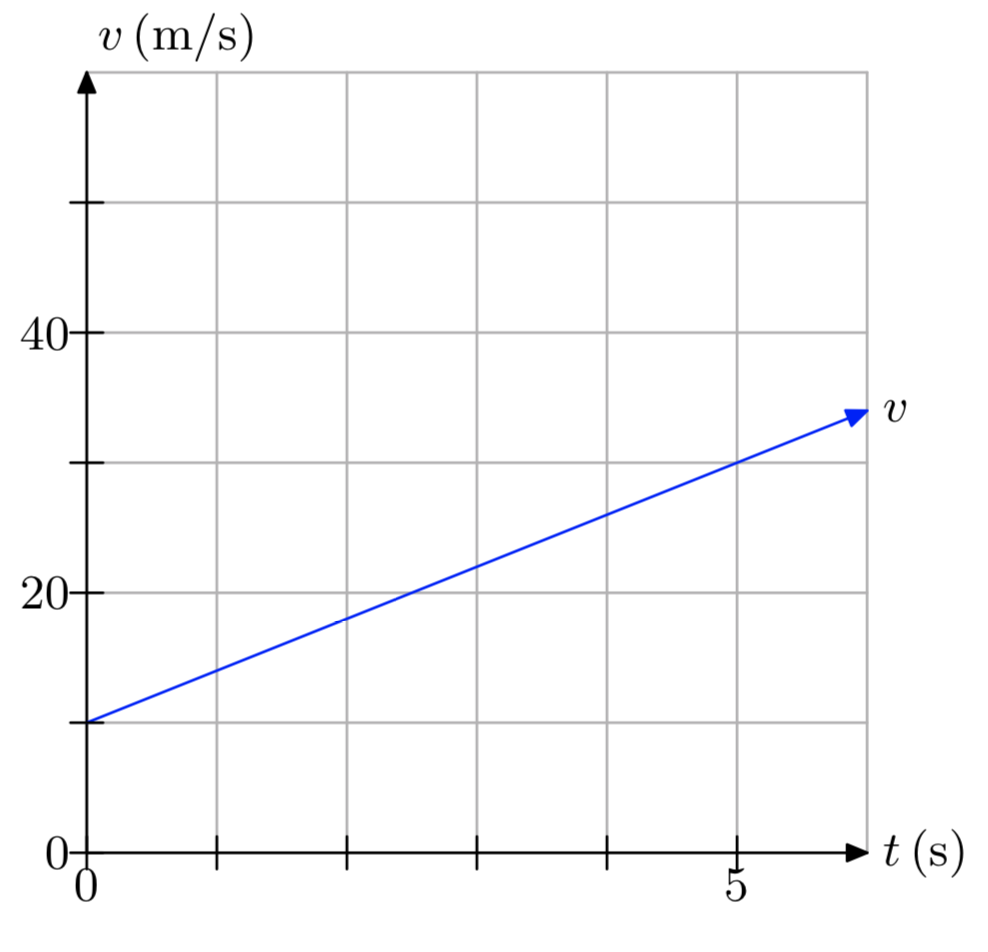
Вправа\(\PageIndex{19}\)

Вам кажуть, що автомобіль рухається з постійним прискоренням 7,5 футів/\(s^2\). Своїми словами поясніть, що це означає.

Відповідь

Це означає, що швидкість автомобіля збільшується зі швидкістю 7,5 футів в секунду кожну секунду.

Вправа\(\PageIndex{20}\)

Вам кажуть, що об'єкт впаде на далеку планету з постійним прискоренням 6,5 м/\(s^2\). Своїми словами поясніть, що це означає.

Вправа\(\PageIndex{21}\)

Вам повідомляють, що прискорення автомобіля становить −18 футів/\(s^2\). Своїми словами поясніть, що це означає.

Відповідь

Це означає, що швидкість автомобіля зменшується зі швидкістю 18 футів в секунду кожну секунду.

Вправа\(\PageIndex{22}\)

Спостерігач на далекій планеті кидає об'єкт у повітря і, рухаючись вгору, повідомляє, що об'єкт має постійне прискорення −4,5 м/\(s^2\). Своїми словами поясніть, що це означає.

У Вправах 23 - 28 виконайте кожне з наступних завдань.

1. Розв'яжіть рівняння\(v = v_{0} + at\) для невідомої величини.
2. Підставте відомі величини (з одиницями) у свій результат, а потім спростіть. Переконайтеся, що блоки скасовують і надають відповідні одиниці для вашого рішення.

Вправа\(\PageIndex{23}\)

Ракета розганяється з відпочинку з постійним прискоренням 15,8 м/\(s^2\). Якою буде швидкість ракети через 3 хвилини?

Відповідь

2, 844 м/с

Вправа\(\PageIndex{24}\)

Камінь скидається з відпочинку на далекій планеті і він розганяється до землі з постійним прискоренням 3.8ft/\(s^2\). Якою буде швидкість каменю через 2 хвилини?

Вправа\(\PageIndex{25}\)

Камінь кидається вниз на далеку планету з початковою швидкістю 20 футів/с Якщо камінь відчуває постійне прискорення 32ft/\(s^2\), якою буде швидкість каменю через 1 хвилину?

Відповідь

1 940 футів/с

Вправа\(\PageIndex{26}\)

М'яч кидається вгору з початковою швидкістю 80 м/с Якщо м'яч відчуває постійне прискорення −9,8 м/\(s^2\), якою буде швидкість м'яча наприкінці 5 секунд?

Вправа\(\PageIndex{27}\)

Об'єкт вистрілюється в повітря з початковою швидкістю 100 м/с Якщо об'єкт відчуває постійне уповільнення 9,8 м/\(s^2\), скільки часу потрібно м'ячу, щоб досягти максимальної висоти?

Відповідь

Приблизно 10,2 секунди.

Вправа\(\PageIndex{28}\)

Об'єкт звільняється від спокою на далекій планеті і через 5 секунд його швидкість становить 98м/с Якщо об'єкт падає з постійним прискоренням, визначте прискорення об'єкта.

У вправах 29 - 42 використовуйте відповідне рівняння руху,\(v = v_{0} + at\) або або\(x = x_{0}+v_{0}t+\frac{1}{2}at^2\) або обидва, для вирішення питання, поставленого у вправі.

1. Виберіть відповідне рівняння руху і вирішіть для невідомої величини.
2. Підставляйте відомі величини (з їх одиницями) у свій результат і спростіть. Переконайтеся, що скасування одиниць забезпечує одиниці, відповідні вашому рішенню.
3. Знайдіть десяткове наближення для вашої відповіді.

Вправа\(\PageIndex{29}\)

Ракета з початковою швидкістю 30 м/с рухається по прямій з постійним прискоренням 2,5 м/\(s^2\). Знайдіть швидкість і відстань, пройдену ракетою в кінці 10 секунд.

Відповідь

Швидкість = 55 м/с, Пройдена відстань = 425 м.

Вправа\(\PageIndex{30}\)

Автомобіль їде зі швидкістю 88 футів/с, коли він застосовує гальма і починає сповільнюватися з постійним уповільненням 5 футів/\(s^2\). Яка його швидкість і як далеко він проїхав наприкінці 5 секунд?

Вправа\(\PageIndex{31}\)

Автомобіль їде зі швидкістю 88 футів/с, коли він застосовує гальма і сповільнюється до 58 футів/с за 10 секунд. Припускаючи постійне уповільнення, знайдіть уповільнення і відстань, пройдену автомобілем, в 10-секундному часовому інтервалі. Підказка: Спочатку обчислити уповільнення.

Відповідь

Прискорення = −3 футів/\(s^2\), Пройдена відстань = 730 футів.

Вправа\(\PageIndex{32}\)

Камінь кидається вниз зверху поверхні далекої планети з початковою швидкістю 45 м/с Після закінчення 10 секунд швидкість каменю 145 м/с Припускаючи постійне прискорення, знайдіть прискорення каменю і відстань, пройдену за 10-секундний проміжок часу.

Вправа\(\PageIndex{33}\)

Об'єкт знімається в повітря з поверхні землі з початковою швидкістю 180 ft/s. знайти максимальну висоту об'єкта і час, який потрібно об'єкту, щоб досягти цієї максимальної висоти.Підказка: Прискорення через гравітацію біля поверхні землі добре відомо.

Відповідь

Час до максимальної висоти = 5. 625 с, Макс висота = 506. 25 футів.

Вправа\(\PageIndex{34}\)

Об'єкт знімається в повітря з поверхні далекої планети з початковою швидкістю 180 м/с Знайти максимальну висоту об'єкта і час, необхідний об'єкту для досягнення цієї максимальної висоти. Припустимо, що прискорення за рахунок гравітації на цій далекій планеті становить 5,8 м/\(s^2\). Підказка: Спочатку розрахуйте час до максимальної висоти.

Вправа\(\PageIndex{35}\)

Автомобіль їде вниз по високому шляху на 55 миль/год, коли водій помічає гірку порід, що покривають дорогу попереду і потрапляє на гальма, забезпечуючи постійне уповільнення 12 футів/с\( ^ 2\). Скільки часу потрібно машині, щоб призупинити і як далеко він проїжджає за цей часовий проміжок?

Відповідь

Час зупинки\(\approx\) 6. 72 s, Відстань пройдена\(\approx\) 271 ft

Вправа\(\PageIndex{36}\)

Автомобіль їде по шосе в Німеччині зі швидкістю 81 км/год, коли водій помічає, що рух зупиняється на дорозі попереду і б'є гальма, забезпечуючи постійне уповільнення 2,3 м/\(s^2\). Скільки часу потрібно машині, щоб призупинити і як далеко він проїжджає за цей часовий проміжок? Примітка: 1 кілометр дорівнює 1000 метрам.

Вправа\(\PageIndex{37}\)

Об'єкт звільняється від спокою на деякій відстані над поверхнею землі. Як далеко (в метрах) впаде об'єкт за 5 секунд і якою буде його швидкість в кінці цього 5-секундного періоду часу? Підказка: Ви повинні знати прискорення за рахунок сили тяжіння біля поверхні землі.

Відповідь

Відстань = 122,5 м, Швидкість = −49 м/с.

Вправа\(\PageIndex{38}\)

Об'єкт звільняється від спокою на деякій відстані над поверхнею далекої планети. Як далеко (в метрах) впаде об'єкт за 5 секунд і якою буде його швидкість в кінці цього 5-секундного періоду часу? Припустимо, що прискорення за рахунок гравітації на далекій планеті становить 13,5 м/\(s^2\).

Вправа\(\PageIndex{39}\)

Об'єкт звільняється від спокою на відстані 352 футів над поверхнею землі. Скільки часу знадобиться об'єкту, щоб вплинути на землю?

Відповідь

Час\(\approx\) 4.69 s

Вправа\(\PageIndex{40}\)

Об'єкт звільняється від спокою на відстані 400 метрів над поверхнею далекої планети. Скільки часу знадобиться об'єкту, щоб вплинути на землю? Припустимо, що прискорення за рахунок гравітації на далекій планеті дорівнює 5,3 м/ (s^2\).

Вправа\(\PageIndex{41}\)

На землі куля кидається вгору з початкової висоти 5 метрів з початковою швидкістю 100 м/с Скільки часу знадобиться м'ячу, щоб повернутися на землю?

Відповідь

Час\(\approx\) 20.5 s

Вправа\(\PageIndex{42}\)

На землі м'яч кидається вгору з початкової висоти 5 футів з початковою швидкістю 100 футів/с Скільки часу буде потрібно м'яч, щоб повернутися на землю?

У повітря біля поверхні землі кидається куля. У вправах 43 - 46 задана початкова висота м'яча і початкова швидкість м'яча. Виконайте наступні завдання.

1. Використовуйте\(y = y_{0} +v_{0}t+\frac{1}{2}at^2\) для встановлення формули висоти у кулі як функції часу t Використовуйте відповідну константу для прискорення за рахунок сили тяжіння поблизу поверхні землі.
2. Завантажте рівняння з попередньої частини в Y1 у свій графічний калькулятор. Налаштуйте вікно перегляду таким чином, щоб була видна і вершина, і час, коли куля повертається на землю. Скопіюйте зображення на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax.
3. Використовуйте нульову утиліту в меню CALC вашого графічного калькулятора, щоб визначити час, коли куля повертається на землю. Запишіть цю відповідь у відповідному місці на вашому графіку.
4. Використовуйте квадратичну формулу, щоб визначити час повернення м'яча на землю. Використовуйте калькулятор, щоб знайти десяткове наближення вашого рішення. Він повинен погодитися з тим, що знайдено за допомогою нульової утиліти на вашому графічному калькуляторі. Будьте вперті! Перевірте свою роботу, поки відповіді не погодяться.

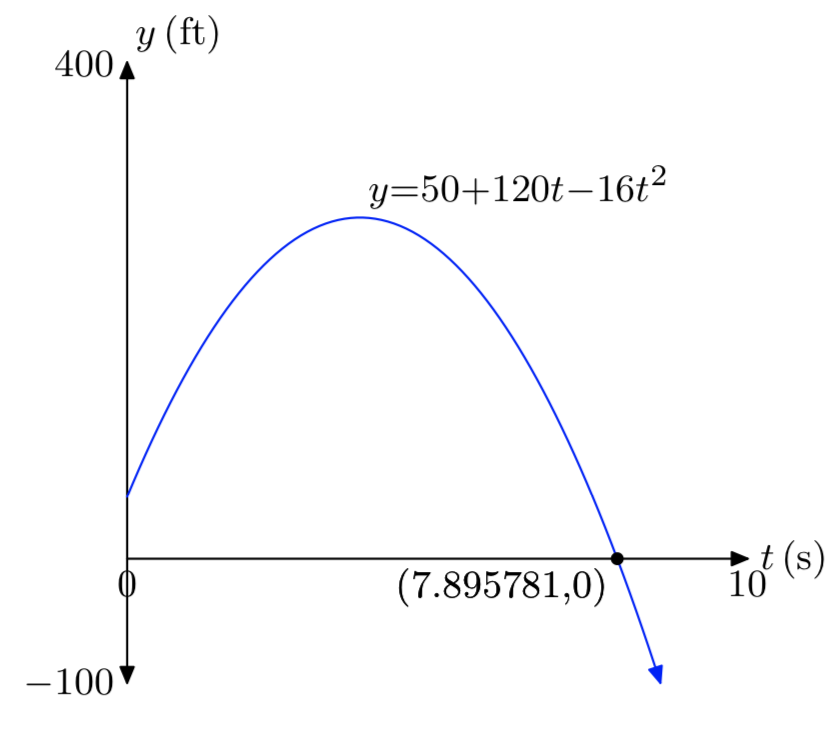
Вправа\(\PageIndex{43}\)

\(y_{0}\)= 50 футів,\(v_{0}\) = 120 футів/с.

Відповідь

Вправа\(\PageIndex{44}\)

\(y_{0}\)= 30 м,\(v_{0}\) = 100 м/с.

Вправа\(\PageIndex{45}\)

\(y_{0}\)= 20м,\(v_{0}\) = 110м/с.

Відповідь

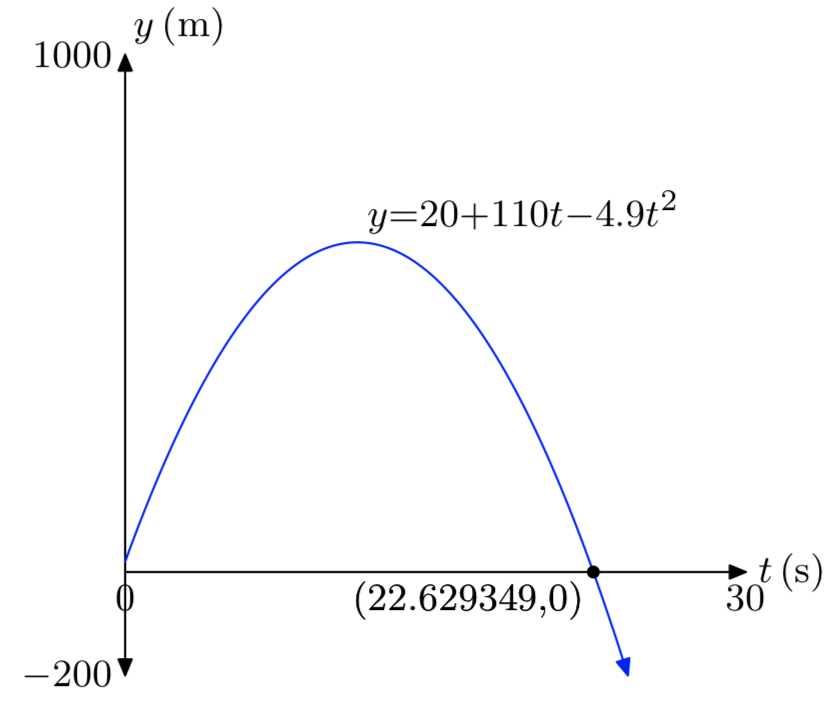
Вправа\(\PageIndex{46}\)

\(y_{0}\)= 100 футів,\(v_{0}\) = 200 футів/с.

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

Вправа\(\PageIndex{47}\)

Скеля кидається вгору з початковою швидкістю 64 футів/с Скільки секунд знадобиться скелі, щоб піднятися на 61 фут? Округлите відповідь до сотих часток секунди.

Відповідь

1. 57 секунд

Вправа\(\PageIndex{48}\)

Копійка скидається вниз з верхівки дерева на початковій швидкості 28 футів/с Скільки секунд знадобиться копійці, щоб впасти 289 футів? Округлите відповідь до сотих часток секунди.

Вправа\(\PageIndex{49}\)

Водяна куля скидається вниз з даху будівлі з початковою швидкістю 24 футів/с. Скільки секунд знадобиться водяній кулі, щоб вдарити об землю? Округлите відповідь до сотих часток секунди.

Відповідь

2. 59 секунд

Вправа\(\PageIndex{50}\)

Скеля кидається вгору з початковою швидкістю 60 футів/с Скільки секунд знадобиться скелі, щоб піднятися на 51 фут? Округлите відповідь до сотих часток секунди.

Вправа\(\PageIndex{51}\)

М'яч кидається вгору з висоти 42 футів на початковій швидкості 63 футів/с Скільки секунд знадобиться м'яч, щоб вдарити об землю? Округлите відповідь до сотих часток секунди.

Відповідь

4. 52 секунди

Вправа\(\PageIndex{52}\)

Скеля кидається вгору з висоти 32 футів на початковій швидкості 25 футів/с Скільки секунд знадобиться скелі, щоб вдарити об землю? Округлите відповідь до сотих часток секунди.

Вправа\(\PageIndex{53}\)

Копійка скидається вниз з верхівки дерева з початковою швидкістю 16 футів/с, дерево висотою 68 футів. Скільки секунд знадобиться копійки, щоб вдарити об землю? Округлите відповідь до сотих часток секунди.

Відповідь

1. 62 секунди

Вправа\(\PageIndex{54}\)

Копійка скидається вниз з краю скелі на початковій швидкості 32 футів/с Скільки секунд знадобиться копійці, щоб впасти 210 футів? Округлите відповідь до сотих часток секунди.