5.1: Парабола

У цьому розділі ви дізнаєтеся, як намалювати графік квадратичної функції, визначеної рівнянням.

$$f(x)=a(x-h)^{2}+k \label{eq1}$$

Ви швидко дізнаєтеся, що графік квадратичної функції має форму «U» і називається параболою. Форма квадратичної функції в Equation\ ref {eq1} називається вершиною форми, так названа тому, що форма легко виявляє вершину або «точку повороту» параболи. Кожна з констант у вершинній формі квадратичної функції відіграє певну роль. Як ви скоро побачите, константа a контролює масштабування (розтягування або стиснення параболи), константа h контролює горизонтальний зсув і розміщення осі симетрії, а постійна$k$ контролює вертикальний зсув. Почнемо з розгляду масштабування квадратики.

Масштабування квадратичної

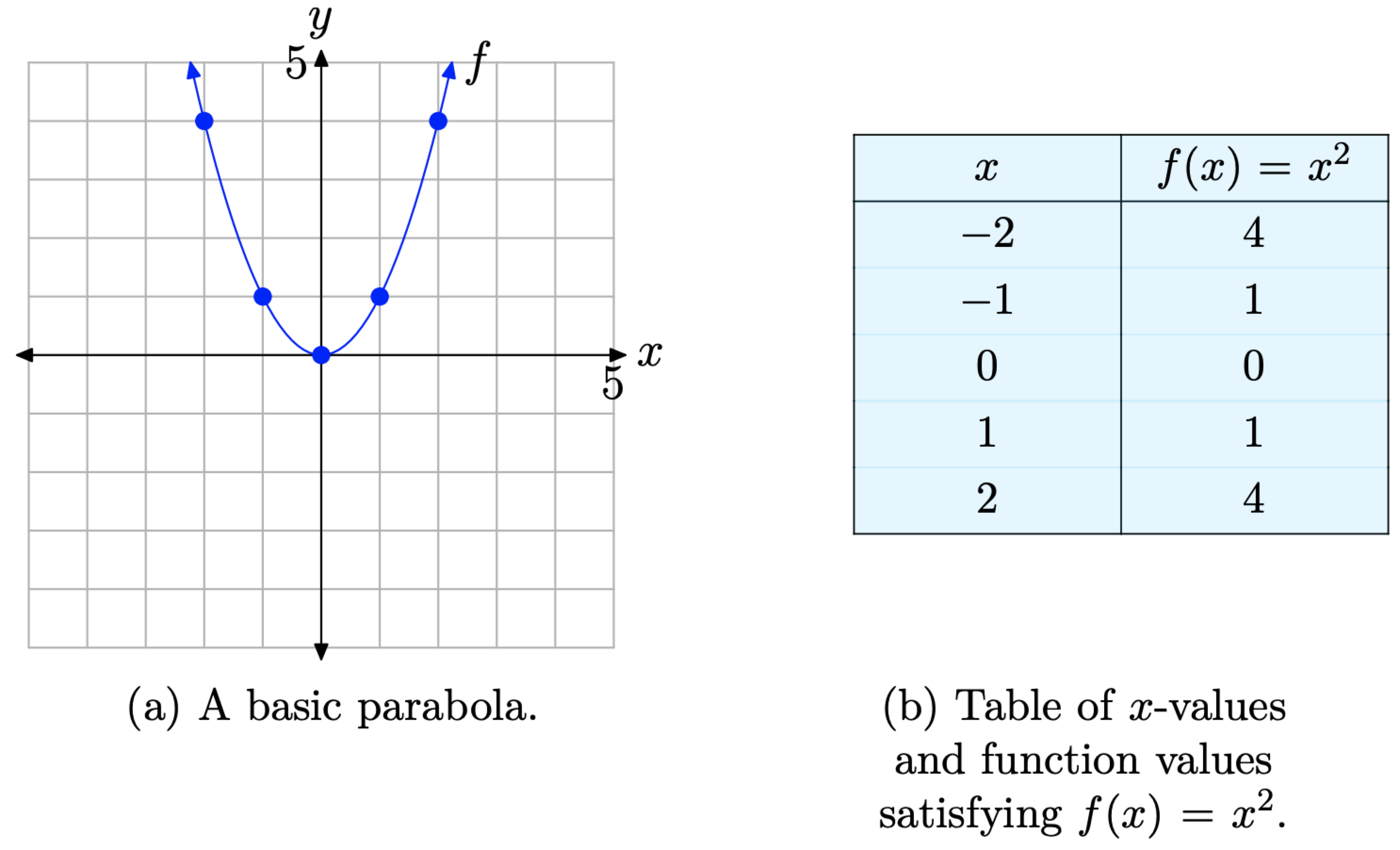
Графік основної квадратичної функції,$f(x)=x^{2}$ показаний на малюнку$\PageIndex{1}$ (а), є параболою. Ми говоримо, що парабола на малюнку$\PageIndex{1}$ (а) «відкривається вгору». Точка в (0, 0), «поворотна точка» параболи, називається вершиною параболи. Ми табулювали кілька пунктів для довідки в таблиці на малюнку$\PageIndex{1}$ (b), а потім наклали ці точки на графіку на$f(x)=x^{2}$ малюнку$\PageIndex{1}$ (а).

Малюнок$\PageIndex{1}$: Графік основної параболи є фундаментальною відправною точкою.

Тепер, коли ми знаємо основну форму параболи$f(x) = x^{2}$, визначену, давайте подивимося, що відбувається, коли ми масштабуємо графік$f(x) = x^{2}$ у вертикальному напрямку. Для прикладу давайте досліджуємо графік$g(x) = 2x^{2}$. Фактор 2 надає ефект подвоєння. Зауважте, що кожне із значень функції g вдвічі перевищує відповідне значення функції f в таблиці на малюнку$\PageIndex{2}$ (b).

Малюнок$\PageIndex{2}$: Розтяжка в 2 рази у вертикальному напрямку.

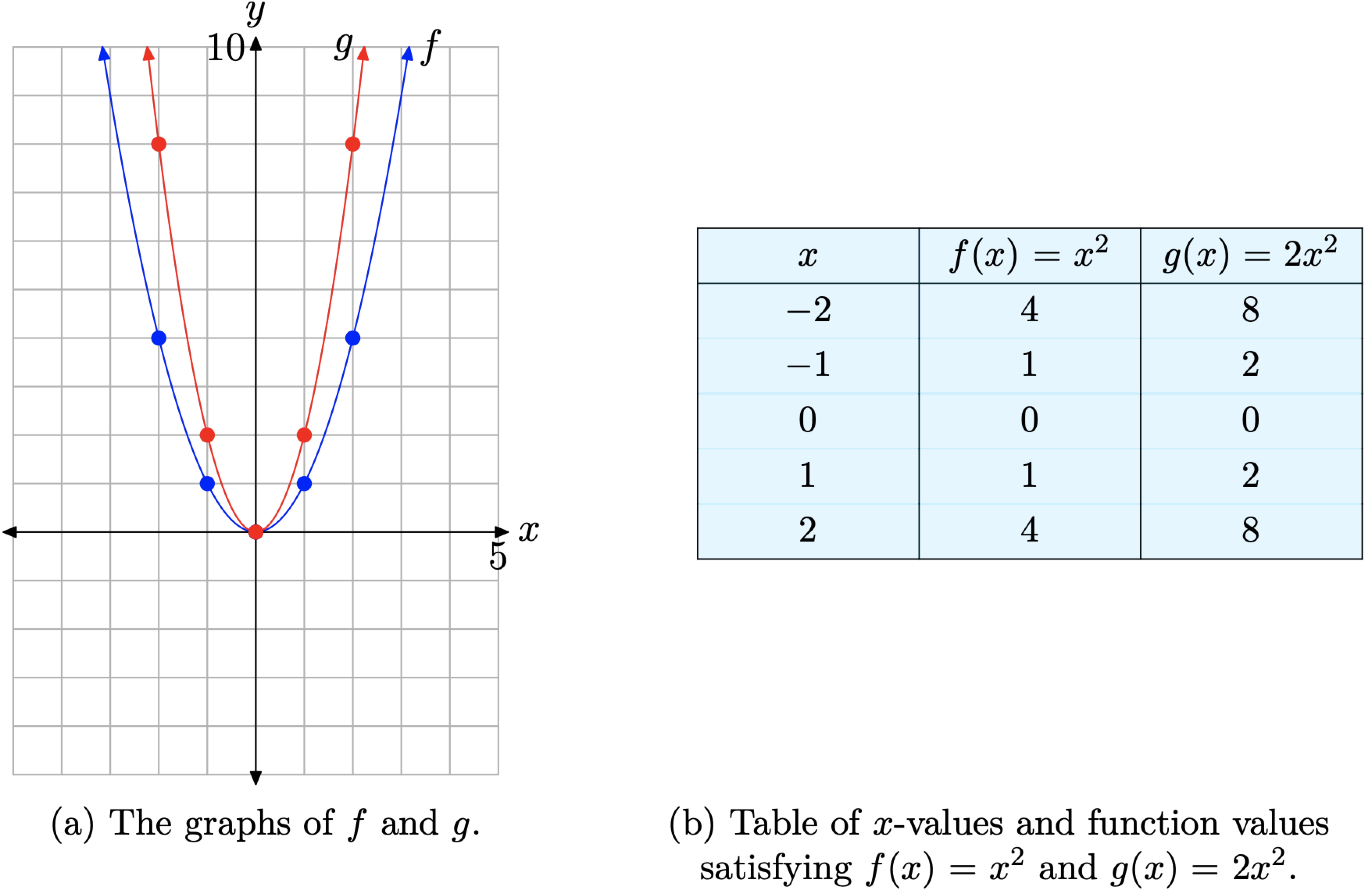
Коли точки в таблиці на малюнку$\PageIndex{2}$ (b) додаються до системи координат на малюнку$\PageIndex{2}$ (а), отриманий графік g розтягується в два рази у вертикальному напрямку. Це як якщо б ми поставили оригінальний графік f на аркуші гумового графіка паперу, схопив верхню і нижню краї аркуша, а потім витягнув кожен край у вертикальному напрямку, щоб розтягнути графік f в два рази. Отже, графік$g(x) = 2x^{2}$ виглядає дещо вужчим за зовнішнім виглядом, як видно в порівнянні з графіком$f(x) = x^{2}$ на малюнку$\PageIndex{2}$ (а). Однак зауважте, що це масштабування не впливає на вершину в початковій точці.

Подібним чином, щоб намалювати графік$h(x) = 3x^{2}$, візьміть графік$f(x) = x^{2}$ і розтягніть графік в три рази, потроюючи значення y кожної точки на вихідному графіку f.

Нерухомість 2

Якщо а - константа більше 1, тобто якщо$a > 1$, то графік$g(x) = ax^{2}$, якщо порівнювати з графом$f(x) = x^{2}$, розтягується на коефіцієнт a.

Приклад$\PageIndex{1}$

Порівняйте графіки$y = x^{2}$$y = 2x ^{2}$, і$y = 3x^{2}$ на графічному калькуляторі.

Рішення

Завантажте функції$y = x^{2}$$y = 2x ^{2}$, і$y = 3x^{2}$ в меню Y=, як показано на малюнку$\PageIndex{3}$ (a). Натисніть кнопку ZOOM і виберіть 6:zStandard, щоб створити зображення, показане на малюнку$\PageIndex{3}$ (b).

Малюнок$\PageIndex{3}$: Креслення$y = x^{2}$$y = 2x ^{2}$, і$y = 3x^{2}$ на графічному калькуляторі.

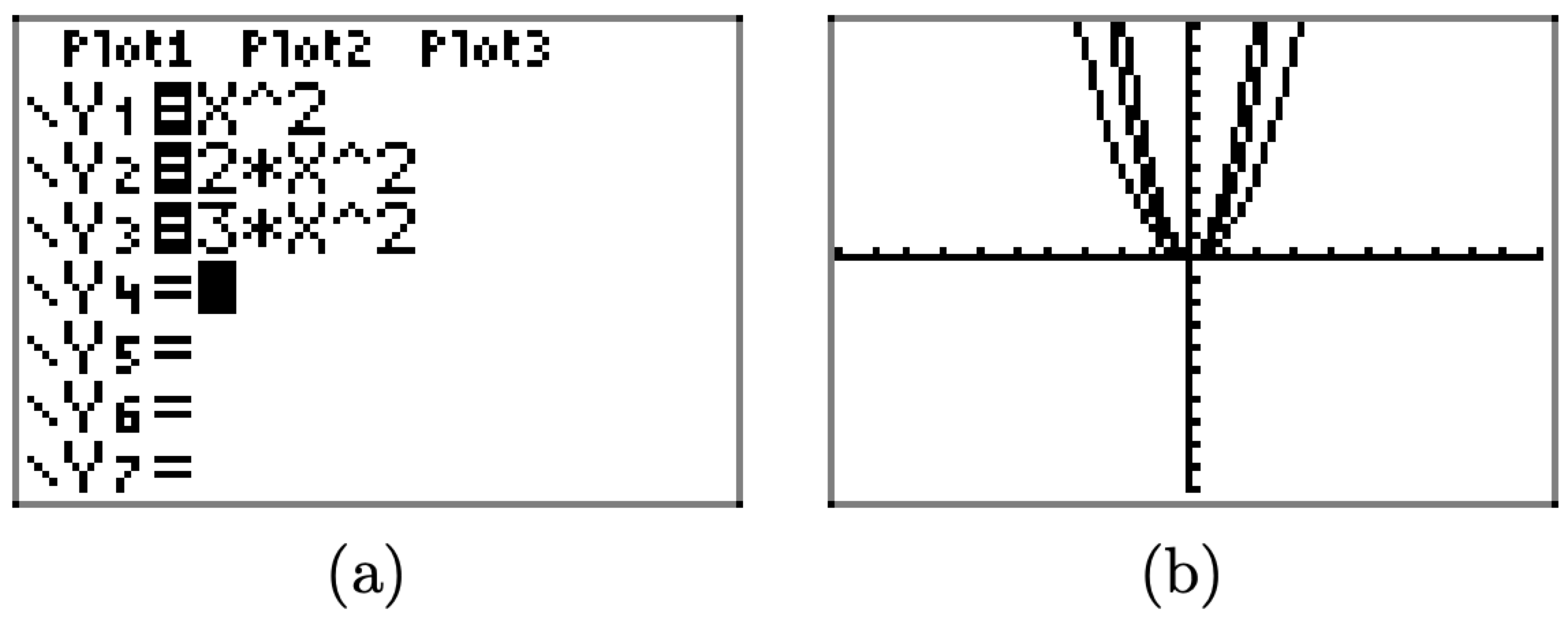
Відзначимо, що у міру$y = ax^{2}$ збільшення «а» в від 1 до 2 до 3 графік$y = ax^{2}$ тягнеться далі і стає, в певному сенсі, більш вузьким за зовнішнім виглядом.

Далі розглянемо, що відбувається, коли ми масштабуємо число, яке менше 1 (але більше нуля - ми розберемося з негативом за мить). Для прикладу давайте досліджуємо графік$g(x) = (1/2)x^{2}$. Фактор 1/2 надає вдвічі ефект. Зверніть увагу, що кожне з значень функції g дорівнює половині відповідного значення функції f в таблиці на малюнку$\PageIndex{4}$ (b).

Малюнок$\PageIndex{4}$: Стиснення в 2 рази у вертикальному напрямку.

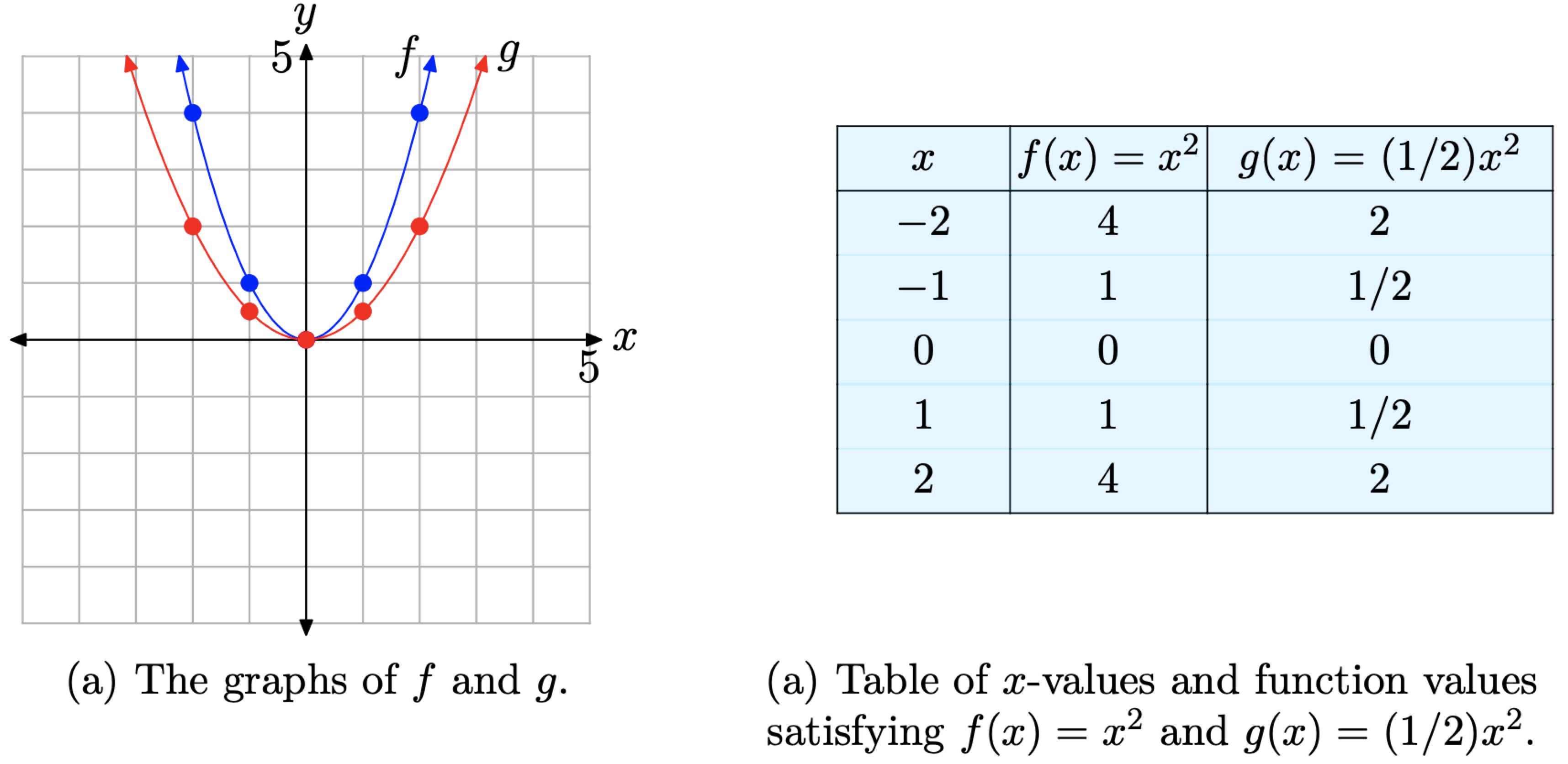
Коли точки в таблиці на малюнку$\PageIndex{4}$ (b) додаються до системи координат на малюнку$\PageIndex{4}$ (а), отриманий графік g стискається в 2 рази у вертикальному напрямку. Це як ніби ми знову помістили графік$f(x) = x^{2}$ на аркуші гумового графського паперу, схопили верхню і нижню частину аркуша, а потім стиснули їх разом в два рази. Отже, графік$g(x) = (1/2)x^{2}$ виглядає дещо ширшим за зовнішнім виглядом, як видно в порівнянні з графіком$f(x) = x^{2}$ на малюнку$\PageIndex{4}$ (а). Знову зауважте, що це масштабування не впливає на вершину в початковій точці.

Нерухомість 4

Якщо a - константа, менша за 1 (але більше нуля), тобто якщо$0 < a < 1$, то графік$g(x) = ax^{2}$, якщо порівнювати з графом$f(x) = x^{2}$, стискається в коефіцієнт 1/а.

Деякі вважають Property 4 дещо неінтуїтивним. Однак, якщо порівняти функцію із$g(x) = (1/2)x^2$ загальною формою$g(x) = ax^2$, ви побачите, що a = 1/2. Властивість 4 стверджує, що графік буде стиснутий в коефіцієнт 1/a. в цьому випадку a = 1/2 і

$$\frac{1}{a}=\frac{1}{1 / 2}=2$$

Таким чином, властивість 4 стверджує, що графік$g(x) = (1/2)x^2$ повинен бути стиснутий коефіцієнтом 1/ (1/2) або 2, що, як видно, має місце на малюнку$\PageIndex{4}$ (а).

Приклад$\PageIndex{2}$

Порівняйте графіки$y=x^{2}, y=(1 / 2) x^{2},$ та$y=(1 / 3) x^{2}$ на графічному калькуляторі.

Рішення

Завантажте рівняння$y=x^{2}, y=(1 / 2) x^{2},$ і$y=(1 / 3) x^{2}$ в Y=, як показано на малюнку$\PageIndex{5}$ (а). Натисніть кнопку ZOOM і виберіть 6:zStandard, щоб створити зображення, показане на малюнку$\PageIndex{5}$ (b).

Малюнок$\PageIndex{5}$: Креслення$y=x^{2}, y=(1 / 2) x^{2},$ і$y=(1 / 3) x^{2}$ на графічному калькуляторі.

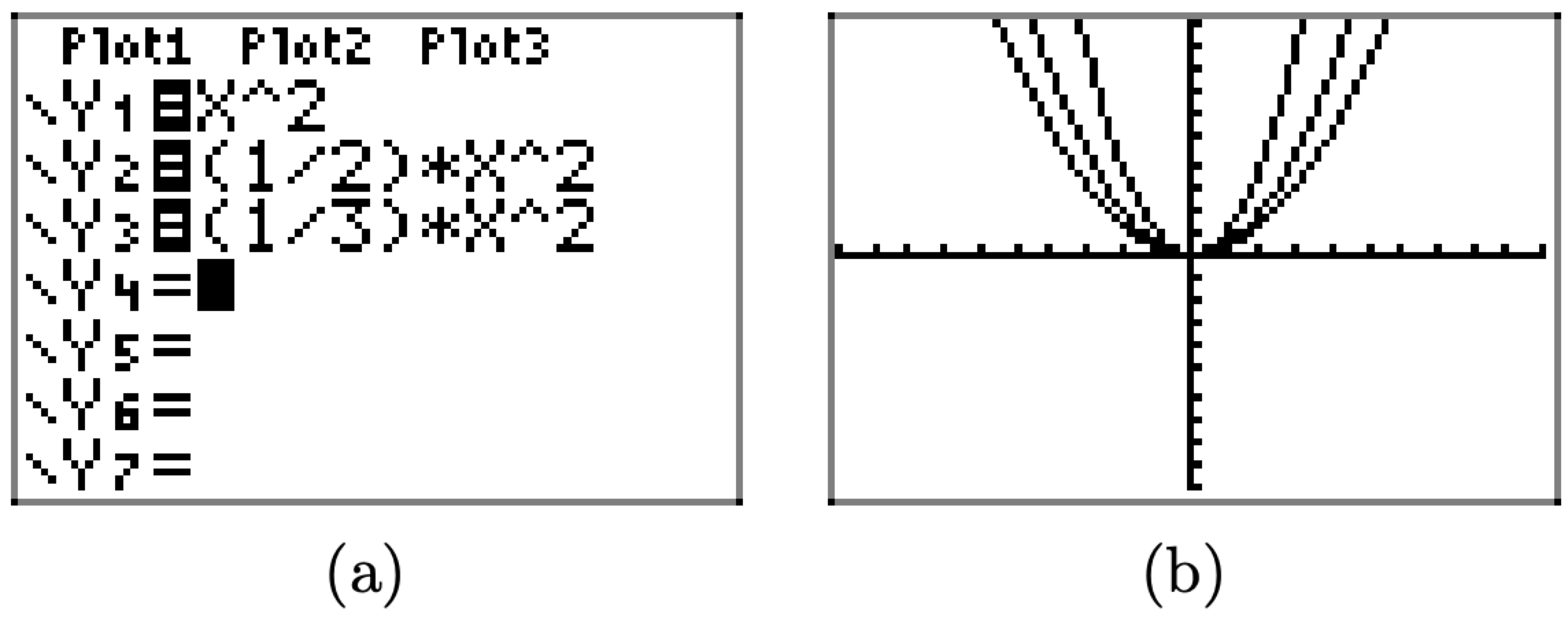
Зверніть увагу, що у міру$y = ax^2$ зменшення «а» в від 1 до 1/2 до 1/3 графік$y = ax^2$ стискається далі і стає, в певному сенсі, ширше за зовнішнім виглядом.

Вертикальні роздуми

Розглянемо графік$g(x) = ax^2$, коли a < 0. Для прикладу розглянемо графіки$g(x)=-x^{2}$ і на$h(x)=(-1 / 2) x^{2}$ малюнку$\PageIndex{6}$

Малюнок$\PageIndex{6}$: Вертикальне відображення поперек осі x.

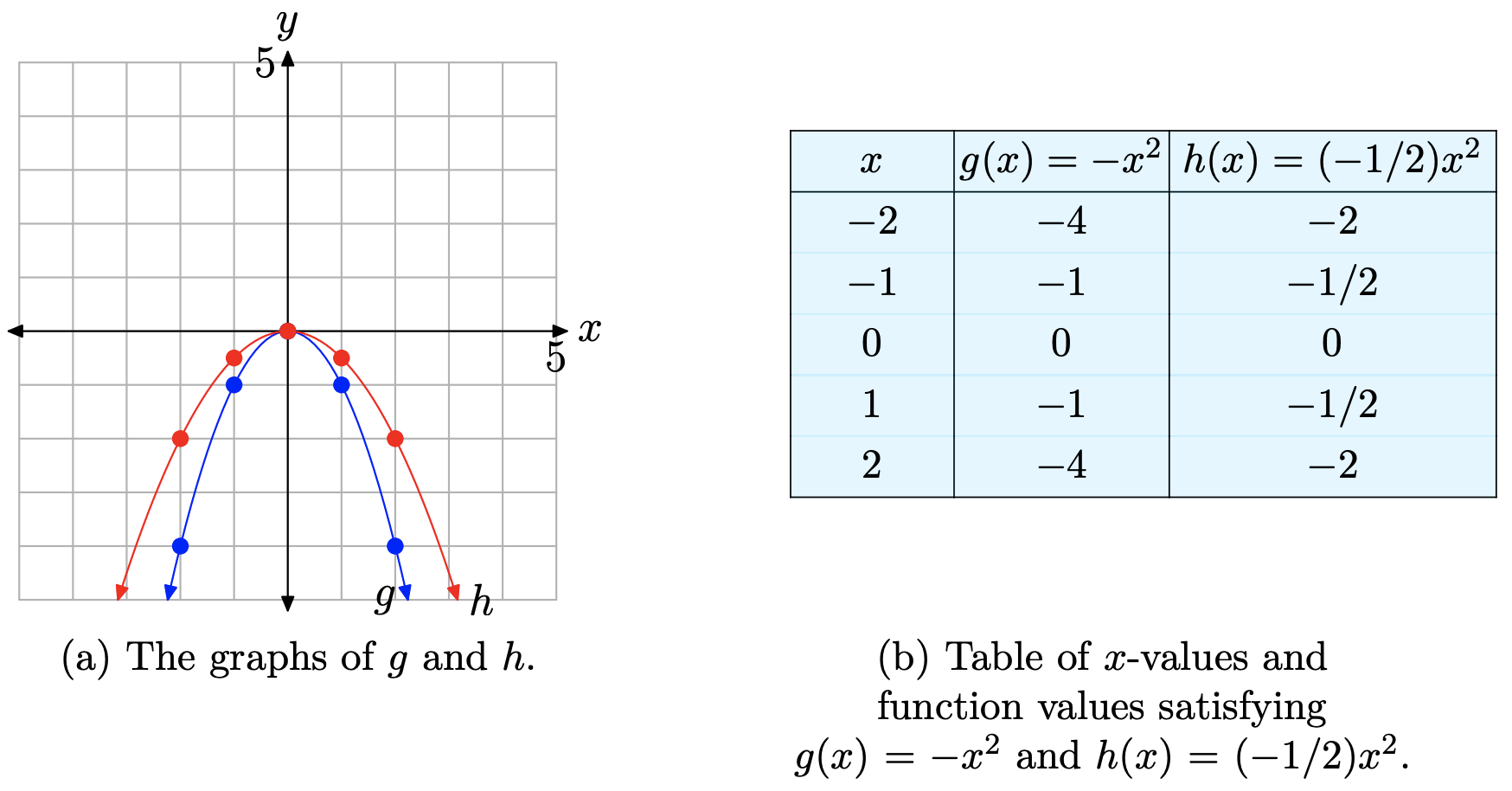
Коли таблиця на малюнку$\PageIndex{6}$ (b) порівнюється з таблицею на малюнку$\PageIndex{4}$ (b), легко побачити, що цифри в останніх двох стовпцях однакові, але вони були заперечені. Результат легко побачити на малюнку$\PageIndex{6}$ (а). Графіки були відображені по осі x. Кожна з парабол тепер «відкривається вниз».

Однак обнадійливо бачити, що масштабування ролі постійної a in не$g(x) = ax^2$ змінилася. У разі$h(x) = (−1/2)x^2$, значення y все ще «стискаються» множником два, але знак мінус заперечує ці значення, змушуючи графік відображатися по осі x. Так, наприклад, можна подумати, що графік$y = −2x^2$ буде розтягнутий у два рази, а потім відображений по осі x. Дійсно, це правильно, і це обговорення призводить до наступного властивості.

Нерухомість 6

Якщо$−1 < a < 0$, то графік$g(x) = ax^2$, якщо порівнювати з графом$f(x) = x^2$, стискається в коефіцієнт 1/|a|, то відбивається по осі x. По-друге, якщо a < −1, то граф$g(x) = ax^2$, якщо порівнювати з графіком$f(x) = x^2$, розтягується на множник |a|, потім відбивається по осі x.

Знову ж таки, деякі вважають Property 6 заплутаним. Однак, якщо порівнювати$g(x) = (−1/2)x^2$ із загальною формою$g(x) = ax^2$, ви побачите, що a = −1/2. Зауважте, що у цьому випадку −1 < a < 0. Властивість 6 стверджує, що граф буде стиснутий коефіцієнтом 1/|a|. У цьому випадку a = −1/2 і

$$\frac{1}{|a|}=\frac{1}{|-1 / 2|}=2$$

Тобто, властивість 6 стверджує, що графік$g(x) = (−1/2)x^2$ стискається коефіцієнтом 1/ (| − 1/2|) або 2, а потім відбивається по осі x, що, як видно, має місце на малюнку$\PageIndex{6}$ (а). Знову зауважте, що це масштабування та відображення не впливає на вершину в початковій точці.

Приклад$\PageIndex{3}$

Намалюйте графіки$y=-2 x^{2}, y=-x^{2},$ та$y=(-1 / 2) x^{2}$ на графічному калькуляторі

Рішення

Кожне з рівнянь було завантажено окремо в Y1 в меню Y=. На кожному з зображень на малюнку ми$\PageIndex{7}$ вибрали 6:ZStandard з меню ZOOM, щоб створити зображення.

Малюнок$\PageIndex{7}$.

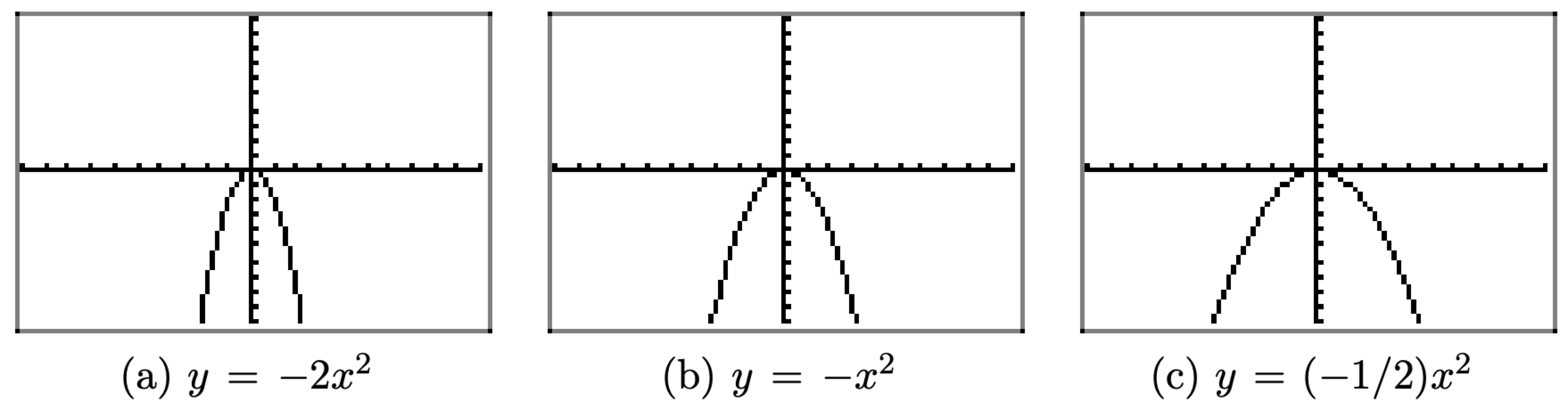
На малюнку$\PageIndex{7}$ (b) графік$y = −x^2$ є відображенням графіка$y = x^2$ поперек осі x і відкривається вниз. На малюнку$\PageIndex{7}$ (а) зверніть увагу, що графік$y = −2x^2$ розтягується вертикально в 2 рази (порівняйте з графіком на$y = −x^2$ малюнку$\PageIndex{7}$ (b)) і відбивається по осі x, щоб відкрити вниз. На малюнку$\PageIndex{7}$ (c) графік$(−1/2)x^2$ стискається в 2 рази, виглядає трохи ширше і відбивається по осі x, щоб відкрити вниз.

Горизонтальні переклади

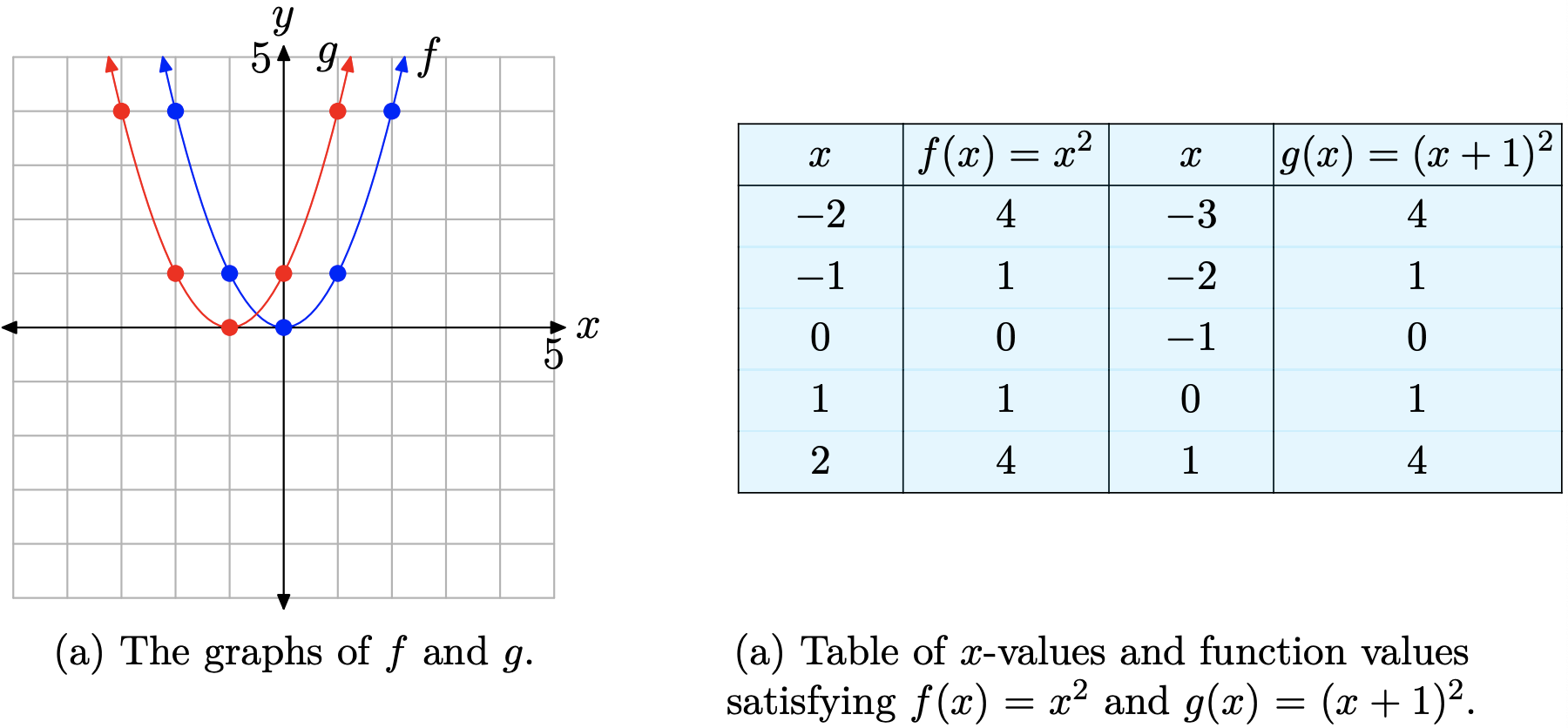
Графік на$g(x) = (x + 1)^2$ малюнку$\PageIndex{8}$ (а) показує основну параболу, яка зсувається на одну одиницю вліво. Вивчіть таблицю на малюнку$\PageIndex{8}$ (b) і зауважте, що рівняння$g(x) = (x + 1)^2$ дає ті ж значення y, що і рівняння$f(x) = x^2$, єдина різниця полягає в тому, що ці значення y обчислюються за значеннями x, які на одиницю менше, ніж ті, що використовуються для$f(x) = x^2$. Отже, графік$g(x) = (x + 1)^2$ повинен зміщуватися на одну одиницю вліво від графіка$f(x) = x^2$, про що свідчить малюнок$\PageIndex{8}$ (а).

Зауважте, що цей результат є контрінтуїтивним. Можна подумати, що заміна x на x + 1 змістила б графік на одну одиницю вправо, але зсув насправді відбувається у зворотному напрямку.

Нарешті, зауважте, що цього разу вершина параболи змістилася на 1 одиницю вліво і тепер знаходиться в точці (−1, 0).

Нас ведуть до наступного висновку.

Нерухомість 8

Якщо c > 0, то графік$g(x) = (x + c)^2$ зсувається c одиниць вліво від графіка$f(x) = x^2$.

Малюнок$\PageIndex{8}$: Горизонтальний зсув або переклад.

Подібне відбувається, коли ви замінюєте x на x − 1, тільки цього разу графік зміщується на одну одиницю вправо.

Приклад$\PageIndex{4}$

Намалюйте графіки$y=x^{2}$ та$y=(x-1)^{2}$ на графічному калькуляторі.

Рішення

Завантажте рівняння$y = x^2$ і$y = (x − 1)^2$ в меню Y=, як показано на малюнку$\PageIndex{9}$ (а). Натисніть кнопку ZOOM і виберіть 6:zStandard, щоб створити зображення, показане на малюнку$\PageIndex{9}$ (b).

Малюнок$\PageIndex{9}$: Креслення$y = x^2$ і$y = (x−1)^2$ на графічному калькуляторі.

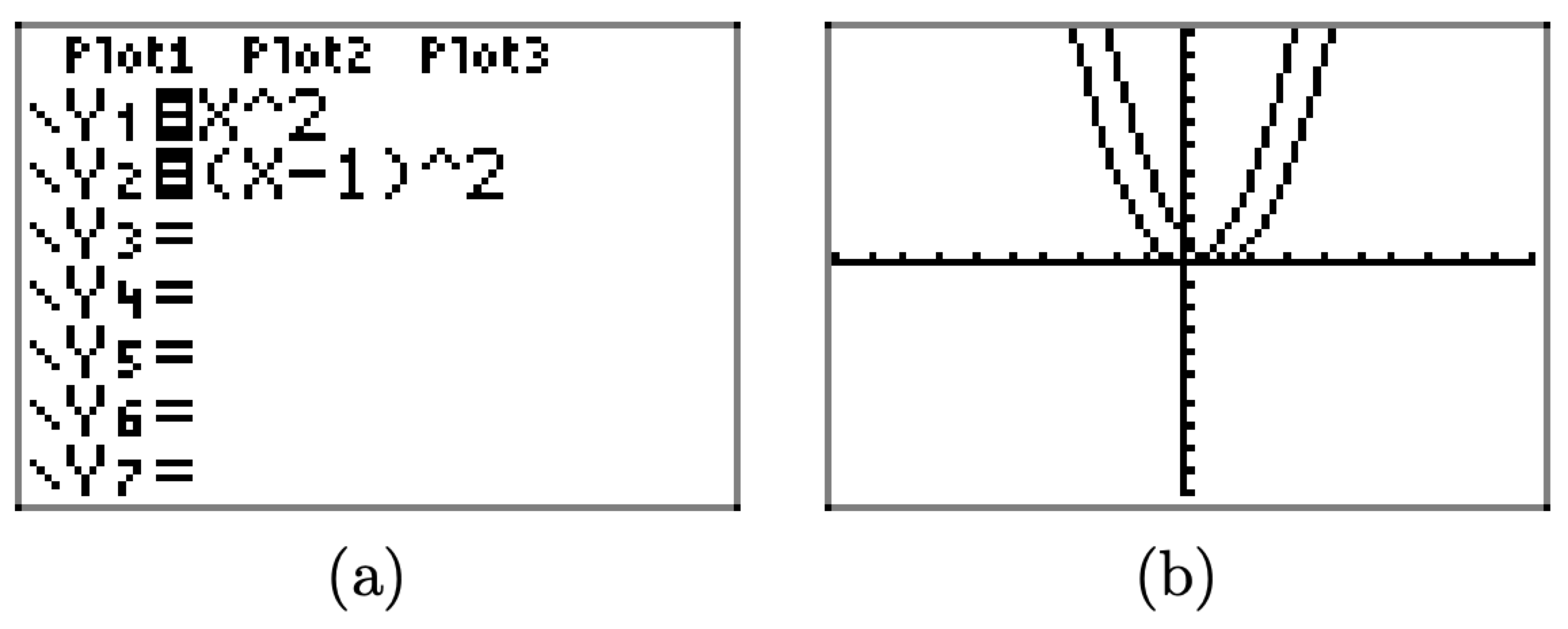
Зверніть увагу, що графік$y = (x − 1)^2$ зсувається на 1 одиницю праворуч від графа$y = x^2$ і вершина графа тепер$y = (x − 1)^2$ знаходиться в точці (1, 0).

Нас ведуть до наступного властивості.

Нерухомість 10

Якщо c > 0, то графік$g(x) = (x − c)^2$ зсувається c одиниць праворуч від графіка$f(x) = x^2$.

Вертикальні переклади

Графік на$g(x) = x^2 + 1$ малюнку$\PageIndex{10}$ (а) зміщений на одну одиницю вгору від графіка$f(x) = x^2$. Це легко побачити, оскільки обидва рівняння використовують однакові значення x у таблиці на малюнку$\PageIndex{10}$ (b), але значення$g(x) = x^2 + 1$ функцій на одиницю більше, ніж відповідні значення функції$f(x) = x^2$.

Зверніть увагу, що вершина графа також змістилася вгору на 1 одиницю і тепер знаходиться в точці (0, 1).$g(x) = x^2 + 1$

Малюнок$\PageIndex{10}$: Вертикальний зсув або переклад.

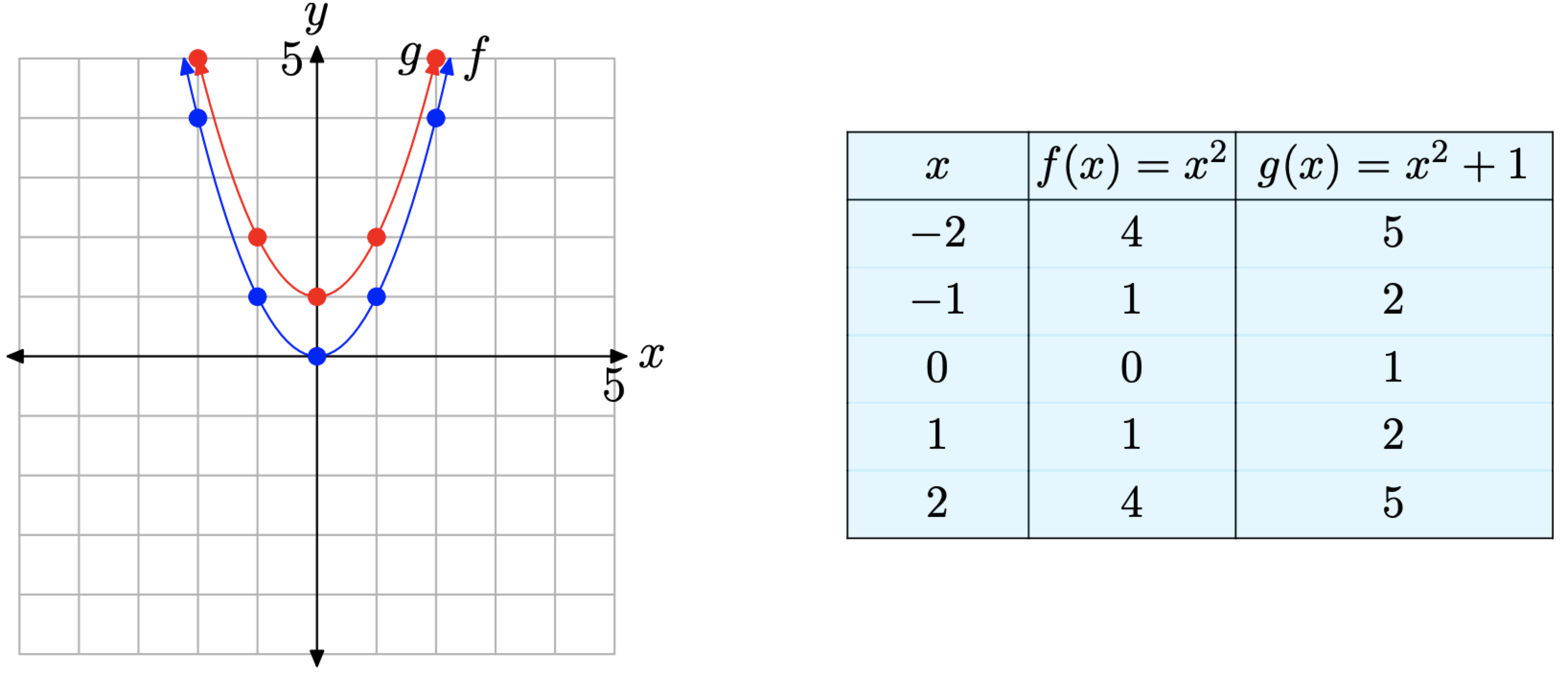
Вищевикладене обговорення призводить до наступного властивості.

Нерухомість 11

Якщо c > 0, графік$g(x) = x^2 + c$ зсувається на c одиниць вгору від графіка$f(x) = x^2$.

Аналогічним чином графік$y = x^2 − 1$ зсувається вниз на одну одиницю від графіка$y = x^2$

Приклад$\PageIndex{5}$

Намалюйте графіки$y = x^2$ та$y = x^2 − 1$ на графічному калькуляторі.

Рішення

Завантажте рівняння$y = x^2$ і$y = x^2 − 1$ в меню Y=, як показано на малюнку$\PageIndex{11}$ (а). Натисніть кнопку ZOOM і виберіть 6:zStandard, щоб створити зображення, показане на малюнку$\PageIndex{11}$ (b).

Зауважте, що граф$y = x^2 − 1$ зсувається на 1 одиницю вниз від графа,$y = x^2$ а вершина графа тепер$y = x^2 − 1$ знаходиться в точці (0, −1).

Малюнок$\PageIndex{11}$: Креслення$y = x^2$ і$y = x^2 − 1$ на графічному калькуляторі.

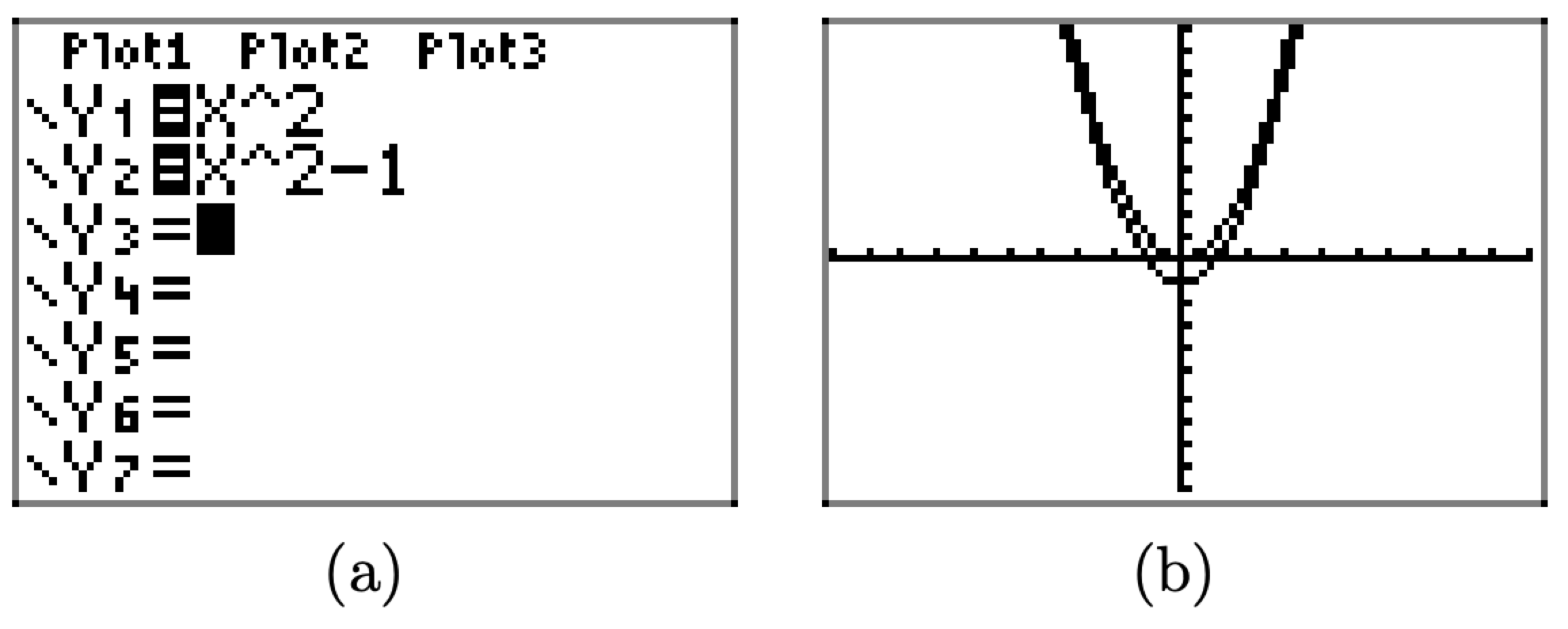
Вищевикладене обговорення призводить до наступного властивості.

Нерухомість 13

Якщо c > 0, графік$g(x) = x^2 − c$ зсувається на c одиниць вниз від графіка$f(x) = x^2$.

Вісь симетрії

На$\PageIndex{1}$ малюнку графік$y = x^2$ симетричний щодо осі y. Одна половина параболи - дзеркальне відображення іншої по відношенню до осі Y. Ми говоримо, що вісь y діє як вісь симетрії.

Якщо парабола відбивається по осі x, як на малюнку 6, вісь симетрії не змінюється. Графік все ще симетричний щодо осі y. Подібні коментарі призначені для масштабування та вертикальних перекладів. Однак якщо графік$y = x^2$ зсувається вправо або вліво, то вісь симетрії зміниться.

Приклад$\PageIndex{6}$

Намалюйте графік$y = −(x + 2)^2 + 3$.

Рішення

Хоча це не потрібно, цей приклад набагато простіший, якщо ви виконуєте роздуми перед перекладами.

Порада 15. Якщо це взагалі можливо, виконайте масштабування і відображення перед перекладами.

У ряді, показаному на малюнку$\PageIndex{12}$, спочатку виконуємо відображення, потім горизонтальний переклад, а потім вертикальний переклад.

• На малюнку$\PageIndex{12}$ (а) графік$y = −x^2$ є відображенням графіка$y = x^2$ поперек осі x і відкривається вниз. Зверніть увагу, що вершина все ще знаходиться в початковій точці.
• На малюнку$\PageIndex{12}$ (b) ми замінили x на x+ 2 у рівнянні,$y = −x^2$ щоб отримати рівняння$y = −(x+ 2)^2$. Ефект полягає$y = −x^2$ у зміщенні графіка на малюнку$\PageIndex{12}$ (а) 2 одиниці вліво, щоб отримати графік на малюнку$\PageIndex{12}$ (b).$y = −(x+ 2)^2$ Зауважте, що вершина тепер знаходиться в точці (−2, 0).
• На малюнку$\PageIndex{12}$ (c) ми додали 3 до рівняння,$y = −(x+ 2)^2$ щоб отримати рівняння$y = −(x+ 2)^2 + 3$. Ефект полягає у зміщенні графіка y = − (x+ 2) 2 на малюнку$\PageIndex{12}$ (b) вгору на 3 одиниці для отримання графіка на$y=-(x+2)^{2}+3$ малюнку$\PageIndex{12}$ (c). Зауважте, що вершина тепер знаходиться в точці (−2, 3).

Рисунок$\PageIndex{12}$: Пошук графіка$y=-(x+2)^{2}+3$ наскрізного ряду перетворень.

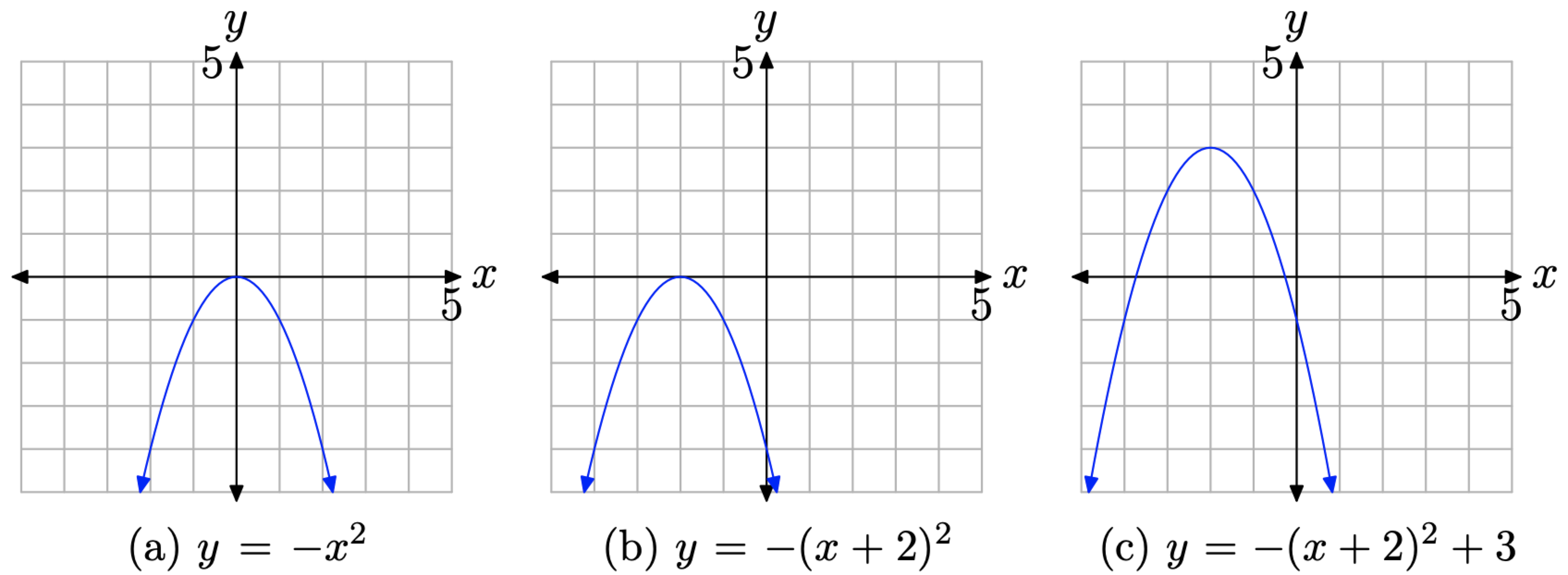
На практиці ми можемо діяти швидше. Проаналізуйте рівняння$y=-(x+2)^{2}+3$. Знак мінус говорить нам про те, що парабола «відкривається вниз». Наявність х + 2 вказує на зсув на 2 одиниці вліво. Нарешті, додавання 3 змістить графік на 3 одиниці вгору. Таким чином, у нас є парабола, яка «відкривається вниз» з вершиною в (−2, 3). Це показано на малюнку$\PageIndex{13}$.

Малюнок$\PageIndex{13}$: Вісь симетрії проходить через вершину.

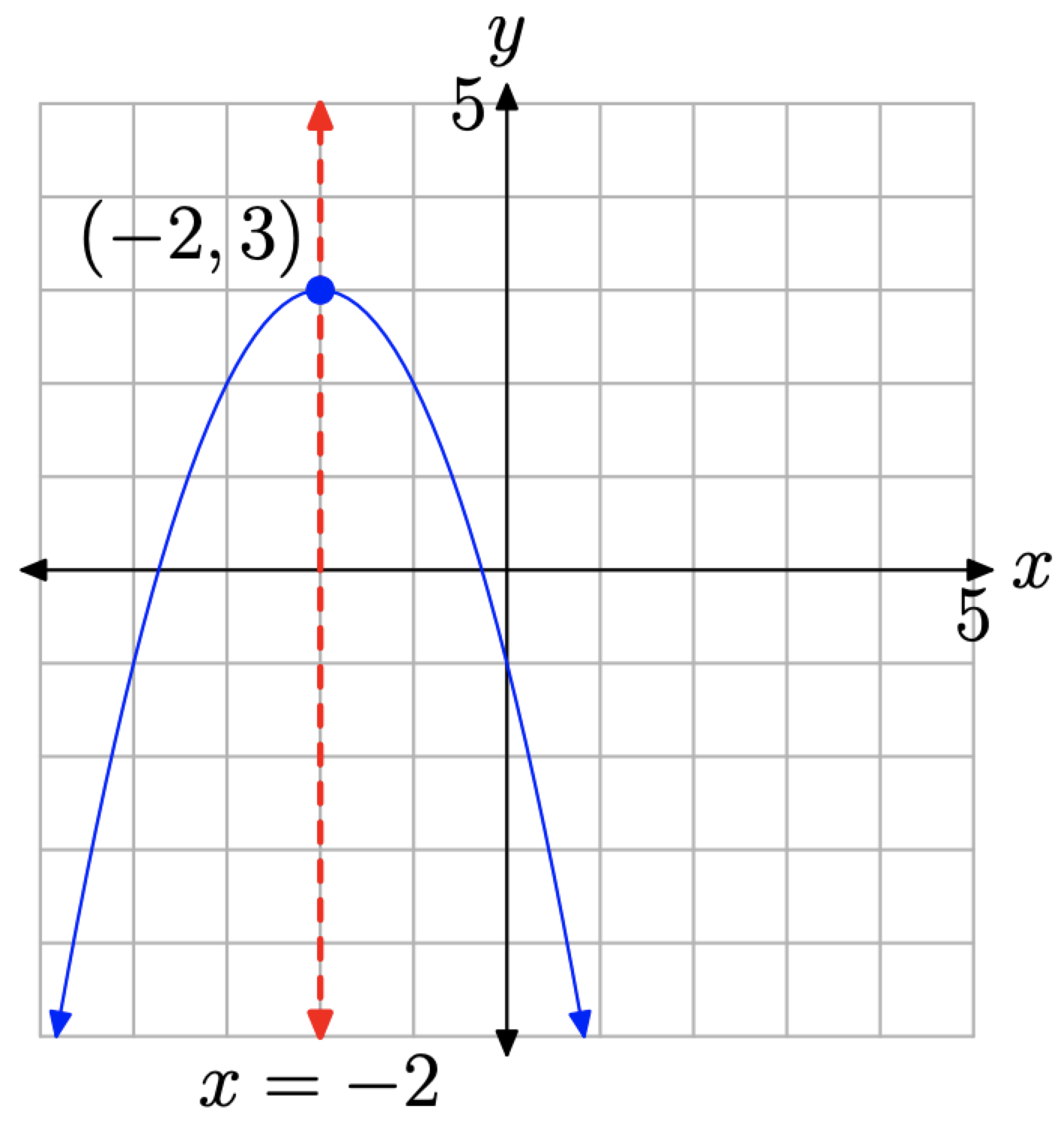
Вісь симетрії проходить через вершину (−2, 3) на малюнку$\PageIndex{13}$ і має рівняння x = −2. Зверніть увагу, що права половина параболи є дзеркальним відображенням її лівої половини поперек цієї осі симетрії. Ми можемо використовувати вісь симетрії, щоб отримати точний графік параболи з мінімальною побудовою точок.

Рекомендації щодо використання осі симетрії

• Почніть з побудови вершини та осі симетрії, як показано на малюнку$\PageIndex{14}$ (а).
• Далі обчислюємо дві точки по обидва боки від осі симетрії. Вибираємо x = −1 і x = 0 і обчислюємо відповідні значення y за допомогою рівняння$y=-(x+2)^{2}+3$

х	$y=-(x+2)^{2}+3$
-1	\ (y=- (x+2) ^ {2} +3\) ">2
0	\ (y=- (x+2) ^ {2} +3\) ">-1

Покладіть точки з таблиці, як показано на малюнку$\PageIndex{14}$ (б).

• Нарешті, побудуйте дзеркальні зображення цих точок поперек осі симетрії, як показано на малюнку$\PageIndex{14}$ (c).

Малюнок$\PageIndex{14}$: Використання осі симетрії для встановлення точності.

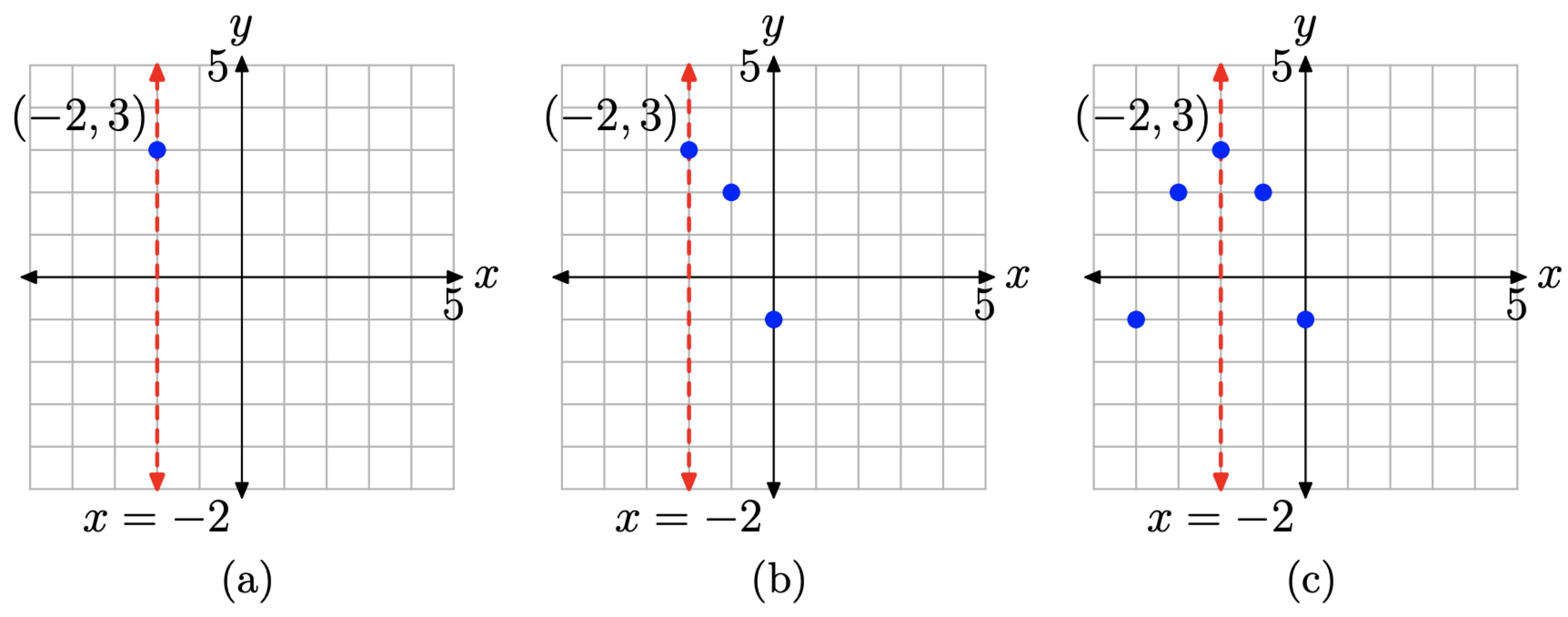
Зображення на малюнку$\PageIndex{14}$ (c) чітко містить достатньо інформації для завершення графіка параболи, що має рівняння на$y=-(x+2)^{2}+3$ малюнку$\PageIndex{15}$.

Малюнок$\PageIndex{15}$: Точний сюжет$y=-(x+2)^{2}+3$.

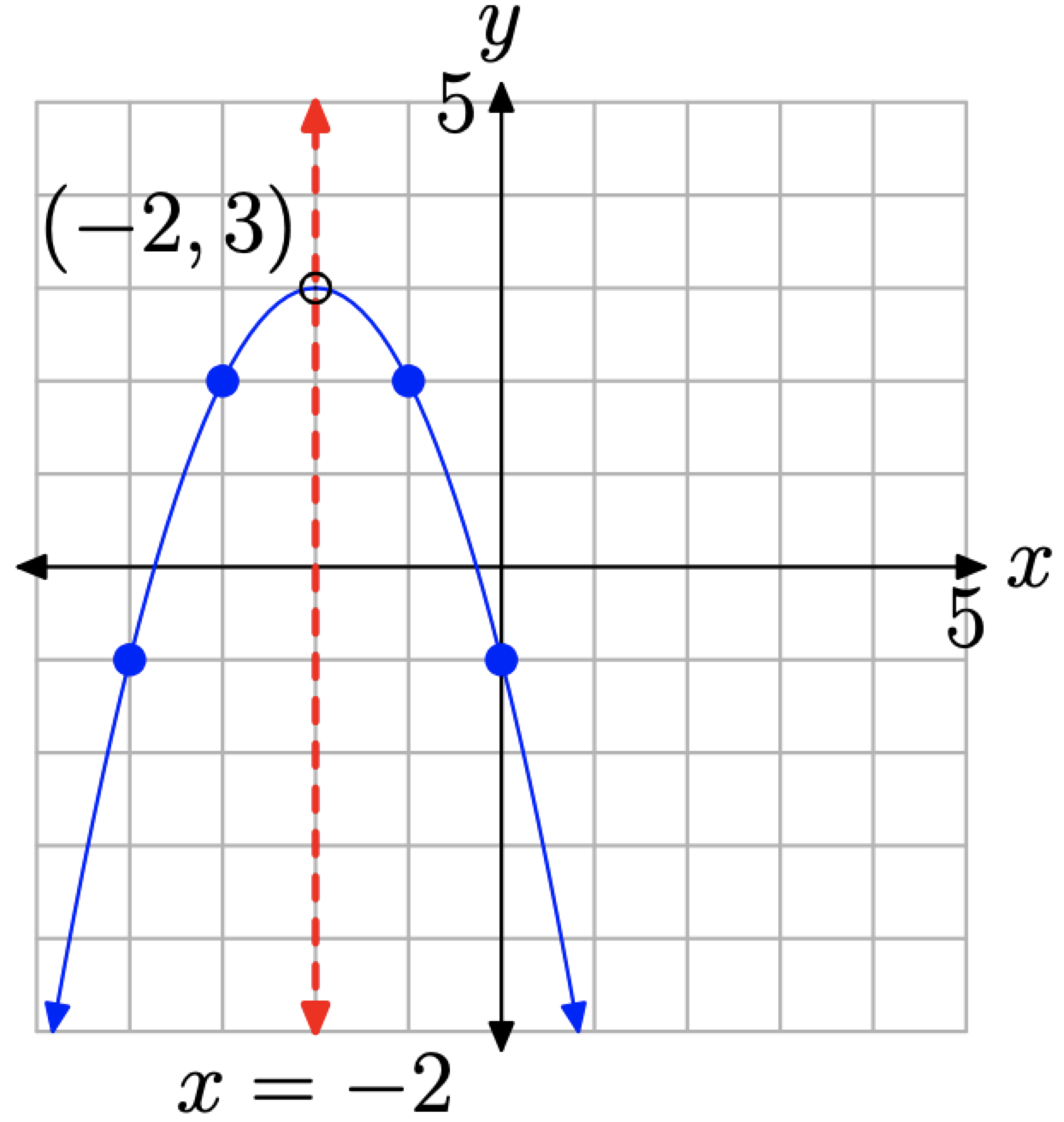
Давайте підсумуємо те, що ми бачили до цих пір.

Резюме 16

Форма квадратичної функції $$f(x)=a(x-h)^{2}+k$$ називається вершиною форми. Графік цієї квадратичної функції є параболою.

1. Графік параболи відкривається вгору, якщо a > 0, вниз, якщо a < 0.
2. Якщо величина а більше 1, то графік параболи розтягується на коефіцієнт а Якщо величина а менше 1, то графік параболи стискається на коефіцієнт 1/а.
3. Парабола перекладається h одиниць вправо, якщо h > 0, і h одиниць ліворуч, якщо h < 0.
4. Парабола перекладається k одиниць вгору, якщо k > 0, і k одиниць вниз, якщо k < 0.
5. Координати вершини - (h, k).
6. Вісь симетрії - вертикальна лінія через вершину, рівняння якої дорівнює x = h.

Давайте розглянемо один остаточний приклад

Приклад$\PageIndex{7}$

Використовуйте техніку Приклад$\PageIndex{6}$, щоб намалювати графік$f(x) = 2(x − 2)^2 − 3$.

Рішення

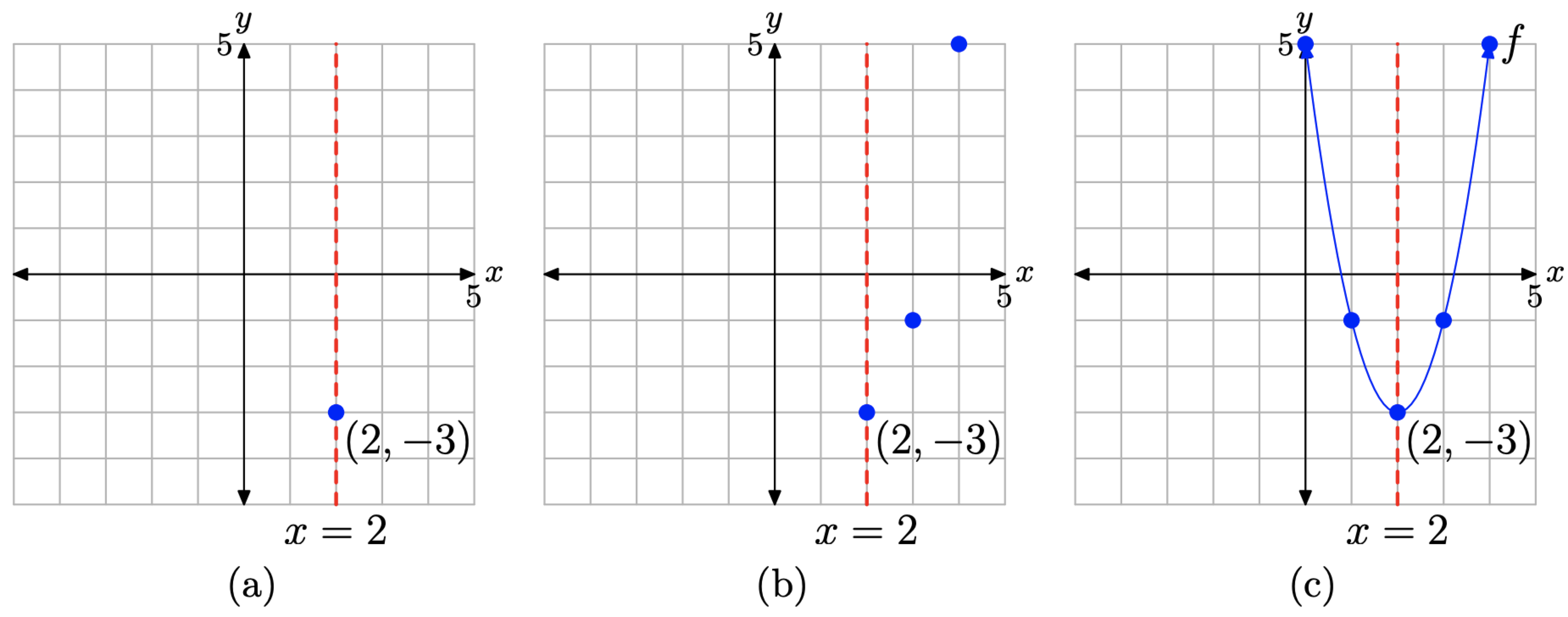
Порівняйте$f(x) = 2(x − 2)^2 − 3$ з$f(x)=a(x-h)^{2}+k$ і зверніть увагу, що a = 2. Значить, парабола була «розтягнута» в 2 рази і відкривається вгору. Наявність x − 2 вказує на зсув на 2 одиниці вправо; а віднімання 3 зміщує параболу на 3 одиниці вниз. Отже, вершина буде розташована в точці (2, −3), а вісь симетрії буде вертикальною лінією, що має рівняння x = 2. Це показано на малюнку$\PageIndex{16}$ (а).

Примітка

Деякі вважають за краще більш суворе порівняння$f(x) = 2(x − 2)^2 − 3$ із загальною формою вершини$f(x)=a(x-h)^{2}+k$, отримуючи a = 2, h = 2, а k = −3. Це одразу визначає вершину в (h, k) або (2, −3).

Далі оцініть функцію$f(x) = 2(x − 2)^2 − 3$ в двох точках, що лежать праворуч від осі симетрії (або ліворуч, якщо хочете). Оскільки вісь симетрії є вертикальною лінією x = 2, ми вибираємо для оцінки функції при x = 3 і 4.

$$\begin{array}{l}{f(3)=2(3-2)^{2}-3=-1} \\ {f(4)=2(4-2)^{2}-3=5}\end{array}$$

Це дає нам дві точки праворуч від осі симетрії, (3, −1) і (4, 5), які ми будуємо на малюнку$\PageIndex{16}$ (b).

Нарешті, ми будуємо дзеркальні зображення (3, −1) та (4, 5) поперек осі симетрії, що дає нам точки (1, −1) та (0, 5) відповідно. Вони побудовані на малюнку$\PageIndex{16}$ (в). Потім ми проводимо параболу через ці точки.

Малюнок$\PageIndex{16}$: Створення графіка$f(x) = 2(x − 2)^2 − 3$.

Закінчимо описом домену і діапазону функції, визначеної правилом$f(x)=2(x-2)^{2}-3$. Якщо ви використовуєте інтуїтивне поняття, що домен - це набір «допустимих значень x», то можна підставити будь-яке число один хоче в рівняння$f(x)=2(x-2)^{2}-3$. Тому домен - це все дійсні числа, які ми можемо записати наступним чином: Domain =$\mathbb{R}$ або Domain =$(-\infty, \infty)$.

Ви також можете проектувати кожну точку на графіку$f(x)=2(x-2)^{2}-3$ на вісь x, як показано на малюнку$\PageIndex{17}$ (а). Якщо зробити це, то вся вісь буде «лежати в тіні», тому ще раз домен - це все дійсні числа.

Рисунок$\PageIndex{17}$: Проектування для пошуку (a) домену та (b) діапазону.

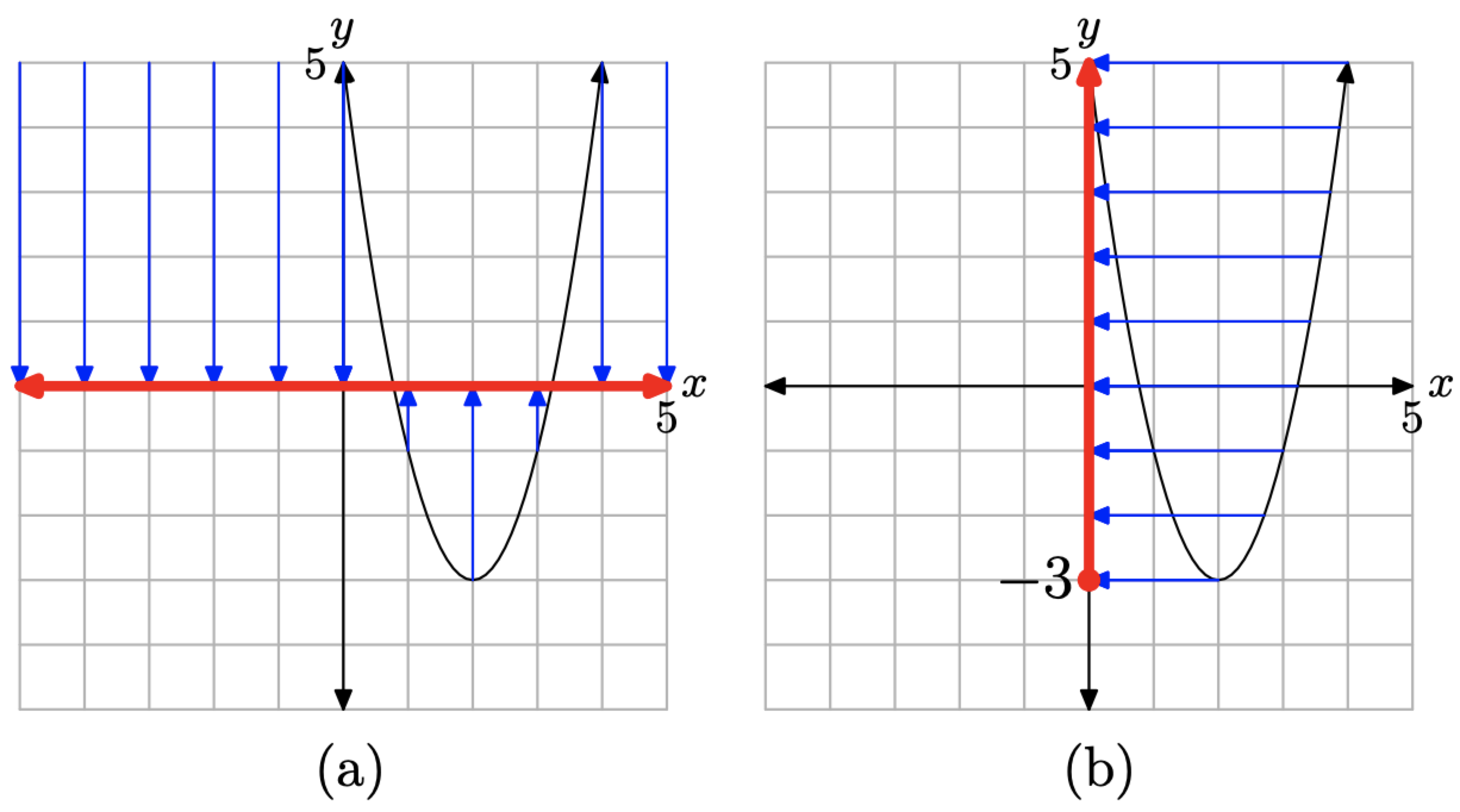
Щоб визначити діапазон функції$f(x)=2(x-2)^{2}-3$, спроектуйте кожну точку на графіку f на вісь y, як показано на малюнку$\PageIndex{17}$ (b). На осі y всі точки, більші або рівні −3, «лежать у тіні», тому діапазон описується за допомогою Range$=\{y : y \geq-3\}=[-3, \infty)$.

Нижче підсумовано, як можна знайти область та діапазон квадратичної функції, яка знаходиться у формі вершини.

Резюме 18

Область квадратичної функції $$f(x)=a(x-h)^{2}+k$$ , незалежно від значень параметрів a, h і k, являє собою набір всіх дійсних чисел, легко описаних за допомогою$\mathbb{R}$ або$(-\infty, \infty)$. З іншого боку, діапазон залежить від значень a і k.

• Якщо a > 0, то парабола відкривається вгору і має вершину в (h, k). Отже, діапазон буде $$[k, \infty)=\{y : y \geq k\}$$ .
• Якщо a < 0, то парабола відкривається вниз і має вершину в (h, k). Отже, діапазон буде $$(-\infty, k]=\{y : y \leq k\}$$ .

Вправа

У Вправи 1 - 6 ескіз зображення екрану калькулятора на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте кожен граф своїм рівнянням. Не забудьте використовувати лінійку, щоб намалювати всі лінії, включаючи осі.

Вправа$\PageIndex{1}$

Використовуйте графічний калькулятор, щоб намалювати графіки$f(x) = x^2$$g(x) = 2x^2$, і$h(x) = 4x^2$ на одному екрані. Напишіть коротке речення, що пояснює, що ви дізналися в цій вправі.

Відповідь

Множення на 2 шкали по вертикалі на коефіцієнт 2. Множення на 4 шкали по вертикалі на коефіцієнт 4.

Вправа$\PageIndex{2}$

Використовуйте графічний калькулятор, щоб намалювати графіки$f(x) = −x^2$$g(x) = −2x^2$, і$h(x) = −4x^2$ на одному екрані. Напишіть коротке речення, що пояснює, що ви дізналися в цій вправі.

Вправа$\PageIndex{3}$

Використовуйте графічний калькулятор, щоб намалювати графіки$f(x) = x^2$$g(x) = (x−2)^2$, і$h(x) = (x−4)^2$ на одному екрані. Напишіть коротке речення, що пояснює, що ви дізналися в цій вправі.

Відповідь

Графік$g(x) = (x−2)^2$ зсувається на 2 одиниці праворуч від$f(x) = x^2$. Графік$h(x) = (x−4)^2$ зсувається на 4 одиниці праворуч від$f(x) = x^2$.

Вправа$\PageIndex{4}$

Використовуйте графічний калькулятор, щоб намалювати графіки$f(x) = x^2$$g(x) = (x+2)^2$, і$h(x) = (x+4)^2$ на одному екрані. Напишіть коротке речення, що пояснює, що ви дізналися в цій вправі.

Вправа$\PageIndex{5}$

Використовуйте графічний калькулятор, щоб намалювати графіки$f(x) = x^2$$g(x) = x^2+2$, і$h(x) = x^2+4$ на одному екрані. Напишіть коротке речення, що пояснює, що ви дізналися в цій вправі.

Відповідь

Графік$g(x) = x^2+2$ зсувається на 2 одиниці вгору від графіка$f(x) = x^2$ .Графік$h(x) = x^2+4$ зсувається на 4 одиниці вгору від графіка$f(x) = x^2$.

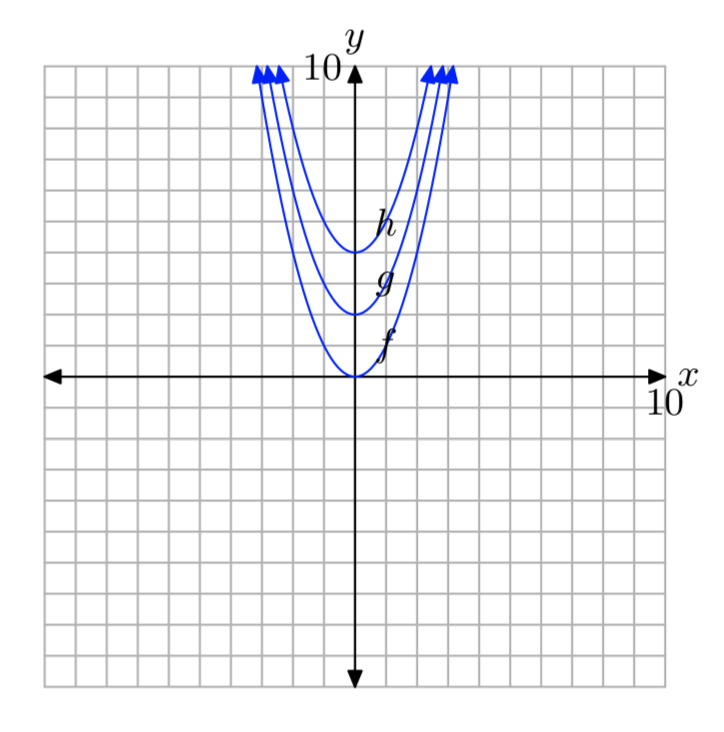
Вправа$\PageIndex{6}$

Використовуйте графічний калькулятор, щоб намалювати графіки$f(x) = x^2$$g(x) = x^2−2$, і$h(x) = x^2−4$ на одному екрані. Напишіть коротке речення, що пояснює, що ви дізналися в цій вправі.

У Вправи 7 - 14 запишіть задану квадратичну функцію на домашній папері, а потім вкажіть координати вершини.

Вправа$\PageIndex{7}$

$f(x) = −5(x−4)^2−5$

Відповідь

(4, −5)

Вправа$\PageIndex{8}$

$f(x) = 5(x+3)^2−7$

Вправа$\PageIndex{9}$

$f(x) = 3(x+1)^2$

Відповідь

(− 1,0)

Вправа$\PageIndex{10}$

$f(x) = \frac{7}{5}(x+\frac{5}{9})^2−\frac{3}{4}$

Вправа$\PageIndex{11}$

$f(x) = −7(x−4)^2+6$

Відповідь

(4, 6)

Вправа$\PageIndex{12}$

$f(x) = −\frac{1}{2}(x−\frac{8}{9})^2+\frac{2}{9}$

Вправа$\PageIndex{13}$

$f(x) = \frac{1}{6}(x+\frac{7}{3})^2+\frac{3}{8}$

Відповідь

$(−\frac{7}{3}, \frac{3}{8})$

Вправа$\PageIndex{14}$

$f(x) = −\frac{3}{2}(x+\frac{1}{2})^2−\frac{8}{9}$

У вправах 15 - 22 викласти рівняння осі симетрії графіка заданої квадратичної функції.

Вправа$\PageIndex{15}$

$f(x) = −7(x−3)^2+1$

Відповідь

х = 3

Вправа$\PageIndex{16}$

$f(x) = −6(x+8)^2+1$

Вправа$\PageIndex{17}$

$f(x) = −\frac{7}{8}(x+\frac{1}{4})^2+\frac{2}{3}$

Відповідь

$x = −\frac{1}{4}$

Вправа$\PageIndex{18}$

$f(x) = −\frac{1}{2}(x−\frac{3}{8})^2−\frac{5}{7}$

Вправа$\PageIndex{19}$

$f(x) = −\frac{2}{9}(x+\frac{2}{3})^2−\frac{4}{5}$

Відповідь

$x = −\frac{2}{3}$

Вправа$\PageIndex{20}$

$f(x) = −7(x+3)^2+9$

Вправа$\PageIndex{21}$

$f(x) = −\frac{8}{7}(x+\frac{2}{9})^2+\frac{6}{5}$

Відповідь

$x = −\frac{2}{9}$

Вправа$\PageIndex{22}$

$f(x) = 3(x+3)^2+6$

У Вправах 23 - 36 виконайте кожне з наступних завдань для заданої квадратичної функції.

1. Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь.
2. Покладіть вершину параболи і позначте її координатами.
3. Намалюйте вісь симетрії і позначте її рівнянням.
4. Налаштуйте таблицю біля вашої системи координат, яка містить точні координати двох точок по обидві сторони від осі симетрії. Покладіть їх на вашу систему координат і їх «дзеркальні зображення» поперек осі симетрії.
5. Намалюйте параболу і позначте її рівнянням.
6. Використовуйте інтервальне позначення для опису як області, так і діапазону квадратичної функції.

Вправа$\PageIndex{23}$

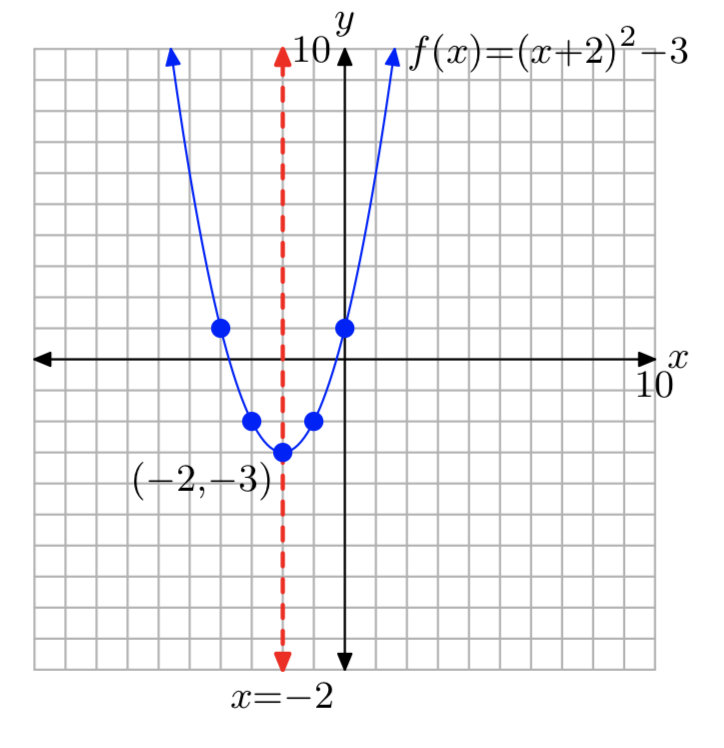
$f(x) = (x+2)^2−3$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= [−3,$\infty$)

Вправа$\PageIndex{24}$

$f(x) = (x−3)^2−4$

Вправа$\PageIndex{25}$

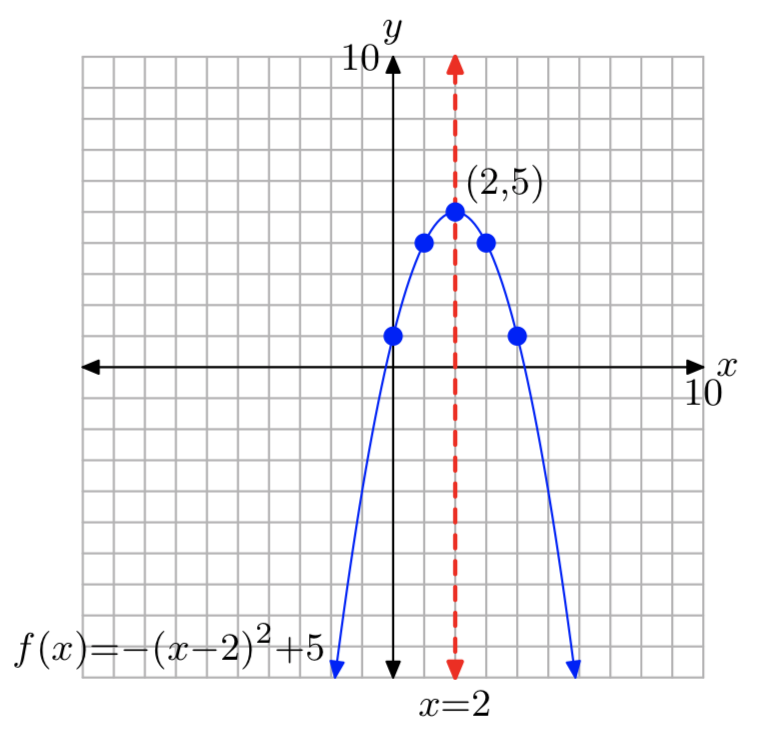
$f(x) = −(x−2)^2+5$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= (−$\infty$, 5]

Вправа$\PageIndex{26}$

$f(x) = −(x+4)^2+4$

Вправа$\PageIndex{27}$

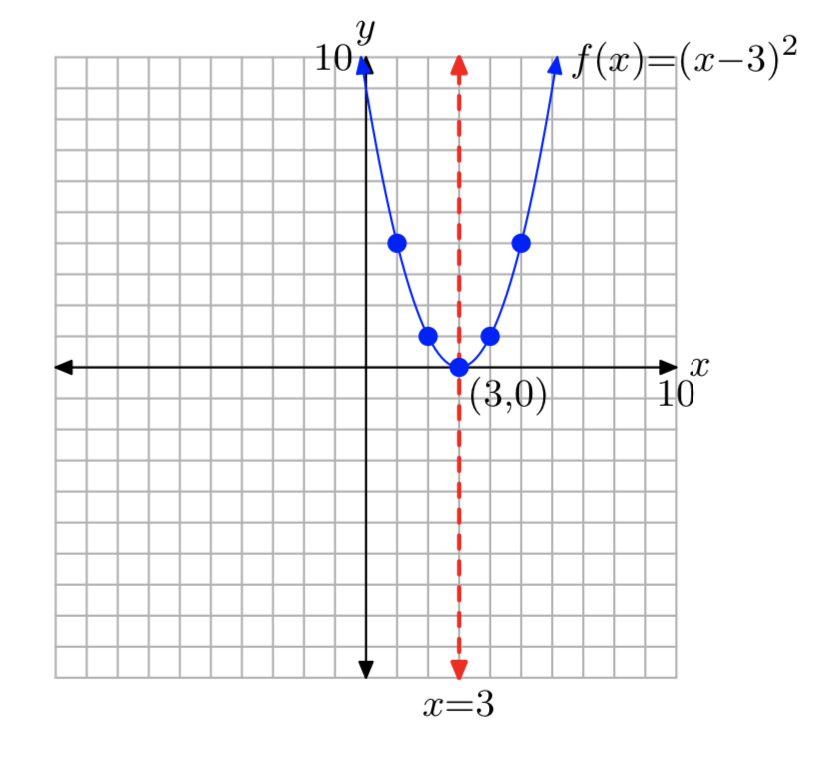
$f(x) = (x−3)^2$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= [0,$\infty$)

Вправа$\PageIndex{28}$

$f(x) = −(x+2)^2$

Вправа$\PageIndex{29}$

$f(x) = −x^2+7$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= (−$\infty$, 7]

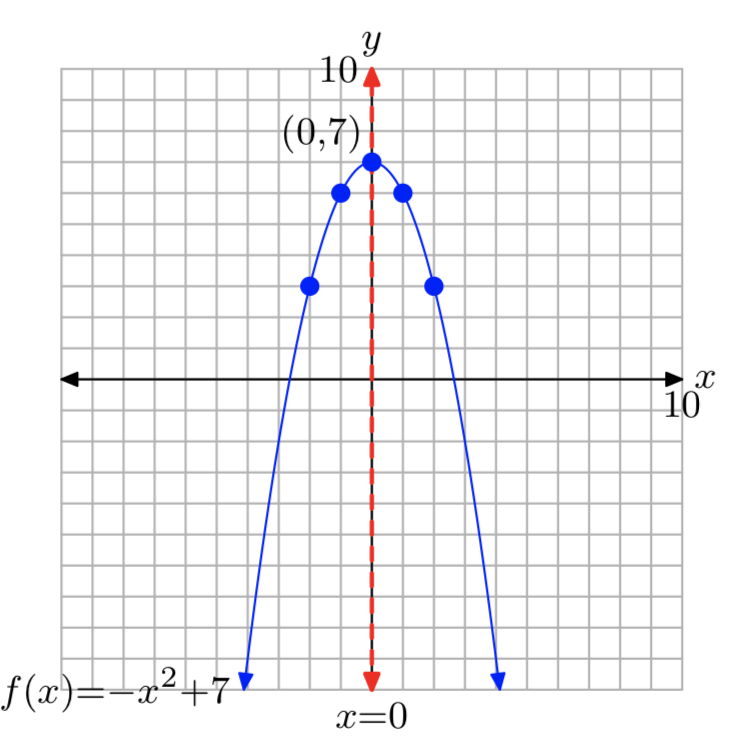
Вправа$\PageIndex{30}$

$f(x) = −x^2+7$

Вправа$\PageIndex{31}$

$f(x) = 2(x−1)^2−6$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= [−6,$\infty$)

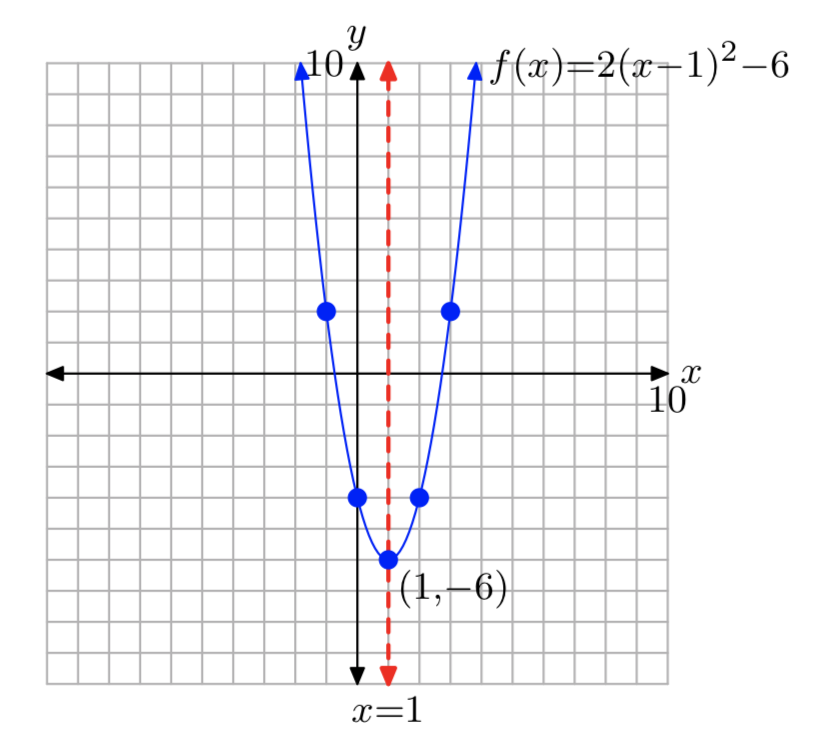
Вправа$\PageIndex{32}$

$f(x) = −2(x+1)^2+5$

Вправа$\PageIndex{33}$

$f(x) = −\frac{1}{2}(x+1)^2+5$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= (−$\infty$, 5]

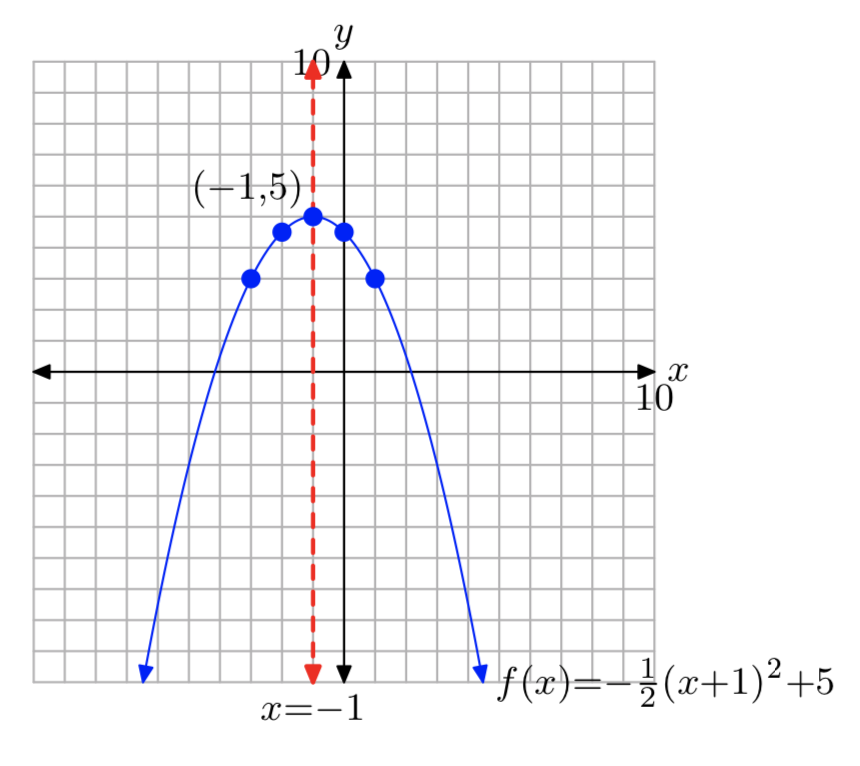
Вправа$\PageIndex{34}$

$f(x) = \frac{1}{2}(x−3)^2−6$

Вправа$\PageIndex{35}$

$f(x) = 2(x−\frac{5}{2})^2−\frac{15}{2}$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон= [−$\frac{15}{2}$,$\infty$)

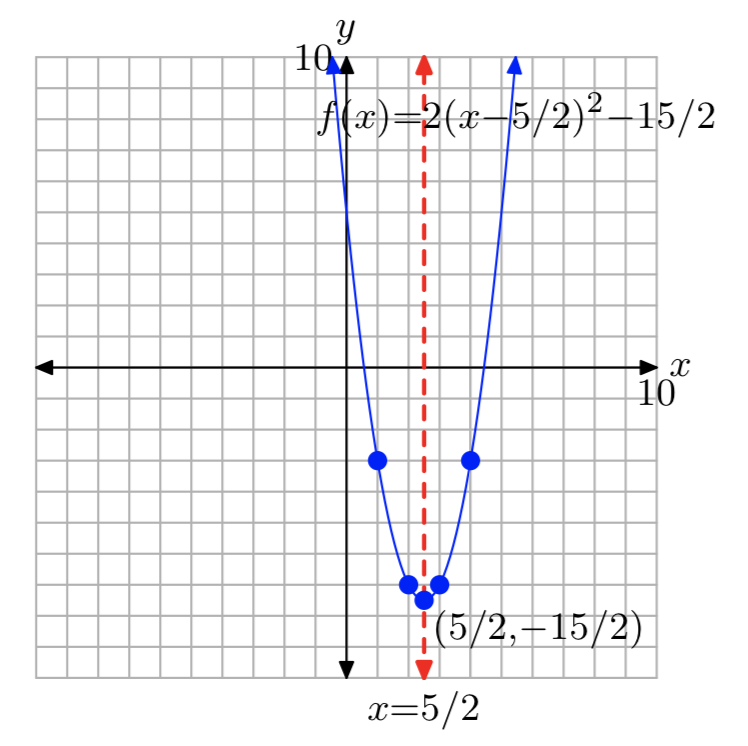
Вправа$\PageIndex{36}$

$f(x) = −3(x+\frac{7}{2})^2+\frac{15}{4}$

У Вправи 37 - 44 запишіть задану квадратичну функцію на домашньому папері, а потім використовуйте конструктор наборів та інтервальні позначення для опису домену та діапазону функції.

Вправа$\PageIndex{37}$

$f(x) = 7(x+6)^2−6$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон = [−6,$\infty$) = {y:$y \ge −6$}

Вправа$\PageIndex{38}$

$f(x) = 8(x+1)^2+7$

Вправа$\PageIndex{39}$

$f(x) = −3(x+4)^2−7$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон = (−$\infty$, −7] = {y:$y \le −7$}

Вправа$\PageIndex{40}$

$f(x) = −6(x−7)^2+9$

Вправа$\PageIndex{41}$

$f(x) = −7(x+5)^2−7$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон = (−$\infty$, −7] = {y:$y \le −7$}

Вправа$\PageIndex{42}$

$f(x) = 8(x−4)^2+3$

Вправа$\PageIndex{43}$

$f(x) = −4(x−1)^2+2$

Відповідь

Домен=$(−\infty, \infty)$; Діапазон = (−$\infty$, 2] = {y:$y \le 2$}

Вправа$\PageIndex{44}$

$f(x) = 7(x−2)^2−3$

У Вправах 45 - 52, використовуючи задане значення a, знайдіть конкретну квадратичну функцію виду$f(x) = a(x−h)^2+k$, яка має показаний графік. Примітка: h і k є цілими числами. Перевірте своє рішення за допомогою графічного калькулятора.

Вправа$\PageIndex{45}$

а = −2

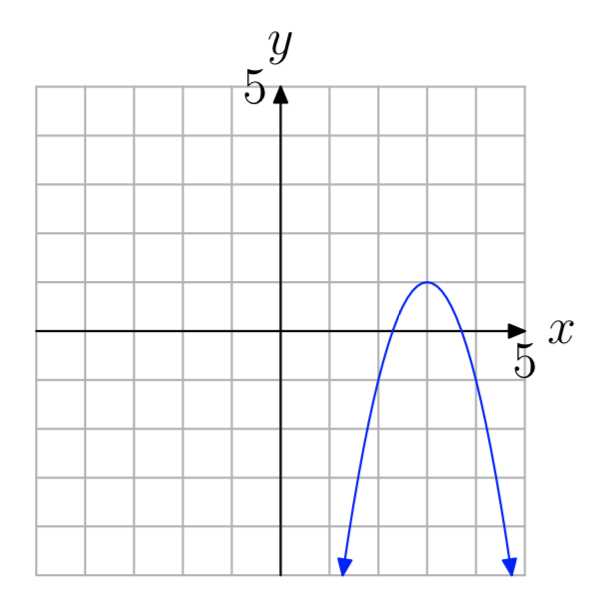
Відповідь

$f(x) = −2(x−3)^2+1$

Вправа$\PageIndex{46}$

а = 0,5

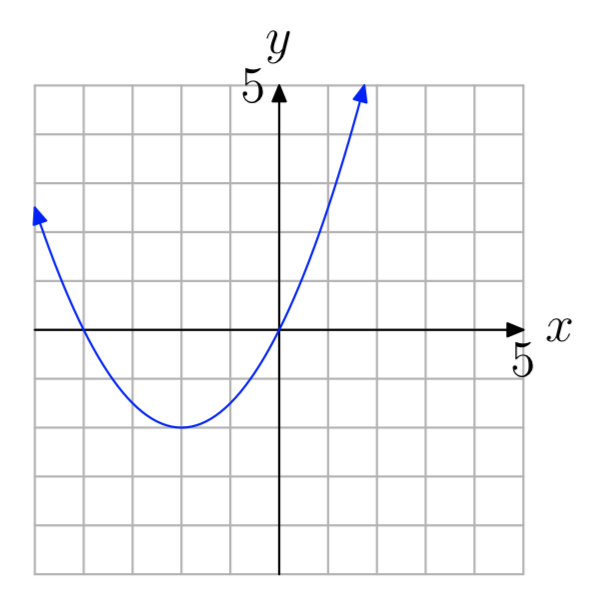
Вправа$\PageIndex{47}$

а = 2

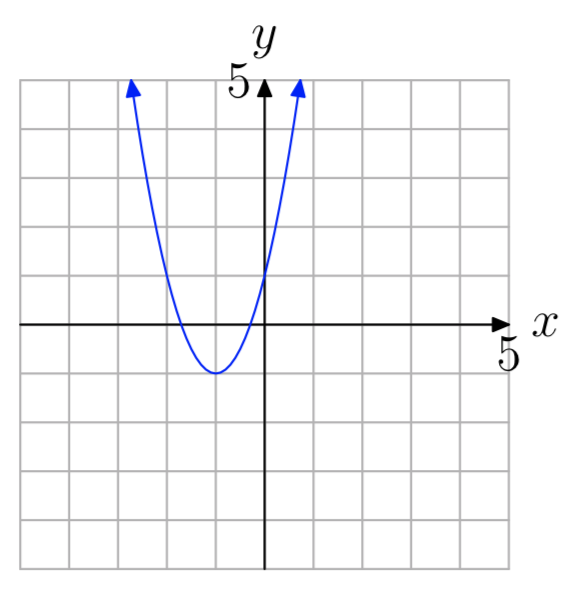
Відповідь

$f(x) = 2(x+1)^2−1$

Вправа$\PageIndex{48}$

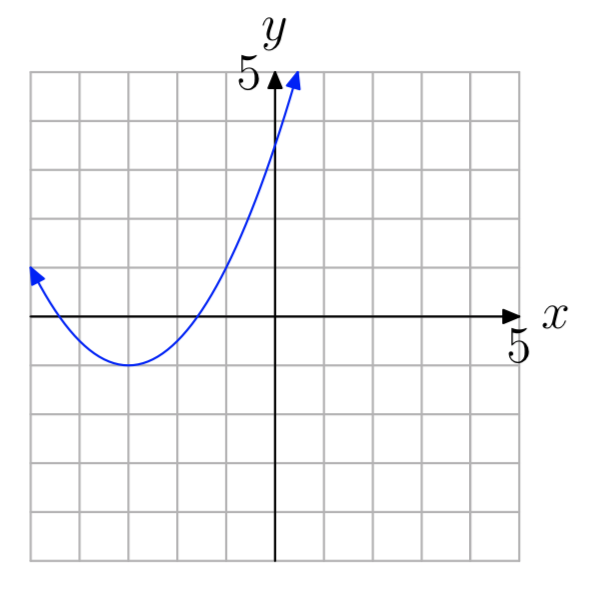
а = 0,5

Вправа$\PageIndex{49}$

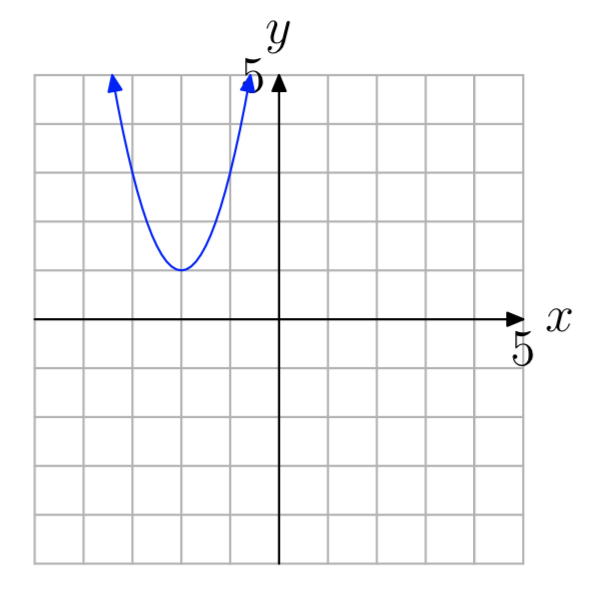
Відповідь

$f(x) = 2(x+2)^2+1$

Вправа$\PageIndex{50}$

а = −0,5

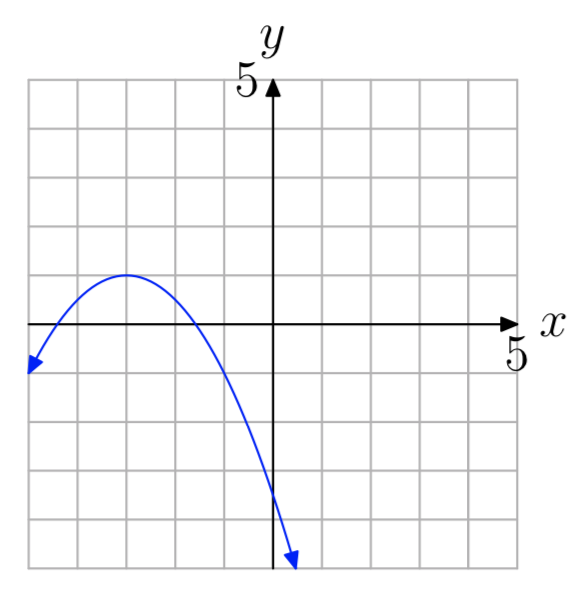
Вправа$\PageIndex{51}$

а = 2

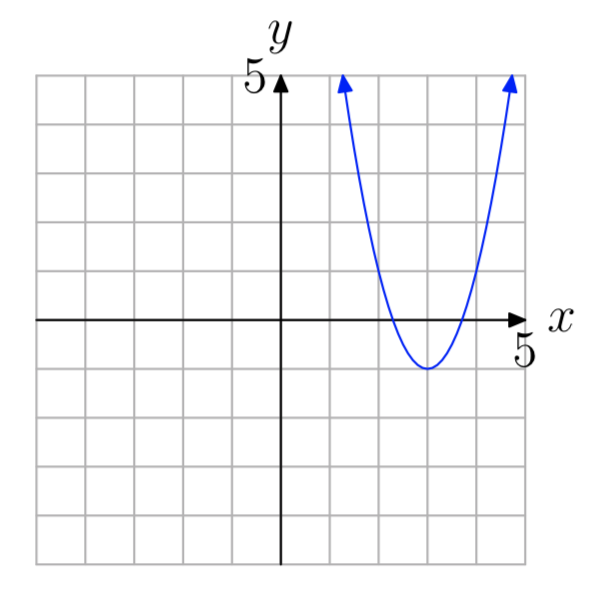
Відповідь

$f(x) = 2(x−3)^2−1$

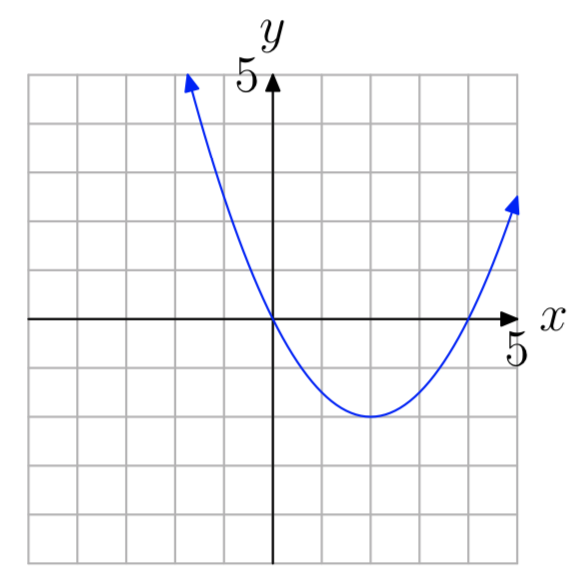
Вправа$\PageIndex{52}$

а = 0,5

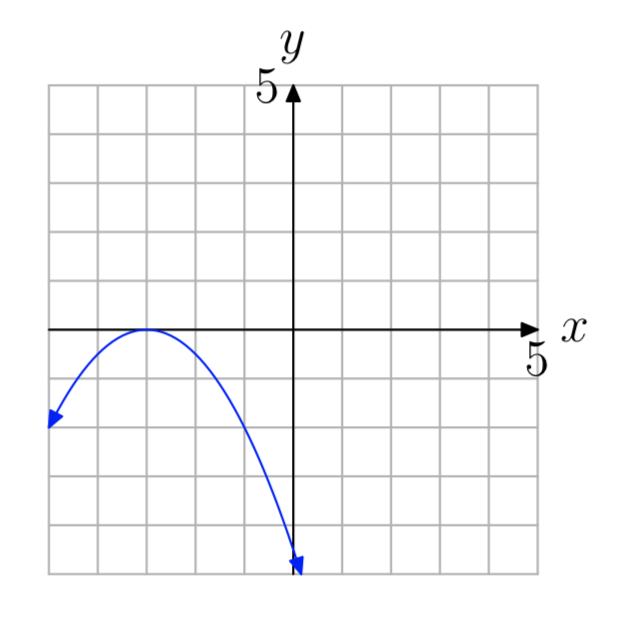
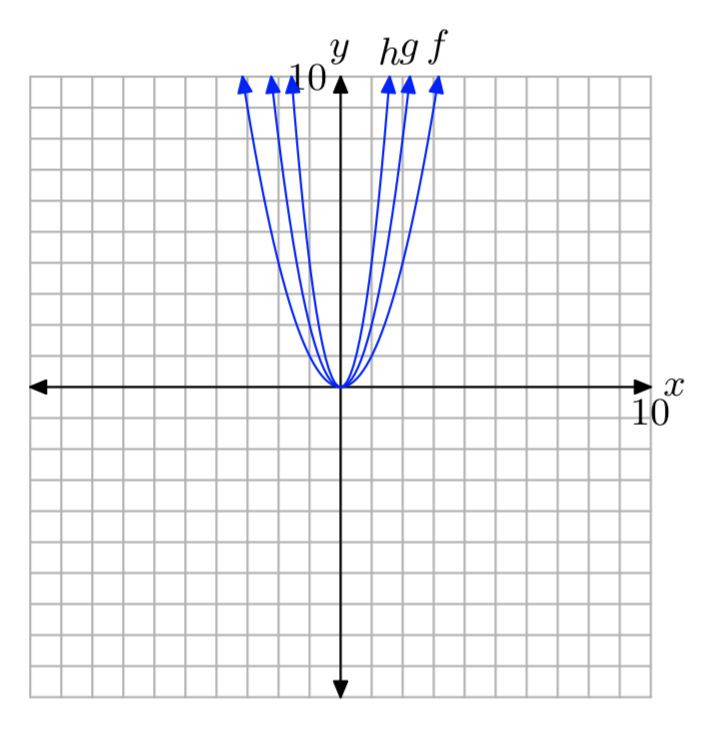
У вправах 53 - 54 використовуйте графік для визначення діапазону функції$f(x) = ax^2+bx+c$ Стрілки на графіку призначені для позначення того, що графік триває нескінченно довго в безперервному шаблоні та напрямку кожної стрілки. Опишіть рішення за допомогою інтервальних позначень.

Вправа$\PageIndex{53}$

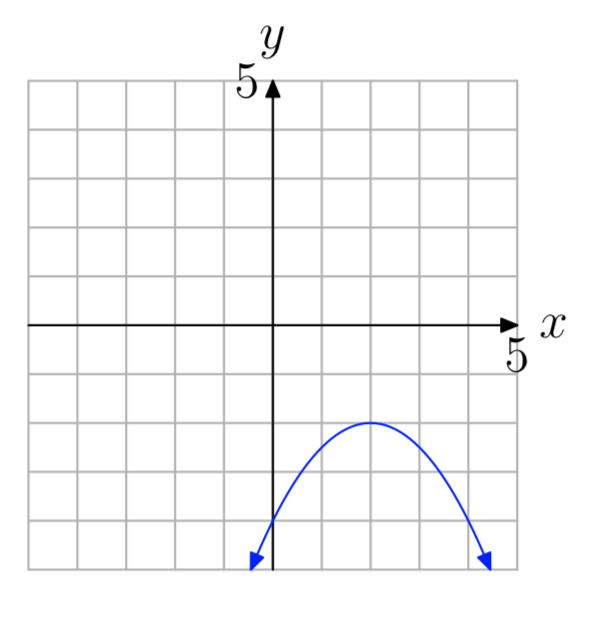
Відповідь

($−\infty$, −2]

Вправа$\PageIndex{54}$

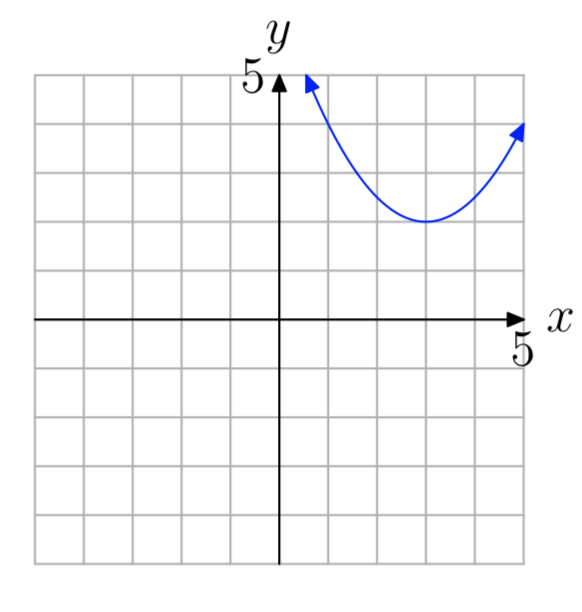
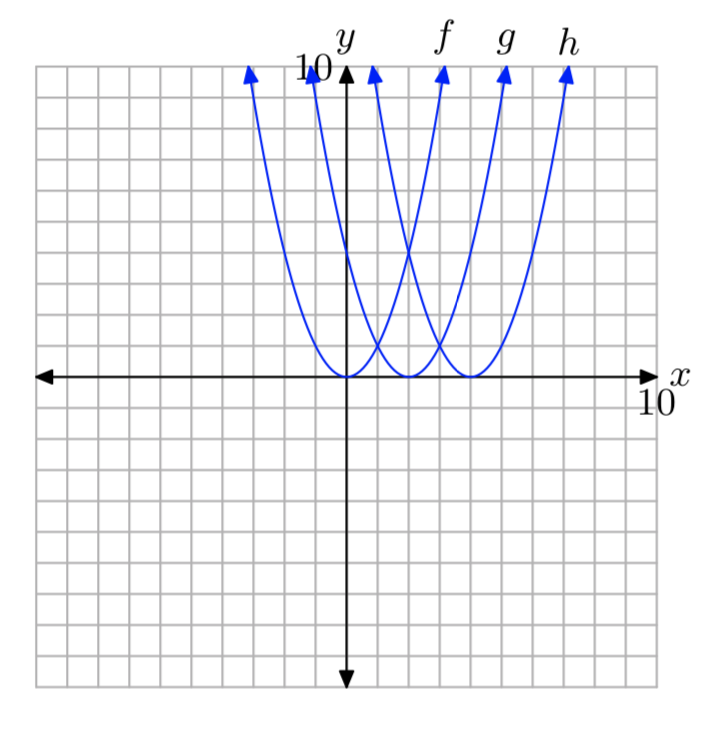
У вправах 55 - 56 використовуйте графік для визначення області функції$f(x) = ax^2+bx+c$. Стрілки на графіку означають, що графік триває нескінченно довго в безперервному шаблоні та напрямку кожної стрілки. Використовуйте інтервальне позначення для опису вашого рішення.

Вправа$\PageIndex{55}$

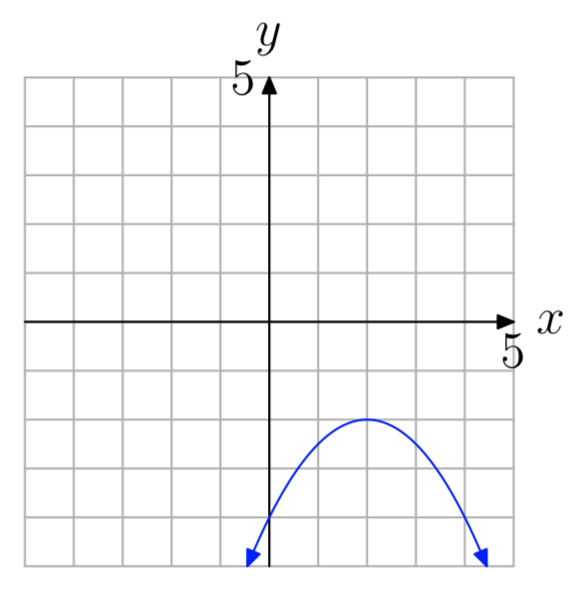
Відповідь

$(−\infty, \infty)$

Вправа$\PageIndex{56}$