3.4: Графік з використанням Y-перехоплення та нахилу
- Page ID
- 58097
Цілі навчання
- Визначте і знайдіть нахил лінії.
- Графік лінії, використовуючи нахил і\(y\) -перехоплення.
Ухил
Крутизну будь-якого ухилу можна виміряти як відношення зміни вертикалі до зміни горизонталі. Наприклад, ухил\(5\)% можна записати як\(\frac{5}{100}\), що означає, що для кожної\(100\) ноги вперед висота\(5\) ноги збільшується.
.png)
Малюнок\(\PageIndex{1}\)
У математиці ми називаємо нахил лінії нахилом і використовуємо букву\(m\) для його позначення. Зміна вертикалі називається підйомом, а зміна горизонталі називається пробігом.
\[\color{Cerulean}{Slope}\quad\color{black}{m=\frac{\text{vertical change}}{\text{horizontal change}}=\frac{rise}{run}}\]
Підйом і біг можуть бути позитивними або негативними. Позитивний підйом відповідає вертикальній зміні вгору, а негативний підйом відповідає вертикальній зміні вниз. Позитивний пробіг позначає зміну горизонталі вправо, а негативний пробіг відповідає горизонтальному зміні вліво. З огляду на графік, ми можемо обчислити нахил, визначивши вертикальні і горизонтальні зміни між будь-якими двома точками.
Приклад\(\PageIndex{1}\)
Знайдіть нахил заданої лінії:
.png)
Малюнок\(\PageIndex{2}\)
Рішення:
З заданих точок на графіку відраховуйте\(3\) одиниці вниз і\(4\) одиниці вправо.
\(m=\frac{rise}{run}=\frac{-3\:\text{units}}{4\:\text{units}}=-\frac{3}{4}\)
Відповідь:
\(m=-\frac{3}{4}\)
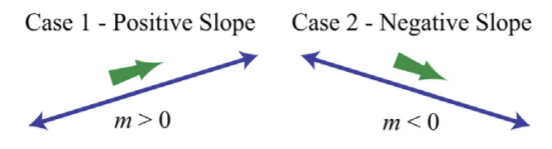
Тут ми маємо негативний нахил, що означає, що для кожної\(4\) одиниці руху вправо зміна вертикалі -\(3\) одиниці вниз. Існує чотири геометричні випадки для значення ухилу.
.png)
Малюнок\(\PageIndex{3}\)
Читаючи графік зліва направо, ми бачимо, що лінії з нахилом вгору мають позитивні нахили, а лінії з ухилом вниз мають негативні нахили.
.png)
Малюнок\(\PageIndex{4}\)
Якщо лінія горизонтальна, то підйом дорівнює\(0\):
\(m=\frac{rise}{run}=\frac{0}{run}=0\)
Ухил горизонтальної лінії - це\(0\). Якщо лінія вертикальна, то прогін такий\(0\):
\(m=\frac{rise}{run}=\frac{rise}{0}\quad\color{Cerulean}{Undefined}\)
Нахил вертикальної лінії невизначений.
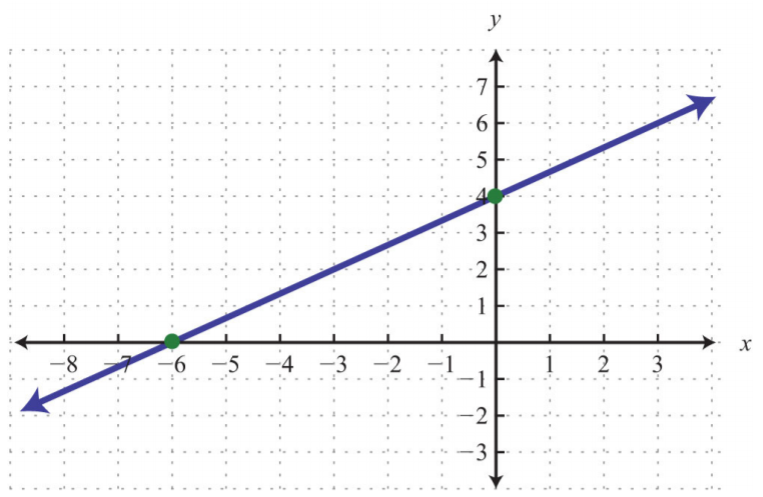
Вправа\(\PageIndex{1}\)
Знайдіть нахил заданої лінії:
.png)
Малюнок\(\PageIndex{5}\)
- Відповідь
-
\(m=\frac{2}{3}\)
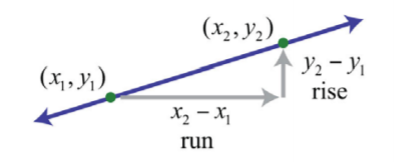
Обчислення нахилу може бути складним, якщо на графіку немає точок з цілочисельними координатами. Тому далі розробляємо формулу, яка дозволяє обчислити ухил алгебраїчно. З огляду на будь-які дві точки\((x_{1}, y_{1})\) і\((x_{2}, y_{2})\), ми можемо отримати підйом і пробіг, віднімаючи відповідні координати.
.png)
Малюнок\(\PageIndex{6}\)
Це призводить нас до формули нахилу. З огляду на будь-які дві точки\((x_{1}, y_{1})\) і\((x_{2}, y_{2})\), нахил задається
\(m=\frac{rise}{run}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Приклад\(\PageIndex{2}\)
Знайти нахил лінії, що проходить через\((−3, −5)\) і\((2, 1)\).
Рішення:
Задано\((−3, −5)\) і\((2, 1)\), обчислити різницю\(y\) -значень, розділених на різницю\(x\) -значень. Оскільки віднімання не є комутативним, подбайте про те, щоб бути послідовним при відніманні координат.
\(\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-3,-5)}&{(2,1)}\end{array}\)
\(\begin{aligned} m&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ &=\frac{1-(-5)}{2-(-3)} \\ &=\frac{1+5}{2+3} \\ &=\frac{6}{5} \end{aligned}\)
Відповідь:
\(m=\frac{6}{5}\)
Ми можемо скласти графік лінії, описану в попередньому прикладі, і перевірити, чи є нахил\(\frac{6}{5}\).
.png)
Малюнок\(\PageIndex{7}\)
Звичайно, графік є необов'язковим; краса формули нахилу полягає в тому, що ми можемо отримати нахил, враховуючи дві точки, використовуючи лише алгебру.
Приклад\(\PageIndex{3}\)
Знайти нахил лінії, що проходить через\((−4, 3)\) і\((−1, −7)\).
Рішення:
\(\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-4,3)}&{(-1,-7)} \end{array}\)
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-7-(3)}{-1-(-4)}=\frac{-7-3}{-1+4}=\frac{-10}{3}\)
Відповідь:
\(m=-\frac{10}{3}\)
Використовуючи формулу нахилу, подбайте про те, щоб бути послідовним, оскільки порядок має значення. Ви повинні відняти координати першої точки з координат другої точки як для чисельника, так і для знаменника в однаковому порядку.
Приклад\(\PageIndex{4}\)
Знайти нахил лінії, що проходить через\((7, −2)\) і\((−5, −2)\).
Рішення:
\(\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(7,-2)}&{(-5,-2)} \end{array}\)
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-(-2)}{-5-(7)}=\frac{-2+2}{-5-7}=\frac{0}{-12}=0\)
Відповідь:
\(m=0\). В якості вправи намітьте задані дві точки і переконайтеся, що вони лежать на горизонтальній лінії.
Приклад\(\PageIndex{5}\)
Знайти нахил лінії, що проходить через\((−4, −3)\) і\((−4, 5)\).
Рішення:
\(\begin{array}{cc}{(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-4,-3)}&{(-4,5)} \end{array}\)
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-(-3)}{-4-(-4)}=\frac{5+3}{-4+4}=\frac{8}{0}\quad\color{Cerulean}{Undefined}\)
Відповідь:
\(m\)Ухил невизначений. В якості вправи намітьте задані дві точки і переконайтеся, що вони лежать на вертикальній лінії.
Вправа\(\PageIndex{2}\)
Обчисліть ухил лінії, що проходить через\((−2, 3)\) і\((5, −5)\).
- Відповідь
-
\(m=-\frac{8}{7}\)
При розгляді ухилу як швидкості зміни важливо включити правильні одиниці.
Приклад\(\PageIndex{6}\)
Corvette Coupe був придбаний новий в 1970 році приблизно за $\(5,200\) і знецінився в ціні з часом, поки він не був проданий в 1985 році за $\(1,300\). У цей момент автомобіль почав вважатися класикою і почав збільшуватися в ціні. У 2000 році, коли автомобілю виповнилося 30 років, його продали на аукціоні за $\(10,450\). Наступний лінійний графік зображує вартість автомобіля з плином часу.
.png)
Малюнок\(\PageIndex{8}\)
- Визначте норму, за якою автомобіль амортизувався в вартості з 1970 по 1985 рік.
- Визначте швидкість, з якою автомобіль цінувався в вартості з 1985 по 2000 рік.
Рішення:
Зверніть увагу, що значення залежить від віку автомобіля і що нахил вимірює ставку в доларах на рік.
а. нахил відрізка лінії, що зображує значення за перші 15 років, дорівнює
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{$1,300-$5,200}{15\text{ years}-0\text{ years}}=\frac{-$3,900}{15\text{ years}}=-$260\text{ per year}\)
б. нахил відрізка лінії, що зображає значення на наступні 15 років, дорівнює
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{$10,450-$1,300}{30\text{ years}-15\text{ years}}=\frac{$9,150}{15\text{ years}}=$610\text{ per year}\)
Відповідь:
- Вартість автомобіля амортизувалася $\(260\) в рік з 1970 по 1985 рік.
- Вартість автомобіля оцінювалася $\(610\) в рік з 1985 по 2000 рік.
Форма перехоплення нахилу лінії
До цього моменту ми навчилися графувати лінії, будуючи точки та використовуючи\(x\) - і\(y\) -перехоплення. Крім того, ми бачили, що нам потрібні лише дві точки для графіка лінії. У цьому розділі ми окреслимо процес легкого визначення двох точок за допомогою\(y\) -перехоплення та нахилу. Рівняння будь-якої невертикальної прямої можна записати у вигляді ухил-перехоплення\(y=mx+b\). У такому вигляді ми можемо визначити нахил\(m\), і\(y\) -перехоплення,\((0, b)\).
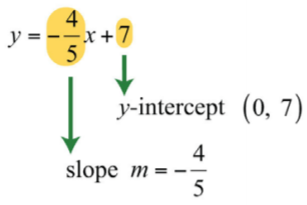
Приклад\(\PageIndex{7}\)
Визначаємо ухил і\(y\) -перехоплення:
\(y=−\frac{4}{5}x+7\).
Рішення:
У такому вигляді коефіцієнт\(x\) - це ухил, а константа\(y\) - значення\(y\) -перехоплення. Тому шляхом огляду ми маємо
.png)
Малюнок\(\PageIndex{9}\)
Відповідь:
\(y\)-Перехоплення є\((0, 7)\), а нахил є\(m=−\frac{4}{5}\).
Не завжди буває так, що лінійне рівняння дається у формі нахилу-перехоплення. Коли він дається в стандартній формі, ви повинні спочатку вирішити,\(y\) щоб отримати схил-перехоплення форми.
Приклад\(\PageIndex{8}\)
\(3x+5y=30\)Висловіть у формі нахилу-перехоплення, а потім визначте нахил і\(y\) -перехоплення.
Рішення:
Почніть з вирішення для\(y\). Для цього застосуйте властивості рівності, щоб спочатку ізолювати,\(5y\) а потім розділити обидві сторони на\(5\).
\(\begin{aligned} 3x+5y&=30 \\ 3x+5y\color{Cerulean}{-3x}&=30\color{Cerulean}{-3x} \\ 5y&=-3x+30 \\ \frac{5y}{\color{Cerulean}{5}}&=\frac{-3x+30}{\color{Cerulean}{5}} \\ y&=\frac{-3x}{5}+\frac{30}{5} \\ y&=-\frac{3}{5}x+6 \end{aligned}\)
Відповідь:
Ухил-перехоплення форма:\(y=−\frac{3}{5}x+6\);\(y\) -перехоплення:\((0, 6)\); нахил:\(m=−\frac{3}{5}\)
Після того, як рівняння знаходиться у формі перехоплення нахилу, ми відразу маємо одну точку для побудови,\(y\) -перехоплення. Від перехоплення можна розмітити ухил, щоб намітити ще одну точку на лінії. З попереднього прикладу ми маємо
\(y=-\frac{3}{5}x+6\)
\(y\)-перехоплення:\((0,6)\)
нахил:\(m=-\frac{3}{5}=\frac{-3}{5}=\frac{rise}{run}\)
Починаючи з точки\((0, 6)\), використовуйте нахил, щоб відзначити іншу точку\(3\) одиниць вниз і\(5\) одиниць вправо.
.png)
Малюнок\(\PageIndex{10}\)
Не потрібно перевіряти, що друга точка, (5, 3), вирішує вихідне лінійне рівняння. Однак ми робимо це тут заради повноти.
\(\begin{aligned} 3x+5y&=30 \\ 3(\color{OliveGreen}{5}\color{black}{)+5(}\color{OliveGreen}{3}\color{black}{)}&=30 \\ 15+15&=30 \\ 30&=30\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Розмітка схилу таким чином виробляє стільки упорядкованих парних рішень, скільки ми хочемо. Зверніть увагу, що якщо ми відзначимо від схилу знову, від точки\((5, 3)\), то отримаємо\(x\) -перехоплення,\((10, 0)\).
Приклад\(\PageIndex{9}\)
Графік:
\(−x+2y=4\).
Рішення:
У цьому прикладі ми окреслимо загальні кроки для побудови графіка лінії за допомогою форми нахилу перехоплення.
Крок 1: Вирішіть\(y\) для отримання форми перехоплення нахилу.
\(\begin{aligned} -x+2y&=4 \\ -x+2y\color{Cerulean}{+x}&=4\color{Cerulean}{+x} \\ 2y&=x+4 \\ \frac{2y}{\color{Cerulean}{2}}&=\frac{x+4}{\color{Cerulean}{2}} \\ y&=\frac{1x}{2}+\frac{4}{2} \\ y&=\frac{1}{2}x+2 \end{aligned}\)
Крок 2: Визначте\(y\) -перехоплення та нахил.
\(y\)-перехоплення:\((0,2)\)
нахил:\(m=\frac{1}{2}=\frac{rise}{run}\)
Крок 3: Побудуйте\(y\) -перехоплення і використовуйте нахил, щоб знайти інше впорядковане рішення пари. Починаючи з\(y\) -перехоплення, відзначте ухил і позначте другу точку. У цьому випадку позначте точку після підйому\(1\) одиниці і пробігу\(2\) одиниць.
.png)
Малюнок\(\PageIndex{11}\)
Крок 4: Проведіть лінію через дві точки прямолінійним краєм.
Відповідь:
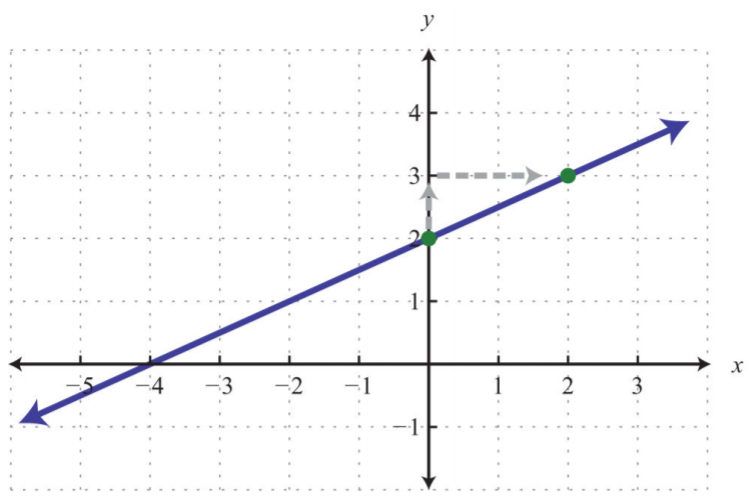.png)
Малюнок\(\PageIndex{12}\)
У цьому прикладі ми помічаємо, що ми могли б отримати\(x\) -intercept, відзначивши схил іншим, але еквівалентним чином. Розглянемо нахил як відношення двох негативних чисел наступним чином:
\(m=\frac{1}{2}=\frac{-1}{-2}=\frac{rise}{run}\)
Ми могли б отримати ще одну точку на лінії, відзначивши еквівалентний нахил вниз\(1\) одиниці і ліві\(2\) одиниці. Робимо це двічі, щоб отримати\(x\) -перехоплення,\((−4, 0)\).
.png)
Малюнок\(\PageIndex{13}\)
Позначення схилу кілька разів не обов'язково завжди дасть нам\(x\) -перехоплення, але коли це відбувається, ми отримуємо цінну точку з невеликими зусиллями. Насправді, гарною практикою є позначення нахилу кілька разів; це дозволяє отримати більше точок на лінії та створити більш точний графік.
Приклад\(\PageIndex{10}\)
Графік і знайдіть\(x\) -перехоплення:
\(y=\frac{3}{4}x−2\).
Рішення:
Рівняння наведено у вигляді ухил-перехоплення. Тому при огляді ми маємо\(y\) -перехоплення і нахил.
\(y\)-перехоплення:\((0,-2)\)
нахил:\(m=\frac{3}{4}=\frac{rise}{run}\)
.png)
Малюнок\(\PageIndex{14}\)
Ми бачимо, що\(x\) -значення\(x\) -intercept є змішаним числом між\(2\) і\(3\). Щоб алгебраїчно знайти\(x\) -перехоплення, нагадаємо, що треба ставити\(y = 0\) і вирішувати для\(x\).
Відповідь:
\(x\)-Перехоплення є\((2\frac{2}{3}, 0)\).
Приклад\(\PageIndex{11}\)
Графік:
\(x−y=0\).
Рішення:
Почніть з вирішення для\(y\).
\(\begin{aligned} x-y&=0\\x-y\color{Cerulean}{-x}&=0\color{Cerulean}{-x} \\ -y&=-x \\ \color{Cerulean}{-1\cdot}\color{black}{(-y)}&=\color{Cerulean}{-1\cdot}\color{black}{(-x)} \\ y&=x \end{aligned}\)
Рівняння\(y=x\) можна записати\(y=1x+0\), і ми маємо
\(y\)-перехоплення:\((0,0)\)
нахил:\(m=1=\frac{1}{1}=\frac{rise}{run}\)
Відповідь:
.png)
Малюнок\(\PageIndex{15}\)
Вправа\(\PageIndex{3}\)
Графік\(−2x+5y=20\) і позначка\(x\) -перехоплення.
- Відповідь
-
.png)
Малюнок\(\PageIndex{16}\)
Ключові винос
- Схил вимірює крутизну лінії як підйом над прогоном. Позитивний підйом позначає зміну вертикалі вгору, а негативний підйом позначає зміну вертикалі вниз. Позитивний пробіг позначає зміну горизонталі вправо, а негативний - горизонтальну зміну вліво.
- Горизонтальні лінії мають ухил в нуль, а вертикальні мають невизначені ухили.
- З огляду на будь-які дві точки на прямій, ми можемо алгебраїчно обчислити нахил, використовуючи формулу нахилу,\(m=\frac{rise}{run}=\frac{y_{2}−y_{1}}{x_{2}−x_{1}}\).
- Будь-яка невертикальна лінія може бути записана у вигляді ухил-перехоплення\(y=mx+b\), по якій ми можемо визначити шляхом огляду нахил\(m\) і\(y\) -перехоплення\((0, b)\).
- Якщо ми знаємо\(y\) -перехоплення і нахил лінії, то ми можемо легко графікувати його. Спочатку сплануйте\(y\) -перехоплення, і з цієї точки використовуйте нахил як підйом над пробігом, щоб відзначити іншу точку на лінії. Нарешті, проведіть лінію через ці дві точки з прямолінійним краєм і додайте стрілку на будь-якому кінці, щоб вказати, що вона триває на невизначений час.
- Ми можемо отримати стільки точок на лінії, скільки хочемо, позначивши схил кілька разів.
Вправа\(\PageIndex{4}\) Slope
Визначте ухил і\(y\) -перехоплення заданого графіка.
1.
.png)
Малюнок\(\PageIndex{17}\)
2.
.png)
Малюнок\(\PageIndex{18}\)
3.
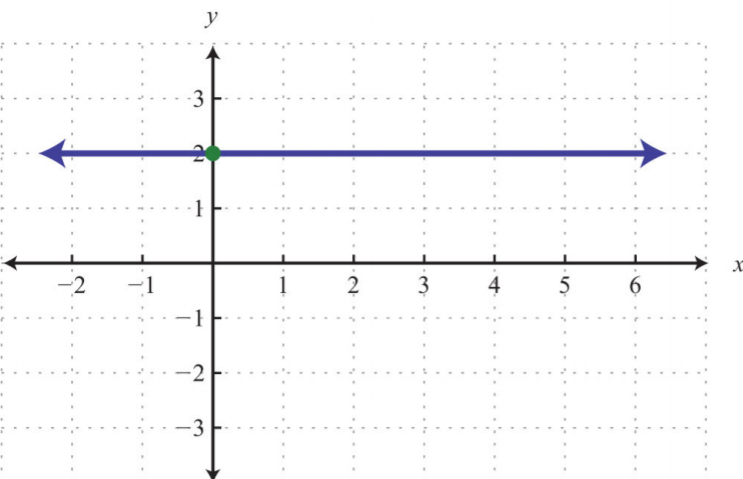.png)
Малюнок\(\PageIndex{19}\)
4.
.png)
Малюнок\(\PageIndex{20}\)
5.
.png)
Малюнок\(\PageIndex{21}\)
6.
.png)
Малюнок\(\PageIndex{22}\)
- Відповідь
-
1. \(y\)-перехоплення:\((0, 3)\); нахил:\(m = −\frac{3}{4}\)
3. \(y\)-перехоплення:\((0, 2)\); нахил:\(m = 0\)
5. \(y\)-перехоплення:\((0, 0)\); нахил:\(m = 2\)
Вправа\(\PageIndex{5}\) Slope
Визначте ухил, враховуючи дві точки.
- \((3, 2)\)і\((5, 1)\)
- \((7, 8)\)і\((−3, 5)\)
- \((2, −3)\)і\((−3, 2)\)
- \((−3, 5)\)і\((7, −5)\)
- \((−1, −6)\)і\((3, 2)\)
- \((5, 3)\)і\((4, 12)\)
- \((−9, 3)\)і\((−6, −5)\)
- \((−22, 4)\)і\((−8, −12)\)
- \((\frac{1}{2}, −\frac{1}{3})\)і\((−\frac{1}{2}, \frac{2}{3})\)
- \((−\frac{3}{4}, \frac{3}{2})\)і\((\frac{1}{4}, −\frac{1}{2})\)
- \((−\frac{1}{3}, \frac{5}{8})\)і\((\frac{1}{2}, −\frac{3}{4})\)
- \((−\frac{3}{5}, −\frac{3}{2})\)і\((\frac{1}{10}, \frac{4}{5})\)
- \((3, −5)\)і\((5, −5)\)
- \((−3, 1)\)і\((−14, 1)\)
- \((−2, 3)\)і\((−2, −4)\)
- \((−4, −4)\)і\((5, 5)\)
- Дах опускає\(4\) ноги на кожну\(12\) ногу вперед. Визначаємо ухил покрівлі.
- Дорога опускає\(300\) ноги на кожну\(5,280\) ногу вперед. Визначаємо ухил дороги.
- Наступний графік дає чисельність населення США осіб віком 65 років і старше. Якими темпами ця чисельність населення збільшувалася з 2000 по 2008 рік?
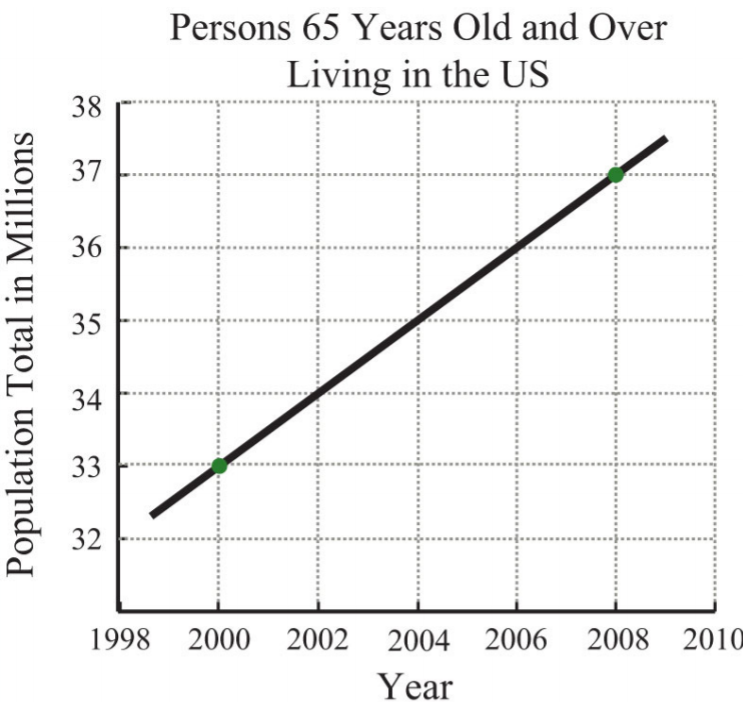.png)
Малюнок\(\PageIndex{23}\): Джерело: Бюро перепису населення США.
20. Наступний графік дає загальний споживчий кредит, непогашений у Сполучених Штатах. Якими темпами зростав споживчий кредит з 2002 по 2008 рік?
.png)
Малюнок\(\PageIndex{24}\): Джерело: Бюро перепису населення США.
21. Комерційний фургон був придбаний новий за $\(20,000\) і, як очікується, буде коштувати $\(4,000\) через 8 років. Визначте швидкість, за якою фургон знецінюється в вартості.
22. Копіювальна машина комерційного класу була придбана нова за $\(4,800\) і буде вважатися нікчемною через 6 років. Визначте швидкість, з якою копіювальний апарат знецінюється в вартості.
23. Знайти,\(y\) якщо нахил лінії, що проходить через\((−2, 3)\) і\((4, y)\) є\(12\).
24. Знайти,\(y\) якщо нахил лінії, що проходить через\((5, y)\) і\((6, −1)\) є\(10\).
25. Знайти,\(y\) якщо нахил лінії, що проходить через\((5, y)\) і\((−4, 2)\) є\(0\).
26. Знайти,\(x\) якщо нахил лінії, що проходить через\((−3, 2)\) і\((x, 5)\) не визначено.
- Відповідь
-
1. \(−\frac{1}{2}\)
3. \(−1\)
5. \(2\)
7. \(−\frac{8}{3}\)
9. \(−1\)
11. \(−\frac{33}{20}\)
13. \(0\)
15. Невизначений
17. \(−\frac{1}{3}\)
19. \(\frac{1}{2}\)млн на рік
21. $\(2,000\) в рік
23. \(75\)
25. \(2\)
Вправа\(\PageIndex{6}\) Slope-Intercept Form
Висловіть задане лінійне рівняння у формі ухил-перехоплення та ідентифікуйте нахил і\(y\) -перехоплення.
- \(6x−5y=30\)
- \(−2x+7y=28\)
- \(9x−y=17\)
- \(x−3y=18\)
- \(2x−3y=0\)
- \(−6x+3y=0\)
- \(\frac{2}{3}x−\frac{5}{4}y=10\)
- \(−\frac{4}{3}x+\frac{1}{5}y=−5\)
- Відповідь
-
1. \(y=\frac{6}{5}x−6\); нахил:\(\frac{6}{5}\);\(y\) -перехоплення:\((0, −6)\)
3. \(y=9x−17\); нахил:\(9\);\(y\) -перехоплення:\((0, −17)\)
5. \(y=\frac{2}{3}x\); нахил:\(\frac{2}{3}\);\(y\) -перехоплення:\((0, 0)\)
7. \(y=\frac{8}{15}x−8\); нахил:\(\frac{8}{15}\);\(y\) -перехоплення:\((0, −8)\)
Вправа\(\PageIndex{7}\) Slope-Intercept Form
Графік лінії з урахуванням нахилу і\(y\) -перехоплення.
- \(m=\frac{1}{3}\)і\((0, −2)\)
- \(m=−\frac{2}{3}\)і\((0, 4)\)
- \(m=3\)і\((0, 1)\)
- \(m=−2\)і\((0, −1)\)
- \(m=0\)і\((0, 5)\)
- \(m\)невизначені і\((0, 0)\)
- \(m=1\)і\((0, 0)\)
- \(m=−1\)і\((0, 0)\)
- \(m=−\frac{15}{3}\)і\((0, 20)\)
- \(m=−10\)і\((0, −5)\)
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{25}\)
3.
.png)
Малюнок\(\PageIndex{26}\)
5.
.png)
Малюнок\(\PageIndex{27}\)
7.
.png)
Малюнок\(\PageIndex{28}\)
9.
.png)
Малюнок\(\PageIndex{29}\)
Вправа\(\PageIndex{8}\) Slope-Intercept Form
Графік з використанням нахилу і\(y\) -перехоплення.
- \(y=\frac{2}{3}x−2\)
- \(y=−\frac{1}{3}x+1\)
- \(y=−3x+6\)
- \(y=3x+1\)
- \(y=\frac{3}{5}x\)
- \(y=−\frac{3}{7}x\)
- \(y=−8\)
- \(y=7\)
- \(y=−x+2\)
- \(y=x+1\)
- \(y=\frac{1}{2}x+\frac{3}{2}\)
- \(y=−\frac{3}{4}x+\frac{5}{2}\)
- \(4x+y=7\)
- \(3x−y=5\)
- \(5x−2y=10\)
- \(−2x+3y=18\)
- \(x−y=0\)
- \(x+y=0\)
- \(\frac{1}{2}x−\frac{1}{3}y=1\)
- \(−\frac{2}{3}x+\frac{1}{2}y=2\)
- \(3x+2y=1\)
- \(5x+3y=1\)
- На одному і тому ж наборі осей намалюйте три лінії, де\(y=\frac{3}{2}x+b\) і\(b = \{−2, 0, 2\}\).
- На одному і тому ж наборі осей намалюйте три лінії, де\(y=mx+1\) і\(m = \{−\frac{1}{2}, 0, \frac{1}{2}\}\).
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{30}\)
3.
.png)
Малюнок\(\PageIndex{31}\)
5.
.png)
Малюнок\(\PageIndex{32}\)
7.
.png)
Малюнок\(\PageIndex{33}\)
9.
.png)
Малюнок\(\PageIndex{34}\)
11.
.png)
Малюнок\(\PageIndex{35}\)
13.
.png)
Малюнок\(\PageIndex{36}\)
15.
.png)
Малюнок\(\PageIndex{37}\)
17.
.png)
Малюнок\(\PageIndex{38}\)
19.
.png)
Малюнок\(\PageIndex{39}\)
21.
.png)
Малюнок\(\PageIndex{40}\)
23.
.png)
Малюнок\(\PageIndex{41}\)
Вправа\(\PageIndex{9}\) Discussion Board Topics
- Назвіть три методи графічних ліній. Обговоріть плюси і мінуси кожного методу.
- Виберіть лінійне рівняння і намалюйте його трьома різними способами. Відскануйте роботу та поділіться нею на дошці обговорень.
- Чому ми використовуємо букву m для нахилу?
- Чим корисні еквівалентні фракції при роботі з укосами?
- Чи можемо ми графувати лінію, знаючи лише її нахил?
- Дослідіть та обговоріть альтернативні позначення для нахилу:\(m=\frac{Δy}{Δx}\).
- Які стратегії графічних ліній слід довести до іспиту? Поясніть
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
5. Відповіді можуть відрізнятися
7. Відповіді можуть відрізнятися
