2.7: Глава 2 Вправи з рішеннями

2.1 Вправи

У Вправи$\PageIndex{1}$ -$\PageIndex{6}$ вкажіть область і діапазон заданого відношення.

Вправа$\PageIndex{1}$

R = {(1, 3), (2, 4), (3, 4)}

Відповідь

Домен - це набір всіх перших координат = {1, 2, 3}. Діапазон - це набір всіх других координат {3, 4} (зауважте, що в наборі ви не перераховуєте об'єкт двічі, тому ми перерахуємо лише 4 рази).

Вправа$\PageIndex{2}$

R = {(1, 3), (2, 4), (2, 5)}

Вправа$\PageIndex{3}$

R = {(1, 4), (2, 5), (2, 6)}

Відповідь

Домен - це набір всіх перших координат = {1, 2} (зверніть увагу, що в наборі ви не перераховуєте об'єкт двічі, тому ми перерахуємо лише 2 рази). Діапазон - це набір всіх других координат {4, 5, 6}.

Вправа$\PageIndex{4}$

R = {(1, 5), (2, 4), (3, 6)}

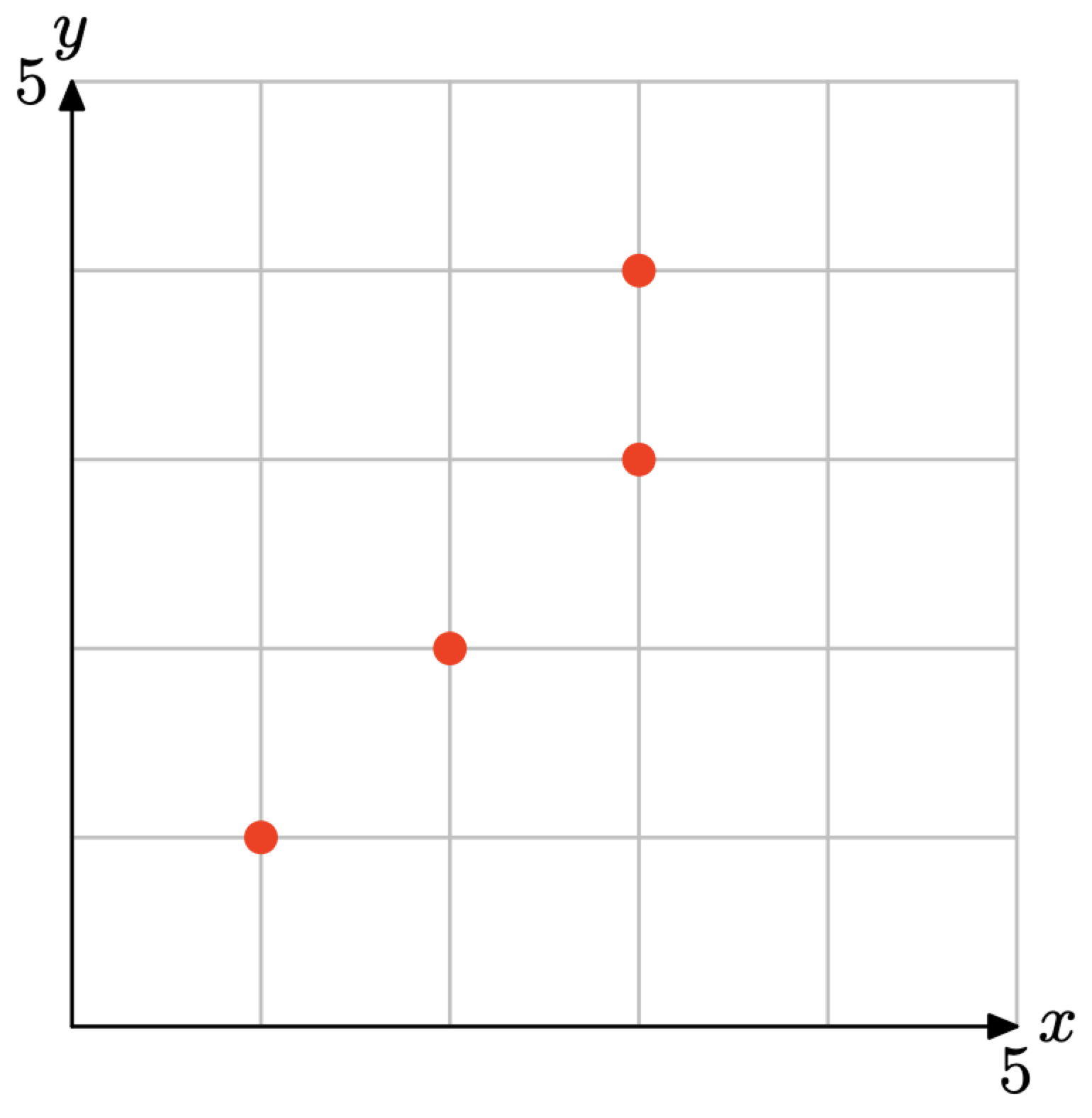
Вправа$\PageIndex{5}$

Відповідь

Прочитайте координату x кожної точки, щоб отримати, що домен є {1, 2, 3}. Потім зчитуйте y-координати, щоб отримати, що діапазон дорівнює {1, 2, 3, 4}

Вправа$\PageIndex{6}$

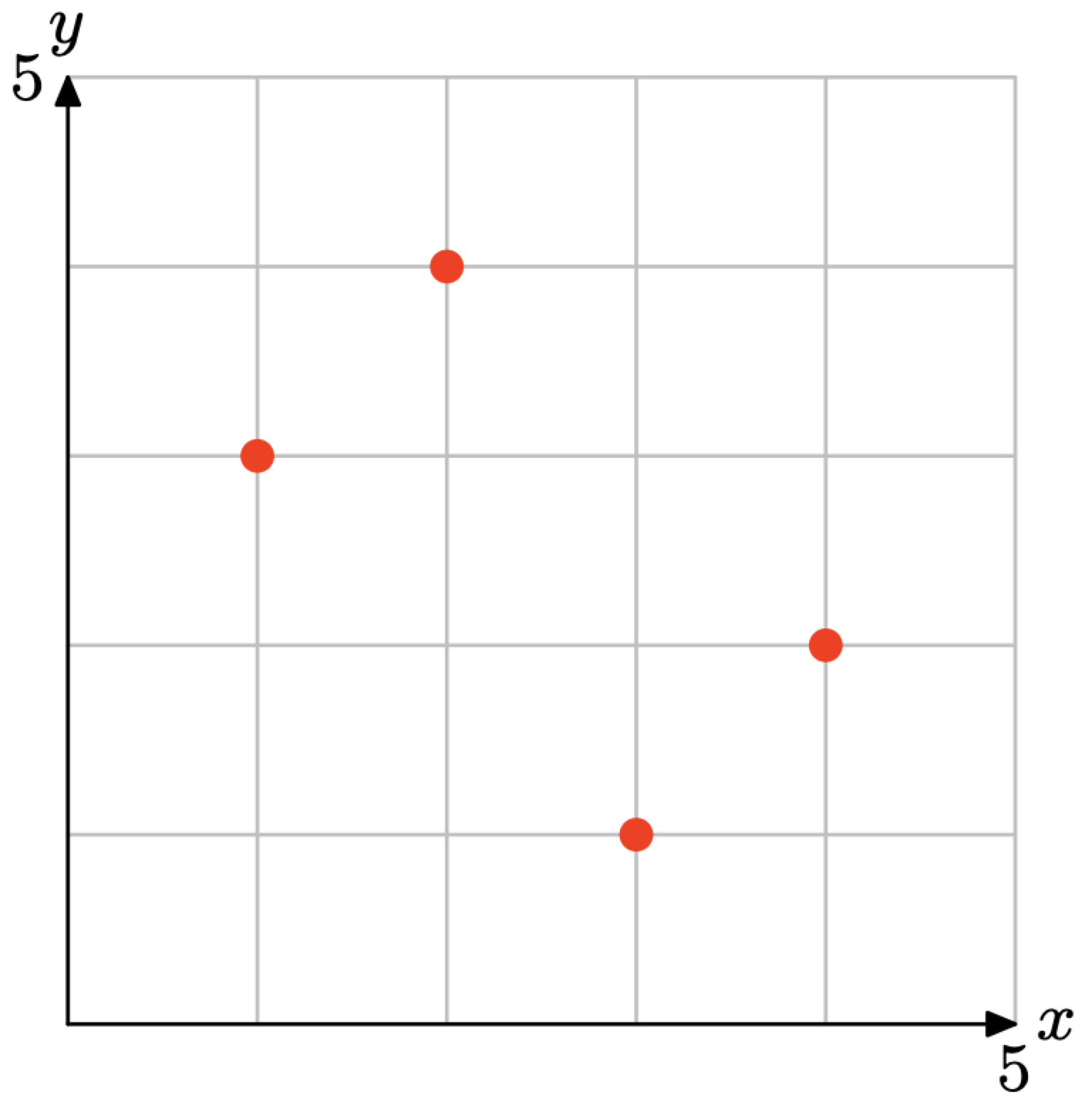
У Вправи$\PageIndex{7}$ -$\PageIndex{12}$ створіть діаграму відображення для заданого відношення та вкажіть, чи є вона функцією чи ні.

Вправа$\PageIndex{7}$

Ставлення у вправах$\PageIndex{1}$.

Відповідь

Створіть діаграму відображення для R.

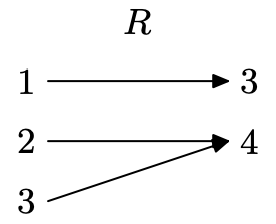
Оскільки жодне значення домену не поєднується з двома значеннями діапазону, це функція (кожен х відповідає одному y). Зауважте, що наявність двох різних значень домену переходить до одного значення діапазону (2 і 3 обидва відображаються на 4) допустимо для функції.

Вправа$\PageIndex{8}$

Ставлення у вправах$\PageIndex{2}$.

Вправа$\PageIndex{9}$

Ставлення у вправах$\PageIndex{3}$.

Відповідь

Створіть діаграму відображення для R.

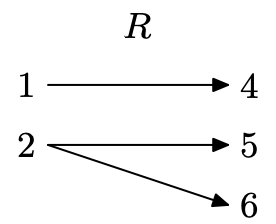
Число 2 зіставляється з двома різними значеннями діапазону (один х відповідає двом y), тому це не функція.

Вправа$\PageIndex{10}$

Ставлення у вправах$\PageIndex{4}$.

Вправа$\PageIndex{11}$

Ставлення у вправах$\PageIndex{5}$.

Відповідь

Створіть діаграму відображення для R.

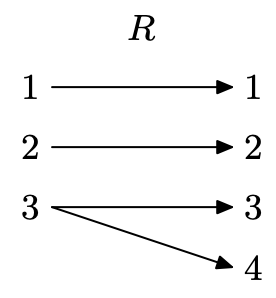
Число 3 зіставляється з двома різними значеннями діапазону (один х відповідає двом y), тому це не функція.

Вправа$\PageIndex{12}$

Ставлення у вправах$\PageIndex{6}$.

Вправа$\PageIndex{13}$

Враховуючи, що g приймає дійсне число і подвоює його, то$g : x \rightarrow ?$.

Відповідь

Подвійний означає «множиться на 2», отже$g : x \rightarrow 2x$.

Вправа$\PageIndex{14}$

З огляду на, що f приймає дійсне число і ділить його на 3, то$f : x \rightarrow ?$.

Вправа$\PageIndex{15}$

З огляду на, що g приймає дійсне число і додає до нього 3, то$g : x \rightarrow ?$.

Відповідь

$g : x \rightarrow x + 3$

Вправа$\PageIndex{16}$

З огляду на, що h приймає дійсне число і віднімає з нього 4, то$h : x \rightarrow ?$.

Вправа$\PageIndex{17}$

З огляду на, що g приймає дійсне число, подвоює його, потім додає 5, потім$g : x \rightarrow ?$

Відповідь

Для х покласти в g, g подвоює його, даючи 2x, а потім додає п'ять, в результаті чого 2x + 5. Тому,$g : x \rightarrow 2x + 5$

Вправа$\PageIndex{18}$

З огляду на, що h приймає дійсне число, віднімає з нього 3, потім ділить результат на 4, потім$h : x \rightarrow ?$

Враховуючи, що функція f визначається правилом$h : x \rightarrow 3x − 5$, визначте, де відображено вхідне число у Вправи$\PageIndex{19}$ -$\PageIndex{22}$.

Вправа$\PageIndex{19}$

$f : 3 \rightarrow ?$

Відповідь

Поставити 3 в f Це означає, замініть x на 3 і обчислити вихід. $f : 3 \rightarrow 3(3) − 5 = 4$, Отже$f : 3 \rightarrow 4$.

Вправа$\PageIndex{20}$

$f : -5 \rightarrow ?$

Вправа$\PageIndex{21}$

$f : a \rightarrow ?$

Відповідь

Покладіть a в f, так само, як ви б число. Це означає, замініть x на a і обчислити вихід. $f : a \rightarrow 3(a) − 5 = 3a − 5$, Отже$f : 3 \rightarrow 3a − 5$.

Вправа$\PageIndex{22}$

$f : 2a+3 \rightarrow ?$

Враховуючи, що функція f визначається правилом$f : x \rightarrow 4-5x$, визначте, де відображено вхідне число у Вправи$\PageIndex{23}$ -$\PageIndex{26}$.

Вправа$\PageIndex{23}$

$f : 2 \rightarrow ?$

Відповідь

Помістіть 2 в f, замінивши x на нього. $f : 2 \rightarrow 4 − 5(2) = −6$, Отже$f : 2 \rightarrow −6$.

Вправа$\PageIndex{24}$

$f : -3 \rightarrow ?$

Вправа$\PageIndex{25}$

$f : a \rightarrow ?$

Відповідь

Помістіть a в f, замінивши x з ним, так само, як і з числом. $f : a \rightarrow 4 − 5(a)$, Отже$f : 2 \rightarrow 4 − 5a$.

Вправа$\PageIndex{26}$

$f : 2a+11 \rightarrow ?$

Враховуючи, що функція f визначається правилом$f : x \rightarrow x^{2}-4x-6$, визначте, де відображено вхідне число у Вправи$\PageIndex{27}$ -$\PageIndex{30}$.

Вправа$\PageIndex{27}$

$f : 1 \rightarrow ?$

Відповідь

Помістіть 1 в f, замінивши x на нього. $f : 1 \rightarrow (1)2 − 4(1) − 6 = 1 − 4 − 6 = −9$, Отже$f : 1 \rightarrow −9$.

Вправа$\PageIndex{28}$

$f : -2 \rightarrow ?$

Вправа$\PageIndex{29}$

$f : -1 \rightarrow ?$

Відповідь

Помістіть −1 у f, замінивши x на нього. $f : −1 \rightarrow (−1)2 −4(−1)−6 = 1+4−6 = −1$, Отже$f : 1 \rightarrow −1$.

Вправа$\PageIndex{30}$

$f : a \rightarrow ?$

Враховуючи, що функція f визначається правилом$f : x \rightarrow 3x-9$, визначте, де відображено вхідне число у Вправи$\PageIndex{31}$ -$\PageIndex{34}$.

Вправа$\PageIndex{31}$

$f : a \rightarrow ?$

Відповідь

Помістіть a в f, замінивши x з ним, так само, як і з числом. $f : a \rightarrow 3a − 9$.

Вправа$\PageIndex{32}$

$f : a+1 \rightarrow ?$

Вправа$\PageIndex{33}$

$f : 2a-5 \rightarrow ?$

Відповідь

Помістіть 2a − 5 у f, замінивши x на нього, так само, як і з числом. Отримуємо$f : 2a − 5 \rightarrow 3(2a − 5) − 9 = 6a − 15 − 9 = 6a − 24$, так$f : 2a − 5 \rightarrow 6a − 24$

Вправа$\PageIndex{34}$

$f : a+h \rightarrow ?$

Враховуючи, що функції f і g визначаються правилами$f : x \rightarrow 2x+3$ і$g : x \rightarrow 4-x$, визначають, де буде відображено вхідне число в Вправи$\PageIndex{35}$ -$\PageIndex{38}$.

Вправа$\PageIndex{35}$

$f : 2 \rightarrow ?$

Відповідь

Покладіть 2 в f, замінивши x на нього. Отримуємо$f : 2 \rightarrow 2(2)+3 = 7$, значить$f : 2 \rightarrow 7$.

Вправа$\PageIndex{36}$

$f : 2 \rightarrow ?$

Вправа$\PageIndex{37}$

$f : a+1 \rightarrow ?$

Відповідь

Покладіть + 1 в f, замінивши x з ним, так само, як і з числом. Отримуємо$f : a + 1 \rightarrow 2(a + 1) + 3 = 2a + 2 + 3 = 2a + 5$, так$f : a + 1 \rightarrow 2a + 5$

Вправа$\PageIndex{38}$

$f : a-3 \rightarrow ?$

Вправа$\PageIndex{39}$

Враховуючи, що g приймає дійсне число і потроює його, то g (x) =?.

Відповідь

Трійки означає «множиться на 3», тому g (x) = 3x

Вправа$\PageIndex{40}$

Враховуючи, що f приймає дійсне число і ділить його на 5, то f (x) =?.

Вправа$\PageIndex{41}$

З огляду на, що g приймає дійсне число і віднімає його з 10, то g (x) =?.

Відповідь

g приймає вхідний x і віднімає його З 10, тому g (x) = 10 − x.

Вправа$\PageIndex{42}$

З огляду на, що f приймає дійсне число, множить його на 5 і потім додає 4 до результату, то f (x) =?.

Вправа$\PageIndex{43}$

З огляду на, що f приймає дійсне число, подвоює його, потім віднімає результат з 11, потім f (x) =?.

Відповідь

f приймає вхід x, подвоює його, щоб отримати 2x, і забирає це від 11, отримуючи 11 − 2x. Отже, f (x) = 11 − 2x.

Вправа$\PageIndex{44}$

З огляду на, що h приймає дійсне число, подвоює його, додає 5, потім приймає квадратний корінь результату, потім h (x) =?.

У Вправи$\PageIndex{45}$ -$\PageIndex{54}$ оцініть задану функцію за заданим значенням b.

Вправа$\PageIndex{45}$

f (х) = 12х + 2 для б = 6.

Відповідь

Підставляємо 6 на х в 12х + 2 і спрощуємо, щоб отримати 74: f (6) = 12 (6) + 2 = 74.

Вправа$\PageIndex{46}$

f (x) = −11x − 4 для b = −3.

Вправа$\PageIndex{47}$

f (x) = −9x − 1 для b = −5.

Відповідь

Замініть −5 на x у −9x−1 та спростіть отримання 44: f (−5) = −9 (−5) −1 = 44.

Вправа$\PageIndex{48}$

f (х) = 11х+ 4 для b = −4.

Вправа$\PageIndex{49}$

f (x) = 4 для b = −12.

Відповідь

f є постійною функцією, тому f (x) = 4 для всіх x, отже, f (−12) = 4.

Вправа$\PageIndex{50}$

f (x) = 7 для b = −7.

Вправа$\PageIndex{51}$

f (x) = 0 для b = −7.

Відповідь

f є постійною функцією, тому f (x) = 0 для всіх x, отже, f (−7) = 0.

Вправа$\PageIndex{52}$

f (х) = 12х+ 8 для b = −3.

Вправа$\PageIndex{53}$

f (x) = −9x + 3 для b = −1.

Відповідь

Заставити −1 на x у −9x+3 та спростити отримання 12: f (−1) = −9 (−1) +3 = 12

Вправа$\PageIndex{54}$

f (x) = 6x − 3 для b = 3.

У Вправи$\PageIndex{55}$ -$\PageIndex{58}$, враховуючи, що функція f визначається правилом f (x) = 2x+ 7, визначаємо, де відображено вхідне число.

Вправа$\PageIndex{55}$

f (а) =?

Відповідь

Помістіть a в f, замінивши x з ним, так само, як і з числом. Це дає f (a) = 2a + 7.

Вправа$\PageIndex{56}$

f (а + 1) =?

Вправа$\PageIndex{57}$

f (3а − 2) =?

Відповідь

Помістіть 3a − 2 у f, замінивши x на нього, так само, як і з числом. Це дає f (3a − 2) = 2 (3a − 2) + 7 = 6a − 4 + 7 = 6а+ 3.

Вправа$\PageIndex{58}$

f (а + ч) =?

У Вправи$\PageIndex{59}$ -$\PageIndex{62}$, враховуючи, що функція g визначається правилом g (x) = 3 − 2x, визначаємо, де відображено вхідне число.

Вправа$\PageIndex{59}$

г (а) =?

Відповідь

Помістіть a в g, замінивши x з ним, так само, як і з числом. Це дає g (a) = 3 − 2a.

Вправа$\PageIndex{60}$

г (а + 3) =?

Вправа$\PageIndex{61}$

g (2 − 5а) =?

Відповідь

Помістіть 2 − 5a у g, замінивши x на нього, так само, як і з числом. Це дає g (2 − 5a) = 3 − 2 (2 − 5a) = 3 − 4 + 10a = −1 + 10a або 10a − 1.

Вправа$\PageIndex{62}$

г (а + ч) =?

Враховуючи, що функції f та g визначаються правилами f (x) = 1 − x та g (x) = 2x + 13, визначте, де буде відображено вхідне число у Вправи$\PageIndex{63}$ -$\PageIndex{66}$.

Вправа$\PageIndex{63}$

f (а) =?

Відповідь

Помістіть a в f, замінивши x з ним, так само, як і з числом. Це дає f (a) = 1 − a.

Вправа$\PageIndex{64}$

г (а) =?

Вправа$\PageIndex{65}$

f (а + 3) =?

Відповідь

Покладіть + 3 в f, замінивши x з ним, так само, як і з числом. Це дає f (a + 3) = 1 − (a + 3) = 1 − a − 3 = −a − 2.

Вправа$\PageIndex{66}$

g (4 − а) =?

Враховуючи, що функції f та g визначаються правилами f (x) = 3x + 4 та g (x) = 2x−5, визначте, де буде відображено вхідне число у Вправи$\PageIndex{67}$ -$\PageIndex{70}$.

Вправа$\PageIndex{67}$

f (г (2)) =?

Відповідь

Спочатку обчислити g (2) = 2 (2) − 5 = −1. Це означає, що f (g (2)) насправді є f (−1). Включивши −1 in для x до функції f, отримаємо f (g (2)) = f (−1) = 3 (−1) + 4 = −3 + 4 = 1.

Вправа$\PageIndex{68}$

г (ф (2)) =?

Вправа$\PageIndex{69}$

f (г (а)) =?

Відповідь

Спочатку обчислити g (a) = 2a−5. Це означає, що f (g (a)) насправді є f (2a−5). Підключивши 2a − 5 in для x до функції f, отримаємо f (g (a)) = f (2a − 5) = 3 (2a − 5) + 4 = 6a − 15 + 4 = 6a − 11.

Вправа$\PageIndex{70}$

г (ф (а)) =?

Враховуючи, що функції f та g визначаються правилами f (x) = 2x − 9 та g (x) = 11, визначте, де буде відображено вхідне число у Вправи$\PageIndex{71}$ -$\PageIndex{74}$.

Вправа$\PageIndex{71}$

f (г (2)) =?

Відповідь

Спочатку обчислити g (2) = 11 (зверніть увагу, що, незалежно від того, що ви ставите в g, він виводить 11). Це означає, що f (g (2)) дійсно f (11). Включивши 11 in для x у функцію f, отримаємо f (g (2)) = f (11) = 2 (11) − 9 = 22 − 9 = 13.

Вправа$\PageIndex{72}$

г (ф (2)) =?

Вправа$\PageIndex{73}$

f (г (а)) =?

Відповідь

Спочатку обчислити g (a) = 11 (зверніть увагу, що, незалежно від того, що ви ставите в g, він виводить 11). Це означає, що f (g (a)) дійсно f (11). Включивши 11 in для x у функцію f, отримаємо f (g (2)) = f (11) = 2 (11) − 9 = 22 − 9 = 13.

Вправа$\PageIndex{74}$

г (ф (а)) =?

Використовуйте нотацію set-builder для опису області кожної з функцій, визначених у Вправи$\PageIndex{75}$ -$\PageIndex{78}$.

Вправа$\PageIndex{75}$

$f(x) = \dfrac{93}{x+98}$

Відповідь

Вхідне значення x = −98 призведе до поділу на нуль, отже −98 не знаходиться у домені. Всі інші можливі входи дійсні. Домен, в позначеннях set-builder, є$\{x : x \neq −98\}$.

Вправа$\PageIndex{76}$

$f(x) = \dfrac{54}{x+65}$

Вправа$\PageIndex{77}$

$f(x) = -\dfrac{87}{x-88}$

Відповідь

Вхід х = 88 призведе до поділу на нуль, тому 88 не знаходиться в області. Всі інші можливі входи дійсні. Домен, в позначеннях set-builder, є$\{x : x \neq 88\}$..

Вправа$\PageIndex{78}$

$f(x) = -\dfrac{30}{x-52}$

Використовуйте set-builder та інтервальні позначення для опису області функцій, визначених у Вправи$\PageIndex{79}$ -$\PageIndex{82}$.

Вправа$\PageIndex{79}$

$f(x) = \sqrt{x+69}$

Відповідь

Квадратний корінь від'ємного числа не визначається як дійсне число. Таким чином, x + 69 повинен бути більше або дорівнює нулю. Потім$x + 69 geq 0$ має на увазі$x \geq −69$, що, таким чином, домен є інтервалом$[−69,\infty)$, або в позначенні set-builder,$\{x : x \geq −69\}$.

Вправа$\PageIndex{80}$

$f(x) = \sqrt{x+62}$

Вправа$\PageIndex{81}$

$f(x) = \sqrt{x-81}$

Відповідь

Квадратний корінь від'ємного числа не визначається як дійсне число. Таким чином, x − 81 має бути більшим або рівним нулю. Потім$x − 81 \geq 0$ має на увазі$x \geq 81$, що, таким чином, домен є інтервалом$[81,\infty)$, або в позначенні set-builder,$\{x : x \geq 81\}$.

Вправа$\PageIndex{82}$

$f(x) = \sqrt{x-98}$

Кажуть, що два цілих числа є відносно простими, якщо їх найбільший спільний дільник дорівнює 1. Наприклад, найбільший спільний дільник 6 і 35 дорівнює 1, тому 6 і 35 є відносно простими. З іншого боку, найбільший спільний дільник 14 і 21 не 1 (це 7), тому 14 і 21 не є відносно простими. $\phi$Функція Ейлера визначається наступним чином:

• Якщо n = 1, то$\phi (n) = 1$.

• Якщо n > 1,$\phi (n)$ то число натуральних чисел менше n$\PageIndex{84}$, які є відносно$\phi$ простими до n.$\PageIndex{83}$

Вправа$\PageIndex{83}$

$\phi (12)$

Відповідь

1, 5, 7 і 11 менше 12 і кожен відносно прості до 12. Тому,$\phi(12) = 4$.

Вправа$\PageIndex{84}$

$\phi (36)$

2.2 Вправи

Виконайте кожне з наступних завдань для функцій, визначених рівняннями в Вправи$\PageIndex{1}$ -$\PageIndex{8}$.

i. встановити таблицю точок, які задовольняють заданому рівнянню. Будь ласка, розмістіть цю таблицю точок поруч із графіком на графічному папері.

II. Налаштуйте систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь, а потім нанесіть кожну точку з таблиці на вашій системі координат.

iii. Якщо ви впевнені, що «бачите» форму графіка, зробіть «стрибок віри» і побудуйте всі пари, які задовольняють заданому рівнянню, намалювавши плавну криву (від руки) на вашій системі координат, яка містить всі раніше побудовані точки (використовуйте лінійку, лише якщо графік рівняння є лінією). Якщо ви не впевнені, що «бачите» форму графіка, додайте більше точок до вашої таблиці, побудуйте їх на вашій системі координат і подивіться, чи допомагає це. Продовжуйте цей процес, поки ви «не побачите» форму графіка і не зможете заповнити решту точок, які задовольняють рівнянню, намалювавши плавну криву (або лінію) у вашій системі координат.

Вправа$\PageIndex{1}$

$f(x) = 2x + 1$

Відповідь

Оцінити функцію$f(x) = 2x + 1$ за значеннями −2, −1, 0 та 1.

$$\begin{array} {ccc} f(−2) &=& 2(−2) + 1 &=& −3 \\ f(−1) & = &2(−1) + 1 &=& −1 \\ f(0) &=& 2(0) + 1 &=& 1 \\ f(1) &=& 2(1) + 1 &=& 3 \end{array}$$

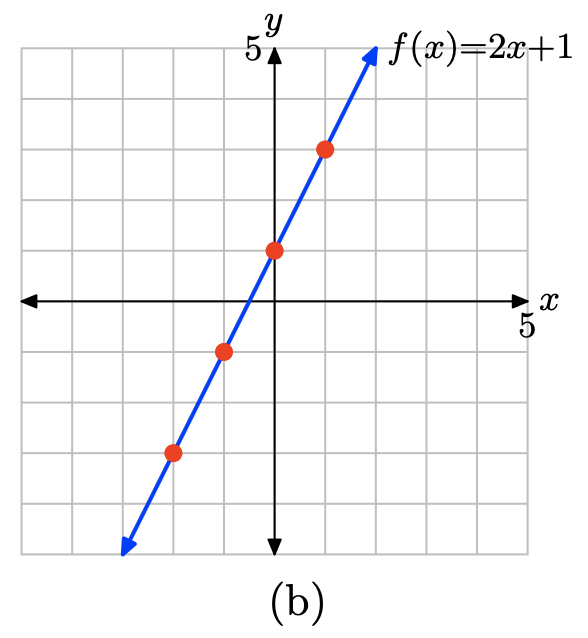
Помістіть ці результати в таблицю (a) і побудуйте їх так, як показано в (b). Тут достатньо доказів, щоб зрозуміти, що графік f - це лінія, показана в (b).

х	$f(x) = 2x + 1$	(х, ф (х))
-2	\ (f (x) = 2х + 1\) ">-3	(−2, −3)
-1	\ (ф (х) = 2х + 1\) ">-1	(−1, −1)
0	\ (f (x) = 2х + 1\) ">1	(0,1)
1	\ (ф (х) = 2х + 1\) ">3	(1,3)

(а)

Вправа$\PageIndex{2}$

$f(x) = 1 − x$

Вправа$\PageIndex{3}$

$f(x) = 3 − \dfrac{1}{2} x$

Відповідь

Оцініть функцію f (x) = 3 − (1/2) x при x = −2, 0, 2 та 4.

$$f(−2) = 3 − (1/2)(−2) = 4 \\ f(0) = 3 − (1/2)(0) = 3 \\ f(2) = 3 − (1/2)(2) = 2 \\ f(4) = 3 − (1/2)(4) = 1$$

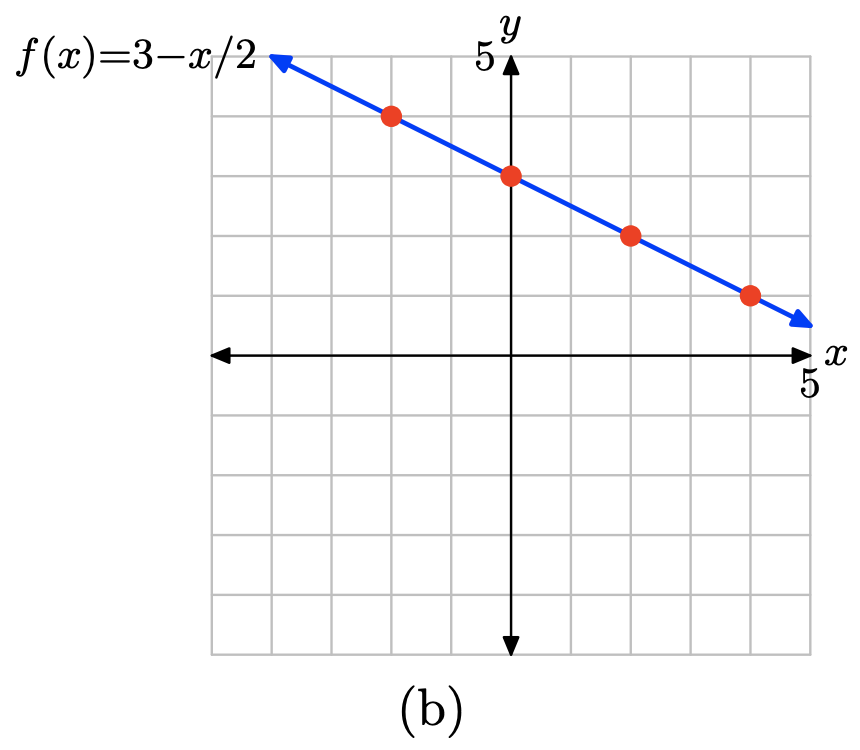
Помістіть ці результати в таблицю (a) і побудуйте їх так, як показано в (b). Тут достатньо доказів, щоб зрозуміти, що графік f - це лінія, показана в (b).

х	$f(x) = 3 - x/2$	(х, ф (х))
-2	\ (f (x) = 3 - х/2\) ">4	(−2, 4)
0	\ (f (x) = 3 - х/2\) ">3	(0,3)
2	\ (f (x) = 3 - х/2\) ">2	(2,2)
4	\ (f (x) = 3 - х/2\) ">1	(4,1)

(а)

Вправа$\PageIndex{4}$

$f(x) = −1 + \dfrac{1}{2}x$

Вправа$\PageIndex{5}$

$f(x) = x^2 − 2$

Відповідь

Оцінити$f(x) = x^2 − 2$ за x = −3, −2, −1, 0, 1, 2 та 3.

$$f(−3) = (−3)^2 − 2 = 7 \\ f(−2) = (−2)^2 − 2 = 2 \\ f(−1) = (−1)^2 − 2 = −1 \\ f(0) = (0)^2 − 2 = −2 \\ f(1) = (1)^2 − 2 = −1 \\ f(2) = (2)^2 − 2 = 2 \\ f(3) = (3)^2 − 2 = 7$$

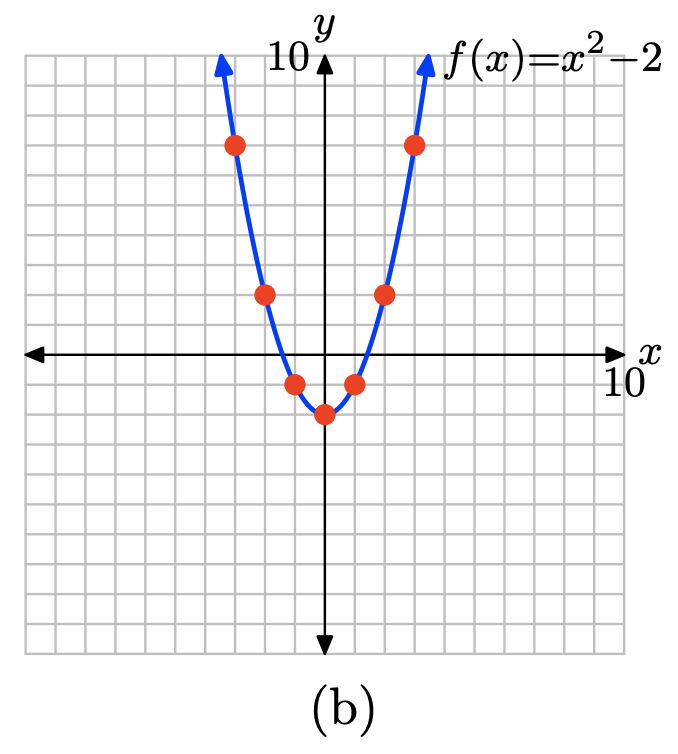
Помістіть ці результати в таблицю (a) і побудуйте їх так, як показано в (b). Тут достатньо доказів, щоб зрозуміти, що графік f - це крива, показана в (b).

х	$f(x) = x^2 − 2$	(х, ф (х))
-3	\ (f (x) = x^2 − 2\) ">7	(−3, 7)
-2	\ (f (x) = x^2 − 2\) ">2	(-2,2)
-1	\ (f (x) = x^2 − 2\) ">-1	(-1, -1)
0	\ (f (x) = x^2 − 2\) ">-2	(0, -2)
1	\ (f (x) = x^2 − 2\) ">-1	(1, -1)
2	\ (f (x) = x^2 − 2\) ">2	(2,2)
3	\ (f (x) = x^2 − 2\) ">7	(3,7)

(а)

Вправа$\PageIndex{6}$

$f(x) = 4 − x^{2}$

Вправа$\PageIndex{7}$

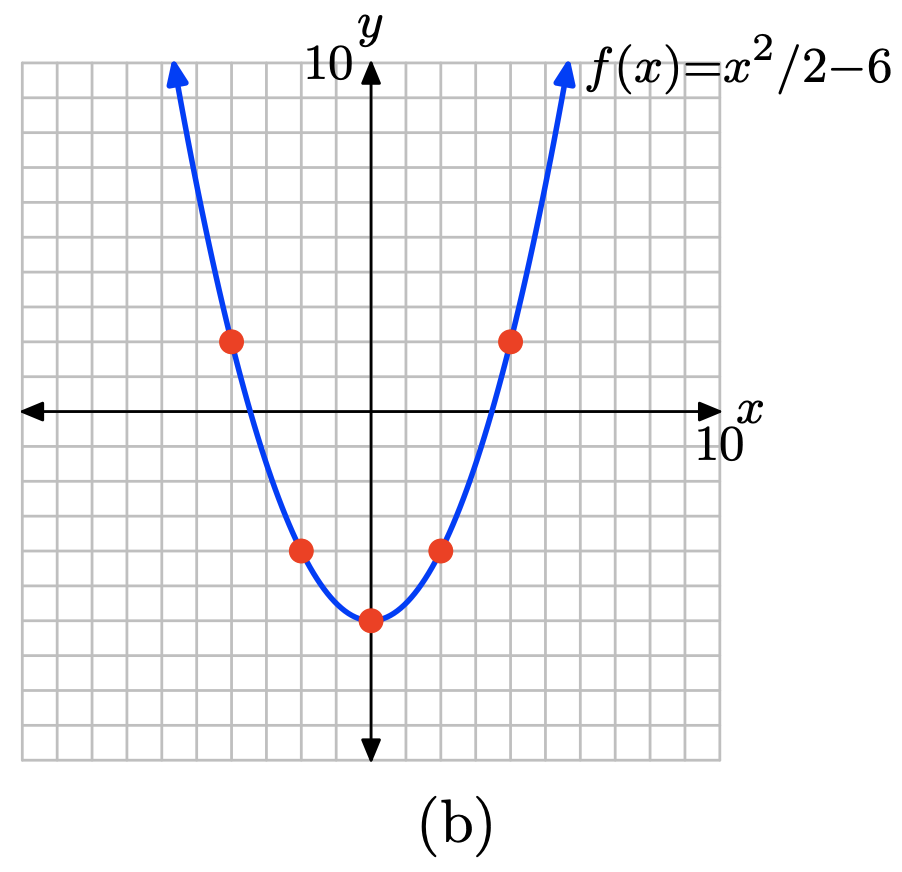
$f(x) = \dfrac{1}{2} x^{2} − 6$

Відповідь

Оцінити$f(x) = x^2/2 − 6$ за x = −4, −2, 0, 2 та 4.

$$f(−4) = (−4)^2/2 − 6 = 2 \\ f(−2) = (−2)^2/2 − 6 = −4 \\ f(0) = (0)^2/2 − 6 = −6 \\ f(2) = (2)^2/2 − 6 = −4 \\ f(4) = (4)^2/2 − 6 = 2$$

Помістіть ці результати в таблицю (a) і побудуйте їх так, як показано в (b). Тут достатньо доказів, щоб зрозуміти, що графік f - це крива, показана в (b).

х	$f(x) = x^2 − 2$	(х, ф (х))
-4	\ (f (x) = x^2 − 2\) ">2	(−4, 2)
-2	\ (f (x) = x^2 − 2\) ">-4	(-2, -4)
0	\ (f (x) = x^2 − 2\) ">-6	(0, -6)
2	\ (f (x) = x^2 − 2\) ">-4	(2, -4)
4	\ (f (x) = x^2 − 2\) ">2	(4,2)

(а)

Вправа$\PageIndex{8}$

$f(x) = 8-\dfrac{1}{2} x^2$

Виконуємо кожне з наступних завдань по функціям Вправи$\PageIndex{9}$ -$\PageIndex{10}$.

i) Налаштуйте систему координат на аркуші графського паперу. Позначте та масштабуйте кожну вісь.

II. Скористайтеся табличною функцією вашого графічного калькулятора, щоб оцінити функцію за заданими значеннями x. Запишіть ці результати у таблиці поруч із вашою системою координат на графічному папері.

iii. Покладіть точки в таблиці на вашій системі координат, а потім використовуйте їх, щоб намалювати графік заданої функції. Позначте графік його рівнянням.

Вправа$\PageIndex{9}$

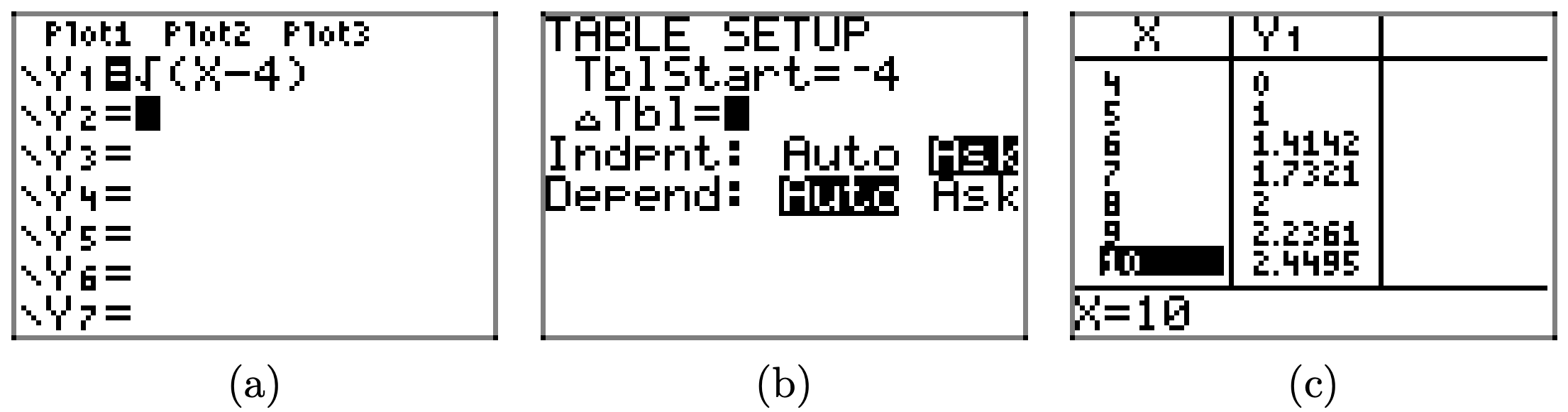
$f(x) = \sqrt{x − 4}$при х = 4, 5, 6, 7, 8, 9 і 10.

Відповідь

Завантажте функцію$f(x) = \sqrt{x − 4}$ в Y1, як показано в (a). Виберіть TBLSET, потім виділіть ASK для незалежної змінної і натисніть ENTER (див. (b)). Не має значення, що введено для TBLStart або Tbl. Виберіть TABLE і введіть значення x 4, 5, 6, 7, 8, 9 та 10, як показано в (c).

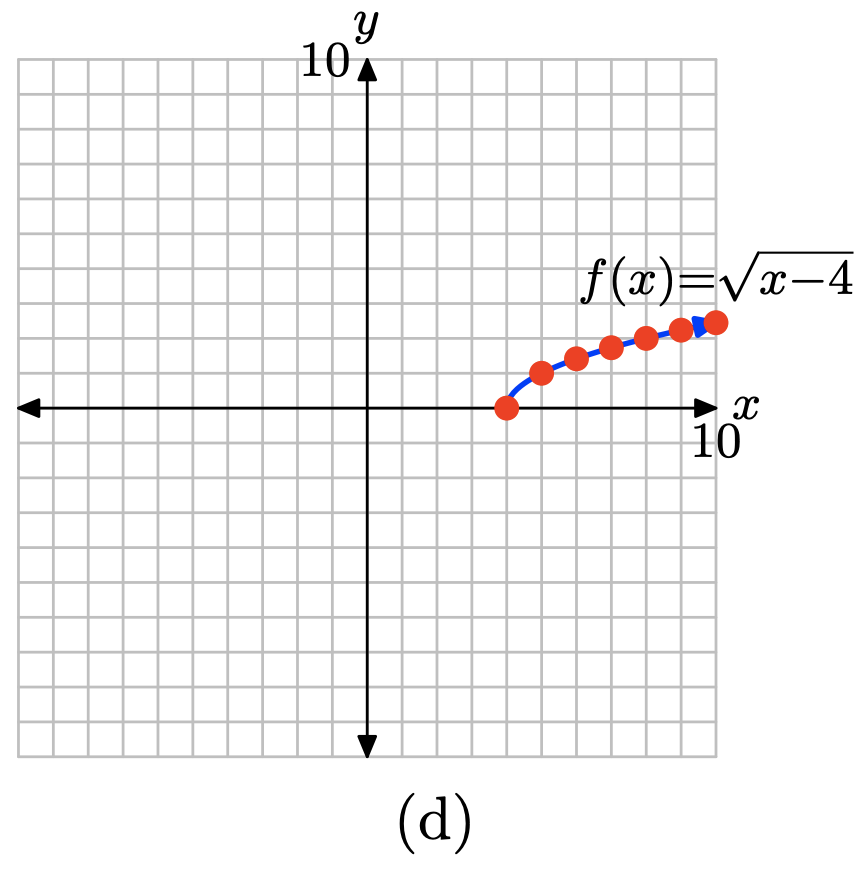
Побудуйте точки в таблиці (c) в (d). Цього достатньо, щоб інтуїтивно визначити, що графік f - це крива, показана в (d).

Вправа$\PageIndex{10}$

$f(x) = \sqrt{4 − x}$при x = −10, −8, −6, −4, −2, 0, 2 та 4.

У Вправи$\PageIndex{11}$ -$\PageIndex{14}$ графіком даної функції є парабола, графік, який має «U-подібну форму». Парабола має лише один переломний момент. Для кожної вправи виконуйте наступні завдання.

i. Завантажте рівняння в меню Y = вашого графічного калькулятора. Налаштуйте параметри WINDOW так, щоб у вікні перегляду була видна «точка перелому» (власне називається вершиною).

II. Зробіть розумну копію зображення в оглядовому вікні на домашній папері. Намалюйте всі лінії лінійкою (включаючи осі), але намалюйте криві від руки. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте графік його рівнянням.

Вправа$\PageIndex{11}$

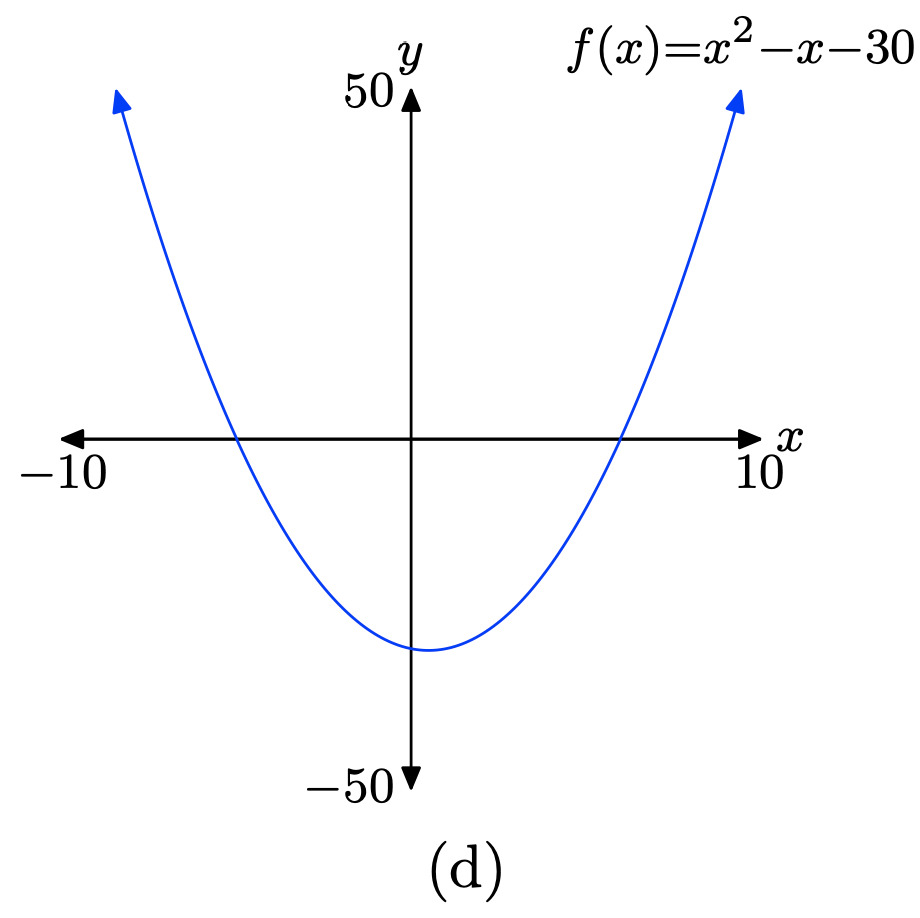
$f(x) = x^{2} − x − 30$

Відповідь

Завантажте функцію$f(x) = x^{2} − x − 30$ в Y1, як показано в (a). Налаштуйте параметри WINDOW, як показано у пункті (b). Натисніть кнопку GRAPH, щоб отримати графік f in (c).

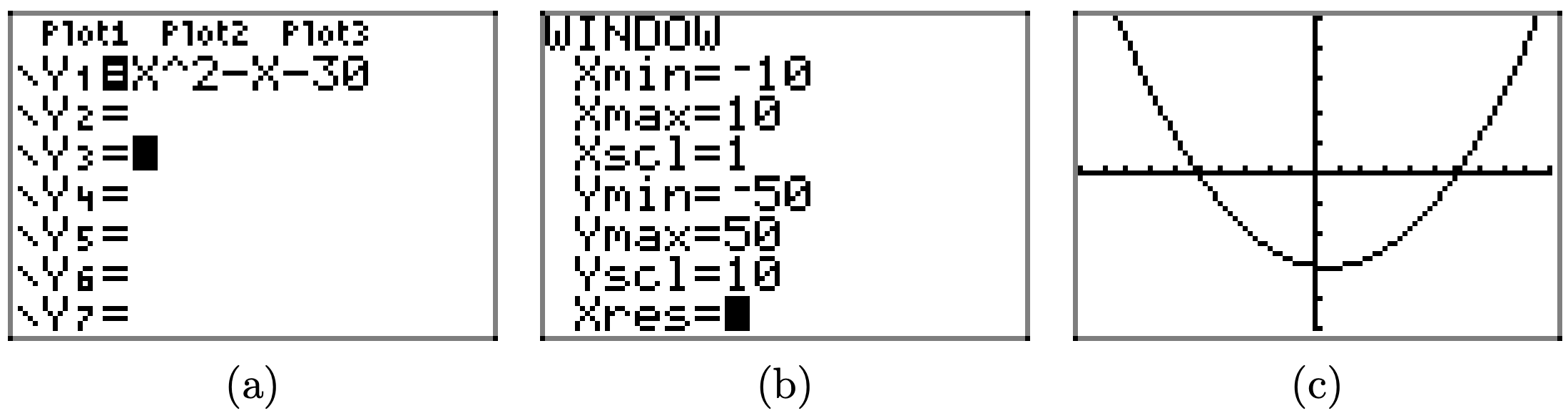
Скопіюйте зображення на домашнє завдання, як показано в (d).

Вправа$\PageIndex{12}$

$f(x) = 24 − 2x − x^2$

Вправа$\PageIndex{13}$

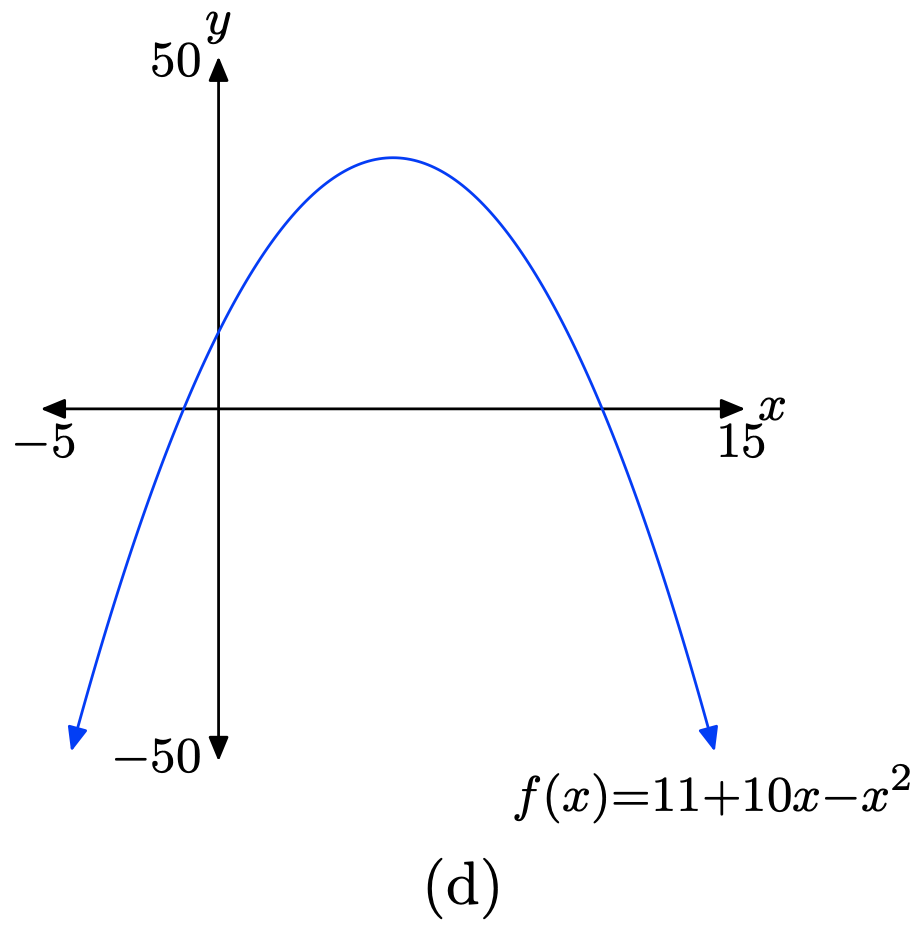
$f(x) = 11 + 10x − x^2$

Відповідь

Завантажте функцію$f(x) = 11 + 10x − x^2$ в Y1, як показано в (a). Налаштуйте параметри WINDOW, як показано у пункті (b). Натисніть кнопку GRAPH, щоб отримати графік f in (c).

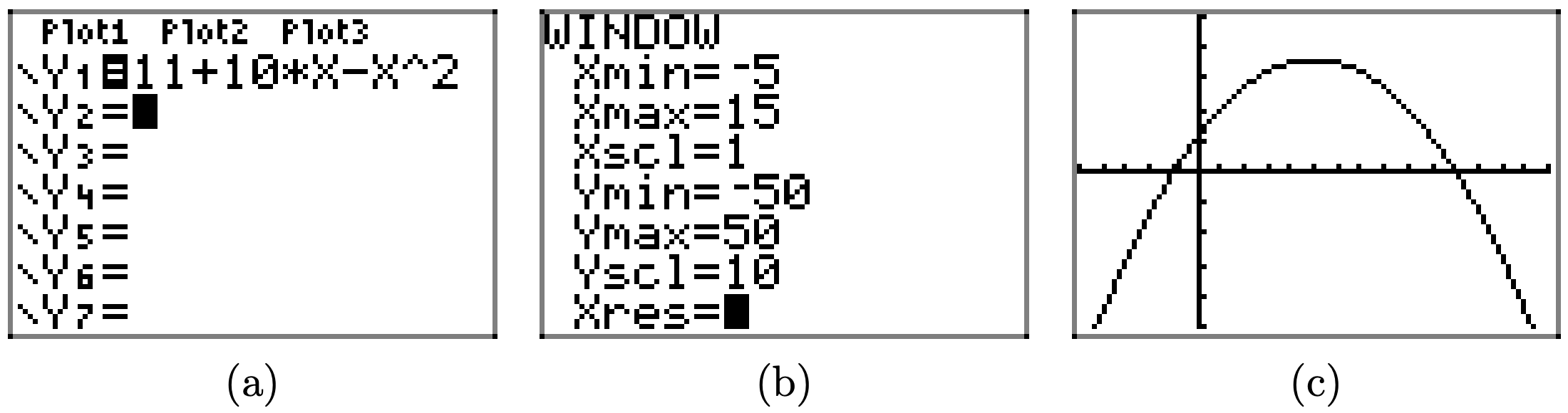
Скопіюйте зображення на домашнє завдання, як показано в (d).

Вправа$\PageIndex{14}$

$f(x) = x^2 + 11x − 12$

Кожне з рівнянь у Вправах$\PageIndex{15}$ -$\PageIndex{18}$ називаються «кубічними поліномами». Кожне рівняння було ретельно підібрано так, щоб його графік мав рівно дві «поворотні точки». Для кожної вправи виконайте кожне з наведених нижче завдань: завантажте рівняння в меню Y= вашого графічного калькулятора і відрегулюйте параметри WINDOW так, щоб обидві «поворотні точки» були видимими у вікні перегляду. ii. Зробіть розумну копію графіка в оглядовому вікні на домашній папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax, а потім позначте графік його рівнянням. Не забудьте намалювати всі лінії лінійкою.

Вправа$\PageIndex{15}$

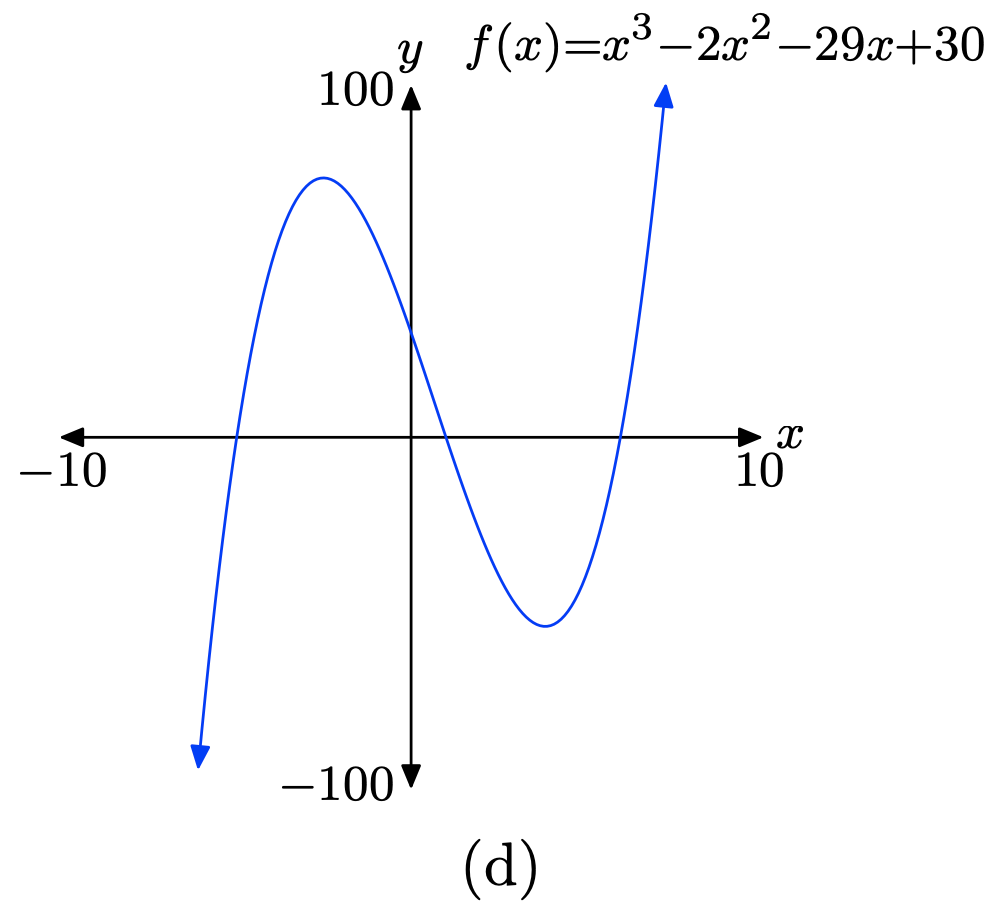
$f(x) = x^3 − 2x^2 − 29x + 30$

Відповідь

Завантажте функцію$f(x) = x^3 − 2x^2 − 29x + 30$ в Y1, як показано в (a). Налаштуйте параметри WINDOW, як показано у пункті (b). Натисніть кнопку GRAPH, щоб отримати графік f in (c).

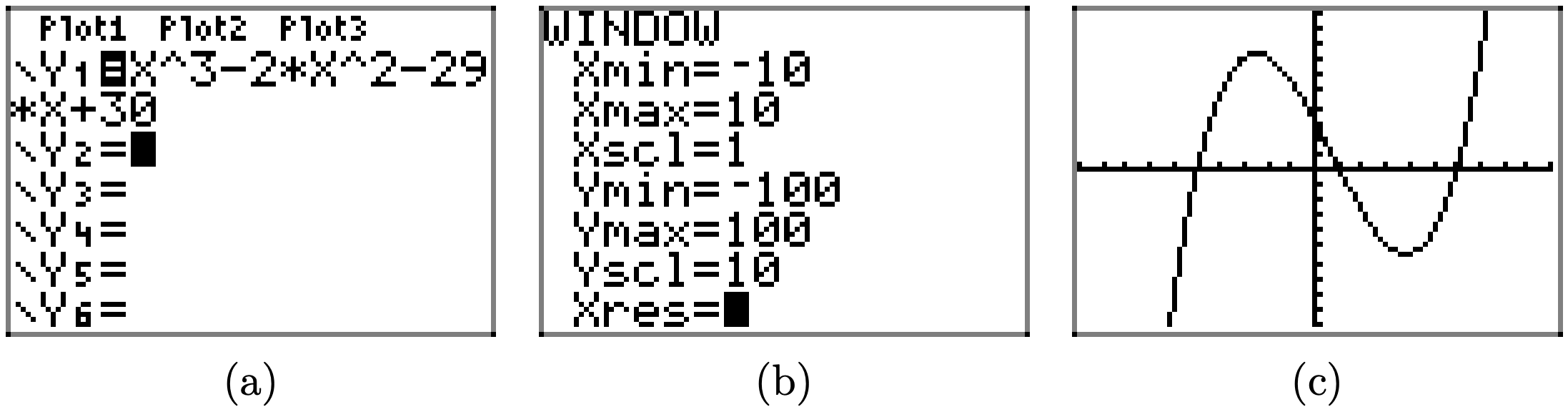
Скопіюйте зображення на домашнє завдання, як показано в (d).

Вправа$\PageIndex{16}$

$f(x) = −x^3 + 2x^2 + 19x − 20$

Вправа$\PageIndex{17}$

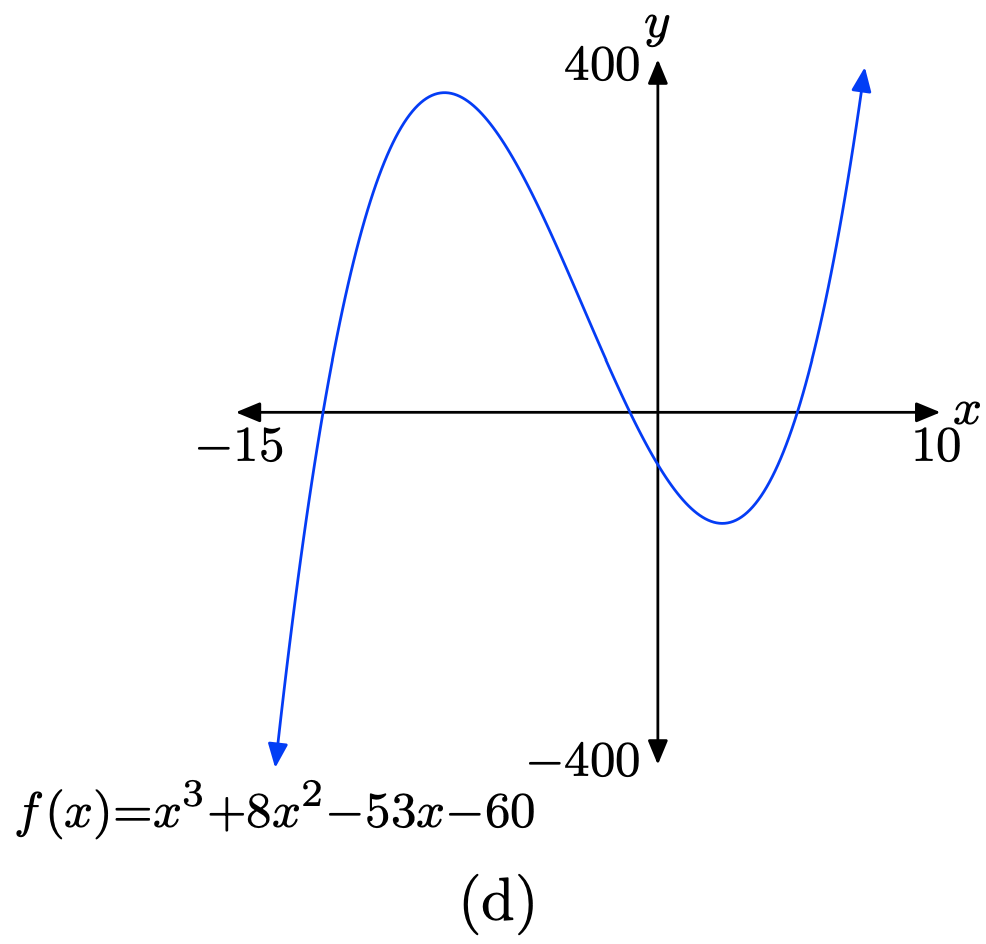
$f(x) = x^3 + 8x^2 − 53x − 60$

Відповідь

Завантажте функцію$f(x) = x^3 + 8x^2 − 53x − 60$ в Y1, як показано в (a). Налаштуйте параметри WINDOW, як показано у пункті (b). Натисніть кнопку GRAPH, щоб отримати графік f in (c).

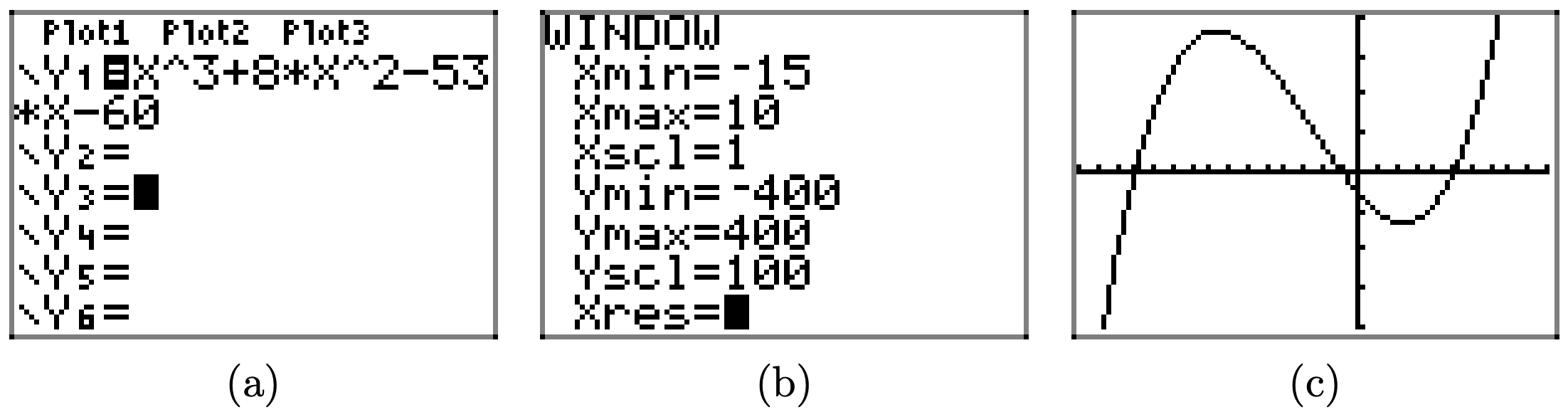
Скопіюйте зображення на домашнє завдання, як показано в (d).

Вправа$\PageIndex{18}$

$f(x) = −x^3 + 16x^2 − 43x − 60$

Виконайте кожне з наступних завдань для рівнянь у Вправи$\PageIndex{19}$ -$\PageIndex{22}$.

i. Завантажте рівняння в меню Y=. Налаштовуйте параметри WINDOW до тих пір, поки не вважаєте, що у вікні перегляду буде видно всю важливу поведінку («поворотні точки» тощо). Примітка: Це складніше, ніж здається, особливо коли ми не маємо заздалегідь уявлення про те, як може виглядати графік. Однак експериментуйте з декількома настройками, поки не «відкриєте» настройки, які демонструють найважливішу поведінку.

II. Скопіюйте зображення на екрані на домашній папір. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax. Позначте графік його рівнянням.

Вправа$\PageIndex{19}$

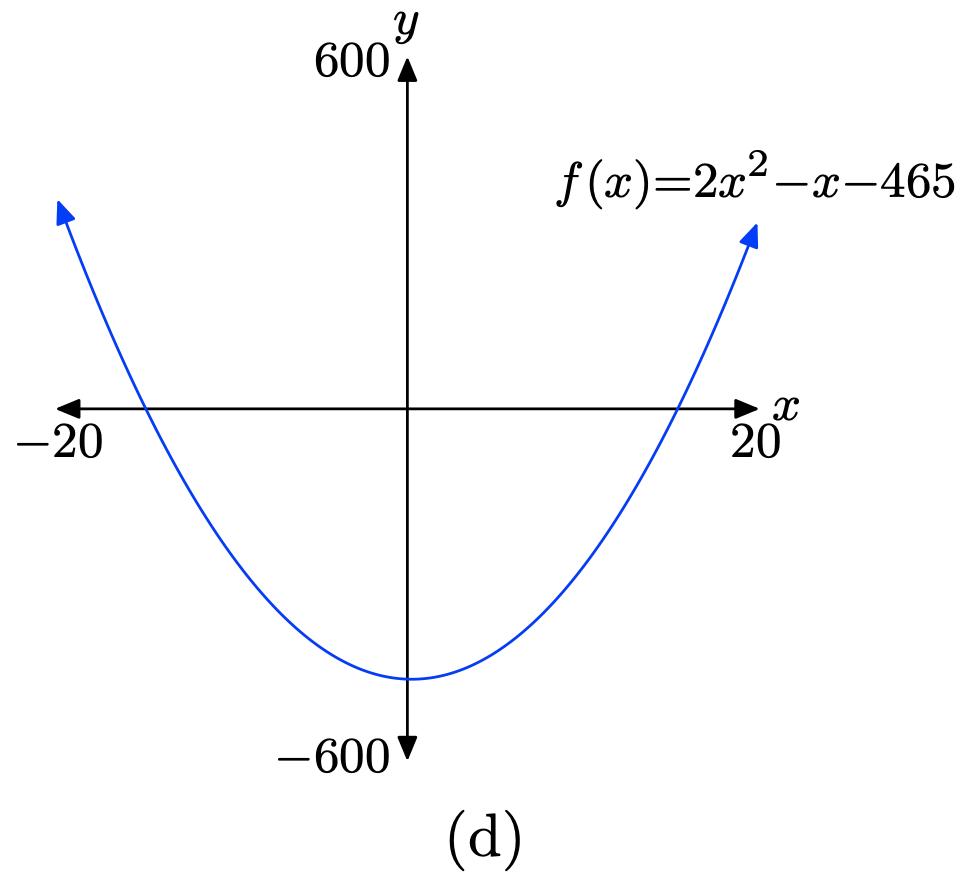
$f(x) = 2x^2 − x − 465$

Відповідь

Завантажте функцію$f(x) = 2x^2 − x − 465$ в Y1, як показано в (a). Налаштуйте параметри WINDOW, як показано у пункті (b). Натисніть кнопку GRAPH, щоб отримати графік f in (c).

Скопіюйте зображення на домашнє завдання, як показано в (d).

Вправа$\PageIndex{20}$

$f(x) = x^3 − 24x^2 + 65x + 1050$

Вправа$\PageIndex{21}$

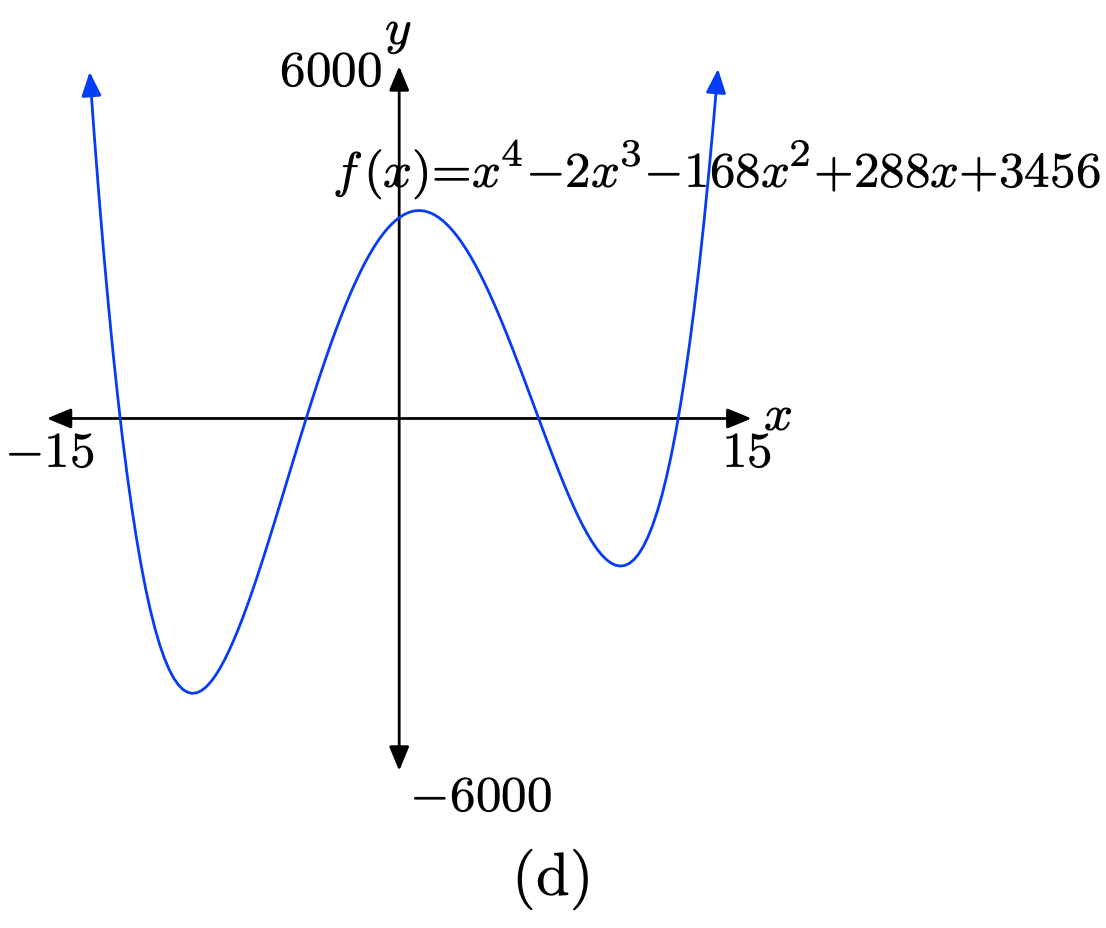
$f(x) = x^4 − 2x^3 − 168x^2 + 288x + 3456$

Відповідь

Завантажте функцію$f(x) = x^4 − 2x^3 − 168x^2 + 288x + 3456$ в Y1, як показано в (a). Налаштуйте параметри WINDOW, як показано у пункті (b). Натисніть кнопку GRAPH, щоб отримати графік f in (c).

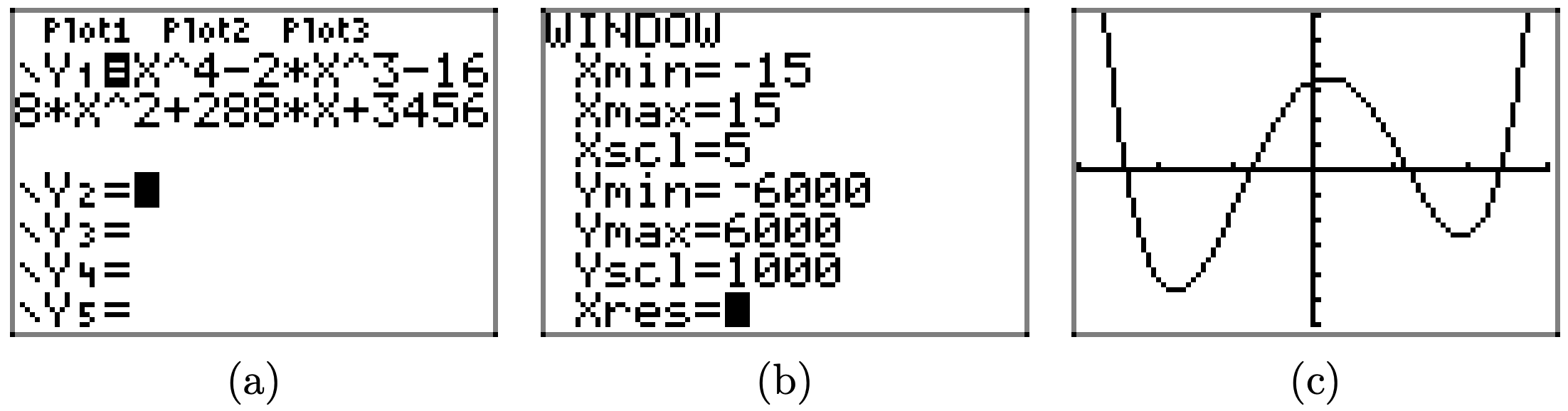
Скопіюйте зображення на домашнє завдання, як показано в (d)

Вправа$\PageIndex{22}$

$f(x) = −x^4 −3x^3 +141x^2 +523x− 660$

2.3 Вправи

Для вправ$\PageIndex{1}$ -$\PageIndex{6}$ виконуйте кожне з наступних завдань.

i. зробіть копію графіка на аркуші графського паперу і застосуйте тест вертикальної лінії.

II. Напишіть повне речення про те, чи є граф функцією. Поясніть причину вашої відповіді.

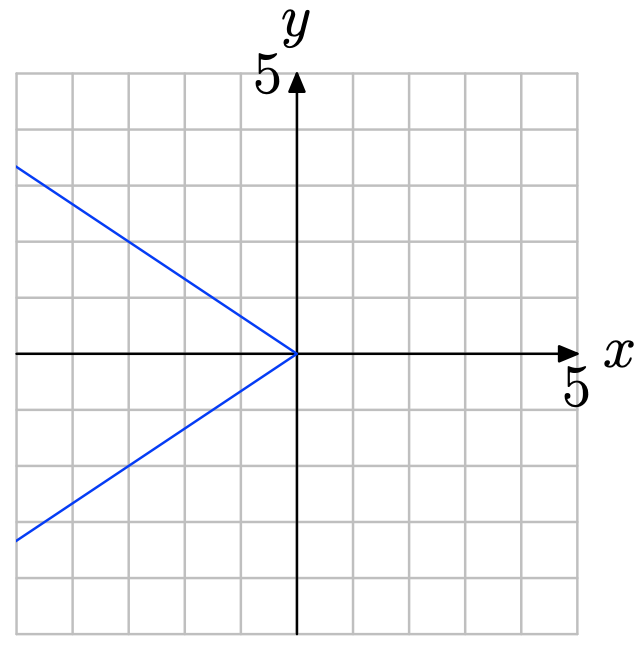
Вправа$\PageIndex{1}$

Відповідь

Зверніть увагу, що на малюнку нижче вертикальна лінія розрізає графік не один раз. Тому графік не представляє графіка функції.

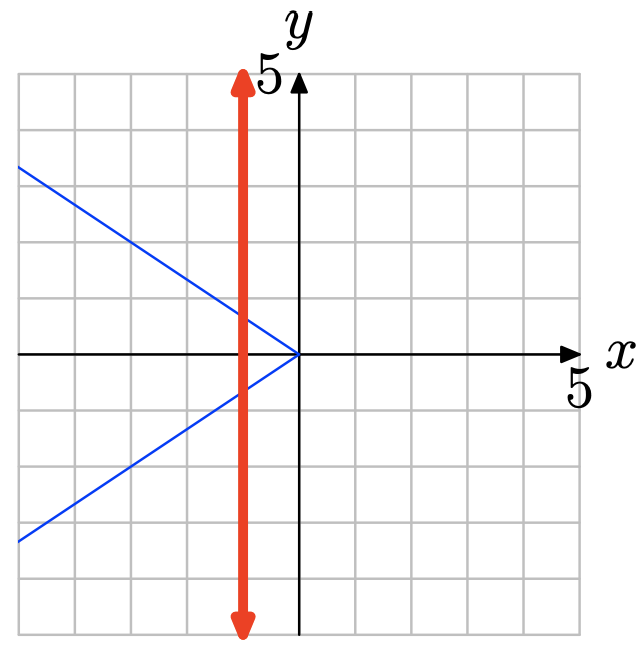
Вправа$\PageIndex{2}$

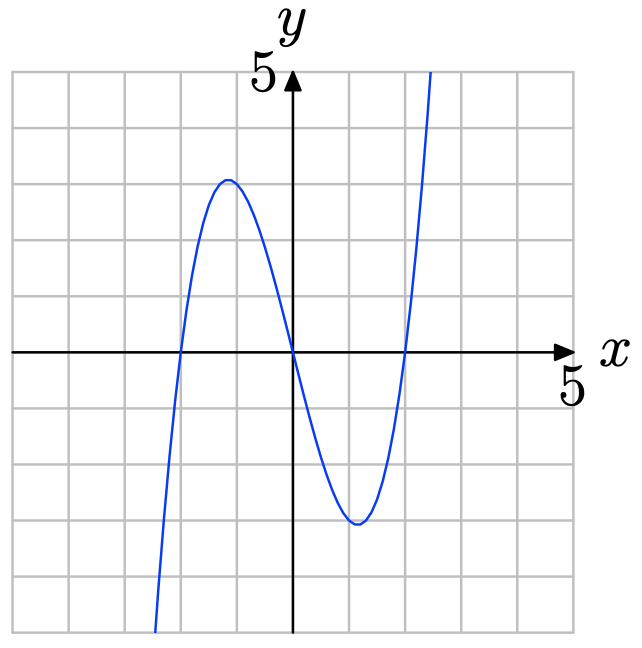
Вправа$\PageIndex{3}$

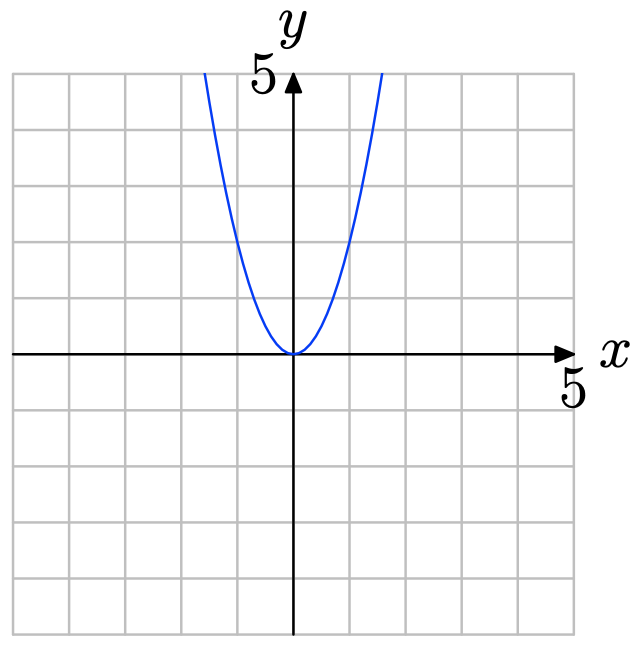
Відповідь

Жодна вертикальна лінія не обрізає графік більше одного разу (див. Малюнок нижче). Тому графік являє собою функцію.

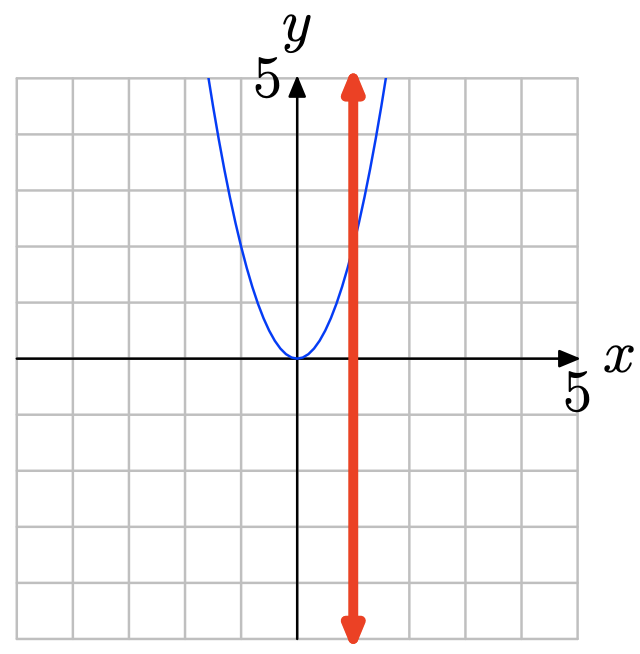
Вправа$\PageIndex{4}$

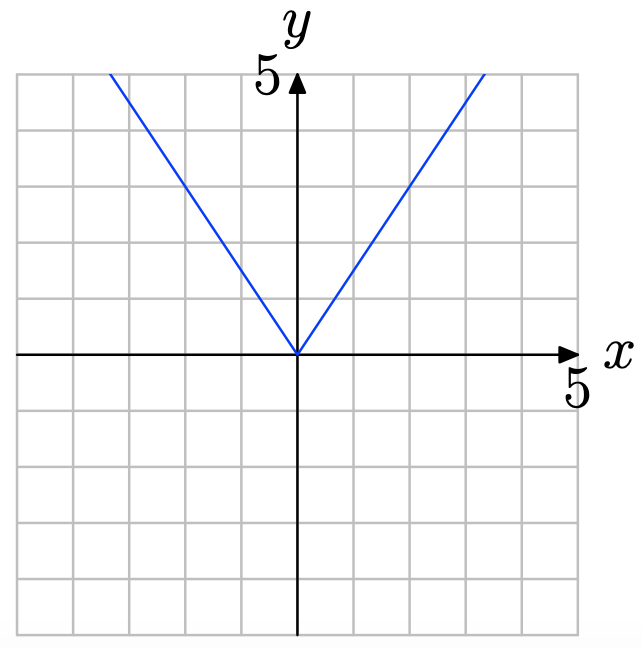
Вправа$\PageIndex{5}$

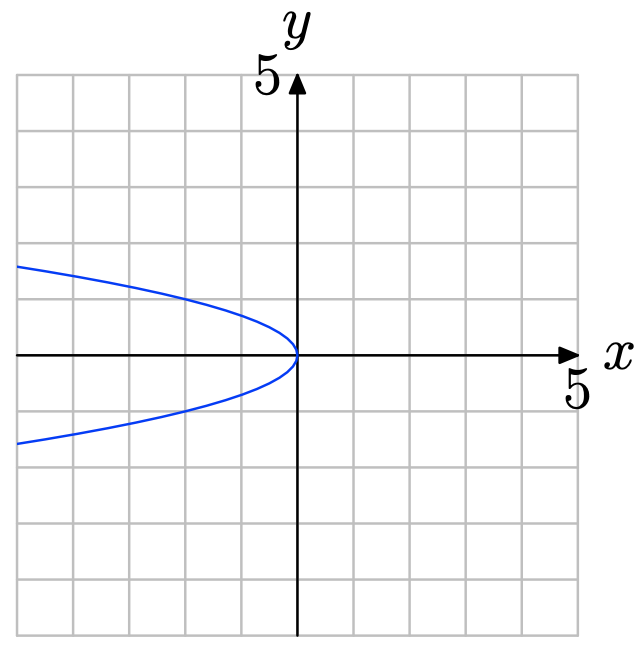
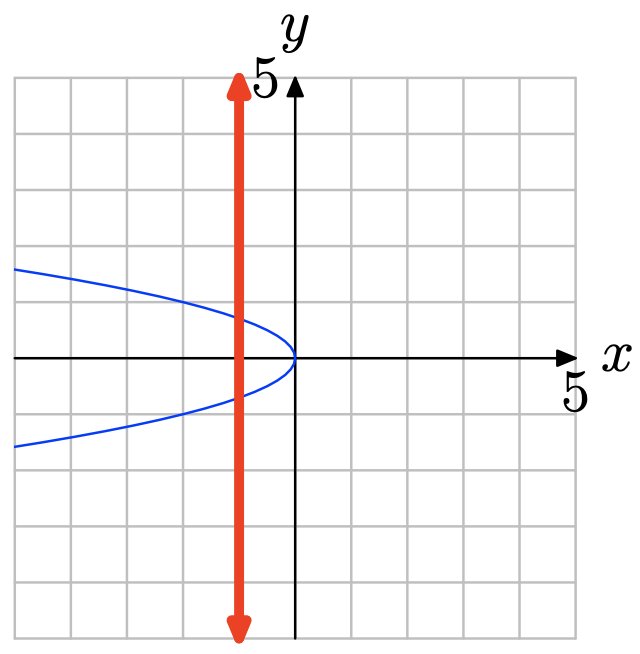
Відповідь

Зверніть увагу, що на малюнку нижче вертикальна лінія розрізає графік не один раз. Тому графік не представляє графіка функції.

Вправа$\PageIndex{6}$

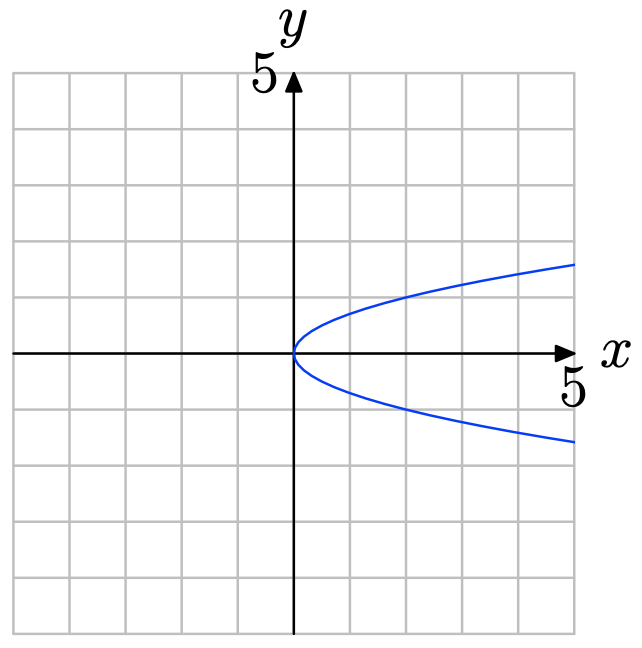
У Вправи$\PageIndex{7}$ -$\PageIndex{12}$ виконуйте кожне з наступних завдань.

тобто зробити точну копію графіка функції f на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.

II. Використовуйте техніку Приклади 3 і 4 в оповіданні для оцінки функції за заданим значенням. Намалюйте та позначте стрілки, як показано на малюнках 4 та 5 в оповіданні.

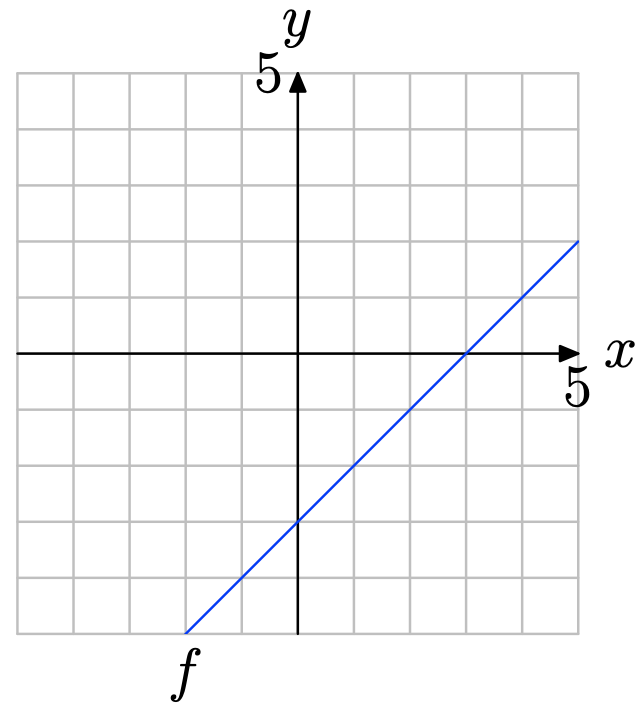
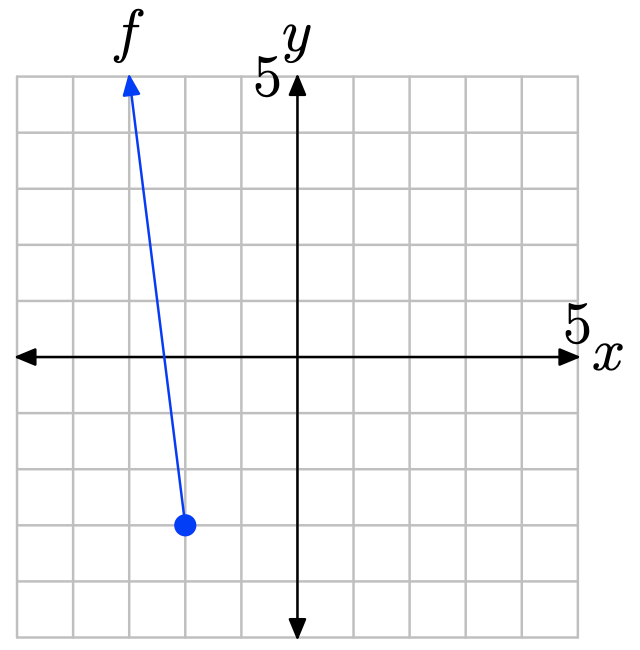
Вправа$\PageIndex{7}$

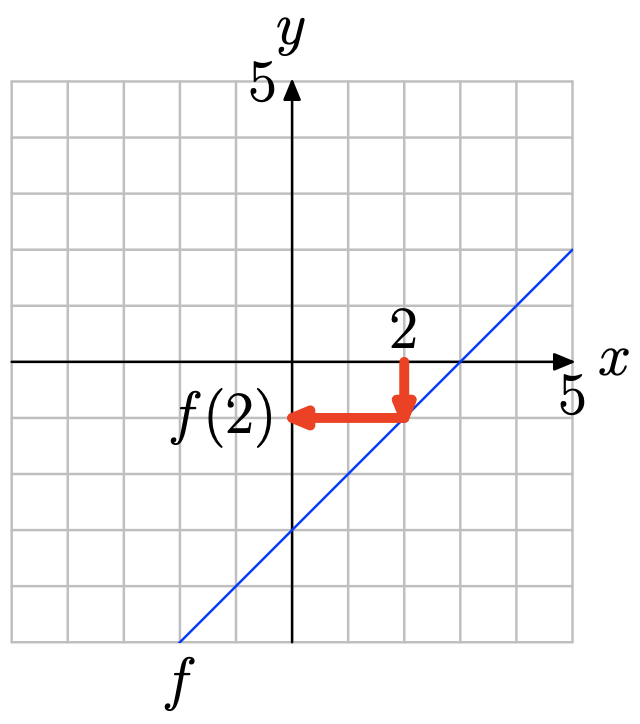
Використовуйте графік f для визначення f (2).

Відповідь

Знайдіть x = 2 на осі x (див. Малюнок нижче), намалюйте вертикальну стрілку до графіка f, потім горизонтальну стрілку до осі y. Таким чином, f (2) = −1.

Вправа$\PageIndex{8}$

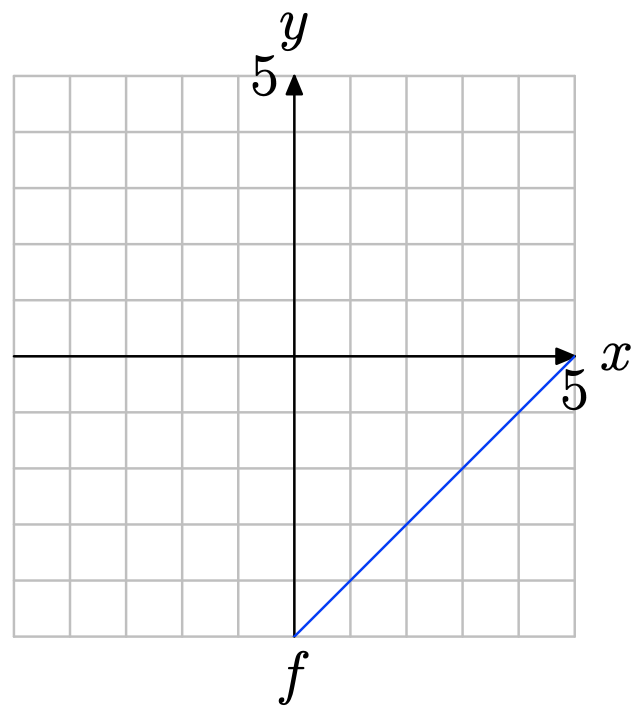
Використовуйте графік f для визначення f (3).

Вправа$\PageIndex{9}$

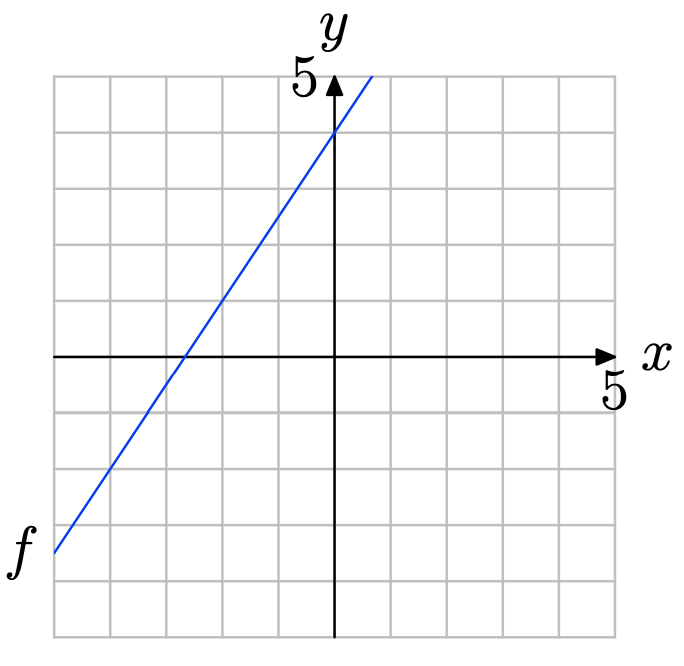
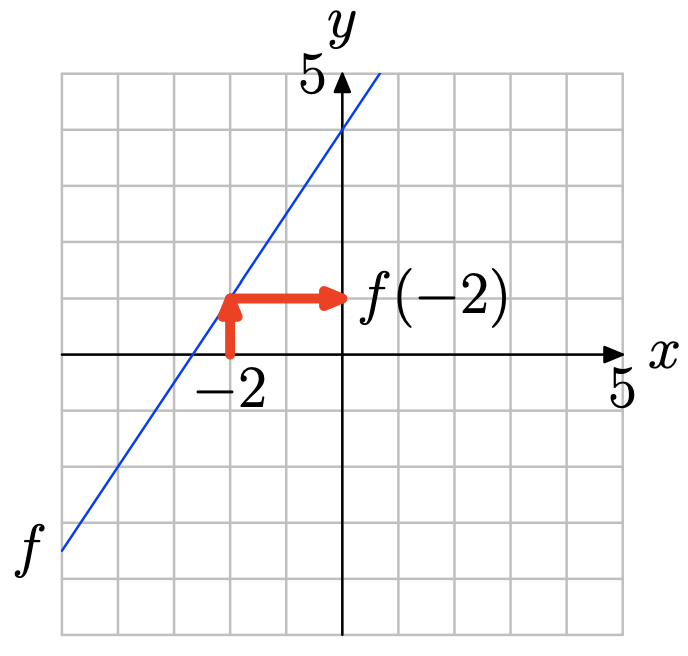
Використовуйте графік f для визначення f (−2).

Відповідь

Знайдіть x = −2 на осі x (див. Малюнок нижче), намалюйте вертикальну стрілку до графіка f, потім горизонтальну стрілку до осі y. Таким чином, f (−2) = 1.

Вправа$\PageIndex{10}$

Використовуйте графік f для визначення f (1).

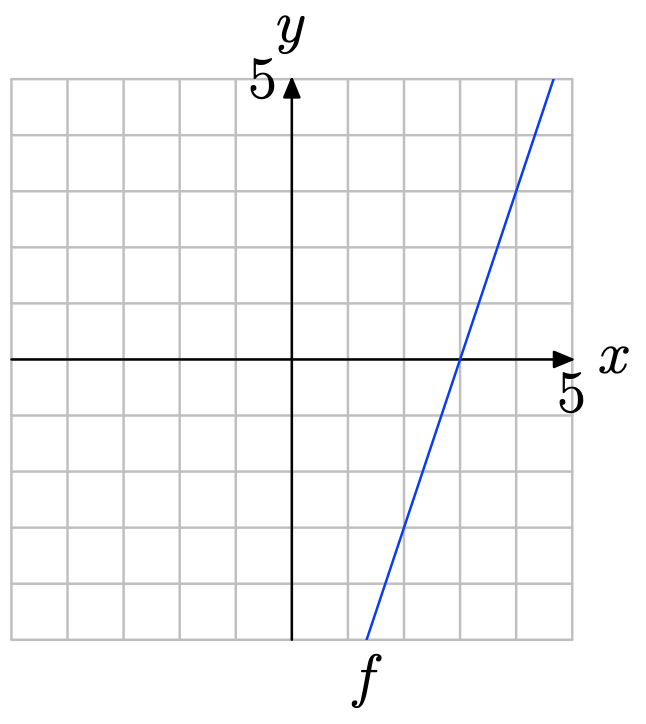
Вправа$\PageIndex{11}$

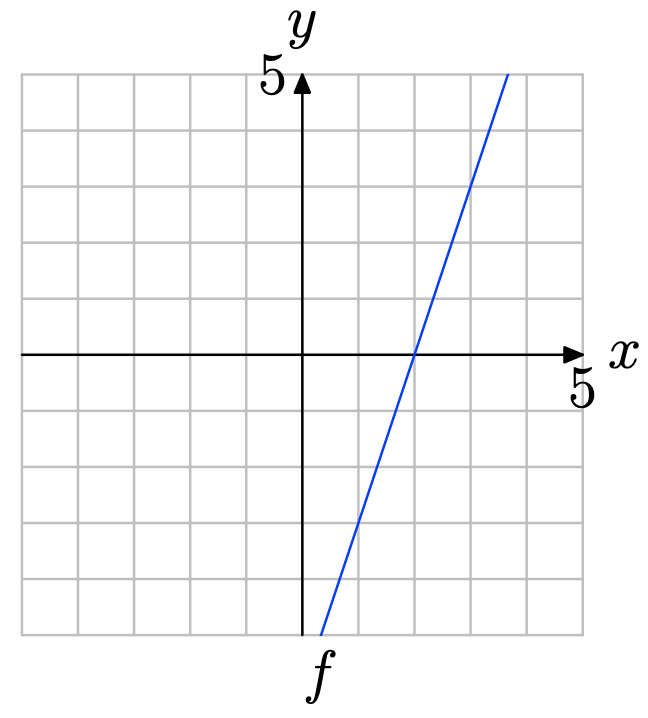
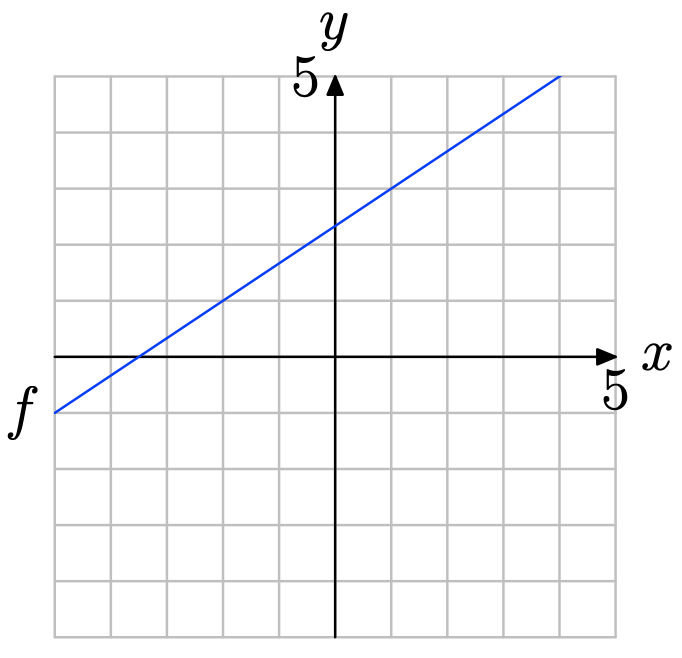
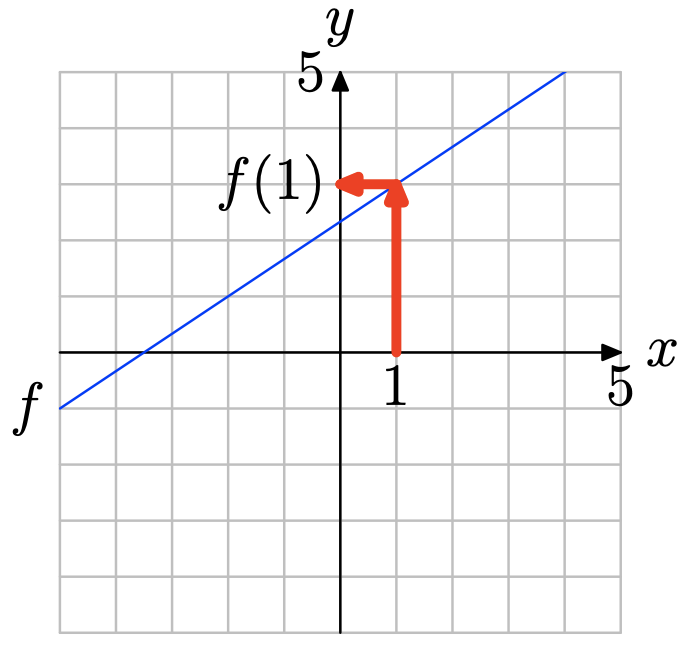
Використовуйте графік f для визначення f (1).

Відповідь

Знайдіть x = 1 на осі x (див. Малюнок нижче), намалюйте вертикальну стрілку до графіка f, потім горизонтальну стрілку до осі y. Таким чином, f (1) = 3.

Вправа$\PageIndex{12}$

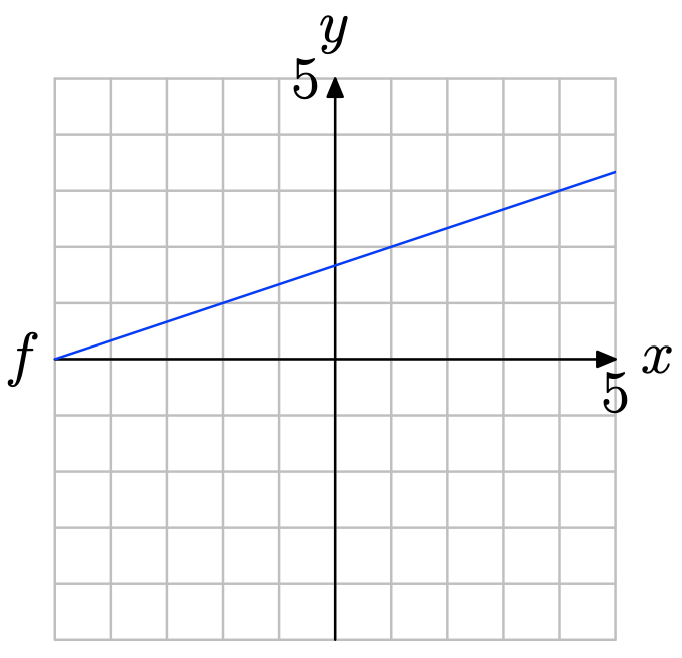
Використовуйте графік f для визначення f (−2).

У Вправи$\PageIndex{13}$ -$\PageIndex{18}$ виконуйте кожне з наступних завдань.

тобто зробити точну копію графіка функції f на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Не забудьте намалювати всі лінії лінійкою.

II. Скористайтеся технікою Прикладу 5 у розповіді, щоб знайти значення x, яке відображає задане значення. Намалюйте і позначте стрілки, як показано на малюнку 6 в оповіданні.

Вправа$\PageIndex{13}$

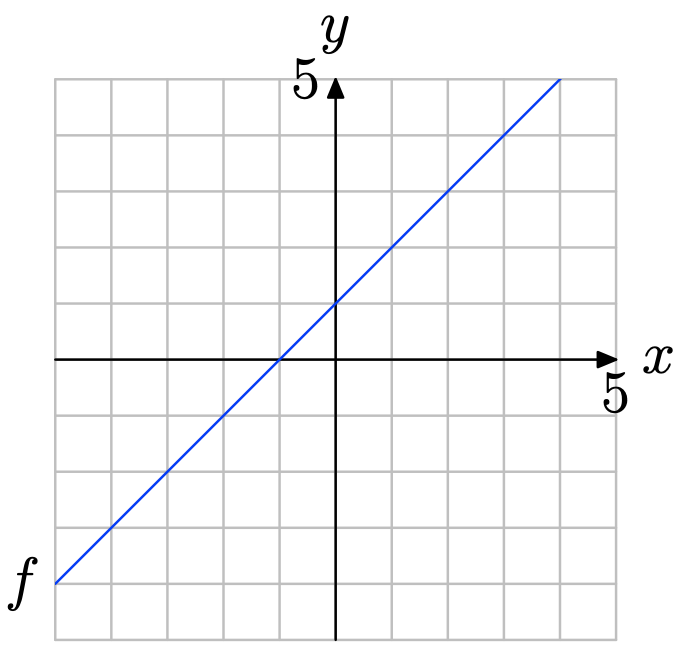
Використовуйте графік f для розв'язання рівняння f (x) = −2.

Відповідь

Знайдіть y = −2 на осі y (див. Малюнок нижче), намалюйте горизонтальну стрілку до графіка f, потім вертикальну стрілку до осі y. Таким чином, розв'язок f (x) = −2 дорівнює x = −3.

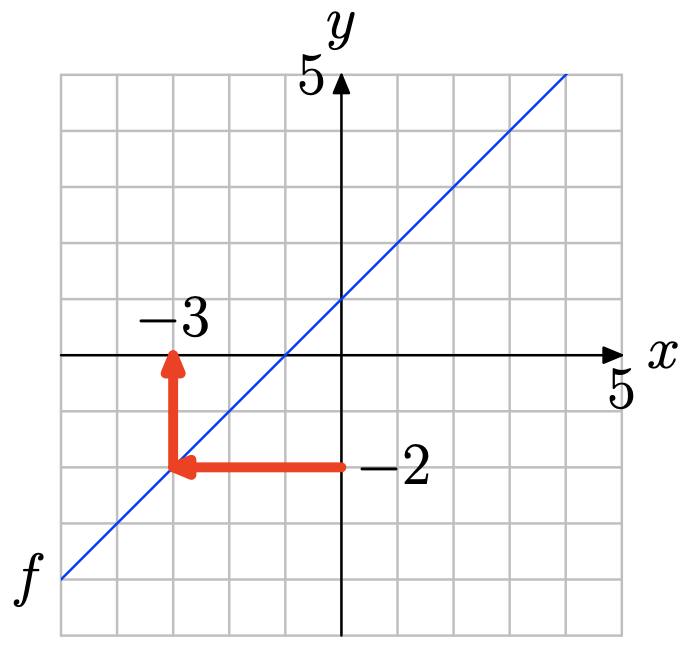
Вправа$\PageIndex{14}$

Використовуйте графік f для вирішення рівняння f (x) = 1.

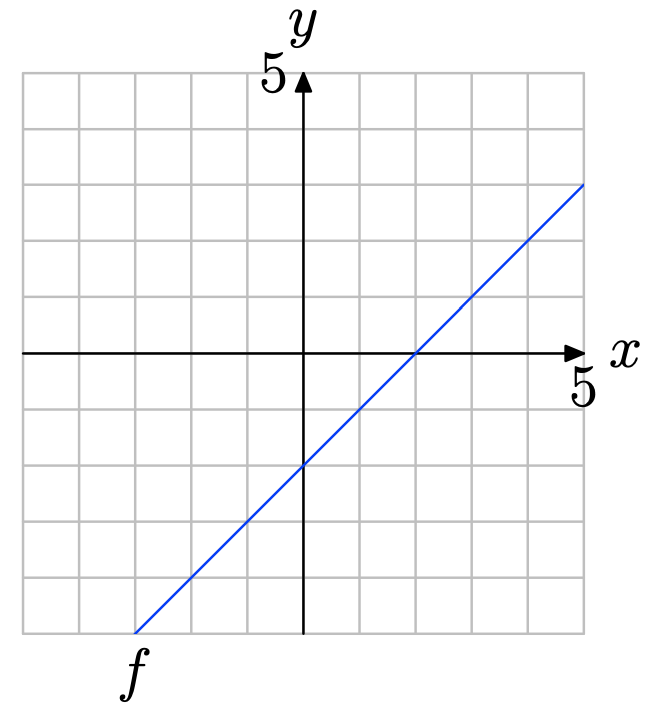
Вправа$\PageIndex{15}$

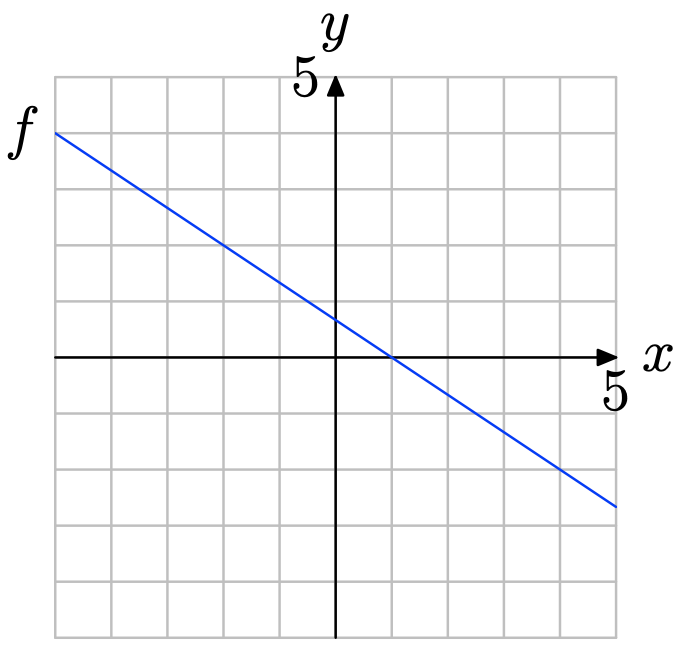
Використовуйте графік f для вирішення рівняння f (x) = 2

Відповідь

Знайдіть y = 2 на осі y (див. Малюнок нижче), намалюйте горизонтальну стрілку до графіка f, потім вертикальну стрілку до осі y. Таким чином, розв'язок f (x) = 2 дорівнює x = −2.

Вправа$\PageIndex{16}$

Використовуйте графік f для розв'язання рівняння f (x) = −2.

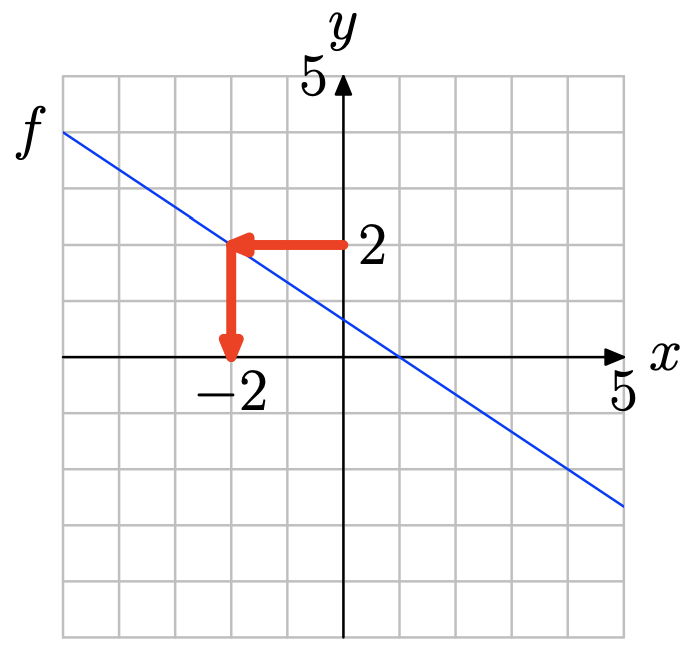
Вправа$\PageIndex{17}$

Використовуйте графік f для вирішення рівняння f (x) = 2.

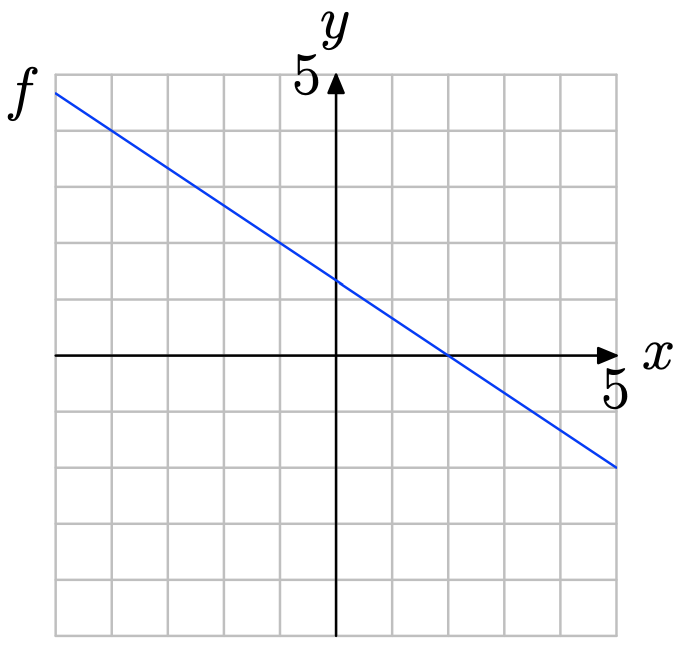
Відповідь

Знайдіть y = 2 на осі y (див. Малюнок нижче), намалюйте горизонтальну стрілку до графіка f, потім вертикальну стрілку до осі y. Таким чином, розв'язок f (x) = 2 дорівнює x = −1.

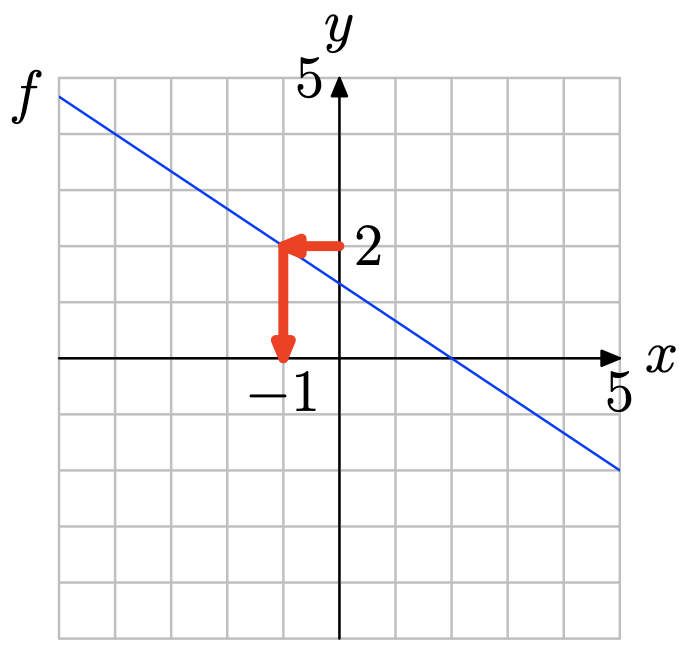
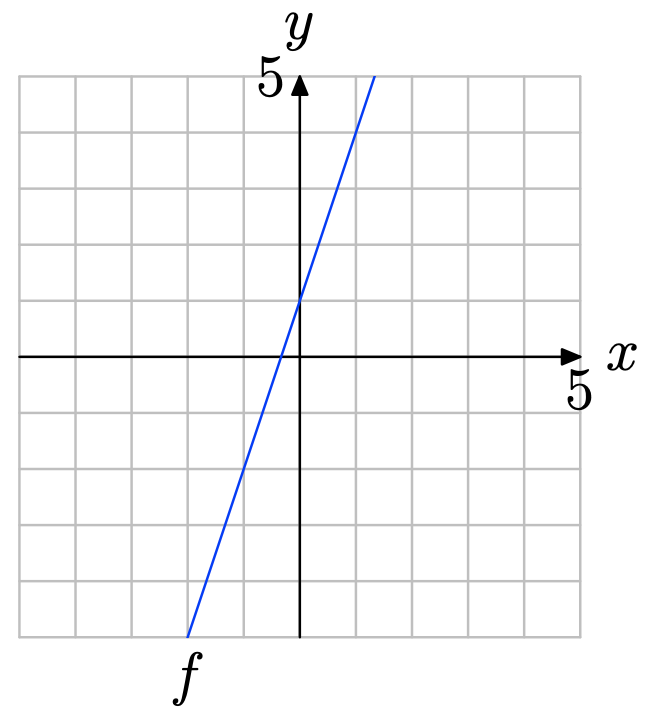
Вправа$\PageIndex{18}$

Використовуйте графік f для розв'язання рівняння f (x) = −3.

У Вправи$\PageIndex{19}$ -$\PageIndex{22}$ виконуйте кожне з наступних завдань.

тобто зробити копію графа f на аркуші графського паперу. Позначте та масштабуйте кожну вісь.

II. Використовуючи ручку або олівець іншого кольору, спроектуйте кожну точку на графіку f на вісь x. Затінюйте отриманий домен на осі x.

iii. Використовуйте як set-builder, так і інтервальні позначення для опису домену.

Вправа$\PageIndex{19}$

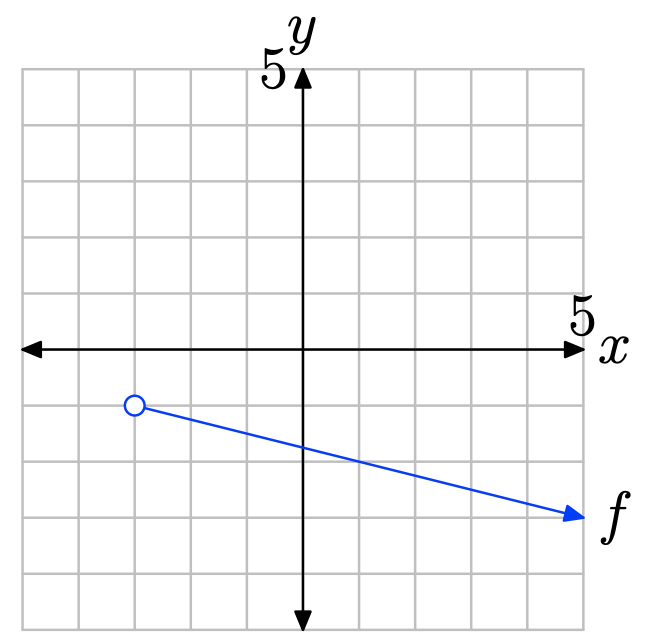
Відповідь

Щоб знайти область функції, спроектуйте графік f на вісь x. Зауважте, що всі значення x, що лежать праворуч від −3, лежать у тіні і, отже, знаходяться в області f. Тому домен найкраще описати за допомогою позначення$\{x : x > −3\} = (−3,\infty)$.

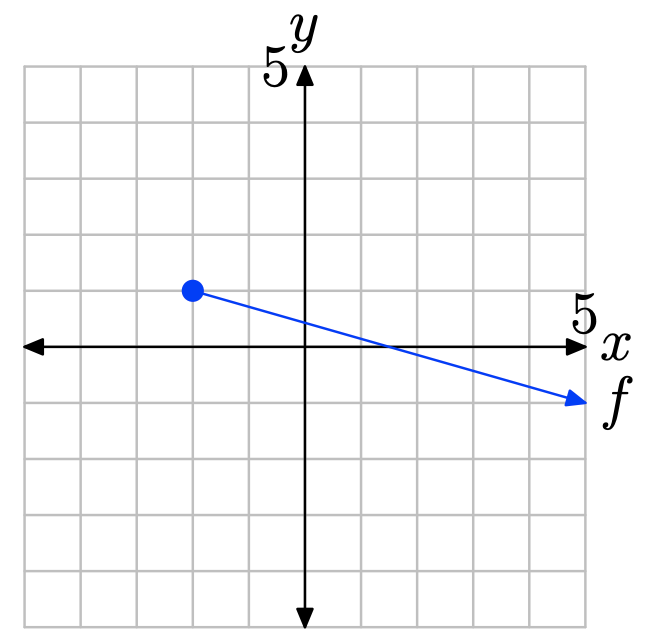
Вправа$\PageIndex{20}$

Вправа$\PageIndex{21}$

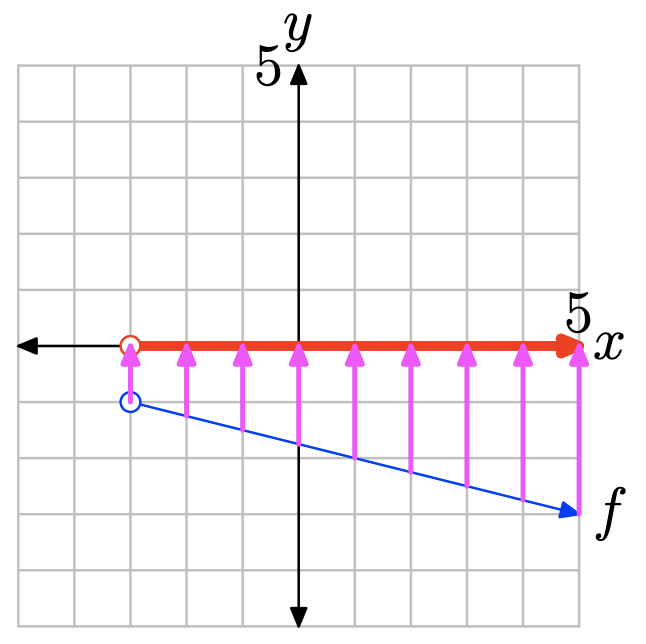
Відповідь

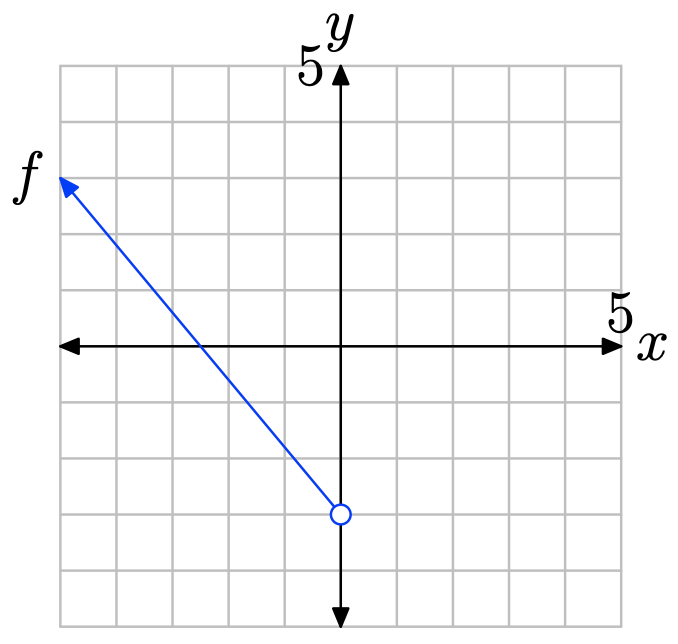
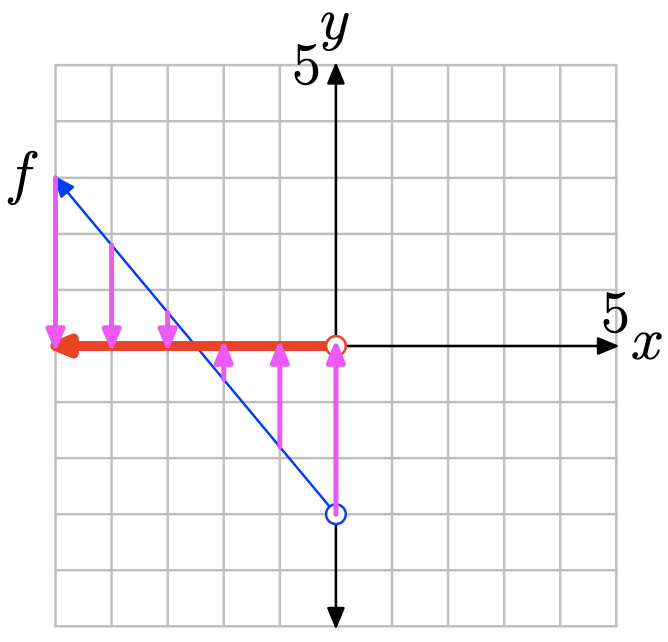
Щоб знайти область функції, спроектуйте графік f на вісь x. Зауважте, що всі значення x, що лежать зліва від 0, лежать в тіні і, отже, знаходяться в області f, тому домен найкраще описувати інтервальними позначеннями$\{x : x < 0\} = (−\infty, 0)$.

Вправа$\PageIndex{22}$

У Вправи$\PageIndex{23}$ -$\PageIndex{26}$ виконуйте кожне з наступних завдань.

тобто зробити копію графа f на аркуші графського паперу. Позначте та масштабуйте кожну вісь.

II. Використовуючи ручку або олівець іншого кольору, спроектуйте кожну точку на графіку f на вісь y. Затіньте отриманий діапазон на осі y. iii. Використовуйте як set-builder, так і інтервальні позначення для опису діапазону.

Вправа$\PageIndex{23}$

Відповідь

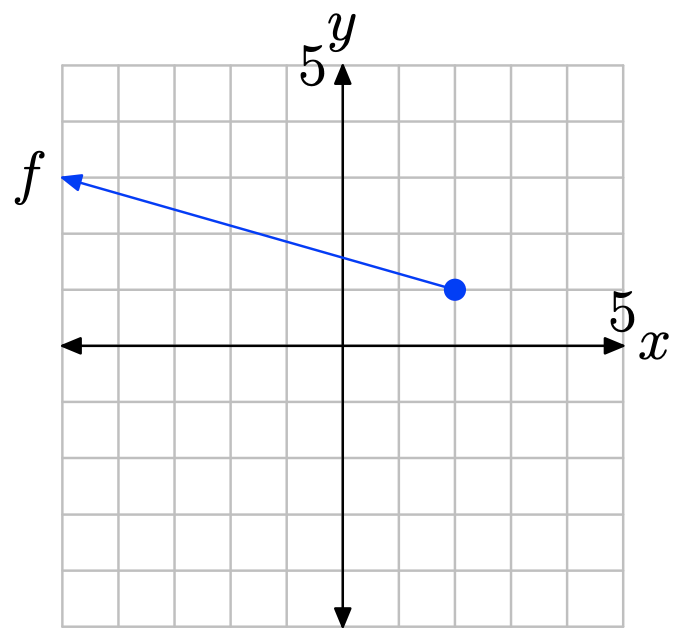
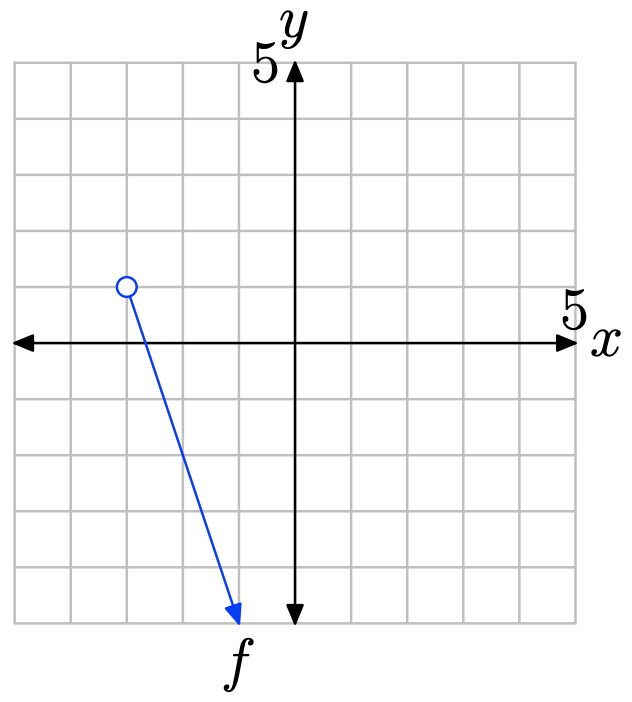
Щоб знайти діапазон функції, спроектуйте графік f на вісь y. Зауважте, що всі значення y, що лежать нижче 1, лежать в тіні і, отже, знаходяться в діапазоні f, тому діапазон найкраще описати інтервальними позначеннями$\{y : y < 1\} = (−\infty, 1)$.

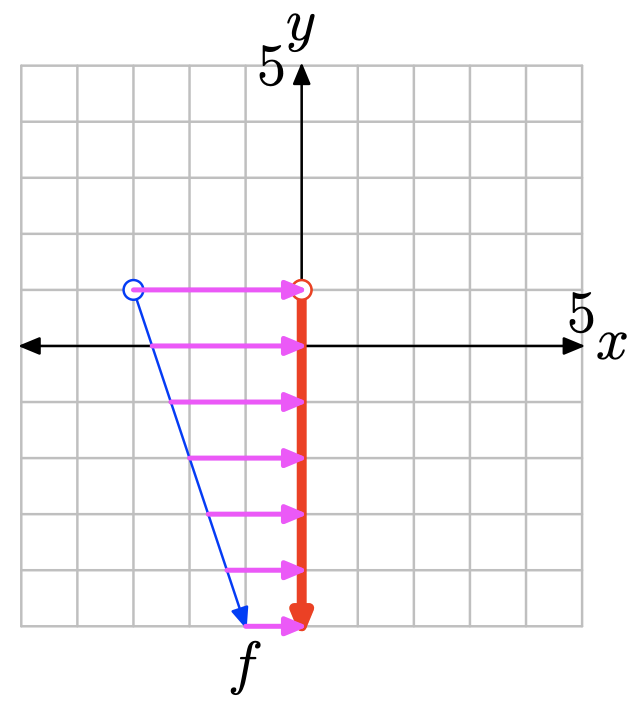
Вправа$\PageIndex{24}$

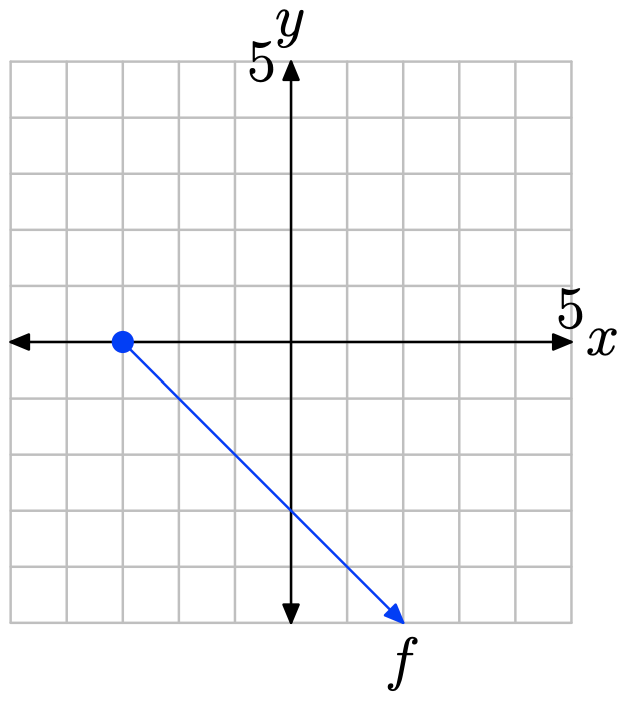
Вправа$\PageIndex{25}$

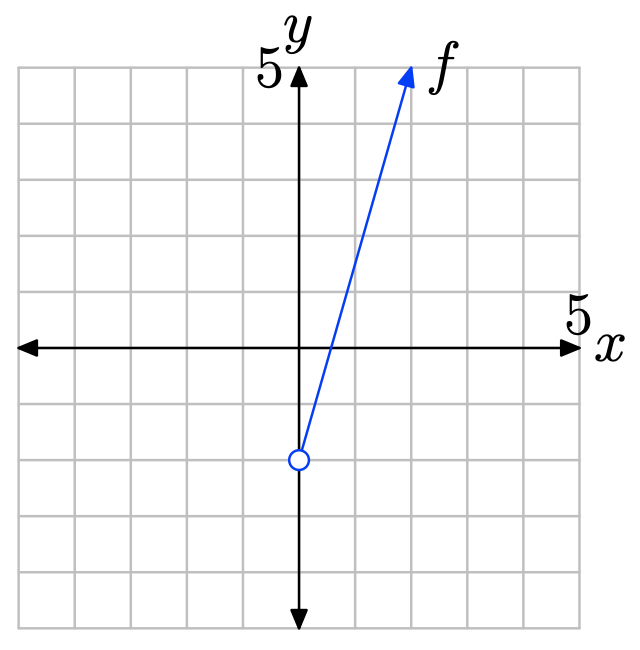
Відповідь

Щоб знайти діапазон функції, спроектуйте графік f на вісь y. Зауважте, що всі значення y, що лежать вище −2, лежать у тіні і, отже, знаходяться в діапазоні f. Тому діапазон найкраще описати інтервальними позначеннями$\{y : y > −2\} = (−2,\infty)$.

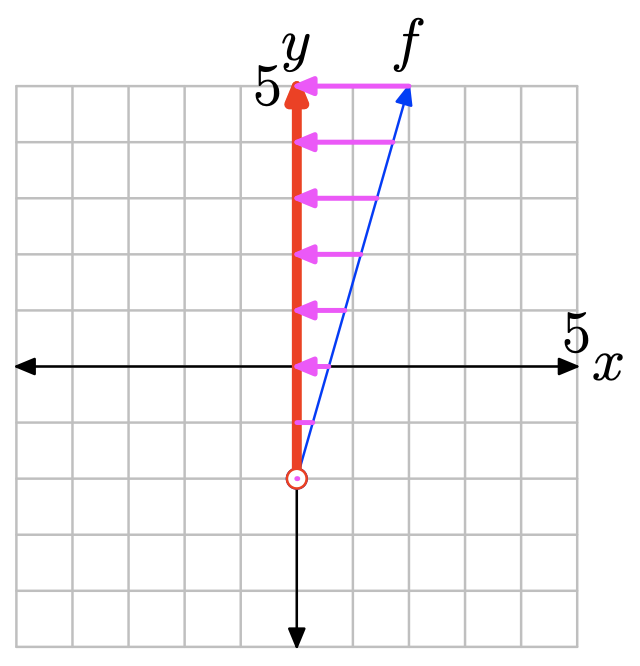
Вправа$\PageIndex{26}$

У Вправи$\PageIndex{27}$ -$\PageIndex{30}$ виконуйте кожне з наступних завдань.

i Використовуйте графічний калькулятор, щоб намалювати графік заданої функції. Зробіть досить точну копію зображення на екрані перегляду на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою параметрів WINDOW xmin, xmax, ymin та ymax. Позначте графік його рівнянням.

II. За допомогою кольорового олівця проектуйте кожну точку на графіку на вісь x; тобто затіньте область на осі x. Для опису домену використовуйте нотації interval та set-builder.

iii. Використовуйте чисто алгебраїчну техніку, як показано в прикладі 8 в оповіданні, щоб знайти область. Порівняйте цей результат з результатом, знайденим у частині (ii).

IV. Використовуючи олівець іншого кольору, спроектуйте кожну точку на графіку на вісь y; тобто затіньте діапазон на осі y. Використовуйте інтервал і позначення set-builder для опису діапазону.

Вправа$\PageIndex{27}$

$f(x) = \sqrt{x + 5}$.

Відповідь

Завантажте функцію$f(x) = \sqrt{x + 5}$ в Y1, як показано в (a). Виберіть 6:ZStandrd в меню ZOOM, щоб створити графік у (b).

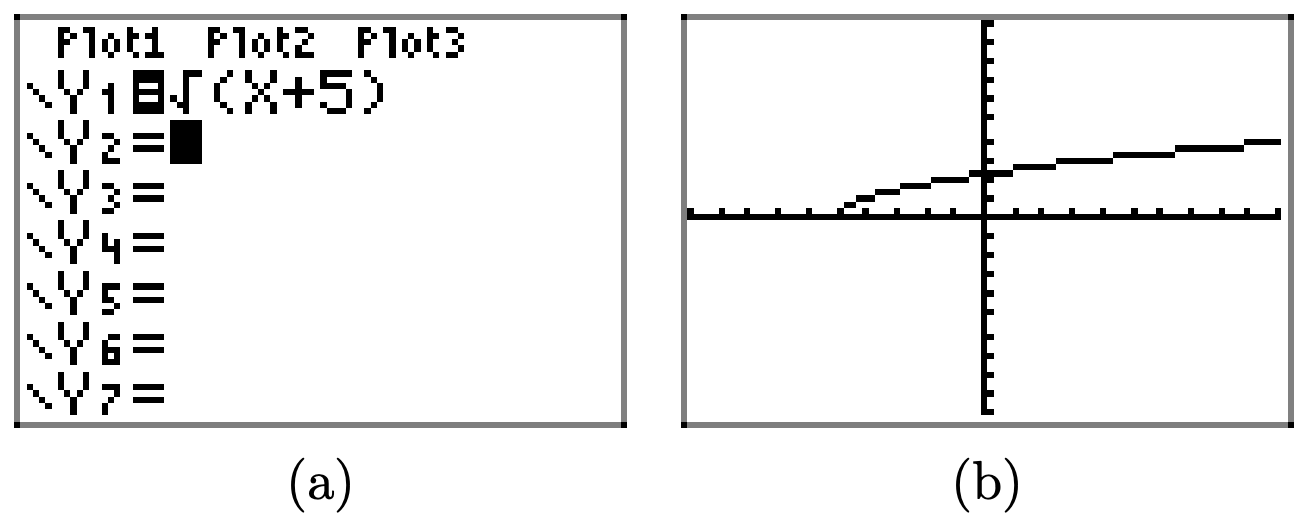
Скопіюйте зображення в (b) на домашній папір, а потім спроектуйте область та діапазон на осі x та y, як показано в (c) та (d) відповідно.

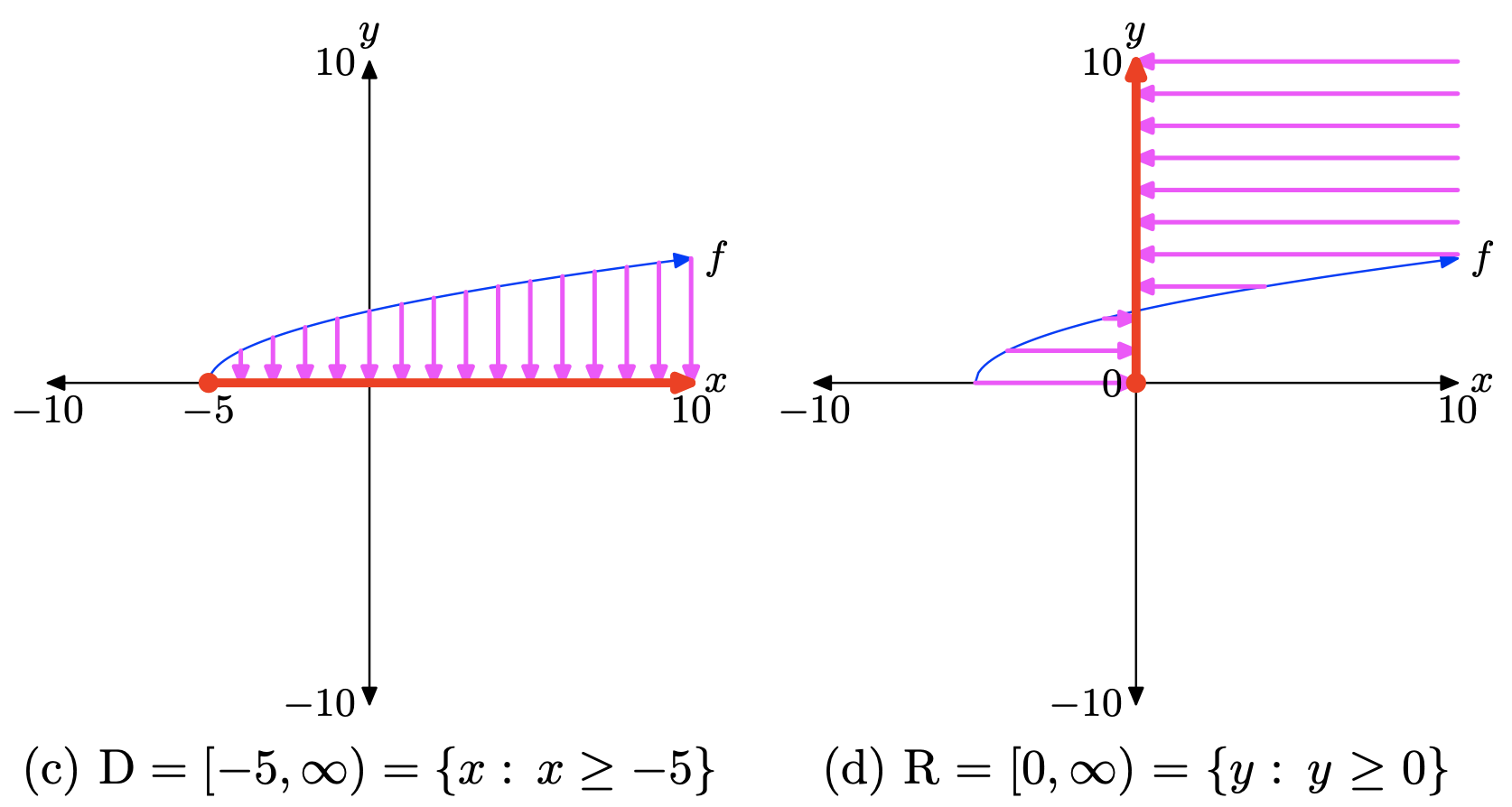
Щоб знайти домен алгебраїчно, зверніть увагу, що ви не можете взяти квадратний корінь від'ємного числа, тому вираз під радикалом in$f(x) = \sqrt{x + 5}$, а саме x+5, має бути або додатним, або нульовим (невід'ємним). Тобто,

$$x + 5 \geq 0$$

або еквівалентно,

$$x\geq -5$$

Таким чином, доменом f є Domain =$[−5,\infty)$, або в позначенні set-builder, Domain =${x : x \geq −5}$.

Вправа$\PageIndex{28}$

$f(x) = \sqrt{5-x}$

Вправа$\PageIndex{29}$

$f(x) = − \sqrt{4 − x}$.

Відповідь

Завантажте функцію$f(x) = − \sqrt{4 − x}$. в Y1, як показано в (a). Виберіть 6:ZStandrd в меню ZOOM, щоб створити графік у (b).

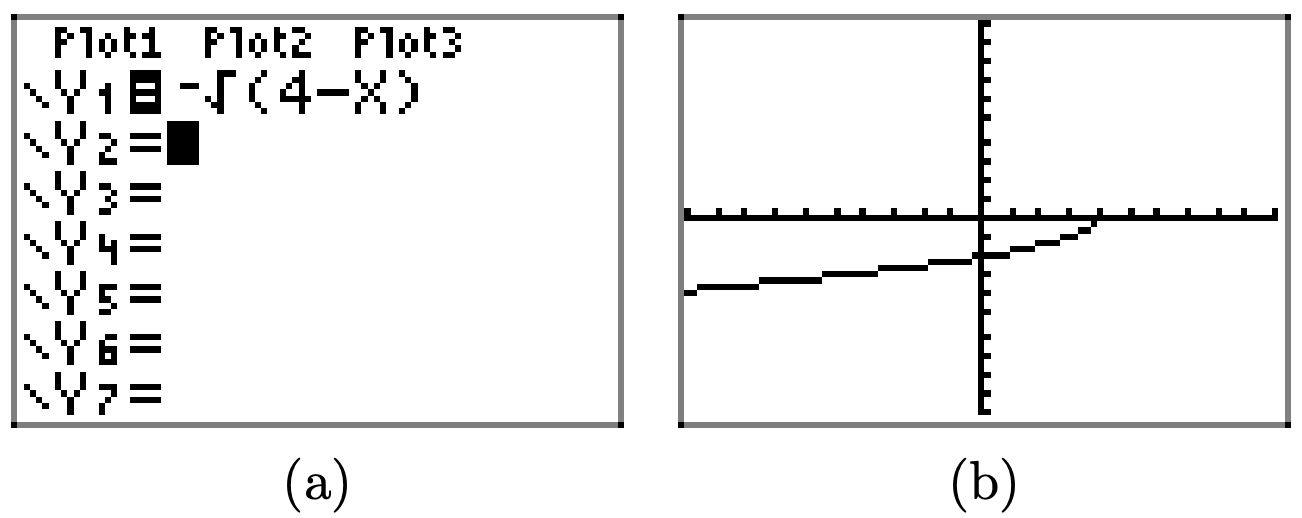
Скопіюйте зображення в (b) на домашній папір, а потім спроектуйте область та діапазон на осі x та y, як показано в (c) та (d) відповідно.

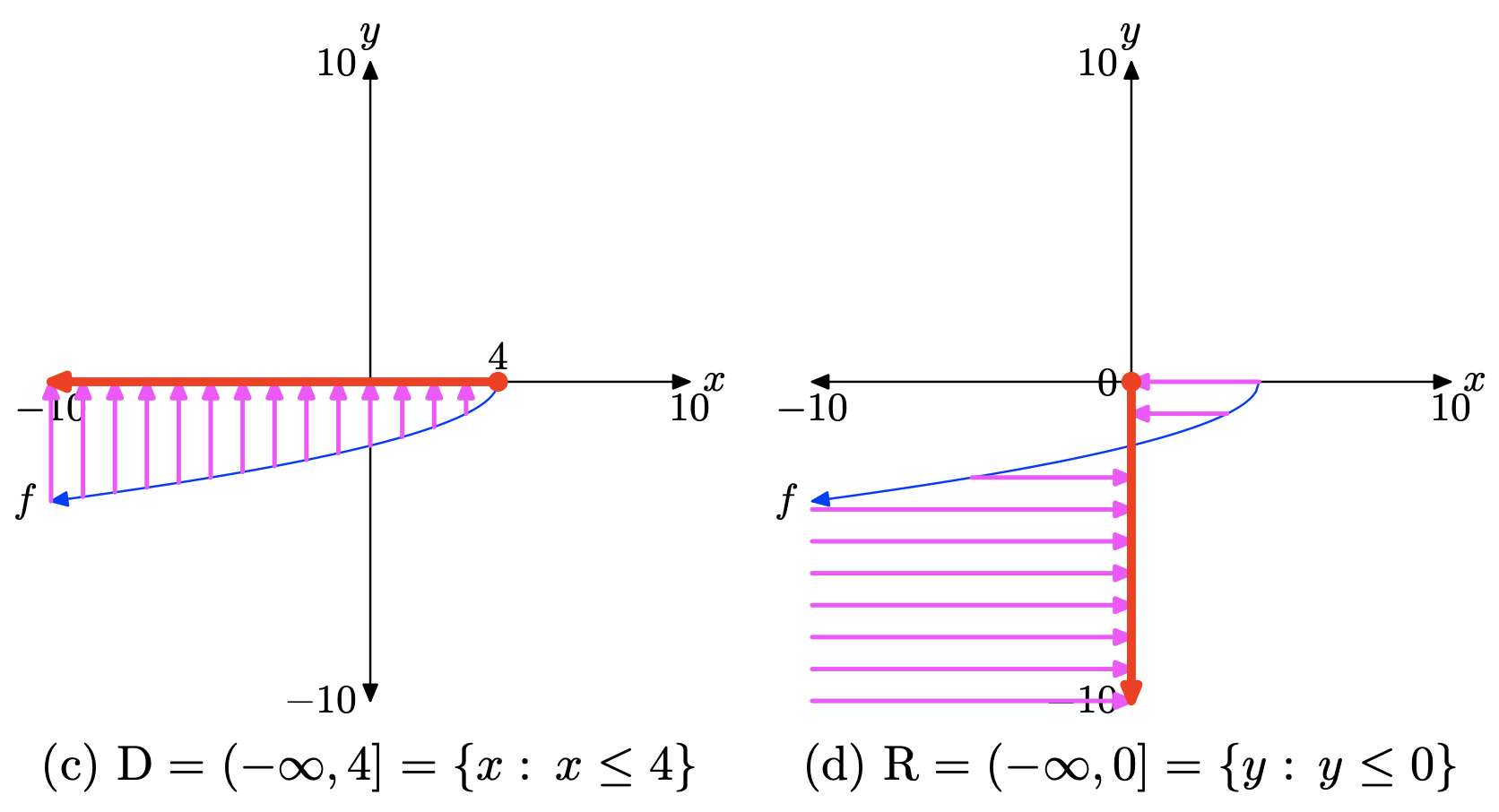
Щоб знайти область алгебраїчно, зауважте, що ви не можете взяти квадратний корінь від'ємного числа, тому вираз під радикалом in$f(x) = − \sqrt{4 − x}$, а саме 4−x, має бути додатним або нулем (невід'ємним). Тобто,

$$4-x\geq 0$$

або еквівалентно,

$$-x \geq -4 \\ x\leq 4$$

Таким чином, доменом f є Domain =$(\infty, 4]$, або в позначенні set-builder, Domain =$\{x : x \leq 4\}$.

Вправа$\PageIndex{30}$

$f(x) = − \sqrt{x + 4}$

2.4 Вправи

У Вправи$\PageIndex{1}$ -$\PageIndex{6}$ дається визначення двох функцій f і g. порівняйте функції, як у прикладі 1 оповідання, при заданих значеннях x.

Вправа$\PageIndex{1}$

f (x) = x+2, g (x) = 4−x при х = −3, 1 і 2.

Відповідь

Задано, що f (x) = x + 2 і g (x) = 4 − x, при x = −3,

$$f(−3) = −3 + 2 = −1 \\ g(−3) = 4 − (−3) = 7$$

Отже, f (−3) < g (−3). При х = 1,

$$f(1) = 1 + 2 = 3 \\ g(1) = 4 − 1 = 3.$$

Тому f (1) = g (1). При х = 2,

$$f(2) = 2 + 2 = 4 \\ g(2) = 4 − 2 = 2.$$

Тому f (2) > g (2).

Вправа$\PageIndex{2}$

f (x) = 2x − 3, g (x) = 3 − х при x = −4, 2 та 5.

Вправа$\PageIndex{3}$

f (x) = 3−x, g (x) = x+9 при x = −4, −3 та −2.

Відповідь

Ми задані, що f (x) = 3 − x і g (x) = x + 9. При х = −4,

$$f(−4) = 3 − (−4) = 7 \\ g(−4) = −4 + 9 = 5$$

Отже, f (−4) > g (−4). При х = −3,

$$f(−3) = 3 − (−3) = 6 \\ g(−3) = −3 + 9 = 6$$

Отже, f (−3) = g (−3). При х = −2,

$$f(−2) = 3 − (−2) = 5 \\ g(−2) = −2 + 9 = 7$$

Отже, f (−2) < g (−2).

Вправа$\PageIndex{4}$

$f(x) = x^2$, g (x) = 4х + 5 при х = −2, 1 і 6.

Вправа$\PageIndex{5}$

$f(x) = x^2$, g (x) = −3x − 2 при x = −3, −1 та 0.

Відповідь

Ми задані, що$f(x) = x^2$ і g (x) = −3x − 2. При х = −3,

$$f(−3) = (−3)2 = 9 \\ g(−3) = −3(−3) − 2 = 7$$

Отже, f (−3) > g (−3). При х = −1,

$$f(−1) = (−1)2 = 1 \\ g(−1) = −3(−1) − 2 = 1$$

Отже, f (−1) = g (−1). При х = 0,

$$f(0) = (0)2 = 0 \\ g(0) = −3(0) − 2 = −2$$

Тому f (0) > g (0).

Вправа$\PageIndex{6}$

f (x) = |x|, g (x) = 4 − х при х = 1, 2 і 3.

У Вправи$\PageIndex{7}$ -$\PageIndex{12}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

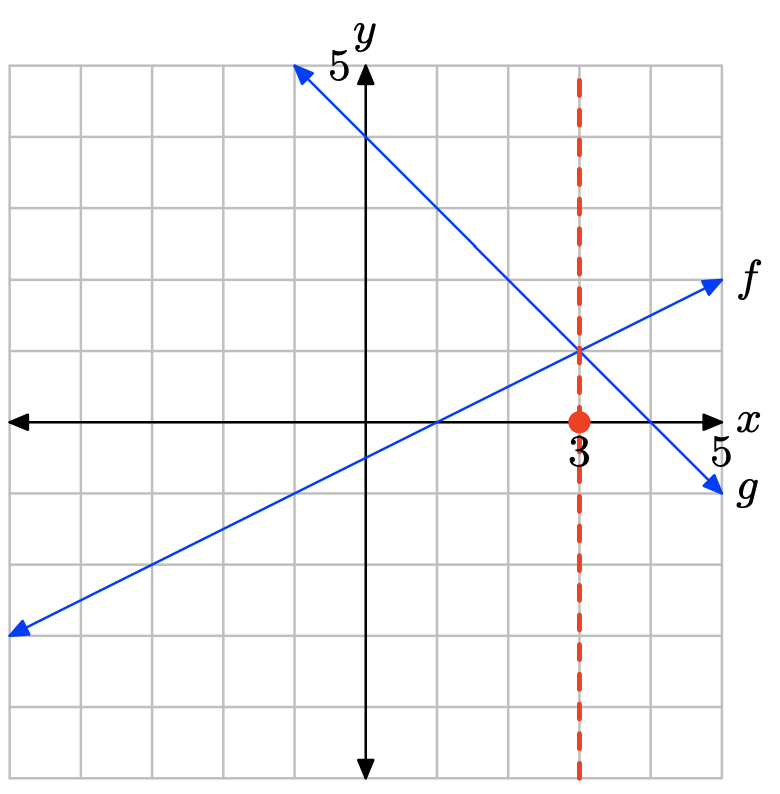
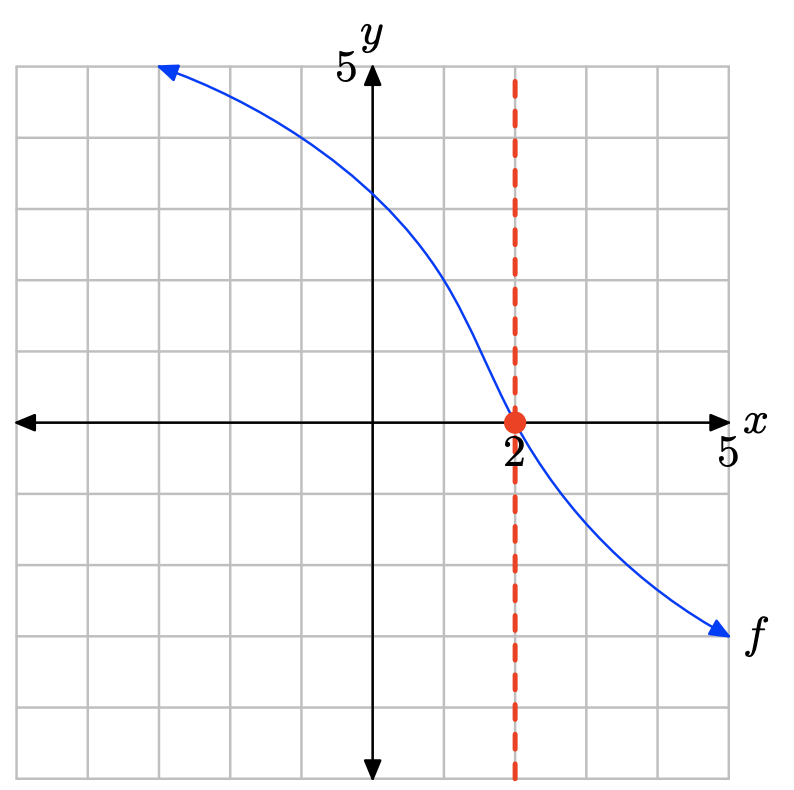
i. Зробіть точну копію зображення на графічному папері (позначте кожне рівняння, позначте і масштабуйте кожну вісь), пропустіть пунктирну вертикальну лінію через точку перетину, потім позначте і затіньте рішення f (x) = g (x) на осі x.

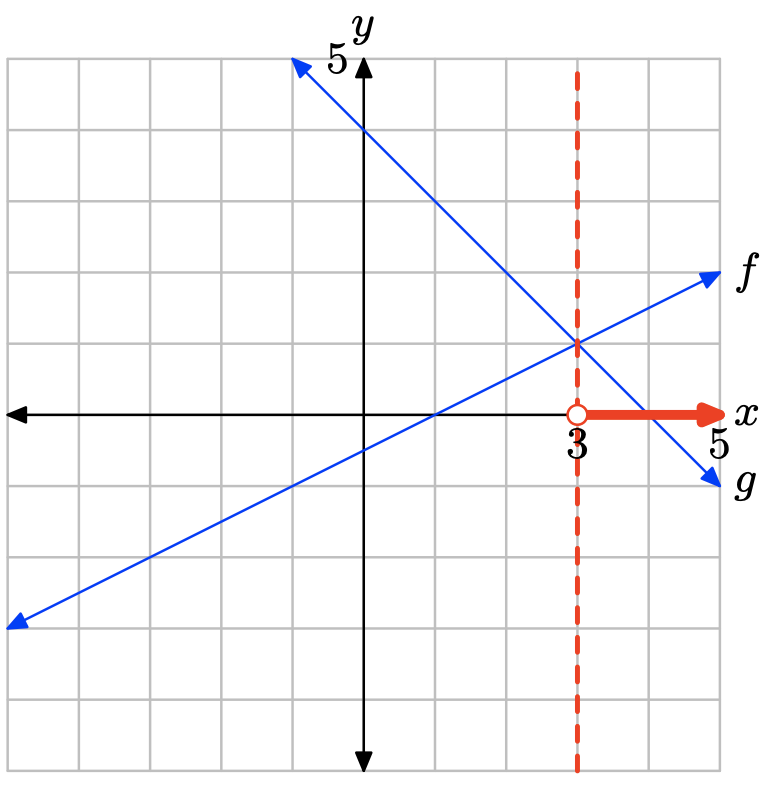
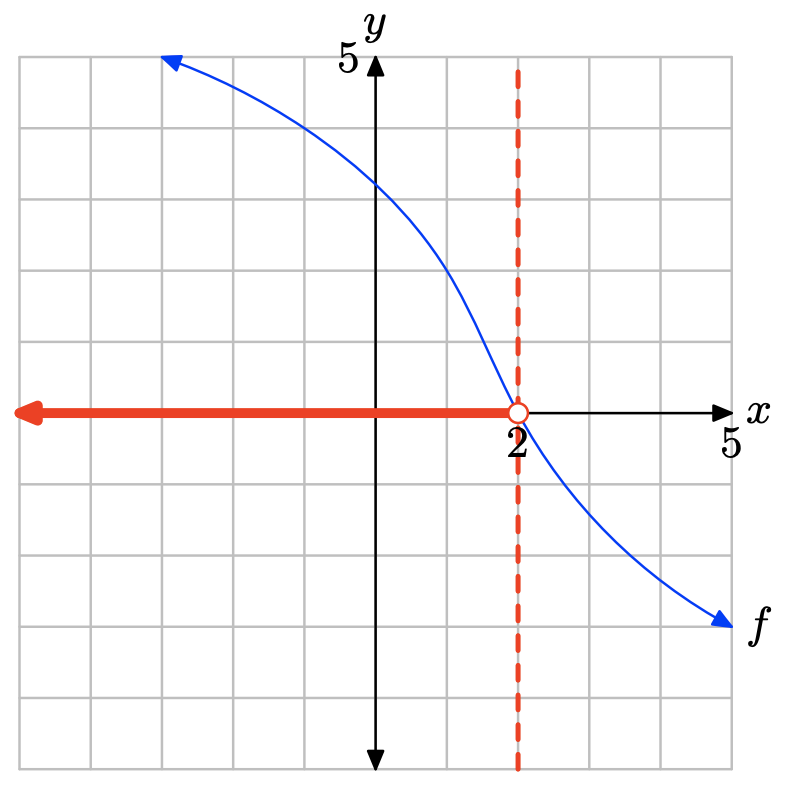
II. Зробіть другу копію зображення на графічному папері, перетягніть пунктирну вертикальну лінію через точку перетину, потім позначте і затіньте рішення f (x) > g (x) на осі x. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

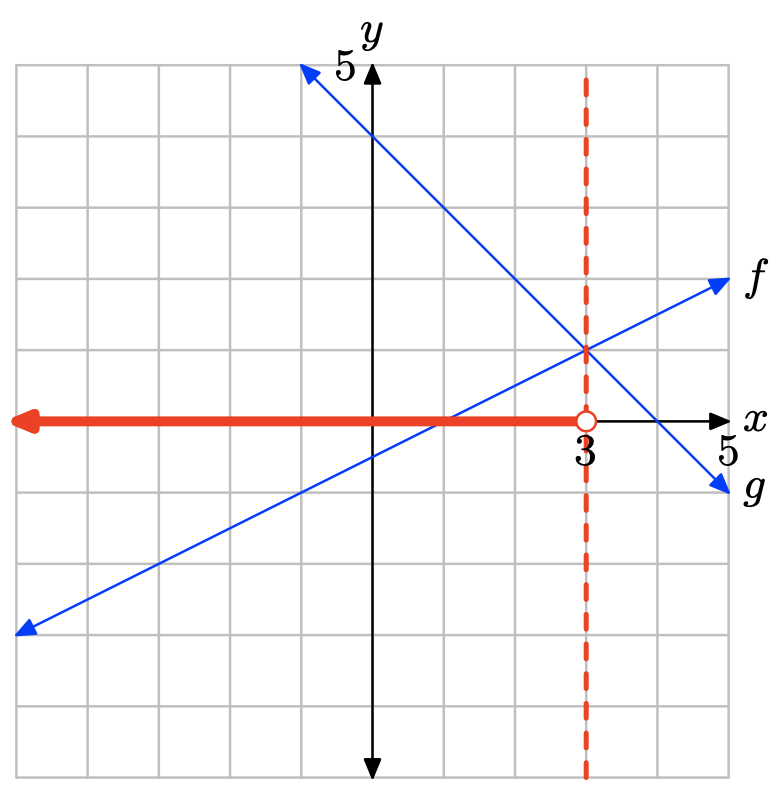
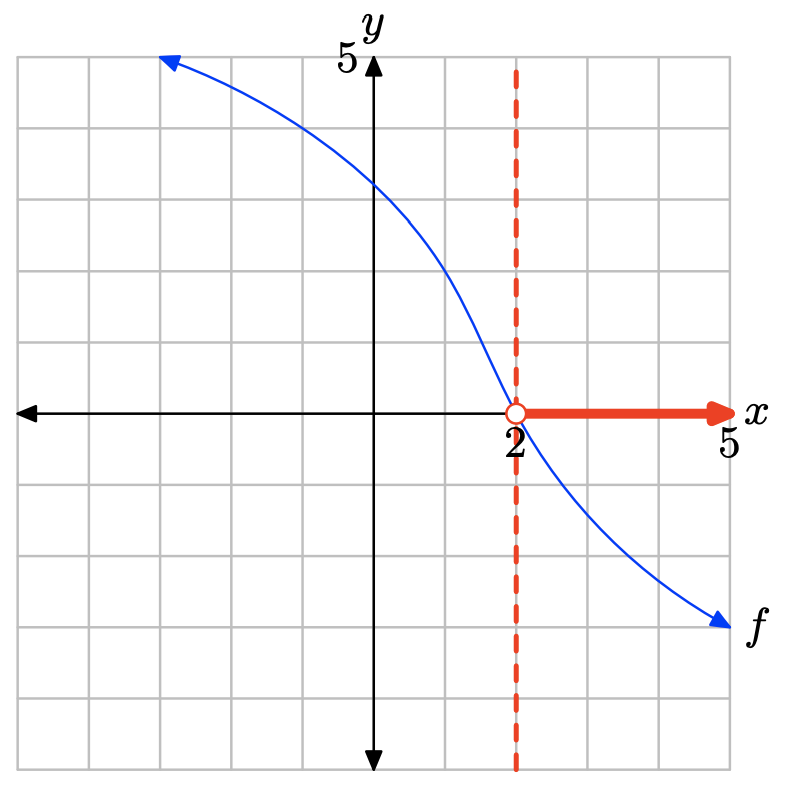
iii. Створіть третю копію зображення на графічному папері, перетягніть пунктирну вертикальну лінію через точку перетину, потім позначте і затіньте рішення f (x) < g (x) на осі x. Використовуйте setbuilder та інтервальні позначення для опису вашого набору рішень.

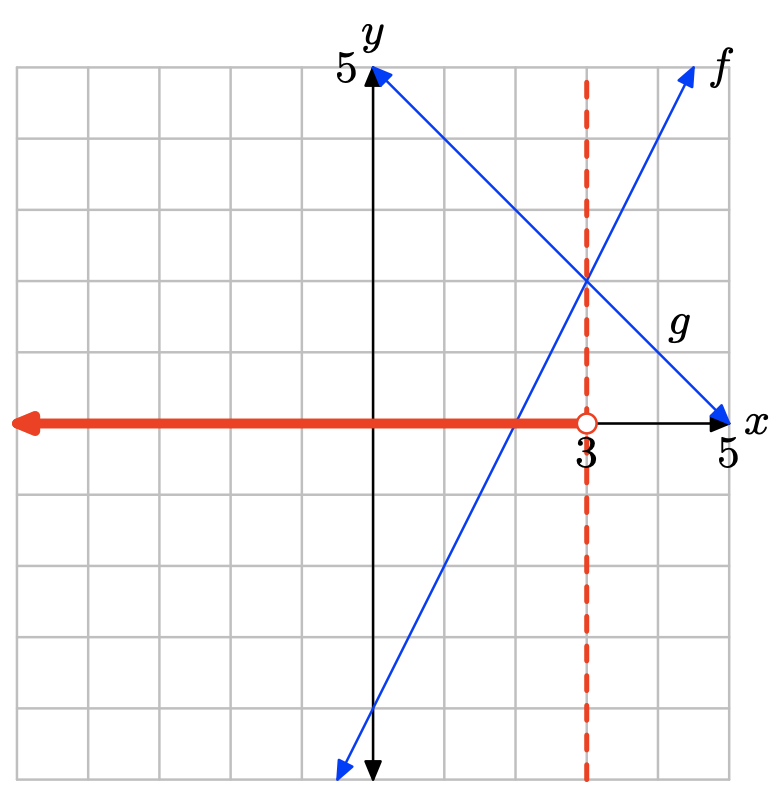
Вправа$\PageIndex{7}$

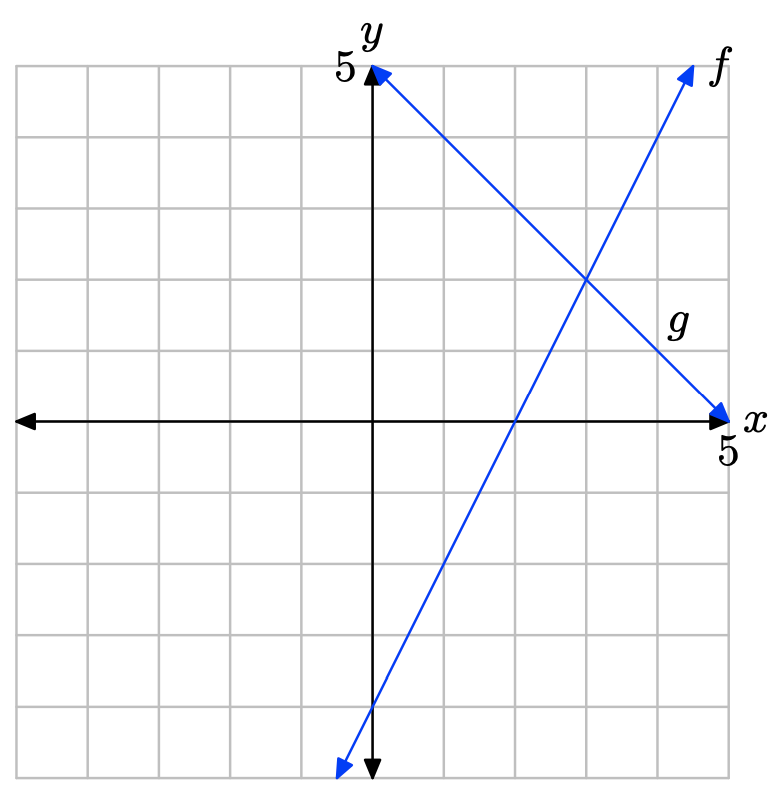
Відповідь

Графік f перетинає граф g при x = 3. Розчин f (х) = g (х) дорівнює х = 3.

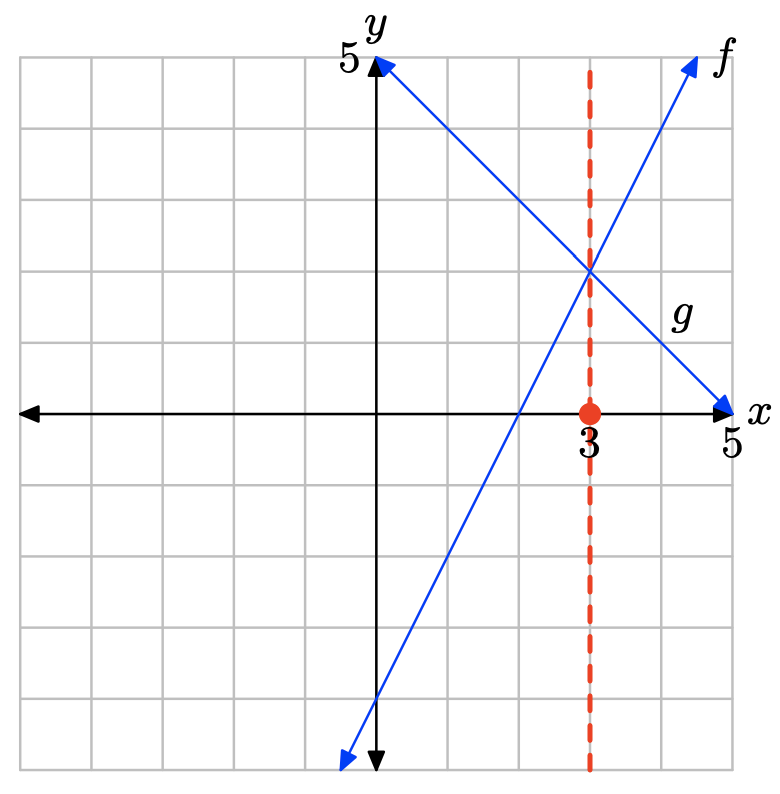
Графік f лежить над графом g праворуч від x = 3. Розчин f (x) > g (x) дорівнює$(3,\infty) = \{x : x > 3\}$.

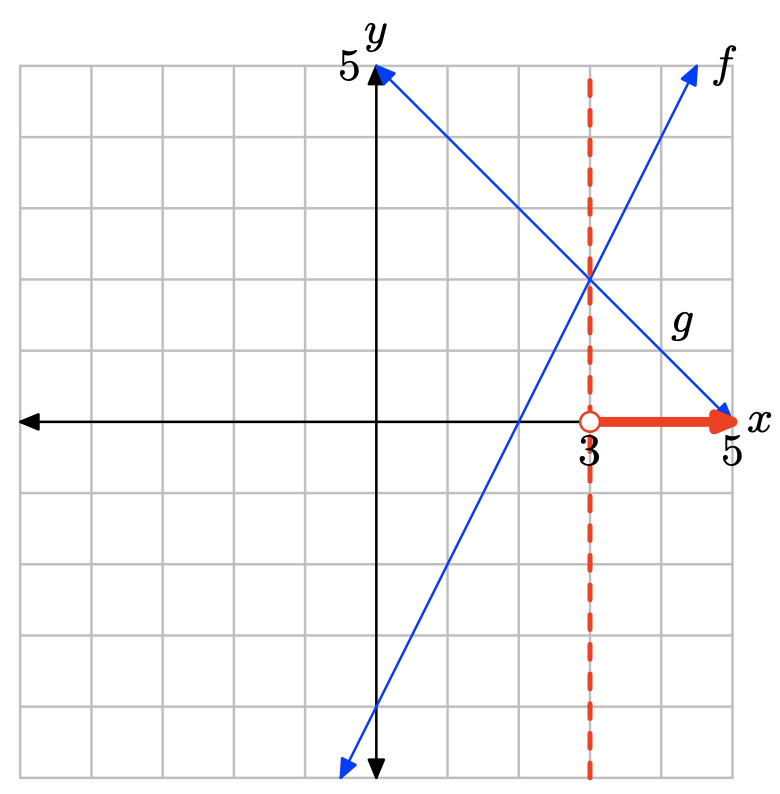
Графік f лежить нижче графіка g зліва від x = 3. Розчин f (x) < g (x) дорівнює$(−\infty, 3) = \{x : x < 3\}$.

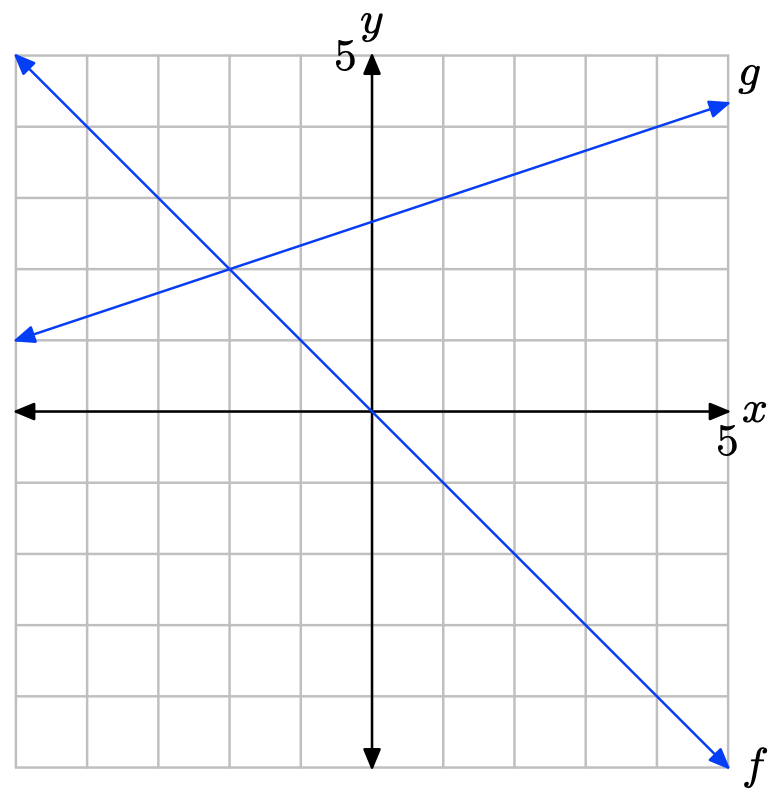
Вправа$\PageIndex{8}$

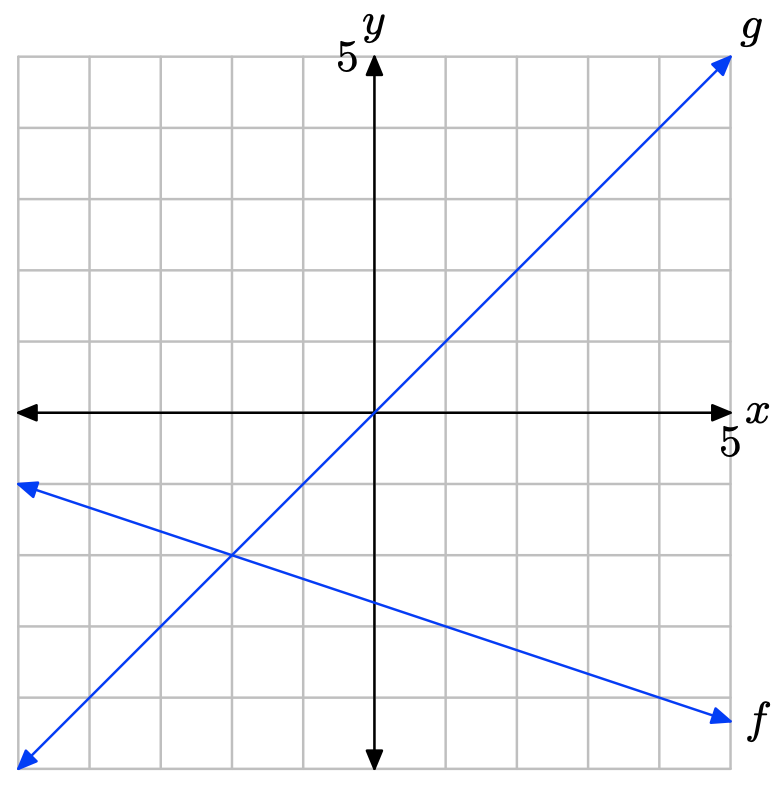
Вправа$\PageIndex{9}$

Відповідь

Графік f перетинає граф g при x = −2. Розв'язок f (x) = g (x) дорівнює x = −2.

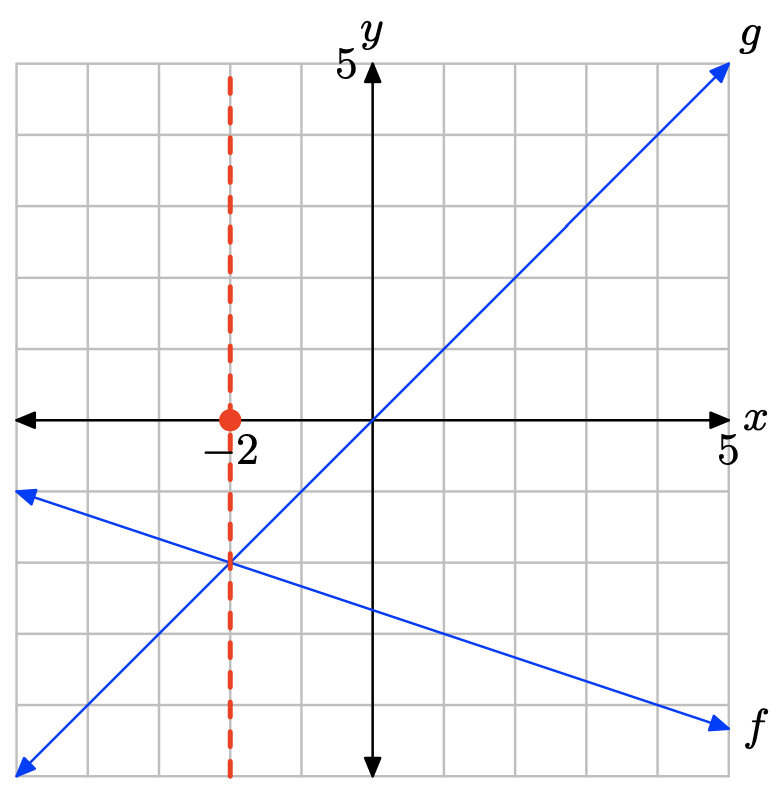
Графік f лежить над графом g ліворуч від x = −2. Розчин f (x) > g (x) дорівнює$(−\infty, −2) = \{x : x < −2\}$.

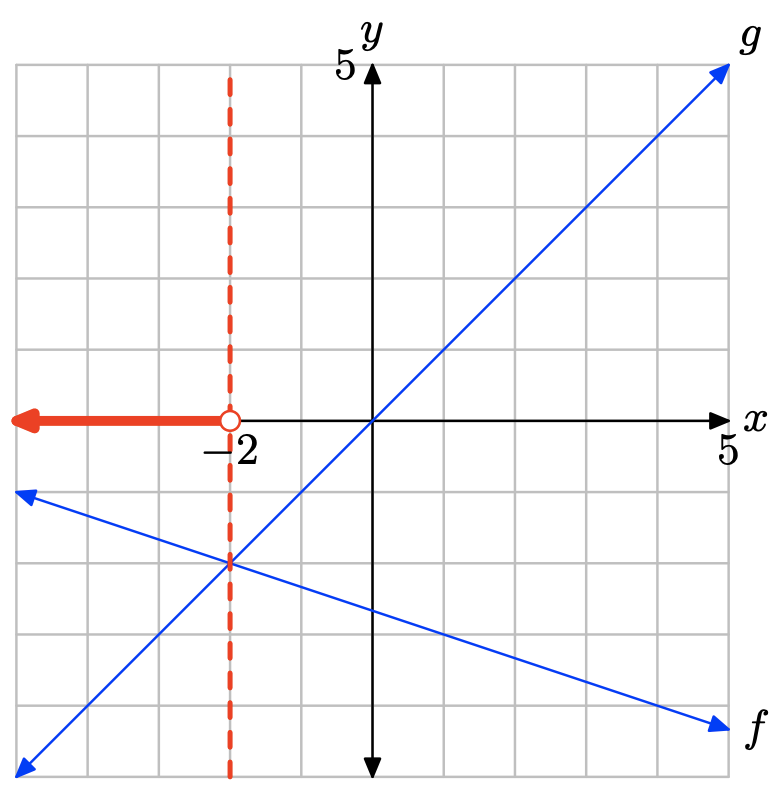
Графік f лежить нижче графа g праворуч від x = −2. Розчин f (x) < g (x) дорівнює$(−2,\infty) = {\x : x > −2\}$.

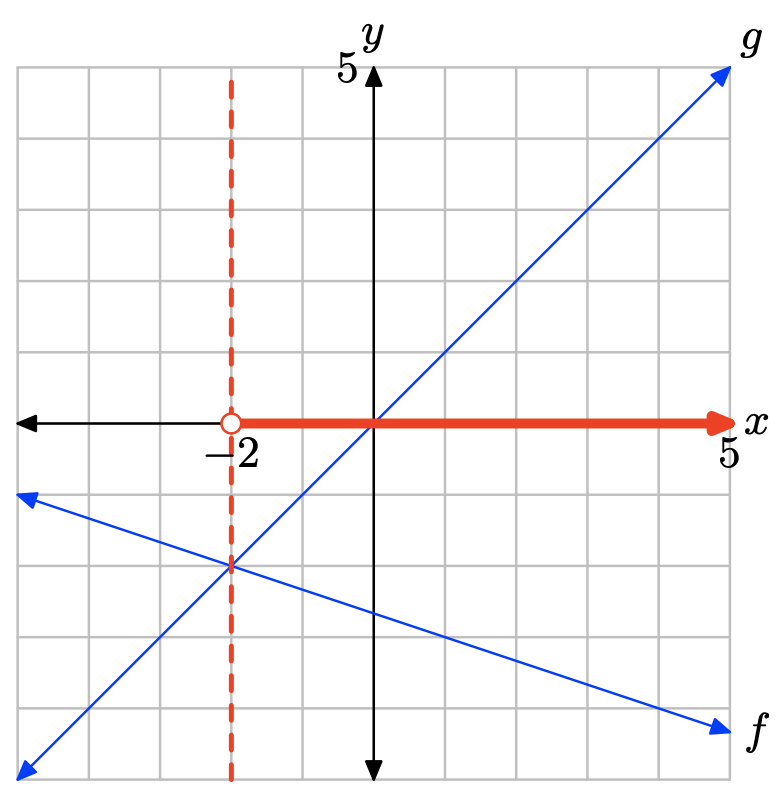
Вправа$\PageIndex{10}$

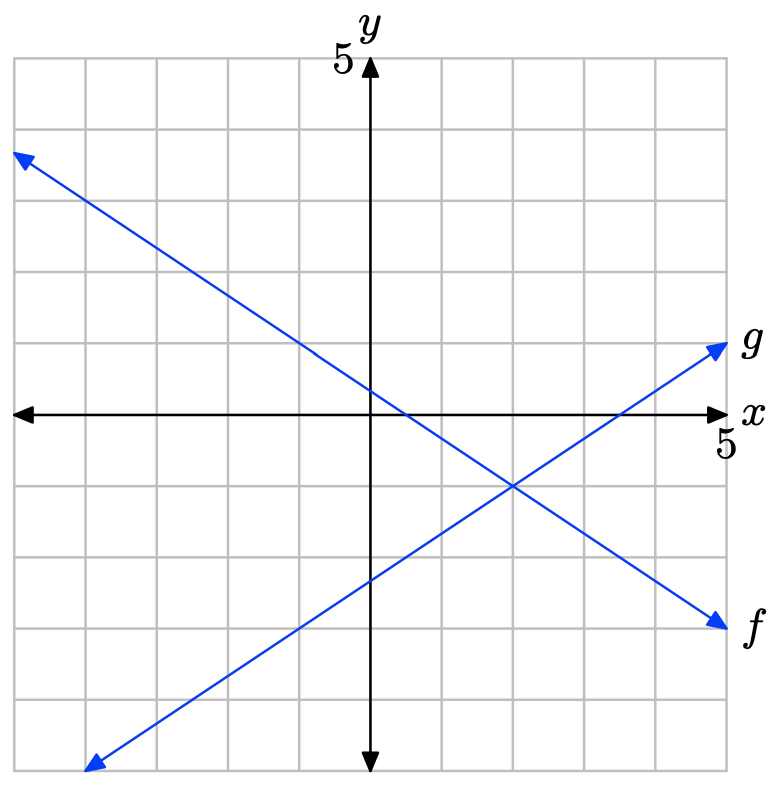
Вправа$\PageIndex{11}$

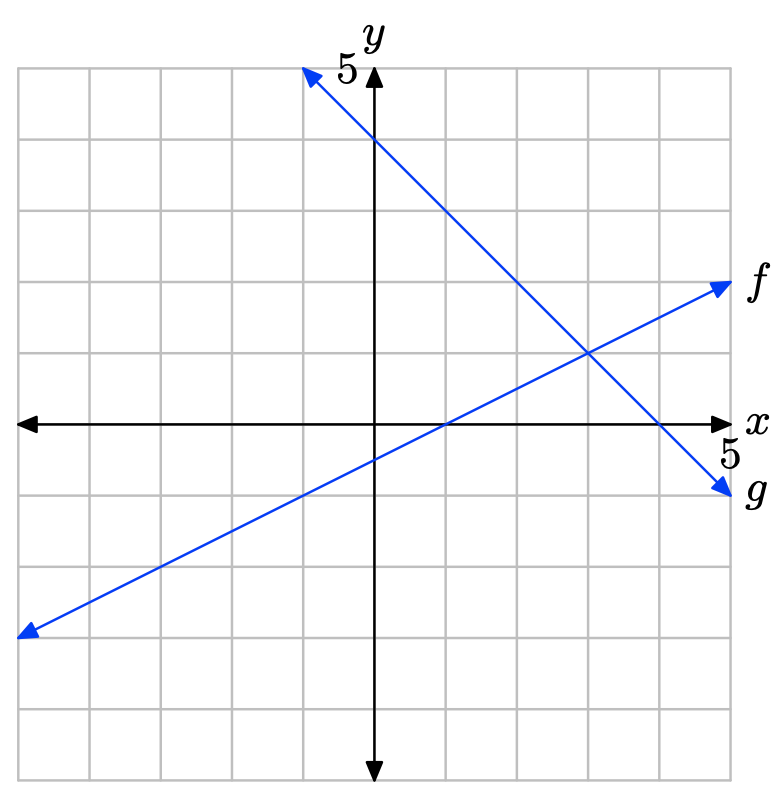
Відповідь

Графік f перетинає граф g при x = 3. Розчин f (х) = g (х) дорівнює х = 3.

Графік f знаходиться над графом g праворуч від x = 3. Розчин f (x) > g (x) дорівнює$(3,\infty) = \{x : x > 3\}$.

Графік f знаходиться нижче графіка g зліва від x = 3. Розчин f (x) < g (x) дорівнює$(−\infty, 3) = \{x : x < 3\}$.

Вправа$\PageIndex{12}$

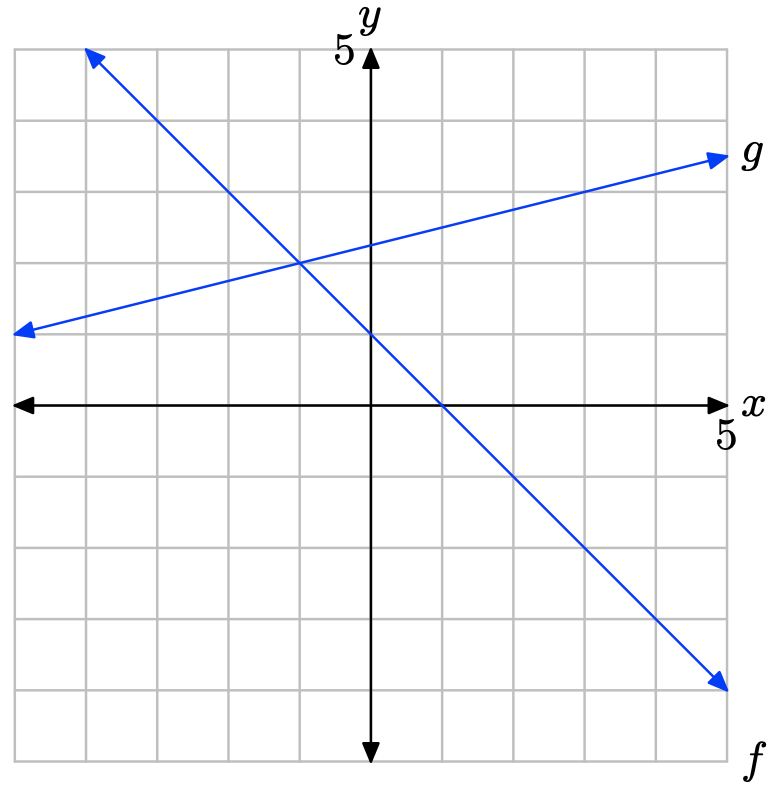
У Вправи$\PageIndex{13}$ -$\PageIndex{16}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Зробіть точну копію зображення на графічному папері, перекиньте пунктирні, вертикальні лінії через точки перетину, потім позначте і затіньте рішення$f(x) \geq g(x)$ на осі х. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

II. Зробіть другу копію зображення на графічному папері, перетягніть пунктирні вертикальні лінії через точки перетину, потім позначте і затіньте рішення f (x) < g (x) на осі x. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

Вправа$\PageIndex{13}$

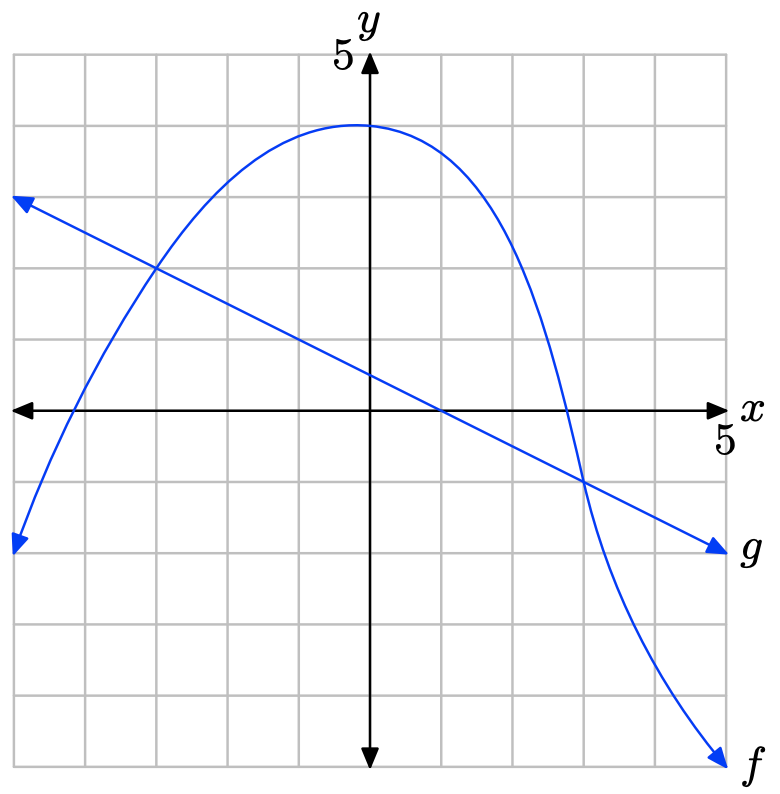
Відповідь

Графік f перетинає граф g при x = −3 і x = 3. Графік f лежить над графом g для значень x, що знаходяться між −3 та 3. Тому рішення$f(x) \geq g(x)$ є$[−3, 3] = \{x : −3 \leq x \leq 3\}$.

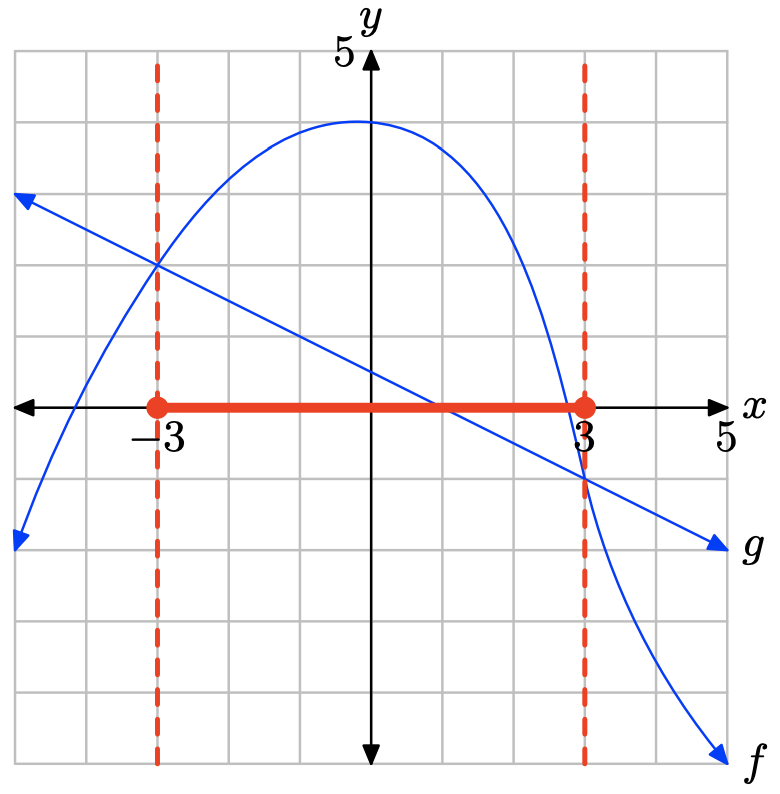
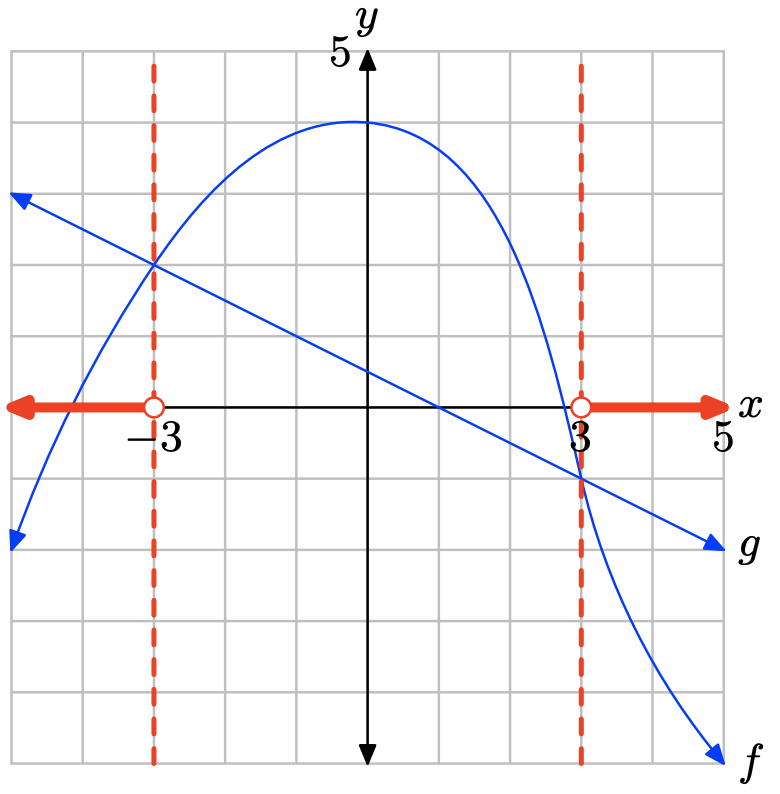
Графік f знаходиться нижче графіка g для значень x, що лежать ліворуч від −3 або праворуч від 3. Тому розчином f (x) < g (x) є$(−\infty, −3) \cup (3,\infty)$ або$\{x : x < −3 or x > 3\}$.

Вправа$\PageIndex{14}$

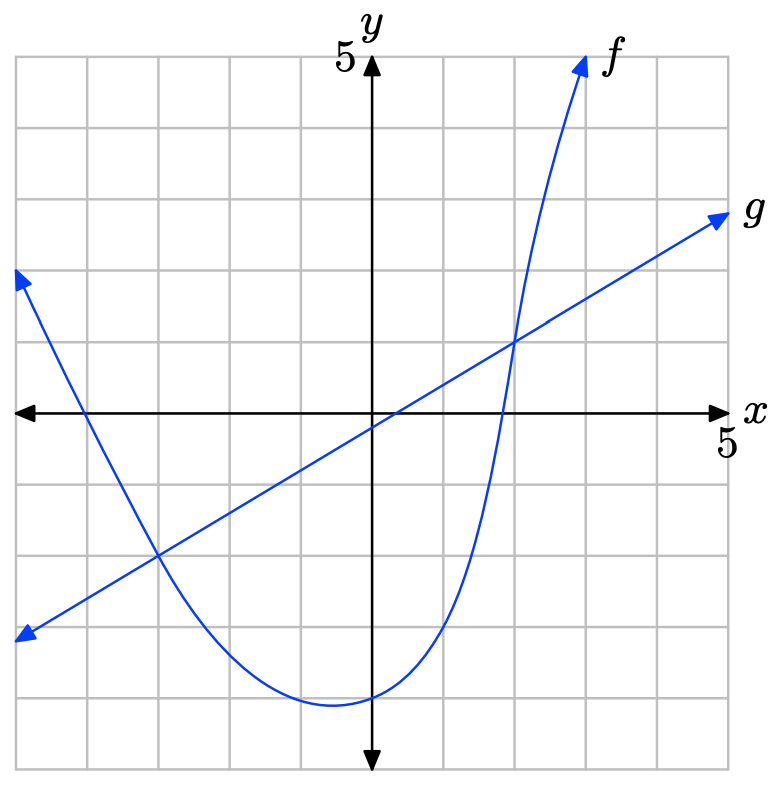
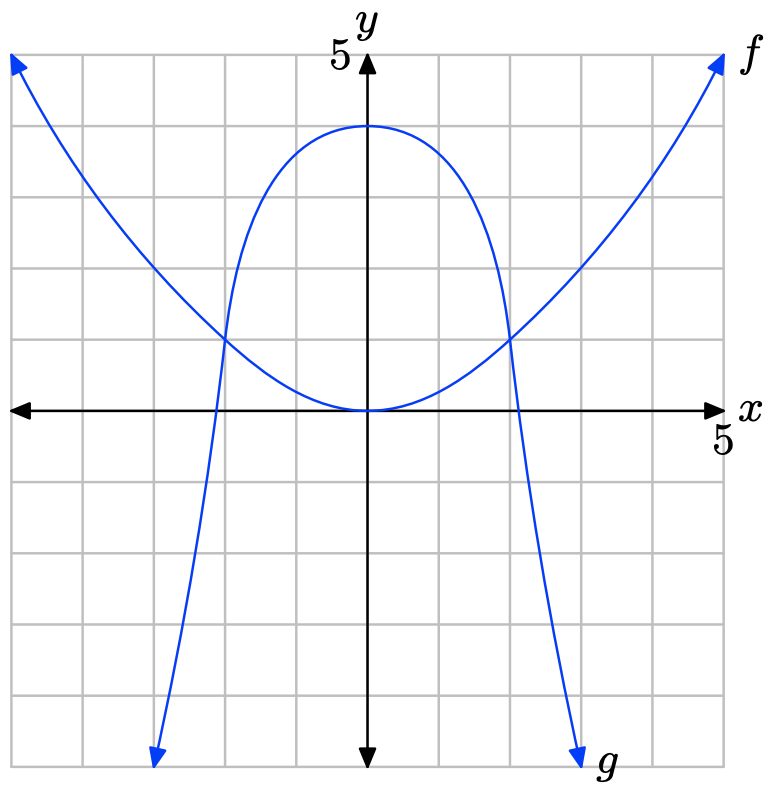
Вправа$\PageIndex{15}$

Відповідь

Графік f перетинає граф g при x = −2 і при x = 2. Графік f лежить над графом g для всіх значень x, що лежать ліворуч від −2 або праворуч від 2. Тому рішення$f(x) \geq g(x)$ є$(−\infty, −2] \cup [2,\infty)$ або$\{x : x \leq −2 or x \geq 2\}$.

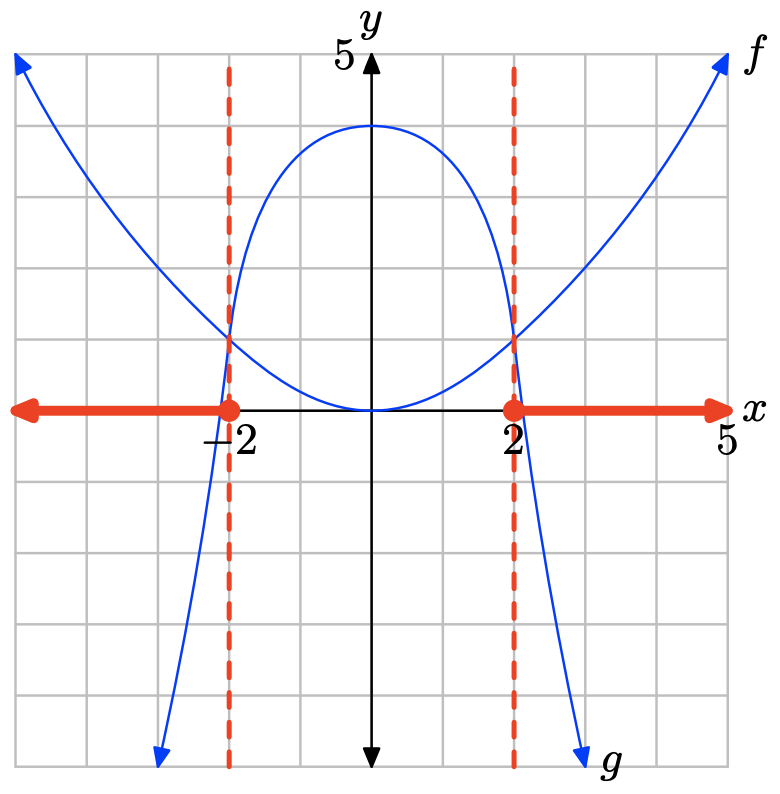
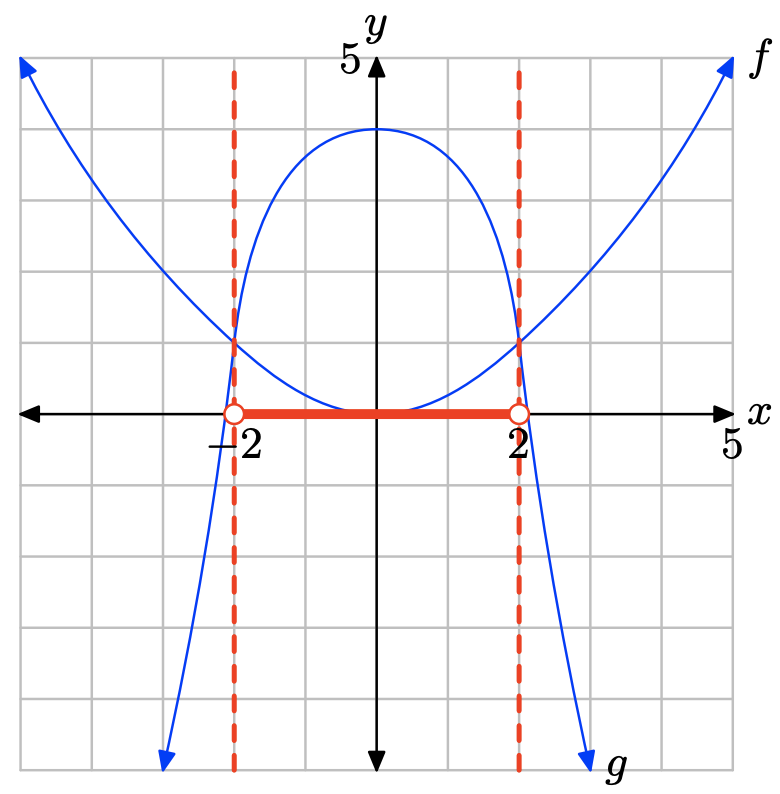
Графік f лежить нижче графіка g для значень x, що знаходяться між −2 та 2. Тому розчином f (x) < g (x) є$(−2, 2) = \{x : −2 < x < 2\}$.

Вправа$\PageIndex{16}$

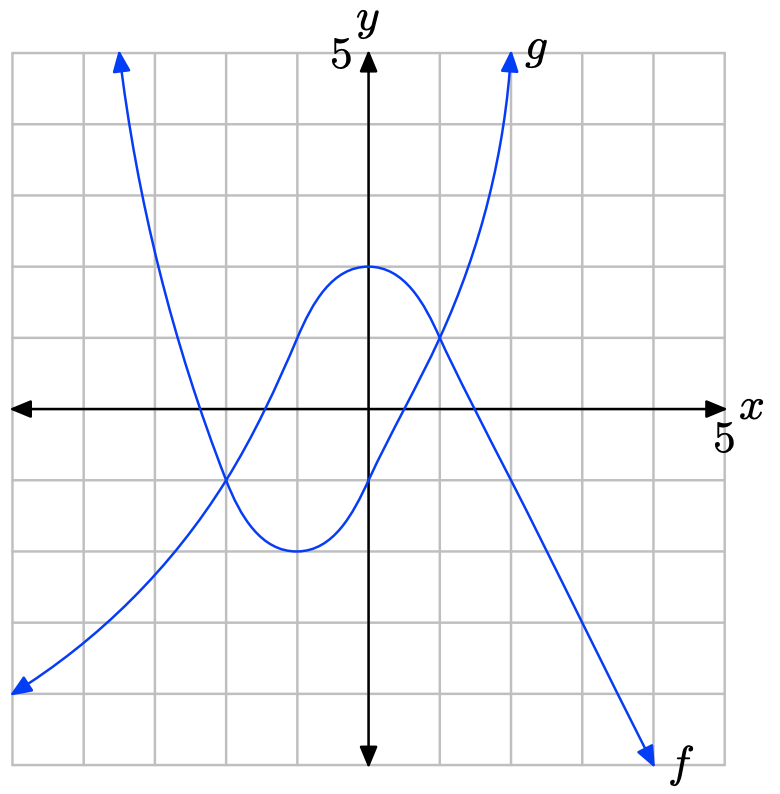
У Вправи$\PageIndex{17}$ -$\PageIndex{20}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Завантажте кожну сторону рівняння в меню Y = вашого калькулятора. Налаштуйте параметри WINDOW так, щоб точка перетину графіків була видна у вікні перегляду. Використовуйте утиліту intersect в меню CALC вашого калькулятора, щоб визначити координату x точки перетину.

II. Зробіть точну копію зображення у вікні перегляду на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax та позначте кожен графік своїм рівнянням.

iii. Проведіть пунктирну вертикальну лінію через точку перетину. Заштрихуйте і позначте рішення рівняння на осі х.

Вправа$\PageIndex{17}$

1.23x − 4.56 = 3.46 − 2,3х

Відповідь

Щоб розв'язати рівняння 1,23x − 4,56 = 3,46 − 2,3x графічно, почніть із завантаження лівої та правої частини рівняння у Y1 та Y2 відповідно, як показано в (а). Використовуйте утиліту intersect в меню CALC, щоб визначити точку перетину, як показано в (c).

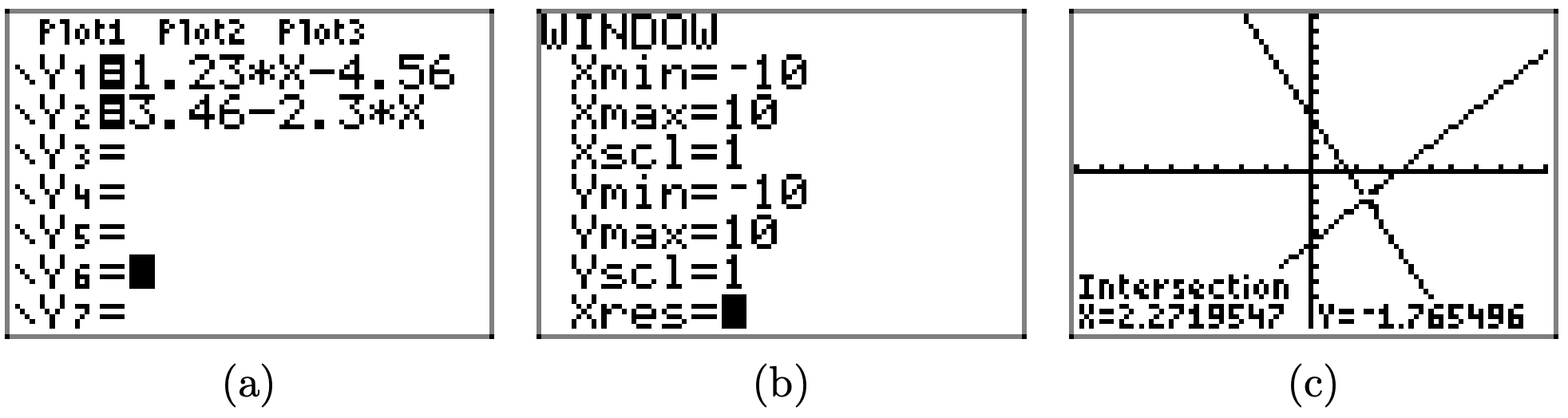
Тому рішення рівняння х = 2.2719547, яке затінено на осі х на наступному зображенні. Відповіді можуть відрізнятися через помилку округлення.

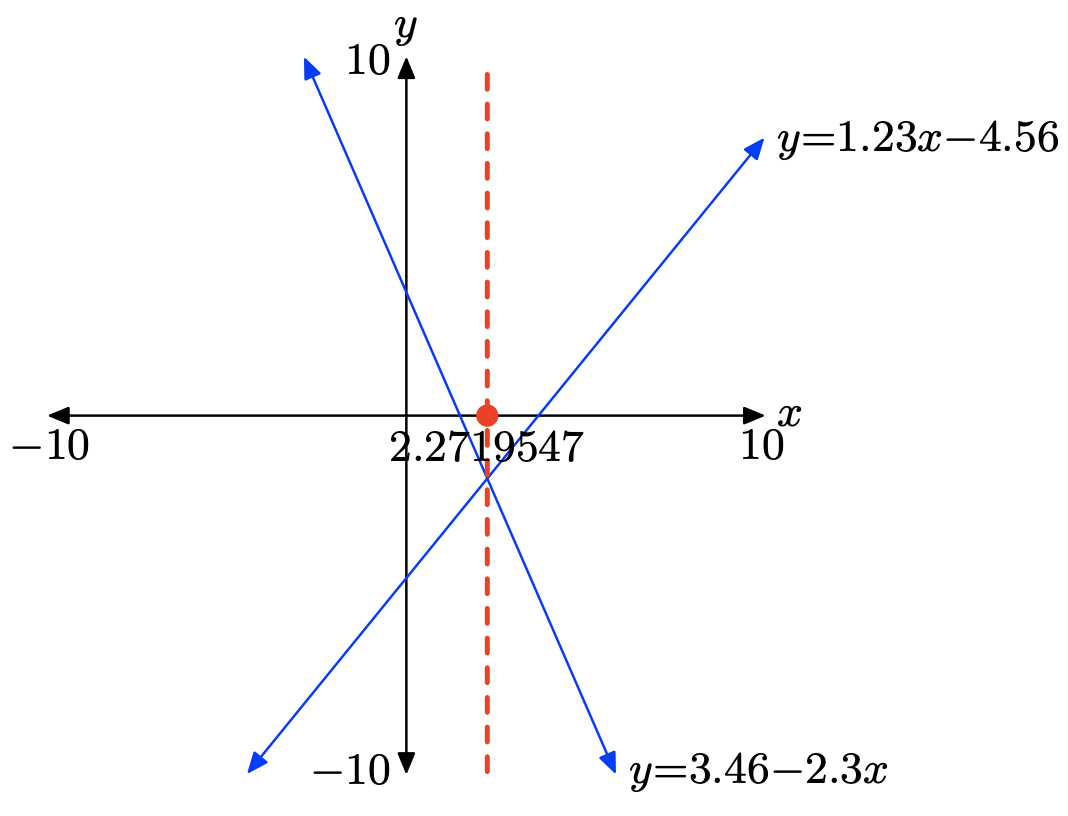
Вправа$\PageIndex{18}$

2.23x − 1.56 = 5.46 − 3,3х

Вправа$\PageIndex{19}$

5.46 − 1.3х = 2.2х − 5.66

Відповідь

Щоб розв'язати рівняння 5.46 − 1.3x = 2.2x − 5.66 графічно, почніть із завантаження лівої та правої частини рівняння в Y1 і Y2 відповідно, як показано в (а). Використовуйте утиліту intersect в меню CALC, щоб визначити точку перетину, як показано в (c).

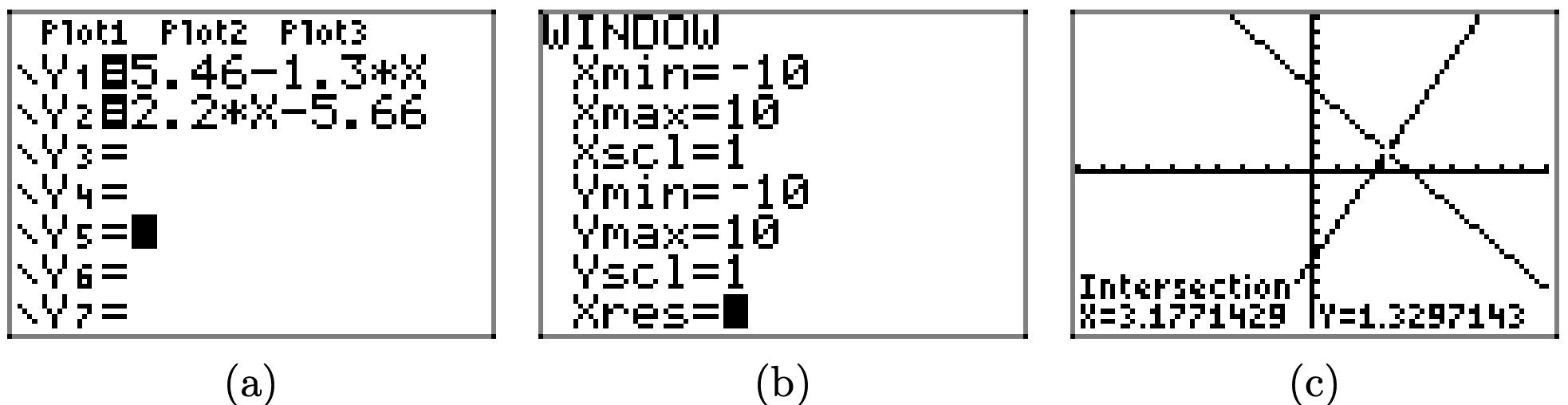
Тому рішення рівняння х = 3,171429, яке затінено на осі х на наступному зображенні. Відповіді можуть відрізнятися через помилку округлення.

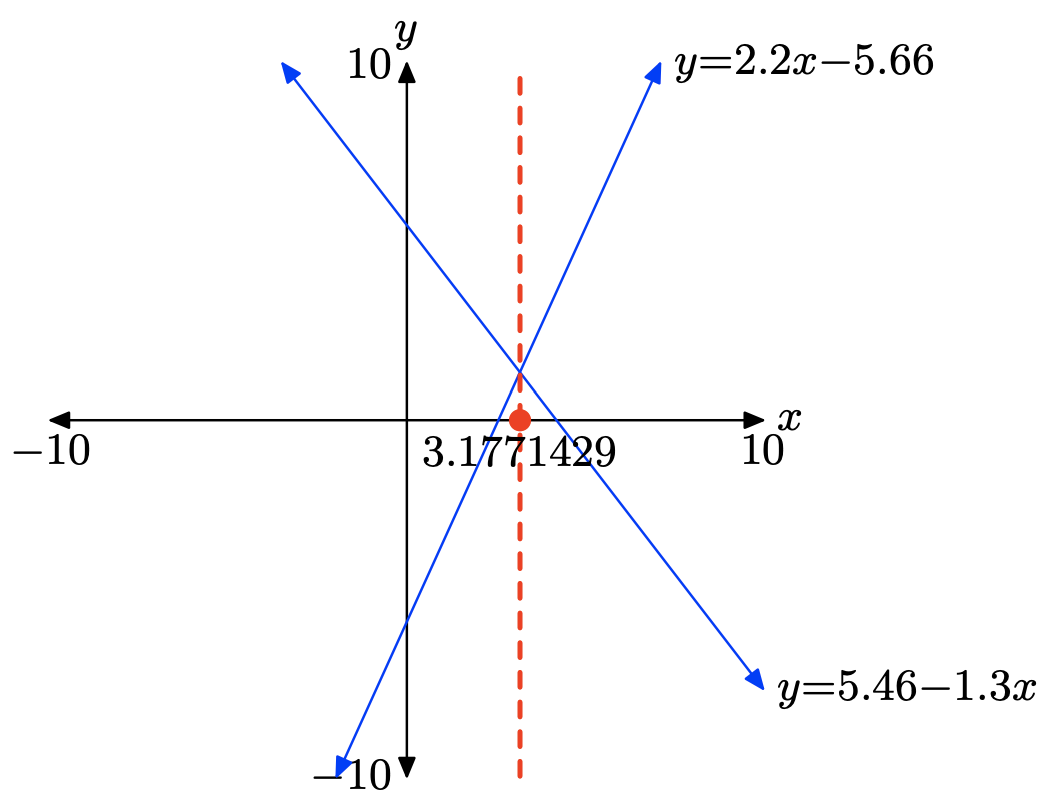
Вправа$\PageIndex{20}$

2.46 − 1.4х = 1.2х − 2.66

У Вправи$\PageIndex{21}$ -$\PageIndex{26}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Завантажте кожну сторону нерівності в меню Y= вашого калькулятора. Налаштуйте параметри WINDOW таким чином, щоб точка (и) перетину графіків була видима у вікні перегляду. Використовуйте утиліту intersect в меню CALC вашого калькулятора, щоб визначити координати точки (ів) перетину.

II. Зробіть точну копію зображення у вікні перегляду на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax та позначте кожен графік своїм рівнянням.

iii. Намалюйте пунктирну вертикальну лінію через точку (и) перетину. Затіньте і позначте розв'язку нерівності на осі x. Використовуйте як set-builder, так і інтервальні позначення для опису набору рішень.

Вправа$\PageIndex{21}$

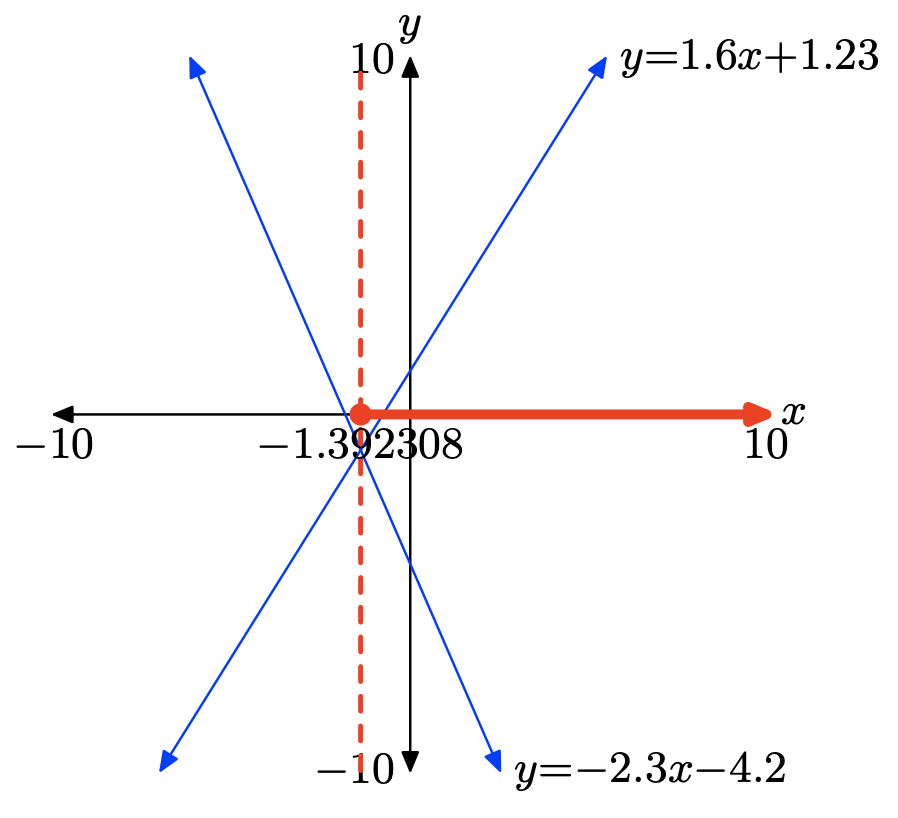
$1.6x + 1.23 \geq −2.3x − 4.2$

Відповідь

Щоб розв'язати нерівність$1.6x+1.23 \geq −2.3x−4.2$ графічно, почніть із завантаження лівої та правої частини нерівності в Y1 та Y2 відповідно, як показано в (а). Використовуйте утиліту intersect в меню CALC, щоб визначити точку перетину, як показано в (c).

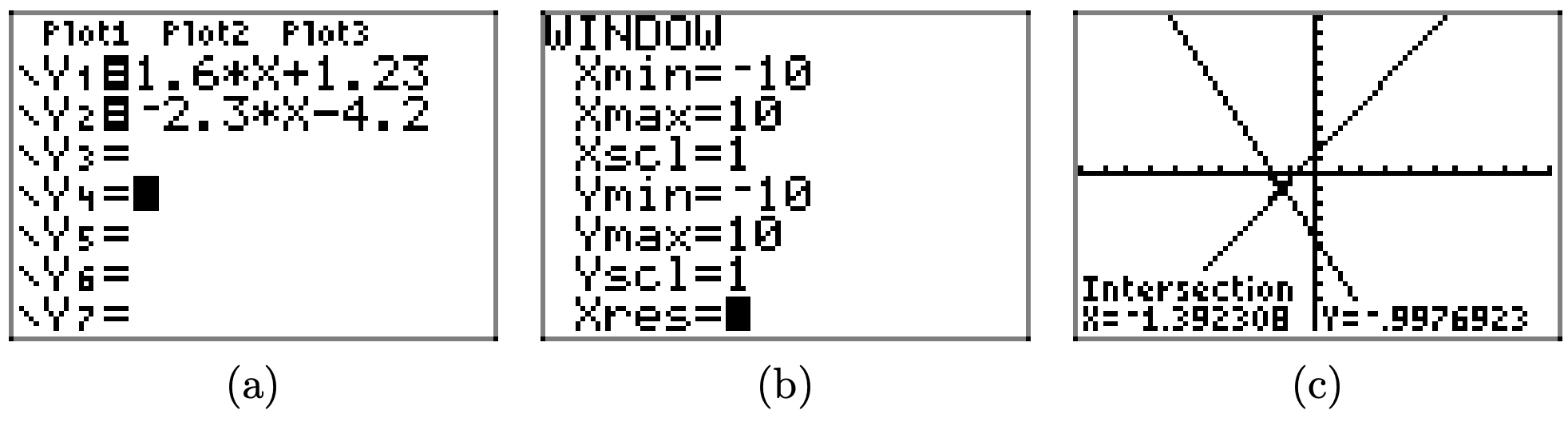
Два графіки перетинаються за x = −1.392308. Графік y = 1.6x + 1.23 знаходиться над графіком y = −2,3x−4.2 для всіх значень x, що лежать праворуч від −1,392308. Тому рішення$1.6x + 1.23 \geq −2.3x − 4.2$ є$[−1.392308,\infty) = \{x : x \geq −1.392308\}$.

Вправа$\PageIndex{22}$

1,24х + 5,6 < 1,2 − 0,52х

Вправа$\PageIndex{23}$

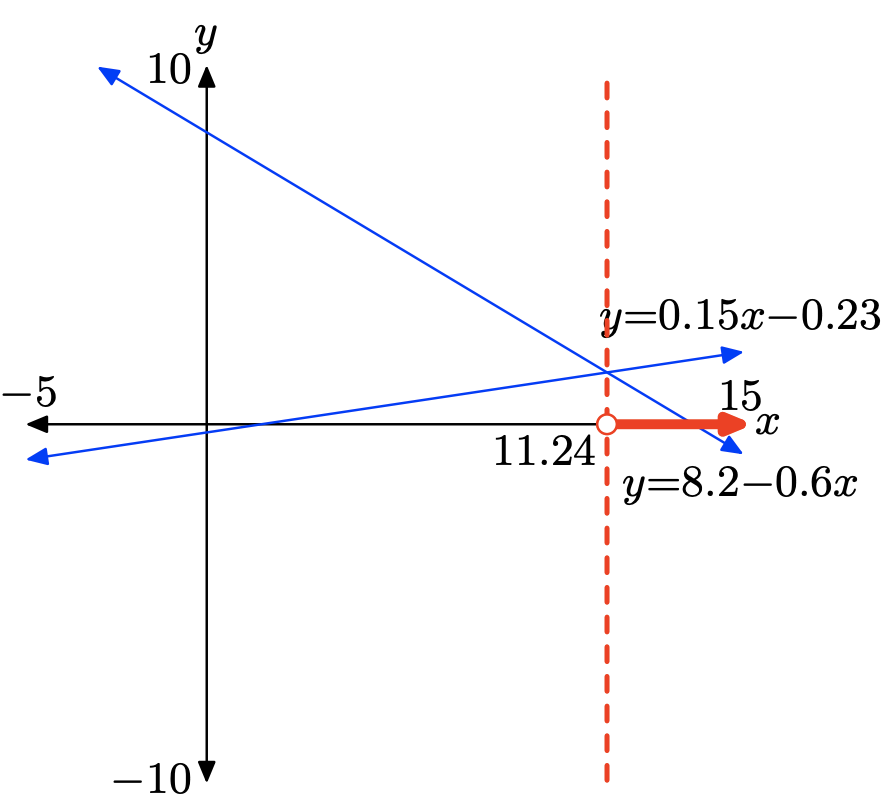
0,15х − 0,23 > 8.2 − 0.6х

Відповідь

Щоб розв'язати нерівність 0,15x − 0,23 > 8,2 − 0,6x графічно, почніть із завантаження лівої та правої частини нерівності у Y1 та Y2 відповідно, як показано у (a). Налаштуйте вікно перегляду, як показано у пункті (b). Використовуйте утиліту intersect в меню CALC, щоб визначити точку перетину, як показано в (c).

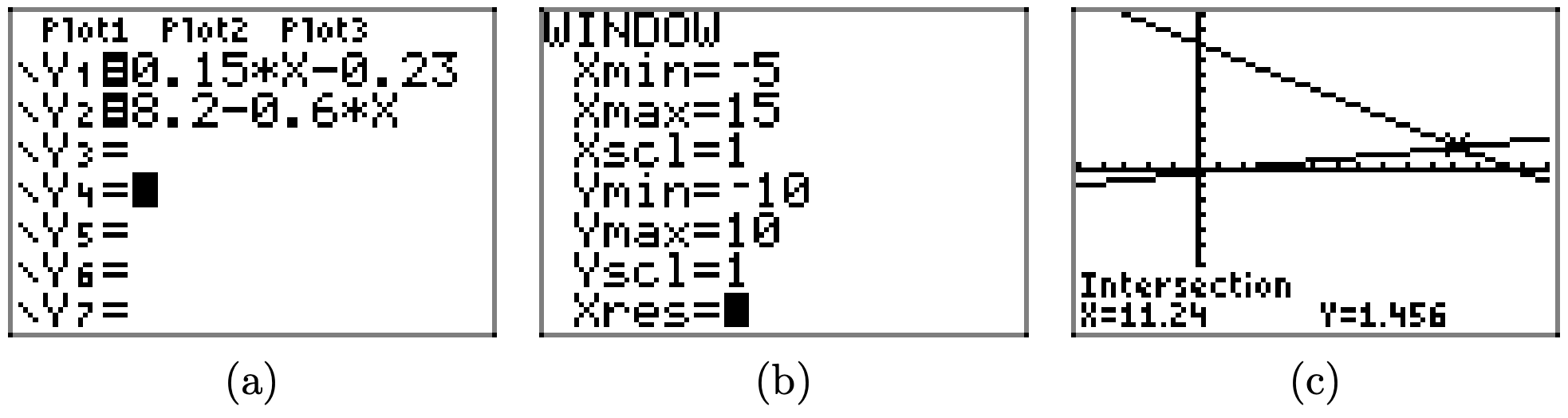
Графік y = 0,15x − 0,23 знаходиться над графіком y = 8.2 − 0.6x для всіх значень x, що лежать праворуч від 11.24. Отже, рішення 0,15x − 0,23 > 8,2 − 0,6x дорівнює$(11.24,\infty) = \{x : x > 11.24\}$

Вправа$\PageIndex{24}$

$−1.23x − 9.76 \leq 1.44x + 22.8$

Вправа$\PageIndex{25}$

$0.5x^2 − 5 < 1.23 − 0.75x$

Відповідь

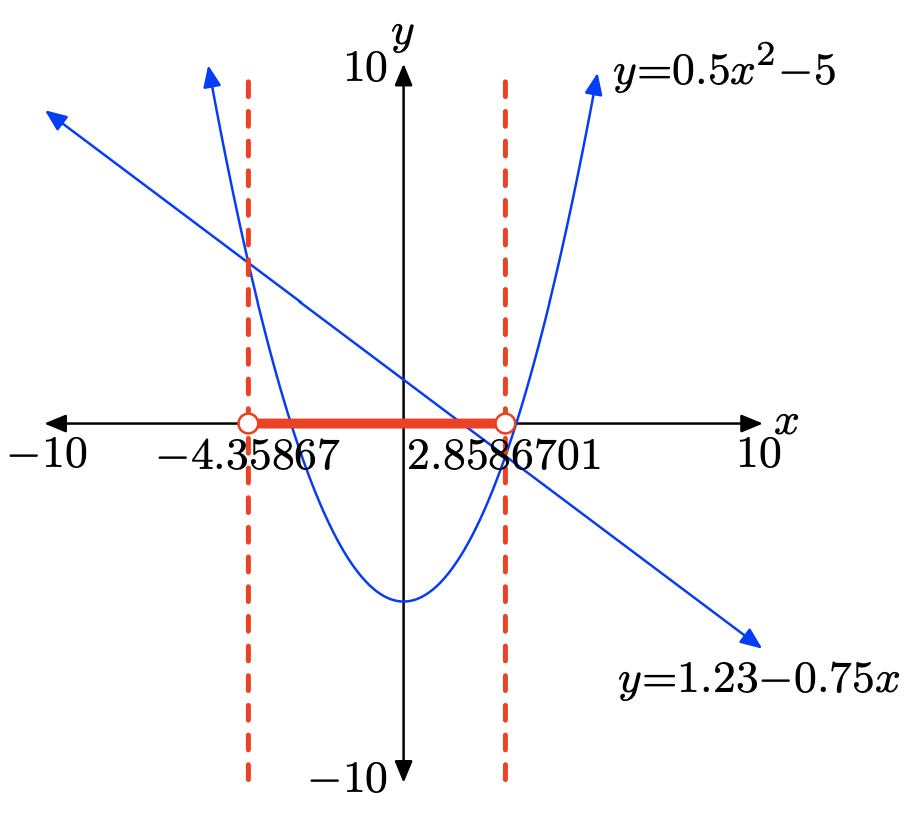
Щоб розв'язати нерівність$0.5x^2 − 5 < 1.23 − 0.75x$ графічно, почніть із завантаження лівої та правої частини нерівності в Y1 та Y2 відповідно, як показано в (а). Використовуйте утиліту intersect в меню CALC для визначення точок перетину, як показано в (b) і (c).

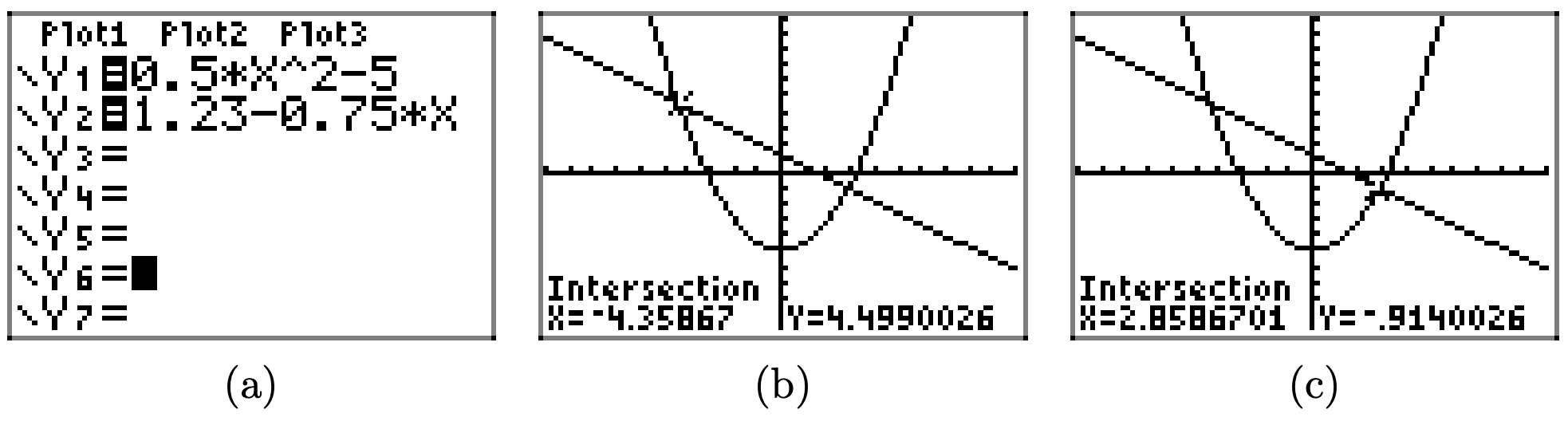
Графік y = 0,5x2−5 знаходиться нижче графіка y = 1,23−0,75x для всіх значень x, що знаходяться між −4,35867 та 2,8586701. Отже, розв'язком$0.5x^2−5 < 1.23−0.75x$ є (−4.35867, 2.8586701) або {x: −4.35867 < x < 2.8586701}.

Вправа$\PageIndex{26}$

$4 − 0.5x^2 \leq 0.72x − 1.34$

У Вправи$\PageIndex{27}$ -$\PageIndex{30}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Зробіть точну копію зображення на графічному папері (позначте графік буквою f і міткою і масштабуйте кожну вісь), пропустіть пунктирну вертикальну лінію через перехоплення x графа f, потім позначте і затіньте рішення f (x) = 0 на осі x. Використовуйте позначення set-builder для опису вашого рішення.

II. Зробіть другу копію зображення на графічному папері, опустіть пунктирну вертикальну лінію через перехоплення x графіка f, потім позначте і затіньте рішення f (x) > 0 на осі x. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

iii. Зробіть третю копію зображення на графічному папері, перетягніть пунктирну вертикальну лінію через перехоплення x графа f, потім позначте і затіньте розв'язок f (x) < 0 на осі x. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

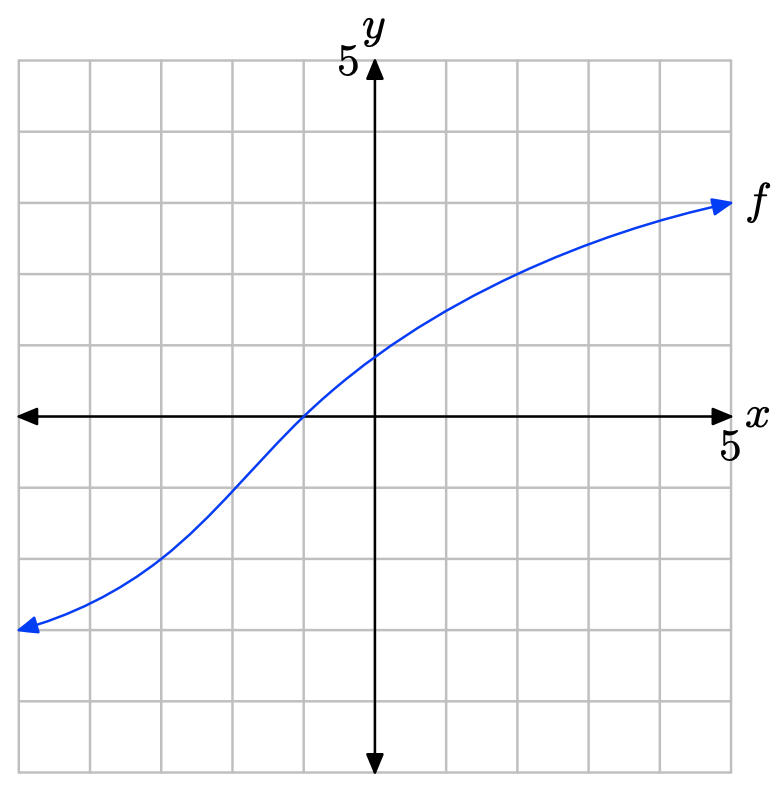
Вправа$\PageIndex{27}$

Відповідь

Графік f перехоплює вісь x при x = −1. Отже, розв'язок f (x) = 0 дорівнює x = −1.

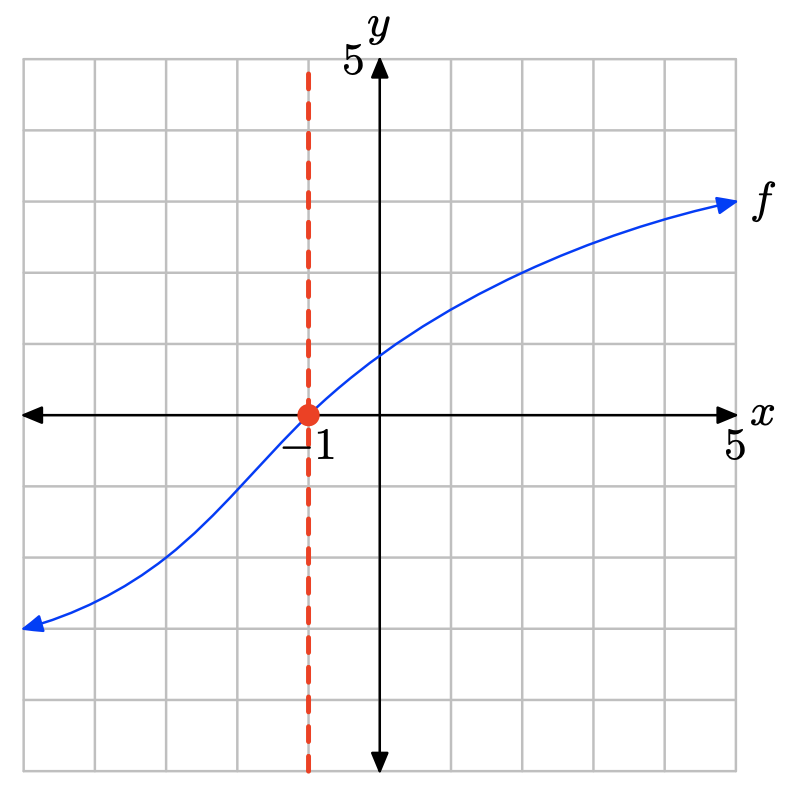
Графік f лежить над віссю x для всіх значень x, що лежать праворуч від −1. Тому розчином f (x) > 0 є$(−1,\infty) = \{x : x > −1\}$.

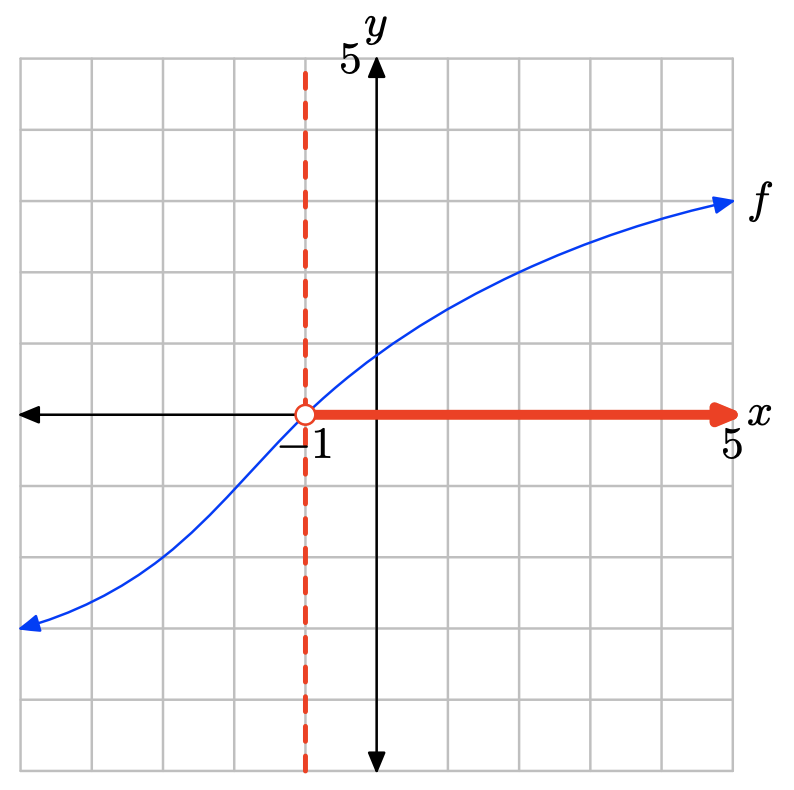
Графік f лежить нижче осі x для всіх значень x, що лежать ліворуч від −1. Тому розв'язок f (x) < 0 дорівнює$(−\infty, −1) = \{x : x < −1\}$

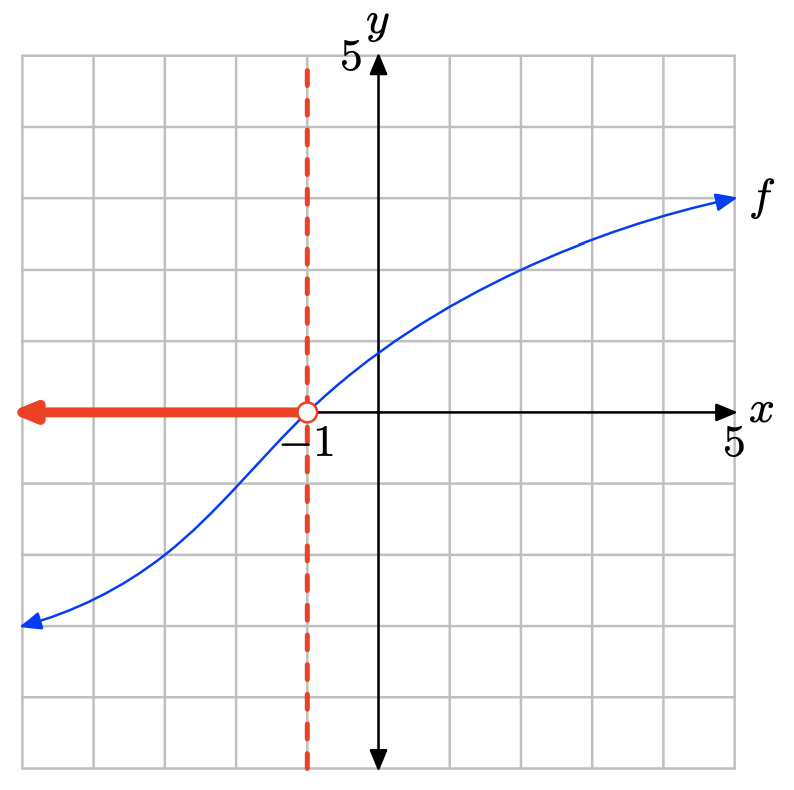
Вправа$\PageIndex{28}$

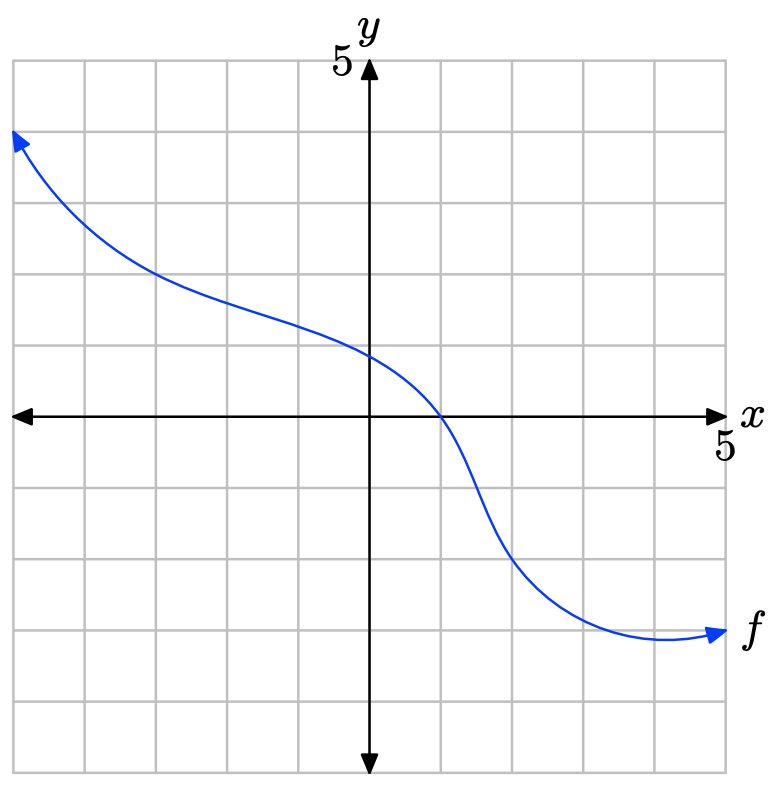
Вправа$\PageIndex{29}$

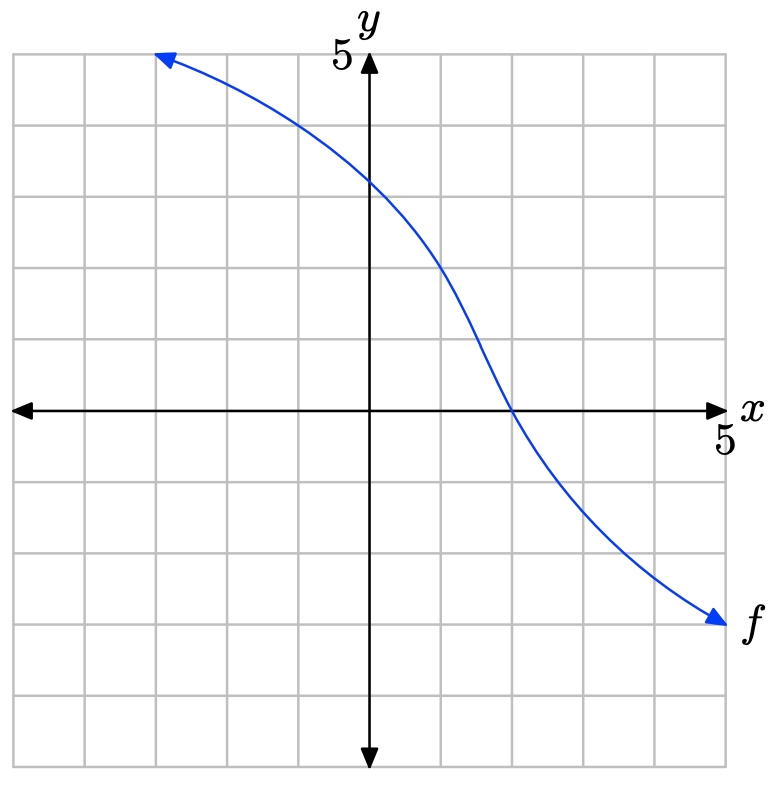
Відповідь

Графік f перехоплює вісь x при x = 2. Тому розчин f (х) = 0 дорівнює х = 2.

Графік f лежить над віссю x для всіх значень x, що лежать ліворуч від x = 2. Тому розчином f (x) > 0 є$(−\infty, 2) = \{x : x < 2\}$.

Графік f лежить нижче осі x для всіх значень x, які лежать праворуч від x = 2. Тому розв'язок f (x) < 0 дорівнює$(2,\infty) = \{x : x > 2\}$

Вправа$\PageIndex{30}$

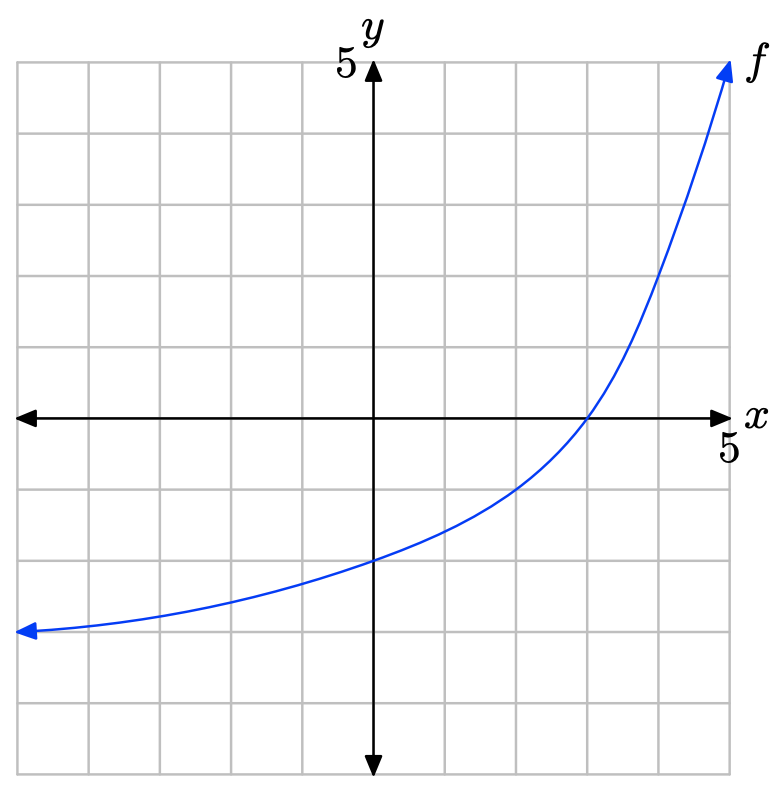
У Вправи$\PageIndex{31}$ -$\PageIndex{34}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Зробіть точну копію зображення на графічному папері, скиньте пунктирні, вертикальні лінії через перехоплення x, потім позначте і затіньте рішення$f(x) \geq 0$ на осі x. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

II. Зробіть другу копію зображення на графічному папері, перетягніть пунктирні вертикальні лінії через перехоплення x, потім позначте і затіньте рішення f (x) < 0 на осі x. Використовуйте set-builder та інтервальні позначення для опису набору рішень.

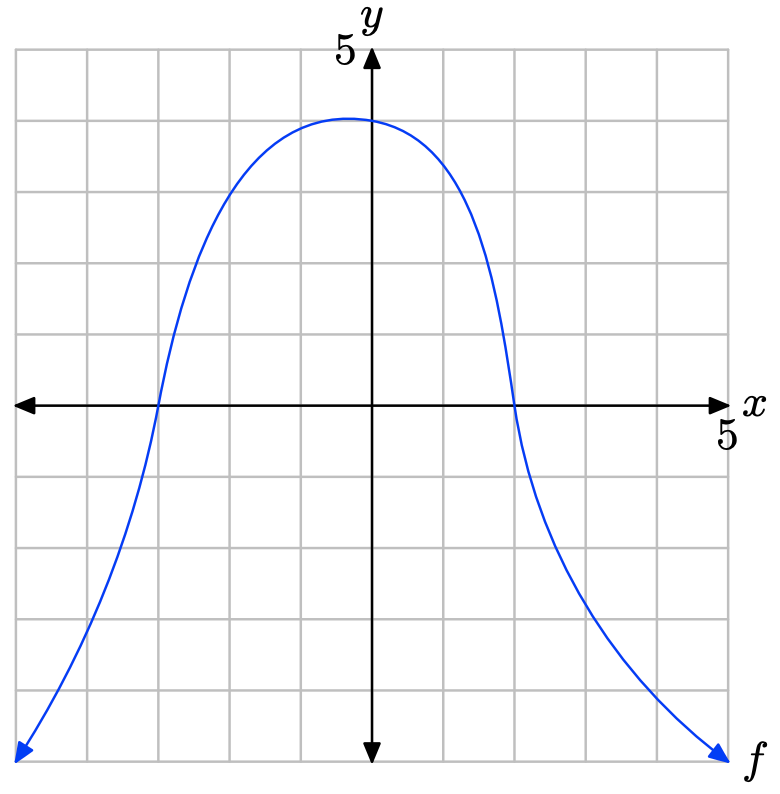
Вправа$\PageIndex{31}$

Відповідь

Графік f перехоплює вісь x при x = −3 і x = 2. Графік f лежить над віссю x для всіх значень x, що знаходяться між x = −3 та x = 2. Тому рішення$f(x) \geq 0$ є$[−3, 2] = \{x : −3 \leq x \leq 2\}$.

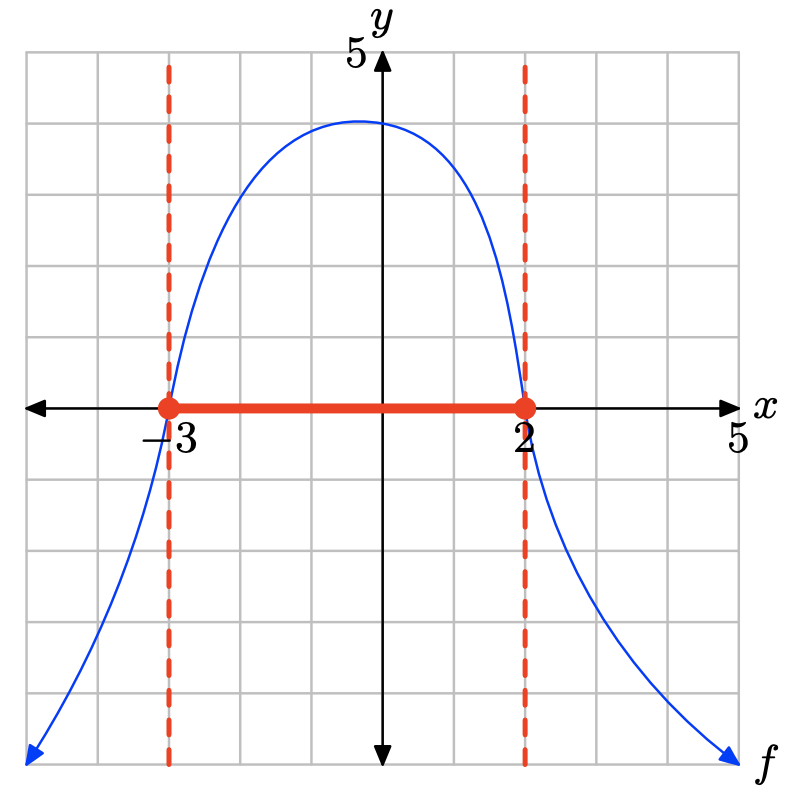
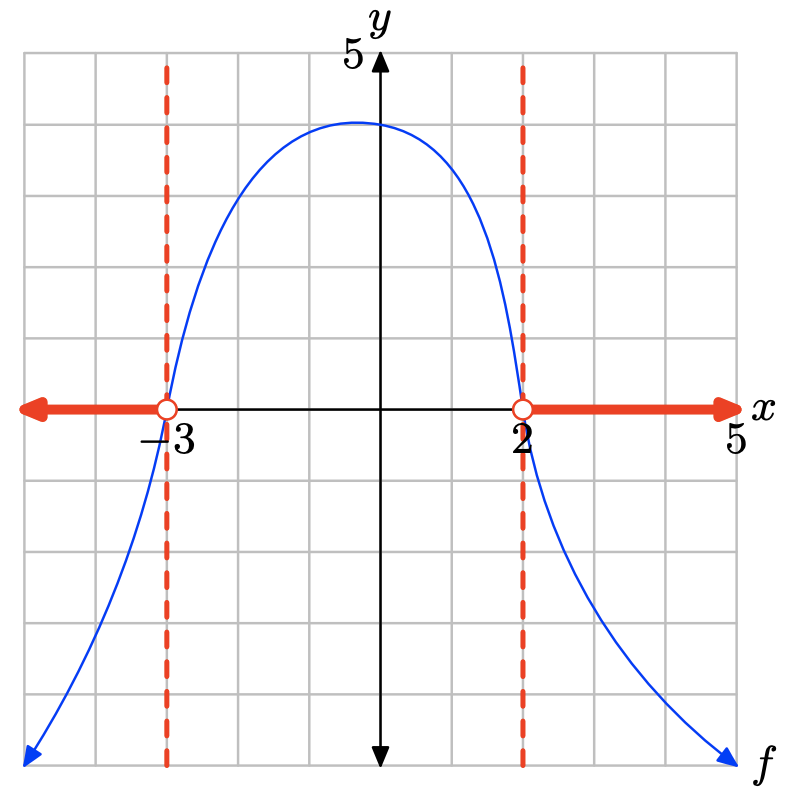
Графік f лежить нижче осі x для всіх значень x, що лежать ліворуч від x = −3 або праворуч від x = 2. Тому розв'язком f (x) < 0 є$(−\infty, −3) \cup (2,\infty) = \{x : x < −3 or x > 2\}$.

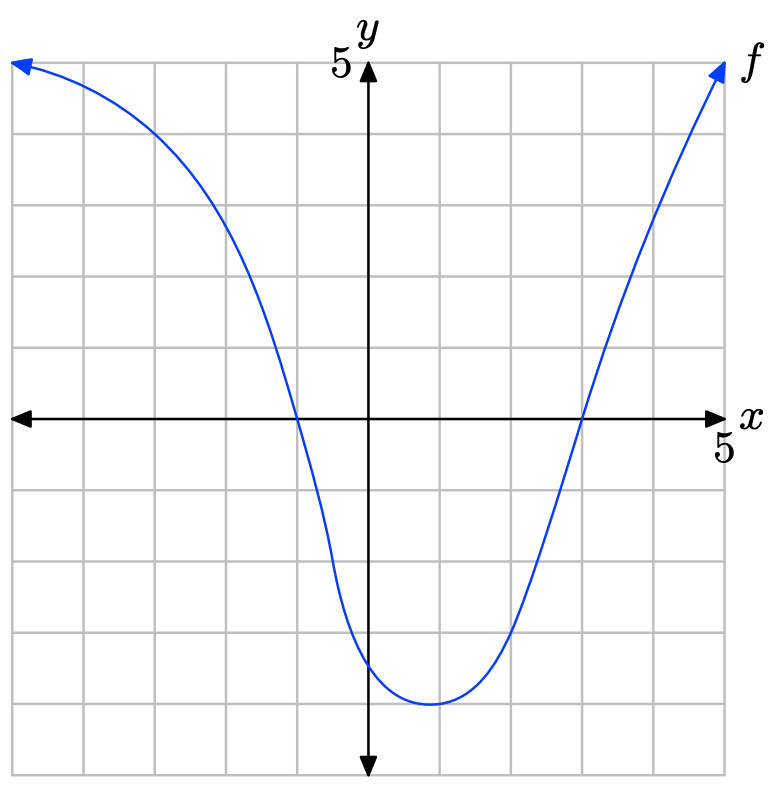
Вправа$\PageIndex{32}$

Вправа$\PageIndex{33}$

Відповідь

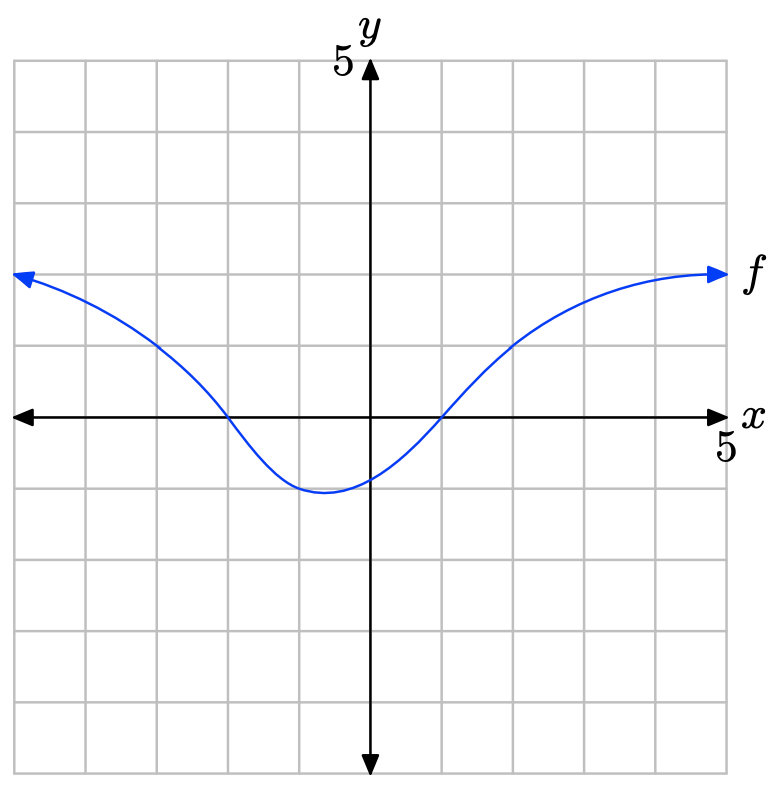
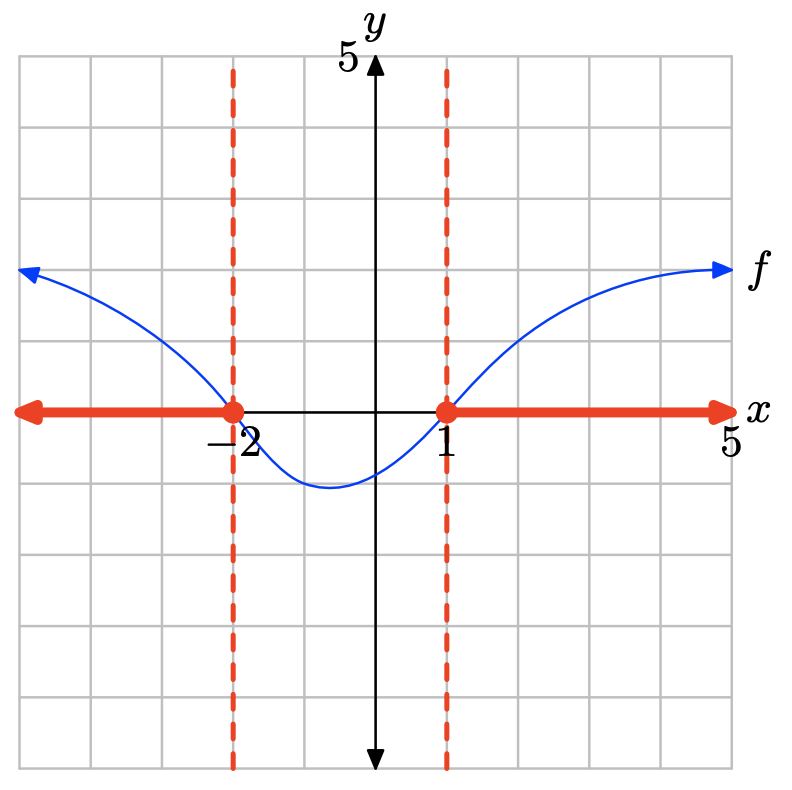
Графік f перехоплює вісь x при x = −2 і x = 1. Графік f лежить над віссю x для всіх значень x, які лежать ліворуч x = −2 або праворуч від x = 1. Тому рішення$f(x) \geq 0$ є$(−\infty, −2] \cup [1,\infty) = \{x : x \leq −2 or x \geq 1\}$.

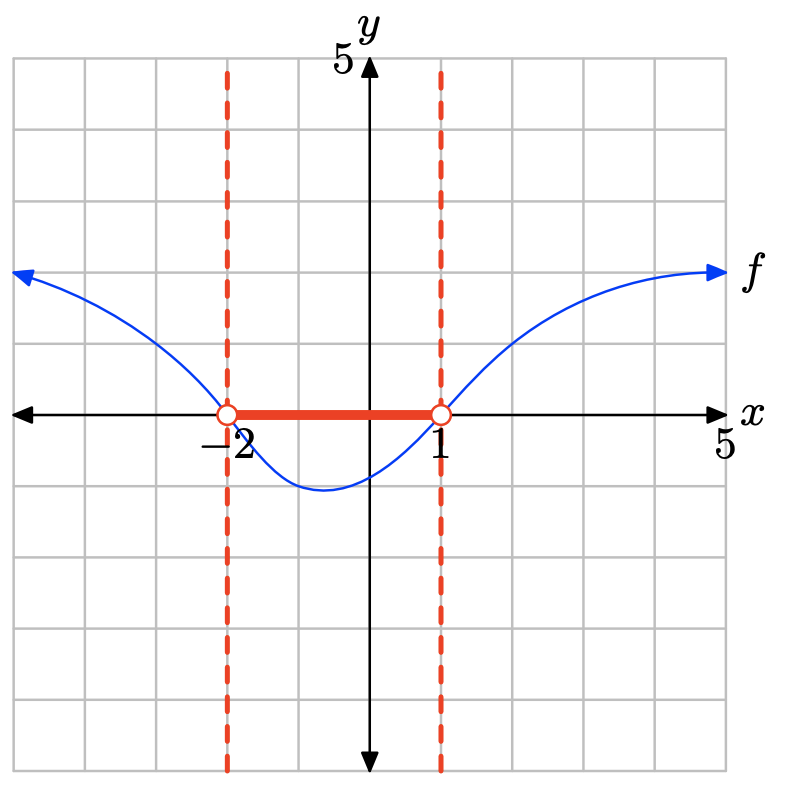
Графік f лежить нижче осі x для всіх значень x, що знаходяться між x = −2 і x = 1. Тому розв'язком f (x) < 0 є$(−2, 1) = \{x : −2 < x < 1\}$.

Вправа$\PageIndex{34}$

У Вправи$\PageIndex{35}$ -$\PageIndex{38}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Завантажте задану функцію f в меню Y= вашого калькулятора. Налаштуйте параметри WINDOW таким чином, щоб у вікні перегляду було видно x-перехоплення (и) графіка f. Використовуйте нульову утиліту в меню CALC вашого калькулятора, щоб визначити координати x-перехоплення (ів) графа f.

II. Зробіть точну копію зображення у вікні перегляду на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax та позначте графік його рівнянням.

iii. Намалюйте пунктирну вертикальну лінію через перехоплення x. Затінюйте і позначте розв'язку нерівності f (x) > 0 на осі x. Використовуйте як set-builder, так і інтервальні позначення для опису набору рішень.

Вправа$\PageIndex{35}$

ф (х) = −1,25х+ 3,58

Відповідь

Щоб розв'язати нерівність f (x) > 0 графічно, почніть із завантаження f (x) = −1,25x+3,58 в Y1. Використовуйте нульову утиліту в меню CALC, щоб визначити нуль f, як показано в (c).

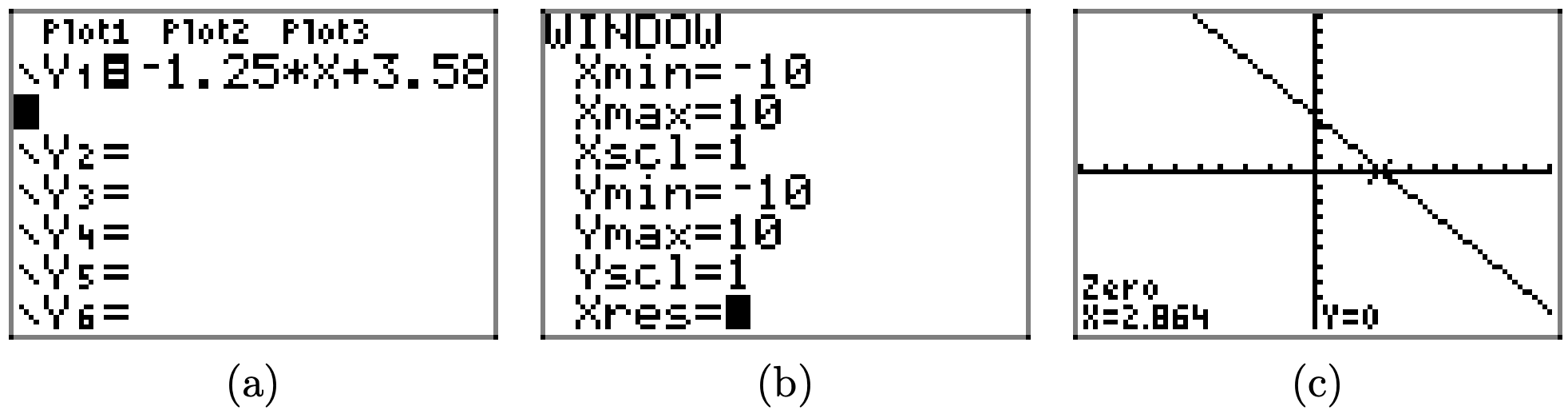
Графік f лежить над віссю x для всіх значень x, що лежать ліворуч від x = 2.864. Тому розчином f (x) > 0 є$(−\infty, 2.864) = \{x : x < 2.864\}$. Відповіді можуть відрізнятися через помилку округлення.

Вправа$\PageIndex{36}$

ф (х) = 1,34х − 4,52

Вправа$\PageIndex{37}$

$f(x) = 1.25x^2 + 4x − 5.9125$

Відповідь

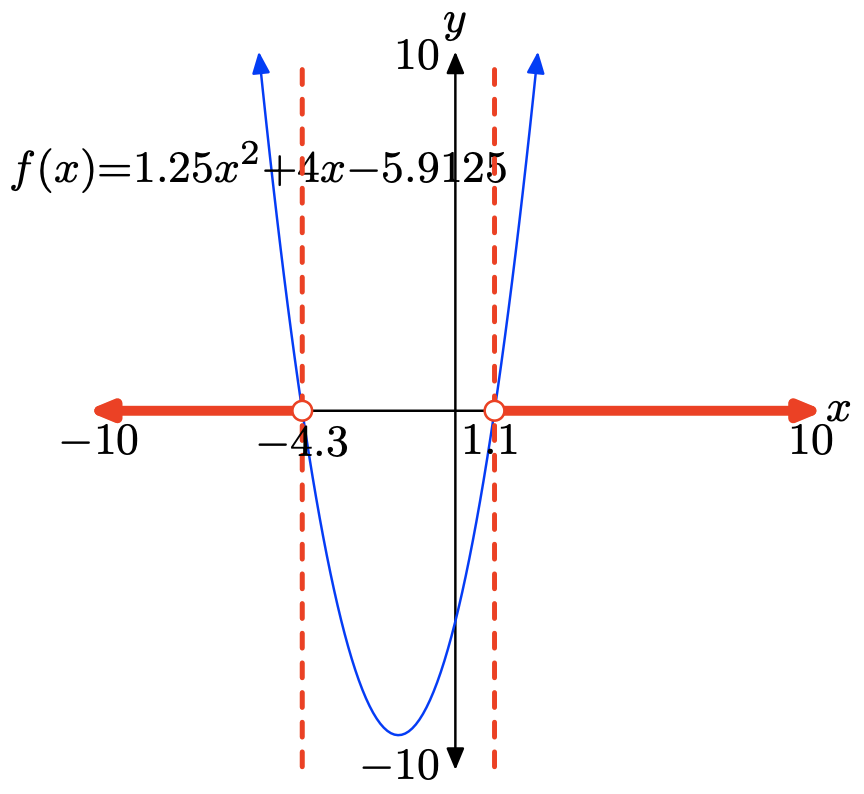
Щоб розв'язати нерівність f (x) > 0 графічно, почніть із завантаження$f(x) = 1.25x^2 + 4x − 5.9125$ в Y1. Використовуйте нульову утиліту в меню CALC для визначення нулів f, як показано в (b) і (c).

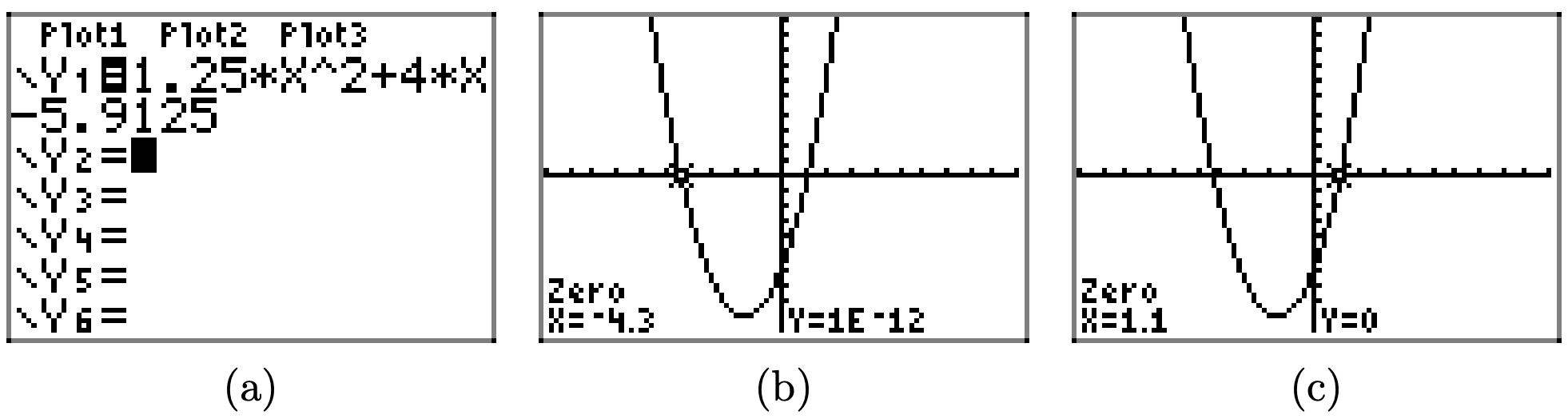
Графік f лежить над віссю x для всіх значень x, що лежать ліворуч від x = −4.3 або праворуч від x = 1.1. Тому розчином f (x) > 0 є$(−\infty, −4.3) \cup (1.1,\infty)$ або$\{x : x < −4.3 or x > 1.1\}$. Відповіді можуть відрізнятися через помилку округлення.

Вправа$\PageIndex{38}$

$f(x) = −1.32x^2 − 3.96x + 5.9532$

У Вправи$\PageIndex{39}$ -$\PageIndex{42}$ виконуйте кожне з наступних завдань. Не забудьте використовувати лінійку, щоб намалювати всі лінії.

i. Завантажте задану функцію f в меню Y= вашого калькулятора. Налаштуйте параметри WINDOW таким чином, щоб у вікні перегляду було видно x-перехоплення (и) графіка f. Використовуйте нульову утиліту в меню CALC вашого калькулятора, щоб визначити координати x-перехоплення (ів) графа f.

II. Зробіть точну копію зображення у вікні перегляду на домашньому папері. Позначте та масштабуйте кожну вісь за допомогою xmin, xmax, ymin та ymax та позначте графік його рівнянням.

iii. Намалюйте пунктирну вертикальну лінію через перехоплення x. Затіньте і позначте розв'язку нерівності$f(x) \leq 0$ на осі x. Використовуйте як set-builder, так і інтервальні позначення для опису набору рішень.

Вправа$\PageIndex{39}$

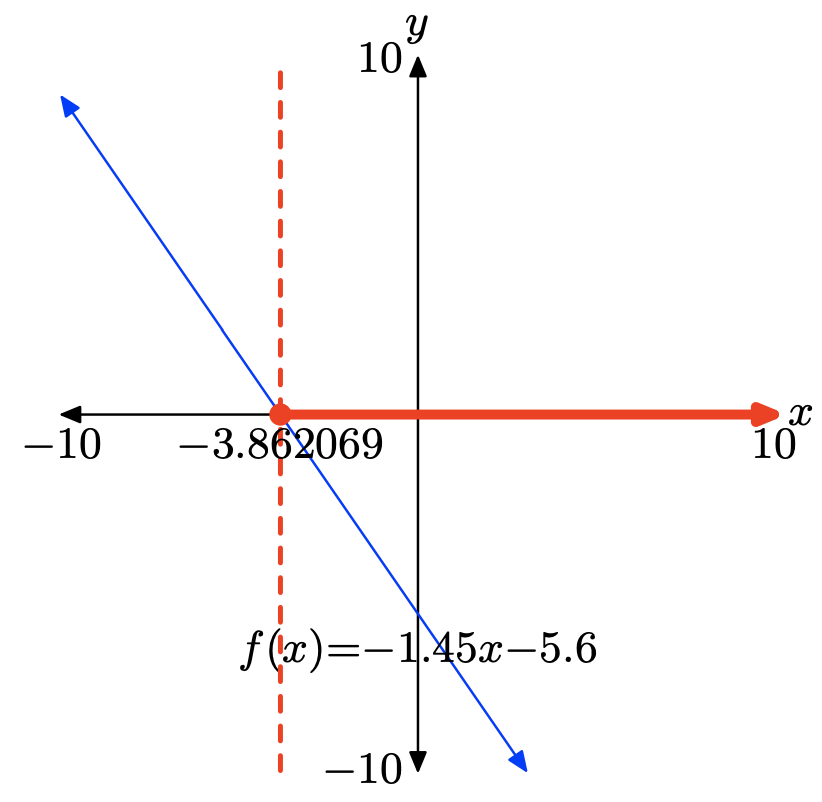
f (x) = −1,45х − 5,6

Відповідь

Щоб розв'язати нерівність$f(x) \leq 0$ графічно, почніть із завантаження f (x) = −1.45x−5.6 у Y1. Використовуйте нульову утиліту в меню CALC, щоб визначити нуль f, як показано в (c).

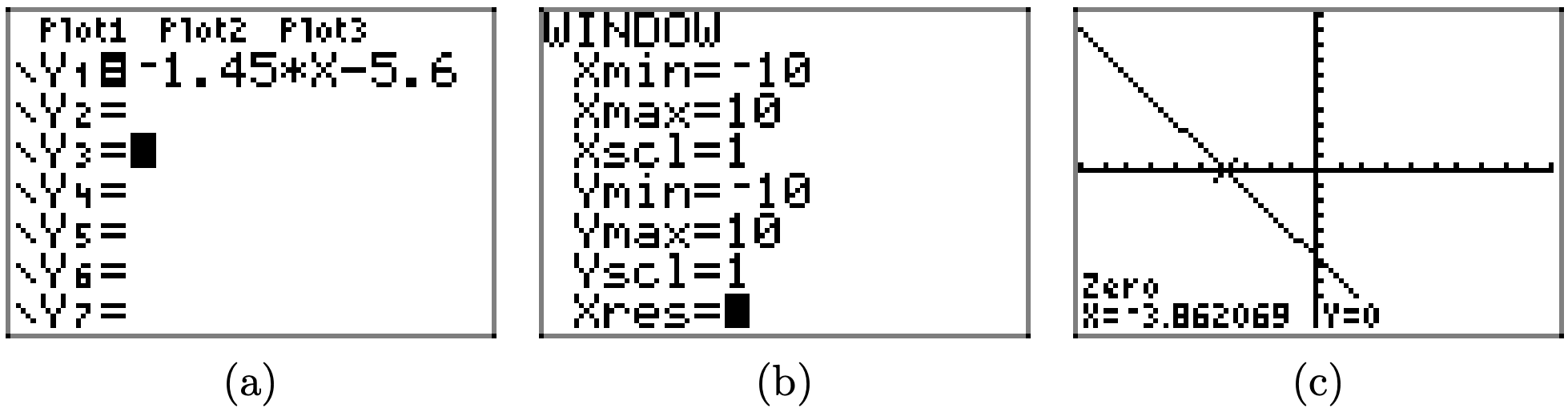
Графік f перехоплює вісь x при x = −3.862069. Графік f лежить нижче осі x для всіх значень x, що лежать праворуч від x = −3.862069. Тому рішення$f(x) \leq 0$ є$[−3.862069,\infty) = \{x : x \geq −3.862069\}$. Відповіді можуть відрізнятися через помилку округлення.

Вправа$\PageIndex{40}$

ф (х) = 1,35х+ 8,6

Вправа$\PageIndex{41}$

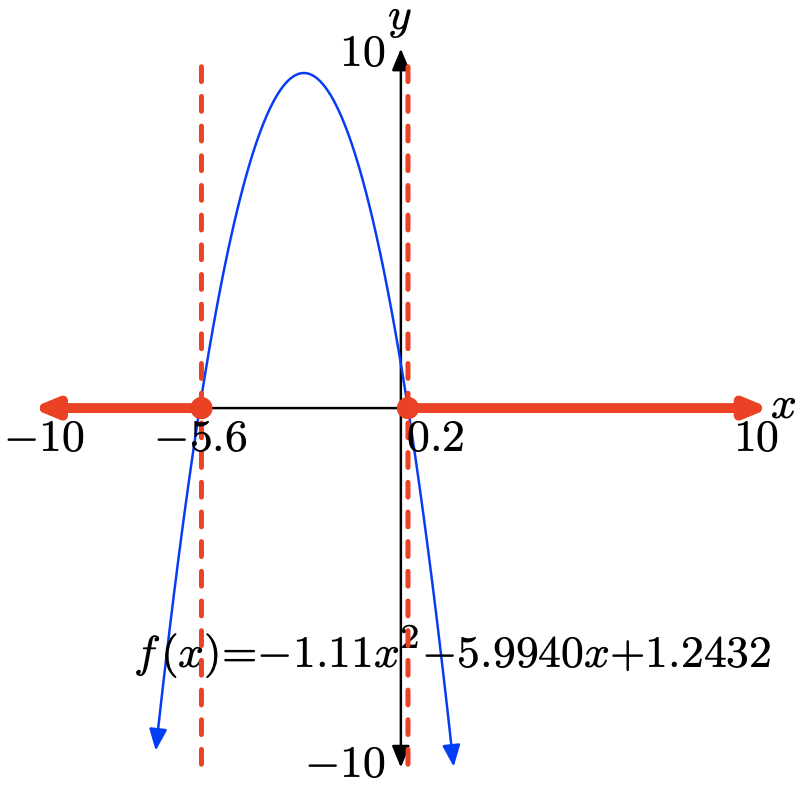
$f(x) = −1.11x^2 −5.9940x+1.2432$

Відповідь

Щоб вирішити нерівність$f(x) \leq 0$ графічно, почніть з завантаження$f(x) = −1.11x^2 − 5.9940x+1.2432$ в Y1. Використовуйте нульову утиліту в меню CALC для визначення нулів f, як показано в (b) і (c).

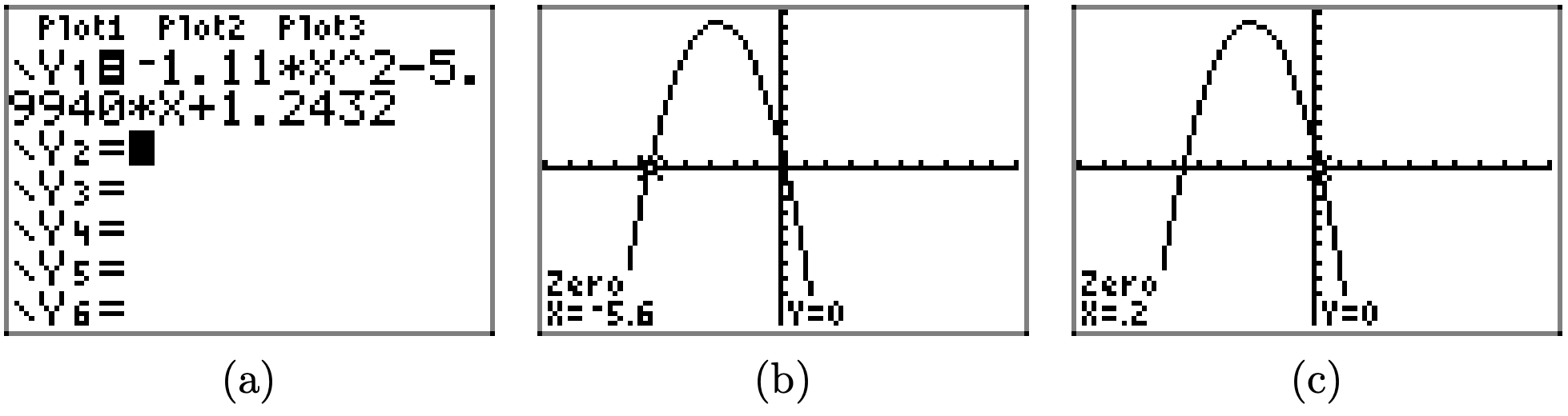
Графік f перехоплює вісь x при x = −5,6 і x = 0,2. Графік f лежить нижче осі x для всіх значень x, що лежать ліворуч від x = −5,6 або праворуч від x = 0,2. Тому рішення$f(x) \leq 0$ є$(−\infty, −5.6] \cup [0.2,\infty)$ або$\{x : x \leq −5.6 or x \geq 0.2\}$. Відповіді можуть відрізнятися через помилку округлення.

Вправа$\PageIndex{42}$

$f(x) = 1.22x^2 − 6.3440x + 1.3176$

2.5 Вправи

На фото нижче наведено графік функції f.

Наступна таблиця обчислює функцію f на графіку за ключовими значеннями x. Зверніть увагу на горизонтальний формат, де першою точкою таблиці є впорядкована пара (−4, 0).

х	-4	-3	0	2	5	6
f (х)	0	4	4	-4	-4	0

Використовуйте графік і таблицю, щоб виконати кожне з наступних завдань для Вправи$\PageIndex{1}$ -$\PageIndex{10}$.

i) Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь, а потім скопіюйте та позначте оригінальний графік f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. Використовуйте оригінальну таблицю, щоб допомогти завершити таблицю для даної функції у вправі.

iii. Використовуючи олівець іншого кольору, побудуйте дані з вашої заповненої таблиці на тій самій системі координат, що і початковий графік f. Використовуйте ці точки, щоб допомогти завершити графік заданої функції у вправі, а потім позначте цей графік рівнянням, вказаним у вправі.

Вправа$\PageIndex{1}$

у = 2ф (х).

х	-4	-3	0	2	5	6
у

Відповідь

Оригінальна таблиця функцій.

х	-4	-3	0	2	5	6
f (х)	0	4	4	-4	-4	0

Оцінити функцію y = 2f (x) при x = −4, −3, 0, 2, 5 та 6.

$$y= 2f(−4) = 2(0) = 0 \\ y = 2f(−3) = 2(4) = 8 \\ y = 2f(0) = 2(4) = 8 \\ y = 2f(2) = 2(−4) = −8 \\ y = 2f(5) = 2(−4) = −8 \\ y = 2f(6) = 2(0) = 0$$

Окуляри задовольняють y = 2f (x).

х	-4	-3	0	2	5	6
у	0	8	8	-8	-8	0

Побудуйте точки в таблиці, щоб отримати графік y = 2f (x).

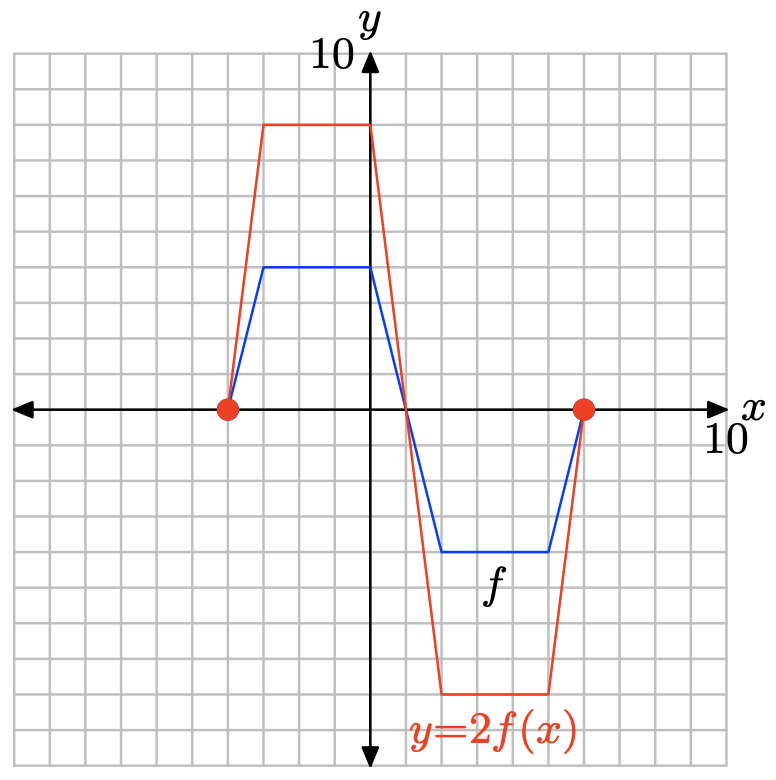
Зверніть увагу, що множення на 2, як у = 2f (x), розтягує графік y = f (x) по вертикалі на коефіцієнт 2.

Вправа$\PageIndex{2}$

у = (1/2) ф (х).

х	-4	-3	0	2	5	6
у

Вправа$\PageIndex{3}$

y = −f (х).

х	-4	-3	0	2	5	6
у

Відповідь

Оригінальна таблиця функцій.

х	-4	-3	0	2	5	6
f (х)	0	4	4	-4	-4	0

Оцінити функцію y = −f (x) при x = −4, −3, 0, 2, 5 та 6.

$$y = −f(−4) = −(0) = 0 \\ y = −f(−3) = −(4) = −4 \\ y = −f(0) = −(4) = −4 \\ y = −f(2) = −(−4) = 4 \\ y = −f(5) = −(−4) = 4 \\ y = −f(6) = −(0) = 0$$

Окуляри, що задовольняють y = −f (x).

х	-4	-3	0	2	5	6
у	0	-4	-4	4	4	0

Побудуйте точки у таблиці, щоб отримати графік y = −f (x).

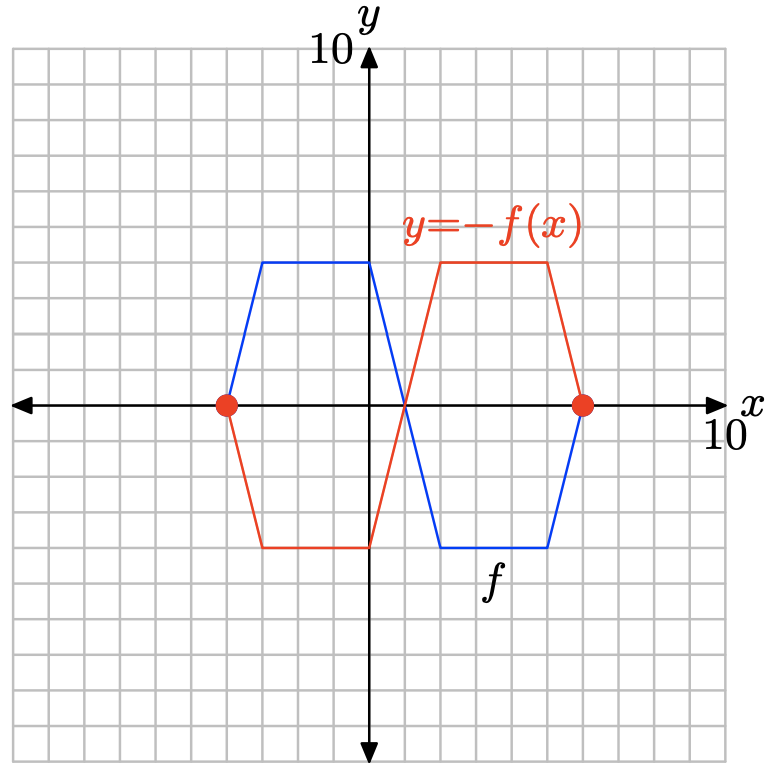
Зауважте, що заперечення функції, як у y = −f (x), відображає графік y = f (x) по осі x.

Вправа$\PageIndex{4}$

y = f (x) − 2.

х	-4	-3	0	2	5	6
у

Вправа$\PageIndex{5}$

у = ф (х) + 4.

х	-4	-3	0	2	5	6
у

Відповідь

Оригінальна таблиця функцій.

х	-4	-3	0	2	5	6
f (х)	0	4	4	-4	-4	0

Оцінити функцію y = f (x) + 4 при x = −4, −3, 0, 2, 5 та 6.

$$y = f(−4) + 4 = (0) + 4 = 4 \\y = f(−3) + 4 = (4) + 4 = 8 \\y = f(0) + 4 = (4) + 4 = 8 \\y = f(2) + 4 = (−4) + 4 = 0 \\y = f(5) + 4 = (−4) + 4 = 0 \\y = f(6) + 4 = (0) + 4 = 4$$

Окуляри задовольняють y = f (x) + 4.

х	-4	-3	0	2	5	6
у	4	8	8	0	0	4

Побудуйте точки в таблиці, щоб отримати графік y = f (x) + 4.

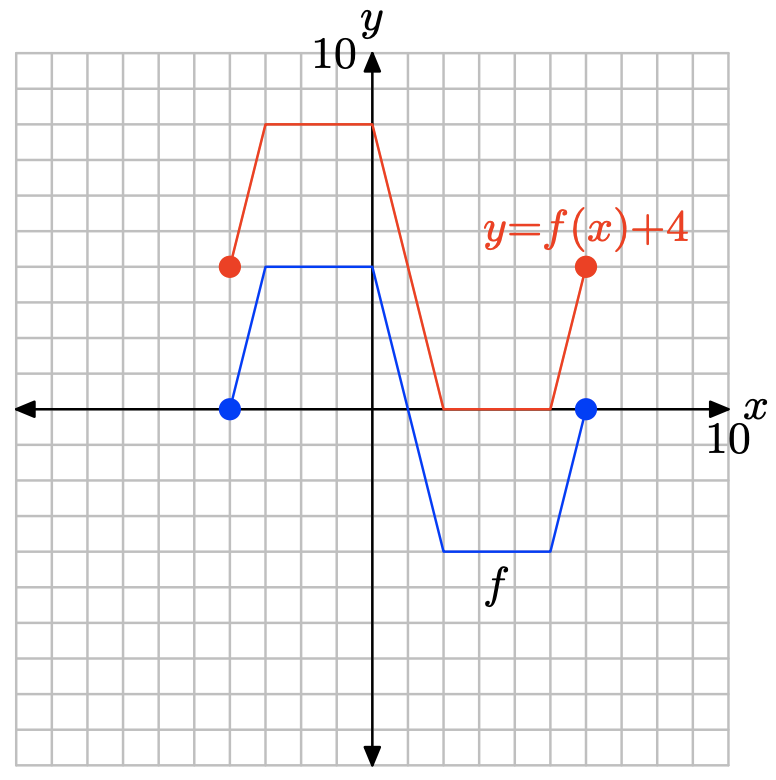
Зверніть увагу, що додавання 4, як і в y = f (x) + 4, переводить графік y = f (x) вгору на 4 одиниці.

Вправа$\PageIndex{6}$

y = −2f (х)

х	-4	-3	0	2	5	6
у

Вправа$\PageIndex{7}$

у = (−1/2) ф (х)

х	-4	-3	0	2	5	6
у

Відповідь

Оригінальна таблиця функцій.

х	-4	-3	0	2	5	6
f (х)	0	4	4	-4	-4	0

Оцінити функцію y = (−1/2) f (x) при x = −4, −3, 0, 2, 5 та 6.

$$y = (−1/2)f(−4) = (−1/2)(0) = 0 \\ y = (−1/2)f(−3) = (−1/2)(4) = −2 \\ y = (−1/2)f(0) = (−1/2)(4) = −2 \\ y = (−1/2)f(2) = (−1/2)(−4) = 2 \\ y = (−1/2)f(5) = (−1/2)(−4) = 2 \\ y = (−1/2)f(6) = (−1/2)(0) = 0$$

Окуляри, що задовольняють y = (−1/2) f (x).

х	-4	-3	0	2	5	6
у	0	-2	-2	2	2	0

Побудуйте точки в таблиці, щоб отримати графік y = (−1/2) f (x).

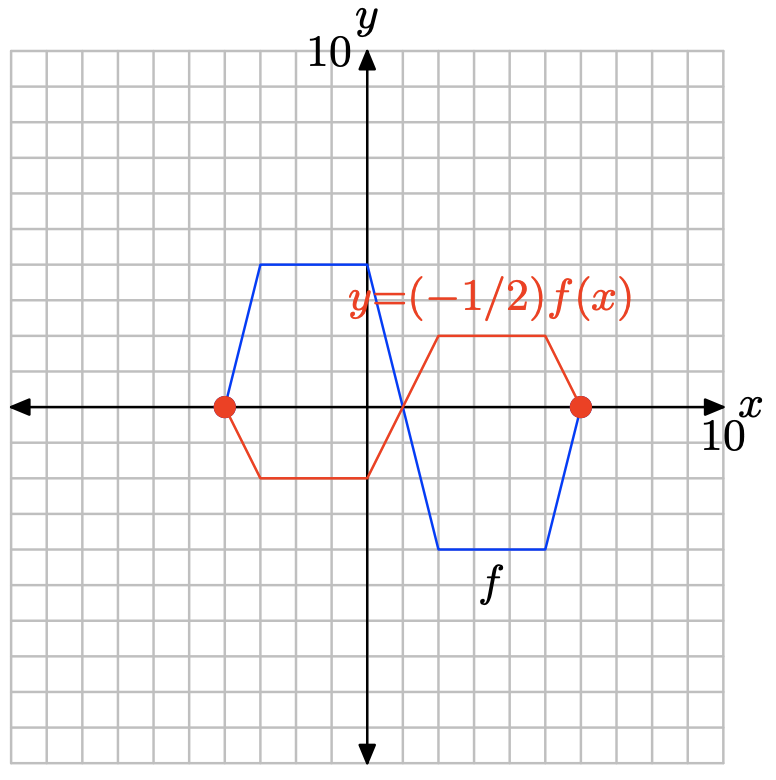
Зауважте, що множення на −1/2, як у y = (−1/2) f (x), стискає графік y = f (x) вертикально на коефіцієнт 2, а потім відображає результат по осі x.

Вправа$\PageIndex{8}$

y = −f (х) + 3.

х	-4	-3	0	2	5	6
у

Вправа$\PageIndex{9}$

y = −f (x) − 2

х	-4	-3	0	2	5	6
у

Відповідь

Оригінальна таблиця функцій.

х	-4	-3	0	2	5	6
f (х)	0	4	4	-4	-4	0

Оцінити функцію y = −f (x) − 2 при x = −4, −3, 0, 2, 5 та 6.

$$y = −f(−4) − 2 = −(0) − 2 = −2 \\ y = −f(−3) − 2 = −(4) − 2 = −6\\ y = −f(0) − 2 = −(4) − 2 = −6 \\y = −f(2) − 2 = −(−4) − 2 = 2 \\y = −f(5) − 2 = −(−4) − 2 = 2 \\y = −f(6) − 2 = −(0) − 2 = −2$$

Окуляри, що задовольняють y = −f (x) − 2.

х	-4	-3	0	2	5	6
у	-2	-6	-6	2	2	-2

Побудуйте точки в таблиці, щоб отримати графік y = −f (x) − 2.

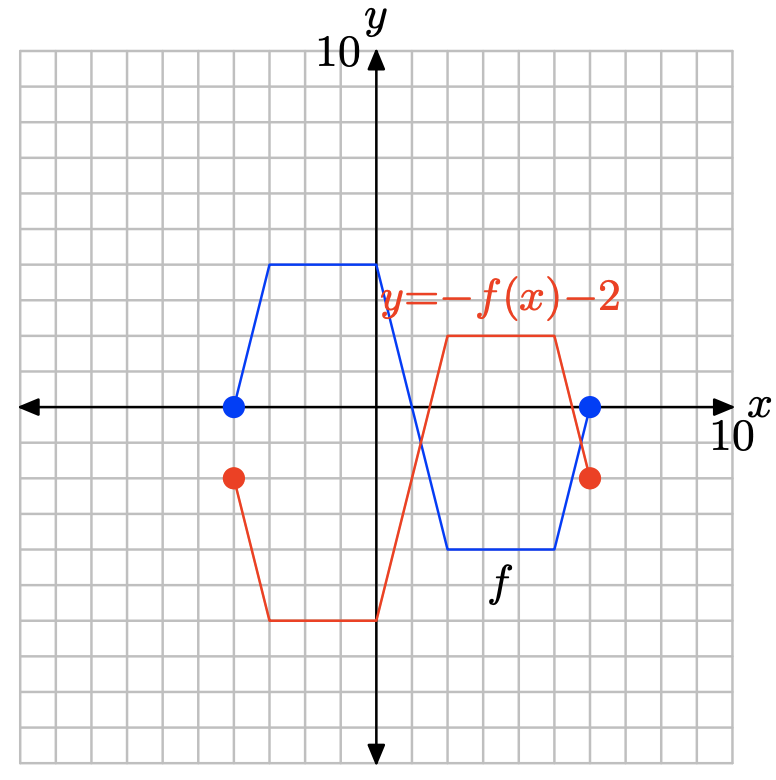
Зауважте, що заперечення потім віднімання 2, як у y = −f (x) − 2, спочатку відображає графік y = f (x) по осі x, потім перекладає отримане відображення на 2 одиниці вниз.

Вправа$\PageIndex{10}$

у = (−1/2) ф (х) + 3

х	-4	-3	0	2	5	6
у

Вправа$\PageIndex{11}$

Використовуйте графічний калькулятор, щоб намалювати графік$y = \sqrt{x}$. Потім намалюйте графік$y = \sqrt{x}$. Своїми словами поясніть, що ви дізналися з цієї вправи.

Відповідь

Спочатку намалюйте графік$y = \sqrt{x}$.

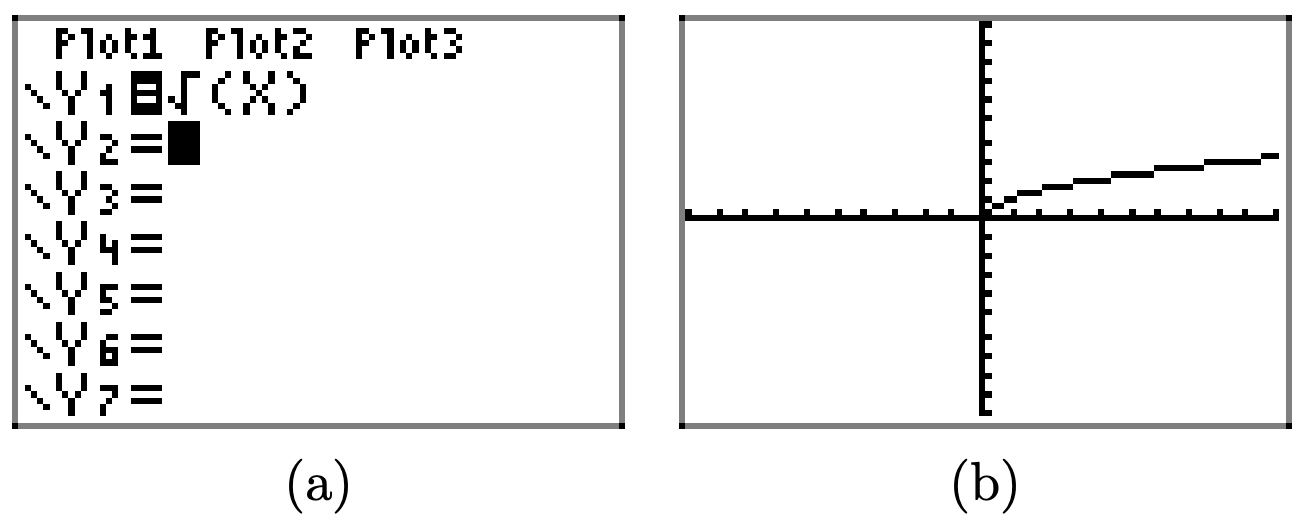
Графік$y = -\sqrt{x}$ є відображенням графіка$y = \sqrt{x}$ поперек осі x.

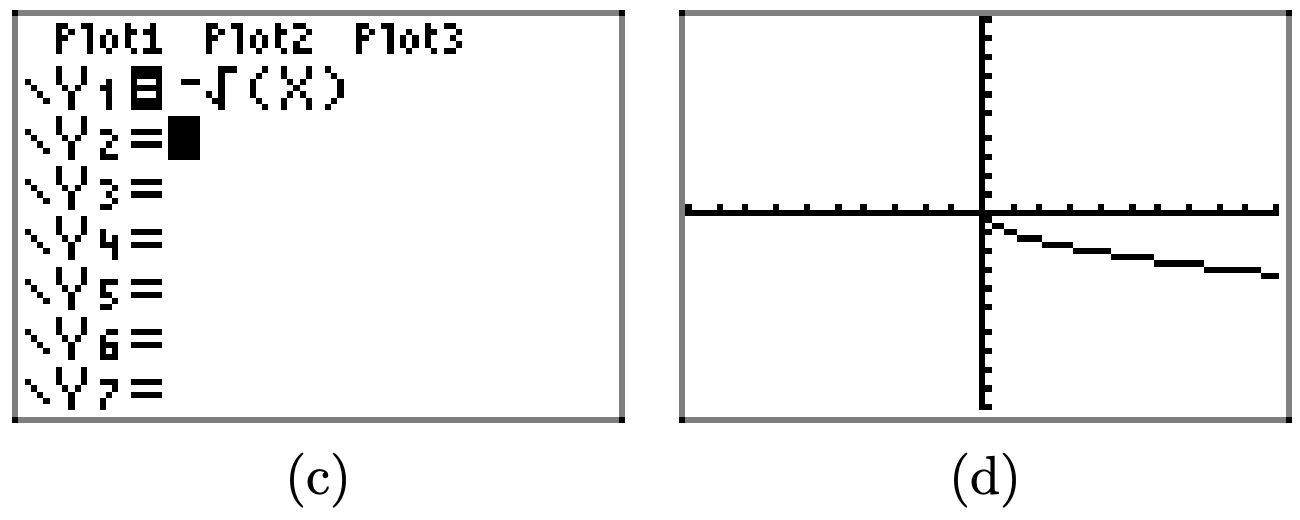
Заперечення функції відображає графік функції по осі x.

Вправа$\PageIndex{12}$

Скористайтеся калькулятором графіків, щоб намалювати графік y = |x|. Потім намалюйте графік y = −|x|. Своїми словами поясніть, що ви дізналися з цієї вправи.

Вправа$\PageIndex{13}$

Використовуйте графічний калькулятор, щоб намалювати графік$y = x^2$. Потім послідовно намалюйте графіки$y = x^2−2$$y = x^2−4$, і$y = x^2 − 6$. Своїми словами поясніть, що ви дізналися з цієї вправи.

Відповідь

Спочатку намалюйте графік$y = x^2$.

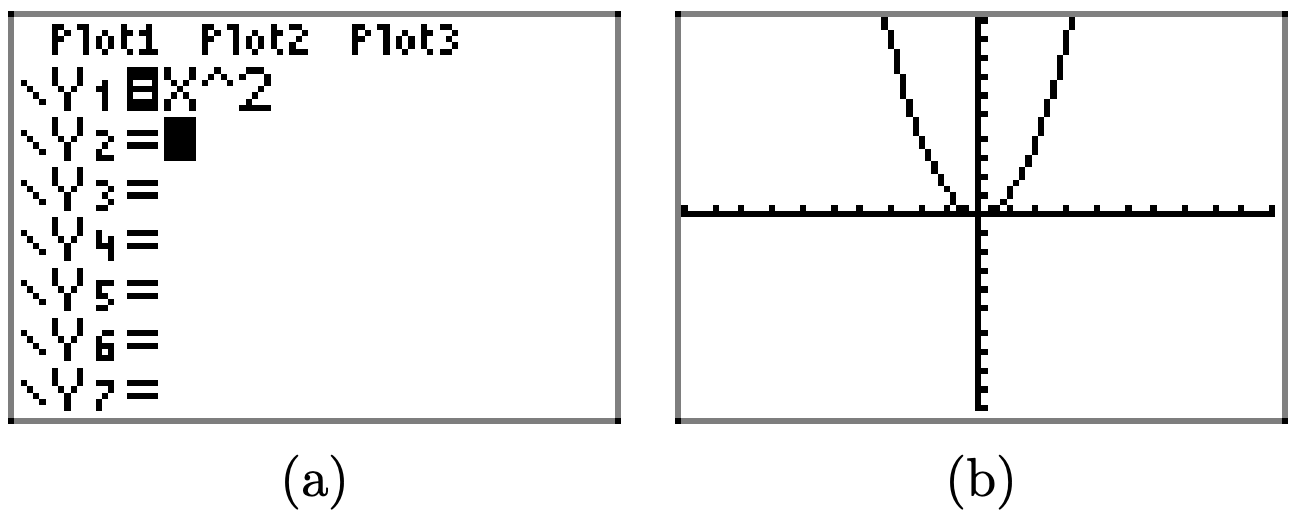
Віднімання 2 (як у$y = x^2-2$) переводить графік$y = x^2$ двох одиниць вниз у напрямку y.

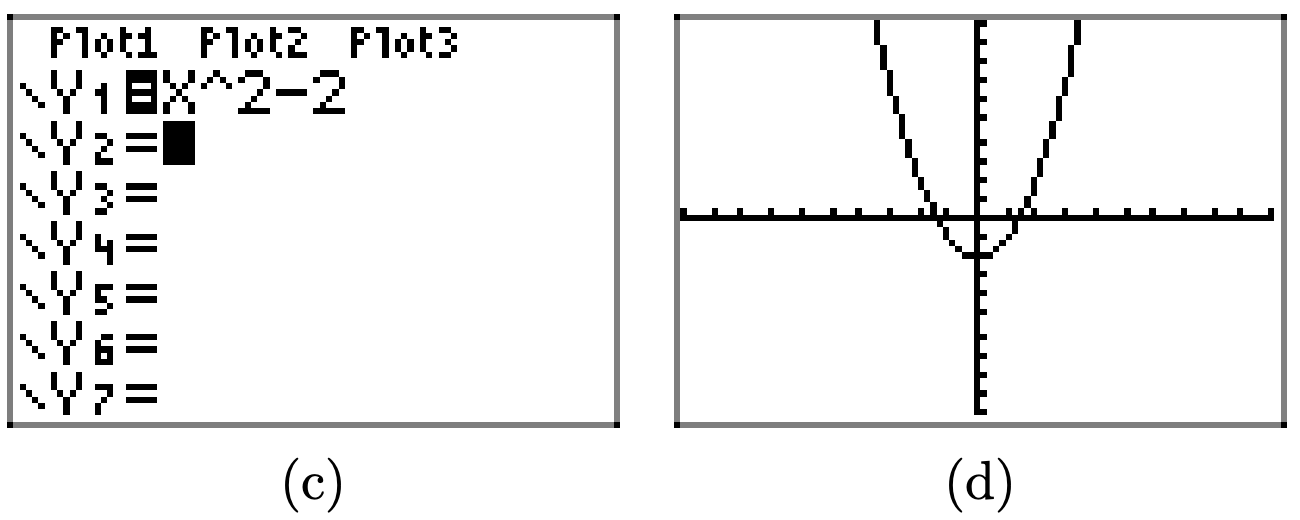
Аналогічно, віднімання 4 і 6 переводить графік$y = x^2$ чотирьох одиниць і 6 одиниць вниз відповідно

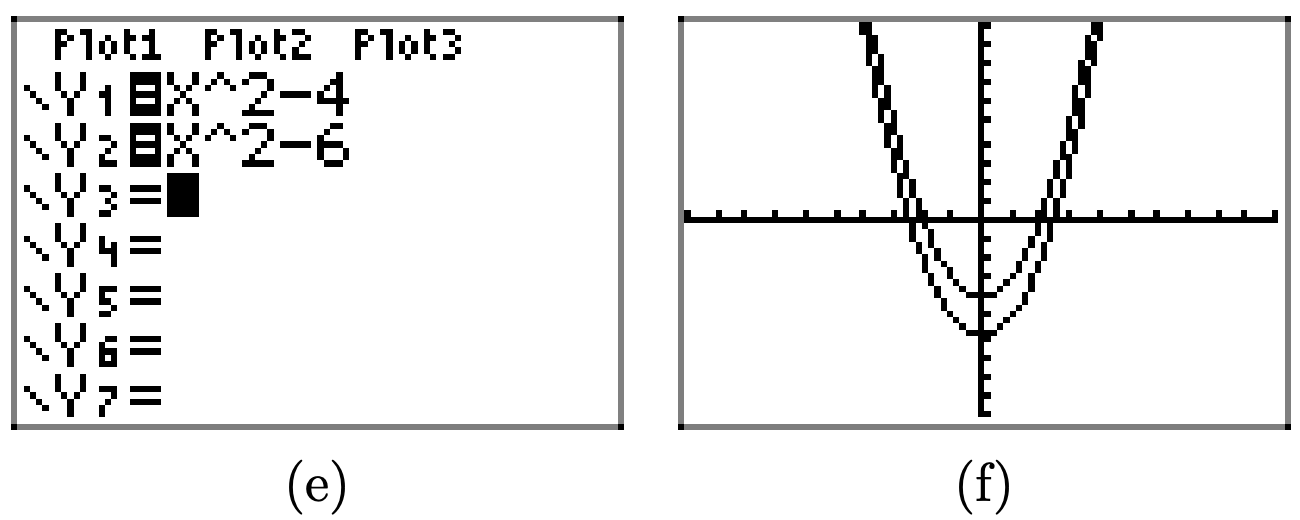
Загалом, якщо c позитивний, то графік y = f (x) − c виходить шляхом перекладу графіка y = f (x) вниз c одиниць.

Вправа$\PageIndex{14}$

Використовуйте графічний калькулятор, щоб намалювати графік$y = x^2$. Потім послідовно намалюйте графіки$y = x^2+2$$y = x^2+4$, і$y = x^2 + 6$. Своїми словами поясніть, що ви дізналися з цієї вправи.

Вправа$\PageIndex{15}$

Скористайтеся калькулятором графіків, щоб намалювати графік y = |x|. Потім послідовно намалюйте графіки y = 2|x|, y = 3|x|, і y = 4|x|. Своїми словами поясніть, що ви дізналися з цієї вправи.

Відповідь

Спочатку намалюйте графік y = |x|.

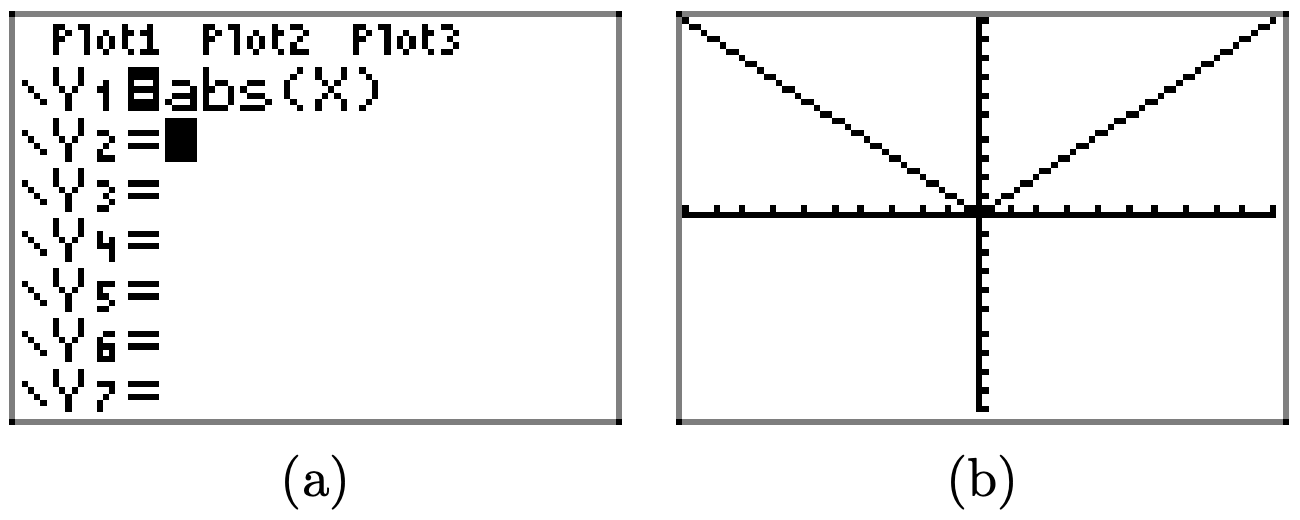
Множивши на 2, як у = 2|x|, розтягує графік y = |x| по вертикалі на коефіцієнт 2.

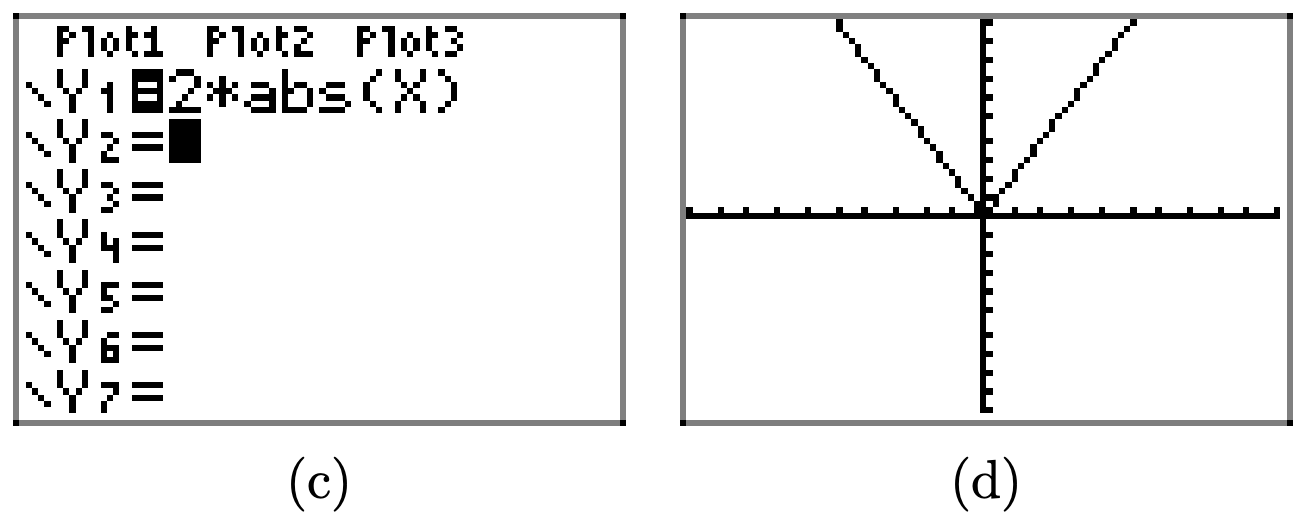
Аналогічно, множивши на 3 і 4, як у = 3|x| і y = 4|x|, розтягує графік y = |x| по вертикалі на множники 3 і 4 відповідно.

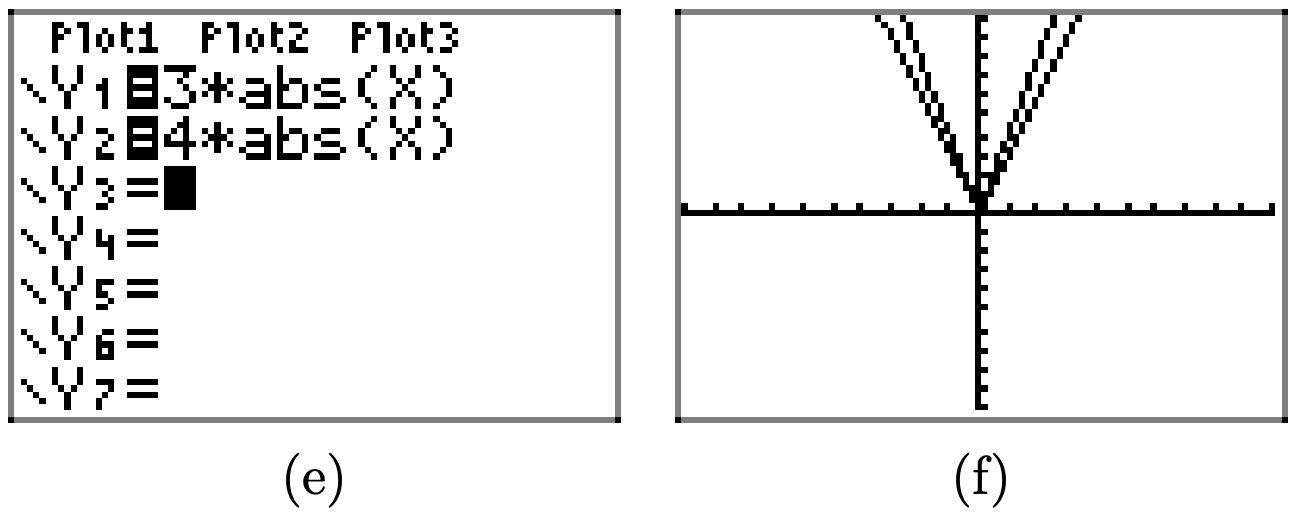
Загалом, якщо a > 1, то графік y = af (x) виходить розтягуванням графа y = f (x) по вертикалі в множник a.

Вправа$\PageIndex{16}$

Скористайтеся калькулятором графіків, щоб намалювати графік y = |x|. Потім послідовно намалюйте графіки y = (1/2) |x|, y = (1/3) |x|, і y = (1/4) |x|. Своїми словами поясніть, що ви дізналися з цієї вправи.

На малюнку нижче наведено графік функції f У Вправи$\PageIndex{17}$ -$\PageIndex{22}$ використовуйте цей графік для виконання кожного з наступних завдань.

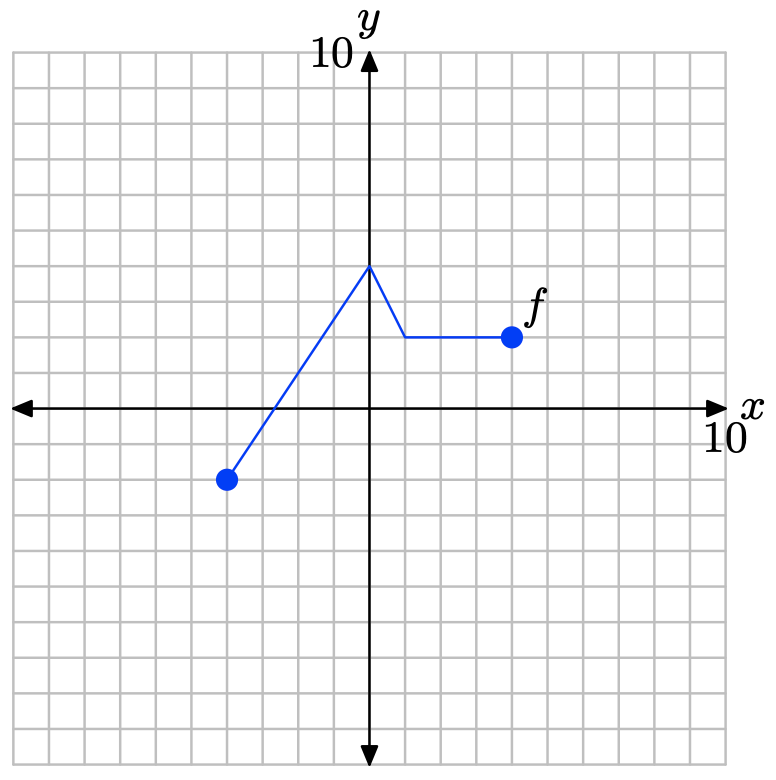
i) Налаштуйте систему координат на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Зробіть точну копію графіка f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. В оповіданні тіньовий ящик в кінці розділу узагальнює поняття та техніку вертикального масштабування, вертикального відображення та вертикального перекладу. Скористайтеся ідеями швидкого доступу, представленими в цьому підведеному вікні тіні, щоб намалювати графіки функцій, які слідують за ними, без використання таблиць.

iii. Використовуйте олівець іншого кольору, щоб намалювати графік функції, наведеної у вправі. Позначте цей графік його рівнянням. Слідкуйте за тим, щоб ключові моменти були точно промальовані. У кожній вправі складіть рівно два графіки на систему координат, графік вихідної функції f та графік функції у вправі.

Вправа$\PageIndex{17}$

у = (1/2) ф (х).

Відповідь

Щоб отримати графік y = (1/2) f (x), просто помножте значення y кожної точки на графіку y = f (x) на 1/2, зберігаючи значення x однаковим.

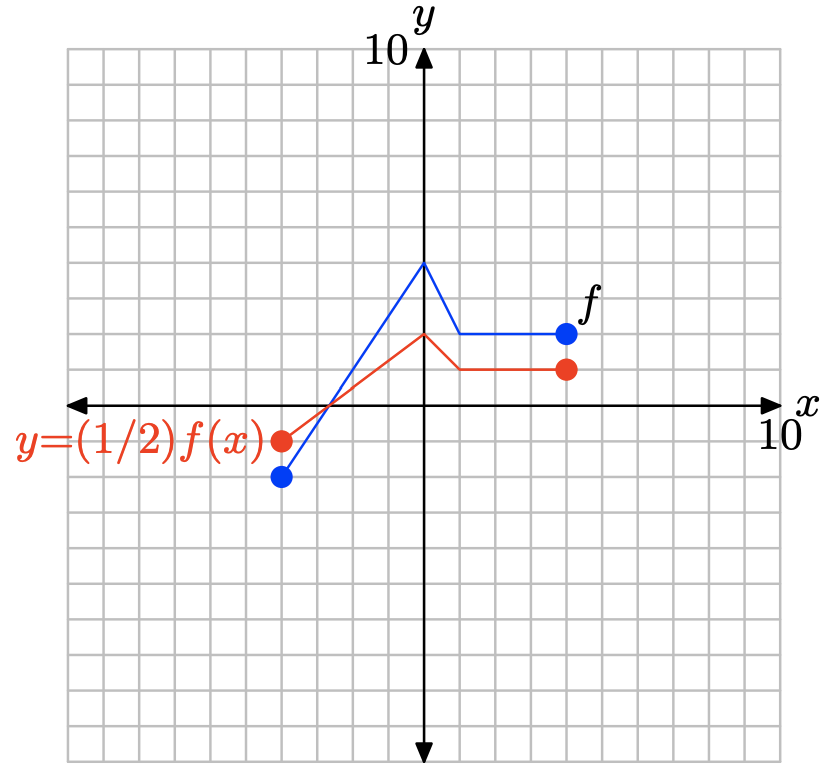
Зверніть увагу, що множення на 1/2, як у = (1/2) f (x), стискає графік y = f (x) по вертикалі на коефіцієнт 2.

Вправа$\PageIndex{18}$

у = 2ф (х).

Вправа$\PageIndex{19}$

y= −f (х).

Відповідь

Щоб отримати графік y = −f (x), просто заперечуйте значення y кожної точки на графіку y = f (x).

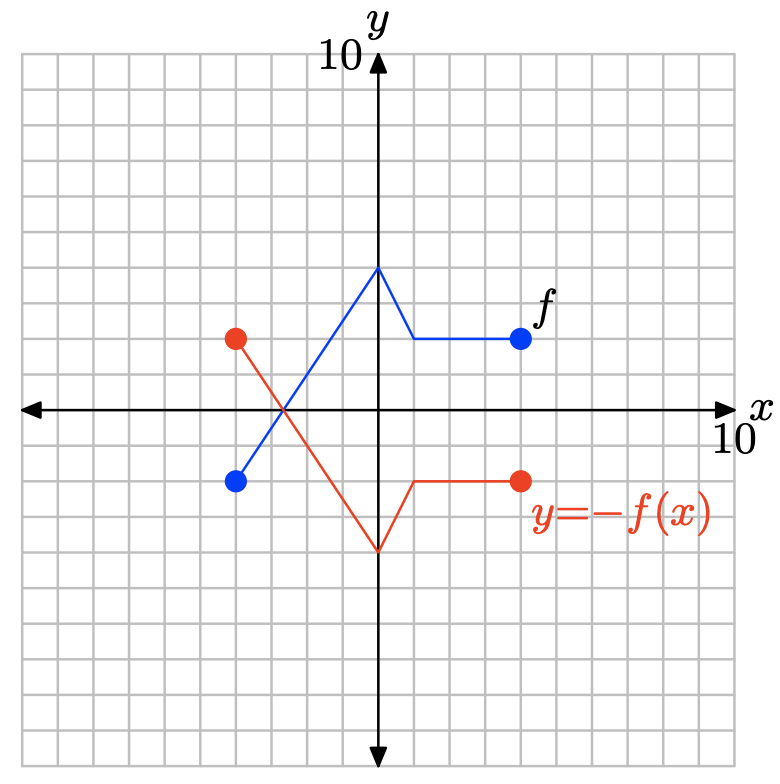
Зауважте, що заперечення, як у y = −f (x), відображає графік y = f (x) по осі x.

Вправа$\PageIndex{20}$

y = ф (х) − 1

Вправа$\PageIndex{21}$

у = ф (х) + 3.

Відповідь

Щоб отримати графік y = f (x) + 3, просто додайте 3 до значення y кожної точки на графіку y = f (x).

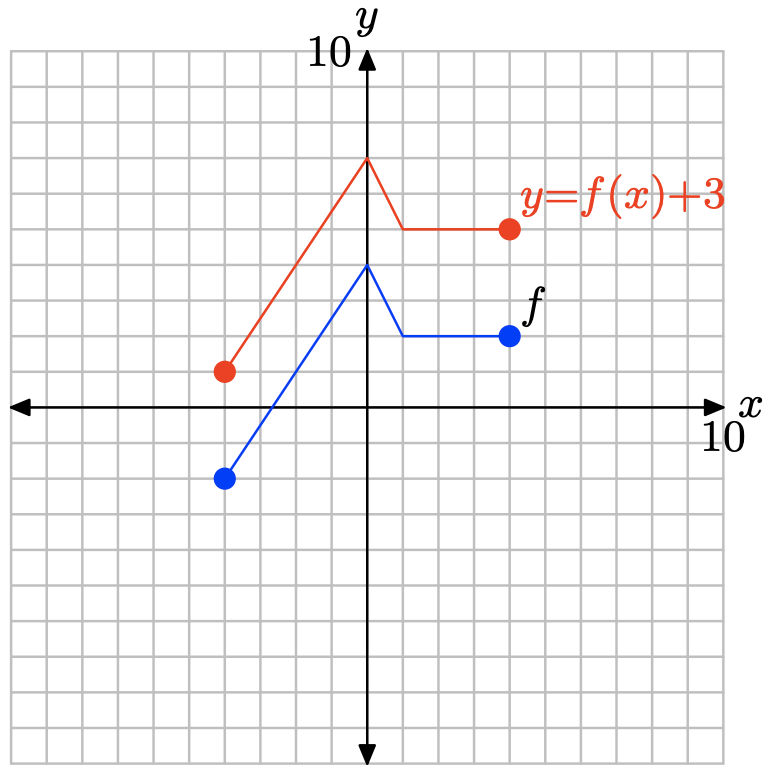
Зверніть увагу, що додавання 3, як і в y = f (x) + 3, переводить графік y = f (x) вгору на 3 одиниці.

Вправа$\PageIndex{22}$

у = ф (х) − 4

На малюнку нижче наведено графік функції f У Вправи$\PageIndex{23}$ -$\PageIndex{28}$ використовуйте цей графік для виконання кожного з наступних завдань.

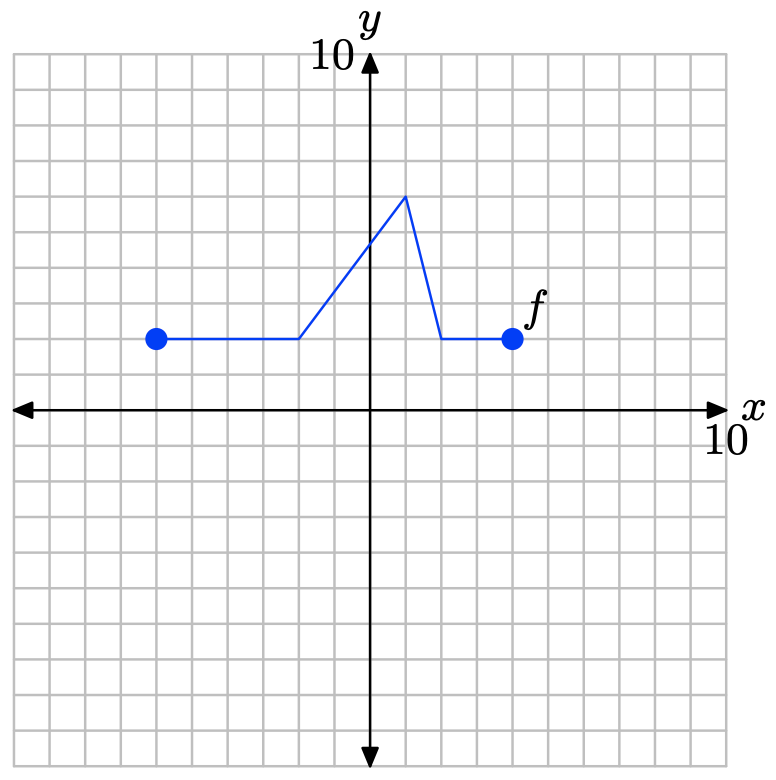
i) Налаштуйте систему координат на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Зробіть точну копію графіка f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. В оповіданні тіньовий ящик в кінці розділу узагальнює поняття та техніку вертикального масштабування, вертикального відображення та вертикального перекладу. Скористайтеся ідеями швидкого доступу, представленими в цьому підведеному вікні тіні, щоб намалювати графіки функцій, які слідують за ними, без використання таблиць.

iii. Використовуйте олівець іншого кольору, щоб намалювати графік функції, наведеної у вправі. Позначте цей графік його рівнянням. Слідкуйте за тим, щоб ключові моменти були точно промальовані. У кожній вправі складіть рівно два графіки на систему координат, графік вихідної функції f та графік функції у вправі.

Вправа$\PageIndex{23}$

у = 2ф (х)

Відповідь

Щоб отримати графік y = 2f (x), просто помножте значення y кожної точки y = f (x) на 2.

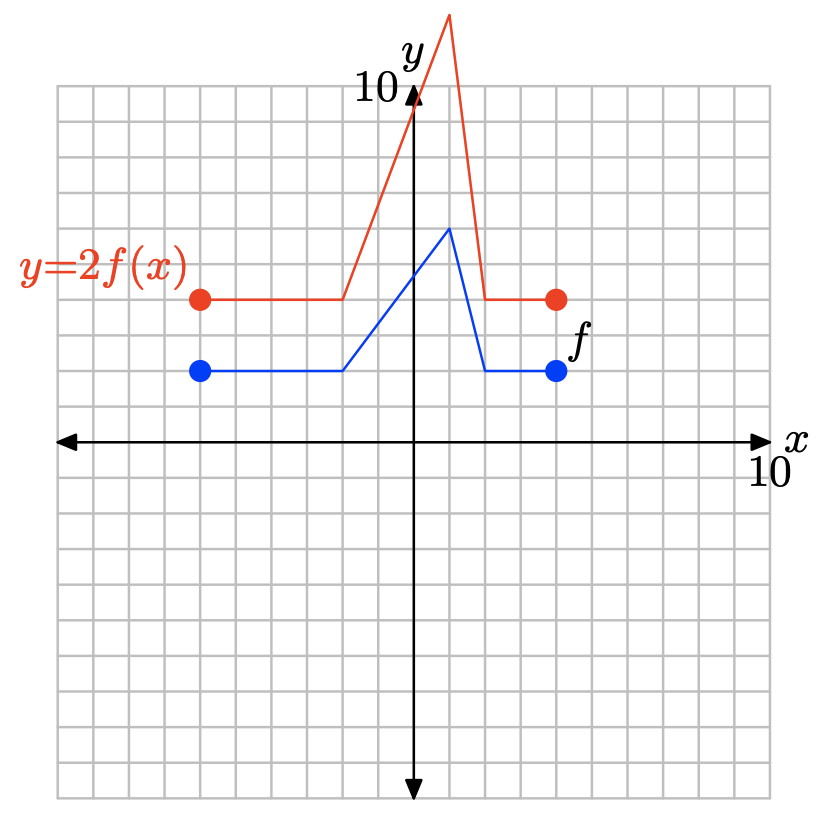
Зверніть увагу, що множення на 2, як у = 2f (x), розтягує графік y = f (x) по вертикалі на коефіцієнт 2.

Вправа$\PageIndex{24}$

у = (1/2) ф (х)

Вправа$\PageIndex{25}$

y = −f (х).

Відповідь

Щоб отримати графік y = −f (x), просто заперечуйте значення y кожної точки на графіку y = f (x).

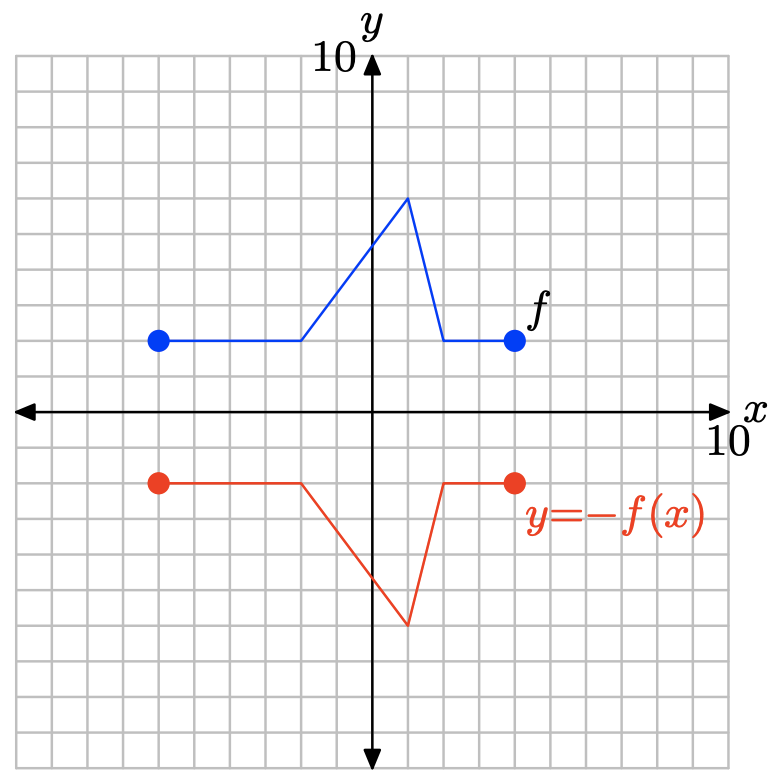
Зауважте, що заперечення функції, як у y = −f (x), відображає графік y = f (x) по осі x.

Вправа$\PageIndex{26}$

у = ф (х) + 3

Вправа$\PageIndex{27}$

y = ф (х) − 2

Відповідь

Щоб отримати графік y = f (x) − 2, просто відніміть 2 від значення y кожної точки на графіку y = f (x).

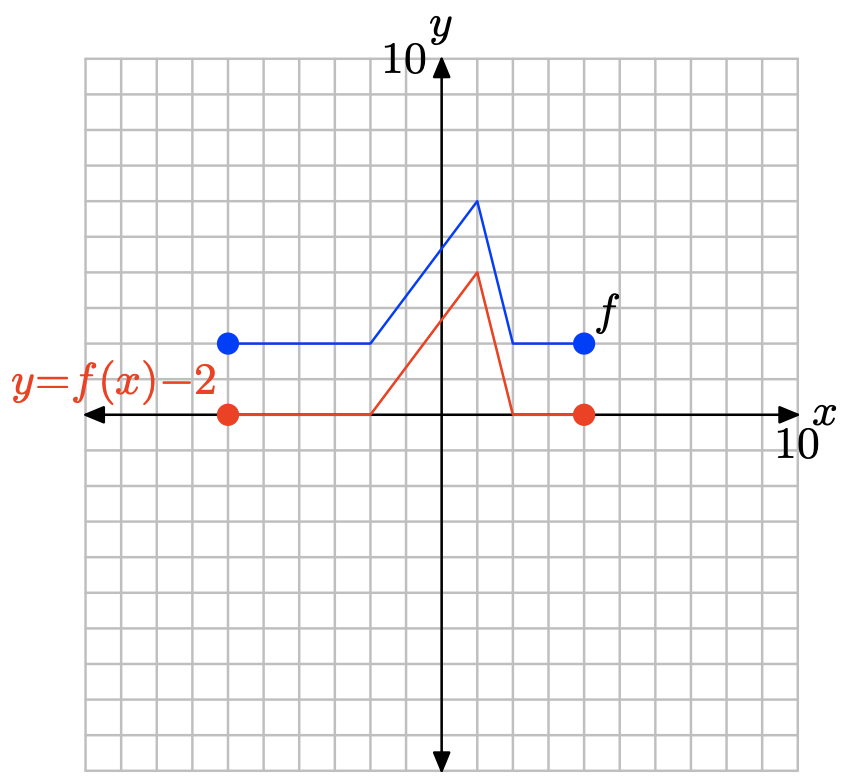
Зауважте, що віднімання 2, як у y = f (x) −2, переводить графік y = f (x) вниз на 2 одиниці.

Вправа$\PageIndex{28}$

y = ф (х) − 1

На малюнку нижче наведено графік функції f У Вправи$\PageIndex{29}$ -$\PageIndex{34}$ використовуйте цей графік для виконання кожного з наступних завдань.

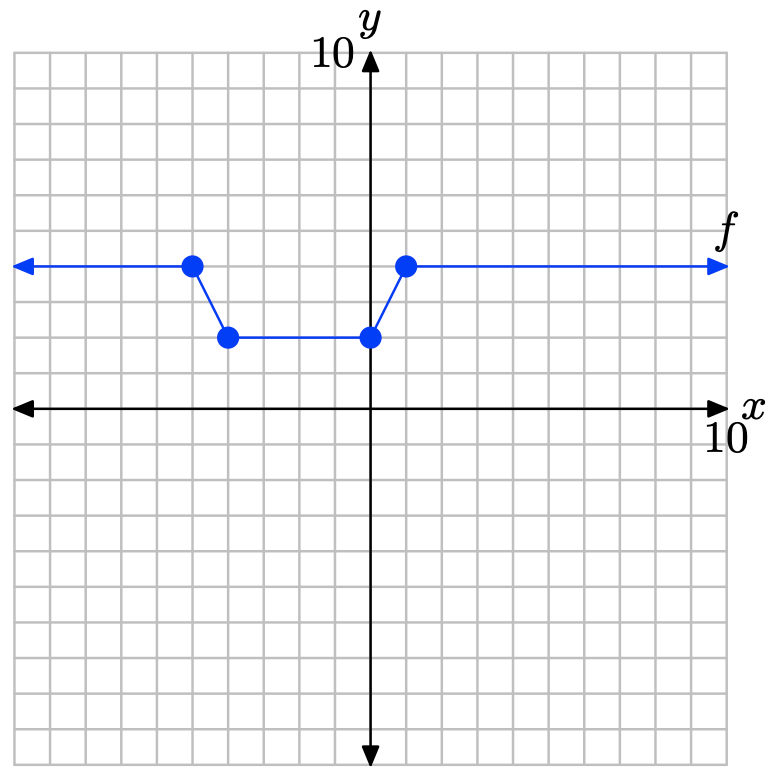
i) Налаштуйте систему координат на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Зробіть точну копію графіка f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. В оповіданні тіньовий ящик в кінці розділу узагальнює поняття та техніку вертикального масштабування, вертикального відображення та вертикального перекладу. Скористайтеся ідеями швидкого доступу, представленими в цьому підведеному вікні тіні, щоб намалювати графіки функцій, які слідують за ними, без використання таблиць.

iii. Використовуйте олівець іншого кольору, щоб намалювати графік функції, наведеної у вправі. Позначте цей графік його рівнянням. Слідкуйте за тим, щоб ключові моменти були точно промальовані. У кожній вправі складіть рівно два графіки на систему координат, графік вихідної функції f та графік функції у вправі.

Вправа$\PageIndex{29}$

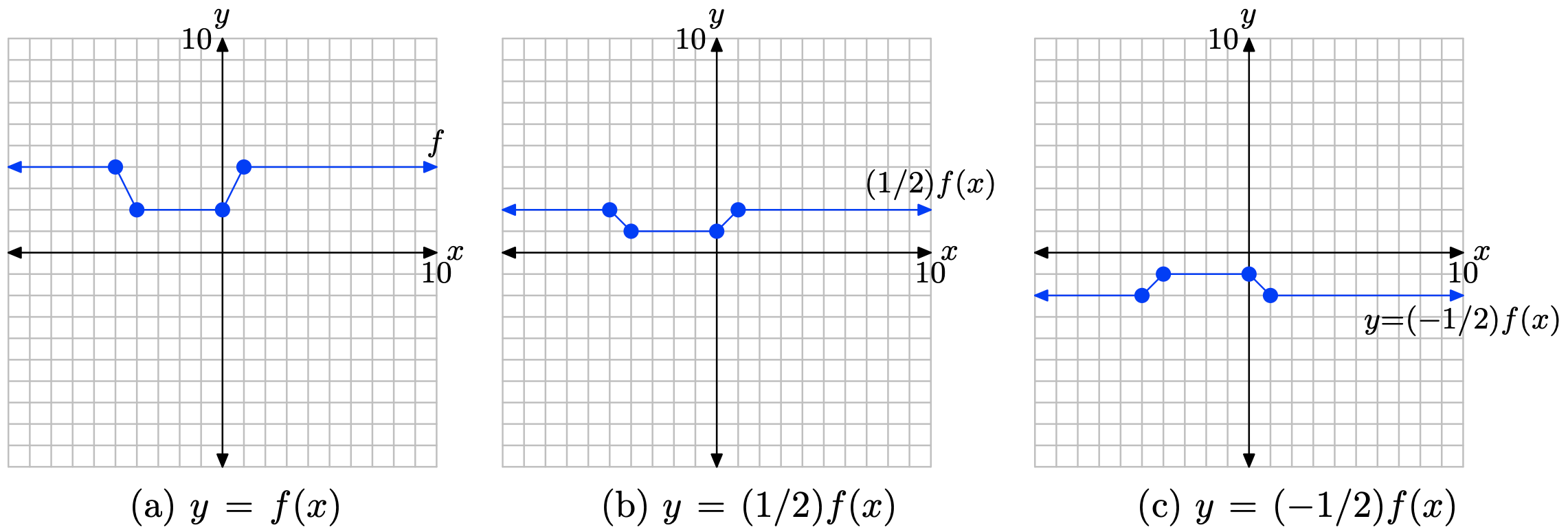
у = (−1/2) ф (х)

Відповідь

Діємо в два етапи:

1. Спочатку помножте значення y кожної точки на графіку y = f (x) на 1/2, щоб отримати графік y = (1/2) f (x) in (b). Це стискає графік y = f (x) в 2 рази.

2. По-друге, помножте значення y кожної точки на графіку y = (1/2) f (x) на −1, щоб отримати графік y = (−1/2) f (x) in (c). Це відображає графік y = (1/2) f (x) по осі x.

Вправа$\PageIndex{30}$

y = −2f (х).

Вправа$\PageIndex{31}$

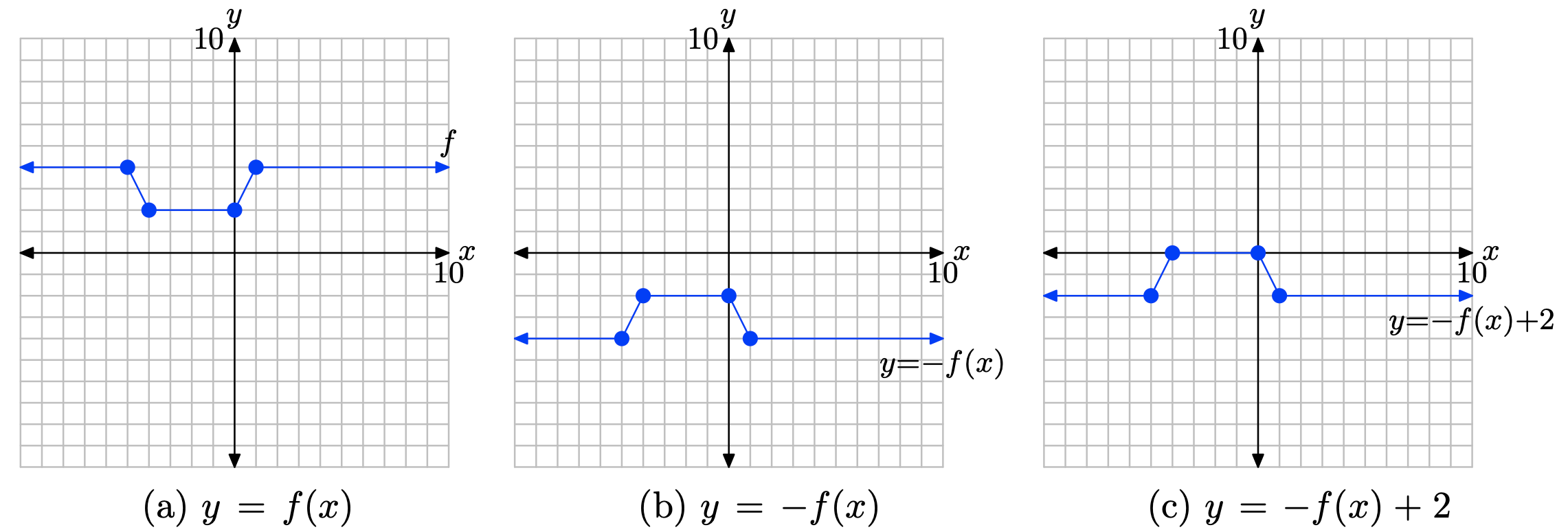
y = −f (х) + 2

Відповідь

Діємо в два етапи:

1. Спочатку помножте значення y кожної точки на графіку y = f (x) на −1, щоб отримати графік y = −f (x) у (b). Це відображає графік y = f (x) по осі x.

2. По-друге, додайте 2 до значення y кожної точки на графіку y = −f (x), щоб отримати графік y = −f (x) + 2 in (c). Це зміщує графік y = −f (x) вгору на 2 одиниці.

Вправа$\PageIndex{32}$

y = −f (x) − 3

Вправа$\PageIndex{33}$

y = 2f (х) − 3.

Відповідь

Діємо в два етапи:

1. Спочатку помножте значення y кожної точки на графіку y = f (x) на 2, щоб отримати графік y = 2f (x) in (b). Це розтягує графік y = f (x) по вертикалі в 2 рази.

2. По-друге, відніміть 3 від значення y кожної точки на графіку y = 2f (x), щоб отримати графік y = 2f (x) − 3 in (c). Це зміщує графік y = 2f (x) вниз на 3 одиниці.

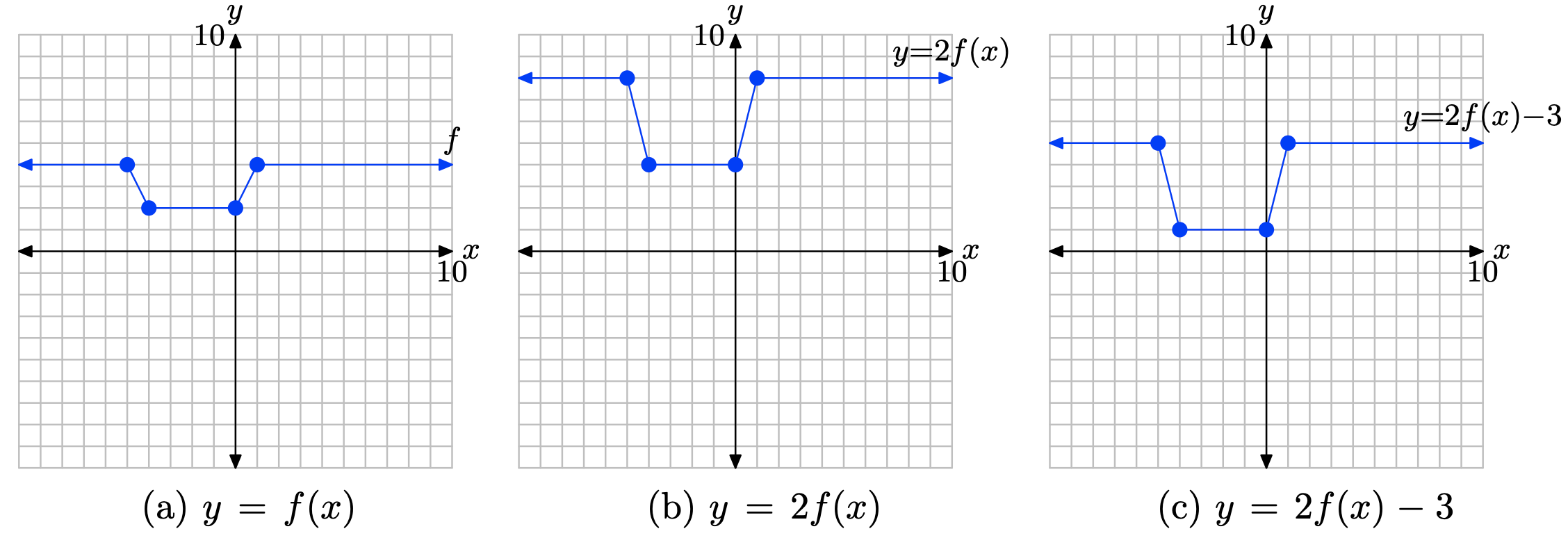
Вправа$\PageIndex{34}$

у = (−1/2) ф (х) + 1

2.6 Вправи

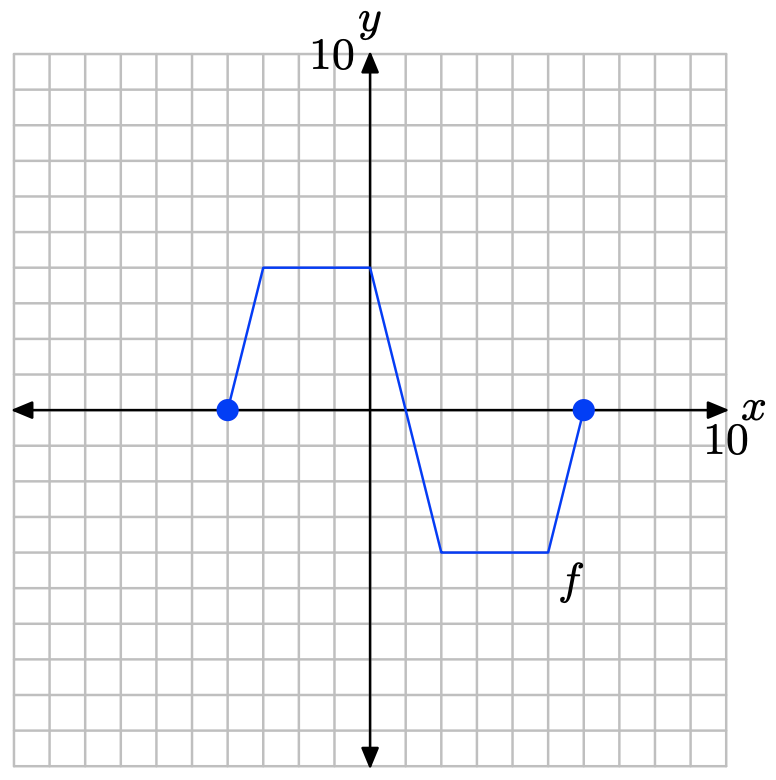
На фото нижче наведено графік функції f.

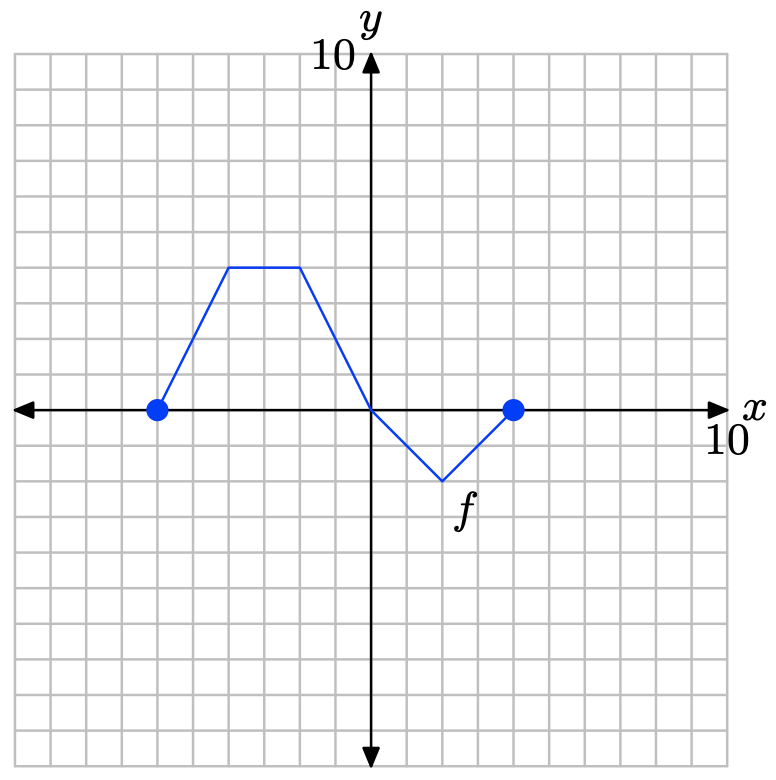
Наведена нижче таблиця обчислює функцію f на графіку за ключовими значеннями x. Зверніть увагу на горизонтальний формат, де першою точкою таблиці є впорядкована пара (−6, 0).

х	-6	-4	-2	0	2	4
f (х)	0	4	4	0	-2	0

Використовуйте графік і таблицю, щоб виконати кожне з наступних завдань для Вправи$\PageIndex{1}$ -$\PageIndex{10}$.

i) Налаштуйте систему координат на графічному папері. Позначте та масштабуйте кожну вісь, а потім скопіюйте та позначте оригінальний графік f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. Використовуйте оригінальну таблицю, щоб допомогти завершити таблицю для даної функції у вправі.

iii. Використовуючи олівець іншого кольору, побудуйте дані з вашої заповненої таблиці на тій самій системі координат, що і початковий графік f. Використовуйте ці точки, щоб допомогти завершити графік заданої функції у вправі, а потім позначте цей графік рівнянням, вказаним у вправі.

Вправа$\PageIndex{1}$

у = ф (2х).

х	-3	-2	-1	0	1	2
у

Відповідь

Оригінальна таблиця функцій.

х	-6	-4	-2	0	2	4
f (х)	0	4	4	0	-2	0

Оцінити функцію y = f (2x) при x = −3, −2, −1, 0, 1 та 2.

$$y = f(2(−3)) = f(−6) = 0 \\ y = f(2(−2)) = f(−4) = 4 \\ y = f(2(−1)) = f(−2) = 4 \\ y = f(2(0)) = f(0) = 0 \\ y = f(2(1)) = f(2) = −2 \\ y = f(2(2)) = f(4) = 0$$

Окуляри задовольняють y = f (2x).

х	-3	-2	-1	0	1	2
у	0	4	4	0	-2	0

Побудуйте точки в таблиці, щоб отримати графік y = f (2x).

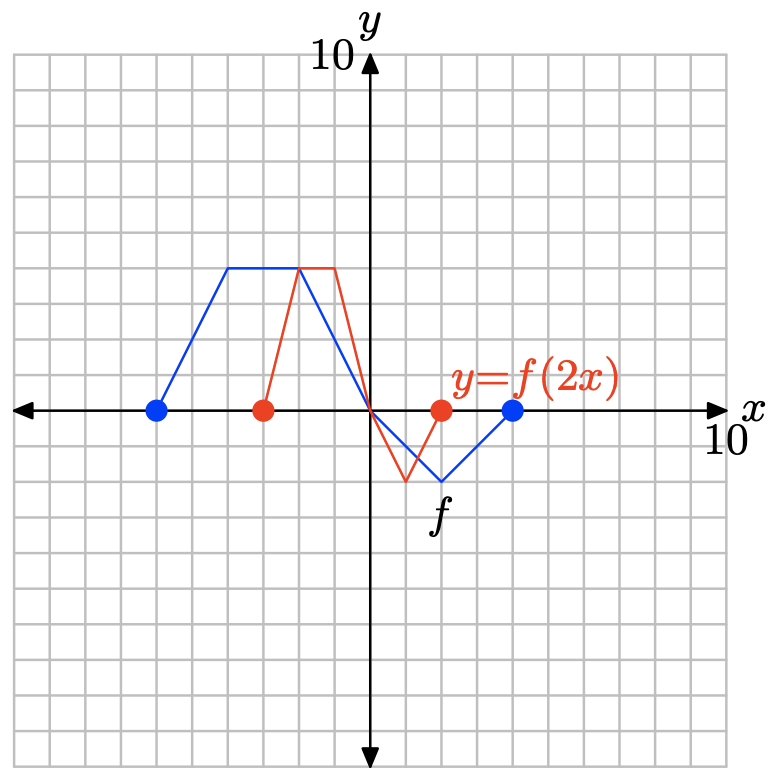
Зверніть увагу, що заміна x на 2x, як у = f (2x), стискає графік y = f (x) по горизонталі в 2 рази.

Вправа$\PageIndex{2}$

у = ф ((1/2) х).

х	-12	-8	-4	0	4	8
у

Вправа$\PageIndex{3}$

y = f (−х).

х	-4	-2	0	2	4	6
у

Відповідь

Оригінальна таблиця функцій.

х	-6	-4	-2	0	2	4
f (х)	0	4	4	0	-2	0

Оцінити функцію y = f (−x) при x = −4, −2, 0, 2, 4 та 6.

$$y = f(−(−4)) = f(4) = 0 \\ y = f(−(−2)) = f(2) = −2 \\ y = f(−(0)) = f(0) = 0 \\ y = f(−(2)) = f(−2) = 4 \\ y = f(−(4)) = f(−4) = 4 \\ y = f(−(6)) = f(−6) = 0$$

Окуляри, що задовольняють y = f (−x).

х	-4	-2	0	2	4	6
у	0	-2	0	4	4	0

Побудуйте точки у таблиці, щоб отримати графік y = f (−x).

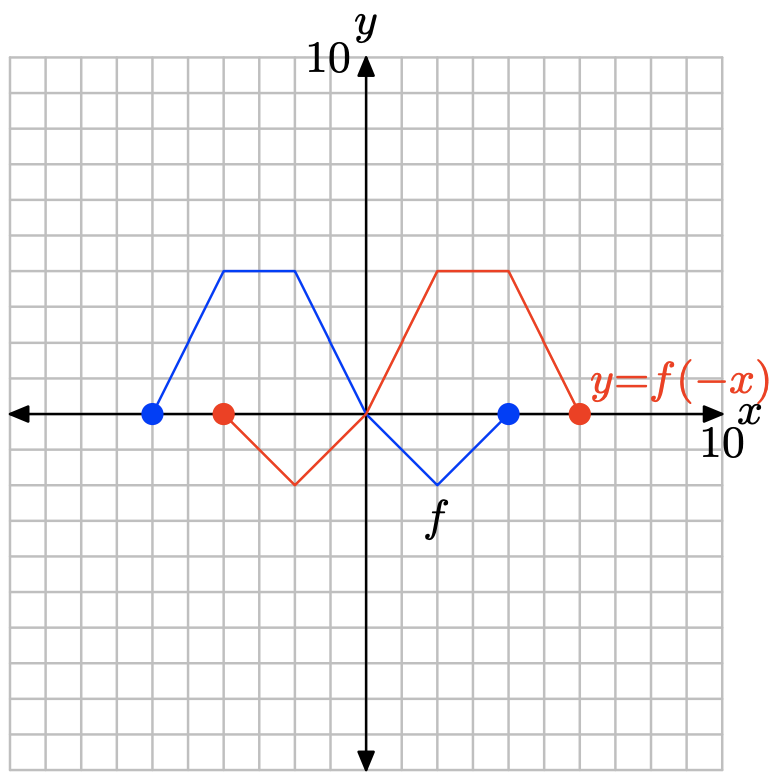
Зауважте, що заміна x на −x, як у y = f (−x), відображає графік y = f (x) по осі y.

Вправа$\PageIndex{4}$

у = ф (х + 3).

х	-9	-7	-5	-3	-1	1
у

Вправа$\PageIndex{5}$

y = f (х − 1).

х	-5	-3	-1	1	3	5
у

Відповідь

Оригінальна таблиця функцій.

х	-6	-4	-2	0	2	4
f (х)	0	4	4	0	-2	0

Оцінити функцію y = f (x − 1) при x = −5, −3, −1, 1, 3 та 5.

$$y = f((−5) − 1) = f(−6) = 0 \\ y = f((−3) − 1) = f(−4) = 4 \\ y = f((−1) − 1) = f(−2) = 4 \\ y = f((1) − 1) = f(0) = 0 \\ y = f((3) − 1) = f(2) = −2 \\ y = f((5) − 1) = f(4) = 0$$

Окуляри, що задовольняють y = f (x − 1).

х	-5	-3	-1	1	3	5
у	0	4	4	0	-2	0

Побудуйте точки в таблиці, щоб отримати графік y = f (x − 1).

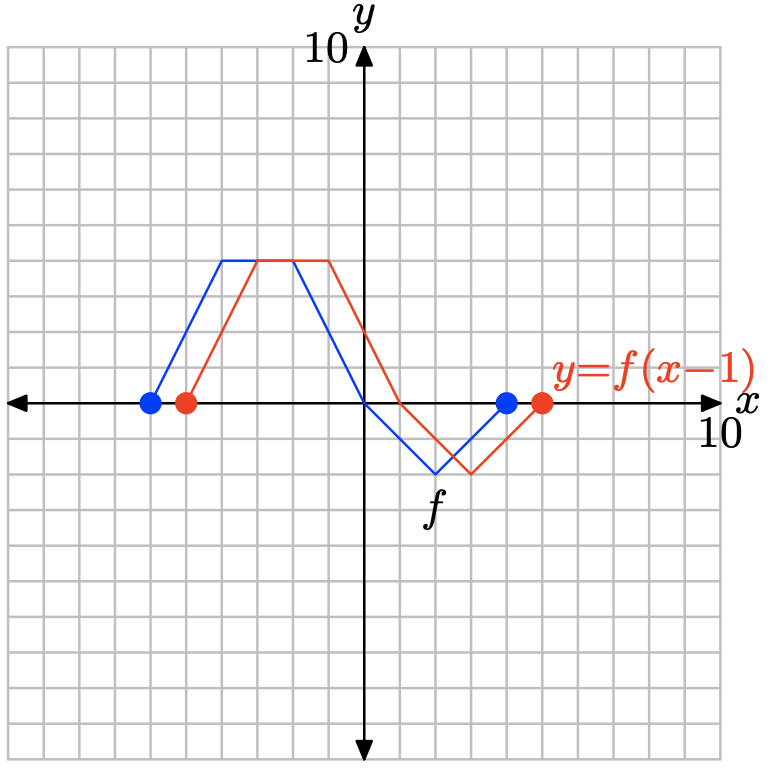
Зауважте, що заміна x на x − 1, як у y = f (x − 1), переводить графік y = f (x) горизонтально на 1 одиницю вправо.

Вправа$\PageIndex{6}$

y = f (−2х).

х	-2	-1	0	1	2	3
у

Вправа$\PageIndex{7}$

y = f ((−1/2) х).

х	-8	-4	0	4	8	12
у

Відповідь

Оригінальна таблиця функцій.

х	-6	-4	-2	0	2	4
f (х)	0	4	4	0	-2	0

Оцінити функцію y = f (((−1/2) x) при x = −8, −4, 0, 4, 8 та 12.

$$y = f((−1/2)(−8)) = f(4) = 0 \\ y = f((−1/2)(−4)) = f(2) = −2 \\ y = f((−1/2)(0)) = f(0) = 0 \\ y = f((−1/2)(4)) = f(−2) = 4 \\ y = f((−1/2)(8)) = f(−4) = 4 \\ y = f((−1/2)(12)) = f(−6) = 0$$

Окуляри, що задовольняють y = f ((−1/2) х).

х	-8	-4	0	4	8	12
у	0	-2	0	4	4	0

Побудуйте точки в таблиці, щоб отримати графік y = f (((−1/2) x).

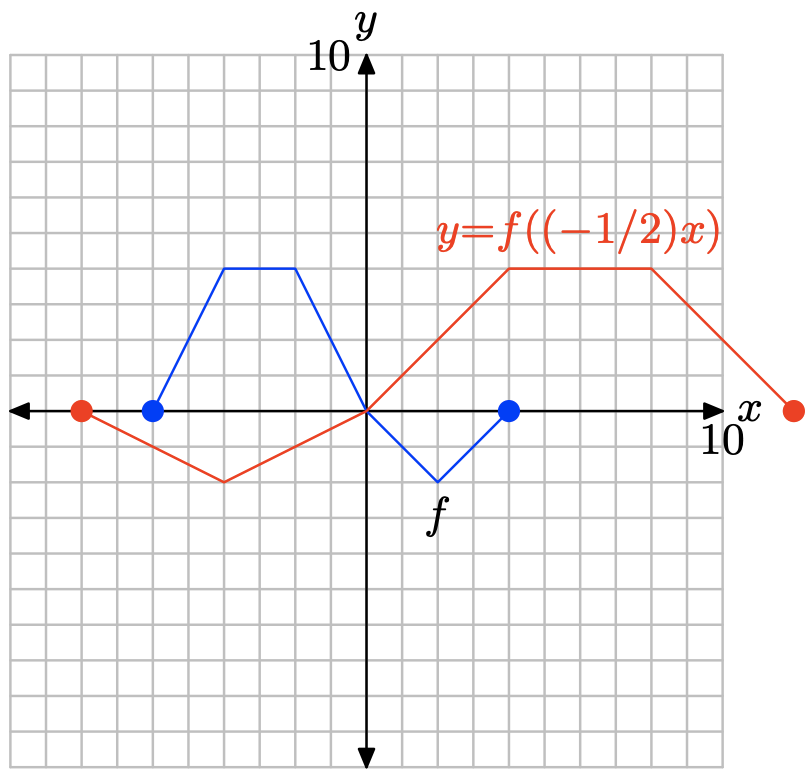
Зауважте, що заміна x на (−1/2) x, як у y = f ((−1/2) x), розтягує графік у 2 рази, а потім відображає результат по осі y.

Вправа$\PageIndex{8}$

y= f (−х − 2)

х	-6	-4	-2	0	2	4
у

Вправа$\PageIndex{9}$

y= f (−х + 1).

х	-3	-1	1	3	5	7
у

Відповідь

Оригінальна таблиця функцій.

х	-6	-4	-2	0	2	4
f (х)	0	4	4	0	-2	0

Оцінити функцію y = f (−x + 1) при x = −3, −1, 1, 3, 5 та 7.

$$y = f(−(−3) + 1) = f(4) = 0 \\ y = f(−(−1) + 1) = f(2) = −2 \\ y = f(−(1) + 1) = f(0) = 0 \\ y = f(−(3) + 1) = f(−2) = 4 \\ y = f(−(5) + 1) = f(−4) = 4 \\ y = f(−(7) + 1) = f(−6) = 0$$

Окуляри, що задовольняють y = f (−x + 1).

х	-3	-1	1	3	5	7
у	0	-2	0	4	4	0

Побудуйте точки у таблиці, щоб отримати графік y = f (−x + 1).

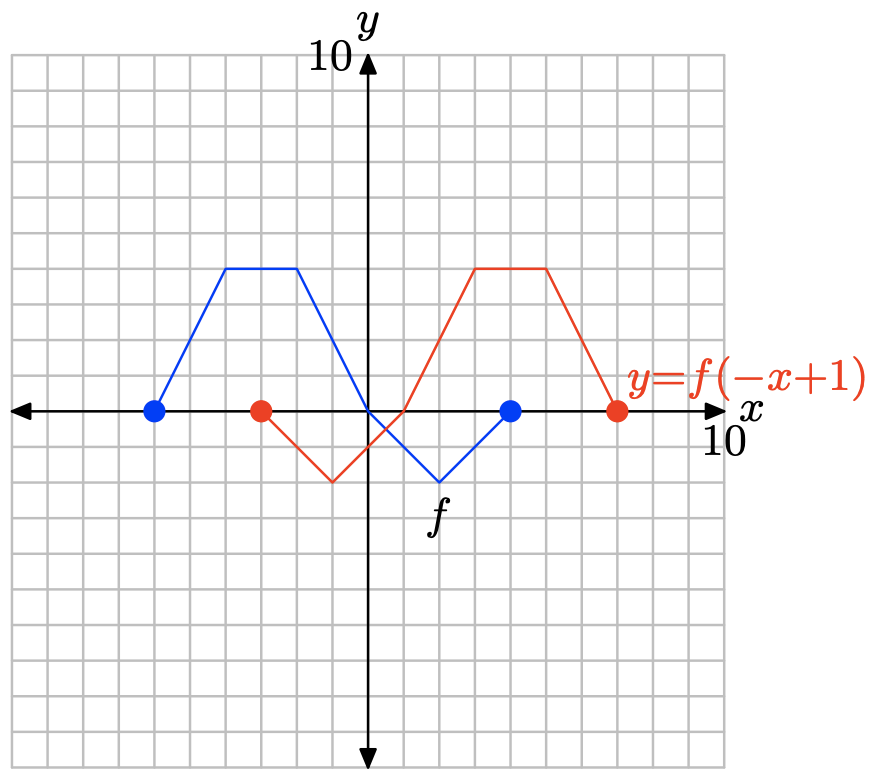
Зауважте, що y = f (−x + 1) збігається з y = f (− (x − 1)). Якщо ми замінимо x на −x, щоб отримати y = f (−x), то x у цьому останньому результаті з x − 1, щоб отримати y = f (− (x − 1)), це спричинить спочатку відображення графіка y = f (x) по осі y, а потім зміщення результату вправо на 1 одиницю.

Вправа$\PageIndex{10}$

y = f (−х/4).

х	-16	-8	0	8	16	24
у

Вправа$\PageIndex{11}$

Використовуйте графічний калькулятор, щоб намалювати графік$y = \sqrt{x}$. Потім намалюйте графік$y = \sqrt{-x}$. Своїми словами поясніть, що ви дізналися з цієї вправи.

Відповідь

Спочатку намалюйте графік$y = \sqrt{x}$.

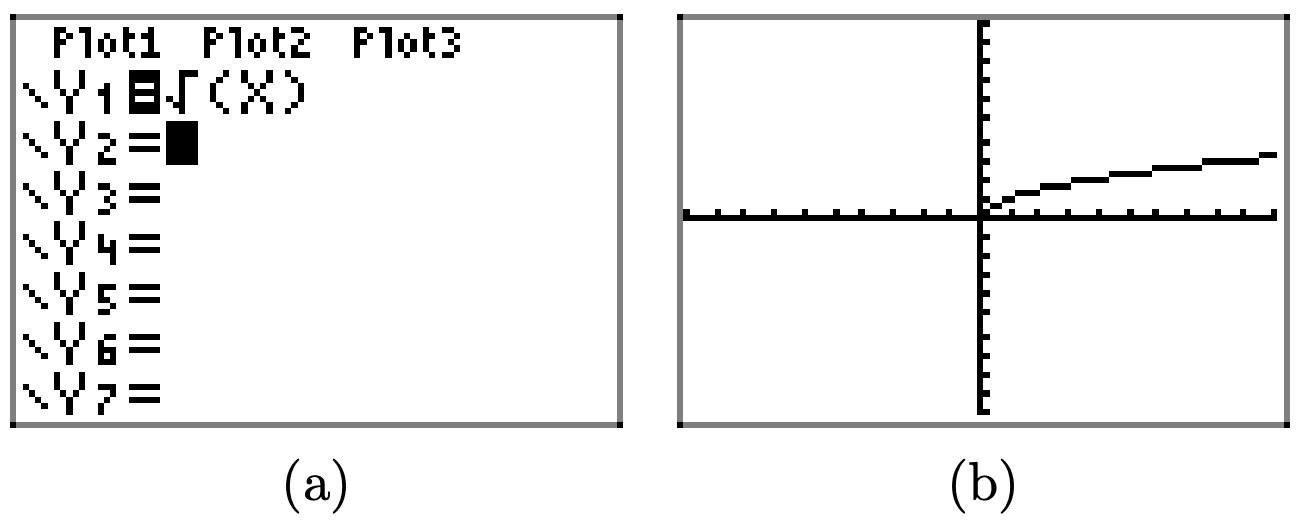
Графік$y = \sqrt{-x}$ є відображенням графіка$y = \sqrt{x}$ поперек осі Y.

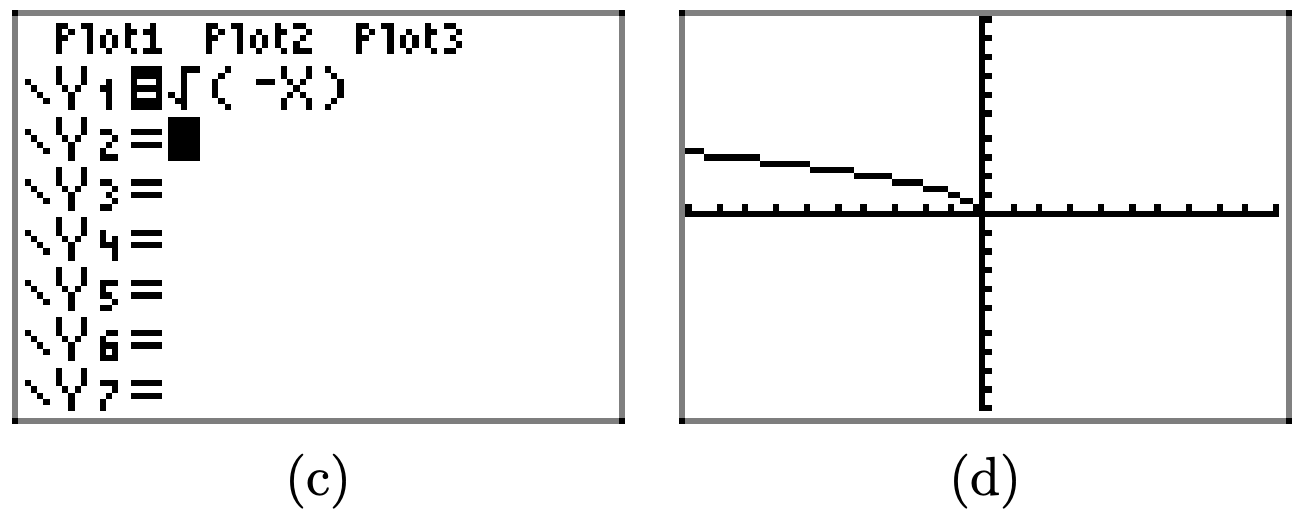
Заміна x на −x, як у y = f (−x), відображає графік y = f (x) по осі y.

Вправа$\PageIndex{12}$

Скористайтеся калькулятором графіків, щоб намалювати графік y = |x|. Потім намалюйте графік y = | − x|. Своїми словами поясніть, що ви дізналися з цієї вправи.

Вправа$\PageIndex{13}$

Використовуйте графічний калькулятор, щоб намалювати графік$y = x^2$. Потім послідовно намалюйте графіки$y = (x − 2)^2, y = (x − 4)^2$, і$y = (x − 6)^2$. Своїми словами поясніть, що ви дізналися з цієї вправи.

Відповідь

Спочатку намалюйте графік$y = x^2$.

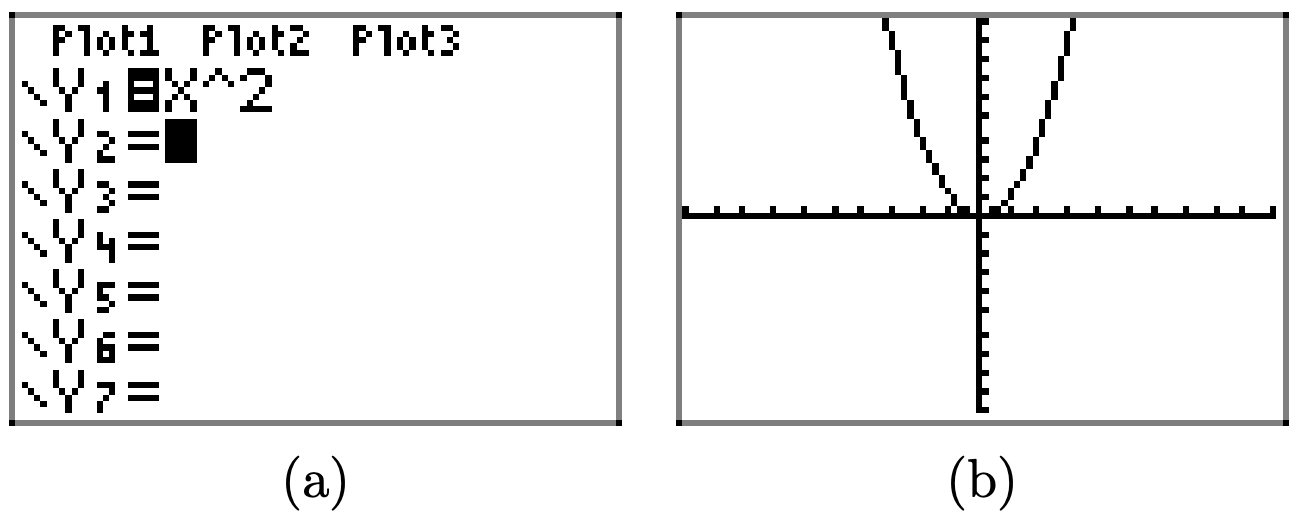
Заміна x на x − 2 переводить графік$y = x^2$ двох одиниць праворуч у горизонтальному напрямку.

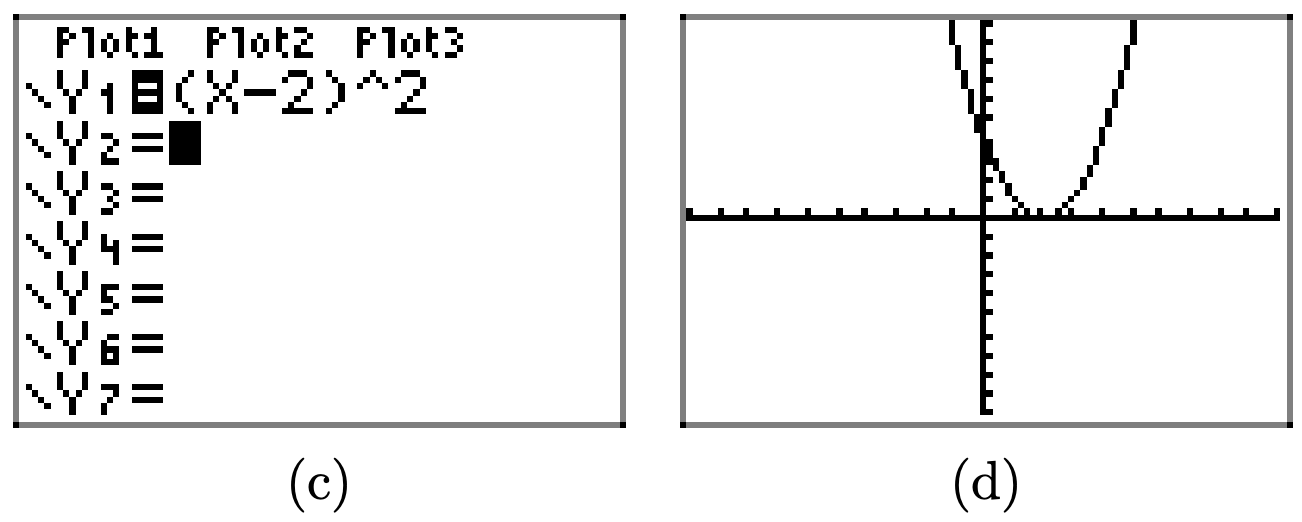
Аналогічно, заміна x на x − 4 та x − 6 переводить графік$y = x^2$ чотирьох одиниць та 6 одиниць праворуч відповідно.

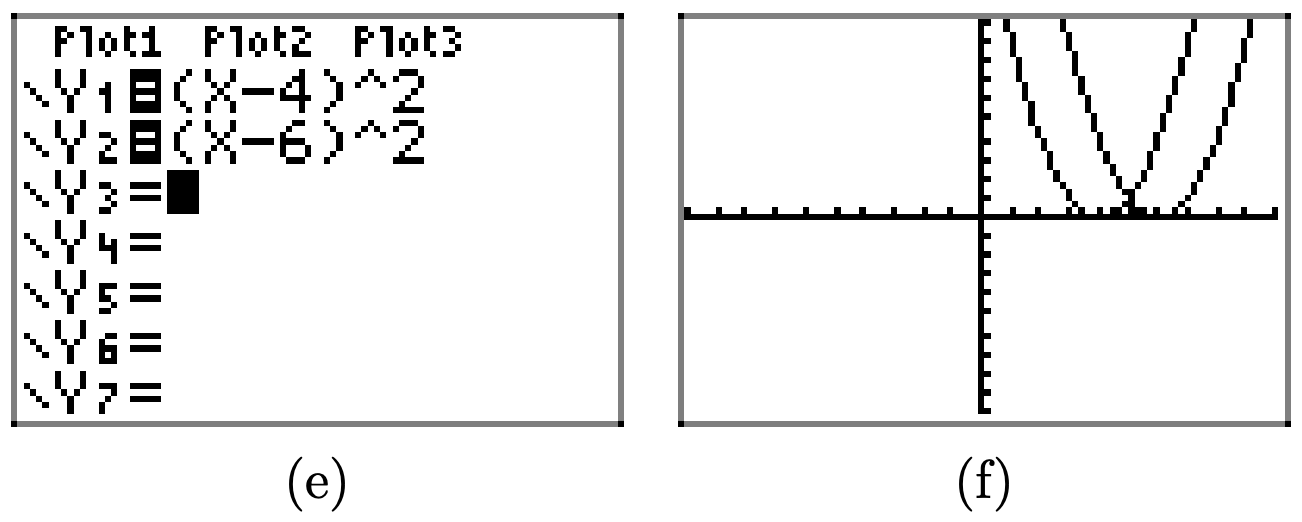
Загалом, якщо c додатне, то графік y = f (x − c) виходить шляхом перекладу графа y = f (x) вправо c одиниць.

Вправа$\PageIndex{14}$

Використовуйте графічний калькулятор, щоб намалювати графік$y = x^2$. Потім послідовно намалюйте графіки$y = (x + 2)^2, y = (x + 4)^2$, і$y = (x + 6)^2$. Своїми словами поясніть, що ви дізналися з цієї вправи.

Вправа$\PageIndex{15}$

Скористайтеся калькулятором графіків, щоб намалювати графік y = |x|. Потім послідовно намалюйте графіки y = |2x|, y = |3x|, і y = |4x|. Своїми словами поясніть, що ви дізналися з цієї вправи.

Відповідь

Спочатку намалюйте графік y = |x|.

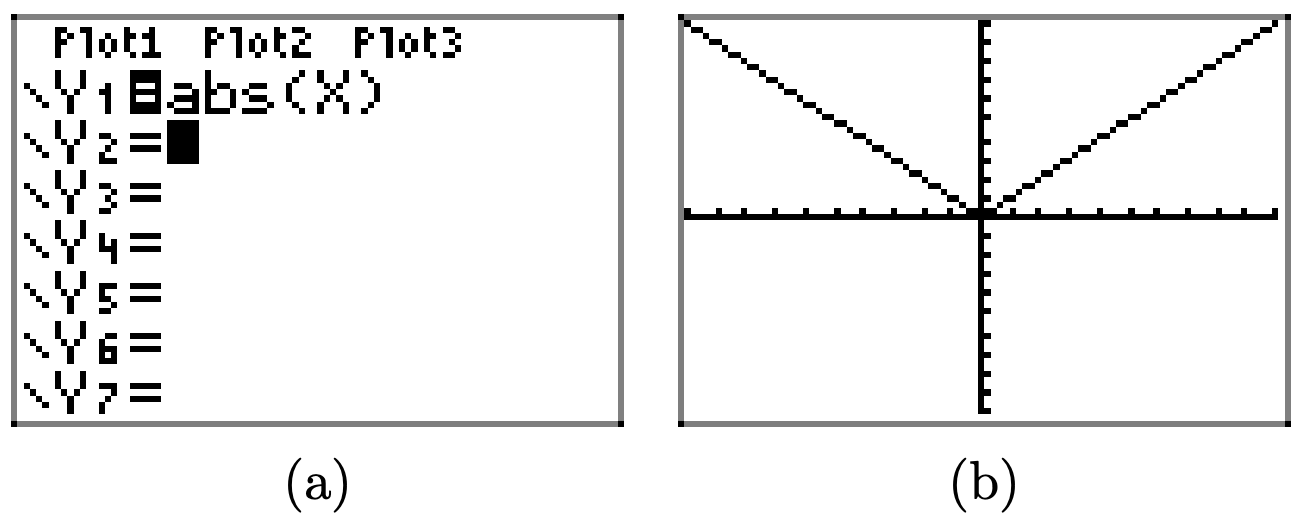
Заміна x на 2x стискає графік y = |x| на коефіцієнт 2 в горизонтальному напрямку.

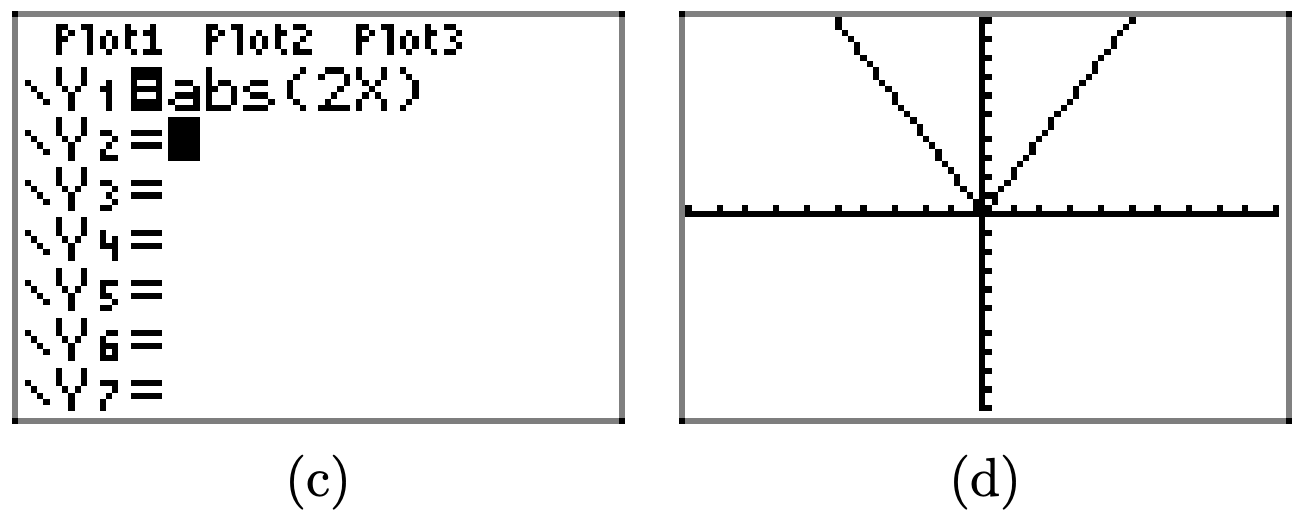
Аналогічно замінюємо х на 3х і 4х на коефіцієнт 3 і 4 в горизонтальному напрямку відповідно.

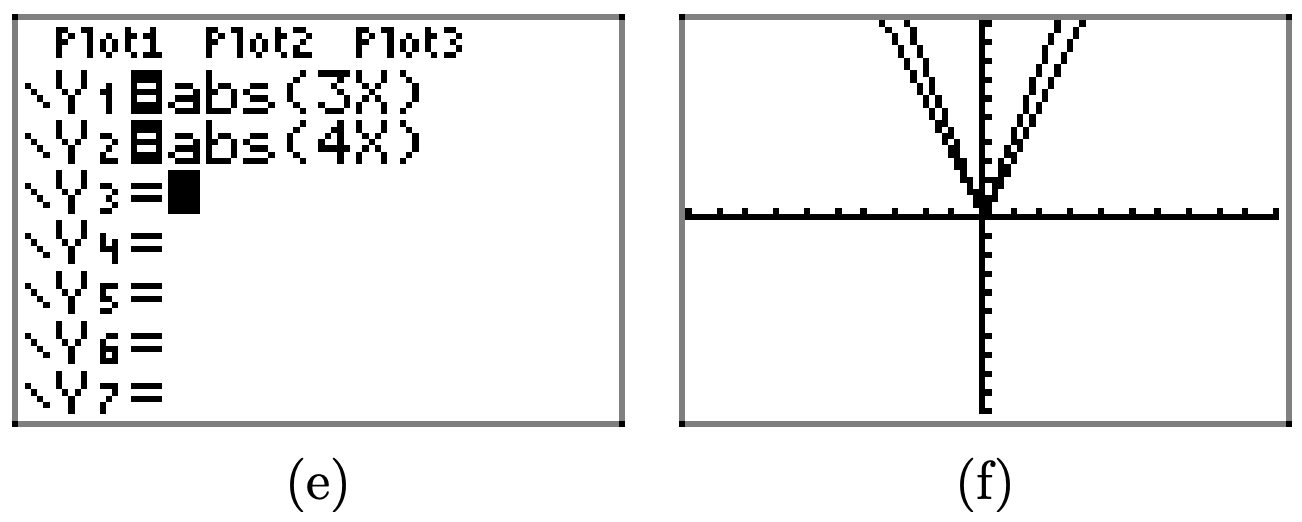
Загалом, якщо a > 1, то графік y = f (ax) виходить стисненням графіка y = f (x) на множник a в горизонтальному напрямку.

Вправа$\PageIndex{16}$

Скористайтеся калькулятором графіків, щоб намалювати графік y = |x|. Потім послідовно намалюйте графіки y = | (1/2) x|, y = | (1/3) x|, і y = | (1/4) x|. Своїми словами поясніть, що ви дізналися з цієї вправи.

На малюнку нижче наведено графік функції f У Вправи$\PageIndex{17}$ -$\PageIndex{22}$ використовуйте цей графік для виконання кожного з наступних завдань.

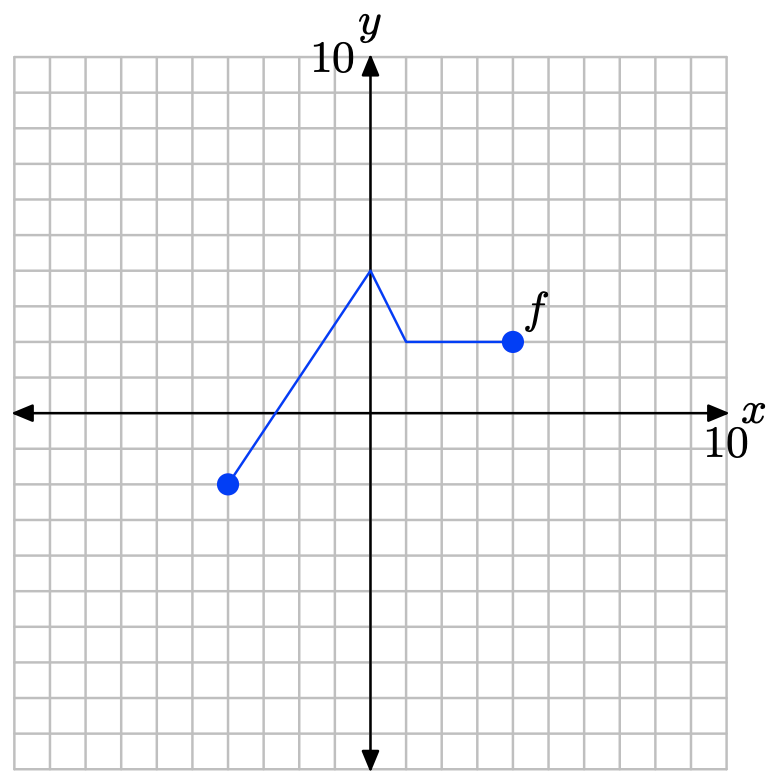
i) Налаштуйте систему координат на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Зробіть точну копію графіка f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. В оповіданні тіньовий ящик в кінці розділу узагальнює поняття та техніку горизонтального масштабування, горизонтального відображення та горизонтального перекладу. Скористайтеся ідеями швидкого доступу, представленими в цьому підведеному вікні тіні, щоб намалювати графіки функцій, які слідують за ними, без використання таблиць.

iii. Використовуйте олівець іншого кольору, щоб намалювати графік функції, наведеної у вправі. Позначте цей графік його рівнянням. Слідкуйте за тим, щоб ключові моменти були точно промальовані. У кожній вправі складіть рівно два графіки на систему координат, графік вихідної функції f та графік функції у вправі.

Вправа$\PageIndex{17}$

у = ф (2х).

Відповідь

Щоб отримати графік для y = f (2x), візьміть кожну точку на графіку y = f (x) і розділіть її значення x на 2, зберігаючи значення y однаковим.

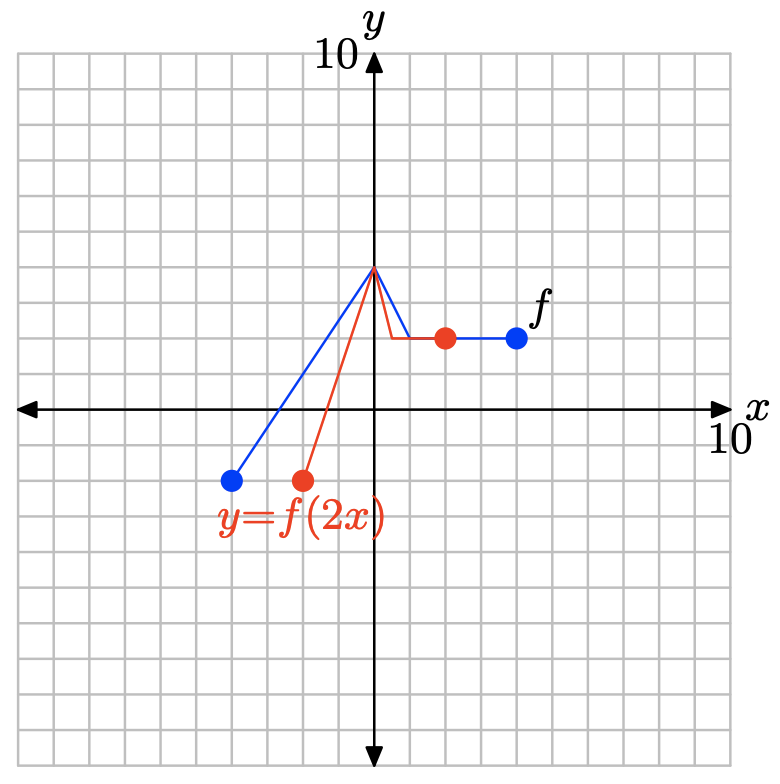
Зверніть увагу, що заміна x на 2x, як у = f (2x), стискає графік y = f (x) в горизонтальному напрямку в 2 рази.

Вправа$\PageIndex{18}$

у = ф ((1/2) х).

Вправа$\PageIndex{19}$

y = f (−х).

Відповідь

Щоб отримати графік y = f (−x), візьміть кожну точку на графіку y = f (x) і змініть її значення x, зберігаючи значення y однаковим.

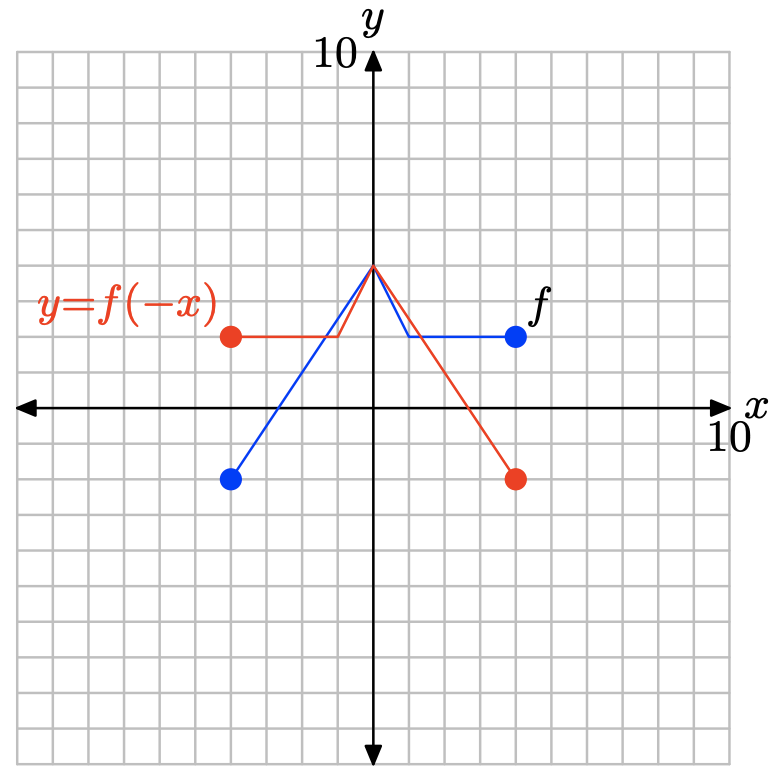
Зауважте, що заміна x на −x, як у y = f (−x), відображає графік f по осі y.

Вправа$\PageIndex{20}$

y = f (х − 1).

Вправа$\PageIndex{21}$

у = ф (х + 3).

Відповідь

Щоб отримати графік y = f (x + 3), візьміть кожну точку на графіку y = f (x) і відніміть 3 з його значення x, зберігаючи значення y однаковим.

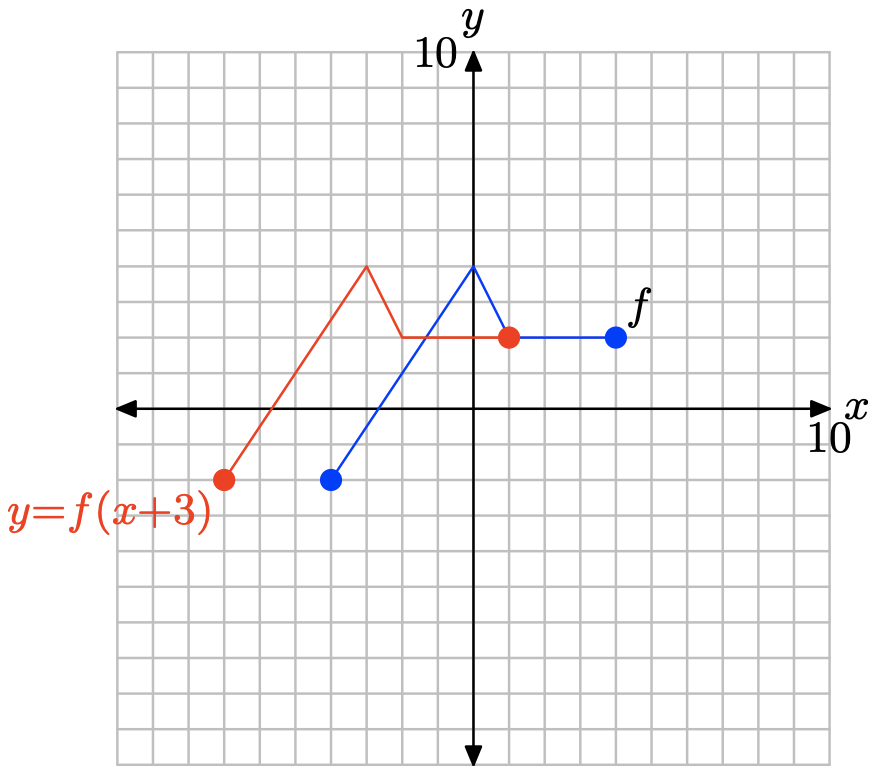
Зверніть увагу, що заміна x на x + 3, як у = f (x + 3), переводить графік y = f (x) вліво 3 одиниці.

Вправа$\PageIndex{22}$

y = f (х − 2).

На малюнку нижче наведено графік функції f У Вправи$\PageIndex{23}$ -$\PageIndex{28}$ використовуйте цей графік для виконання кожного з наступних завдань.

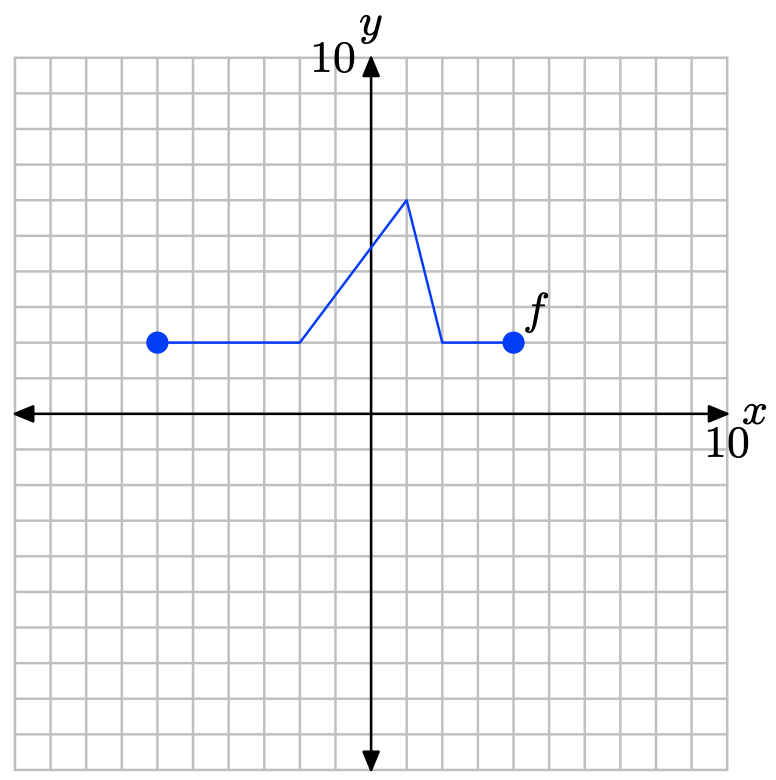
i) Налаштуйте систему координат на аркуші графського паперу. Позначте та масштабуйте кожну вісь. Зробіть точну копію графіка f у вашій системі координат. Не забудьте намалювати всі лінії лінійкою.

II. В оповіданні тіньовий ящик в кінці розділу узагальнює поняття та техніку горизонтального масштабування, горизонтального відображення та горизонтального перекладу. Скористайтеся ідеями швидкого доступу, представленими в цьому підведеному вікні тіні, щоб намалювати графіки функцій, які слідують за ними, без використання таблиць.

iii. Використовуйте олівець іншого кольору, щоб намалювати графік функції, наведеної у вправі. Позначте цей графік його рівнянням. Слідкуйте за тим, щоб ключові моменти були точно промальовані. У кожній вправі складіть рівно два графіки на систему координат, графік вихідної функції f та графік функції у вправі.

Вправа$\PageIndex{23}$

у = ф (2х).

Відповідь

Щоб отримати графік y = f (2x), візьміть кожну точку на графіку y = f (x) і розділіть її значення x на 2, зберігаючи значення y однаковим.

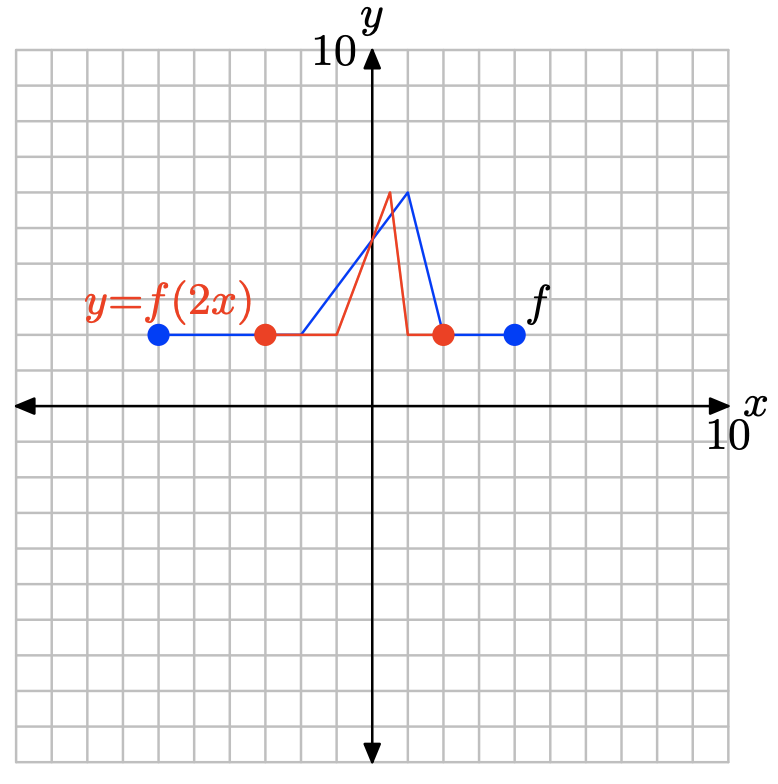
Замінивши x на 2x, як у = f (2x), стискає графік y = f (x) по горизонталі в 2 рази.

Вправа$\PageIndex{24}$

у = ф ((1/2) х).

Вправа$\PageIndex{25}$

y = f (−х).

Відповідь

Щоб отримати графік y = f (−x), візьміть кожну точку на графіку y = f (x) і скасовуйте її значення x, зберігаючи однакове значення y.

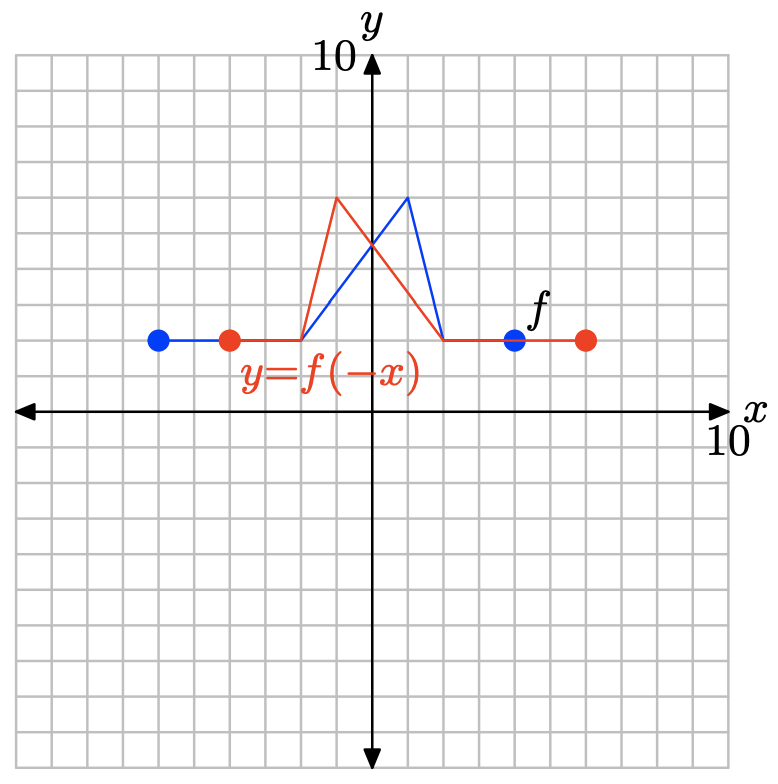
Заміна x на −x, як у y = f (−x), відображає графік y = f (x) по осі y.

Вправа$\PageIndex{26}$

у = ф (х + 3)

Вправа$\PageIndex{27}$

y= f (х − 2).

Відповідь

Щоб отримати графік y = f (x − 2), візьміть кожну точку на графіку y = f (x) і додайте 2 до її значення x, зберігаючи її значення y однаковим.

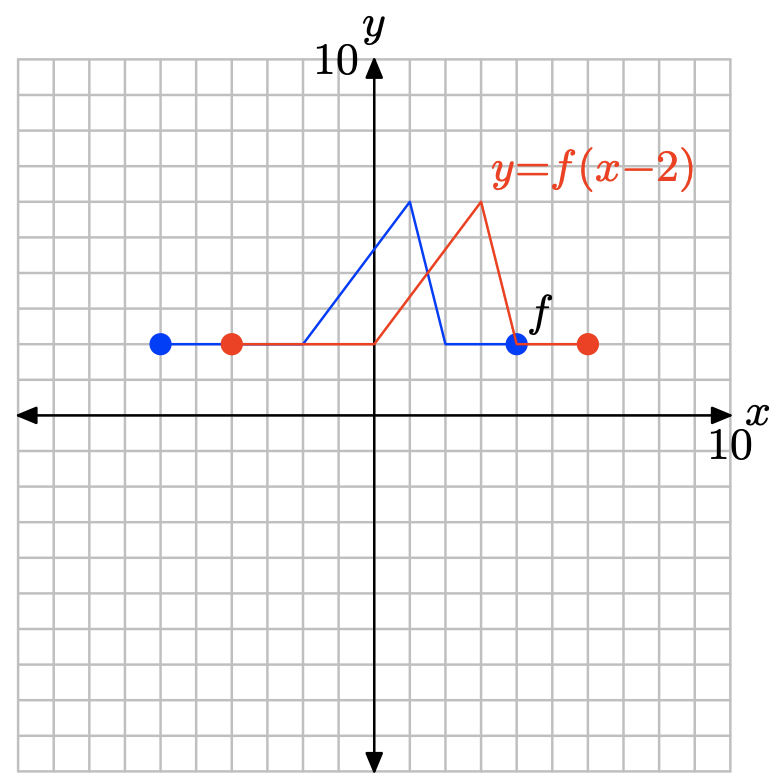
Заміна x на x − 2, як у y = f (x − 2), зрушує графік y = f (x) вправо на 2 одиниці.

Вправа$\PageIndex{28}$

у = ф (х + 1).