2.1: Вступ до функцій

Наш розвиток концепції функції є сучасним, але досить швидким, особливо з огляду на те, що сьогоднішнє визначення зайняло понад 300 років, щоб досягти свого теперішнього стану. Почнемо з визначення відношення.

Відносини

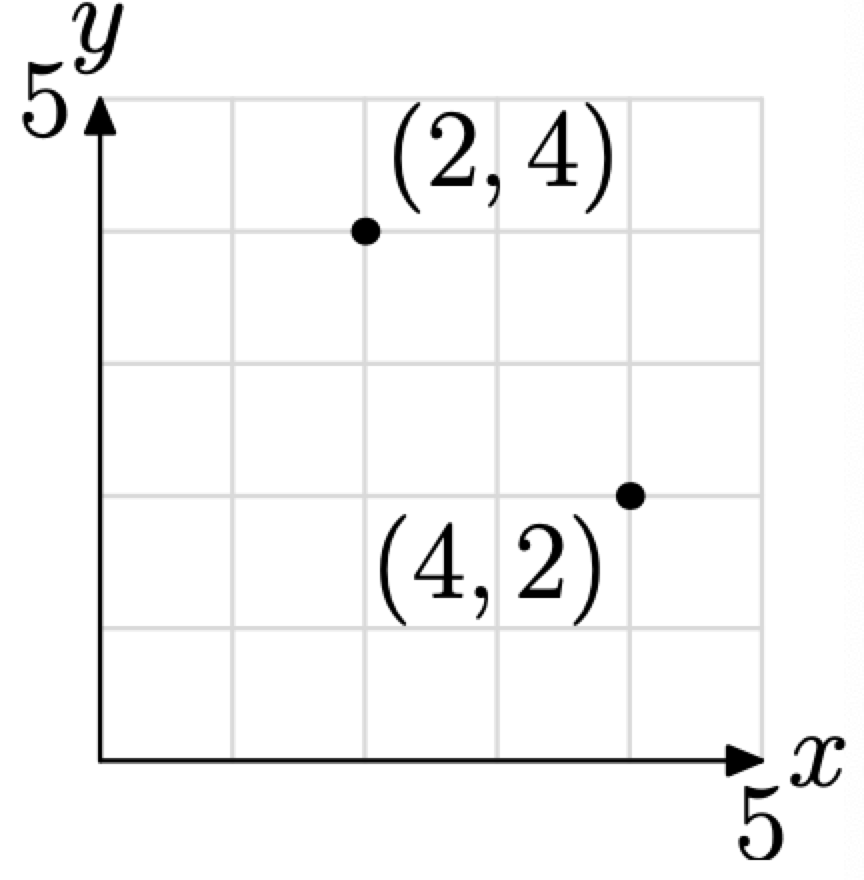
Використовуємо позначення (2, 4) для позначення того, що називається впорядкованою парою. Якщо думати про позиції, зайняті впорядкованими парами (4, 2) і (2, 4) в координатній площині (див. Рис.\(\PageIndex{1}\)), то відразу видно, чому важливий порядок. Впорядкована пара (4, 2) просто не така, як упорядкована пара (2, 4).

Малюнок\(\PageIndex{1}\)

Перший елемент впорядкованої пари називається її абсцисою. Другий елемент впорядкованої пари називається її ординатою. Так, наприклад, абсциса (4, 2) дорівнює 4, тоді як ордината (4, 2) дорівнює 2.

Визначення

Колекція впорядкованих пар називається відношенням. (2)

Наприклад, колекція впорядкованих пар\[R=\{(0,1),(0,2),(3,4)\}\] - це відношення.

Визначення

Домен відношення - це колекція всіх абсцис кожної впорядкованої пари.

Таким чином, область відношення R в (2) дорівнює\[\text { Domain }=\{0,3\}\]

Відзначимо, що кожну абсцису ми перераховуємо тільки один раз.

Визначення

Діапазон відношення - це колекція всіх ординат кожної впорядкованої пари.

Таким чином, діапазон відношення R in (2) дорівнює\[\text { Range }=\{1,2,4\}\]

Давайте розглянемо приклад.

Приклад\(\PageIndex{1}\)

Розглянемо відношення T, визначене\[T=\{(1,2),(3,2),(4,5)\}\]

Що таке домен і діапазон цього відношення?

Рішення

Домен являє собою колекцію абсцис кожної впорядкованої пари. Отже, домен T є\[\text { Domain }=\{1,3,4\}\]

Діапазон - це колекція ординат кожної впорядкованої пари. Значить, діапазон T дорівнює\[\text { Range }=\{2,5\}\]

Зверніть увагу, що ми перераховуємо кожну ординату в діапазоні лише один раз.

У\(\PageIndex{1}\) прикладі відношення описується шляхом перерахування впорядкованих пар. Це не єдиний спосіб, яким можна описати відношення. Наприклад, графік, безумовно, являє собою сукупність впорядкованих пар.

Приклад\(\PageIndex{2}\)

Розглянемо графік співвідношення S, показаний на малюнку\(\PageIndex{2}\).

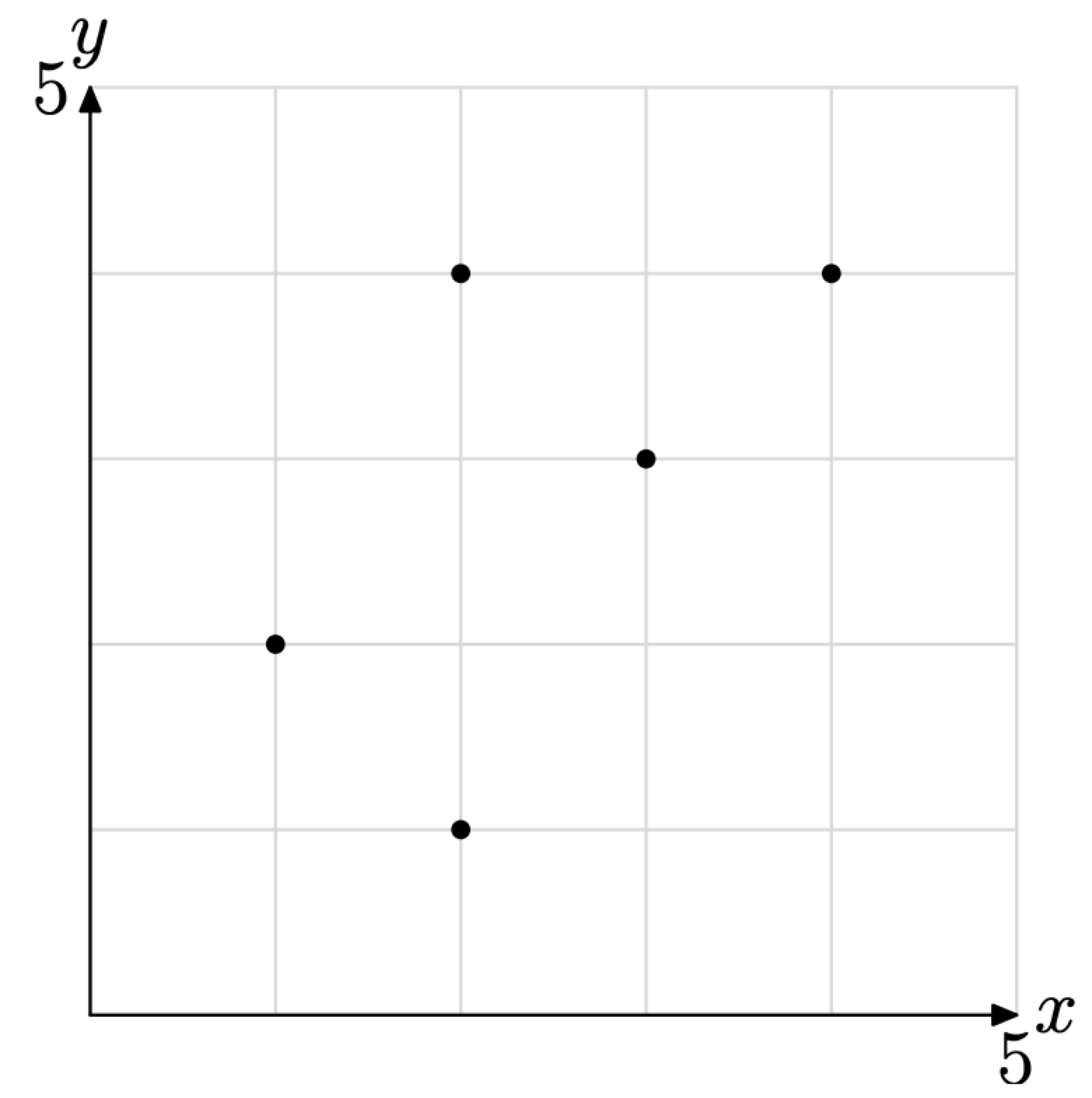
\(\PageIndex{2}\)Малюнок Графік відношення.

Що таке домен і діапазон відношення S?

Рішення

Існує п'ять впорядкованих пар (точок), побудованих на малюнку\(\PageIndex{2}\). Вони є\[S=\{(1,2),(2,1),(2,4),(3,3),(4,4)\}\]

Отже, відношення S має домен = {1, 2, 3, 4} і діапазон = {1, 2, 3, 4}. У випадку з діапазоном, зверніть увагу, як ми відсортували ординати кожної впорядкованої пари у порядку зростання, дбаючи про те, щоб не перераховувати жодної ординати більше одного разу.

Функції

Функція - це дуже особливий тип відношення. Почнемо з формального визначення.

Визначення

Відношення - це функція тоді і лише тоді, коли кожен об'єкт у своїй області сполучається з одним і тільки одним об'єктом у своєму діапазоні.

Це непросте визначення, тому давайте не поспішаємо і розглянемо кілька прикладів. Розглянемо, якщо хочете, відношення R в (2), повторене тут ще раз для зручності.

\[R=\{(0,1),(0,2),(3,4)\}\]

Доменом є {0, 3}, а діапазон - {1, 2, 4}. Зверніть увагу, що число 0 в області R сполучається з двома числами з діапазону, а саме 1 і 2. Тому R не є функцією.

Існує конструкція, яка називається діаграмою відображення, яка може бути корисною для визначення того, чи є зв'язок функцією. Щоб створити діаграму відображення, спочатку перерахуйте домен зліва, потім діапазон праворуч, потім використовуйте стрілки, щоб вказати впорядковані пари у вашому відношенні, як показано на малюнку\(\PageIndex{3}\).

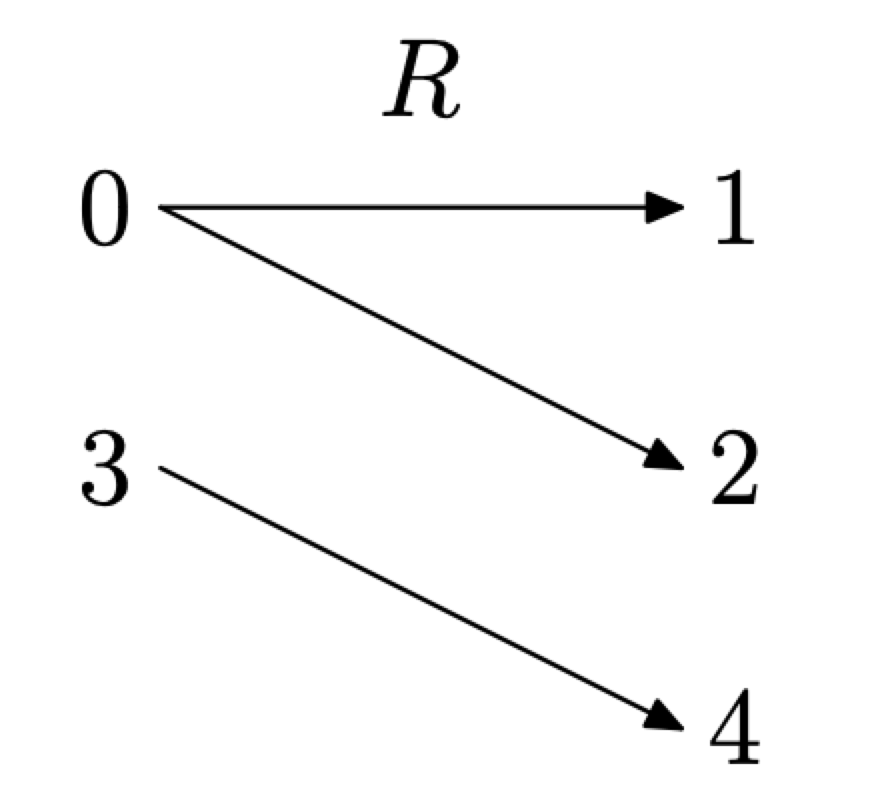
\(\PageIndex{3}\)Рисунок Діаграма відображення для R.

З діаграми відображення на малюнку зрозуміло\(\PageIndex{3}\), що число 0 в області сполучається (зіставляється) з двома різними об'єктами діапазону, а саме 1 і 2. Таким чином, R не є функцією.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{3}\)

Чи є відношення, описане в\(\PageIndex{1}\) прикладі, функцією?

Рішення

Для початку давайте повторимо перерахування відношення T тут для зручності.

\[T=\{(1,2),(3,2),(4,5)\}\]

Далі побудуйте діаграму відображення для відношення Т. Перерахуйте домен зліва, діапазон праворуч, потім за допомогою стрілок вказуйте пари, як показано на малюнку\(\PageIndex{4}\).

З діаграми відображення на малюнку ми бачимо\(\PageIndex{4}\), що кожен об'єкт області зліва парний (зіставлений) з рівно одним об'єктом діапазону праворуч. Значить, відношення T є функцією.

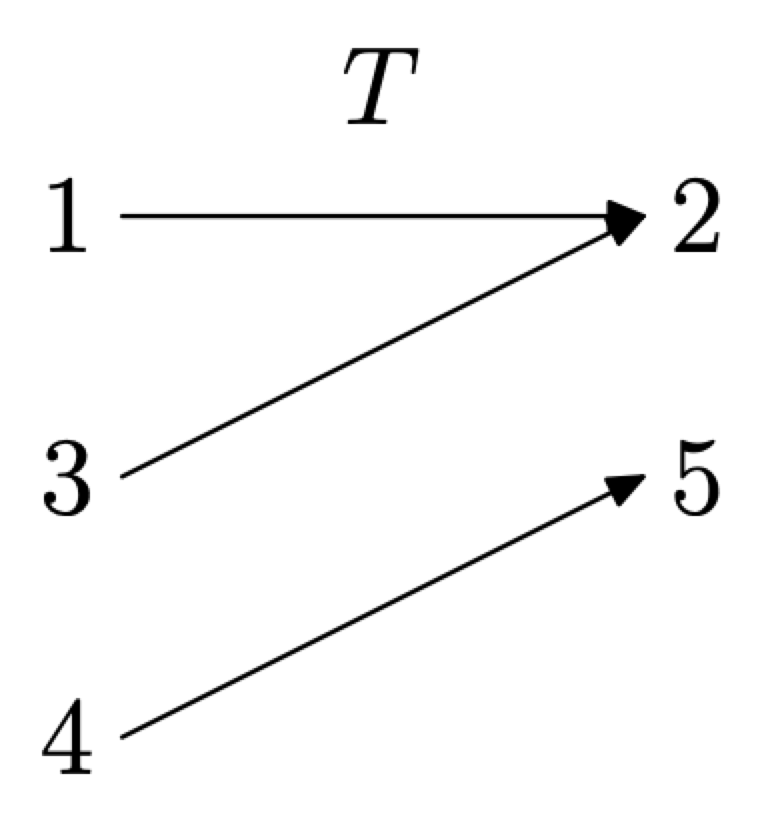
Малюнок\(\PageIndex{4}\). Діаграма відображення для Т.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{4}\)

Чи є відношення Прикладу\(\PageIndex{2}\), зображеного на малюнку\(\PageIndex{2}\), функцією?

Рішення

Спочатку ми повторюємо графік відношення з Прикладу\(\PageIndex{2}\) тут для зручності. Це показано на малюнку\(\PageIndex{5}\) (а). Далі перерахуємо впорядковані пари відношення S.

\[S=\{(1,2),(2,1),(2,4),(3,3),(4,4)\}\]

Потім ми створюємо діаграму відображення, спочатку перерахувавши домен зліва, діапазон праворуч, потім за допомогою стрілок для позначення пар, як показано на малюнку\(\PageIndex{5}\) (b).

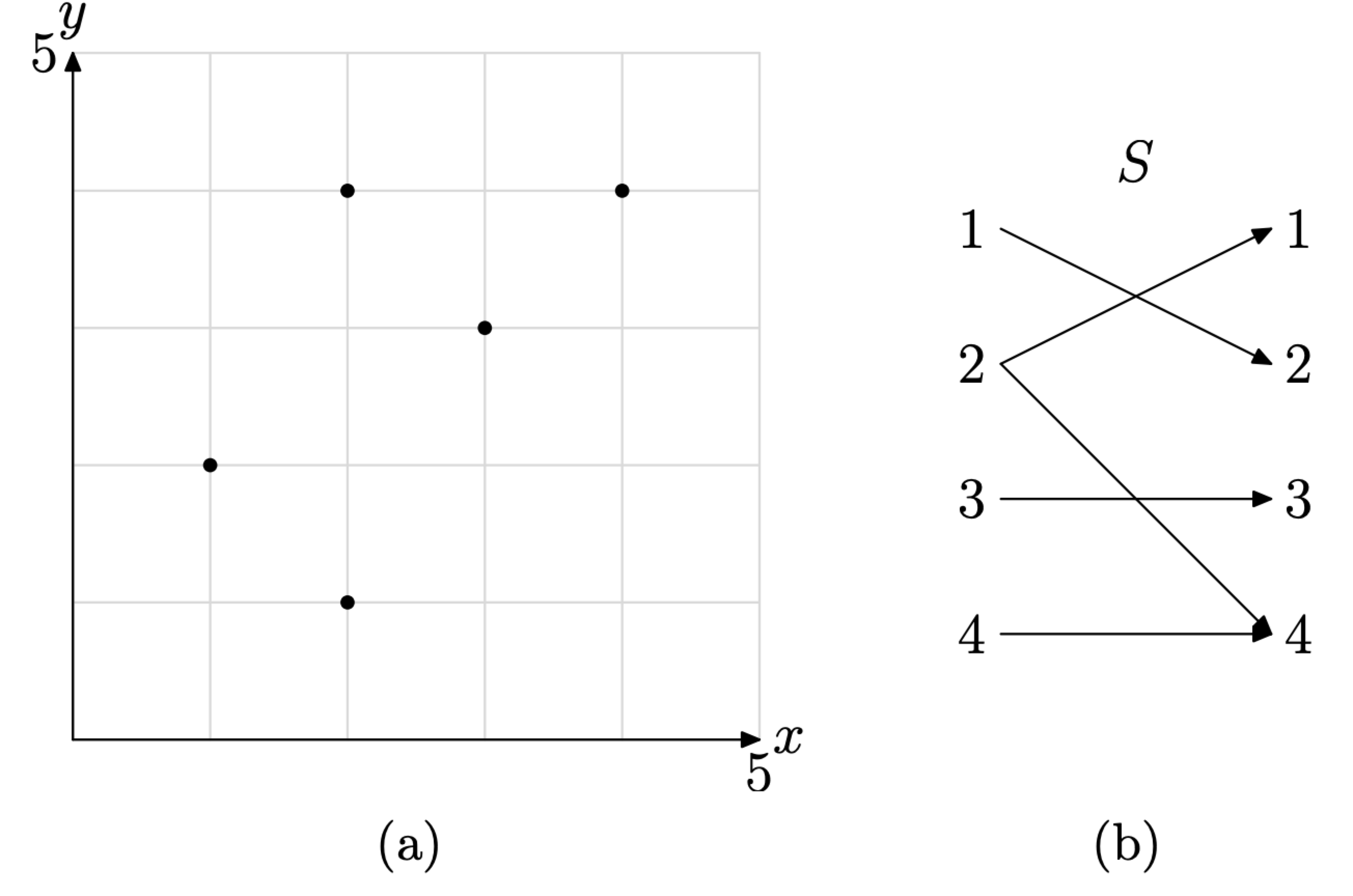
\(\PageIndex{5}\)Рисунок: Графік відношення S та відповідна діаграма відображення

Кожен об'єкт у домені S зіставляється рівно з одним об'єктом діапазону за одним винятком. Об'єкт домену 2 сполучається з двома об'єктами діапазону, а саме 1 і 4. Отже, S не є функцією.

Це хороший момент, щоб підсумувати те, що ми дізналися про функції до цих пір.

Резюме

Функція складається з трьох частин:

1. набір об'єктів, які математики називають доменом,
2. другий набір об'єктів, які математики називають діапазоном,
3. і правило, яке описує, як призначити унікальний об'єкт діапазону кожному об'єкту в домені.

Правило може приймати різні форми. Наприклад, ми можемо використовувати набори впорядкованих пар, графіків та діаграм відображення для опису функції. У наступних розділах ми вивчимо інші способи опису функції, наприклад, через використання рівнянь і простих описів слів.

Функція позначення

Ми використовували слово «mapping» кілька разів у попередніх прикладах. Це не слово, яке слід сприймати легковажно; це важливе поняття. У випадку діаграми відображення на малюнку\(\PageIndex{5}\) (b), ми б сказали, що число 1 в області S «відображено» (або «відправлено») на число 2 в діапазоні S.

Існує ряд різних позначень, які ми могли б використовувати, щоб вказати, що число 1 в домені «відображено» або «відправлено» на число 2 в діапазоні. Однією з можливих позначень є

\[S : 1 \longrightarrow 2\]

який ми б прочитали так: «Відносини S карти (посилає) 1 до 2». Аналогічним чином ми бачимо на малюнку\(\PageIndex{5}\) (b), що об'єкти домену 3 і 4 зіставляються (відправляються) на об'єкти діапазону 3 і 4 відповідно. У символах ми б писали

\[\begin{array}{l}{S : 3 \longrightarrow 3, \text { and }} \\ {S : 4 \longrightarrow 4}\end{array}\]

Складність виникає, коли ми вивчаємо, що відбувається з об'єктом домену 2. Є дві можливості, або

\[S : 2 \longrightarrow 1\]або\[S : 2 \longrightarrow 4\]

Який нам вибрати? У 1? Або 4? Таким чином, S не є чітко визначеним і не є функцією, оскільки ми не знаємо, який об'єкт діапазону з'єднати з об'єктом домену 1.

Ідея відображення дає нам альтернативний спосіб опису функції. Можна сказати, що функція - це правило, яке присвоює унікальний об'єкт у своєму діапазоні кожному об'єкту в його області. Візьмемо, наприклад, функцію, яка відображає кожне дійсне число на його квадрат. Якщо ми назвемо функцію f, то f відображає 5 на 25, від 6 до 36, −7 до 49 тощо. У символах ми б писали

\[f : 5 \longrightarrow 25, \quad f : 6 \longrightarrow 36, \quad \text { and } \quad f :-7 \longrightarrow 49\]

Загалом, ми могли б написати

\[f : x \longrightarrow x^{2}\]

Зверніть увагу, що кожне дійсне число x прив'язується до унікального числа в діапазоні f, а саме,\(x^{2}\). Отже, функція f чітко визначена. Нам вдалося написати правило, яке повністю визначає функцію f.

Як інший приклад, давайте визначимо функцію, яка приймає дійсне число, подвоює його, а потім додає 3. Якщо ми назвемо функцію g, то g візьме число 7, подвоїти його, а потім додати 3. Тобто,

\[g : 7 \longrightarrow 2(7)+3\]

Спрощення,\(g : 7 \longrightarrow 17\). Аналогічно, g взяв би число 9, подвоїти його, потім додати 3. Тобто,

\[g : 9 \longrightarrow 2(9)+3\]

Спрощення,\(g : 9 \longrightarrow 21\). Загалом, g приймає дійсне число x, подвоює його, потім додає три. У символах ми б писали

\[g : x \longrightarrow 2 x+3\]

Зверніть увагу, що кожне дійсне число x зіставляється за допомогою g до унікального числа в його діапазоні. Тому ми знову визначили правило, яке повністю визначає функцію g.

Корисно думати про функцію як про машину. Машина отримує вхід, обробляє його за якимось правилом, потім виводить результат. Щось йде (вхід), потім щось виходить (вихід). У випадку функції, описаної правилом\(f : x \longrightarrow x^{2}\), «f-машина» отримує вхід x, потім застосовує своє «квадратне правило» до входу і виходів\(x^{2}\), як показано на малюнку\(\PageIndex{6}\) (а). У випадку функції, описаної правилом\(g : x \longrightarrow 2 x+3\), «g-машина» отримує вхід x, потім застосовує правила «double», потім «додати 3», потім виводить\(2x + 3\), як показано на малюнку\(\PageIndex{6}\) (b).

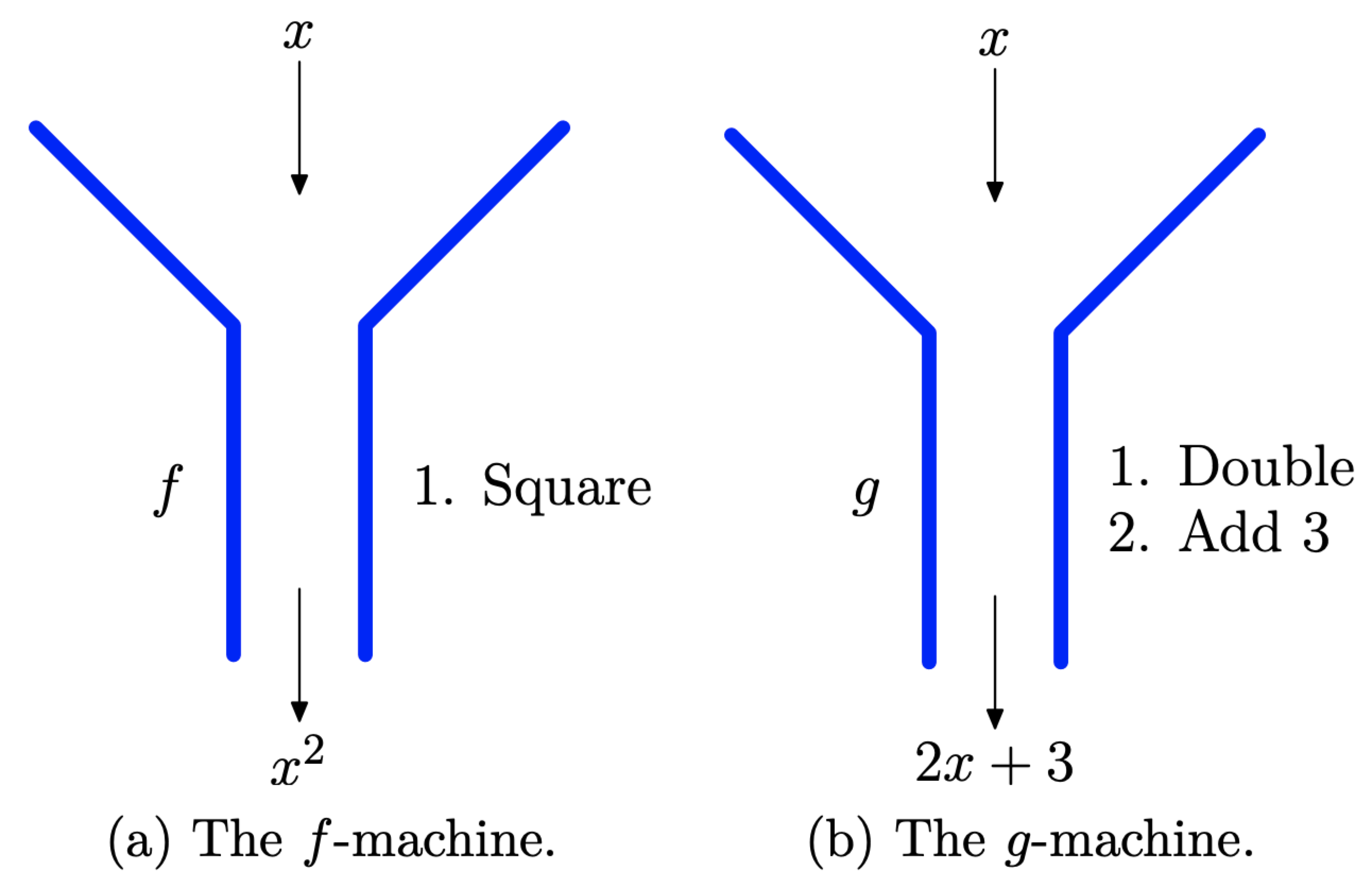
Малюнок\(\PageIndex{6}\) Функція машини.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{5}\)

Припустимо, що f визначається наступним правилом. Для кожного дійсного числа x,

\[f : x \longrightarrow x^{2}-2 x-3\]

Де f відображає число −3? Це функція f?

Рішення

Підставляємо −3 на x у правилі для f і отримуємо

\[f :-3 \longrightarrow(-3)^{2}-2(-3)-3\]

Спрощення,

\[f :-3 \longrightarrow 9+6-3\]

або,

\[f :-3 \longrightarrow 12\]

Таким чином, f відображає (надсилає) число −3 до числа 12. Повинно бути зрозуміло, що кожне дійсне число x буде зіставлено (відправлено) на унікальне дійсне число, як визначено правилом\(f : x \longrightarrow x^{2}-2 x-3\). Тому f - це функція.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{6}\)

Припустимо, що g визначається наступним правилом. Для кожного дійсного числа x, яке більше або дорівнює нулю,

\[g : x \longrightarrow \pm \sqrt{x}\]

Де g відображає число 4? Чи є g функцією?

Рішення

Знову підставляємо 4 на х в правило для g і отримуємо

\[g : 4 \longrightarrow \pm \sqrt{4}\]

Спрощення,

\[g : 4 \longrightarrow \pm 2\]

Таким чином, g відображає (посилає) число 4 до двох різних об'єктів у своєму діапазоні, а саме 2 і −2. Отже, g не є чітко визначеним і не є функцією.

Давайте розглянемо інший приклад

Приклад\(\PageIndex{7}\)

Припустимо, що у нас є функції f і g, визначені

\[f : x \longrightarrow x^{4}+11 \quad \text { and } \quad g : x \longrightarrow(x+2)^{2}\]

Куди ж відправляє 5?

Рішення

У цьому прикладі ми бачимо явну перевагу позначення функцій. Оскільки наші функції мають різні імена, ми можемо просто посилатися на ім'я функції, яку ми хочемо використовувати наші читачі. У цьому випадку нас запитують, куди функція g посилає число 5, тому підставляємо 5 для х в

\[g : x \longrightarrow(x+2)^{2}\]

Тобто,

\[g : 5 \longrightarrow(5+2)^{2}\]

Спрощення,\(g : 5 \longrightarrow 49\).

Сучасні позначення

Функція позначення є відносно новою, причому деякі з найдавніших символізму вперше відбулися в 17 столітті. У листі до Лейбніца (1698) Йоганн Бернуллі написав: «Для позначення будь-якої функції змінної кількості x, я вважаю за краще використовувати велику літеру, що має таку ж назву X або грецьку\(\xi\), бо вона з'являється відразу про те, яка змінна це функція; це полегшує пам'ять».

Математики захоплюються позначеннями\[f : x \longrightarrow x^{2}-2 x\]

тому що він передає відчуття того, що робить функція; а саме, вона «відображає» або «посилає» число х до числа\(x^{2}-2 x\). Це те, що функції роблять, вони поєднують кожен об'єкт у своїй області з унікальним об'єктом у своєму діапазоні. Аналогічно, функції «відправляють» кожен об'єкт у своїй області на унікальний об'єкт у своєму діапазоні.

Однак в поширених обчислювальних ситуаціях позначення «стрілка» може бути трохи незграбним, тому математики, як правило, віддають перевагу дещо іншим позначенням. Замість того, щоб писати

\[f : x \longrightarrow x^{2}-2 x\]

математики, як правило, віддають перевагу позначенню

\[f(x)=x^{2}-2 x\]

Важливо з самого початку розуміти, що ці дві різні позначення еквівалентні; вони представляють одну і ту саму функцію f, яка поєднує кожне дійсне число x у своїй області з дійсним числом\(x^{2}-2 x\) у своєму діапазоні.

Перше позначення\(f : x \longrightarrow x^{2}-2 x\), передає сенс, що функція f є відображенням. Якщо ми читаємо це позначення вголос, ми повинні вимовити його як «f посилає (або карти) x to»\(x^{2}-2 x\). Друге позначення\(f(x) = x^{2}-2 x\), вимовляється «f з х дорівнює»\(x^{2}-2 x\).

Примітка

Фраза «f з x» є прикро, оскільки наші читачі могли б згадати, як навчалися з самого раннього віку, щоб з'єднати слово «of» з операцією множення. Наприклад, 1/2 з 12 дорівнює 6, як в\(1 / 2 \times 12=6\). Однак у контексті позначення функції, хоча f (x) читається вголос як «f з x», це не означає «f разів x». Дійсно, якщо ми нагадуємо собі, що позначення\(f(x)=x^{2}-2 x\) еквівалентно позначенню\(f : x \longrightarrow x^{2}-2 x\), то навіть якщо ми можемо сказати «f з х», ми повинні думати «f посилає х» або «f карти х». Ми не повинні думати «f раз х».

Тепер давайте подивимося, як працює кожна з цих позначень на цифрі 5. У першому випадку, використовуючи позначення «стрілка»,

\[f : x \longrightarrow x^{2}-2 x\]

Щоб знайти, куди f посилає 5, підставляємо 5 на х наступним чином.

\[f : 5 \longrightarrow(5)^{2}-2(5)\]

Спрощення,\(f : 5 \longrightarrow 15\). Тепер, оскільки обидва позначення еквівалентні, щоб обчислити f (5), ми знову підставляємо 5 для х в

\[f(x)=x^{2}-2 x\]

Таким чином,

\[f(5)=(5)^{2}-2(5)\]

Спрощення,\(f(5)=15\). Цей результат читається вголос як «f 5 дорівнює 15», але ми хочемо думати «f посилає 5 до 15».

Давайте розглянемо приклади, в яких використовується ця сучасна позначення.

Приклад\(\PageIndex{8}\)

Дано\(f(x)=x^{3}+3 x^{2}-5,\) визначити\(f(-2)\)

Рішення

Просто замініть −2 на x. Тобто,

\[\begin{aligned} f(-2) &=(-2)^{3}+3(-2)^{2}-5 \\ &=-8+3(4)-5 \\ &=-8+12-5 \\ &=-1 \end{aligned}\]

Таким чином,\(f(−2) = −1\). Знову ж таки, хоча це вимовляється «f з −2 дорівнює −1», ми все одно повинні думати «f посилає −2 до −1».

Приклад\(\PageIndex{9}\)

Дано\[f(x)=\frac{x+3}{2 x-5}\] визначення f (6).

Рішення

Просто підставити 6 на х. тобто,\[\begin{aligned} f(6) &=\frac{6+3}{2(6)-5} \\ &=\frac{9}{12-5} \\ &=\frac{9}{7} \end{aligned}\]

Таким чином,\(f(6) = 9/7\). Знову ж таки, незважаючи на те, що це вимовляється «f з 6 дорівнює 9/7», ми все одно повинні думати «f посилає 6 до 9/7».

Приклад\(\PageIndex{10}\)

Дано\(f(x)=5 x-3,\) визначити\(f(a+2)\).

Рішення

Якщо ми думаємо з точки зору відображення позначення, то\[f : x \longrightarrow 5 x-3\]

Подумайте про це відображення як «машину». Що б ми не ставили в автомат, його спочатку множать на 5, потім з результату віднімають 3, як показано на малюнку\(\PageIndex{7}\). Наприклад, якщо ми ставимо в автомат 4, то правило функції вимагає, щоб ми помножили введення 4 на 5, потім віднімаємо з результату 3. Тобто,

\[f : 4 \longrightarrow 5(4)-3\]

Спрощення,\(f : 4 \longrightarrow 17\)

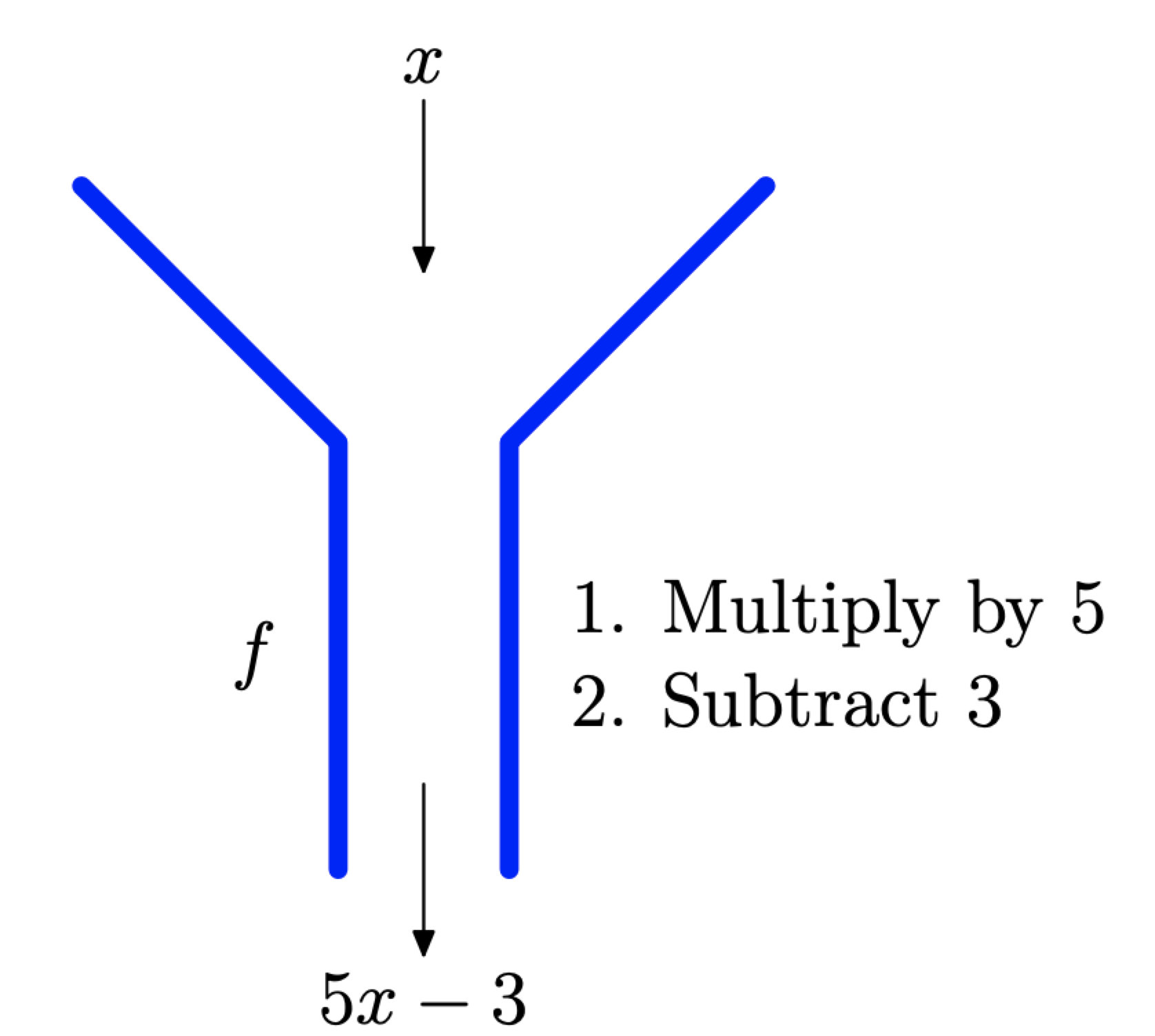
Малюнок\(\PageIndex{7}\). Помножте на 5, потім відніміть 3 машини.

Аналогічно, якщо ми ставимо a + 2 в машину, то правило функції вимагає, щоб ми помножили вхід a + 2 на 5, потім віднімаємо з результату 3. Тобто,

\[f : a+2 \longrightarrow 5(a+2)-3\]

Використовуючи сучасні позначення функцій, ми б написали

\[f(a+2)=5(a+2)-3\]

Зверніть увагу, що це знову проста заміна, де ми замінюємо кожне входження х у формулі\(f(x) = 5x − 3\) виразом a + 2. Нарешті, використовуйте розподільну властивість, щоб спочатку помножити на 5, потім відняти 3.

\[\begin{aligned} f(a+2) &=5 a+10-3 \\ &=5 a+7 \end{aligned}\]

Нам часто потрібно буде підставити результат оцінки однієї функції на другу функцію для оцінки. Давайте розглянемо приклад.

Приклад\(\PageIndex{11}\)

Дано дві функції,\(f(x) = 3x + 2\) визначені і\(g(x) = 5 − 4x\), знайдіть f (g (2)).

Рішення

Вкладені дужки у виразі f (g (2)) працюють так само, як і з вкладеними виразами. Правило полягає в тому, щоб спочатку працювати з найпотаємнішими символами групування, виходячи назовні, коли ви працюєте. Ми спочатку оцінимо g (2), потім оцінюємо f в результаті.

Починаємо. Спочатку оцініть g (2), підставивши 2 на x у визначальному рівнянні\(g(x) = 5 − 4x\). Зверніть увагу\(g(2) = 5 − 4(2)\), що, потім спростити.

\[f(g(2))=f(5-4(2))=f(5-8)=f(-3)\]

Щоб завершити оцінку, ми підставимо −3 для x у визначальному рівнянні\(f(x) = 3x + 2\), а потім спростимо.

\[f(-3)=3(-3)+2=-9+2=-7\]

Отже,\(f(g(2))=-7\).

Традиційно влаштовувати роботу в одному суміжному блоці, наступним чином.

\[\begin{aligned} f(g(2)) &=f(5-4(2)) \\ &=f(-3) \\ &=3(-3)+2 \\ &=-7 \end{aligned}\]

Ви можете скоротити завдання ще більше, якщо готові зробити підміну і спрощення функції в голові. Спочатку оцініть g на 2, потім f в результаті.

\[f(g(2))=f(-3)=-7\]

Давайте розглянемо ще один приклад цього унікального способу об'єднання функцій.

Приклад\(\PageIndex{12}\)

Дано\(f(x) = 5x + 2\) і\(g(x) = 3 − 2x\), оцінити\(g(f(a))\) і спростити результат.

Рішення

\(g(f(a))\)Спочатку ми працюємо з оцінкою внутрішньої функції у виразі. Таким чином, для оцінки f (a) підставляємо a для x у визначенні,\(f(x) = 5x + 2\) щоб отримати

\[g(f(a))=g(5 a+2)\]

Тепер треба оцінити\(g(5a + 2)\). Для цього підставляємо x\(5a + 2\) у визначенні,\(g(x) = 3 − 2x\) щоб отримати

\[g(5 a+2)=3-2(5 a+2)\]

Ми можемо розширити цей останній результат і спростити. Таким чином,

\[g(f(a))=3-10 a-4=-10 a-1\]

Знову ж таки, прийнято влаштовувати роботу в один суцільний блок, наступним чином.

\[\begin{aligned} g(f(a)) &=g(5 a+2) \\ &=3-2(5 a+2) \\ &=3-10 a-4 \\ &=-10 a-1 \end{aligned}\]

Отже,\(g(f(a))=-10 a-1\).

Витяг області функції

Ми бачили, що область відношення або функції - це набір всіх перших координат його впорядкованих пар. Однак якщо функціональний зв'язок визначається рівнянням, таким як\(f(x) = 3x − 4\), то не практично перераховувати всі впорядковані пари, визначені цим співвідношенням. Для будь-якого реального значення x ви отримуєте впорядковану пару. Наприклад, якщо x = 5, то\(f(5) = 3(5) − 4 = 11\), що веде до впорядкованої пари (5, f (5)) або (5, 11). Як бачите, кількість таких впорядкованих пар нескінченно. Для кожного нового значення x отримуємо ще одне значення функції та іншу впорядковану пару.

Тому легше звернути нашу увагу на значення х, які дають реальні числові відповіді в рівнянні\(f(x) = 3x − 4\). Це призводить до наступної ключової ідеї.

Визначення

Якщо функція визначається рівнянням, то областю функції є набір «допустимих значень x», значень, які виробляють реакцію дійсного числа, визначеного рівнянням.

Іноді ми хотіли б сказати, що область функції є набір «OK x-значення для використання в рівнянні». Наприклад, якщо ми визначимо функцію за допомогою правила\(f(x) = 3x − 4\), відразу видно, що ми можемо використовувати будь-яке значення, яке ми хочемо для x у правилі\(f(x) = 3x − 4\). Таким чином, домен f - це всі дійсні числа. Ми можемо написати, що домен\(D=\mathbb{R}\), або ми можемо використовувати інтервальні позначення і написати, що домен\(D=(-\infty, \infty)\).

Це не так, що x може бути будь-яким дійсним числом у функції, визначеній правилом\(f(x)=\sqrt{x}\). Неможливо взяти квадратний корінь від'ємного числа.2 Тому x має бути або нулем, або додатним дійсним числом. У нотації set-builder ми можемо описати домен за допомогою\(D=\{x : x \geq 0\}\). У інтервальних позначеннях пишемо\(D=[0, \infty)\).

Ми також повинні усвідомлювати той факт, що ми не можемо розділити на нуль. Якщо ми визначимо функцію з правилом\(f(x)=x /(x-3)\), то відразу побачимо, що x = 3 поставить нуль в знаменник. Ділення на нуль не визначено. Тому 3 не знаходиться в області f. Жодне інше значення x не викличе проблеми. Домен f найкраще описати за допомогою позначення set-builder як\(D=\{x : x \neq 3\}\).

Функції без формул

У попередньому розділі ми визначали функції за допомогою формули, наприклад, як в

\[f(x)=\frac{x+3}{2-3 x}\]

Ейлер був би задоволений цим визначенням, бо, як ми вже говорили раніше, Ейлер думав про функції як аналітичні вирази.

Однак насправді не потрібно надавати вираз або формулу для визначення функції. Є й інші форми, які ми можемо використовувати для вираження функціонального зв'язку: графік, таблиця або навіть опис оповідання. Єдине, що дійсно важливо, це вимога, щоб функція була чітко визначена, і під «чітко визначеною» ми маємо на увазі, що кожен об'єкт в області функції парний з одним і тільки одним об'єктом у своєму діапазоні.

Як приклад, розглянемо спеціальну функцію\(\pi\) на натуральних числах3, яка повертає кількість простих чисел, менших або рівних заданому натуральному числу. Наприклад, прості числа менше або рівні числу 23 - це 2, 3, 5, 7, 11, 13, 17, 19 і 23, всього дев'ять чисел. Тому кількість простих чисел менше або дорівнює 23 дорівнює дев'яти. У символах ми б писали

\[\pi(23)=9\]

Зверніть увагу на відсутність формули у визначенні цієї функції. Дійсно, визначення носить описовий характер, тому ми могли б написати

\[\pi(n)=\text { number of primes less than or equal to } n\]

Важливим є не те, як ми визначаємо цю спеціальну функцію π, а те, що вона чітко визначена; тобто для кожного натурального числа n існує фіксована кількість простих чисел менше або дорівнює n. таким чином, кожне натуральне число в області π парне з одним і тільки одним числом в своєму діапазоні.

Тепер, тільки тому, що наша функція не надає вираз для обчислення кількості простих чисел менше або дорівнює заданому натуральному числу n, це не зупиняє математиків шукати таку формулу. Евклід Олександрійський (325-265 рр. До н.е.), грецький математик, довів, що кількість простих чисел нескінченно, але саме німецький математик і вчений Йоганн Карл Фрідріх Гаусс (1777-1855) вперше запропонував, що кількість простих чисел менше або дорівнює n можна наблизити за формулою

\[\pi(n) \approx \frac{n}{\ln n}\]

де ln n - «натуральний логарифм» від n (пояснюється в главі 9). Це наближення стає все кращим і кращим при більших і більших значеннях n Формулу уточнив Гаусс, який не надав доказів, і задача стала називатися теоремою простих чисел. Лише в 1896 році Жак Саломон Адамар (1865-1963) та Шарль Жан Гюстав Ніколас Барон де ла Валле Пуссен (1866-1962), працюючи самостійно, надали доказ теореми про просте число.