2.2: Графік функції

Рене Декарт (1596-1650) був французьким філософом і математиком, який добре відомий відомою фразою «cogito ergo sum» (Я думаю, тому я), яка з'являється в його Discours de la methode pour bien conduire sa raison, et chercher la verite dans les sciences (Дискурс про метод справедливо Проведення розуму, і пошук істини в науках). У тому ж трактаті Декарт вводить свою систему координат, метод представлення точок на площині за допомогою пар дійсних чисел. Дійсно, декартова площина сучасності так названа на честь Рене Декарта, якого деякі називають «Батьком сучасної математики».

Робота Декарта, яка назавжди пов'язувала геометрію та алгебру, була продовжена в додатку до Discourse on Method під назвою La Geometrie, який деякі вважають початком сучасної математики. Звичайно, і Ньютон, і Лейбніц, розробляючи обчислення, побудовані на фундаменті, наданому в цій роботі Декарта.

Декартова система координат складається з пари осей, зазвичай намальованих під прямим кутом один до одного в площині, однієї горизонтальної (позначеної x) і однієї вертикальної (позначеної y), як показано на малюнку$\PageIndex{1}$. Квадранти нумеруються I, II, III та IV в порядку проти годинникової стрілки, а зразки впорядкованих пар виду (x, y) показані в кожному квадранті декартової системи координат на рис$\PageIndex{1}$.

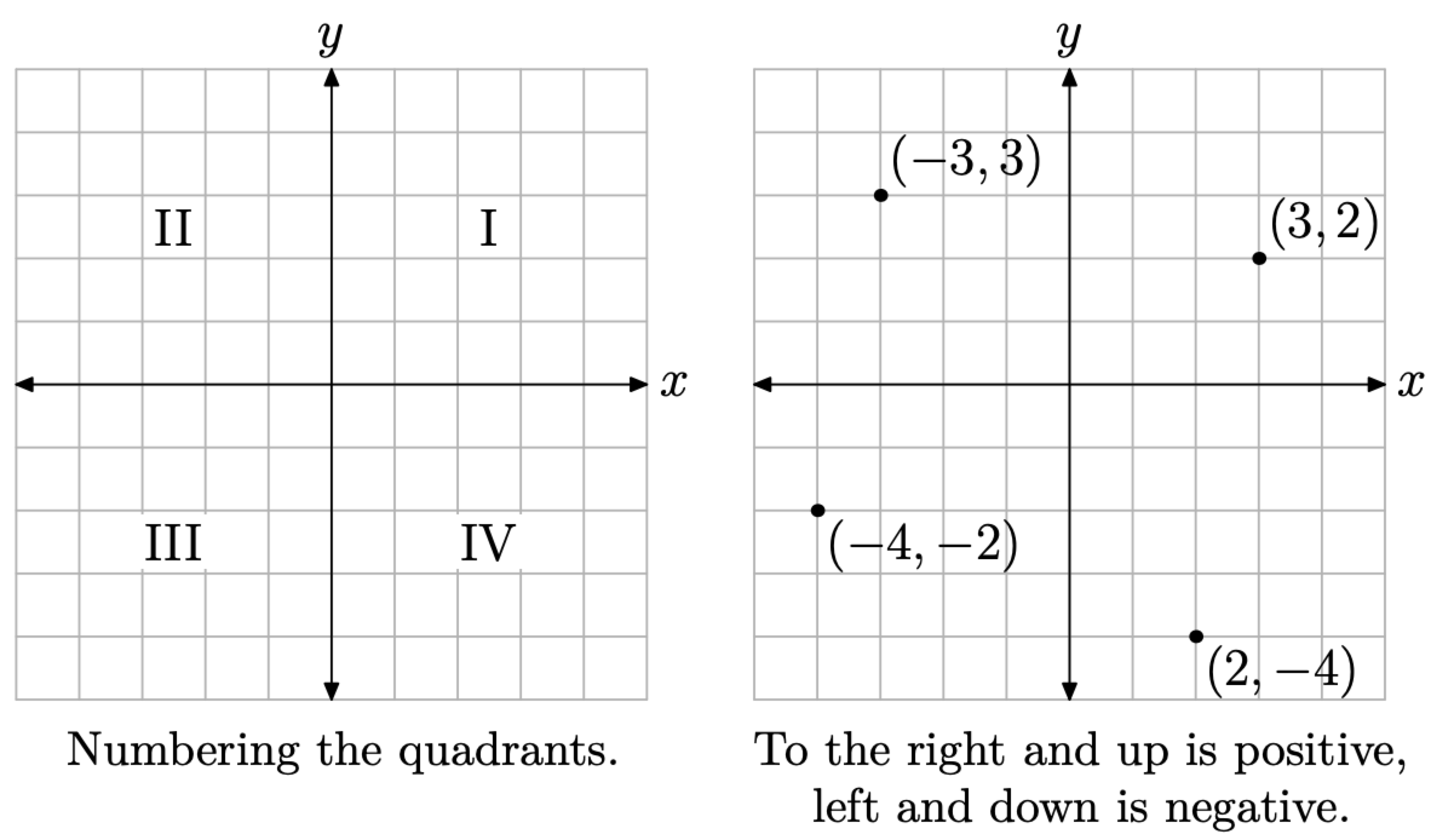
Малюнок$\PageIndex{1}$. Декартова система координат.

Тепер припустимо, що у нас є відношення $$R=\{(1,2),(3,1),(3,4),(4,3)\}$$

Нагадаємо, що відношення - це назва, дане колекції впорядкованих пар. На малюнку$\PageIndex{2}$ (b) ми побудували кожну з впорядкованих пар у співвідношенні R. Це називається графом відношення R.

Визначення

Графік відношення - це сукупність всіх впорядкованих пар відношення. Зазвичай вони представлені у вигляді точок у декартовій системі координат.

Малюнок$\PageIndex{2}$ A діаграма відображення та її графік.

На малюнку$\PageIndex{2}$ (a) ми створили діаграму відображення впорядкованих пар. Зверніть увагу, що об'єкт домену 3 поєднується з двома елементами діапазону, а саме 1 і 4. Звідси відношення R не є функцією. Цікаво відзначити, що на графіку R на малюнку$\PageIndex{2}$ (b) є дві точки, які мають однакову першу координату, а саме (3, 1) та (3, 4). Це сигнал про те, що графік відношення R не є функцією. У наступному розділі ми обговоримо тест вертикальної лінії, який буде використовувати це подвійне використання першої координати, щоб визначити, коли відношення не є функцією.

Створення графіка функції

Деякі тексти будуть говорити про графік рівняння, наприклад «Намалюйте графік рівняння»$y=x^{2}$. Дана інструкція викликає ряд труднощів.

• По-перше, інструкція не дає вказівки читачеві; тобто що означає інструкція? Це не дуже корисно.
• По-друге, інструкція невірна. Ви не малюєте графіки рівнянь. Швидше за все, ви малюєте графіки відносин і/або функцій. Графік - це просто ще один спосіб представлення функції, відношення, яке поєднує кожен елемент у своїй області з точно одним елементом у своєму діапазоні.

Отже, в чому полягає правильна інструкція? Спочатку ми надамо формальне визначення графіка функції, потім розбимо його за допомогою прикладів.

Визначення

Графік функції - це колекція всіх впорядкованих пар функції. Зазвичай вони представлені у вигляді точок у декартовій системі координат.

Як приклад розглянемо функцію

$$f=\{(1,2),(2,4),(3,1),(4,3)\}$$

Читачі відзначать, що кожен об'єкт в області пов'язаний з одним і тільки одним об'єктом в діапазоні, як видно на діаграмі відображення Рисунок$\PageIndex{3}$ (а).

Таким чином, у нас є два уявлення функції f, колекція впорядкованих пар (3) та діаграма відображення на малюнку$\PageIndex{3}$ (а). Третє подання функції f - графік впорядкованих пар функції, показаний на декартовій площині на малюнку$\PageIndex{3}$ (b).

Малюнок$\PageIndex{3}$ A діаграма відображення та її графік.

Коли функція представлена рівнянням або формулою, то ми дещо коригуємо своє визначення її графіка.

Визначення

Графік f - це множина всіх впорядкованих пар$(x, f(x))$ таким чином, що x знаходиться в області f.

$$\text {Graph of } f=\{(x, f(x)) : x \text { is in the domain of } f .\}$$

Це останнє визначення найпростіше пояснити на прикладі. Отже, давайте визначимо функцію f що відображає будь-яке дійсне число х до дійсного числа$x^{2}$; тобто давайте$f(x)=x^{2}$. Тепер, згідно з Визначенням, граф f - це множина всіх точок$(x, f(x))$, таких, що х знаходиться в області f.

Шляхи тепер зрозумілі. Почнемо зі створення таблиці точок$(x, f(x))$, де x знаходиться в області функції f, визначеної$f(x) = x^{2}$. Вибір x є суб'єктивним та експериментальним, тому ми починаємо з вибору цілих значень x між −3 та 3. Потім ми оцінюємо функцію на кожному з цих x-значень (наприклад,$f(-3)=(-3)^{2}=9$). Результати наведені в таблиці на малюнку$\PageIndex{4}$ (а). Потім ми будуємо точки в нашій таблиці в декартовій площині, як показано на малюнку$\PageIndex{4}$ (b).

Малюнок$\PageIndex{4}$. Побудова пар, що задовольняють функціональну залежність, визначену рівнянням$f(x)=x^{2}$.

Хоча це хороший початок, графік на малюнку$\PageIndex{4}$ (b) далеко не повний. Визначення вимагає побудови впорядкованих пар$(x, f(x))$ для кожного значення x, що знаходиться в області f. Ми тільки побудували сім таких точок, тому ми не закінчили. Давайте додамо більше точок до графіка f, оцінимо функцію на кожному з x-значень, показаних у таблиці на малюнку$\PageIndex{5}$ (a), а потім побудуємо додаткові пари$(x, f(x))$ з таблиці в декартовій площині, як показано на малюнку$\PageIndex{5}$ (b).

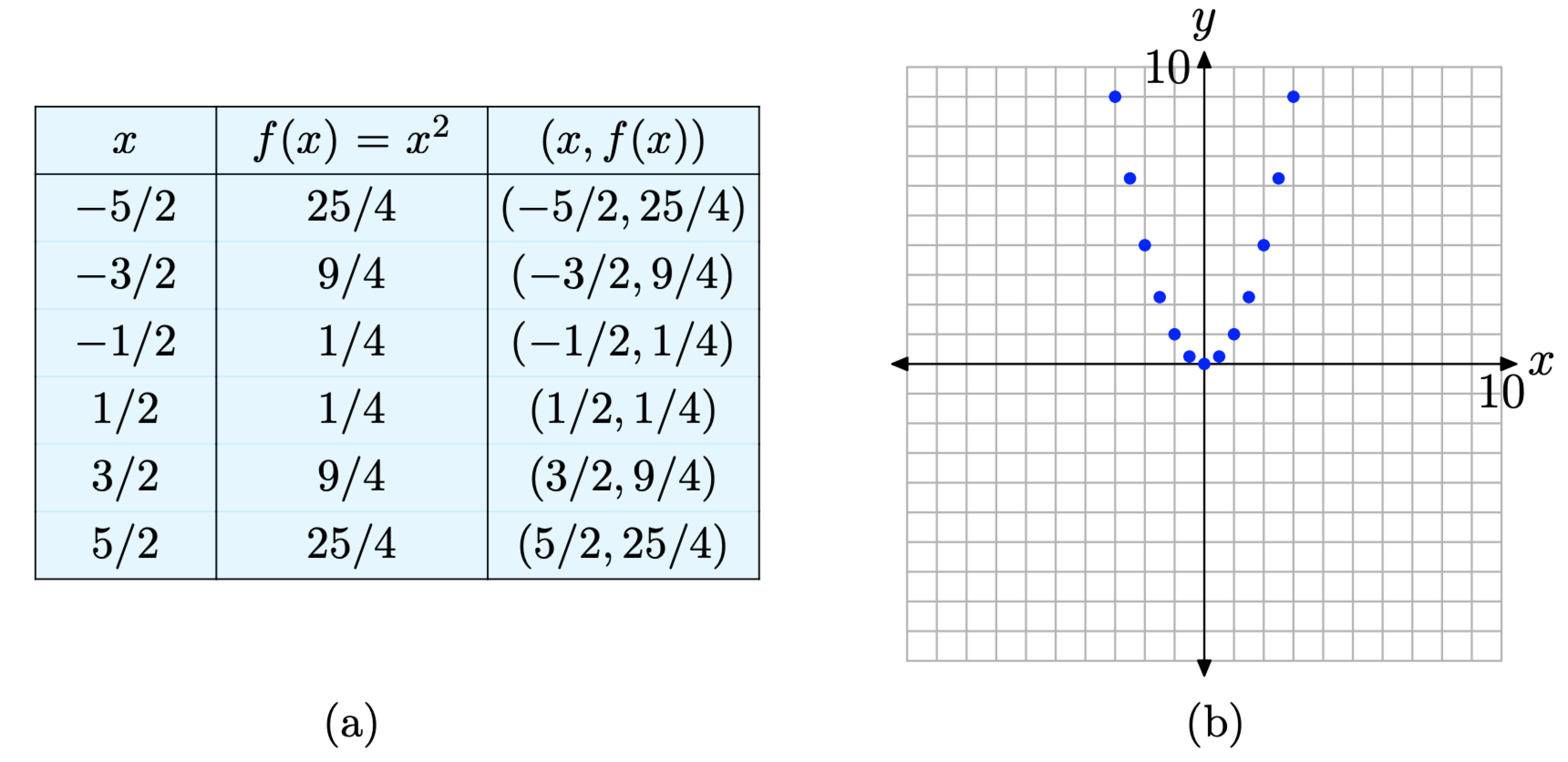
Малюнок$\PageIndex{5}$. Побудова додаткових пар,$(x, f(x))$ визначених рівнянням$f(x) = x^{2}$.

Ми все ще не закінчили, тому що ми тільки намітили 13 пар$(x, f(x))$, такі, що$f(x) = x^{2}$. Визначення 4 вимагає побудови впорядкованих пар$(x, f(x))$ для кожного значення x в області f.

Однак закономірність, безумовно, встановлює себе, як видно на малюнку$\PageIndex{5}$ (b). У якийсь момент нам потрібно «зробити стрибок віри», і побудувати всі впорядковані пари$(x, f(x))$, таким чином, що х знаходиться в області f$\PageIndex{6}$.

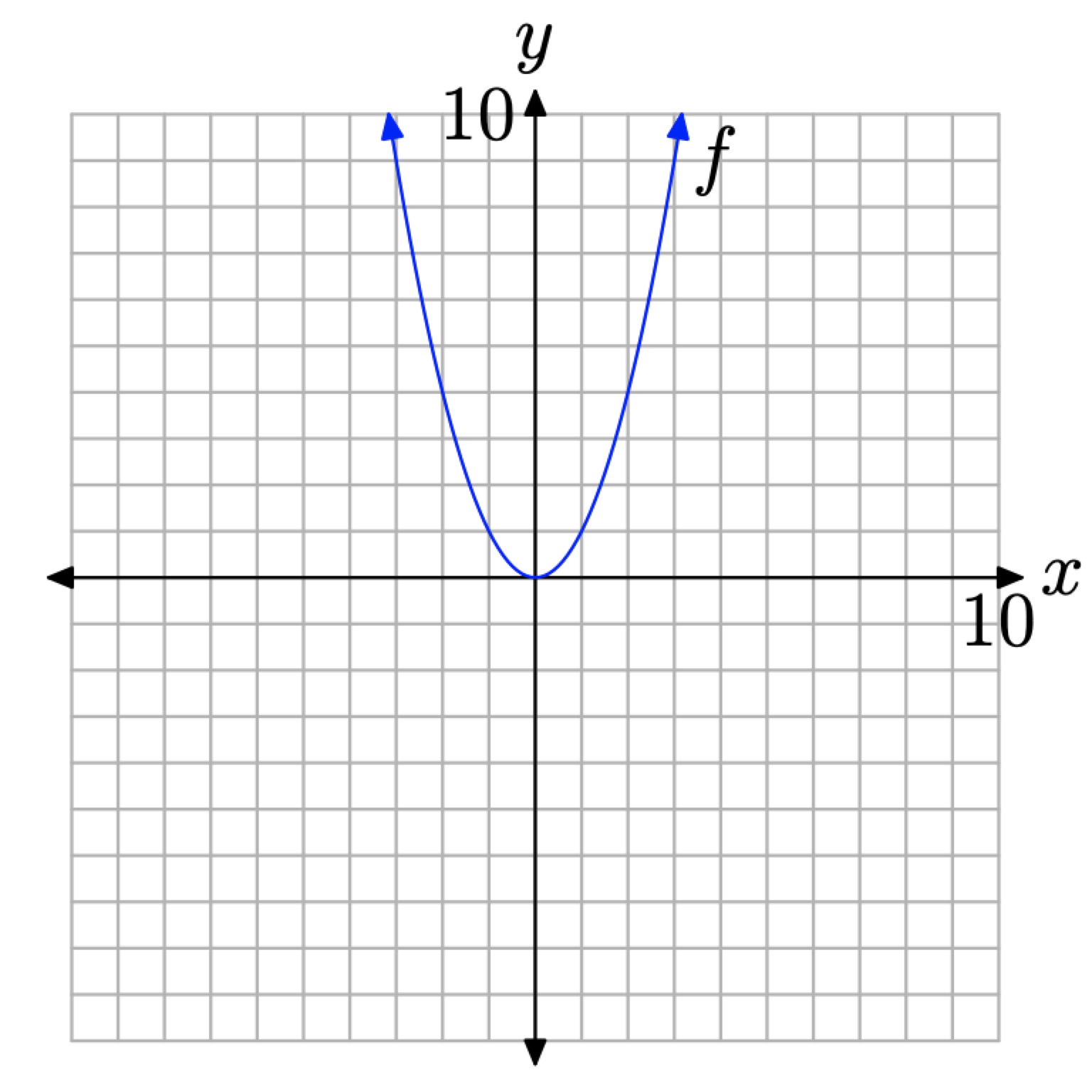
Малюнок$\PageIndex{6}$. Побудова всіх пар$(x, f(x))$ так, щоб х знаходився в області f.

Є кілька важливих моментів, які нам потрібно зробити щодо кінцевого результату на малюнку$\PageIndex{6}$.

• Коли ми малюємо плавну криву, таку як показано на малюнку$\PageIndex{6}$, важливо розуміти, що це просто ярлик для побудови всіх пар (x, f (x)), де$f(x) = x^{2}$ і х знаходиться в області f.
• Важливо розуміти, що ми НЕ «з'єднуємо точки», ні лінійкою, ні з вигнутими відрізками. Швидше, крива на малюнку$\PageIndex{6}$ є результатом побудови всіх окремих пар$(x, f(x))$.
• «Стрілки» на кожному кінці кривої мають важливе значення. Оскільки крапки в кінці прогресії$2,4,6, \dots$ означають «et-cetera», стрілки на кожному кінці кривої мають подібне значення. Стрілка в кінці лівої половини кривої вказує на те, що графік продовжує відкриватися вгору і вліво, тоді як стрілка в кінці правої половини кривої вказує на те, що графік продовжує відкриватися вгору і вправо.

Створення графіків вручну

Ми розглянемо кілька основних графіків, які ми створимо, використовуючи стратегію, яка використовується для створення графіка$f(x) = x^{2}$. Для початку давайте підсумуємо цей процес.

Резюме

Якщо функція визначається рівнянням, ви можете створити графік функції наступним чином.

1. Виберіть кілька значень x в області функції f.
2. Використовуйте вибрані значення x для створення таблиці пар (x, f (x)), які задовольняють рівнянню, що визначає функцію f.
3. Створіть декартову систему координат на аркуші графічного паперу. Позначте та масштабуйте кожну вісь, а потім побудуйте пари (x, f (x)) з таблиці на вашій системі координат.
4. Якщо побудовані пари (x, f (x)) надають достатньо шаблону, щоб ви зрозуміли форму графіка f, зробіть «стрибок віри» і побудуйте всі пари, які задовольняють рівнянню, що визначає f, намалювавши плавну криву на вашій системі координат. Звичайно, ця крива повинна містити всі раніше побудовані пари.
5. Якщо ваші побудовані пари не забезпечують достатньо шаблону для визначення остаточної форми графіка f, додайте більше пар до вашої таблиці та побудуйте їх у вашій декартовій системі координат. Продовжуйте таким чином, поки не будете впевнені у формі графіка f.

Давайте розглянемо приклад.

Приклад$\PageIndex{1}$

Намалюйте графік функції, визначеної рівнянням$f(x)=x^{3}$.

Рішення

Ми почнемо з x-значень$-2,-1,0,1,$ і 2, а потім використаємо рівняння$f(x)=x^{3}$ для визначення пар (x, f (x)) (наприклад,$f(-2)=(-2)^{3}=-8$). Вони наведені в таблиці на малюнку$\PageIndex{7}$ (а). Потім ми розміщуємо точки з таблиці на декартовій системі координат, як показано на малюнку$\PageIndex{7}$ (b).

Малюнок$\PageIndex{7}$. Побудова пар (x, f (x)) визначається рівнянням$f(x)=x^{3}$.

Ми трохи не впевнені в формі графіка f, так що ми додамо ще кілька пар до нашої таблиці і побудувати їх. Це показано на малюнках$\PageIndex{8}$ (a) і (b).

Малюнок$\PageIndex{8}$. Побудова додаткових пар (x, f (x)), визначених рівнянням$f(x)=x^{3}$.

Додаткові пари заповнюють форму f на малюнку$\PageIndex{8}$ (b) трохи краще, ніж на малюнку$\PageIndex{7}$ (b), достатньо, щоб ми були достатньо впевнені, щоб зробити «стрибок віри» і намалювати остаточну форму графіка на$f(x)=x^{3}$ малюнку$\PageIndex{9}$.

Малюнок$\PageIndex{9}$. Фінальний графік$f(x)=x^{3}$.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{2}$

Намалюйте графік$f(x)=\sqrt{x}$

Рішення

Знову ж таки, ми почнемо з вибору декількох значень x в області f, в цьому випадку$f(x)=\sqrt{x}$, і неможливо взяти квадратний корінь від'ємного числа. Крім того, якщо ми створюємо таблицю пар вручну, це хороша стратегія для вибору відомих квадратів. Таким чином, ми будемо використовувати x = 0, 1, 4 і 9 для початку.

Малюнок$\PageIndex{10}$. Побудова пар (x, f (x)) визначається рівнянням$f(x)=\sqrt{x}$.

Деякі можуть бути готові зробити «стрибок віри» на основі цих початкових результатів. Інші можуть захотіти використовувати калькулятор для обчислення десяткових наближень для додаткових квадратних коренів. Отримані пари показані в таблиці на малюнку$\PageIndex{11}$ (а), а додаткові пари - на малюнку$\PageIndex{11}$ (б).

Малюнок$\PageIndex{11}$ Побудова додаткових пар (x, f (x)), визначених рівнянням$f(x)=\sqrt{x}$

Візерунок на малюнку$\PageIndex{11}$ (b) досить зрозумілий, щоб зробити «стрибок віри» і завершити графік, як показано на малюнку$\PageIndex{12}$.

Малюнок$\PageIndex{12}$. Графік f визначається рівнянням$f(x)=\sqrt{x}$.

Використання функції таблиці графічного калькулятора

Функція ТАБЛИЦЯ на вашому графічному калькуляторі може надати величезну допомогу при створенні таблиць точок, які задовольняють рівнянню, що визначає функцію f.

Приклад$\PageIndex{3}$

Намалюйте графік$f(x)=|x|$

Рішення

Введіть функцію$f(x)=|x|$ в$\mathrm{Y}=$ меню наступним чином.

1. Натисніть кнопку Y = на калькуляторі. Це відкриє меню Y =, як показано на малюнку$\PageIndex{13}$ (a). Використовуйте клавіші зі стрілками і кнопку CLEAR на калькуляторі, щоб видалити всі існуючі функції.
2. Натисніть кнопку MATH, щоб відкрити меню, показане на малюнку$\PageIndex{13}$ (b).
3. Натисніть стрілку праворуч на калькуляторі, щоб вибрати підменю NUM, як показано на малюнку$\PageIndex{13}$ (c).
4. Виберіть 1: abs (, потім введіть X і закрийте дужки, як показано на малюнку$\PageIndex{13}$ (d).

Малюнок$\PageIndex{13}$. Вхід$f(x)=|x|$ в$\mathrm{Y}=$ меню.

Тепер ми будемо використовувати функцію TABLE графічного калькулятора, щоб допомогти створити таблицю пар (x, f (x)), що задовольняють рівнянню$f(x) = |x|$. Дійте наступним чином.

1. Виберіть 2nd TBLSET (тобто натисніть 2-ю кнопку, а потім TBLSET), яка знаходиться над кнопкою WINDOW. Введіть tblStart=-3$\Delta \mathrm{Tb} 1=1$, і встановіть незалежні і залежні змінні на Auto (це робиться виділенням Auto і натисканням кнопки Enter), як показано на малюнку$\PageIndex{14}$ (a).
2. Натисніть 2-у ТАБЛИЦЮ, яка розташована над кнопкою GRAPH, щоб скласти таблицю пар (x, f (x)), зображену на малюнку$\PageIndex{14}$ (b).

Ми побудували пари безпосередньо з калькулятора на декартовій системі координат на графічному папері на малюнку$\PageIndex{14}$ (c).

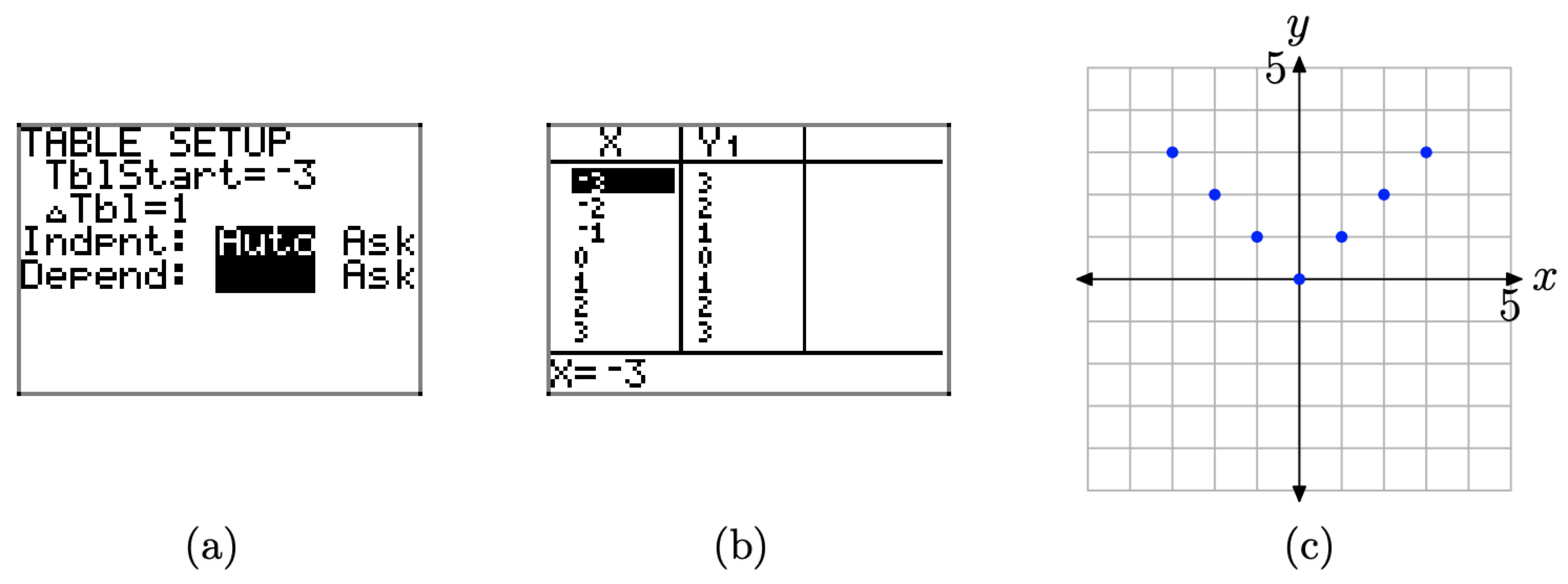
Малюнок$\PageIndex{14}$. Створення таблиці з функцією TABLE графічного калькулятора.

Виходячи з того, що ми бачимо на малюнку$\PageIndex{14}$ (c), ми готові зробити «стрибок віри» і намалювати графік f, показаний на малюнку$\PageIndex{15}$.

Малюнок$\PageIndex{15}$. Графік f визначається$f(x) = |x|$.

Крім того, або як чек, ми можемо мати графічний калькулятор намалювати графік для нас. Натисніть кнопку ZOOM, потім виберіть 6:zStandard (показано на малюнку$\PageIndex{16}$ (a)), щоб створити графік, показаний на малюнку$\PageIndex{16}$ (b).

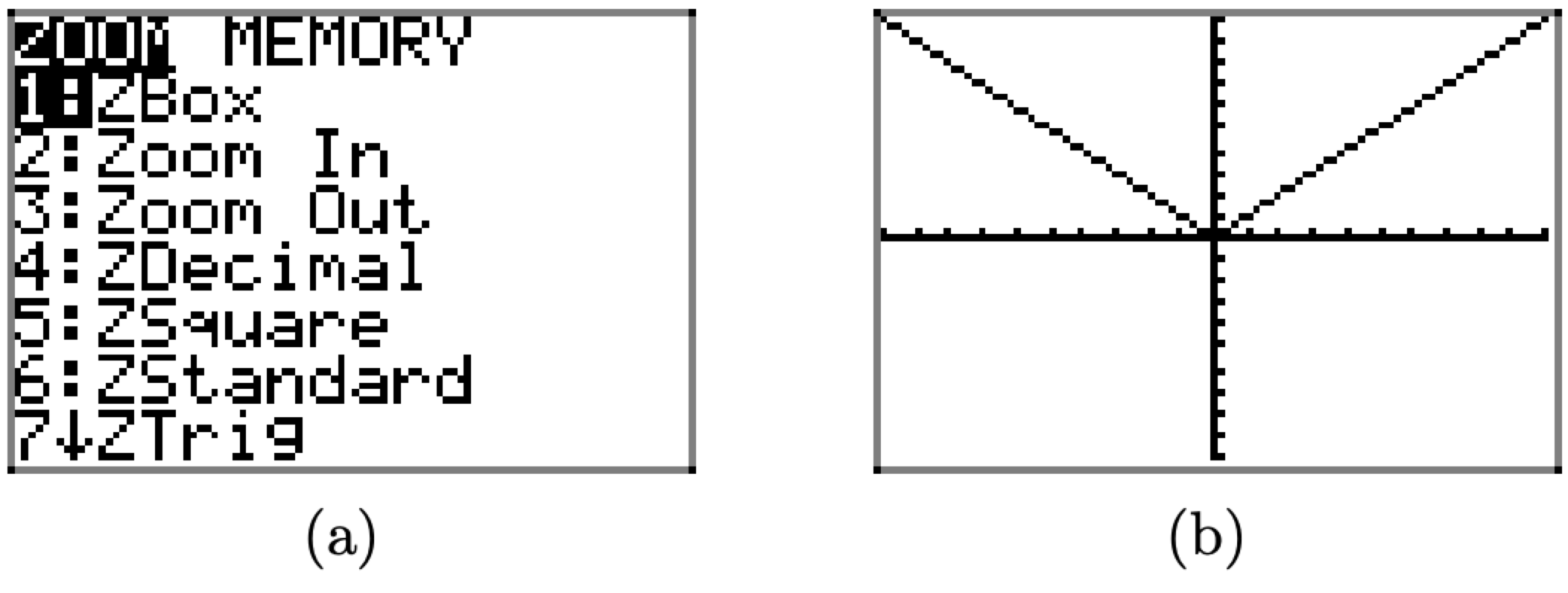
Малюнок$\PageIndex{16}$. Створення графіка за$f(x) = |x|$ допомогою графічного калькулятора.

Налаштування вікна перегляду

У прикладі$\PageIndex{3}$ ми використовували графічний калькулятор, щоб намалювати графік функції, визначеної рівнянням$f(x) = |x|$. Для функцій, з якими ми стикалися досі, малювання їх графіків за допомогою графічного калькулятора досить тривіально. Просто введіть рівняння в меню Y =, потім натисніть кнопку ZOOM і виберіть 6:ZStandard. Однак, якщо графік функції не поміщається (або навіть відображається) у «стандартному» вікні перегляду, знайти оптимальні параметри перегляду може бути досить складно, щоб були видимі важливі функції графіка.

Дійсно, як можна навіть не знати, на які «важливі» функції шукати, установка оглядового вікна, як правило, дуже суб'єктивна і експериментальна за своєю природою. Давайте розглянемо кілька прикладів.

Приклад$\PageIndex{4}$

Використовуйте графічний калькулятор для ескізу графіка$f(x)=56-x-x^{2}$. Експериментуйте з настройками WINDOWS, поки не відчуєте, що у вас є вікно перегляду, яке демонструє важливі особливості графіка.

Рішення

Спочатку почніть з введення функції в меню Y=, як показано на малюнку$\PageIndex{17}$ (а). Каретка на клавіатурі використовується для експонентів. Натисніть кнопку ZOOM і виберіть 6:zStandard, щоб створити графік, показаний на малюнку$\PageIndex{17}$ (b).

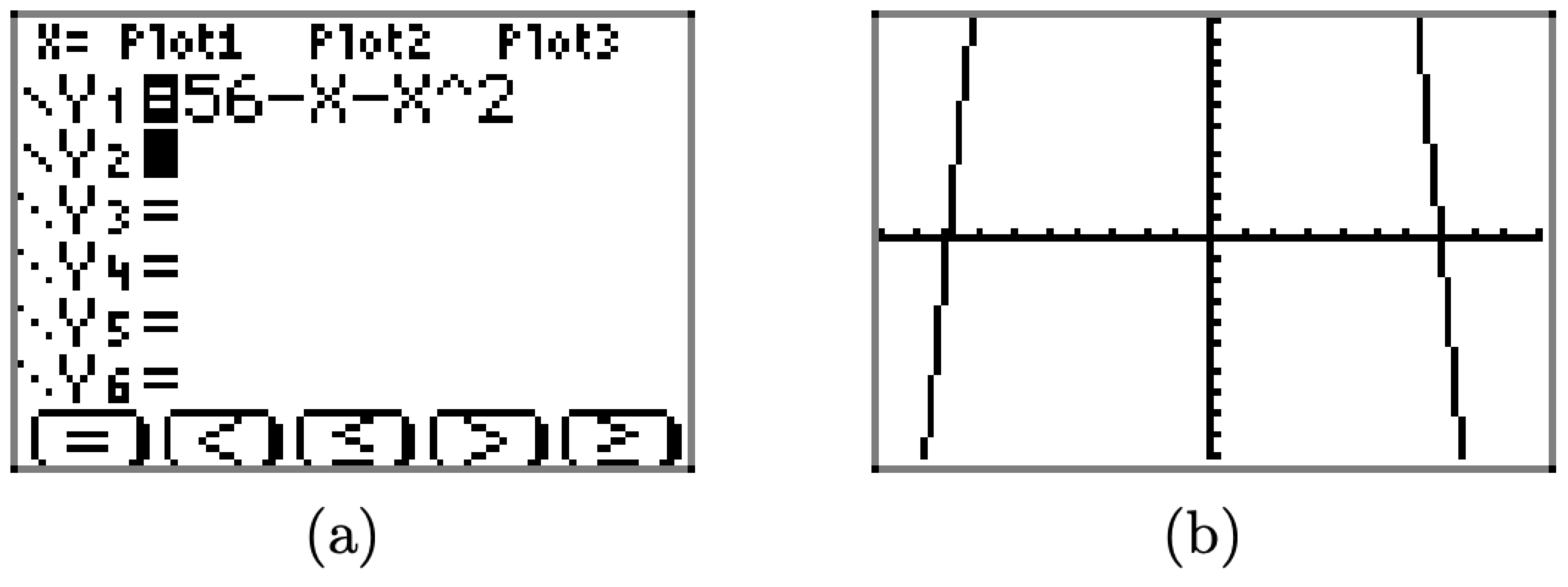
Малюнок$\PageIndex{17}$. Графік$f(x)=56-x-x^{2}$ в «стандартному» вікні перегляду.

Коли графік малюється, зауважте, що графік піднімається знизу екрана, залишає верхню частину екрана, потім повертається, падаючи з верхньої частини екрана і знову залишаючи внизу екрана. Це означало б, що повинен бути якийсь «поворотний момент», який не видно у верхній частині екрана.

Натисніть кнопку WINDOW, щоб відкрити параметри «стандартного вікна перегляду», показані на малюнку$\PageIndex{18}$ (а). Наступна легенда пояснює кожен з параметрів WINDOW на малюнку$\PageIndex{18}$ (a).

\ (\ begin {масив} {lll} Xmin & ==& x значення лівого краю оглядового вікна\\

Xmax &=& x значення правого краю вікна перегляду\\

Xscl &=Приріст галочки по осі x\\

Y min &=& y значення нижнього краю оглядового вікна\\

Y max &=& y значення верхнього краю вікна перегляду\\

Y scl &=& Y приріст тика по осі\ end {масив}\)

Легко оцінити функцію$f(x)=56-x-x^{2}$ при$x = 0$. Дійсно,$f(0) = 56−0−0^2 = 56$. Це говорить про те, що графік f повинен проходити через точку (0, 56). Це дає нам підказку про те, як ми повинні встановити верхню межу на нашому оглядовому вікні. Встановіть Ymax = 60, як показано на малюнку$\PageIndex{18}$ (b), потім натисніть кнопку GRAPH, щоб створити графік та вікно перегляду, показані на малюнку$\PageIndex{18}$ (c).

Малюнок$\PageIndex{18}$. Зміна оглядового вікна.

Хоча вікно перегляду на малюнку$\PageIndex{18}$ (c) показує «поворотну точку» графіка f, ми внесемо деякі додаткові зміни в налаштування вікна, як показано на малюнку$\PageIndex{19}$ (а). Спочатку трохи «розширюємо» оглядове вікно, встановивши Xmin = -15 і Xmax = 15, потім ставимо галочки на осі х через кожні 5 одиниць з Xscl = 5. Далі, щоб створити маленьку кімнату у верхній частині екрану, встановлюємо Ymax = 100, потім «балансуємо» цю настройку Ymin = -100. Нарешті, ми встановлюємо галочки на осі y кожні 10 одиниць з Yscl = 10.

Натисніть кнопку GRAPH, щоб переглянути наслідки цих змін до параметрів WINDOW на малюнку$\PageIndex{19}$ (b). Зверніть увагу, що ці налаштування є дуже суб'єктивними, і те, що один читач може здатися цілком приємним, не обов'язково знайде прихильність інших читачів.

Однак важливим є той факт, що ми зафіксували «важливі риси» графіка$f(x)=56-x-x^{2}$. Відзначимо, що це дуже спірне твердження. Якщо хтось тільки починає дізнаватися про графіки функцій, як визначити, які «важливі особливості» графіка? На жаль, відповідь на це питання «через досвід». Безсумнівно, це дуже неприємна фраза для читачів, але, принаймні, правдива. Чим більше графіків ви намалюєте, тим більше ви дізнаєтеся, як шукати «поворотні точки», «кінцева поведінка», «x- і y-перехоплення» тощо.

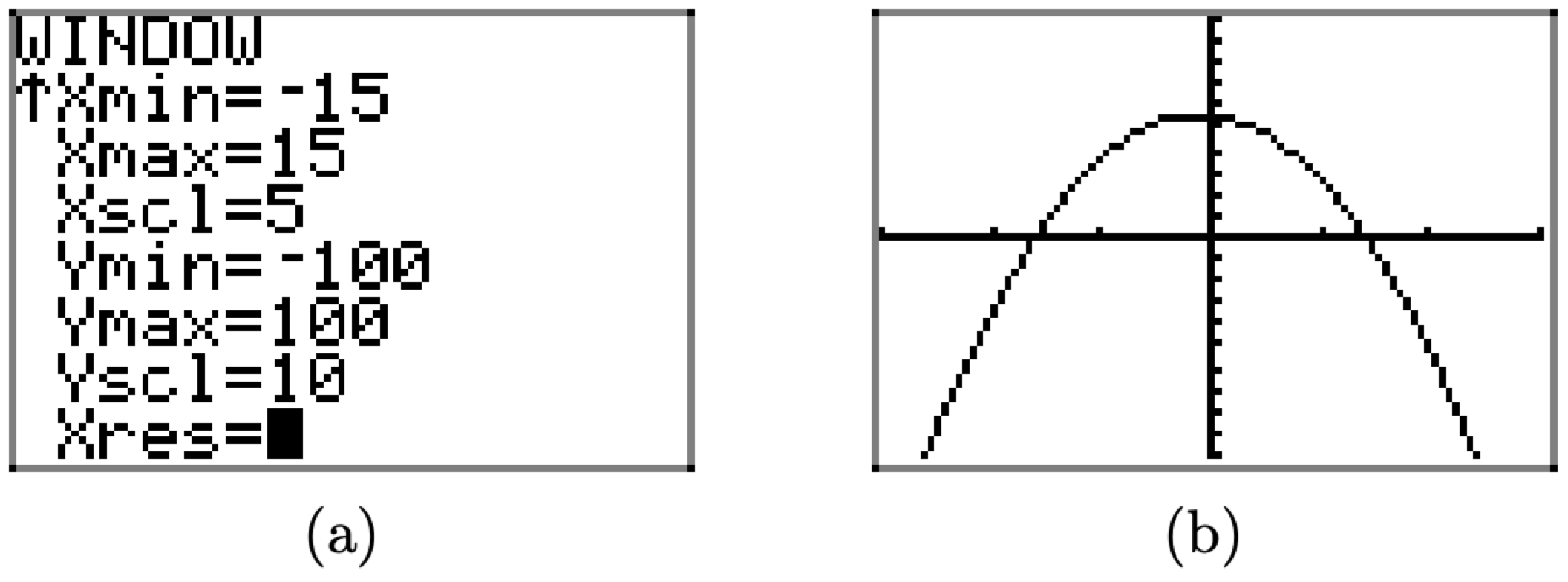
Малюнок$\PageIndex{19}$. Поліпшення налаштувань WINDOW.

Наприклад, як ми знаємо, що налаштування WINDOW на малюнку$\PageIndex{19}$ (а) визначають вікно перегляду (рис.$\PageIndex{19}$ (b)), яке розкриває всі «важливі особливості» графіка? Відповідь на цей момент: «ми цього не робимо, не без подальшого експерименту». Наприклад, уважний читач може захотіти спробувати налаштування вікна Xmin=-50, Xmax=50, Xscl = 10, Ymin=-500, Ymax=500 та Yscl = 100, щоб побачити, чи виникає будь-яка несподівана поведінка.

Давайте розглянемо останній приклад.

Приклад$\PageIndex{5}$

Намалюйте графік функції f, визначеної рівнянням$f(x) = x^{4}+9 x^{3}-117 x^{2}-265 x+2100$.

Рішення

Завантажте функцію в меню Y= (показано на малюнку$\PageIndex{20}$ (a)) і виберіть 6:ZStandard, щоб створити графік, показаний на малюнку$\PageIndex{20}$ (b).

Малюнок$\PageIndex{20}$ Ескіз графіка$f(x) = x^{4}+9 x^{3}-117 x^{2}-265 x+2100$.

У міру малювання графіка спостерігайте, що він піднімається з нижньої частини оглядового вікна, залишає верхню частину оглядового вікна, потім повертається, щоб впасти з нижньої частини оглядового вікна, потім знову повертається і піднімається з верхньої частини оглядового вікна.

Ми помічаємо, що f (0) = 2100, тому нам потрібно встановити у верхній частині вікна перегляду цього значення або вище. Маючи на увазі цю думку, ми встановимо Ymax = 3000, а потім встановити Ymin=-3000 для балансу, а потім, щоб уникнути мільйона маленьких галочок, ми встановимо Yscl = 1000, все це показано на малюнку$\PageIndex{21}$ (а). Натискання кнопки GRAPH потім створює зображення, показане на малюнку$\PageIndex{21}$ (b).

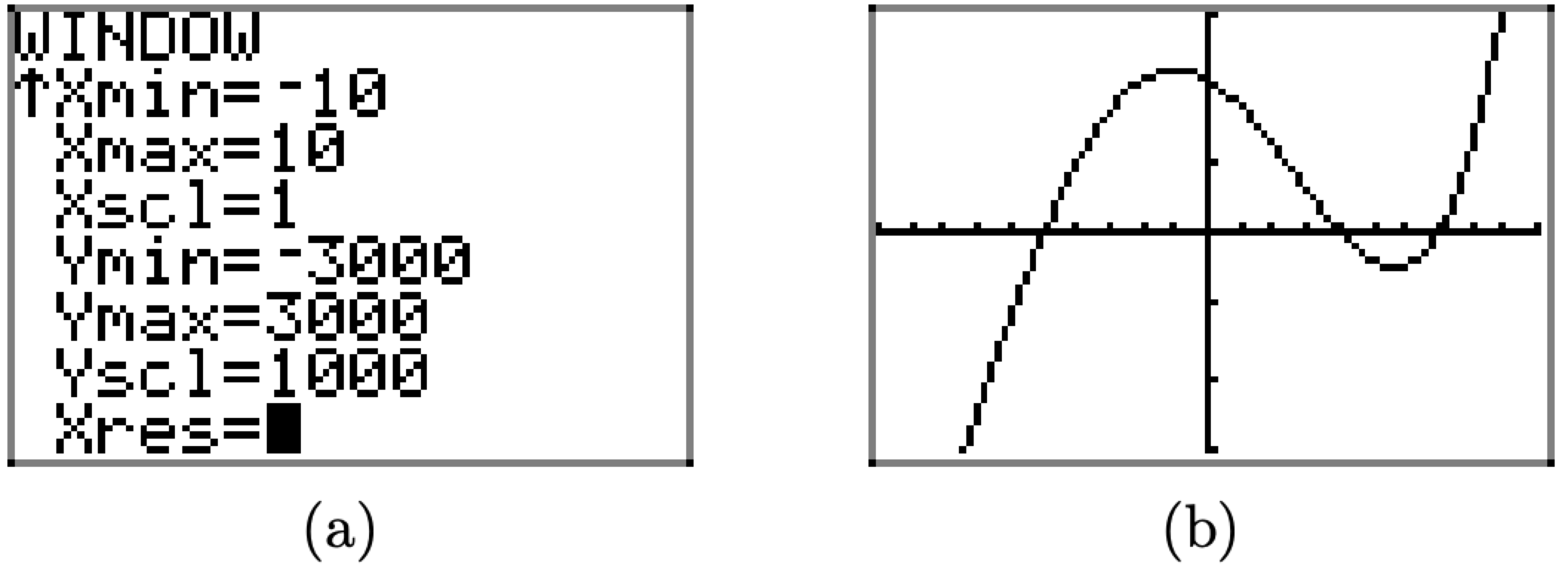
$\PageIndex{21}$Малюнок Налаштування оглядового вікна.

Чи здається, що у нас є всі «важливі функції» цього графіка, відображені в нашому вікні перегляду? Зауважимо, що ми експериментували не дуже багато. Можливо, нам слід спробувати розширити вікно трохи більше, щоб побачити, чи не пропустили ми якусь важливу поведінку. Маючи на увазі цю думку, ми встановлюємо Xmin=-20, Xmax = 20, і щоб уникнути тонни галочок, Xscl = 5, як показано на малюнку$\PageIndex{22}$ (а). Натискання кнопки GRAPH створює зображення на малюнку$\PageIndex{22}$ (b).

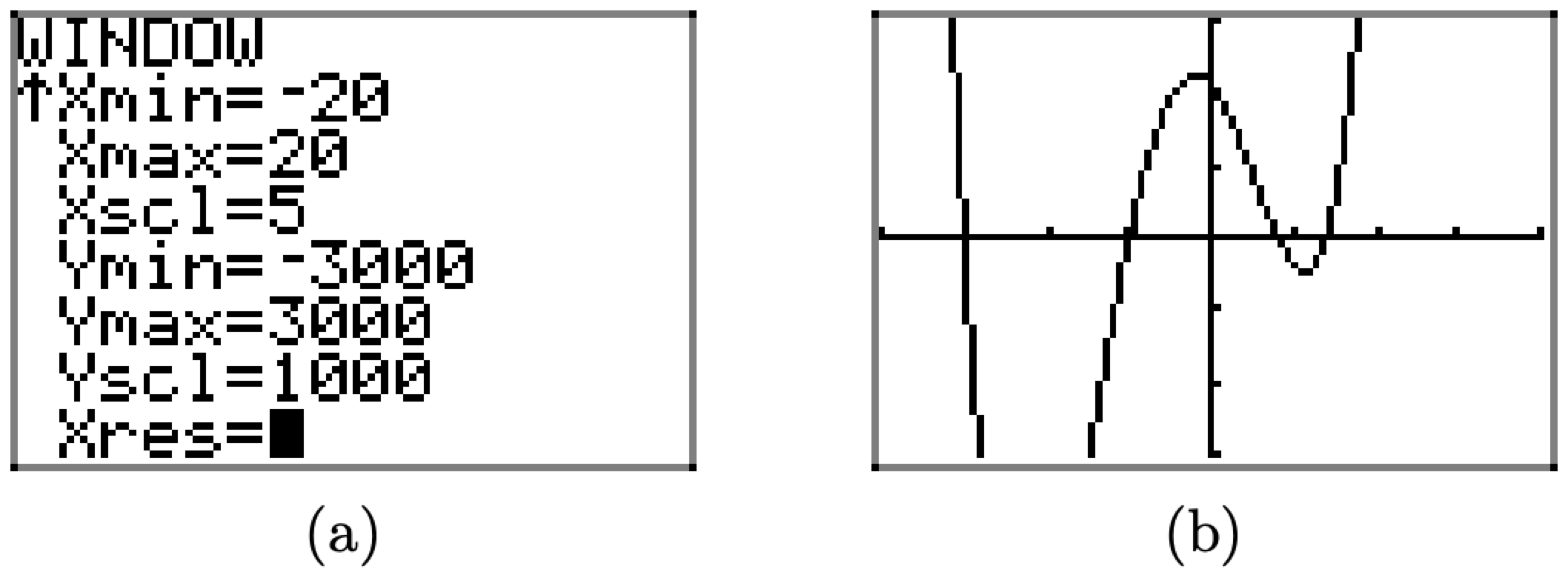
Рисунок$\PageIndex{22}$ Налаштування вікна перегляду знову показує поведінку, яку не видно.

Зауважте, що вікно перегляду на малюнку$\PageIndex{22}$ (b) показує поведінку, яку не видно у вікні перегляду малюнка$\PageIndex{21}$ (b). Якби ми не експериментували далі, якби ми не розширили оглядове вікно, ми б не бачили цієї нової поведінки. Це важливе заняття.

Зверніть увагу, що одна з «поворотних точок» графіка на малюнку$\PageIndex{22}$ (b) лежить в нижній частині оглядового вікна. Ми зробимо ще одне коригування, щоб включити цю важливу функцію. Встановіть Ymin=-10000, Ymax = 10000, і Yscl = 5000, як показано на малюнку$\PageIndex{23}$ (a), потім натисніть кнопку GRAPH, щоб створити зображення, показане на малюнку$\PageIndex{23}$ (b).

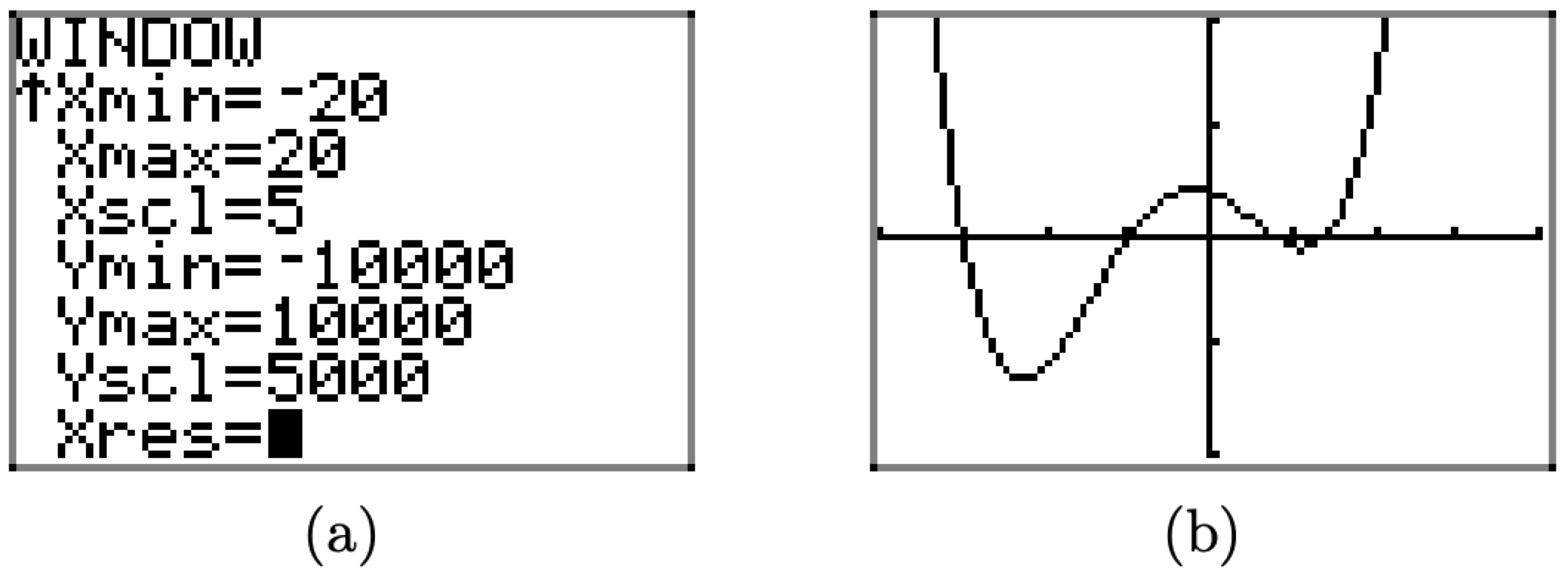
Малюнок$\PageIndex{23}$. Налаштування вікна перегляду знову виявляє поведінку, яку не видно.

Графік на малюнку$\PageIndex{23}$ (b) показує всі «важливі особливості» графіка f, але уважний читач продовжить експериментувати, розширюючи вікно перегляду, щоб переконатися в істинності цього твердження.