2.6: Горизонтальні перетворення

У попередньому розділі ми ввели поняття перетворень. Ми зробили зміну базового рівняння y = f (x), наприклад y = af (x), y = −f (x), y = f (x) − c, або y = f (x) + c, потім вивчили, як ці зміни вплинули на форму графіка y = f (x). У цьому розділі ми зосередилися строго на перетвореннях, які застосовуються у вертикальному напрямку. У цьому розділі ми вивчимо перетворення, які будуть впливати на форму графіка в горизонтальному напрямку.

Ми починаємо наше завдання з прикладу, який вимагає, щоб ми прочитали графік функції, щоб захопити кілька ключових точок, які лежать на графіку функції.

Приклад\(\PageIndex{1}\)

Розглянемо графік f, представлений на малюнку\(\PageIndex{1}\) (а). Використовуйте графік f, щоб заповнити таблицю на малюнку\(\PageIndex{1}\) (b).

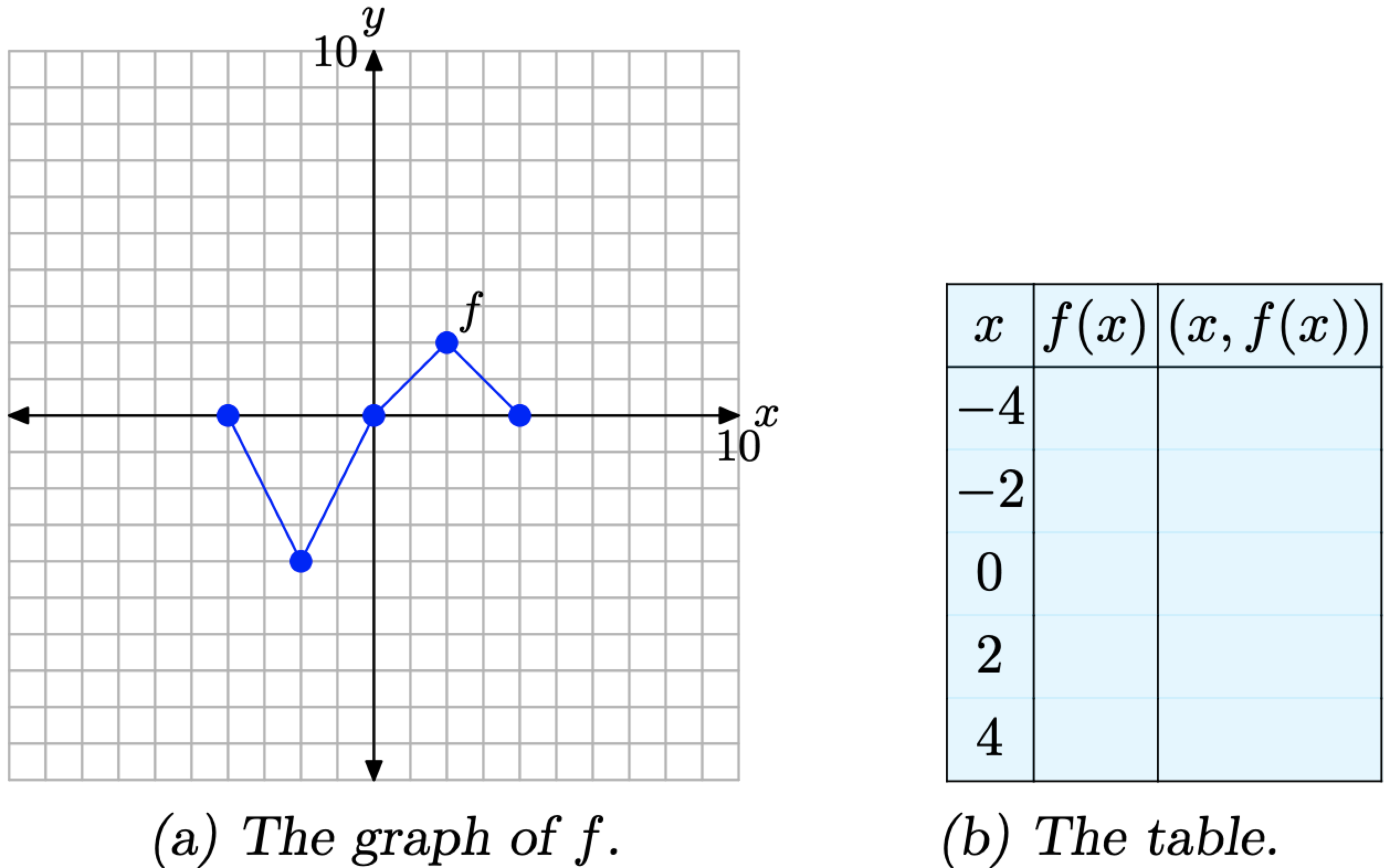
Малюнок\(\PageIndex{1}\). Читання ключових значень з графіка f.

Рішення

Наприклад, щоб обчислити f (−2), ми спочатку знайдемо −2 на осі x, намалюємо вертикальну стрілку до графіка f, потім горизонтальну стрілку до осі y, як показано на малюнку\(\PageIndex{2}\) (a). Значенням y цього кінцевого пункту призначення є значенням f (−2). Тобто f (−2) = −4. Це дозволяє нам заповнити один запис у таблиці, як показано на малюнку\(\PageIndex{2}\) (b). Продовжуйте таким чином, щоб завершити всі записи в таблиці. Результат показаний на малюнку\(\PageIndex{2}\) (в).

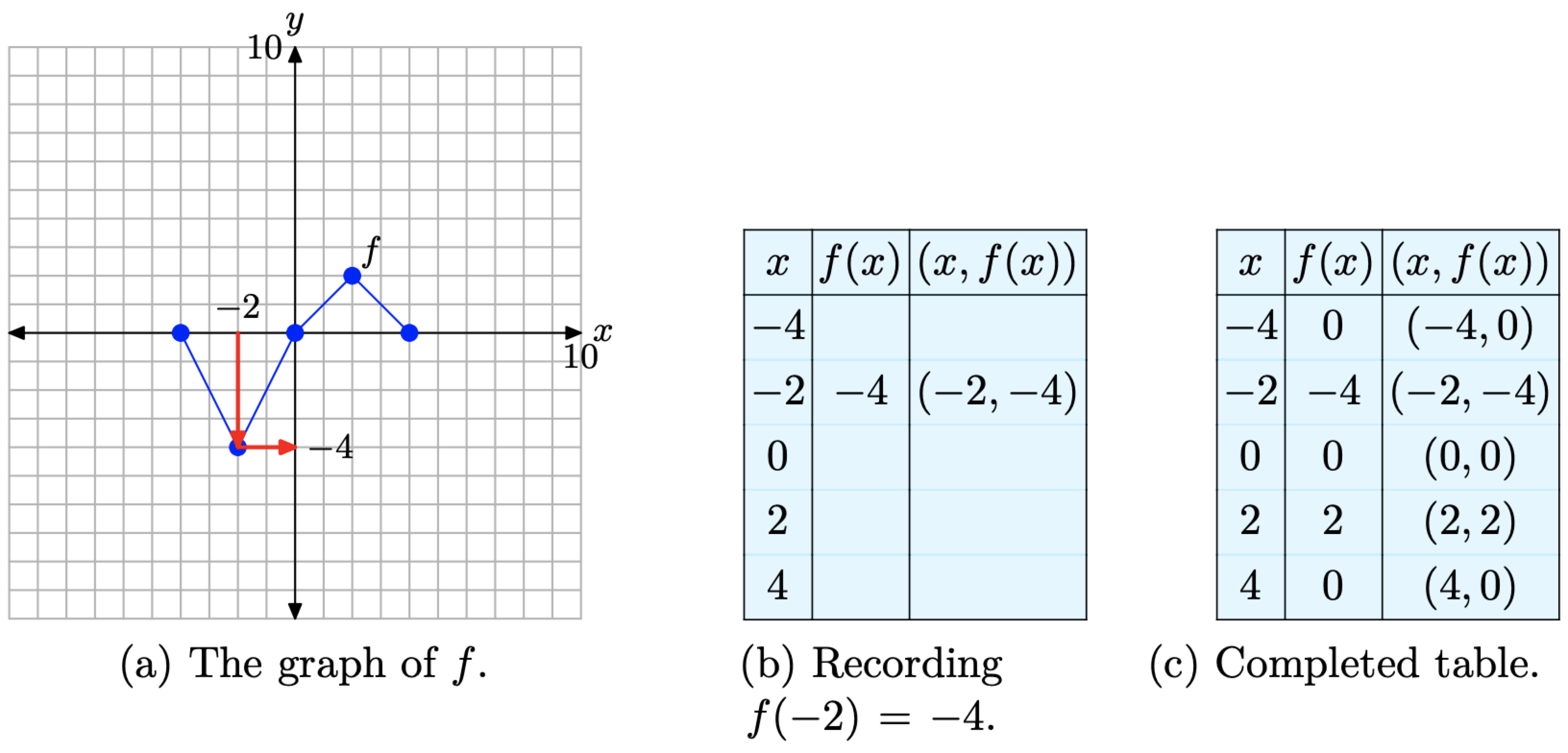
Малюнок\(\PageIndex{2}\). Запис координат точок на графіку f в таблицях

Горизонтальне масштабування

У наступному розповіді ми матимемо повторну потребу в графіку на малюнку\(\PageIndex{2}\) (а) та таблиці на малюнку\(\PageIndex{2}\) (c). Вони характеризують основну функцію, яка стане відправною точкою для понять масштабування, рефлексії та перекладу, які ми розробляємо в цьому розділі. Отже, давайте розмістимо їх пліч-о-пліч для акценту на малюнку\(\PageIndex{3}\).

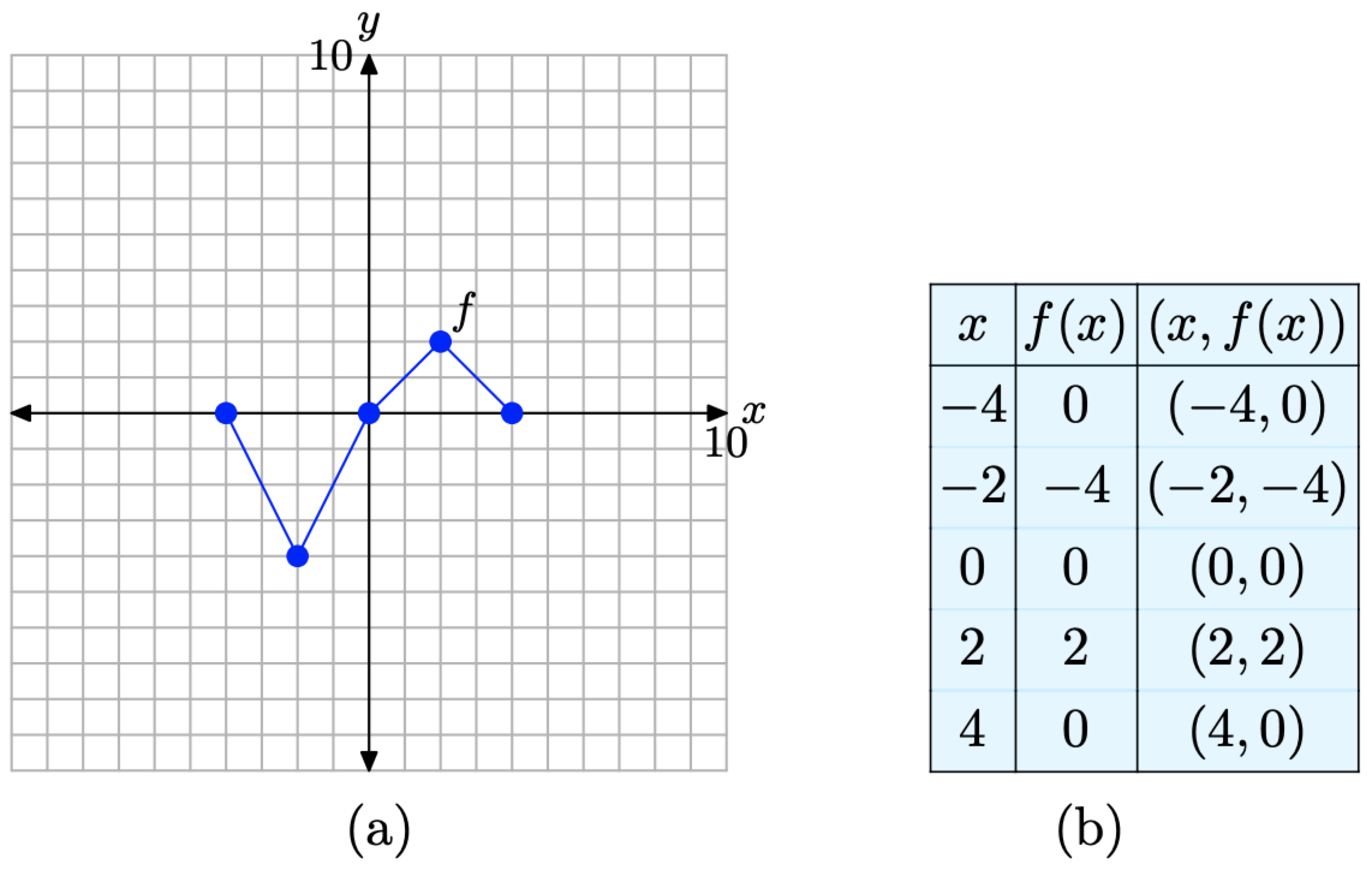
Малюнок\(\PageIndex{3}\). Вихідний графік f і таблиця ключових точок на графіку f

Тепер ми збираємося масштабувати графік f в горизонтальному напрямку.

Приклад\(\PageIndex{2}\)

Якщо y = f (x) має графік, показаний на малюнку\(\PageIndex{3}\) (a), намалюйте графік y = f (2x).

Рішення

У попередньому розділі ми досліджували графік y = 2f (x). Число 2 виявилося поза позначенням функції і в результаті ми розтягнули графік y = f (x) по вертикалі в 2 рази. Однак зауважте, що 2 тепер знаходиться всередині позначення функції y = f (2x). Інтуїція вимагатиме, щоб це могло мати щось спільне з масштабуванням у напрямку x (горизонтальному напрямку), але як?

Знову ж таки, коли ми не впевнені в формі графіка, ми покладаємося на побудова таблиці точок. Ми починаємо з вибору цих значень x: x = −2, −1, 0, 1 і 2. Зверніть увагу, що це рівно половина кожного з x-значень, представлених в таблиці на малюнку\(\PageIndex{3}\) (b). Тепер ми будемо оцінювати функцію y = f (2x) на кожному з цих x-значень. Наприклад, щоб обчислити y = f (2x) при x = −2, ми спочатку вставляємо x = −2 для x, щоб отримати\[y=f(2(-2))=f(-4)\]

Щоб завершити обчислення, ми повинні оцінити f (−4). Однак цей результат заноситься в таблицю на малюнку\(\PageIndex{3}\) (б). Там ми знаходимо, що f (−4) = 0, і ми можемо завершити обчислення, розпочате вище.

\[y=f(2(-2))=f(-4)=0\]

Аналогічно, щоб оцінити функцію y = f (2x) при x = −1, спочатку підставляємо x = −1 у y = f (2x), щоб отримати

\[y=f(2(-1))=f(-2)\]

Тепер зауважте, що f (−2) є наступним записаним значенням у таблиці на малюнку\(\PageIndex{3}\) (b). Там ми знаходимо, що f (−2) = −4, тож ми можемо завершити обчислення, розпочате вище.

\[y=f(2(-1))=f(-2)=-4\]

На цьому етапі ви можете побачити, чому ми вибрали значення x: −2, −1, 0, 1 і 2. Це рівно половина x-значень в таблиці вихідних значень для функції y = f (x) на малюнку\(\PageIndex{3}\) (b). Коли значення −2, −1, 0, 1 і 2 підставляються у функцію y = f (2x), вони спочатку подвоюються, перш ніж ми перейдемо до пошуку значення функції в таблиці на рисунку\(\PageIndex{3}\) (b).

Продовжуючи таким чином, оцінюємо функцію y = f (2x) при інших значеннях x, а саме 0, 1 і 2.

\[\begin{aligned} y &=f(2(0))=f(0)=0 \\ y &=f(2(1))=f(2)=2 \\ y &=f(2(2))=f(4)=0 \end{aligned}\]

Ці значення вводимо в таблицю на малюнку 4 (б) і будуємо їх для визначення графіка y = f (2x) на малюнку\(\PageIndex{4}\) (а).

На даний момент існує ряд порівнянь, які ви можете зробити.

1. Порівняйте дані в таблиці на малюнку\(\PageIndex{4}\) (b) з вихідними даними функції в таблиці на малюнку\(\PageIndex{3}\) (b). Зверніть увагу, що значення y в кожній таблиці ідентичні. Однак зауважте, що кожне значення x в таблиці малюнка\(\PageIndex{4}\) (b) дорівнює рівно половині відповідного значення x в таблиці рисунка\(\PageIndex{3}\) (b).

2. Порівняйте графік y = f (2x) на малюнку\(\PageIndex{4}\) (а) з вихідним графіком y = f (x) на малюнку\(\PageIndex{3}\) (а). Зверніть увагу, що кожне значення x у кожній точці на графіку y = f (2x) в

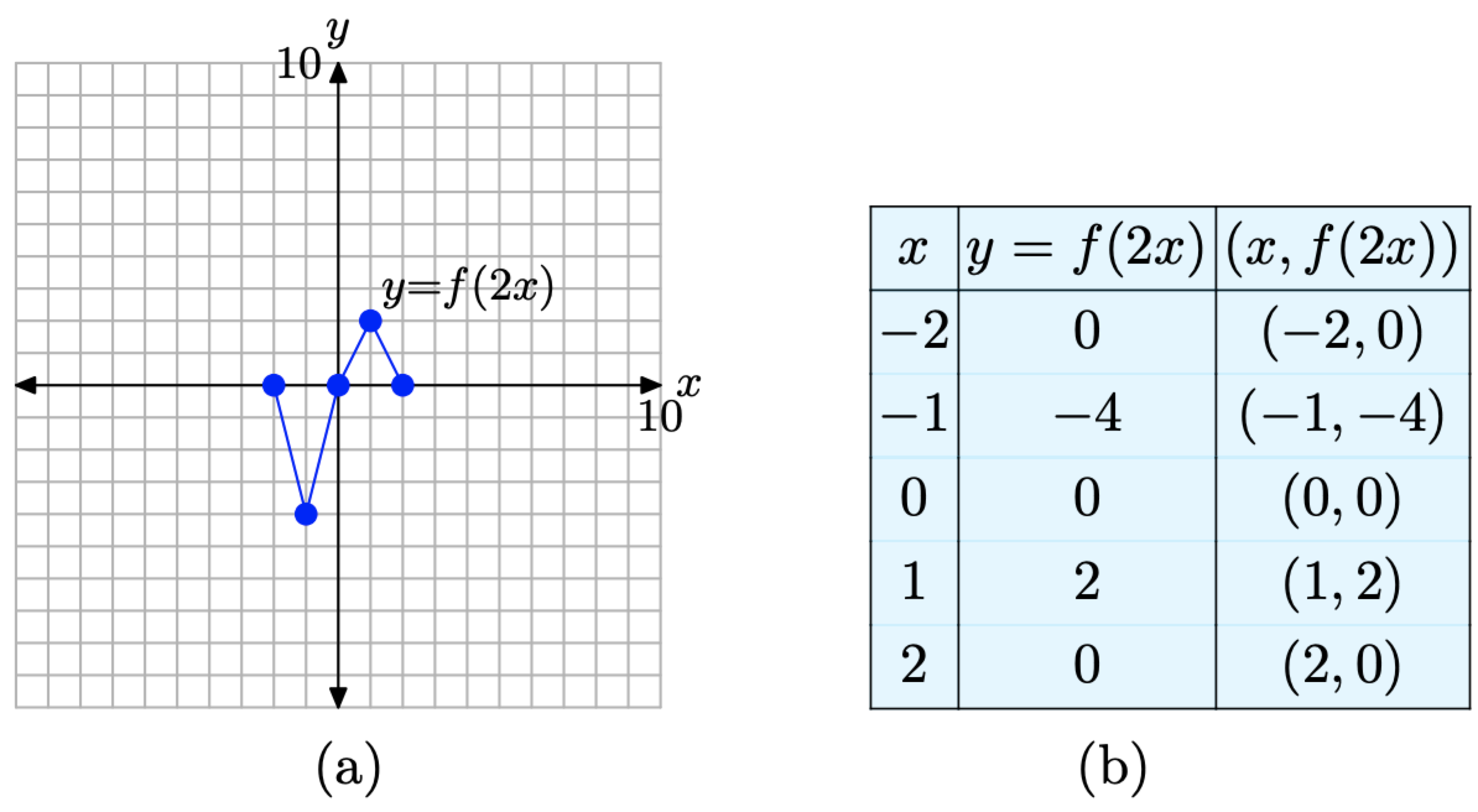
Малюнок\(\PageIndex{4}\). Точки в таблиці - це точки на графіку y = f (2x).

Рисунок\(\PageIndex{4}\) (а) точно дорівнює половині значення x відповідної точки на графіку y = f (x) на малюнку\(\PageIndex{3}\) (а).

Зверніть увагу на результат. Графік y = f (2x) стискається горизонтально (до осі y), як позитивно, так і негативно, в 2 рази. Зверніть увагу, що це прямо протилежне тому, що ви могли б очікувати по інтуїції, але уважне вивчення даних в таблицях на малюнках\(\PageIndex{3}\) (b) і\(\PageIndex{4}\) (b) пояснить чому.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{3}\)

Якщо y = f (x) має графік, показаний на малюнку\(\PageIndex{3}\) (а), намалюйте графік y = f (((1/2) x).

Рішення

Замість того, щоб подвоювати кожне значення x на початку, ця функція спочатку вдвічі збільшує кожне значення x. Таким чином, ми хочемо оцінити функцію y = f (((1/2) x) при x = −8, −4, 0, 4 та 8. Наприклад, щоб оцінити функцію y = f ((1/2) x) при x = −8, спочатку підставляємо x = −8, щоб отримати\[y=f((1 / 2)(-8))=f(-4)\]

Тепер знайдіть це значення в таблиці на малюнку\(\PageIndex{3}\) (b) і зауважте, що f (−4) = 0. Таким чином, ми можемо завершити обчислення наступним чином.

\[y=f((1 / 2)(-8))=f(-4)=0\]

Аналогічно, щоб оцінити функцію y = f ((1/2) x) при x = −4, спочатку підставляємо x = −4, щоб отримати

\[y=f((1 / 2)(-4))=f(-2)\]

Тепер знайдіть це значення в таблиці на малюнку\(\PageIndex{3}\) (b) і зауважте, що f (−2) = −4. Таким чином, ми можемо завершити обчислення наступним чином.

\[y=f((1 / 2)(-4))=f(-2)=-4\]

На цьому етапі ви побачите, чому ми обрали значення x: −8, −4, 0, 4 та 8. Ці значення точно вдвічі перевищують значення x в таблиці вихідних значень для функції y = f (x) на малюнку\(\PageIndex{3}\) (b). Коли значення −8, −4, 0, 4 та 8 підставляються у функцію y = f ((1/2) x), вони спочатку зменшуються вдвічі, перш ніж ми перейдемо до пошуку значення функції в таблиці на рисунку\(\PageIndex{3}\) (b). Це скорочення вдвічі призводить до значень −4, −2, 0, 2 та 4, які є саме значеннями, доступними у таблиці на рис.\(\PageIndex{3}\) (b).

Робимо аналогічні обчислення при інших значеннях x, а саме x = 0, 4 і 8.

\[\begin{aligned} y &=f((1 / 2)(0))=f(0)=0 \\ y &=f((1 / 2)(4))=f(2)=2 \\ y &=f((1 / 2)(8))=f(4)=0 \end{aligned}\]

Сподіваємось, ці обчислення пояснюють наш вибір x-значень вище. Кожен з цих результатів записується в таблицю на малюнку\(\PageIndex{5}\) (б) і наноситься на графік, показаний на малюнку\(\PageIndex{5}\) (а).

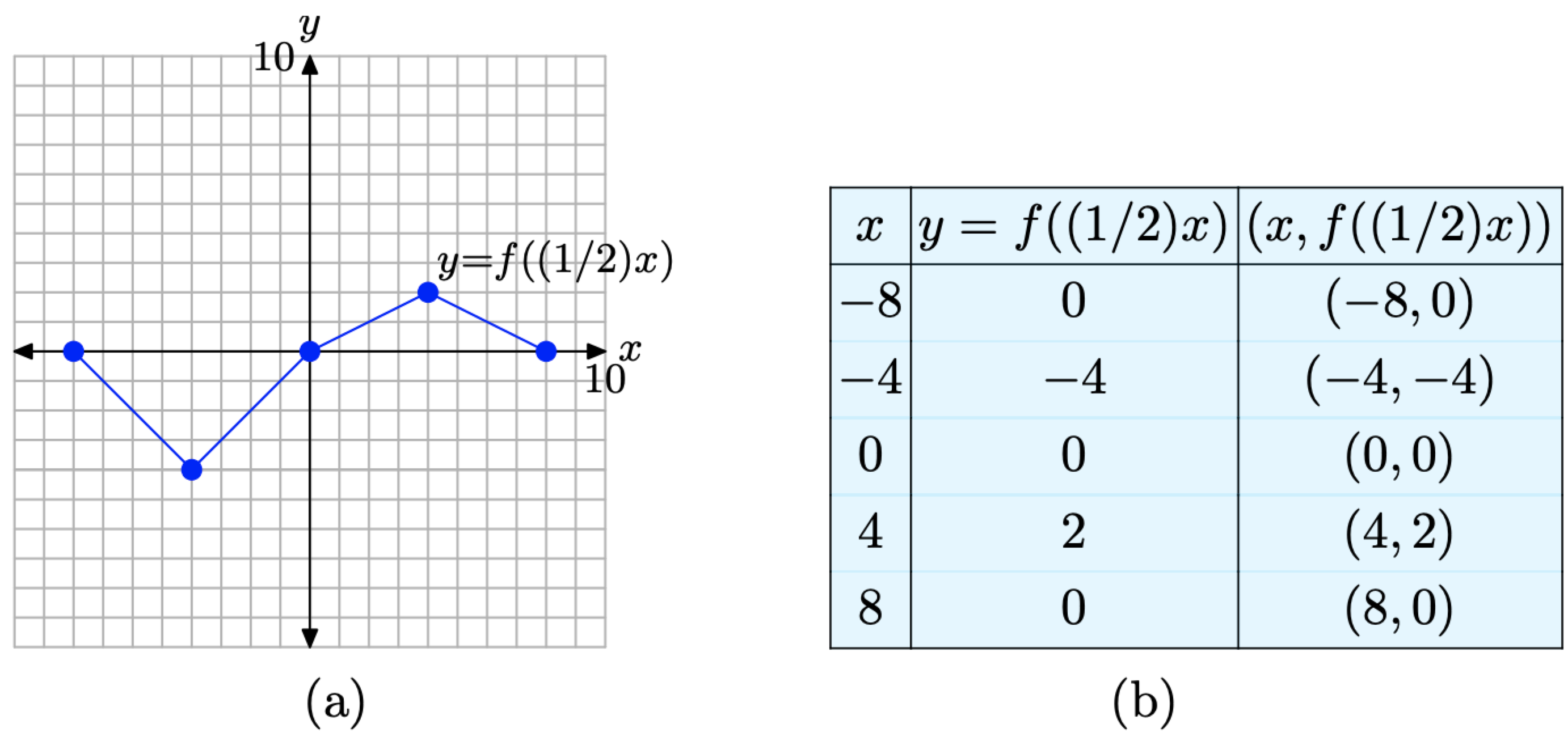
Малюнок\(\PageIndex{5}\). Точки в таблиці - це точки на графіку y = f ((1/2) х).

Знову зауважте, що значення y в таблиці на малюнку\(\PageIndex{5}\) (b) ідентичні значенням y в таблиці на малюнку\(\PageIndex{3}\) (b). Однак кожне значення x у таблиці на малюнку\(\PageIndex{5}\) (b) точно вдвічі перевищує відповідне значення x у таблиці на малюнку\(\PageIndex{3}\) (b).

Це подвоєння значень x видно на графіку y = f ((1/2) x), показаному на малюнку\(\PageIndex{5}\) (а), де графік розтягується на коефіцієнт 2 по горизонталі (далеко від осі y), як позитивно, так і негативно. Зверніть увагу, що це прямо протилежне тому, що ви могли б очікувати по інтуїції, але уважне вивчення даних в таблицях на малюнках\(\PageIndex{3}\) (b) і\(\PageIndex{5}\) (b) пояснить чому.

Давайте підсумуємо наші висновки.

Візуальний підсумок - горизонтальне масштабування

Розглянемо зображення на малюнку\(\PageIndex{6}\).

• На малюнку\(\PageIndex{6}\) (a) ми бачимо на фото графік вихідної функції y = f (x).
• На малюнку\(\PageIndex{6}\) (b) зверніть увагу, що кожна ключова точка на графіку y = f (2x) має значення x, яке точно дорівнює половині значення x відповідної точки на графіку y = f (x) на малюнку\(\PageIndex{6}\) (а).
• На малюнку\(\PageIndex{6}\) (c) зверніть увагу, що кожна ключова точка на графіку y = f ((1/2) x) має значення x, яке вдвічі перевищує значення x відповідної точки на графіку y = f (x) на малюнку\(\PageIndex{6}\) (а).
• Зауважте, що значення y кожної трансформованої точки залишається незмінним.

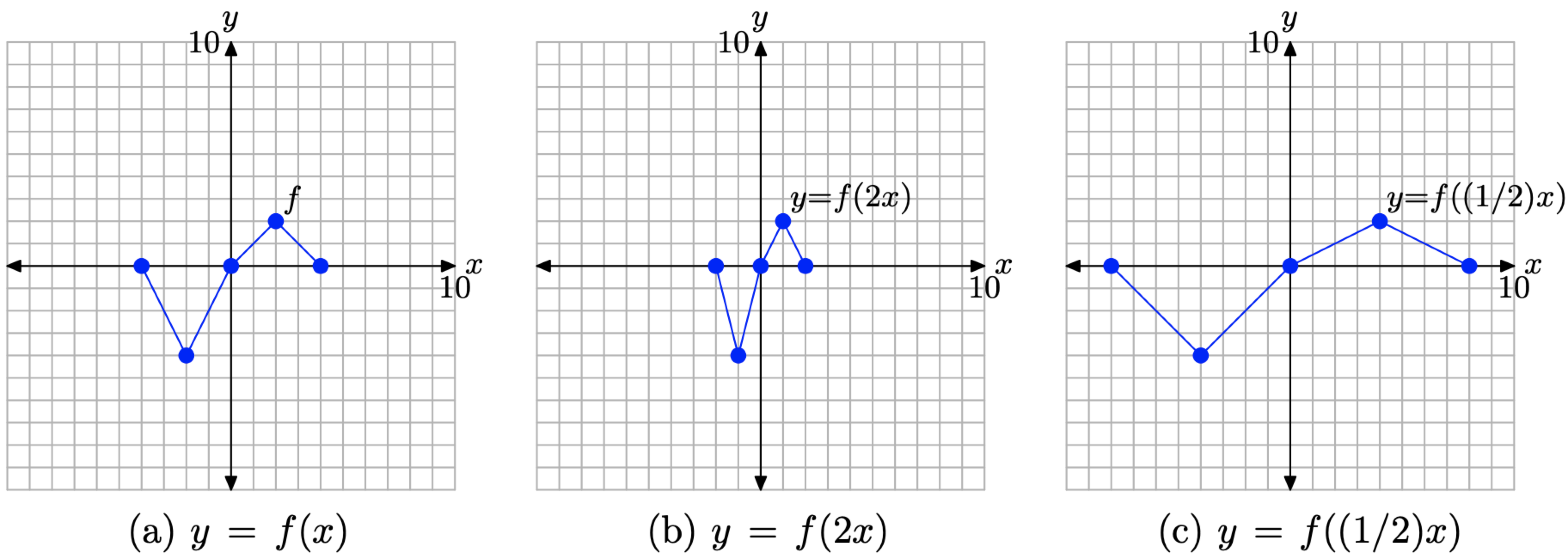
Малюнок\(\PageIndex{6}\). Графік y = f (2x) стискає горизонтально (до осі y) в 2 рази. Графік y = f ((1/2) x) розтягується горизонтально (від осі y) в 2 рази.

Візуальне резюме на малюнку\(\PageIndex{6}\) робить ескіз графіків y = f (2x) та y = f (1/2) x) легким завданням.

• З огляду на графік y = f (x), щоб намалювати графік y = f (2x), просто візьміть кожну точку на графіку y = f (x) і розріжте її значення x навпіл, зберігаючи однакове значення y.
• З огляду на графік y = f (x), щоб намалювати графік y = f ((1/2) x), просто візьміть кожну точку на графіку y = f (x) і подвоїти її значення x, зберігаючи однакове значення y.

Виконайте ті ж процедури для інших факторів масштабування. Наприклад, у випадку y = f (3x) візьміть кожну точку на графіку y = f (x) і розділіть її значення x на 3, зберігаючи однакове значення y. З іншого боку, щоб намалювати графік y = f ((1/3) x), візьміть кожну точку на графіку f і помножте її значення x на 3, зберігаючи однакове значення y.

Загалом, можна констатувати наступне.

резюме

Припустимо, нам дано графік y = f (x).

• Якщо a > 1, графік y = f (ax) стискається горизонтально (до осі y), як позитивно, так і негативно, в рази a.
• Якщо 0 < a < 1, графік y = f (ax) розтягується горизонтально (від осі y), як позитивно, так і негативно, в рази 1/a.

У випадку з першим пунктом в Summary, коли ми порівнюємо загальну форму y = f (ax) з y = f (2x), ми бачимо, що a = 2. При цьому зверніть увагу, що a > 1 і графік y = f (2x) стискає горизонтально в 2 рази при порівнянні з графіком y = f (x)\(\PageIndex{6}\) (див. Рис.

У випадку з другим пунктом в Summary, коли ми порівнюємо загальний вигляд y = f (ax) з рівнянням y = f (((1/2) х), ми бачимо, що a = 1/2, тому

\[\frac{1}{a}=\frac{1}{1 / 2}=2\]

Другий пункт в резюме 4 говорить про те, що при 0 < a < 1 графік y = f (ax) розтягується горизонтально в коефіцієнт 1/a. дійсно, це саме те, що сталося у випадку y = f (((1/2) x), який розтягнувся в горизонтальному напрямку на коефіцієнт 1/ (1/2), або 2\(\PageIndex{6}\) (див. Рис.

Горизонтальні відбиття

Для зручності починаємо з повторення вихідного графіка y = f (x) і супутніх до нього даних на рис\(\PageIndex{7}\). Тепер ми збираємося відобразити графік y = f (x) в горизонтальному напрямку (поперек осі y).

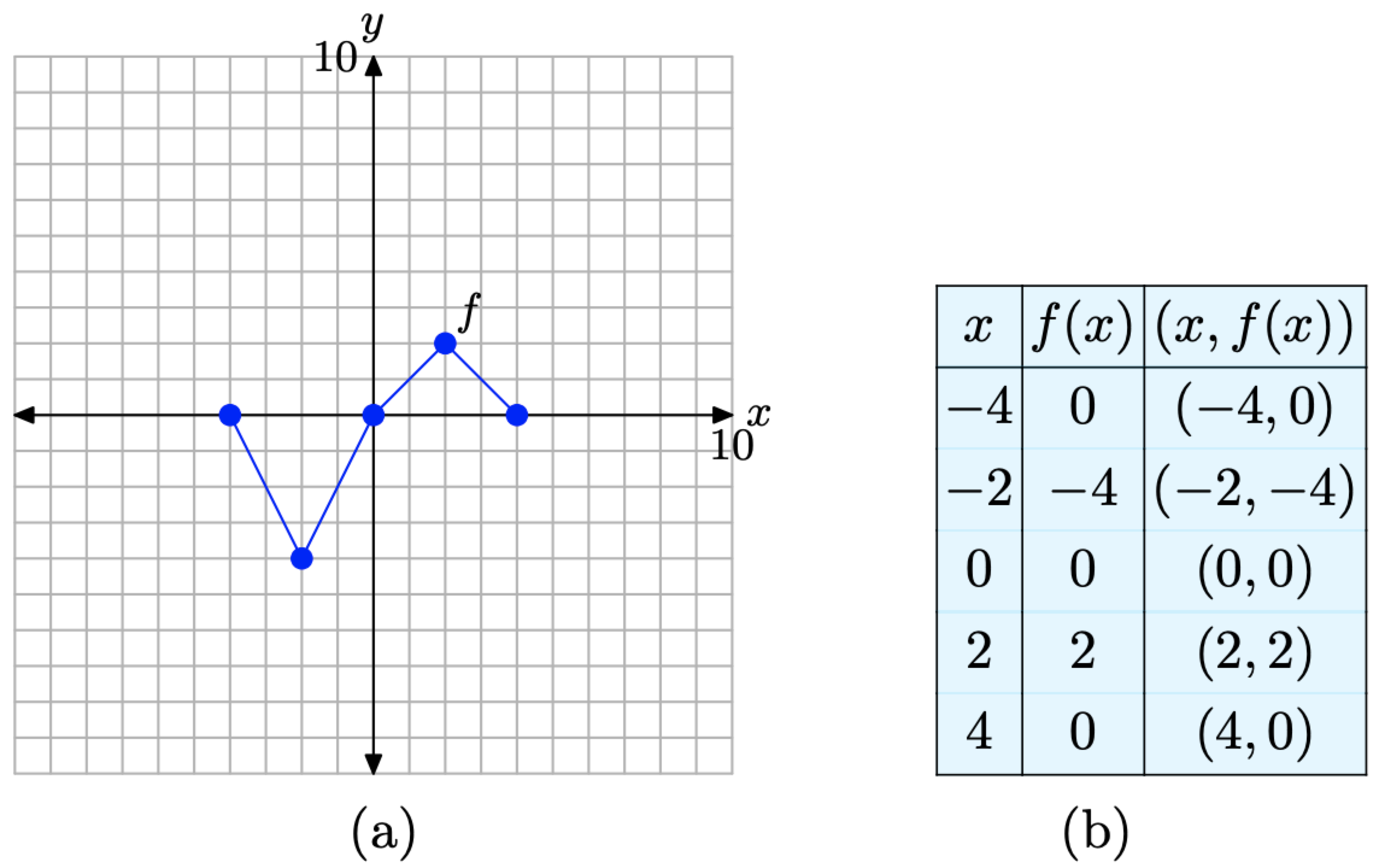
Малюнок\(\PageIndex{7}\). Вихідний графік f і таблиця ключових точок на графіку f

Приклад\(\PageIndex{4}\)

Якщо y = f (x) має графік, показаний на малюнку\(\PageIndex{7}\) (a), намалюйте графік y = f (−x).

Рішення

У попередньому розділі нам було запропоновано намалювати графік y = −f (x). Зверніть увагу, як знак мінус з'являється на зовнішній стороні функції. Зрозуміло, що y-значення y = −f (x) повинні бути протилежні за знаком y-значень y = f (x). Саме тому графік y = −f (x) був відображенням графіка y = f (x) по осі x.

Однак у цьому прикладі знак мінус знаходиться всередині функції, залишаючи один, щоб зрозуміти, що це значення x, а не значення y, які заперечуються. Ми виберемо такі значення x: x = 4, 2, 0, −2 та −4. Це трохи оманливо, так як схоже, ми вибираємо ті ж значення x, тільки в зворотному порядку. Це не так. Ми вибираємо негатив кожного значення x в таблиці на малюнку\(\PageIndex{7}\) (b).

Щоб оцінити y = f (−x) при нашому першому значенні x, а саме x = 4, ми виконуємо наступний розрахунок. Спочатку підставляємо x = 4, щоб отримати

\[y=f(-(4))=f(-4)\]

Тепер знайдіть це значення в таблиці на малюнку\(\PageIndex{7}\) (b) і зауважте, що f (−4) = 0. Таким чином, ми можемо завершити обчислення наступним чином.

\[y=f(-(4))=f(-4)=0\]

Аналогічно, щоб оцінити функцію y = f (−x) при x = 2, спочатку підставляємо x = 2, щоб отримати

\[y=f(-(2))=f(-2)\]

Тепер знайдіть це значення в таблиці на малюнку\(\PageIndex{7}\) (b) і зауважте, що f (−2) = −4. Таким чином, ми можемо завершити обчислення наступним чином.

\[y=f(-(2))=f(-2)=-4\]

На цьому етапі ви побачите, чому ми обрали значення x: 4, 2, 0, −2 та −4. Ці значення є негативами x-значень в таблиці вихідних значень для функції y = f (x) на малюнку\(\PageIndex{7}\) (b). Коли значення 4, 2, 0, −2 та −4 підставляються у функцію y = f (−x), вони спочатку заперечуються перед тим, як ми перейдемо до пошуку значення функції у таблиці на рисунку\(\PageIndex{7}\) (b). Це заперечення призводить до значень −4, −2, 0, 2 і 4, які є саме значеннями, доступними в таблиці на рис.\(\PageIndex{7}\) (b).

Аналогічні обчислення проводимо за рештою значень x, а саме x = 0, −2 та −4.

\[\begin{array}{l}{y=f(-(0))=f(0)=0} \\ {y=f(-(-2))=f(2)=2} \\ {y=f(-(-4))=f(4)=0}\end{array}\]

Ми організуємо ці точки в таблиці на малюнку\(\PageIndex{8}\) (b), потім будуємо їх на малюнку\(\PageIndex{8}\) (а).

Коли ви порівнюєте записи в таблиці на малюнку\(\PageIndex{8}\) (b) з тими, що знаходяться в таблиці на малюнку\(\PageIndex{7}\) (b), зверніть увагу, що значення y з'являються в тому ж порядку, але значення x таблиці на малюнку\(\PageIndex{7}\) (b) були заперечені в таблиці на малюнку\(\PageIndex{8}\) (b). Це означає, що колишня точка (−2, −4) перетворюється на точку (2, −4), яка є відображенням точки (−2, −4) поперек осі y.

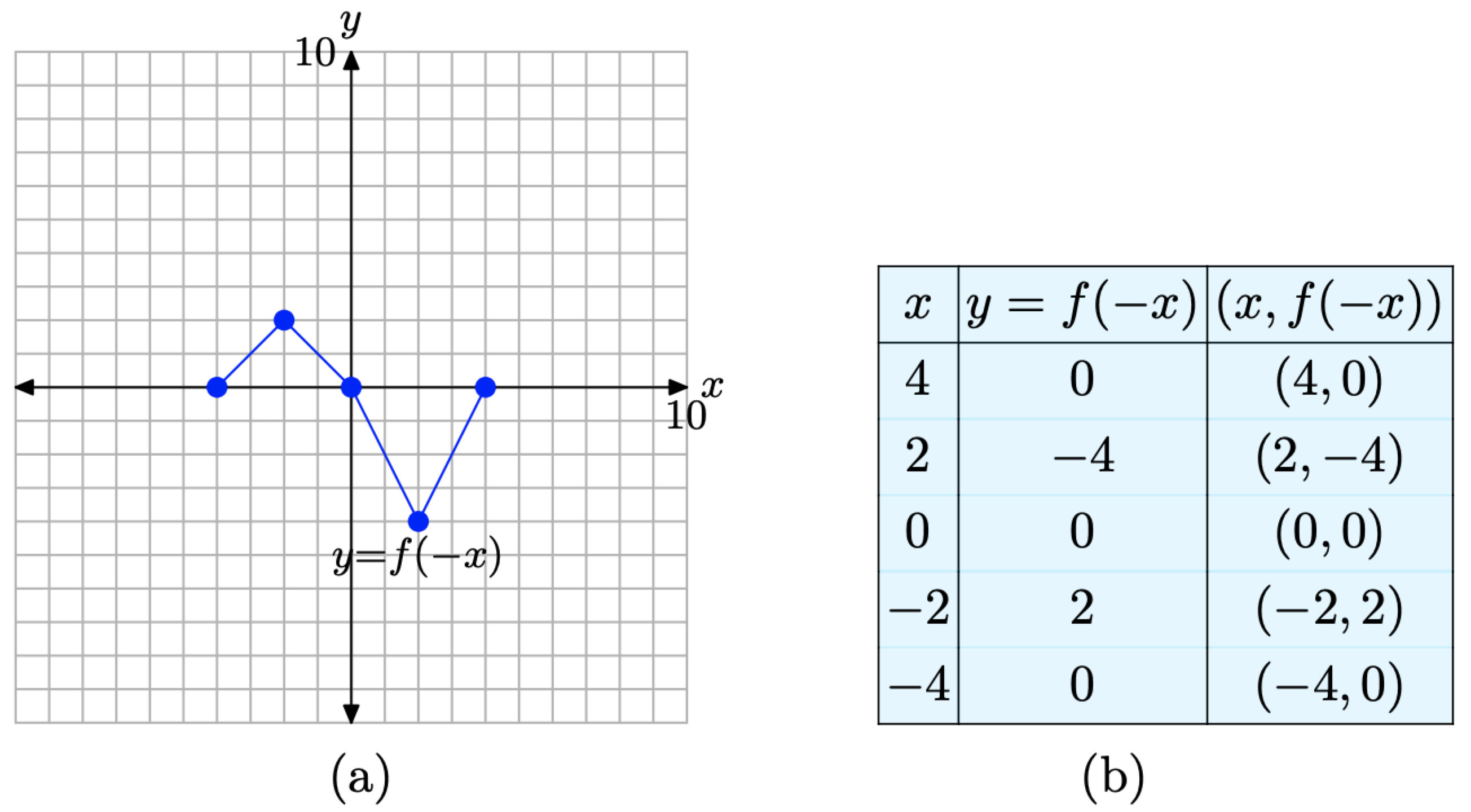
Малюнок\(\PageIndex{8}\). Графік y = f (−x) та таблиця ключових точок на графіку.

Таким чином, щоб отримати графік y = f (−x), просто відобразіть графік y = f (x) по осі y.

Давайте підсумуємо те, що ми дізналися про горизонтальні відбиття.

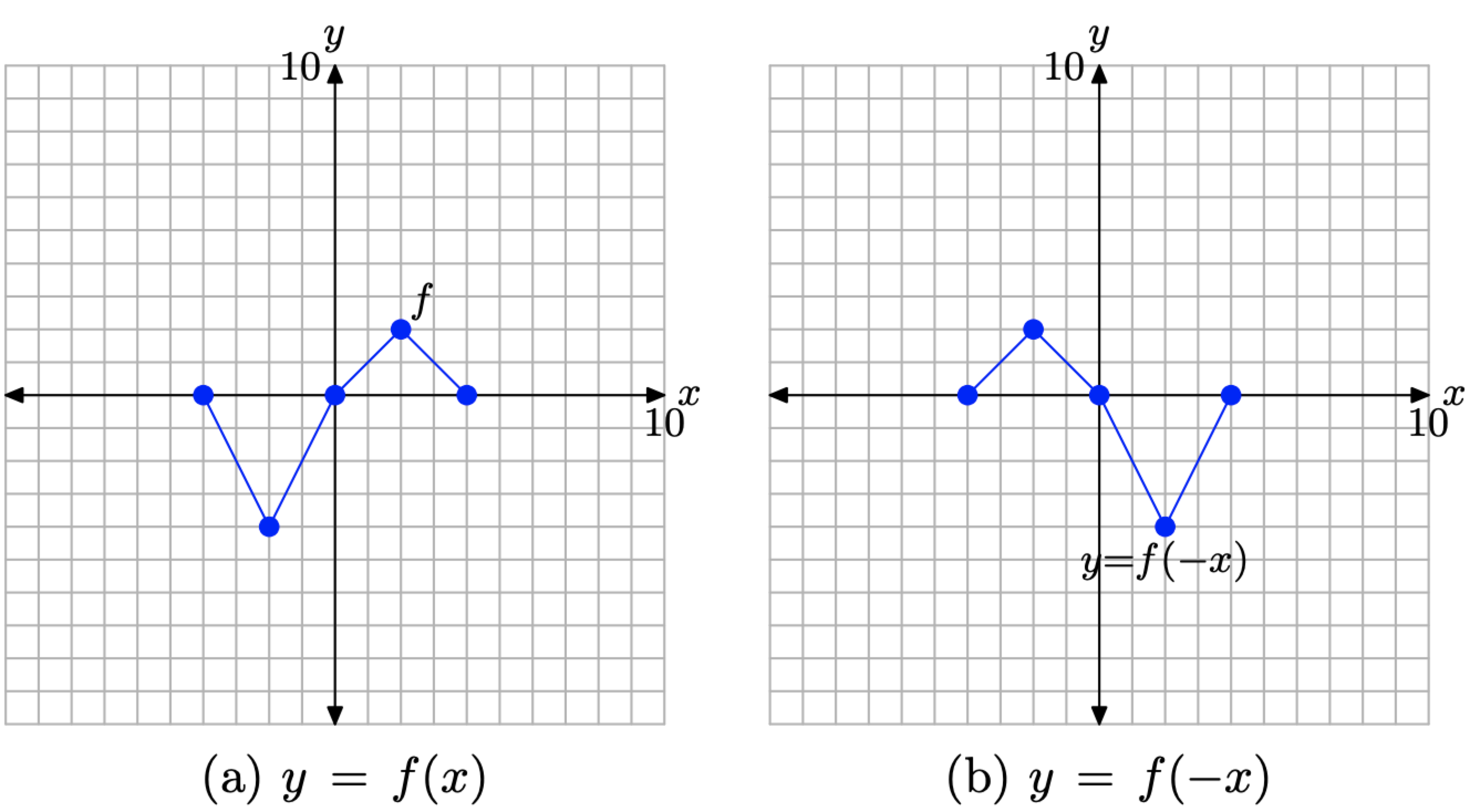
Малюнок\(\PageIndex{9}\). Графік y = f (−x) є відображенням графіка y = f (x) по осі y.

Візуальний підсумок - горизонтальні роздуми

Розглянемо зображення на малюнку\(\PageIndex{9}\).

• На малюнку\(\PageIndex{9}\) (а) ми бачимо на фото оригінальний графік y = f (x).
• На малюнку\(\PageIndex{9}\) (b) графік y = f (−x) є відображенням графіка y = f (x) по осі y.

Таким чином, враховуючи графік y = f (x), намалювати графік y = f (−x) є простим завданням.

• Щоб намалювати графік y = f (−x), візьміть кожну точку на графіку y = f (x) і відобразіть її по осі y, зберігаючи значення y однаковим, але заперечуючи значення x.

Горизонтальні переклади

У попередньому розділі ми бачили, що графіки y = f (x) + c і y = f (x) − c були вертикальними перекладами графа y = f (x). Якщо c є додатним числом, то графік y = f (x) + c зміщує c одиниць вгору, тоді як графік y = f (x) − c зміщує c одиниць вниз.

У цьому розділі ми вивчимо горизонтальні переклади. Для зручності почнемо з повторення вихідного графіка y = f (x) і супутніх до нього даних на малюнку 10.

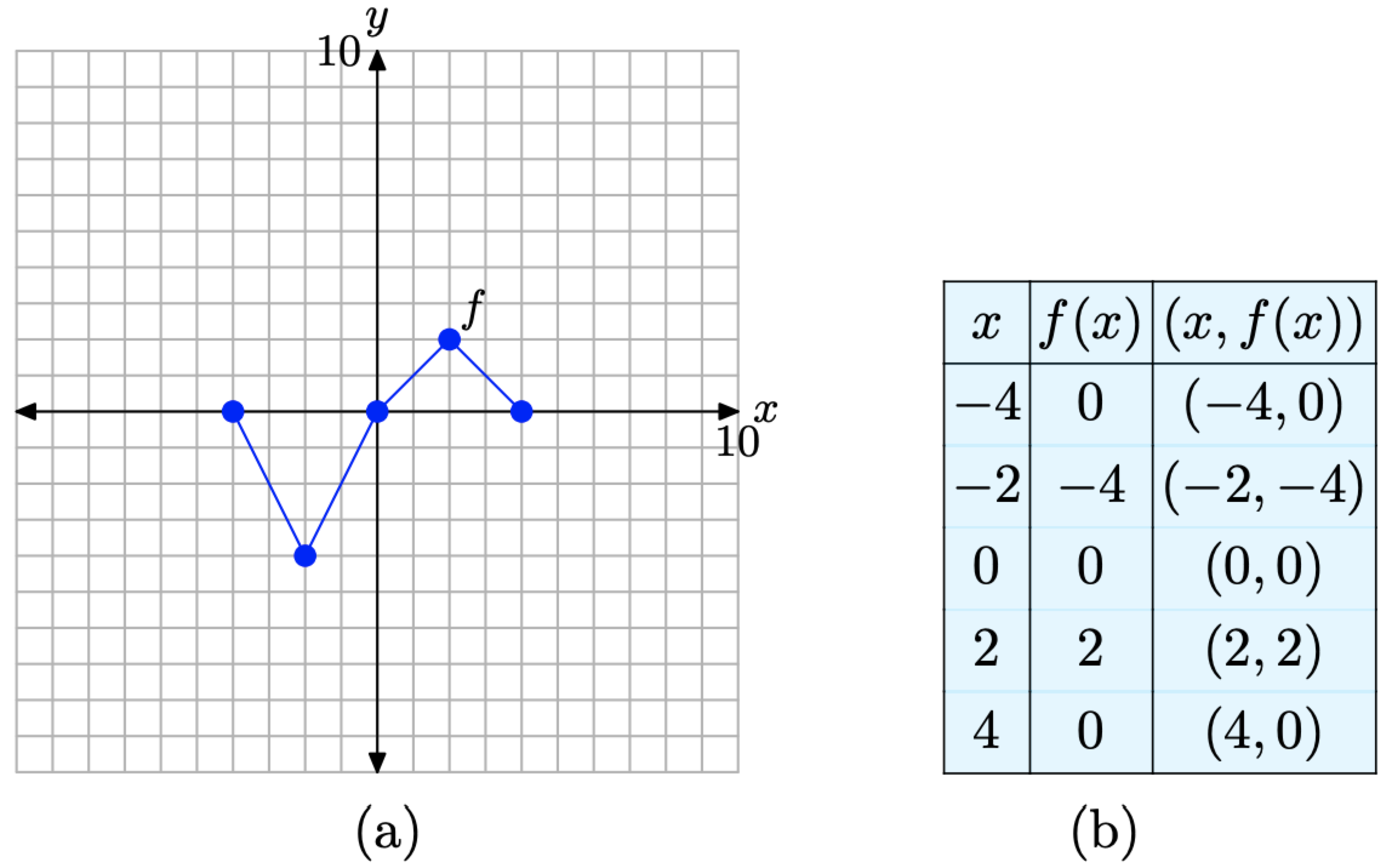
Малюнок\(\PageIndex{10}\). Вихідний графік f і таблиця ключових точок на графіку f

Приклад\(\PageIndex{5}\)

Якщо y = f (x) має графік, показаний на малюнку\(\PageIndex{10}\) (a), намалюйте графік y = f (x + 1).

Рішення

У попередньому розділі ми намалювали графік y = f (x) +1. Зверніть увагу, що в y = f (x) +1 число 1 знаходиться поза функцією. Результатом став графік, який був зміщений на 1 одиницю вгору в напрямку y.

У цьому випадку y = f (x + 1) і 1 знаходиться всередині позначення функції, що призводить до інтуїції того, що переклад може бути в горизонтальному напрямку (x-direction). Але як?

Знову встановимо таблицю точок, які задовольняють рівнянню y = f (x + 1), потім розставимо їх. Оскільки ця функція вимагає спочатку додати 1 до кожного значення x перед тим, як вставляти його у функцію, ми виберемо значення x відповідним чином, а саме x = −5, −3, −1, 1 та 3. Через мить буде зрозуміло, чому ми вибрали саме ці значення х, можливо, ви вже бачите чому?

Потрібно обчислити функцію y = f (x + 1) на кожному з цих обраних значень x. щоб оцінити y = f (x+ 1) за першим значенням, а саме x = −5, вставляємо x = −5 і робимо розрахунок\[y=f(-5+1)=f(-4)\]

Щоб завершити обчислення, ми повинні оцінити f (−4). Однак цей результат заноситься в таблицю на малюнку\(\PageIndex{10}\) (б). Там ми знаходимо, що f (−4) = 0, і ми можемо завершити розрахунок, розпочатий вище.

\[y=f(-5+1)=f(-4)=0\]

Аналогічним чином ми можемо оцінити функцію y = f (x+1) при x = −3. По-перше, підставити x = −3 у y = f (x + 1), щоб отримати

\[y=f(-3+1)=f(-2)\]

Щоб завершити обчислення, ми повинні оцінити f (−2). Однак цей результат заноситься в таблицю на малюнку\(\PageIndex{10}\) (б). Там ми знаходимо, що f (−2) = −4, і ми можемо завершити обчислення, розпочате вище.

\[y=f(-3+1)=f(-2)=-4\]

На цьому етапі ви можете побачити, чому ми вибрали значення x: −5, −3, −1, 1 і 3. Це точно на одиницю менше, ніж значення x в таблиці вихідних значень для функції y = f (x) на малюнку\(\PageIndex{10}\) (b). Коли значення −5, −3, −1, 1 і 3 підставляються у функцію y = f (x + 1), ми спочатку додаємо 1 до кожного значення, перш ніж шукати значення функції в таблиці на рисунку\(\PageIndex{10}\) (b). Це додавання 1 призводить до значень −4, −2, 0, 2 та 4, які є саме значеннями, доступними у таблиці на рисунку\(\PageIndex{10}\) (b).

Продовжуючи таким чином, ми оцінюємо функцію y = f (x + 1) за рештою значень x, а саме −1, 1 і 3.

\[\begin{aligned} y &=f(-1+1)=f(0)=0 \\ y &=f(1+1)=f(2)=2 \\ y &=f(3+1)=f(4)=0 \end{aligned}\]

Ми збираємо ці результати в таблиці на малюнку\(\PageIndex{11}\) (b) і будуємо їх на малюнку\(\PageIndex{11}\) (а).

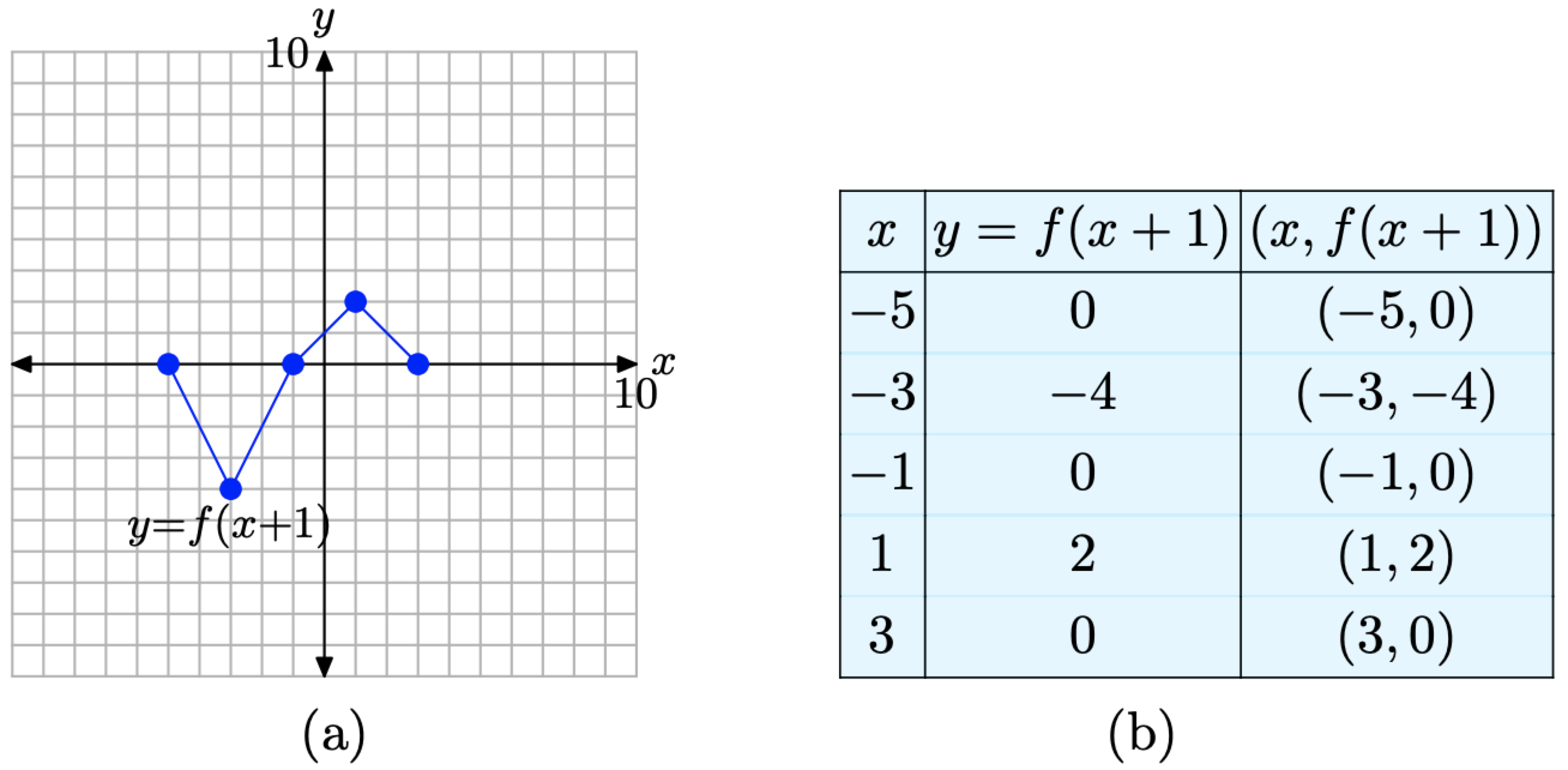
Малюнок\(\PageIndex{11}\). Графік y = f (x + 1) і таблиця ключових точок на графіку

Коли ви порівнюєте точки на графіку y = f (x+1) в таблиці на малюнку\(\PageIndex{11}\) (b) з початковими точками на графіку y = f (x) в таблиці на малюнку\(\PageIndex{10}\) (b), зверніть увагу, що значення y ідентичні, але значення x в таблиці на малюнку\(\PageIndex{11}\) (b) все на 1 одиницю менше відповідні значення x в таблиці на малюнку\(\PageIndex{10}\) (b). Не дивно, що графік y = f (x + 1) на малюнку\(\PageIndex{11}\) (a) зміщений на 1 одиницю вліво від вихідного графіка y = f (x) на малюнку\(\PageIndex{10}\) (a).

Зверніть увагу, що це дещо контрінтуїтивно, тому що ми, здавалося б, додаємо 1 до кожного значення x у = f (x + 1). Чому графік не рухається на одну одиницю вправо? Ну а ретельне порівняння x-значень в таблицях на малюнках\(\PageIndex{10}\) (b) і\(\PageIndex{11}\) (b) виявляє відповідь. Для того, щоб використовувати дані в таблиці на малюнку\(\PageIndex{10}\) (b), ми повинні спочатку відняти 1 з кожного значення x, щоб отримати значення x в таблиці на малюнку\(\PageIndex{11}\) (b). Ось чому графік y = f (x + 1) переміщує 1 одиницю вліво замість 1 одиниці вправо.

Ви також можете згадати, що функція y = f (2x) стискається множником 2, що також протилежно тому, що інтуїція може диктувати. Аналогічно функція y = f ((1/2) x) розтягується в 2 рази, що теж йде врозріз з інтуїцією. Маючи на увазі ці думки, не дивно, що y = f (x+ 1) зміщує одну одиницю вліво. Все-таки порівняння значень x в таблицях на малюнках\(\PageIndex{10}\) (b) і\(\PageIndex{11}\) (b) дають незаперечні докази того, що зсув становить 1 одиницю вліво.

Давайте розглянемо інший приклад.

Приклад\(\PageIndex{6}\)

Якщо y = f (x) має графік, показаний на малюнку\(\PageIndex{10}\) (a), намалюйте графік y = f (x − 2).

Рішення

Знову створимо таблицю точок, які задовольняють рівнянню y = f (x − 2), а потім побудуємо їх. Оскільки ця функція вимагає спочатку відняти 2 від кожного значення x перед тим, як вставляти його у функцію, ми виберемо значення x: −2, 0, 2, 4 та 6. Нам потрібно обчислити функцію y = f (x − 2) при кожному з цих значень x.

Щоб оцінити y = f (x − 2) за першим значенням, а саме x = −2, вставте x = −2 у функцію y = f (x − 2), щоб отримати\[y=f(-2-2)=f(-4)\]

У таблиці на малюнку\(\PageIndex{10}\) (b) ми знаходимо, що f (−4) = 0, що дозволяє завершити обчислення вище.

\[y=f(-2-2)=f(-4)=0\]

Аналогічним чином ми оцінюємо y = f (x − 2) при x = 0 для отримання

\[y=f(0-2)=f(-2)\]

У таблиці на малюнку\(\PageIndex{10}\) (b) ми знаходимо, що f (−2) = −4, що дозволяє завершити обчислення вище.

\[y=f(0-2)=f(-2)=-4\]

Сподіваємось, ви зрозумієте, чому ми обрали значення x: −2, 0, 2, 4 та 6. Ці значення на 2 більше, ніж значення x в таблиці вихідних значень для функції y = f (x) на малюнку\(\PageIndex{10}\) (b). Коли значення −2, 0, 2, 4 і 6 підставляються у функцію y = f (x − 2), ми спочатку віднімаємо 2 з кожного значення, перш ніж шукати значення функції в таблиці на рисунку\(\PageIndex{10}\) (b). Це віднімання 2 призводить до −4, −2, 0, 2 та 4, саме до значень, доступних у таблиці на рис.\(\PageIndex{10}\) (b).

Продовжуючи таким чином, ми оцінюємо y = f (x − 2) за рештою значень x, а саме x = 2, 4 і 6.

\[\begin{array}{l}{y=f(2-2)=f(0)=0} \\ {y=f(4-2)=f(2)=2} \\ {y=f(6-2)=f(4)=0}\end{array}\]

Ми збираємо ці результати в таблиці на малюнку\(\PageIndex{12}\) (b) і будуємо їх на малюнку\(\PageIndex{12}\) (а).

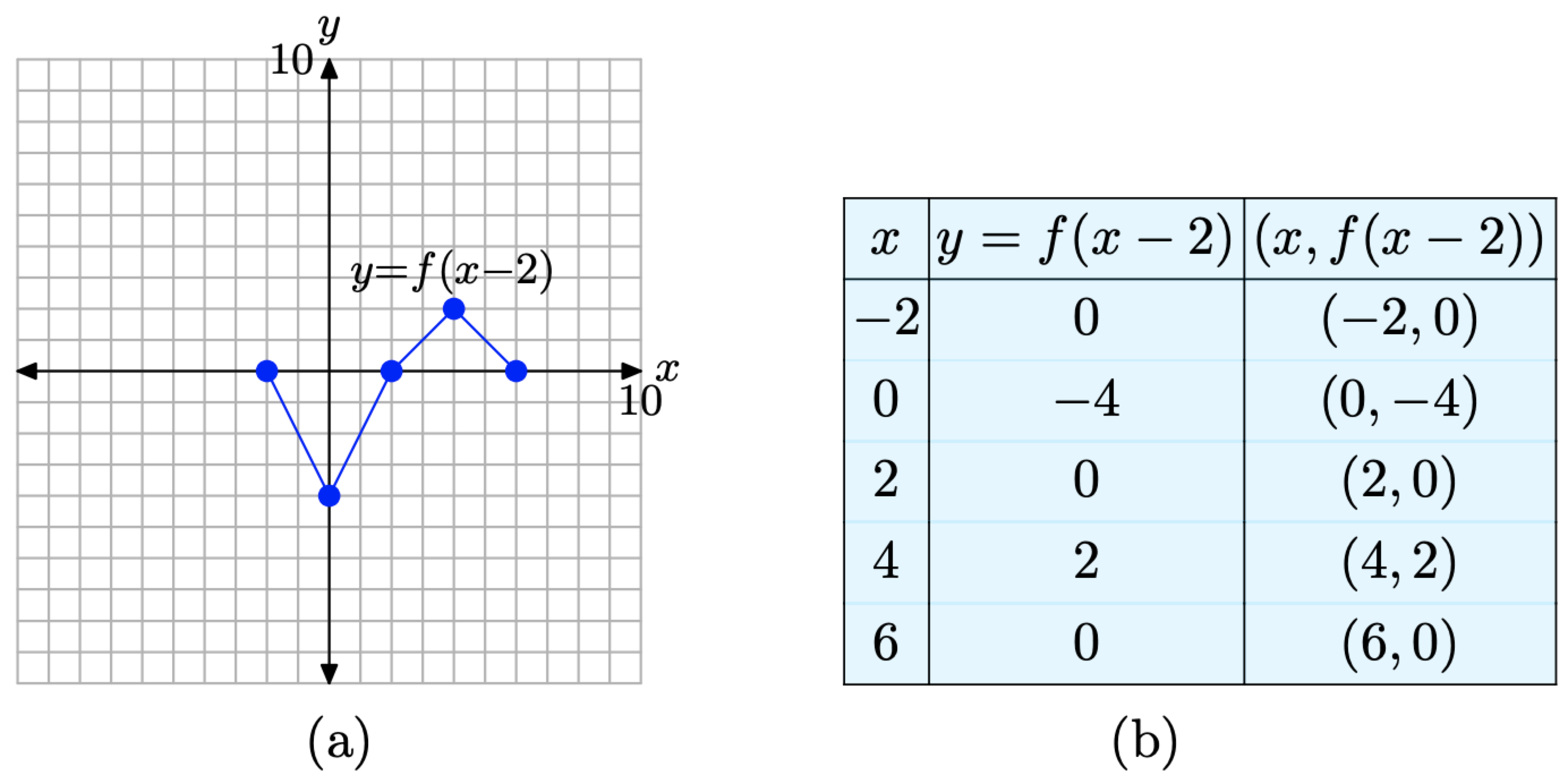
Малюнок\(\PageIndex{12}\). Графік y = f (x − 2) та таблиця ключових точок на графіку.

Коли ви порівнюєте точки на графіку y = f (x−2) в таблиці на малюнку\(\PageIndex{12}\) (b) з початковими точками на графіку y = f (x) в таблиці на малюнку\(\PageIndex{10}\) (b), зверніть увагу, що значення y ідентичні, але значення x в таблиці на малюнку\(\PageIndex{12}\) (b) все на 2 більше відповідних x-значення в таблиці на малюнку\(\PageIndex{10}\) (b). Не дивно, що графік y = f (x − 2) на малюнку\(\PageIndex{12}\) (a) зміщений на 2 одиниці праворуч від початкового графіка y = f (x) на малюнку\(\PageIndex{10}\) (a).

Знову ж таки, це працює неінтуїтивно (чому графік y = f (x − 2) не зміщує 2 одиниці вліво?) , але порівняння значень x в таблицях на малюнках\(\PageIndex{10}\) (b) і\(\PageIndex{12}\) (b) явно вказує на зсув вправо.

Давайте підсумуємо те, що ми дізналися про горизонтальні переклади.

Візуальний підсумок - Горизонтальні переклади (зрушення)

Розглянемо зображення на малюнку\(\PageIndex{13}\).

• На малюнку\(\PageIndex{13}\) (a) ми бачимо на фото графік вихідної функції y = f (x).
• На малюнку\(\PageIndex{13}\) (b) зверніть увагу, що кожна точка на графіку y = f (x + 1) має значення x, яке на 1 одиницю менше значення x відповідної точки на графіку y = f (x) на малюнку\(\PageIndex{13}\) (а).
• На малюнку\(\PageIndex{13}\) (c) зверніть увагу, що кожна точка на графіку y = f (x − 2) має значення x, яке на 2 одиниці перевищує значення x відповідної точки на графіку y = f (x) на малюнку\(\PageIndex{13}\) (а).
• Зауважте, що значення y кожної трансформованої точки залишається незмінним.

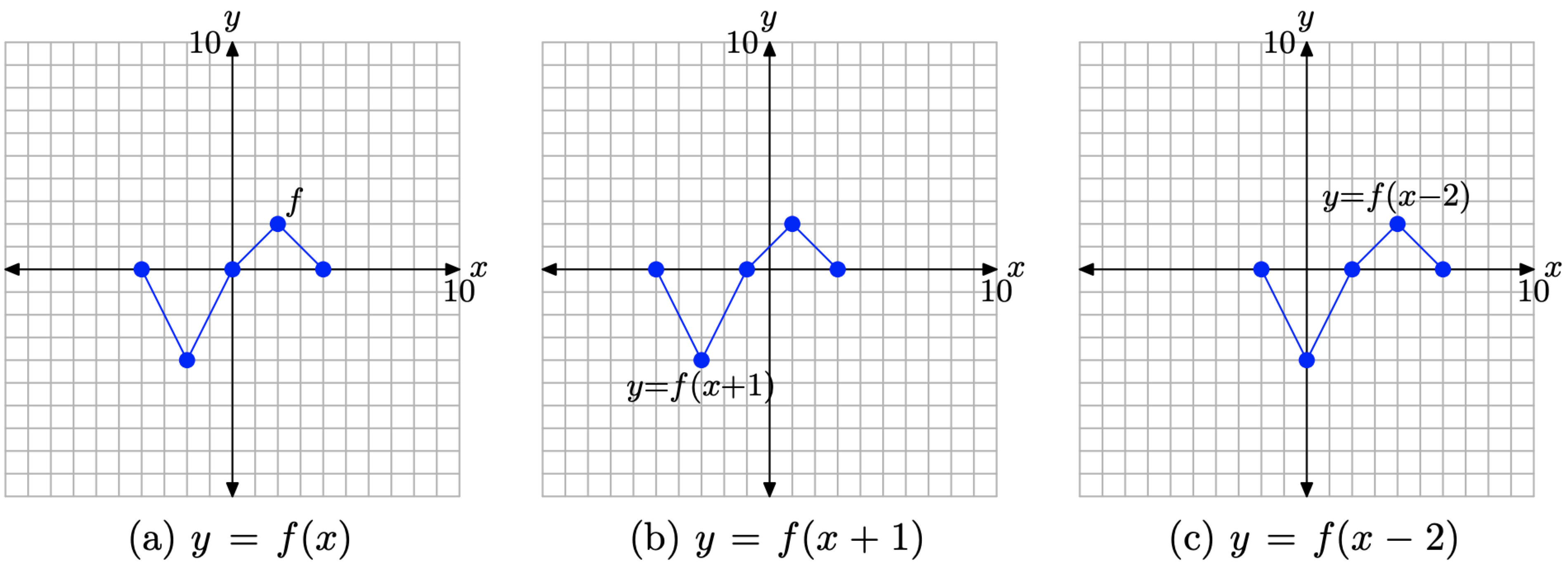
Малюнок\(\PageIndex{13}\). Графік y = f (x + 1) формується зміщенням (по горизонталі) графіка y = f (x) на одну одиницю вліво. Графік y = f (x − 2) формується зміщенням (горизонтально) графіка y = f (x) на дві одиниці вправо.

Візуальне резюме на малюнку\(\PageIndex{13}\) робить ескіз графіків y = f (x + 1) та y = f (x − 2) легким завданням.

• З огляду на графік y = f (x), щоб намалювати графік y = f (x + 1), просто візьміть кожну точку на графіку y = f (x) і змістіть її на 1 одиницю вліво, зберігаючи однакове значення y.
• З огляду на графік y = f (x), щоб намалювати графік y = f (x − 2), просто візьміть кожну точку на графіку y = f (x) і зрушіть її на 2 одиниці вправо, зберігаючи однакове значення y.

Загалом, можна констатувати наступне.

Резюме

Припустимо, що нам дано графік y = f (x) і припустимо, що c - будь-яке додатне дійсне число.

• Графік y = f (x+c) зміщений c одиницями вліво від графа y = f (x).
• Графік y = f (x−c) зміщений на c одиниць праворуч від графа y = f (x).

Коли ми розглядали вертикальні переклади в попередньому розділі, переклад був описаний спочатку уявляючи графік на аркуші прозорого пластику, потім ковзаючи прозорість (не обертаючи її) по системі координат на аркуші графічного паперу. Горизонтальні переклади можна розглядати так само, як ковзання графіка на прозорість c одиниць вліво або c одиниць вправо.

Додаткова практика

У цьому розділі давайте візьмемо поняття з Візуальних резюме і поставимо їх для роботи над деякими остаточними прикладами.

Приклад\(\PageIndex{7}\)

Розглянемо графік f на малюнку\(\PageIndex{14}\).

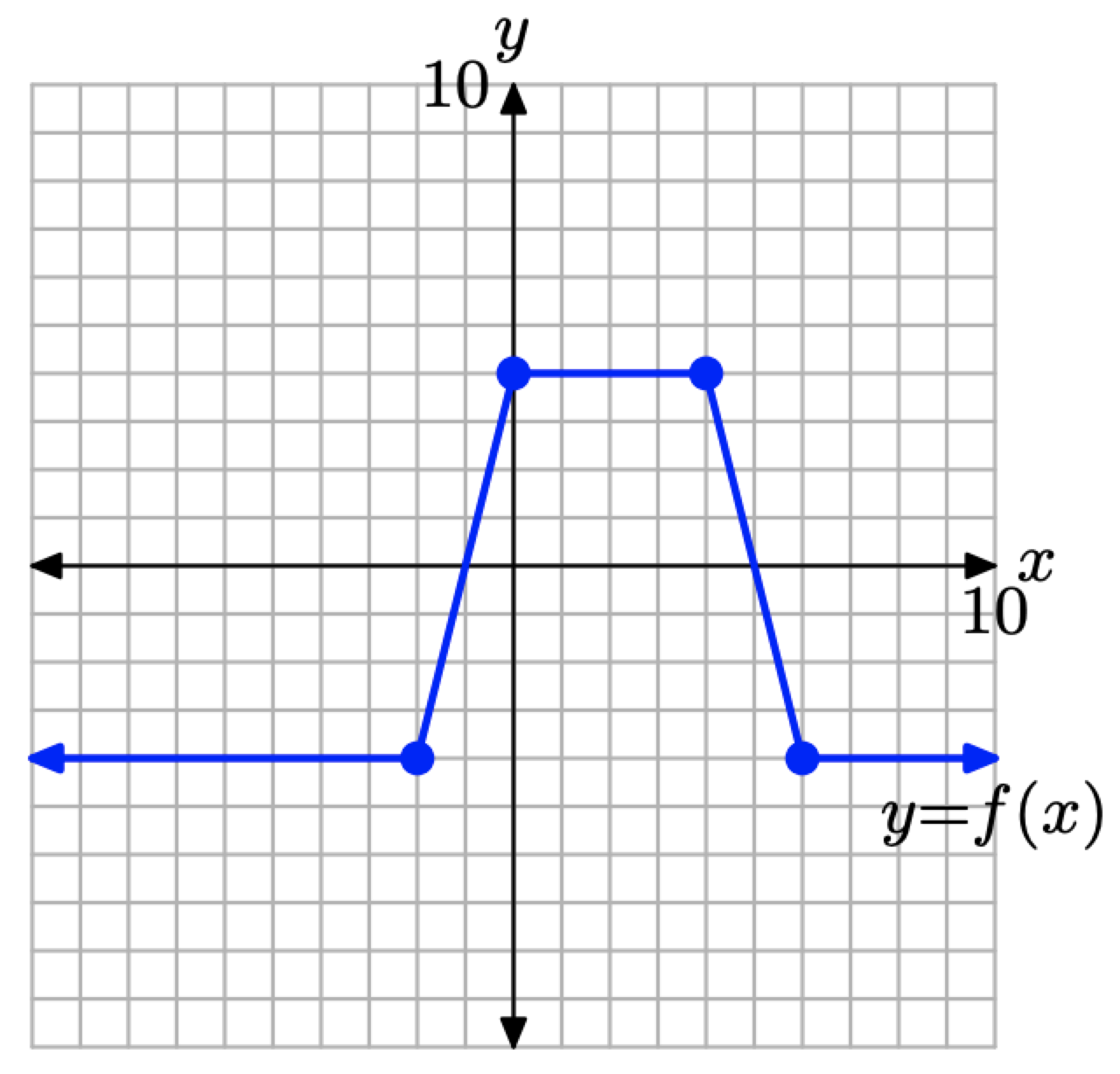
Малюнок\(\PageIndex{14}\). Графік y = f (x) наприклад\(\PageIndex{7}\).

Використовуйте концепції з Візуальних резюме (масштабування, відображення та переклад), щоб намалювати графіки y = f (2x), y = f (−x) та y = f (x + 2) без створення та звернення до таблиць.

Рішення

Щоб намалювати графік y = f (2x), просто візьміть кожну точку на графіку y = f (x) на малюнку\(\PageIndex{15}\) (a) і розділіть її значення x на 2, зберігаючи однакове значення y. Результат показаний на малюнку\(\PageIndex{15}\) (б).

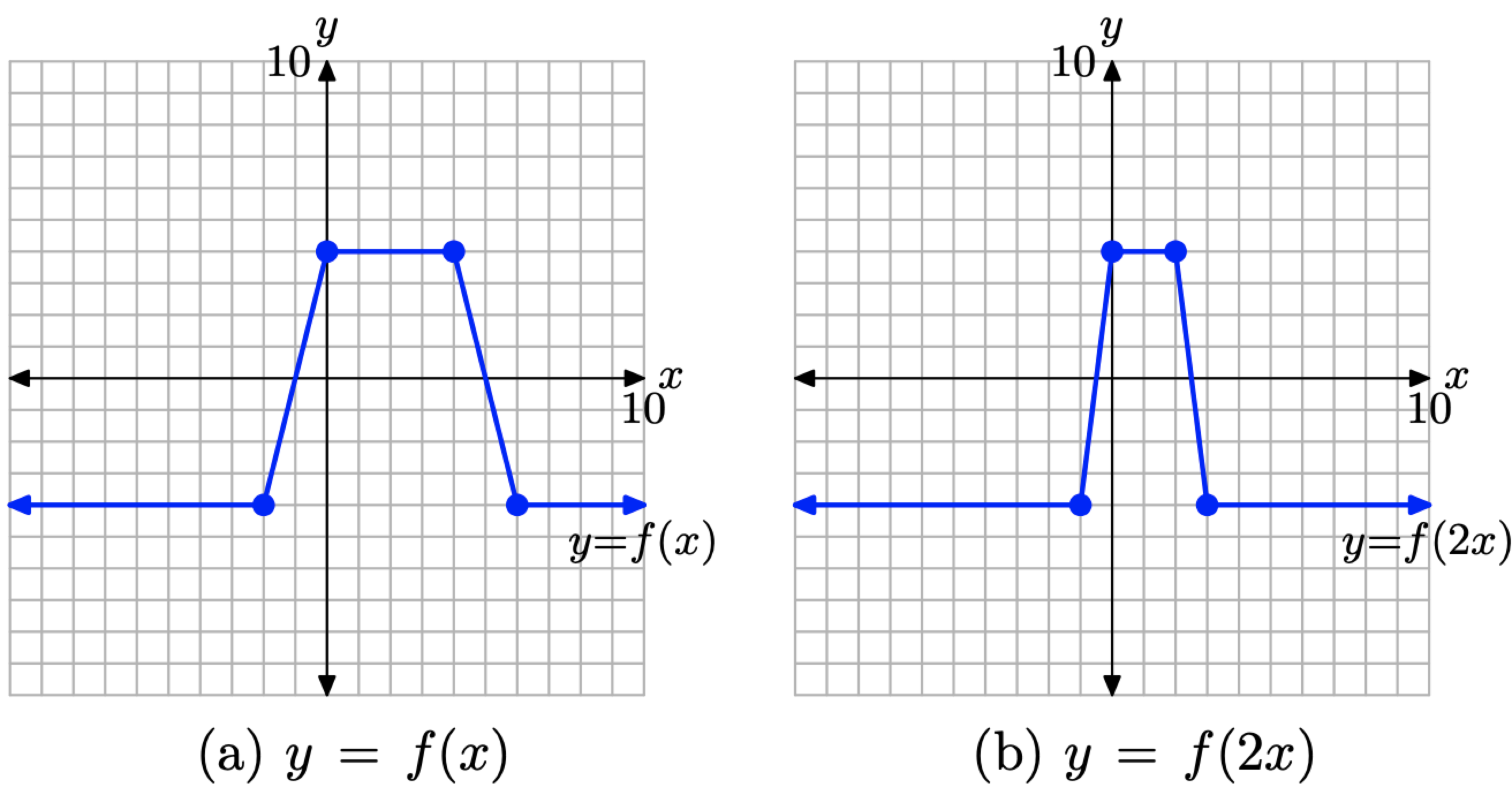
Малюнок\(\PageIndex{15}\). Стисніть графік y = f (x) множником 2, щоб отримати графік y = f (2x).

Щоб намалювати графік y = f (−x), просто візьміть кожну точку на графіку y = f (x) на малюнку\(\PageIndex{16}\) (a) і змініть її значення x, зберігаючи однакове значення y. Результат показаний на малюнку\(\PageIndex{16}\) (б).

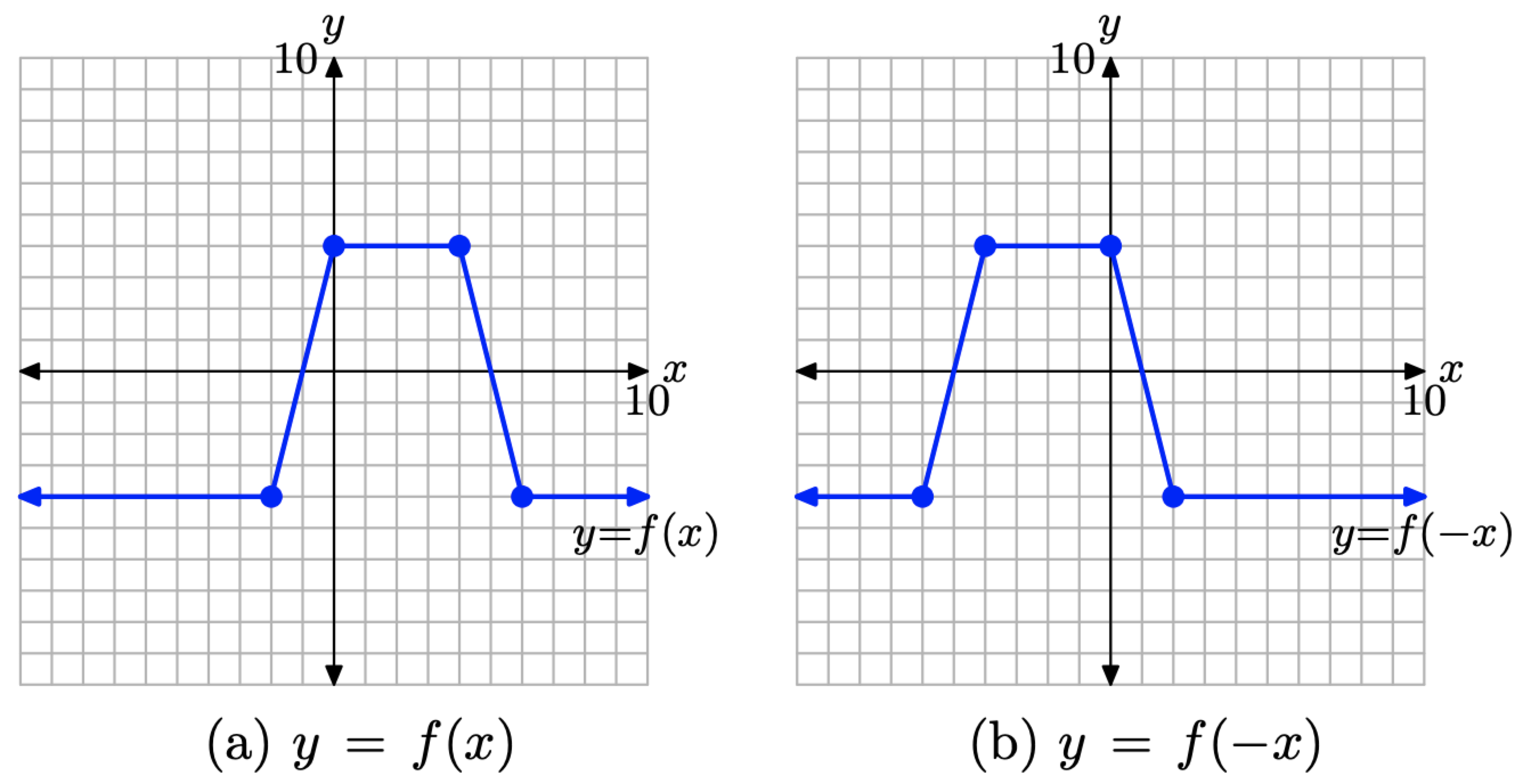
Малюнок\(\PageIndex{16}\). Відобразіть графік y = f (x) по осі y, щоб отримати графік y = f (−x).

Щоб намалювати графік y = f (x + 2), просто візьміть кожну точку на графіку y = f (x) на малюнку\(\PageIndex{17}\) (a) і відніміть 2 від його значення x, зберігаючи однакове значення y. Результат показаний на малюнку\(\PageIndex{17}\) (б).

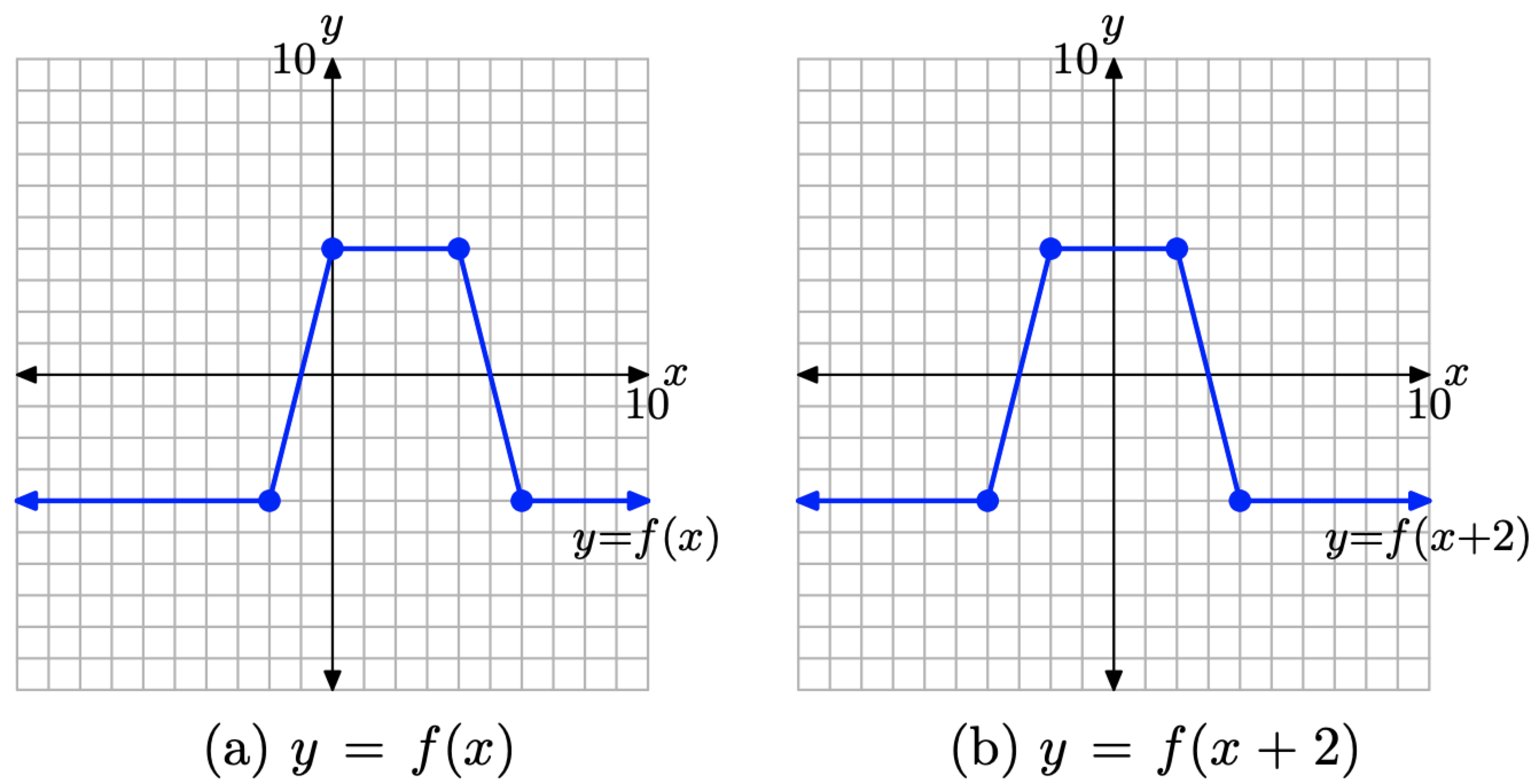
Малюнок\(\PageIndex{17}\). Зсуньте графік y = f (x) вліво на 2 одиниці, щоб отримати графік y = f (x + 2).

Резюме

У цьому розділі ми бачили, як кілька перетворень значно покращують наші можливості графіків. Ми закінчуємо цей розділ перерахуванням перетворень, представлених у цьому розділі, та їх впливу на графік функції.

Вертикальні перетворення

Припустимо, нам дано графік y = f (x).

• Якщо a > 1, графік y = f (ax) стискається горизонтально (до осі y), як позитивно, так і негативно, в рази a.
• Якщо 0 < a < 1, графік y = f (ax) розтягується горизонтально (від осі y), як позитивно, так і негативно, в рази 1/a.
• Графік y = f (−x) є відображенням графіка y = f (x) по осі y.
• Якщо c > 0, то графік y = f (x + c) зміщується c одиницями вліво від графа y = f (x).
• Якщо c > 0, то графік y = f (x − c) зміщується c одиницями праворуч від графа y = f (x).