2.3: Інтерпретація графа функції

У попередньому розділі ми почали з функції, а потім намалювали графік даної функції. У цьому розділі ми почнемо з графіка функції, а потім зробимо ряд інтерпретацій на основі даного графіка: оцінки функцій, область і діапазон функції, а також розв'язування рівнянь і нерівностей.

Тест вертикальної лінії

Розглянемо графік співвідношення R, показаний на малюнку$\PageIndex{1}$ (а). Нагадаємо, що раніше ми визначали відношення як набір впорядкованих пар. Звичайно, графік, показаний на малюнку$\PageIndex{1}$ (а), являє собою набір впорядкованих пар. Дійсно, це нескінченний набір впорядкованих пар, настільки багато, що графік є суцільною кривою.

На малюнку$\PageIndex{1}$ (b) зверніть увагу, що ми можемо намалювати вертикальну лінію, яка розрізає графік більше одного разу. На малюнку$\PageIndex{1}$ (b) ми намалювали вертикальну лінію, яка розрізає графік у двох місцях, один раз$\left(x, y_{1}\right)$, потім знову в$\left(x, y_{2}\right)$, як показано на малюнку$\PageIndex{1}$ (c). Це означає, що об'єкт домену x поєднується з двома різними об'єктами діапазону, а саме$y_{1}$ і$y_{2}$, тому відношення R не є функцією.

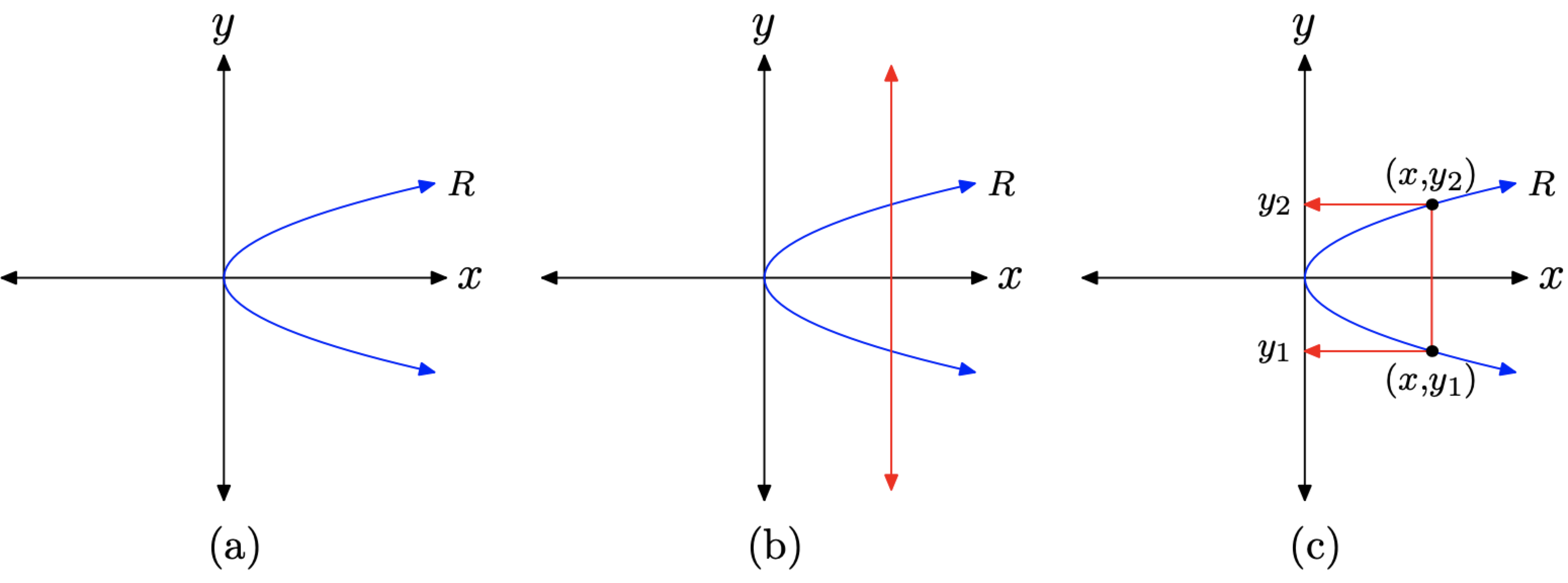
Малюнок$\PageIndex{1}$. Пояснення тесту вертикальної лінії для функцій.

Згадаймо визначення функції.

Визначення

Відношення - це функція тоді і лише тоді, коли кожен об'єкт у своїй області сполучається з одним і тільки одним об'єктом у своєму діапазоні.

Розглянемо діаграму відображення на малюнку$\PageIndex{2}$, де ми використовували стрілки для позначення впорядкованих пар$\left(x, y_{1}\right)$ і на$\left(x, y_{2}\right)$ малюнку$\PageIndex{1}$ (c). Зверніть увагу, що x, об'єкт у області R, зіставляється з двома об'єктами в діапазоні R, а саме$y_{1}$ і$y_{2}$. Отже, відношення R не є функцією.

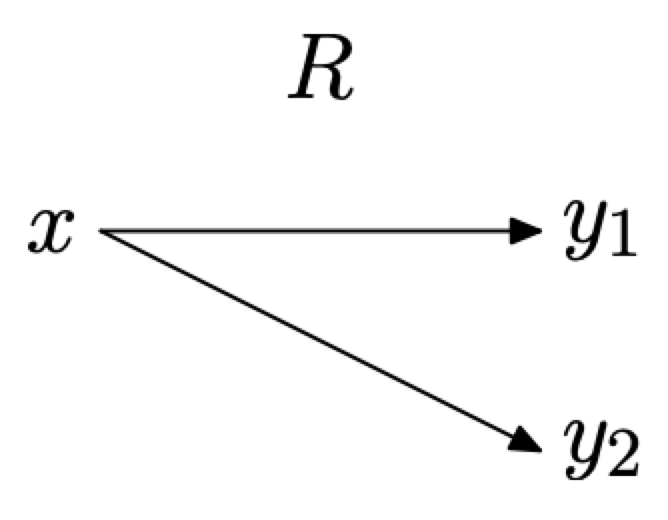
Малюнок$\PageIndex{2}$. Діаграма відображення, що представляє точки$\left(x, y_{1}\right)$ і$\left(x, y_{2}\right)$ на малюнку$\PageIndex{1}$ (c).

Це обговорення призводить до наступного результату, який називається тестом вертикальної лінії для функцій.

Тест вертикальної лінії

Якщо будь-яка вертикальна лінія розрізає графік відношення більше одного разу, то відношення НЕ є функцією.

Отже, коло, зображений на малюнку$\PageIndex{3}$ (а), є відношенням, але це не графік функції. Можна вирізати графік кола не один раз вертикальною лінією, як показано на малюнку$\PageIndex{3}$ (а). З іншого боку, парабола, показана на малюнку$\PageIndex{3}$ (b), є графіком функції, оскільки жодна вертикальна лінія не розрізає графік більше одного разу.

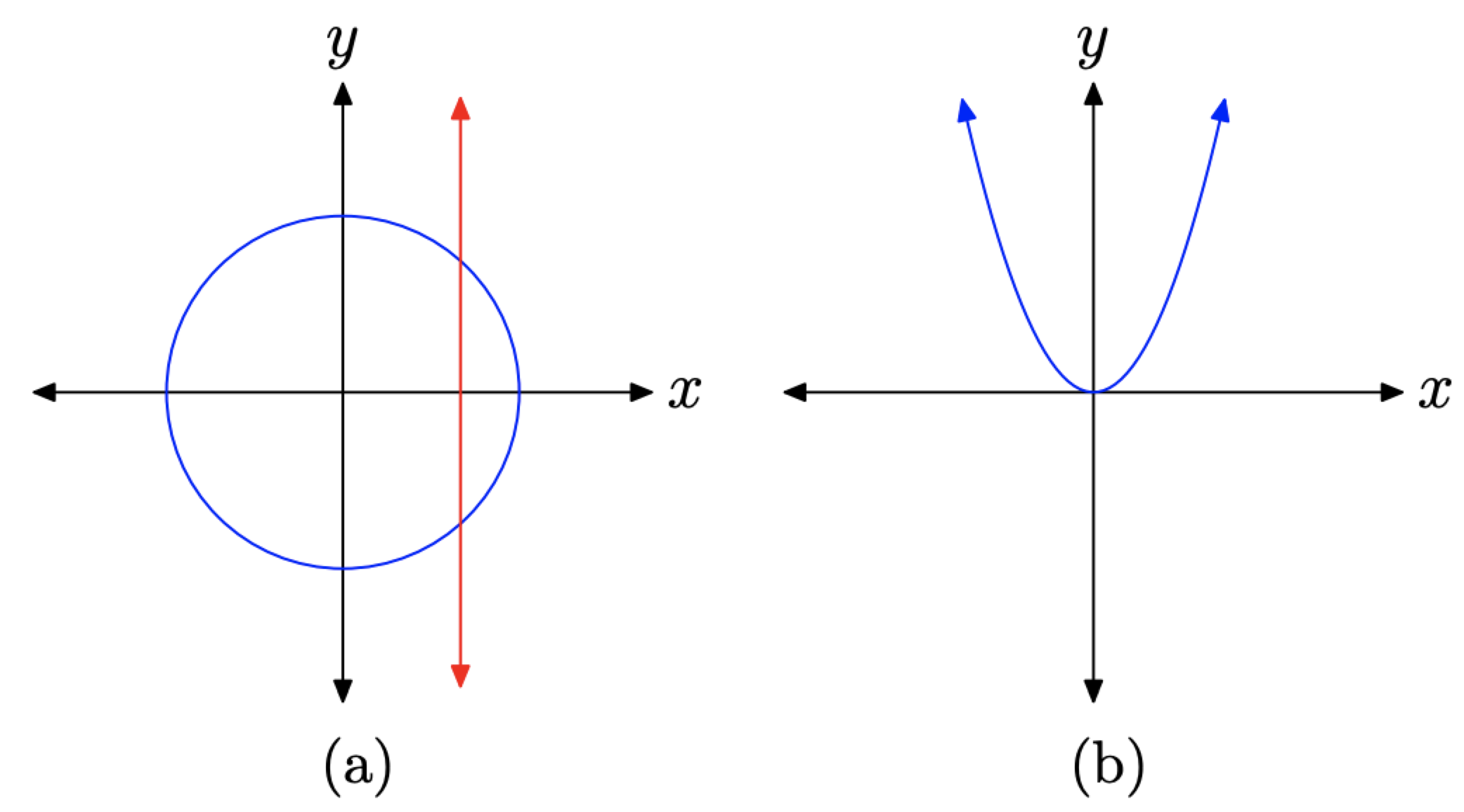
Малюнок$\PageIndex{3}$. Використовуйте тест вертикальної лінії, щоб визначити, чи є графік функції.

Читання графіка для значень функцій

Ми знаємо, що графік f, зображений на малюнку,$\PageIndex{4}$ є графіком функції. Ми знаємо це тому, що жодна вертикальна лінія не буде різати графік f більш ніж один раз.

Ми раніше визначили графік f як сукупність всіх впорядкованих пар$(x, f(x))$, так що х знаходиться в області f. отже, якщо ми виділимо точку P на графіку f, як на малюнку$\PageIndex{4}$ (a), ми позначаємо точку P (x, f (x)). Однак ми також можемо позначити цей пункт як$P(x, y)$, як показано на малюнку$\PageIndex{4}$ (b). Це призводить до нової інтерпретації f (x) як значення y точки P. Тобто f (x) - це значення y, яке парне з x.

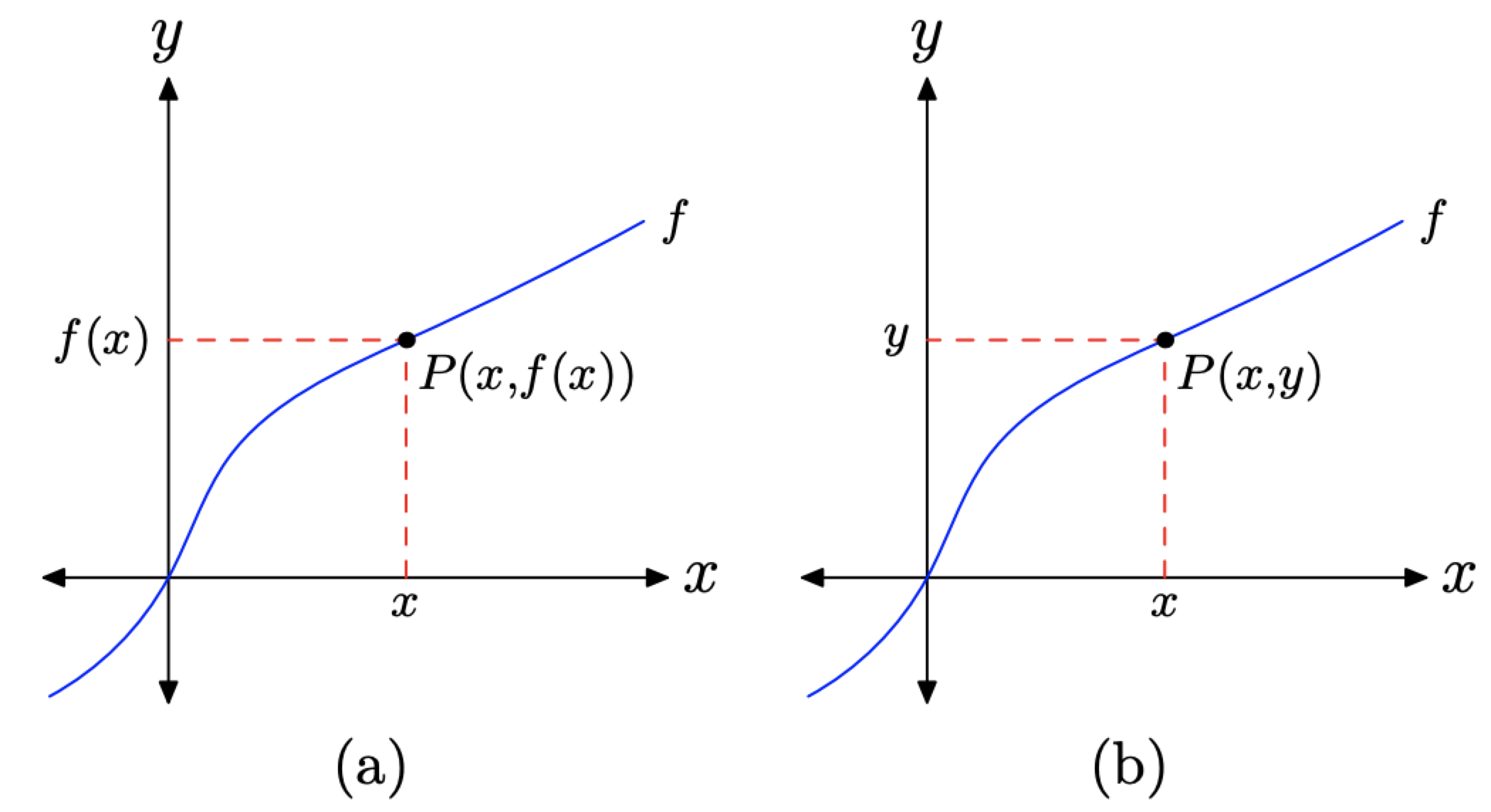
Малюнок$\PageIndex{4}$. Читання графіка функції.

Визначення

f (x) - значення y, яке поєднується з x.

Ще два зауваження по порядку. На малюнку$\PageIndex{4}$ (а) вибираємо точку Р на графіку f.

1. Щоб знайти значення x точки P, ми повинні спроектувати точку P на вісь x.
2. Щоб знайти f (x), значення y, яке поєднується з x, ми повинні спроектувати точку P на вісь y.

Давайте розглянемо приклад.

Приклад$\PageIndex{1}$

За заданим графіком f на малюнку$\PageIndex{5}$ (a) знайдіть f (4).

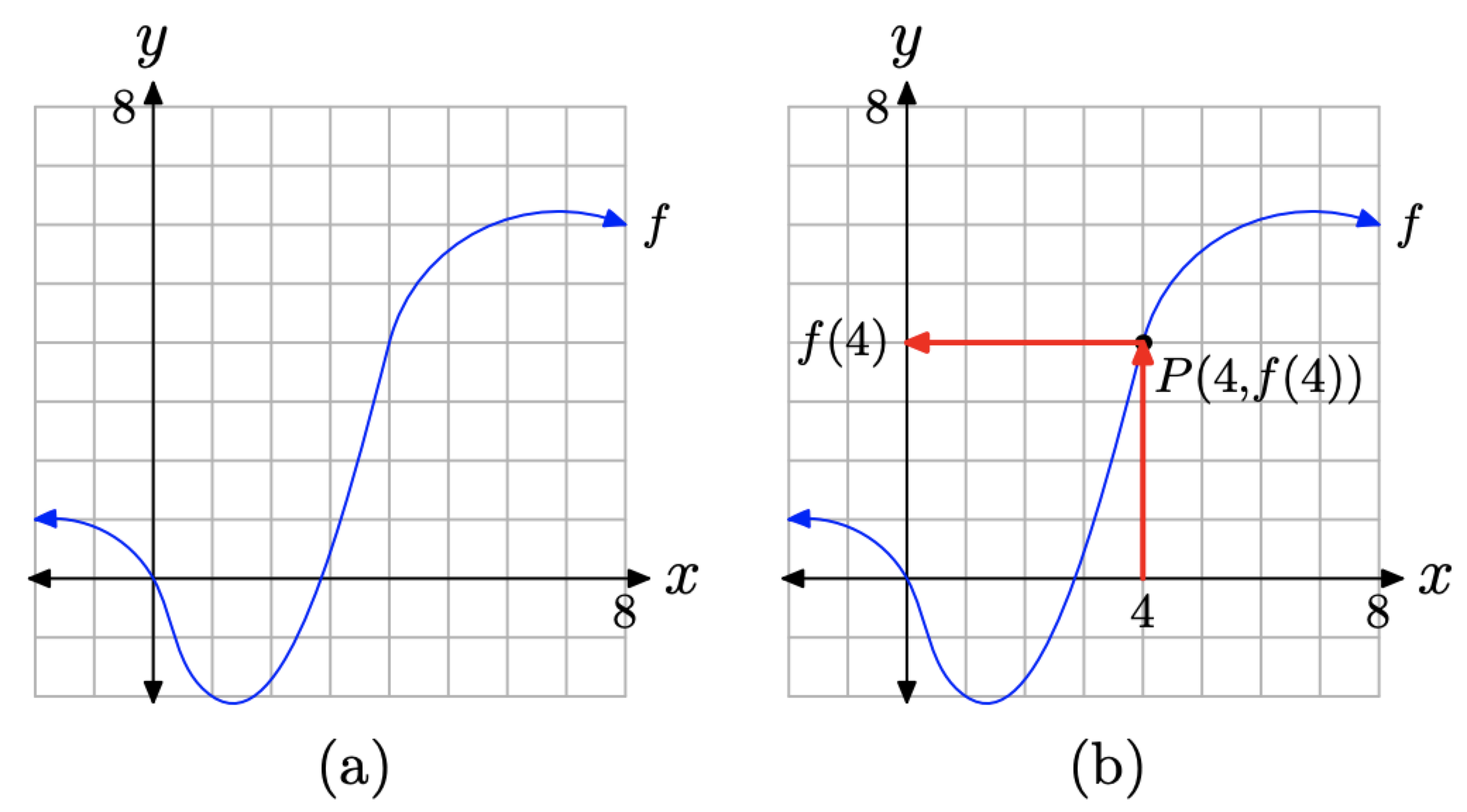
Малюнок (\ Індекс сторінки {5}\). Знаходження значення f (4).

Рішення

По-перше, зауважте, що графік f представляє функцію. Жодна вертикальна лінія не розрізає графік f більше одного разу.

Оскільки f (4) представляє значення y, яке поєднується зі значенням x 4, ми спочатку знаходимо 4 на осі x, як показано на малюнку (\ pageIndex {5}\) (b). Потім малюємо вертикальну стрілку, поки не перехопимо графік f в точці P (4, f (4)). Нарешті, ми малюємо горизонтальну стрілку з точки Р, поки не перехопимо вісь Y. Проекція точки Р на вісь y - це значення f (4).

Оскільки у нас є сітка, яка показує масштаб на кожній осі, ми можемо наблизити значення f (4). Здавалося б, що значення y точки P дорівнює приблизно 4. Таким чином,$f(4) \approx 4$.

Давайте розглянемо інший приклад.

Приклад$\PageIndex{2}$

За заданим графіком f на малюнку (\ pageIndex {6}\) (a) знайдіть f (5).

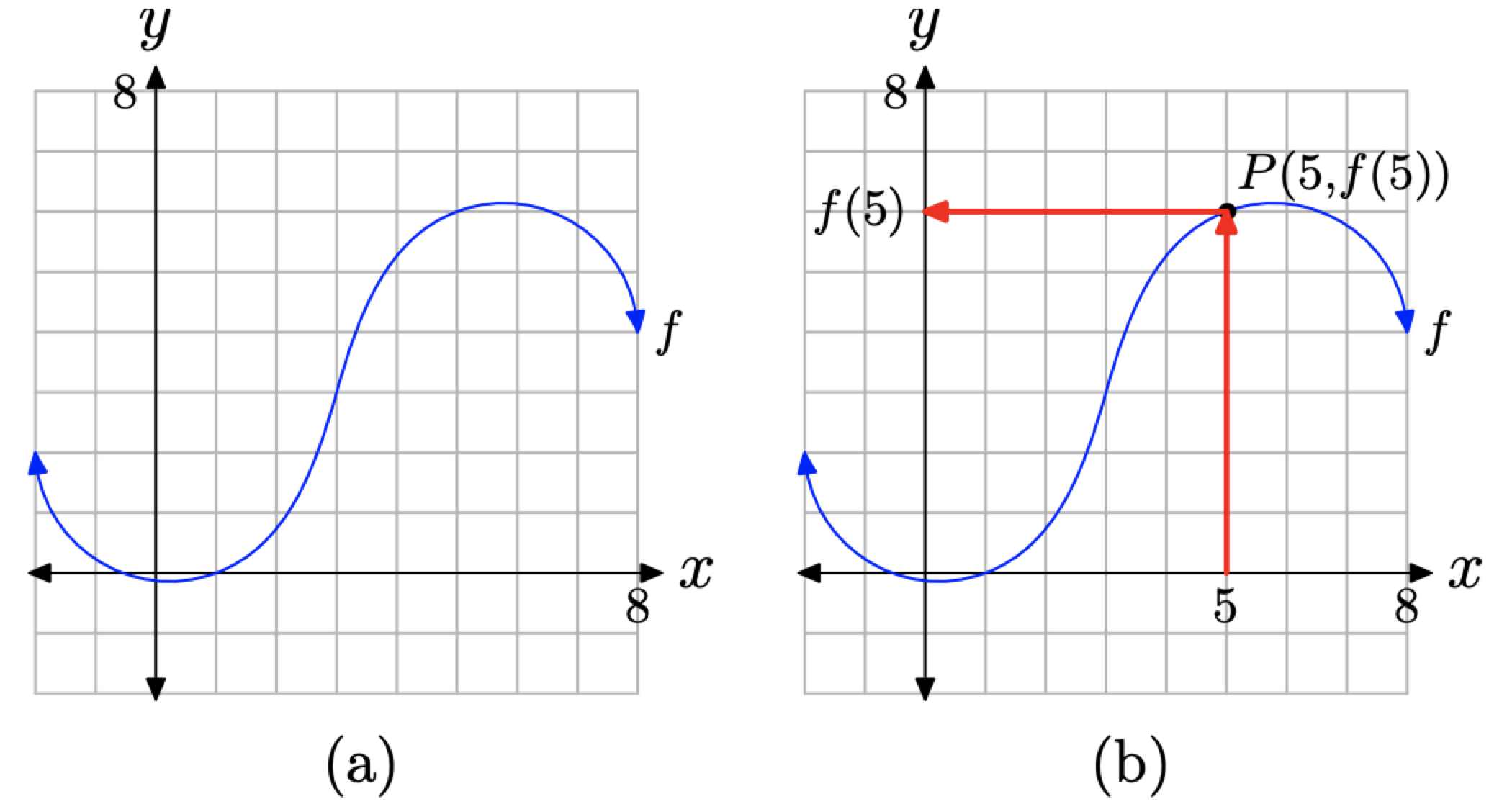
Малюнок (\ Індекс сторінки {6}\). Знаходження значення f (5).

Рішення

По-перше, зауважте, що графік f представляє функцію. Жодна вертикальна лінія не розрізає графік f більше одного разу.

Оскільки f (5) представляє значення y, яке поєднується зі значенням x 5, ми спочатку знаходимо 5 на осі x, як показано на малюнку (\ pageIndex {6}\) (b). Потім малюємо вертикальну стрілку, поки не перехопимо графік f в точці P (5, f (5)). Нарешті, ми малюємо горизонтальну стрілку з точки Р, поки не перехопимо вісь Y. Проекція точки Р на вісь y - це значення f (5).

Оскільки у нас є сітка, яка показує масштаб на кожній осі, ми можемо наблизити значення f (5). Здавалося б, що значення y точки P дорівнює приблизно 6. Таким чином,$f(5) \approx 6$.

Давайте повернемо тлумачення в іншому прикладі.

Приклад$\PageIndex{3}$

Враховуючи графік f на малюнку (\ pageIndex {7}\) (a), для якого значення x робить f (x) = −4?

Рішення

Знову ж таки, графік на рисунку (\ pageIndex {7}\) проходить тест вертикальної лінії і представляє графік функції.

Цього разу в$f(x) = −4$ рівнянні нам дано значення y, рівне −4. Отже, ми повинні змінити процес, який використовується в Example$\PageIndex{1}$ і Example$\PageIndex{2}$. Спочатку ми знаходимо значення y −4 на осі y, потім намалюємо горизонтальну стрілку, поки не перехопимо

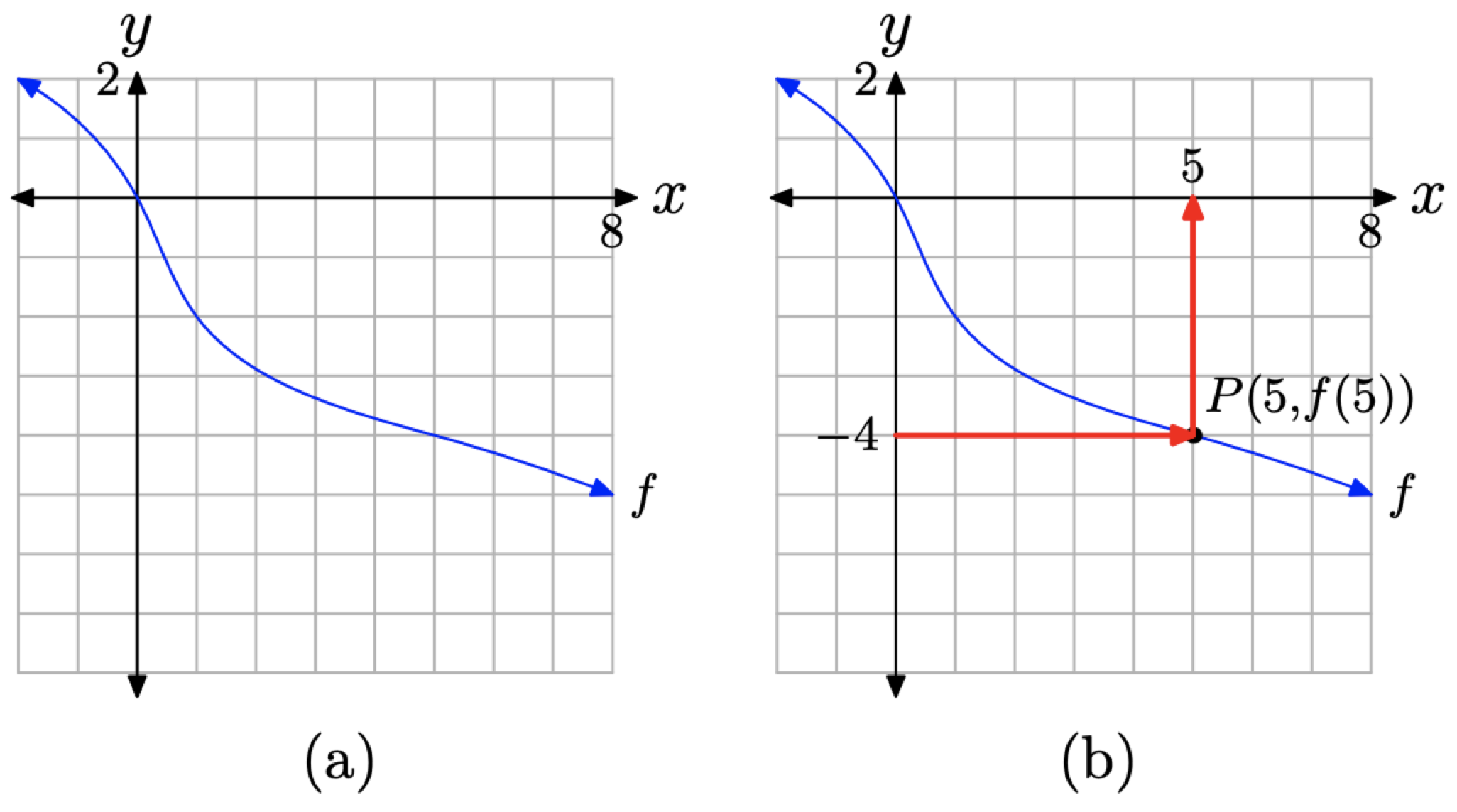
Малюнок (\ Індекс сторінки {7}\). Знайшовши х так, що$f(x) = −4$.

графік f в P, як показано на малюнку (\ pageIndex {7}\) (b). Нарешті, ми малюємо вертикальну стрілку з точки Р, поки не перехопимо вісь х. Проекція точки Р на вісь х є рішенням$f(x) = −4$.

Оскільки у нас є сітка, яка показує масштаб на кожній осі, ми можемо наблизити значення x точки P. Здається, що$x \approx 5$. Таким чином, позначаємо точку Р (5, f (5)), а$f(x) = −4$ розчин приблизно$x \approx 5$.

Це рішення можна легко перевірити, обчисливши f (5). Просто почніть з 5 на осі x, а потім поверніть порядок стрілок, показаних на малюнку (\ pageIndex {7}\) (b). Ви повинні накрутити на −4 на осі y, демонструючи це$f(5) = −4$.

Домен та діапазон функції

Ми можемо використовувати графік функції для визначення її області та діапазону. Для прикладу розглянемо графік функції, показаний на малюнку (\ pageIndex {8}\) (a).

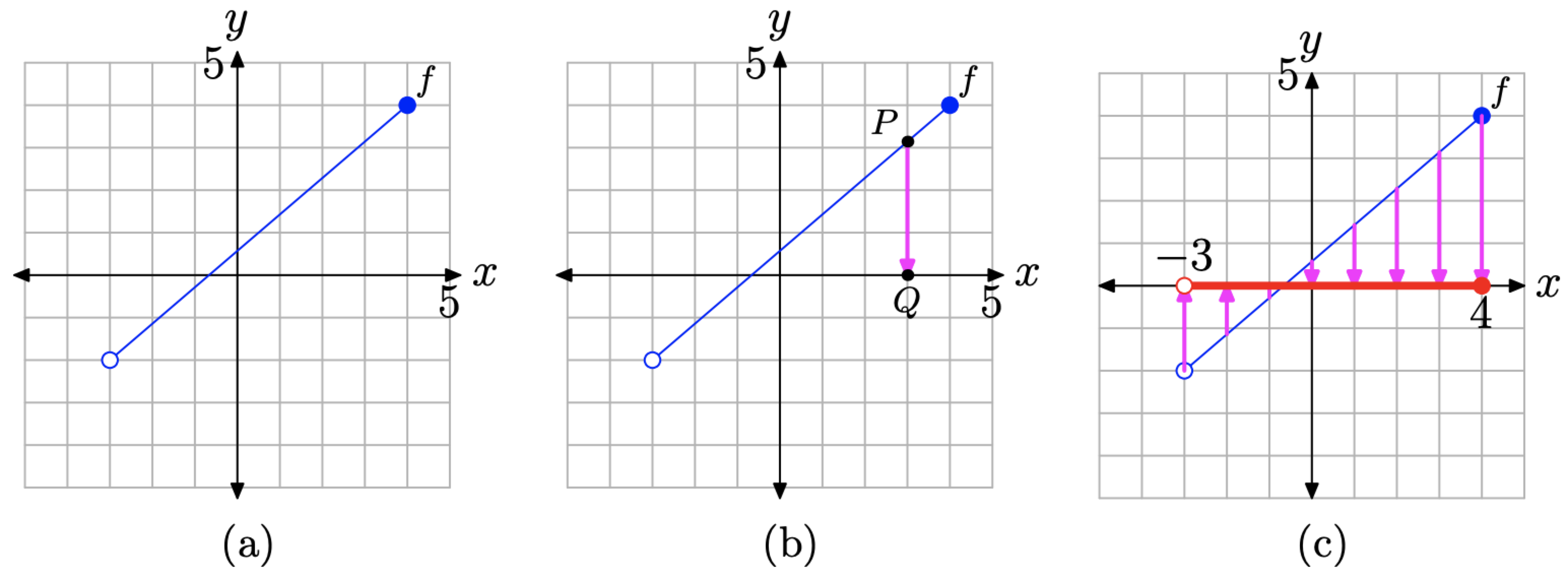
Малюнок (\ Індекс сторінки {8}\). Визначення області функції за її графіком.

Зауважте, що жодна вертикальна лінія не розрізає графік f більше одного разу, тому графік f представляє функцію.

Щоб визначити область, ми повинні зібрати значення x (перші координати) кожної точки на графіку f. На малюнку (\ pageIndex {8}\) (b) ми вибрали точку P на графіку f, яку потім проектуємо на вісь x. Зображення цієї проекції - точка Q, а значення x точки Q - елемент в області f.

Подумайте про проекцію, показану на малюнку (\ pageIndex {8}\) (b) наступним чином. Уявіть собі джерело світла над точкою P. Точка P блокує світло, а його тінь падає на вісь x у точці Q, тобто думайте про точку Q як «тінь», яку точка P створює, коли вона проектується вертикально на вісь x.

Тепер, щоб знайти область функції f, ми повинні спроектувати кожну точку на графіку f на вісь x. Ось питання: якщо ми проектуємо кожну точку на графіку f на вісь x, яка частина осі x буде «лежати в тіні», коли процес завершиться? Відповідь наведено на малюнку (\ pageIndex {8}\) (c).

На рисунку (\ pageIndex {8}\) (c) зауважте, що «тінь», створена проектуванням кожної точки на графіку f на вісь x, затінена червоним кольором (більш товста лінія, якщо ви переглядаєте це чорно-білим кольором). Ця колекція значень x є доменом функції f. Є три критичні точки, які нам потрібно зробити щодо «тіні» на осі x на малюнку (\ pageIndex {8}\) (c).

1. Всі точки, що лежать між$x = −3$ ними,$x = 4$ були затінені на осі x червоним кольором.
2. Ліва кінцева точка графа f - це відкрите коло. Це вказує на те, що в цій кінцевій точці немає точки. Отже, немає сенсу проектувати на вісь x, і це пояснює відкрите коло в лівому кінці нашої «тіні» на осі x.
3. З іншого боку, права кінцева точка графа f є заповненою кінцевою точкою. Це вказує на те, що це побудована точка і частина графіка f Отже, коли ця точка проектується на вісь x, тінь падає при x = 4. Це пояснює заповнену кінцеву точку в правому кінці нашої «тіні» на осі x.

Ми можемо описати значення x «тіні» на осі x за допомогою нотації set-builder.

$$\text { Domain of } f=\{x :-3<x \leq 4\}$$

Зауважте, що ми не включаємо −3 до цього опису, оскільки лівий кінець тіні на осі x є порожнім колом. Зауважте, що ми включаємо 4 в цей опис, оскільки правий кінець тіні на осі x - це заповнене коло.

Ми також можемо описати значення x «тіні» на осі x за допомогою інтервальних позначень.

$$\text { Domain of } f=(-3,4]$$

Ми нагадуємо нашим читачам, що дужка зліва означає, що ми не включаємо −3, тоді як дужка праворуч означає, що ми включаємо 4.

Щоб знайти діапазон функції, зобразіть ще раз графік f, показаний на малюнку$\PageIndex{9}$ (а). Продовжуйте аналогічно, тільки на цей раз проект вказує на графік f на вісь y, як показано на малюнках$\PageIndex{9}$ (b) і (c).

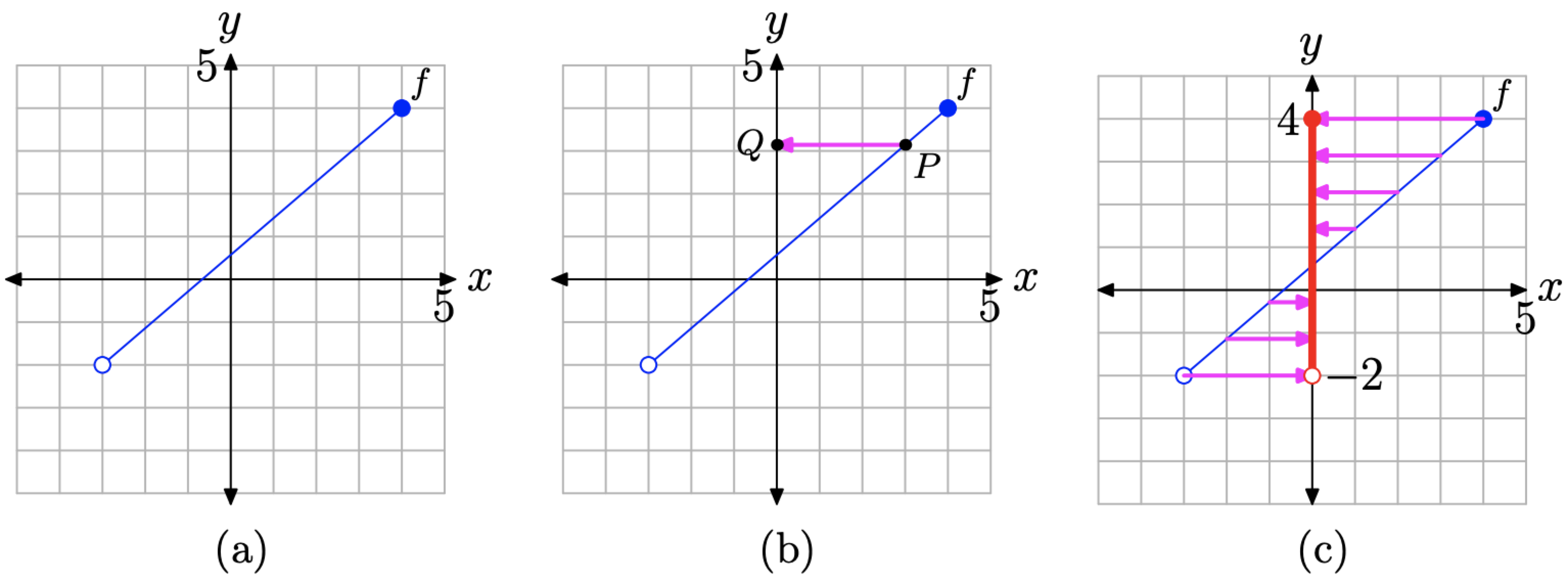
Малюнок$\PageIndex{9}$. Визначення діапазону функції за її графіком.

Зверніть увагу, яка частина осі y «лежить у тіні», коли ми спроектували всі точки на графіку f на вісь y.

1. Усі точки, що лежать між ними$y = −2$ та$y = 4$ були затінені на осі y червоним кольором (товстіший стиль лінії, якщо ви переглядаєте це чорно-білим кольором).
2. Ліва кінцева точка графіка f є порожнім колом, тому немає сенсу проектувати на вісь y. Отже,$y = −2$ на осі y немає «тіні», а точка залишається незаштрихованою (порожнє коло).
3. Права кінцева точка графа f - це заповнене коло, тому$y = 4$ на осі y є «тінь», і ця точка затінена (заповнене коло).

Тепер ми можемо легко описати діапазон як в set-builder, так і в інтервальному позначенні.

$$\text { Range of } f=(-2,4]=\{y :-2<y \leq 4\}$$

Давайте розглянемо інший приклад.

Приклад$\PageIndex{4}$

Використовуйте set-builder та інтервальні позначення для опису області та діапазону функції, представленої графіком на малюнку$\PageIndex{10}$ (a).

Малюнок$\PageIndex{10}$. Визначення домену за графом f.

Рішення

Щоб визначити область f, спроектуйте кожну точку на графіку f на вісь x. Ця проекція позначається «тінню» на осі x на малюнку$\PageIndex{10}$ (b). З приводу цієї «тіні» або проекції потрібно зробити два важливих моменти.

1. Ліва кінцева точка графіка f порожня (позначається відкритим колом), тому вона не має проекції на вісь x. На це вказує розімкнуте коло на лівому кінці (в$x = −4$) «тіні» або проекції на вісь x.

2. Стрілка на правому кінці графіка f вказує на те, що графік f триває вниз і вправо нескінченно. Отже, проекція на вісь х - це тінь, яка рухається нескінченно вправо. Це позначається стрілкою в правому кінці «тіні» або проекцією на вісь x.

Отже, область f - це сукупність значень x, представлених «тінню» або проекцією на вісь x. Зауважте, що всі значення x праворуч від них$x = −4$ затінені на осі x. Отже,

$$\text { Domain of } f=(-4, \infty)=\{x : x>-4\}$$

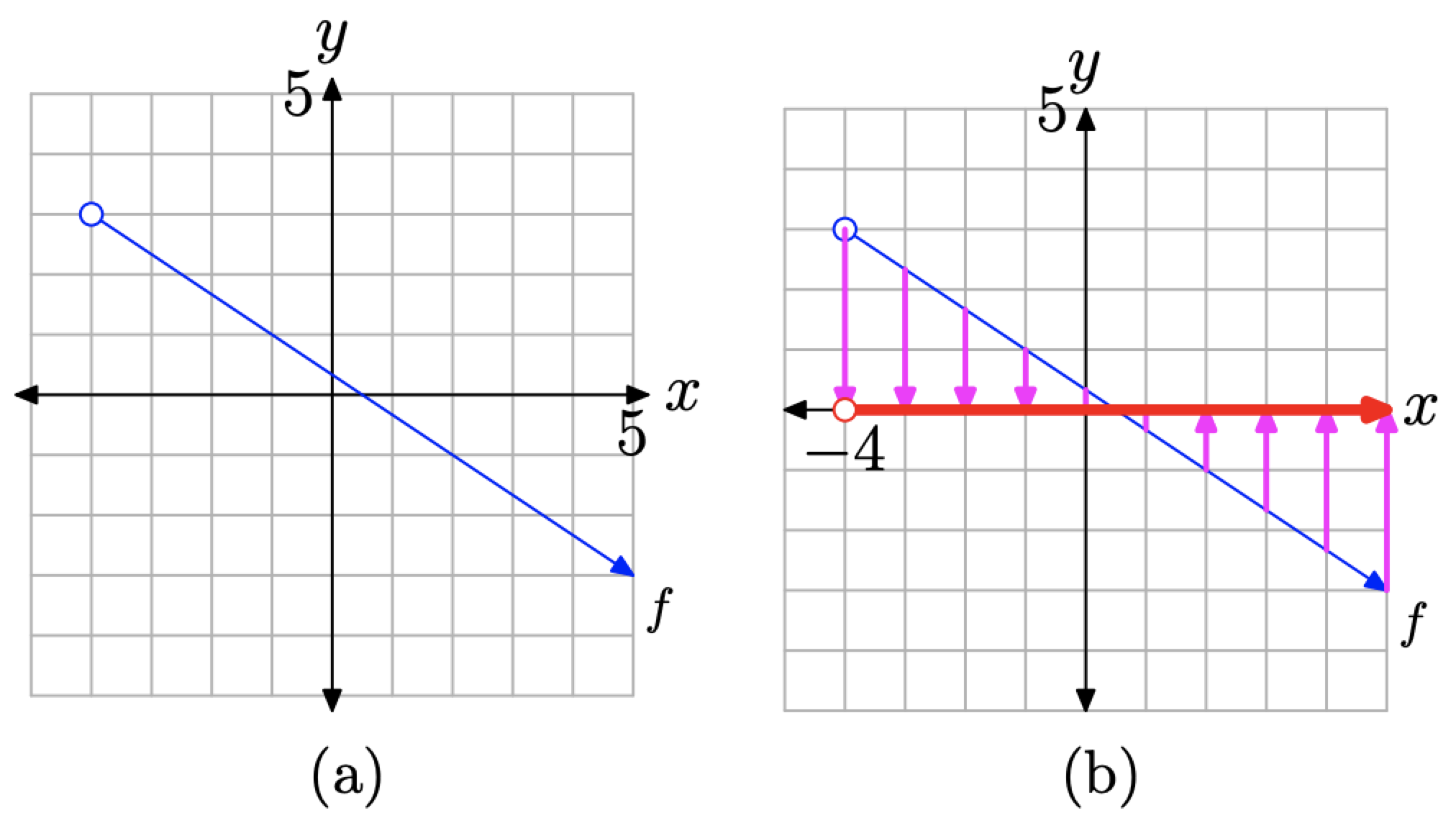
Щоб знайти діапазон, ми повинні спроектувати кожну точку на графіку f (перемальований на малюнку$\PageIndex{11}$ (a)) на вісь y. Проекція позначається «тінню» або проекцією на вісь y, як показано на малюнку$\PageIndex{11}$ (b). З приводу цієї «тіні» або проекції потрібно зробити два важливих моменти.

Малюнок$\PageIndex{11}$. Визначення діапазону з графіка f.

1. Ліва кінцева точка графіка f порожня (позначається відкритим колом), тому вона не має проекції на вісь y. Це позначається відкритим колом у верхньому кінці (at$y = 3$) «тіні» на осі y.
2. Стрілка на правому кінці графіка f вказує на те, що графік f триває вниз і вправо нескінченно. Отже, проекція графіка f на вісь y - це тінь, яка рухається нескінченно вниз. На малюнку$\PageIndex{11}$ (b) зверніть увагу на те, як проекції точок на графіку f, не видимих у вікні перегляду, заходять з правого нижнього кута і відкидають «тіні» на вісь y.

Отже, діапазон f - це сукупність значень y, затінених на осі y системи координат, показаної на малюнку$\PageIndex{11}$ (b). Зауважте, що всі значення y, нижчі$y = 3$ за, затінені на осі y. Таким чином, діапазон f дорівнює

$$\text { Range of } f=(-\infty, 3)=\{y : y<3\}$$

Давайте розглянемо інший приклад.

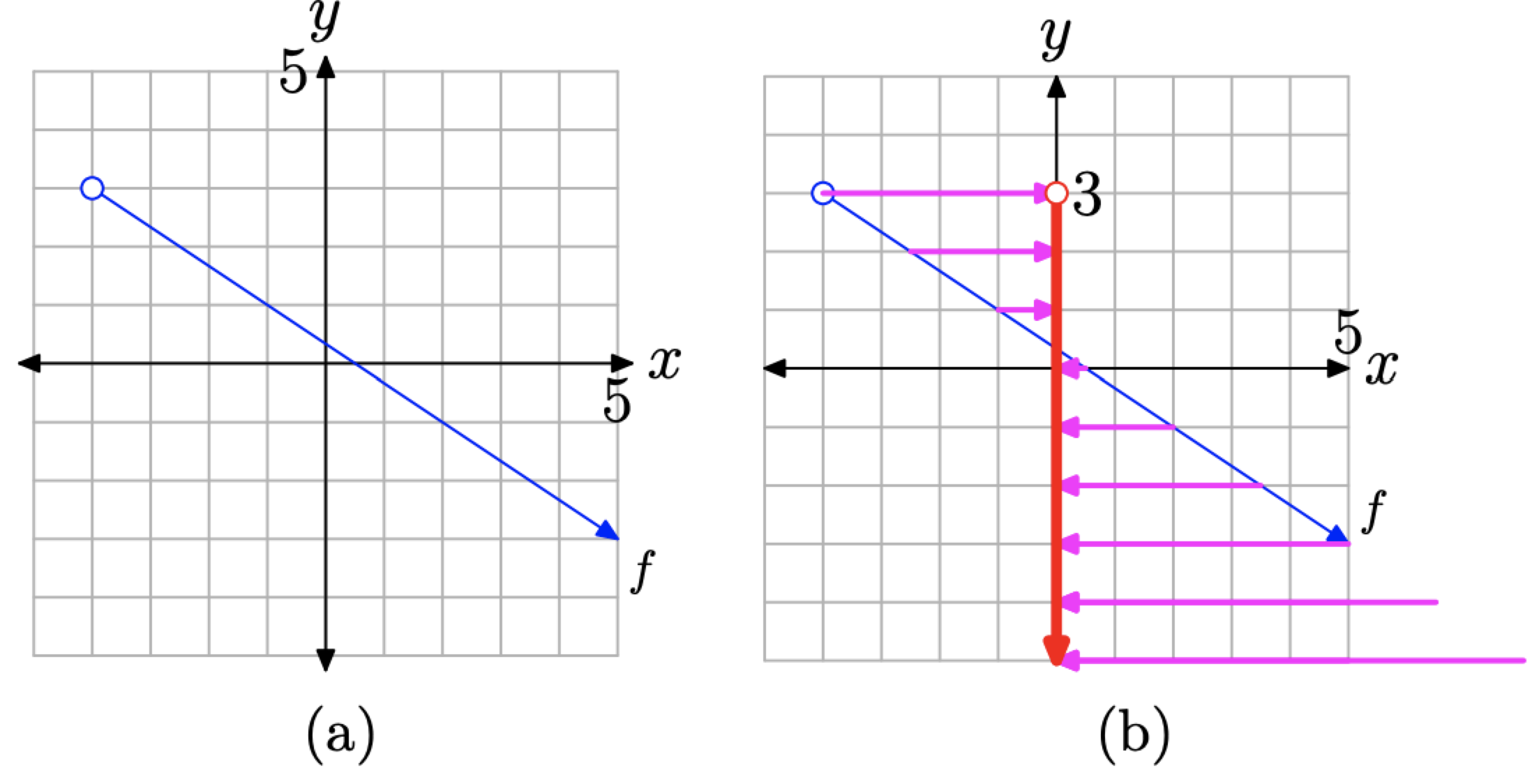
Приклад$\PageIndex{5}$

Використовуйте set-builder та інтервальні позначення для опису області та діапазону функції, представленої графіком на малюнку$\PageIndex{12}$ (a).

Малюнок$\PageIndex{12}$. Визначення домену за графом f.

Рішення

Щоб визначити область f, ми повинні спроектувати всі точки на графіку f на вісь x. Ця проекція позначається червоною «тінню» (або більш товстим стилем лінії, якщо ви переглядаєте це чорно-білим кольором), показаним на осі x на малюнку$\PageIndex{12}$ (b). З приводу цієї «тіні» або проекції потрібно зробити два важливих моменти.

1. Стрілка в кінці лівої половини графіка f на малюнку$\PageIndex{12}$ (а) вказує на те, що ця половина графіка f відкривається нескінченно вліво і вгору. Отже, коли точки на лівій половині графіка f проектуються на вісь x, «тінь» або проекція поширюється на невизначений термін вліво. Зверніть увагу, як точки на графіку, які потрапляють за межі вікна перегляду, потрапляють з лівого верхнього кута і відкидають «тіні» на вісь x.
2. Стрілка в кінці правої половини графіка f на малюнку$\PageIndex{12}$ (а) вказує на те, що ця половина графіка f відкривається нескінченно вправо і вгору. Отже, коли точки на цій половині графіка f проектуються на вісь x, «тінь» або проекція поширюється на невизначений термін вправо.

Отже, вся вісь x лежить в «тіні», що робить область f бути

$$\text { Domain of } f=(-\infty, \infty)=\{x : x \in \mathbb{R}\}$$

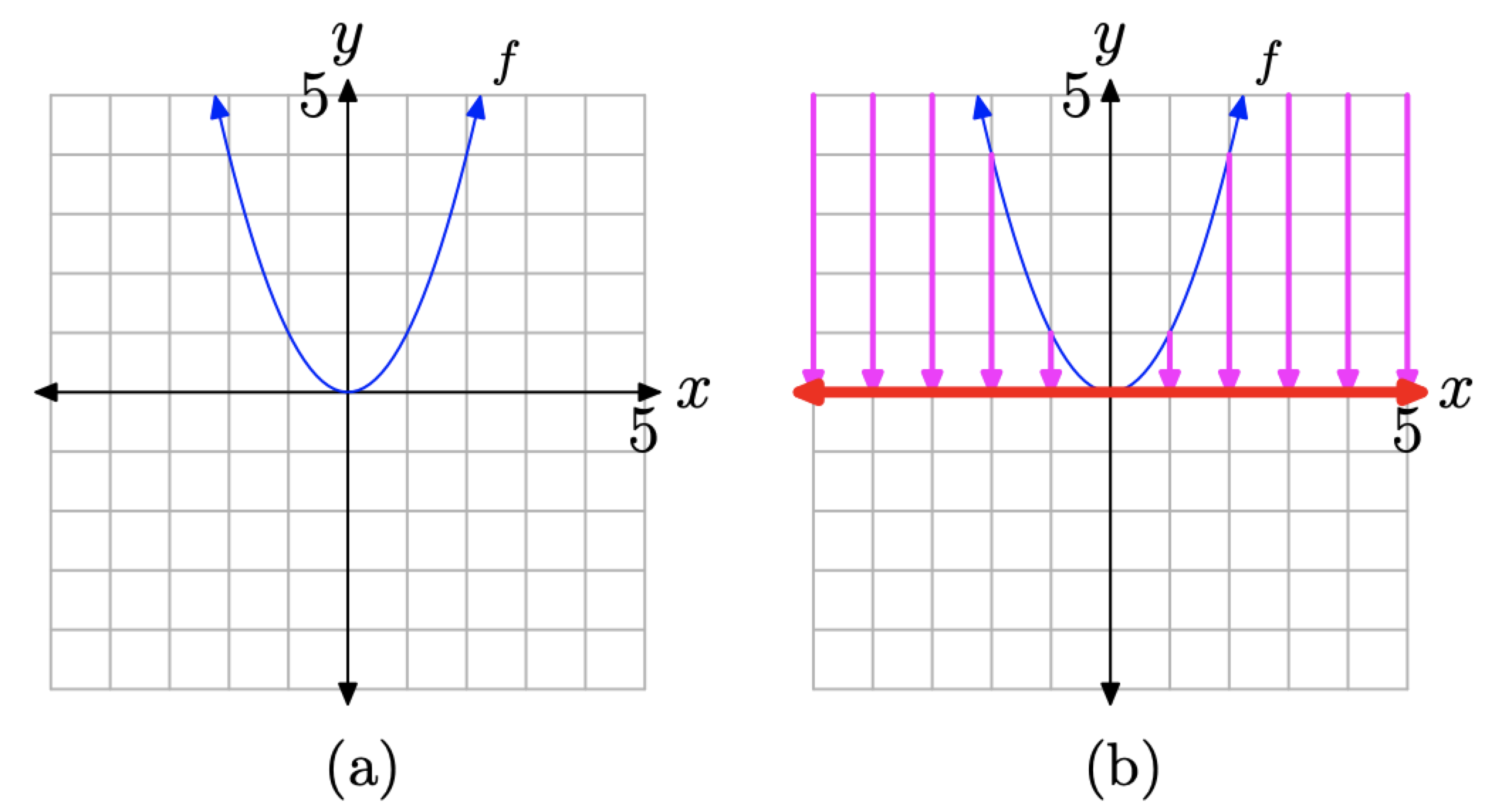
Щоб визначити діапазон f, ми повинні спроектувати всі точки на графіку f на вісь y. Ця проекція позначається червоною «тінню» (або більш товстою лінією, якщо ви переглядаєте її чорно-білим кольором), показаною на осі y на малюнку$\PageIndex{13}$ (b). Два важливих моменти потрібно зробити з приводу цієї «тіні» або проекції.

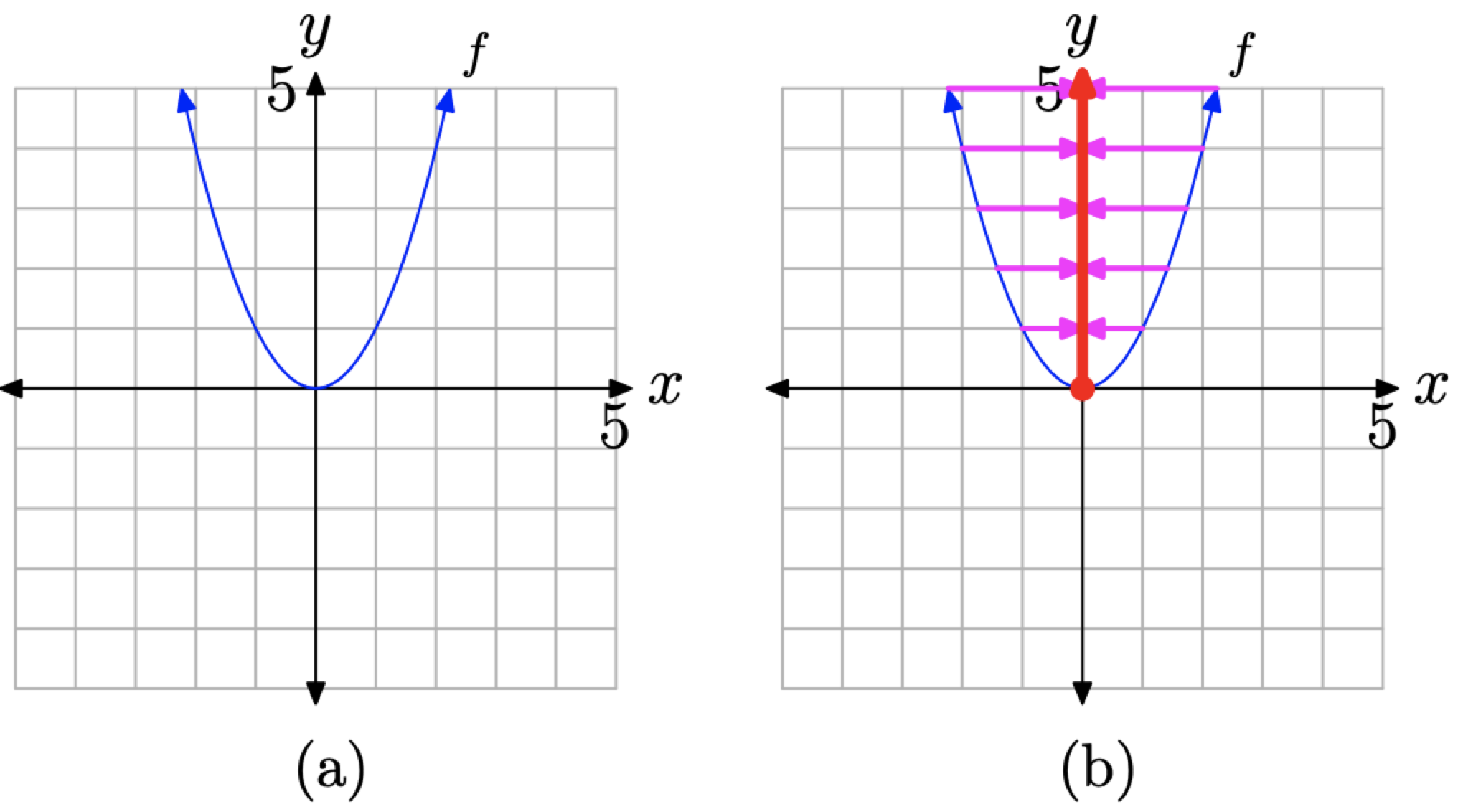
Малюнок$\PageIndex{13}$. Визначення діапазону з графіка f.

1. Графік f проходить через початок (точка (0, 0)). Це найнижча точка на графіку і, отже, її тінь є кінцевою точкою на нижньому кінці затіненої області на осі y.
2. Стрілки в кінці кожної половини графіка f вказують на те, що графік відкривається вгору нескінченно довго. Отже, коли точки на графіку f проектуються на вісь y, «тінь» або проекція поширюється вгору на невизначений термін. Про це вказує стрілка на верхньому кінці «тіні» на осі у.

Отже, всі точки на осі Y вище і включаючи точку на початку «лежать в тіні». Таким чином, діапазон f дорівнює

$$\text { Range of } f=[0, \infty)=\{y : y \geq 0\}$$

Використання графічного калькулятора для визначення домену та діапазону

Ми дізналися, як знайти область і діапазон функції, подивившись на її графік. Тому, якщо ми визначимо функцію за допомогою виразу, наприклад$f(x)=\sqrt{4-x}$, то ми повинні мати можливість захопити область і діапазон f з її графіка, за умови, звичайно, що ми можемо намалювати графік f Ми знайдемо графічний калькулятор буде зручним інструментом для цієї вправи.

Приклад$\PageIndex{6}$

Використовуйте set-builder та інтервальне позначення для опису домену та діапазону функції, визначеної правилом

$$f(x)=\sqrt{4-x}$$

Рішення

Завантажте вираз, що визначає f, у меню Y=, як показано на малюнку$\PageIndex{14}$ (a). Виберіть 6:ZStandard у меню ZOOM, щоб створити графік f, показаний на малюнку$\PageIndex{14}$ (b).

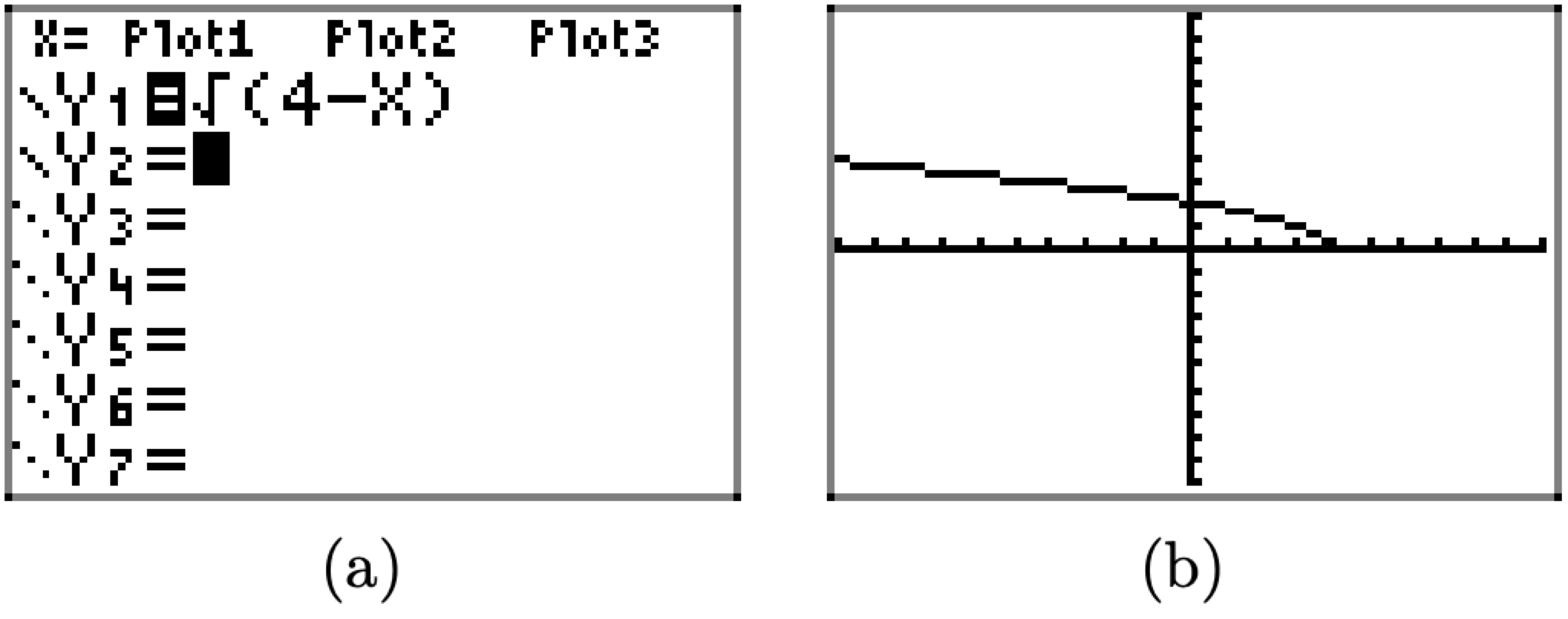
Малюнок$\PageIndex{14}$. Начерк графіка$f(x)=\sqrt{4-x}$.

Скопіюйте зображення на малюнку$\PageIndex{14}$ (b) на аркуш графічного паперу. Позначте та масштабуйте кожну вісь за допомогою параметрів WINDOW xmin, xmax, ymin та ymax, як показано на малюнку$\PageIndex{15}$ (а).

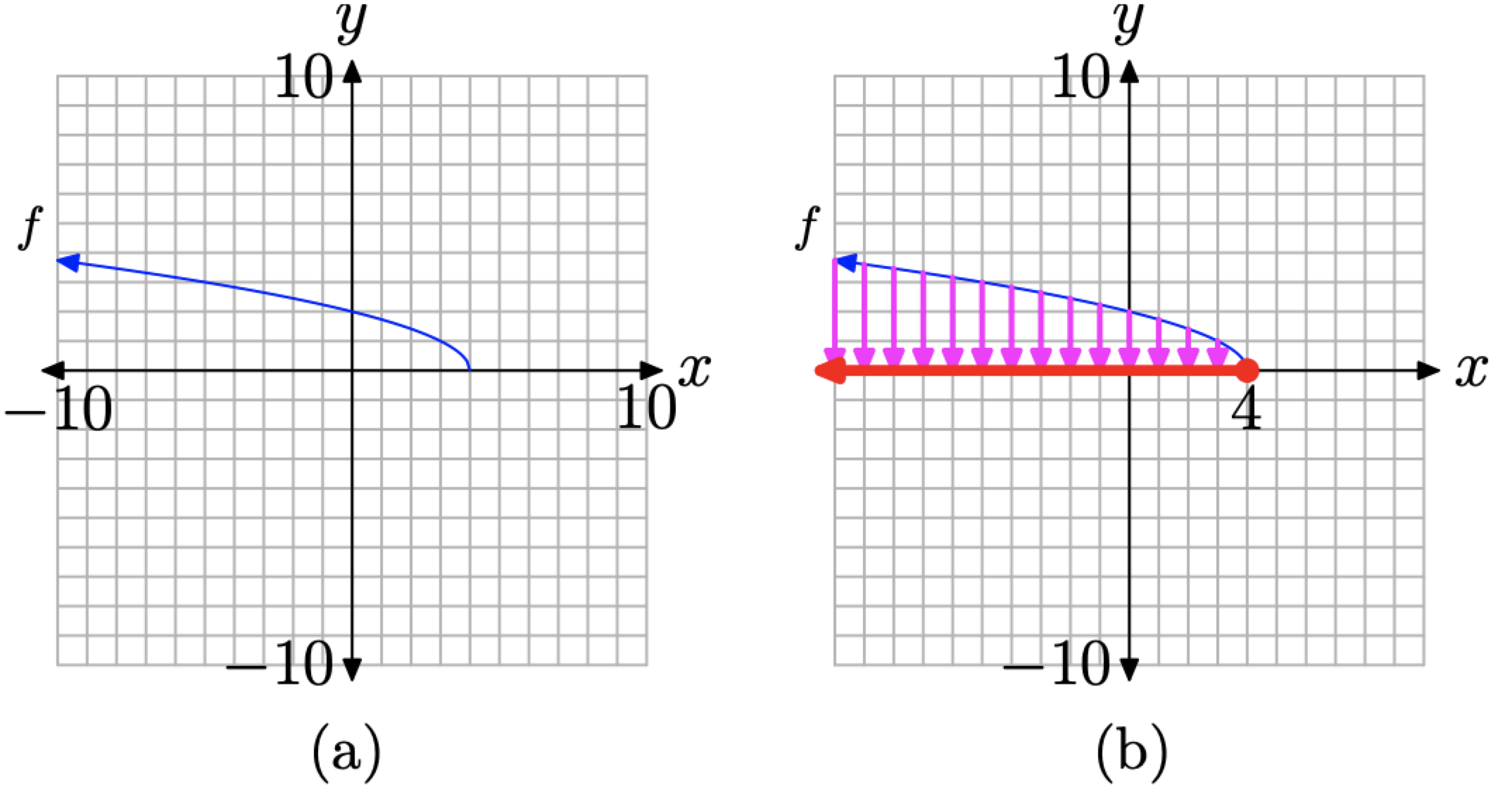
Малюнок$\PageIndex{15}$. Захоплення домену$f(x)=\sqrt{4-x}$ з його графа.

Далі спроектуйте кожну точку на графіку f на вісь x, як показано на малюнку$\PageIndex{15}$ (b). Зауважте, що ми зробили два припущення щодо графіка f.

1. У лівому кінці графіка на рисунках$\PageIndex{14}$ (b) і$\PageIndex{15}$ (b) припускаємо, що графік f триває вгору і вліво до нескінченності. Значить, «тінь» або проекція на вісь x будуть рухатися на невизначений час вліво. Це вказується прикріпленням наконечника стрілки до лівого кінця області, яка «лежить у тіні» на осі x, як показано на малюнку$\PageIndex{15}$ (b).
2. Також припустимо, що правий кінець графіка закінчується в точці$(4, 0)$. Це враховує «заповнену крапку», коли ця точка на графіку f проектується на вісь x.

Зверніть увагу, що «тінь» або проекція на вісь x на малюнку$\PageIndex{15}$ (b) включає всі значення x менше або дорівнює 4. Таким чином, доменом f є

$$\text { Domain of } f=(-\infty, 4]=\{x : x \leq 4\}$$

Ми можемо інтуїтивно зрозуміти цей результат, розглядаючи вираз, що визначає f. тобто розглянути правило або визначення

$$f(x)=\sqrt{4-x}$$

Нагадаємо, що раніше ми визначали область f як набір «допустимих» x-значень. У цьому випадку неможливо взяти квадратний корінь негативного числа, тому ми повинні бути обережними, вибираючи значення x, які ми використовуємо в цьому правилі. Відзначимо,$x = 4$ що допустимо, як

$$f(0)=\sqrt{4-4}=\sqrt{0}=0$$

Однак цифри більше 4 не можуть бути використані в цьому правилі. Наприклад, розглянемо, що відбувається, коли ми намагаємося використовувати$x = 5$.

$$f(x)=\sqrt{4-5}=\sqrt{-1}$$

Ми залишимо це нашим читачам, щоб перевірити інші значення х, які менше 4. Вони також дадуть реальні відповіді, коли вони вводяться в правило$f(x)=\sqrt{4-x}$. Зауважте, що це також підтверджує нашу попередню гіпотезу про те, що «тінь» або проекція, показана на малюнку$\PageIndex{15}$ (b), триває нескінченно ліворуч.

Замість того, щоб «гадати і перевіряти», ми можемо прискорити аналіз області,$f(x)=\sqrt{4-x}$ зазначивши, що вираз під радикалом не повинно бути негативним числом. Отже,$4 − x$ повинен бути або більше, або дорівнює нулю. Цей аргумент створює нерівність, яка легко вирішується для x.

$$\begin{aligned} 4-x & \geq 0 \\-x & \geq-4 \\ x & \leq 4 \end{aligned}$$

Цей останній результат перевіряє, що область f - це всі значення x, які менше або рівні 4, що повністю узгоджується з «тінню» або проекцією на вісь x, показану на малюнку$\PageIndex{15}$ (b).

Щоб визначити діапазон f, ми повинні спроектувати кожну точку на графіку f на вісь y, як показано на малюнку$\PageIndex{16}$ (b).

Знову зробимо два припущення про графі f.

1. У лівому кінці графіка на$f(x)=\sqrt{4-x}$ рисунках$\PageIndex{14}$ (b) і$\PageIndex{16}$ (b) ми вважаємо, що графік f триває вгору і вліво до нескінченності. Таким чином, коли точки на графіку f проектуються на вісь y, з'являться проекції, що виходять з верхнього лівого краю від точок на графіку f, які не видно у вікні перегляду, вибраному на малюнку$\PageIndex{14}$ (b). Отже, «тінь» або проекція на осі y, показану на малюнку$\PageIndex{16}$ (b), продовжують вгору нескінченно довго. Це позначається стрілкою у верхньому кінці «тіні» на осі y на малюнку$\PageIndex{16}$ (b).

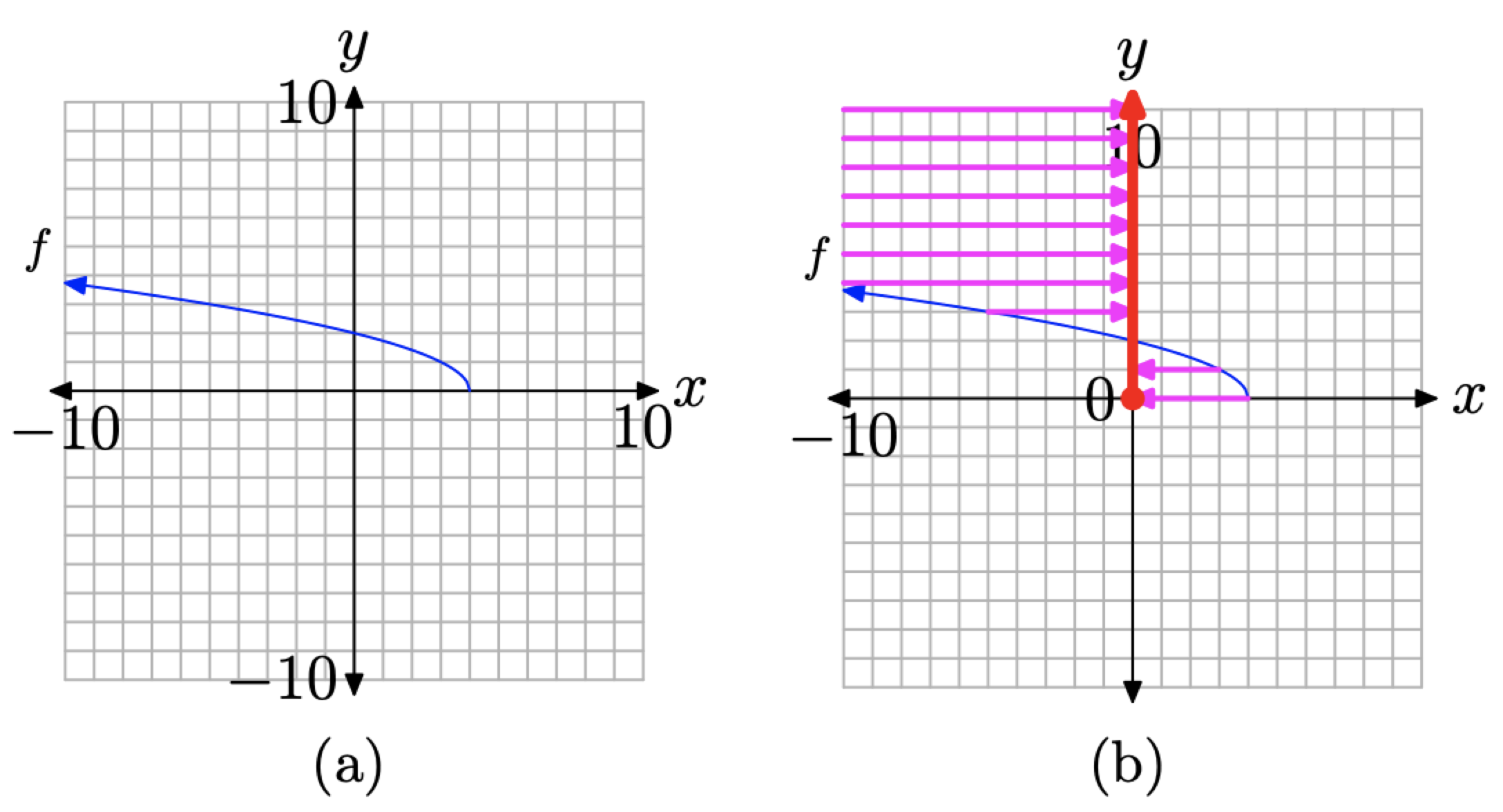
Малюнок$\PageIndex{16}$. Визначення діапазону$f(x)=\sqrt{4-x}$ за своїм графіком.

2. Знову припускаємо, що правий кінець графіка f закінчується в точці$(4, 0)$. Проекція цієї точки на вісь y створює «заповнену» кінцеву точку на початку, показаному на малюнку$\PageIndex{16}$ (b).

Зверніть увагу, що «тінь» або проекція на вісь y на малюнку$\PageIndex{16}$ (b) включає всі значення y, які більше або рівні нулю. Отже,

$$\text { Range of } f=[0, \infty)=\{y : y \geq 0\}$$