7.6: Застосування раціональних рівнянь
- Page ID
- 58056
Цілі навчання
- Вирішувати додатки, що включають відносини між дійсними числами.
- Вирішуйте програми, що включають рівномірний рух (задачі відстані).
- Вирішувати додатки з нормою роботи.
Проблеми з числом
Нагадаємо, що зворотне ненульового числа\(n\) є\(\frac{1}{n}\). Наприклад,\(5\) взаємне є\(\frac{1}{5}\) і\(5\cdot \frac{1}{5} = 1\). У цьому розділі додатки часто будуть включати ключове слово «взаємний». Коли це так, ми побачимо, що алгебраїчна установка призводить до раціонального рівняння.
Приклад\(\PageIndex{1}\)
Додатне ціле число\(4\) менше іншого. Сума зворотних двох натуральних чисел дорівнює\(\frac{10}{21}\). Знайдіть два цілих числа.
Рішення:
Почніть з присвоєння змінних невідомим.
\(n\)Дозволяти представляти більше натуральне число.
\(n-4\)Дозволяти представляти найменше натуральне число.
Далі використовуйте взаємні\(\frac{1}{n}\) і\(\frac{1}{n−4}\) для перекладу речень в алгебраїчне рівняння.
\(\begin{array}{ccc}{\color{Cerulean} { the\:sum\:of\:the\:reciprocals }} & {\color{Cerulean} { is }} \\ {\qquad \frac{1}{n}+\frac{1}{n-4}} & {=} & {\frac{10}{21}}\end{array}\)
Ми можемо вирішити цей раціональний вираз, помноживши обидві сторони рівняння на найменш спільний знаменник (РК). В даному випадку РК-дисплей є\(21n(n−4)\).
\(\begin{array}{cl}{\frac{1}{n}+\frac{1}{n-4}=\frac{10}{21}}&{} \\ {\color{Cerulean}{21n(n-4)} \color{black}{\cdot \left(\frac{1}{n}+\frac{1}{n-4} \right)}=\color{Cerulean}{21n(n-4)}\color{black}{ \cdot\left(\frac{10}{21}\right)}}&{\color{Cerulean}{Multiply\:both\:sides}}\\{}&{\color{Cerulean}{by\:the\:LCD.}} \\ {\color{Cerulean}{21n (n-4)}\color{black}{ \cdot \frac{1}{n}+}\color{Cerulean}{21n (n-4)}\color{black}{ \cdot \frac{1}{n-4}}=\color{Cerulean}{21n (n-4)}\color{black}{ \cdot\left(\frac{10}{21}\right)}}&{\color{Cerulean}{Distribute\:and}}\\{}&{\color{Cerulean}{then\:cancel.}} \\ {21(n-4)+21n =10 n(n-4)}\end{array}\)
Розв'яжіть отримане квадратне рівняння.
\(\begin{array}{rlrl}{5 n-6} & {=0} & {\text { or }} & {n-7=0} \\ {5 n} & {=6} && {n=7} \\ {n} & {=\frac{6}{5}}\end{array}\)
Питання вимагає цілих чисел і єдиним цілим рішенням є\(n=7\). Звідси ігнорування\(\frac{6}{5}\). Використовуйте вираз,\(n−4\) щоб знайти менше ціле число.
\(n-4=7-4=3\)
Відповідь:
Два натуральних числа -\(3\) і\(7\). Чек залишається на зчитувач.
Приклад\(\PageIndex{2}\)
Додатне ціле число\(4\) менше іншого. Якщо зворотне від меншого цілого числа віднімається з подвійного зворотного більшого, то результат є\(\frac{1}{30}\). Знайдіть два цілих числа.
Рішення:
\(n\)Дозволяти представляти більше натуральне число.
\(n-4\)Дозволяти представляти менше натуральне число.
Налаштуйте алгебраїчне рівняння.
Розв'яжіть це раціональне вираз, множивши обидві сторони на РК-дисплей. РК-дисплей є\(30n(n−4)\).
\(\begin{aligned}\frac{2}{n}-\frac{1}{n-4}&=\frac{1}{30} \\ \color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{2}{n}-\frac{1}{n-4}\right)}&=\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{1}{30}\right)} \\ \color{Cerulean}{30 n(n-4)}\color{black}{ \cdot \frac{2}{n}-}\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot \frac{1}{n-4}}&=\color{Cerulean}{30 n(n-4)}\color{black}{ \cdot\left(\frac{1}{30}\right)}\end{aligned}\)
\(\begin{array}{rlrl}{n-10} & {=0 \quad \text { or }} & {n-24} & {=0} \\ {n} & {=10} & { n=24}\end{array}\)
Тут ми маємо дві життєздатні можливості для більшого цілого числа. З цієї причини у нас буде два рішення цієї проблеми.
Якщо\(n=10\), то\(n-4=10-4=6\).
Якщо\(n=24\), то\(n-4=24-4=20\).
В якості перевірки виконайте операції, зазначені в проблемі.
\(\begin{array}{r|r}{\text { Check } 6 \text { and } 10 .} &{\text{Check} \:20\:\text{and}\:24.}\\{2\left(\frac{1}{\color{OliveGreen}{10}}\right)-\frac{1}{\color{OliveGreen}{6}}=\frac{1}{5}-\frac{1}{6}}&{2\left(\frac{1}{\color{OliveGreen}{24}}\right)-\frac{1}{\color{OliveGreen}{20}}=\frac{1}{12}-\frac{1}{20}}\\{=\frac{6}{30}-\frac{5}{30}}&{=\frac{5}{60}-\frac{3}{60}}\\{=\frac{1}{30}\quad\color{Cerulean}{\checkmark}}&{=\frac{1}{30}\quad\color{Cerulean}{\checkmark}} \end{array}\)
Відповідь:
Дві множини натуральних чисел вирішують цю задачу: {\(6, 10\)} та {\(20, 24\)}.
Вправа\(\PageIndex{1}\)
Різниця між зворотними двома послідовними натуральними непарними чисел дорівнює\(\frac{2}{15}\). Знайти цілі числа.
- Відповідь
-
Цілими числами є\(3\) і\(5\).
Проблеми рівномірного руху
Проблеми рівномірного руху, які також називають проблемами відстані, включають формулу
\[D=rt\]
де відстань\(D\), задається як добуток середньої ставки\(r\), так і час\(t\), пройдений з цією швидкістю. Якщо розділити обидві сторони на середню норму\(r\), то отримаємо формулу
\[t=\frac{D}{r}\]
З цієї причини, коли невідома величина є часом, алгебраїчна установка для задач відстані часто призводить до раціонального рівняння. Аналогічно, коли невідома величина є швидкістю, налаштування також може призвести до раціонального рівняння.
Ми починаємо будь-яку задачу рівномірного руху, спочатку організувавши наші дані за допомогою діаграми. Використовуйте цю інформацію, щоб налаштувати алгебраїчне рівняння, яке моделює додаток.
Приклад\(\PageIndex{5}\)
Мері провела перші 120 миль своєї дорожньої поїздки в пробці. Коли рух розчистився, вона змогла проїхати вдвічі швидше за інші 300 миль. Якщо загальна поїздка зайняла 9 годин, то як швидко вона рухалася в пробці?
Рішення:
Спочатку визначте невідому кількість і впорядкуйте дані.
Давайте\(x\) представляємо середню швидкість Марії (милі на годину) в русі.
Нехай\(2x\) уявляють її середню швидкість після того, як трафік розчистився.
.png)
Щоб уникнути введення ще двох змінних для стовпчика часу, скористайтеся формулою\(t=\frac{D}{r}\). Тут час для кожного відрізка поїздки розраховується наступним чином:
\(\begin{array}{c} {\color{Cerulean} { Time\:spent\:in\:traffic:}\:\:\color{black}{ t=\frac{D}{r}=\frac{120}{x}}} \\{\color{Cerulean}{Time\:clear\:of\:traffic:}\:\:\color{black}{t=\frac{D}{r}}=\frac{300}{2x}} \end{array}\)
Використовуйте ці вирази для завершення діаграми.
.png)
Алгебраїчне налаштування визначається стовпчиком часу. Додайте час для кожного відрізка поїздки, щоб отримати в цілому 9 годин:
\(\begin{array}{ccccc}{\color{Cerulean}{time\:spent\:in\:traffic}}&{}&{\color{Cerulean}{time\:clear\:of\:traffic}}&{}&{\color{Cerulean}{total\:time\:of\:trip}} \\ {\overbrace{\frac{120}{x}}}&{+}&{\overbrace{\frac{300}{2x}}}&{=}&{\overbrace{9}} \end{array}\)
Ми починаємо розв'язувати це рівняння спочатку множивши обидві сторони на РК-дисплей,\(2x\).
\(\begin{aligned} \frac{120}{x}+\frac{300}{2 x} &=9 \\ \color{Cerulean}{2x }\color{black}{ \cdot\left(\frac{120}{x}+\frac{300}{2 x}\right)} &=\color{Cerulean}{2 x}\color{black}{ \cdot 9} \\ \color{Cerulean}{2 x}\color{black}{ \cdot \frac{120}{x}+}\color{Cerulean}{2 x}\color{black}{ \cdot \frac{300}{2 x}} &=\color{Cerulean}{2 x}\color{black}{ \cdot 9} \\ 240+300 &=18 x \\ 540 &=18 x \\ 30 &=x \end{aligned}\)
Відповідь:
Мері в середньому 30 миль на годину в пробці.
Приклад\(\PageIndex{6}\)
Пасажирський поїзд може проїхати, в середньому,\(20\) милі на годину швидше, ніж вантажний поїзд. Якщо пасажирський поїзд охоплює\(390\) милі в той же час, що він приймає вантажний поїзд, щоб подолати\(270\) милі, то наскільки швидко кожен поїзд?
Рішення:
Спочатку визначте невідомі величини та організуйте дані.
Дозвольте\(x\) уявити середню швидкість вантажного поїзда.
\(x+20\)Дозволяти представляти швидкість пасажирського поїзда.
Далі організуйте дані в діаграмі.
.png)
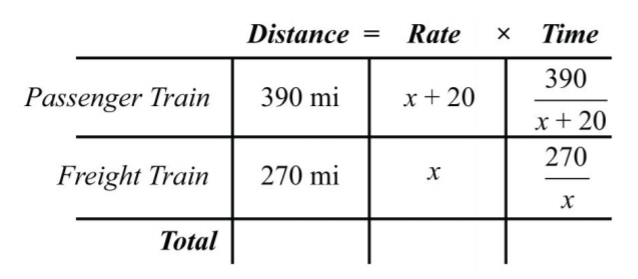
Використовуйте формулу\(t=\frac{D}{r}\), щоб заповнити стовпчик часу для кожного поїзда.
\(\begin{array}{c} {\color{Cerulean} { Passenger\: train: }\:\:\color{black}{ t=\frac{D}{r}=\frac{390}{x+20}}} \\ {\color{Cerulean}{Freight\:train:}\:\:\color{black}{t=\frac{D}{r}=\frac{270}{x}}} \end{array}\)
.png)
Оскільки поїзди подорожують однакову кількість часу, завершіть алгебраїчну настройку, прирівнюючи вирази, що представляють час:
\(\frac{390}{x+20}=\frac{270}{x}\)
Вирішіть це рівняння, попередньо помноживши обидві сторони на РК-дисплей,\(x(x+20)\).
\(\begin{aligned} \color{Cerulean}{x(x+20)}\color{black}{ \cdot\left(\frac{390}{x+20}\right)} &=\color{Cerulean}{x(x+20)}\color{black}{ \cdot\left(\frac{270}{x}\right) }\\ 390 x &=270(x+20) \\ 390 x &=270 x+5400 \\ 120 x &=5400 \\ x &=45 \end{aligned}\)
Використовуйте\(x+20\) для пошуку швидкості пасажирського поїзда.
\(x+20=\color{OliveGreen}{45}\color{black}{+20=65}\)
Відповідь:
Швидкість пасажирського поїзда становить\(65\) милі на годину, а швидкість вантажного поїзда -\(45\) милі на годину.
Приклад\(\PageIndex{7}\)
Бретт живе на річці\(8\) милі вище за течією від міста. Коли течія становить\(2\) милі на годину, він може грести свій човен вниз за течією до міста для поставок і назад в\(3\) години. Яка його середня швидкість веслування в негазованій воді?
Рішення:
\(x\)Уявімо середню швидкість веслування Бретта в негазованій воді.
Веслуючи вниз за течією, течія збільшує його швидкість, а його швидкість становить\(x + 2\) милі на годину. Веслуючи вгору за течією, течія знижує свою швидкість, а його швидкість становить\(x − 2\) милі на годину. Почніть з організації даних у наступній діаграмі:
.png)
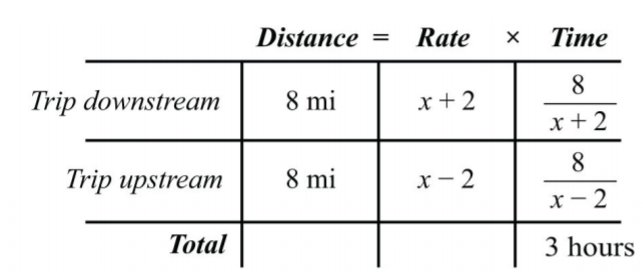
Використовуйте формулу\(t=\frac{D}{r}\), щоб заповнити стовпчик часу для кожного етапу поїздки.
\(\begin{array}{c} {\color{Cerulean} { Trip\: downstream: } \:\:\color{black}{ t=\frac{D}{r}=\frac{8}{x+2}}}\\{\color{Cerulean}{Trip\:upstream:}\:\:\color{black}{t=\frac{D}{r}=\frac{8}{x-2}}} \end{array}\)
.png)
Алгебраїчне налаштування визначається стовпчиком часу. Додайте час для кожного відрізка поїздки, щоб отримати в цілому 3 години:
\(\begin{array}{ccccc}{\color{Cerulean}{time\:rowing\:downstream}}&{}&{\color{Cerulean}{time\:rowing\:upstream}}&{}&{\color{Cerulean}{total\:time\:of\:trip}}\\{\overbrace{\frac{8}{x+2}}}&{+}&{\overbrace{\frac{8}{x-2}}}&{=}&{\overbrace{3}} \end{array}\)
Вирішіть це рівняння, попередньо помноживши обидві сторони на РК-дисплей,\((x+2)(x−2)\).
Далі вирішуємо отримане квадратне рівняння.
\(\begin{array}{rlrl}{3 x+2} & {=0} & {\text { or }} & {x-6=0} \\ {3 x} & {=-2} & {} & {x=6} \\ {x} & {=\frac{-2}{3}}\end{array}\)
Використовуйте тільки позитивне рішення,\(x=6\) милі на годину.
Відповідь:
Його швидкість веслування становить\(6\) милі на годину.
Вправа\(\PageIndex{2}\)
Дуейн проїхав\(18\) милі до аеропорту, щоб забрати батька, а потім повернувся додому. У зворотній поїздці він зміг проїхати в середньому\(15\) милі на годину швидше, ніж він робив там поїздку. Якщо загальний час руху становив\(1\) годину, то якою була його середня швидкість їзди до аеропорту?
- Відповідь
-
Його середня швидкість їзди до аеропорту становила\(30\) милі на годину.
Проблеми з робочим тарифом
Швидкість, з якою може виконуватися завдання, називається нормою роботи.
Приклад\(\PageIndex{8}\)
Наприклад, якщо художник може пофарбувати кімнату за 8 годин, то завдання полягає в тому, щоб пофарбувати кімнату, а ми можемо написати
\(\frac{1 \text { task }}{8 \text { hours }} \quad \color{Cerulean} { Work\: rate }\)
Іншими словами, художник може виконати\(\frac{1}{8}\) завдання за годину.
Рішення
Якщо він пропрацює менше 8 годин, то виконає частку завдання. Наприклад,
\(\begin{array}{cc} {\color{Cerulean}{work\:rate}\color{black}{\times}\color{Cerulean}{time}\color{black}{=}\color{Cerulean}{work\:completed}}&{}\\{\frac{1}{8}\times 2\text{hrs}=\frac{1}{4}}&{\color{Cerulean}{One-quarter\:of\:the\:room\:painted}}\\{\frac{1}{8}\times 4\text{hrs}=\frac{1}{2}}&{\color{Cerulean}{One-half\:of\:the\:room\:painted}}\\{\frac{1}{8}\times 8\text{hrs}=1}&{\color{Cerulean}{One\:whole\:room\:painted}} \end{array}\)
Отримати суму виконаного завдання, помноживши норму робіт на кількість часу роботи маляра. Як правило, проблеми з нормою роботи включають людей, які працюють разом для виконання завдань. Коли це так, ми можемо організувати дані на діаграмі, так само, як ми це робили з проблемами відстані.
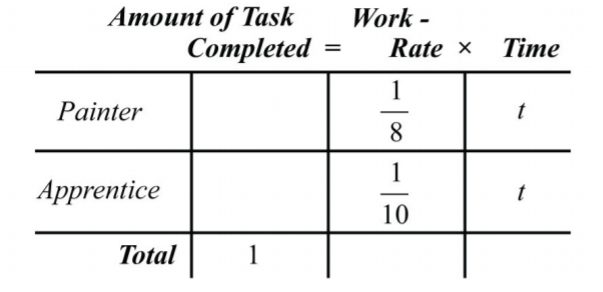
Припустимо, що підмайстер художник може самостійно пофарбувати ту ж кімнату за кілька\(10\) годин. Тоді скажемо, що він може виконати\(\frac{1}{10}\) завдання за годину.
Нехай\(t\) уявляють час, який потрібно обом художникам, працюючи разом, щоб пофарбувати кімнату.
.png)
Для завершення графіка помножте норму роботи на час для кожної людини.
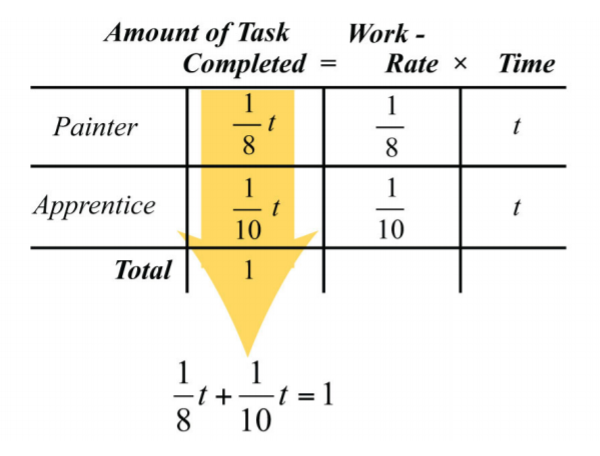
Частина кімнати, яку кожен може розфарбувати, додає в цілому\(1\) виконане завдання.
Це представлено рівнянням, отриманим з першого стовпця діаграми:
.png)
Ця установка призводить до раціонального рівняння, яке можна вирішити\(t\) шляхом множення обох сторін на РК-дисплей,\(40\).
\(\begin{aligned} \frac{1}{8}t+\frac{1}{10}t &=1 \\ \color{Cerulean}{40}\color{black}{\cdot \left(\frac{1}{8}t+\frac{1}{10}t\right)}&=\color{Cerulean}{40}\color{black}{\cdot 1} \\ \color{Cerulean}{40}\color{black}{\cdot\frac{t}{8}+}\color{Cerulean}{40}\color{black}{\cdot\frac{t}{10}}&=\color{Cerulean}{40}\color{black}{\cdot 1}\\ 5t+4t &=40 \\ 9t & =40 \\ t & = \frac{40}{9} \\ t & = 4 \frac{4}{9} \end{aligned}\)
Тому два живописця, працюючи разом, виконують завдання за\(4 \frac{4}{9}\) години.
Загалом, ми маємо наступну формулу норми роботи:
\[\frac{1}{t_{1}}t + \frac{1}{t_{2}}t = 1\]
\(\frac{1}{t_{2}}\)Ось\(\frac{1}{t_{1}}\) і індивідуальні показники роботи, і\(t\) це час, необхідний для виконання одного завдання, працюючи разом. Якщо врахувати час\(t\), а потім розділити обидві сторони на\(t\), то отримаємо еквівалентну формулу норми роботи:
\(\begin{array}{c} {\frac{1}{t_{1}}t + \frac{1}{t_{2}}t = 1} \\ {t\left( \frac{1}{t_{1}}+\frac{1}{t_{2}} \right)=1} \\ {\frac{1}{t_{1}}+\frac{1}{t_{2}}=\frac{1}{t}} \end{array}\)
Підсумовуючи, ми маємо такі еквівалентні формули робочого тарифу:
\(\begin{array}{ccccc}{}&{}&{\color{Cerulean}{Work\:rate\:formulas:}}&{}&{} \\ {\frac{1}{t_{1}}t}&{\text{or}}&{\frac{t}{t_{1}}+\frac{t}{t_{2}}=1}&{\text{or}}&{\frac{1}{t_{1}}+\frac{1}{t_{2}}=\frac{1}{t}}\end{array}\)
Приклад\(\PageIndex{9}\)
Працюючи один, тато Біллі може завершити роботу двору за 3 години. Якщо Біллі допомагає татові, то робота двору займає 2 години. Скільки часу знадобиться Біллі, працюючи на самоті, щоб завершити роботу у дворі?
Рішення:
Наведена інформація говорить нам про те, що тато Біллі має індивідуальну норму роботи\(\frac{1}{3}\) завдання на годину. Якщо ми дозволимо\(x\) представити час, який потрібен Біллі, працюючи на самоті, щоб завершити роботу на дворі, то індивідуальний рівень роботи Біллі є\(\frac{1}{x}\), і ми можемо написати
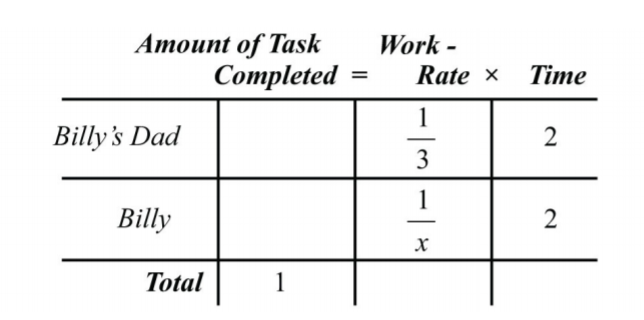.png)
Працюючи разом, вони можуть виконати завдання за лічені\(2\) години. Помножте окремі показники роботи на\(2\) години, щоб заповнити діаграму.
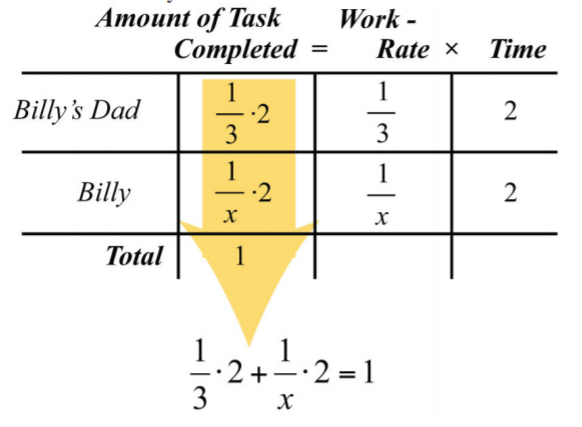.png)
Сума виконання кожного завдання складе 1 виконане завдання. Щоб вирішити для\(x\), ми спочатку множимо обидві сторони на РК-дисплей,\(3x\).
\(\begin{aligned} \frac{1}{3}\cdot 2+\frac{1}{x}\cdot 2 &=1 \\ \color{Cerulean}{3x}\color{black}{\cdot \left(\frac{2}{3}+\frac{2}{x} \right)}&=\color{Cerulean}{3x}\color{black}{\cdot1} \\ \color{Cerulean}{3x}\color{black}{\cdot \frac{2}{3} +}\color{Cerulean}{3x}\color{black}{\cdot \frac{2}{x}}&=\color{Cerulean}{3x}\color{black}{\cdot 1} \\ 2x+6&=3x \\ 6&=x \end{aligned}\)
Відповідь:
Це займає Біллі\(6\) годин, щоб завершити роботу двору в поодинці.
Зрозуміло, одиниця часу на норму роботи не завжди повинна бути в годині.
Приклад\(\PageIndex{10}\)
Працюючи разом, дві будівельні бригади можуть побудувати сарай за\(5\) добу. Працюючи окремо, менш досвідченому екіпажу потрібно в два рази більше часу на будівництво сараю, ніж більш досвідченому екіпажу. Працюючи окремо, скільки часу потрібно кожному екіпажу, щоб побудувати сарай?
Рішення:
Нехай\(x\) уявляють час, який потрібен більш досвідченому екіпажу, щоб побудувати сарай.
Нехай\(2x\) уявляють час, який потрібно менш досвідченому екіпажу, щоб побудувати сарай.
Працюючи разом, завдання завершується за лічені\(5\) дні. Це дає наступну настройку:
.png)
Перший стовпець на діаграмі дає нам алгебраїчне рівняння, яке моделює проблему:
\(\begin{aligned} \frac{1}{x}\cdot 5+\frac{1}{2x}\cdot 5 &=1 \\ \frac{5}{x}+\frac{5}{2x}&=1 \end{aligned}\)
Вирішити рівняння шляхом множення обох сторін на\(2x\).
\(\begin{aligned} \color{Cerulean}{2x}\color{black}{\cdot \left(\frac{5}{x}+\frac{5}{2x} \right)}&=\color{Cerulean}{2x}\color{black}{\cdot 1}\\ \color{Cerulean}{2x}\color{black}{\cdot \frac{5}{x} +}\color{Cerulean}{2x}\color{black}{\cdot \frac{5}{2x}}&=\color{Cerulean}{2x}\color{black}{\cdot 1} \\ 10+5&=2x \\ 15&=2x \\ \frac{15}{2}&=x \quad\text{or}\quad x=7\frac{1}{2}\:\text{days} \end{aligned}\)
Щоб визначити час, який займає менш досвідчений екіпаж, ми використовуємо\(2x\):
\(\begin{aligned} 2x&= 2\color{black}{\left(\color{OliveGreen}{\frac{15}{2}} \right) } \\ &= 15\:\text{days} \end{aligned}\)
Відповідь:
Працюючи окремо, досвідченому екіпажу потрібні\(7\frac{1}{2}\) дні, щоб побудувати сарай, а менш досвідченому екіпажу потрібні\(15\) дні, щоб побудувати сарай.
Вправа\(\PageIndex{3}\)
Садовий шланг Джо заповнює басейн за\(12\) години. Його сусід має більш тонкий шланг, який наповнює басейн за\(15\) годинами. Скільки часу знадобиться для заповнення басейну за допомогою обох шлангів?
- Відповідь
-
Буде потрібно обидва шланги\(6\frac{2}{3}\) години для заповнення басейну.
Ключові винос
- У цьому розділі застосовуються всі кроки, описані для вирішення загальних проблем слів. Шукайте нове ключове слово «взаємний», яке вказує на те, що слід записати величину в знаменнику дробу з чисельником\(1\).
- При вирішенні задач відстані, де елемент часу невідомий, використовуйте еквівалентну форму формули рівномірного руху\(t=\frac{D}{r}\), щоб уникнути введення більшої кількості змінних.
- При вирішенні завдань з нормою роботи помножте індивідуальну норму роботи на час, щоб отримати частину виконаного завдання. Сума частин завдання призводить до загального обсягу виконаної роботи.
Вправа\(\PageIndex{4}\) Number Problems
Використовуйте алгебру для вирішення наступних програм.
- Додатне ціле число вдвічі більше. Сума зворотних двох натуральних чисел дорівнює\(\frac{3}{10}\). Знайдіть два цілих числа.
- Додатне ціле число вдвічі більше. Сума зворотних двох натуральних чисел дорівнює\(\frac{3}{12}\). Знайдіть два цілих числа.
- Додатне ціле число вдвічі більше. Різниця взаємних двох натуральних чисел дорівнює\(\frac{1}{8}\). Знайдіть два цілих числа.
- Додатне ціле число вдвічі більше. Різниця взаємних двох натуральних чисел дорівнює\(\frac{1}{18}\). Знайдіть два цілих числа.
- Додатне ціле число\(2\) менше іншого. Якщо сума зворотного меншого і подвійного зворотного більшого дорівнює\(\frac{5}{12}\), то знайдіть два цілих числа.
- Додатне ціле число\(2\) більше, ніж інше. Якщо сума зворотного меншого і подвійного зворотного більшого дорівнює\(\frac{17}{35}\), то знайдіть два цілих числа.
- Сума зворотних двох послідовних натуральних чисел дорівнює\(\frac{11}{60}\). Знайдіть два парних цілих числа.
- Сума зворотних двох послідовних натуральних непарних чисел дорівнює\(\frac{16}{63}\). Знайти цілі числа.
- Різниця взаємних двох послідовних натуральних чисел дорівнює\(\frac{1}{24}\). Знайдіть два парних цілих числа.
- Різниця взаємних двох послідовних натуральних непарних чисел дорівнює\(\frac{2}{99}\). Знайти цілі числа.
- Якщо\(3\) раз зворотне більшого з двох послідовних цілих чисел віднімається з\(2\) разів зворотного меншого, то результат є\(\frac{1}{2}\). Знайдіть два цілих числа.
- Якщо\(3\) раз зворотне меншого з двох послідовних цілих чисел віднімається з\(7\) разів зворотного більшого, то результат є\(\frac{1}{2}\). Знайдіть два цілих числа.
- Додатне ціле число\(5\) менше іншого. Якщо зворотне від меншого цілого числа віднімається з\(3\) разів зворотне більшого, то результат є\(\frac{1}{12}\). Знайдіть два цілих числа.
- Додатне ціле число\(6\) менше іншого. Якщо зворотне від меншого цілого числа віднімається з\(10\) разів зворотне більшого, то результат є\(\frac{3}{7}\). Знайдіть два цілих числа.
- Відповідь
-
1. {\(5, 10\)}
3. {\(4, 8\)}
5. {\(6, 8\)}
7. {\(10, 12\)}
9. {\(6, 8\)}
11. {\(1, 2\)} або {\(−4, −3\)}
13. {\(4, 9\)} або {\(15, 20\)}
Вправа\(\PageIndex{5}\) Uniform Motion Problems
Використовуйте алгебру для вирішення наступних програм.
- Джеймс може бігати підтюпцем вдвічі швидше, ніж він може ходити. Він зміг пробігти перші\(9\) кілометри до бабусиного будинку, але потім втомився і пройшов залишилися\(1.5\) кілометри. Якщо загальна поїздка зайняла\(2\) години, то якою була його середня швидкість бігу підтюпцем?
- У відрядженні виконавчий пройшов\(720\) милі на реактивних літаках, а потім ще\(80\) милі на вертольоті. Якщо реактивний літак\(3\) усереднював швидкість вертольота і загальна поїздка зайняла\(4\) години, то якою була середня швидкість реактивного літака?
- Саллі змогла проїхати в середньому\(20\) милі на годину швидше на своєму автомобілі після того, як рух розчистився. Вона проїхала\(23\) милі в пробці перед тим, як він розчистився, а потім проїхав ще\(99\) Якщо загальна поїздка зайняла\(2\) години, то яка у неї середня швидкість руху?
- Гаррі проїхав\(15\) милі в автобусі, а потім ще\(72\) милі на поїзді. Якщо поїзд був на\(18\) милі на годину швидше автобуса і загальна поїздка зайняла\(2\) години, то якою була середня швидкість поїзда?
- Автобус в середньому\(6\) милі на годину швидше, ніж тролейбус. Якщо автобус проїжджає\(90\) милі в той же час він приймає тролейбус, щоб проїхати\(75\) милі, то яка швидкість кожного?
- Легковий автомобіль в середньому\(16\) милі на годину швидше, ніж автобус. Якщо автобус проїжджає\(56\) милі в той же час, коли пасажирський автомобіль проїжджає\(84\) милі, то яка швидкість кожного?
- Легкий літак проїжджає\(2\) милі на годину менше, ніж вдвічі швидше, ніж легковий автомобіль. Якщо пасажирський автомобіль може проїхати\(231\) милі в той же час, який займає літак, щоб пройти\(455\) милі, то яка середня швидкість кожного?
- Мері може пробігти\(1\) милю на годину більш ніж в два рази швидше, ніж Білл може ходити. Якщо Білл може пройти\(3\) милі в той же час, коли Мері\(7.2\) пробігає милі, то яка середня швидкість ходьби Білла?
- Літак, що подорожує з\(20\) -миля на годину попутного вітру охоплює\(270\) милі. У зворотній поїздці проти вітру він долає\(190\) кілометри за однакову кількість часу. Яка швидкість літака в нерухомому повітрі?
- Реактивний авіалайнер, який подорожує з\(30\) -миля на годину попутного вітру охоплює\(525\) милі в тій же кількості часу, коли він здатний подорожувати\(495\) милями після того, як попутний вітер полегшується до\(10\) миль на годину. Яка швидкість авіалайнера в нерухомому повітрі?
- Човен в середньому\(16\) милі на годину в негазованій воді. З течією човен може проїхати\(95\) милі в той же час, коли вона подорожує\(65\) милями проти нього. Яка швидкість струму?
- Річковий екскурсійний човен в середньому\(7\) милі на годину в негазованій воді. Якщо загальна\(24\) -миля тур вниз по річці і\(24\) миль назад займає\(7\) години, то як швидко течія річки?
- Якщо течія річки протікає в середньому\(3\) милі на годину, то екскурсійний човен робить\(9\) -мильний тур вниз за течією з течією і назад\(9\) милями проти течії в\(4\) годинами. Яка середня швидкість човна в негазованій воді?
- Джейн гребла її каное проти\(1\) -миля на годину поточних\(12\) миль вгору за течією, а потім повернула\(12\) милі назад за течією. Якщо загальна поїздка зайняла\(5\) години, то з якою швидкістю Джейн може грести в негазованій воді?
- Хосе проїхав\(15\) милі, щоб забрати сестру, а потім повернувся додому. На зворотній поїздці він зміг в середньому\(15\) милі на годину швидше, ніж він зробив у поїздці, щоб забрати її. Якщо загальна поїздка зайняла\(1\) годину, то якою була середня швидкість Хосе на зворотній поїздці?
- Баррі проїхав\(24\) милі до міста, а потім назад за\(1\) годину. На зворотній поїздці він зміг в середньому\(14\) милі на годину швидше, ніж він усереднений під час поїздки в місто. Якою була його середня швидкість під час поїздки в місто?
- Джеррі веслував на байдарці вгору за течією проти\(1\) -милі на годину протягом\(12\) миль. Зворотна поїздка вниз за течією з\(1\) -миля на годину струму зайняла\(1\) годину менше часу. Як швидко Джеррі може веслувати байдарку в негазованій воді?
- Легкому літаку потрібно\(1\) годину більше часу, щоб пролетіти\(360\) милі проти\(30\) - милі на годину зустрічного вітру, ніж це робить, щоб пролетіти однакову відстань з ним. Яка швидкість літака в спокійному повітрі?
- Відповідь
-
1. \(6\)миль на годину
3. \(46\)миль на годину
5. Тролейбус:\(30\) милі на годину; автобус:\(36\) милі на годину
7. Легковий автомобіль:\(66\) милі на годину; літак:\(130\) милі на годину
9. \(115\)миль на годину
11. \(3\)миль на годину
13. \(6\)миль на годину
15. \(40\)миль на годину
17. \(5\)миль на годину
Вправа\(\PageIndex{6}\) Work-Rate Problems
Використовуйте алгебру для вирішення наступних програм.
- Джеймс може малювати офіс сам за кілька\(7\) годин. Менні малює офіс за\(10\) годинами. Скільки часу знадобиться їм, щоб розфарбувати офіс, що працюють разом?
- Баррі може самостійно прокласти цегляну під'їзну дорогу за\(12\) лічені години. Роберт виконує ту ж роботу за\(10\) годинами. Скільки часу знадобиться їм, щоб укласти цегляну під'їзну доріжку, що працює разом?
- Джеррі може деталізувати автомобіль самостійно за\(50\) лічені хвилини. Саллі виконує ту ж роботу за\(1\) годину. Скільки часу знадобиться їм, щоб деталізувати автомобіль, який працює разом?
- Хосе може побудувати невеликий сарай самостійно за кілька\(26\) годин. Олексій будує такий же невеликий сарай за\(2\) кілька днів. Скільки часу знадобиться їм, щоб побудувати сарай, який працює разом?
- Еллісон може самостійно завершити маршрут продажів за кілька\(6\) годин. Працюючи з асоційованим, вона завершує маршрут за\(4\) лічені години. Скільки часу знадобилося б її співрозмовнику, щоб самостійно завершити маршрут?
- Джеймс може підготувати і пофарбувати будинок самостійно за кілька\(5\) днів. Працюючи зі своїм братом Брайаном, вони можуть це зробити за кілька\(3\) днів. Скільки часу знадобилося б Брайану, щоб підготувати і пофарбувати будинок самостійно?
- Джо може зібрати комп'ютер самостійно за\(1\) годину. Працюючи з помічником, він може зібрати комп'ютер за\(40\) лічені хвилини. Скільки часу займе його помічник, щоб зібрати комп'ютер, що працює самостійно?
- Помічник вчителя може оцінювати класні домашні завдання самостійно за\(1\) годину. Якщо вчитель допомагає, то оцінку можна завершити за\(20\) лічені хвилини. Скільки часу знадобиться вчителю, щоб оцінювати документи, що працюють поодинці?
- Більша труба заповнює резервуар для води в два рази швидше, ніж труба меншого розміру. Коли використовуються обидві труби, вони заповнюють бак за\(5\) годинами. Якщо більшу трубу залишити, то скільки часу займе менша труба, щоб заповнити бак?
- Новіший принтер може друкувати вдвічі швидше, ніж старий принтер. Якщо обидва принтери, що працюють разом, можуть надрукувати партію флаєрів за\(45\) лічені хвилини, то скільки часу знадобиться новішому принтеру, щоб надрукувати партію, що працює поодинці?
- Працюючи поодинці, Генрі займає\(9\) години довше, ніж Мері, щоб очистити килими у всьому офісі. Працюючи разом, вони прибирають килими за\(6\) годинами. Скільки часу знадобилося б Мері, щоб очистити офісні килими, якби Генрі не був там, щоб допомогти?
- Працюючи поодинці, Монік займає\(4\) години довше, ніж Одрі, щоб записати інвентар всього магазину. Працюючи разом, вони проводять інвентаризацію за\(1.5\) годинами. Скільки часу знадобилося б Одрі, щоб записати інвентар, що працює поодинці?
- Джеррі може укласти плитковий підлогу в\(3\) години менше часу, ніж Джейк. Якщо вони працюють разом, підлога займає\(2\) години. Скільки часу займе Джеррі, щоб укласти підлогу самостійно?
- Джеремі може побудувати модельний літак за\(5\) години менше часу, ніж його брат. Працюючи разом, їм потрібні\(6\) години, щоб побудувати літак. Скільки часу знадобиться Джеремі, щоб побудувати модель літака, що працює поодинці?
- Гаррі може намалювати сарай сам за кілька\(6\) годин. Джеремі може пофарбувати той же сарай сам за кілька\(8\) годин. Скільки часу знадобиться їм, щоб пофарбувати два сараї, що працюють разом?
- Джо збирає комп'ютер сам за\(1\) годину. Працюючи з помічником, він може збирати\(10\) комп'ютери за\(6\) годинами. Скільки часу займе його помічник, щоб зібрати\(1\) комп'ютер, що працює поодинці?
- Джеррі може укласти плитковий підлогу за\(3\) годинами, а його помічник може виконати ту ж роботу за кілька\(4\) годин. Якщо Джеррі почне роботу і його помічник приєднується до нього через 1 годину, то скільки часу знадобиться, щоб укласти підлогу?
- Працюючи поодинці, Монік займає\(6\) години, щоб записати інвентаризацію всього магазину, тоді як Одрі займає лише\(4\) години, щоб виконати ту ж роботу. Скільки часу вони працюватимуть разом, якщо Моніка піде на\(2\) години раніше?
- Відповідь
-
1. \(4 \frac{2}{17}\)годин
3. \(27 \frac{3}{11}\)хвилин
5. \(12\)годин
7. \(2\)годин
9. \(15\)годин
11. \(9\)годин
13. \(3\)годин
15. \(6\frac{6}{7}\)годин
17. \(2 \frac{1}{7}\)годин
