7.1: Спрощення раціональних виразів

Last updated
Save as PDF

Page ID: 58065

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте обмеження до області раціонального виразу.
Спростіть раціональні вирази.
Спростіть вирази з протилежними біноміальними факторами.
Спростити і оцінити раціональні функції.

Раціональні вирази, оцінка та обмеження

Раціональне число, або дріб$\frac{a}{b}$, - це дійсне число, яке визначається як частка двох цілих чисел a та b, де$b≠0$. Аналогічно ми визначаємо раціональний вираз$\frac{P}{Q}$, або алгебраїчний дріб, як частку двох многочленів P і Q, де$Q≠0$. Нижче наведено кілька прикладів раціональних виразів:

Приклад$\frac{x+3}{x-5}$ складається з лінійних виразів як в чисельнику, так і в знаменнику. Оскільки знаменник містить змінну, цей вираз визначається не для всіх значень x.

Приклад$\PageIndex{1}$

Оцініть$\frac{x+3}{x-5}$ для множини x -значень$\{-3,4,5\}$.

Рішення:

Підставляємо значення в для x.

$\begin{array}{c|c}{x=-3} & {x=4} & {x=5} \\ \hline \frac{x+3}{x-5}=\frac{(\color{OliveGreen}{-3}\color{black}{)}+3}{(\color{OliveGreen}{-3}\color{black}{)}-5} & {\frac{x+3}{x-5}=\frac{(\color{OliveGreen}{4}\color{black}{)}+3}{(\color{OliveGreen}{4}\color{black}{)}-5}} & {\frac{x+3}{x-5}=\frac{(\color{OliveGreen}{5}\color{black}{)}+3}{(\color{OliveGreen}{5}\color{black}{)}-5}} \\ {=\frac{0}{-8}}&{=\frac{7}{-1}}&{=\frac{8}{0}\:\:\color{Cerulean}{Undefined}}\\{=0}&{=-7}&{}\end{array}$

Відповідь:

Коли$x=−3$, значення раціонального виразу є$0$; коли$x=4$, значення раціонального виразу є$−7$; а коли$x=5$, значення раціонального виразу невизначено.

Цей приклад ілюструє, що змінні обмежені значеннями, які не роблять знаменник рівним 0. Домен раціонального виразу - це сукупність дійсних чисел, для яких воно визначено, а обмеження - дійсні числа, для яких вираз не визначено. Ми часто виражаємо область раціонального вираження з точки зору його обмежень.

Приклад$\PageIndex{2}$

Знайдіть домен наступного:

$\frac{x+7}{2 x^{2}+x-6}$

Рішення:

У цьому прикладі чисельник$x+7$ є лінійним виразом, а знаменник$2x^{2}+x−6$ - квадратичним виразом. Якщо перерахувати знаменник, то отримаємо еквівалентний вираз.

$\frac{x+7}{2 x^{2}+x-6}=\frac{x+7}{(2 x-3)(x+2)}$

Оскільки раціональні вирази невизначені, коли знаменник дорівнює 0, ми хочемо знайти значення для x, які роблять його 0. Для цього застосовують властивість нульового добутку. Встановіть кожен множник в знаменнику рівним 0 і вирішуйте.

$(2 x-3)(x+2)=0$

$\begin{array}{ll}{2 x-3=0} & {\text { or } \quad x+2=0} \\ {2 x=3} &\qquad\quad {x=-2} \\ {x=\frac{3}{2}}\end{array}$

Зроблено висновок, що вихідний вираз визначено для будь-якого дійсного числа, крім$\frac{3}{2}$ і$−2$. Ці два значення є обмеженнями для домену. Важливо зазначити, що$−7$ це не є обмеженням для домену, оскільки вираз визначається як 0, коли чисельник дорівнює 0.

$\begin{aligned} \frac{x+7}{2 x^{2}+x-6} &=\frac{(\color{OliveGreen}{-7}\color{black}{)}+7}{2(\color{OliveGreen}{-7}\color{black}{)}^{2}+(\color{OliveGreen}{-7}\color{black}{)}-6} \\ &=\frac{0}{98-7-6} \\ &=\frac{0}{85} \\ &=0 \end{aligned}$

Відповідь:

Домен складається з будь-якого дійсного числа x, де$x≠\frac{3}{2}$ і$x≠−2$.

Ми можемо висловити домен попереднього прикладу за допомогою позначення наступним чином:

$\begin{array}{cc}{\color{Cerulean} { Set-builder\: notation}} & {\color{Cerulean} {Interval\: notation}} \\ {\left\{x | x \neq-2, \frac{3}{2}\right\}} & {(-\infty,-2) \cup\left(-2, \frac{3}{2}\right) \cup\left(\frac{3}{2}, \infty\right)}\end{array}$

Обмеження до області раціонального виразу визначаються знаменником. Ігноруйте чисельник при знаходженні цих обмежень.

Приклад$\PageIndex{3}$

Визначаємо домен:

$\frac{x^{4}+x^{3}-2x^{2}-x}{x^{2}-1}$

Рішення:

Щоб знайти обмеження на домен, встановіть знаменник рівний 0 і вирішіть:

$\begin{array}{r}{x^{2}-1=0} \\ {(x+1)(x-1)=0}\end{array}$

$\begin{array}{rlrl}{x+1} & {=0} & {\text { or }} & {x-1=0} \\ {x} & {=-1} & &{x=1}\end{array}$

Ці два значення призводять до того, що знаменник дорівнює 0. Отже, вони обмежені з домену.

Відповідь:

Домен складається з будь-якого дійсного числа x, де$x≠±1$.

Приклад$\PageIndex{4}$

Визначаємо домен:

$\frac{x^{2}-25}{4}$

Рішення:

У знаменнику немає змінної і, отже, немає обмежень для домену.

Відповідь:

Домен складається з усіх дійсних чисел, R.

Спрощення раціональних виразів

При спрощенні дробів шукайте загальні чинники, які скасовують. Наприклад,

$\frac{12}{60}=\frac{1 \cdot \color{Cerulean}{\cancel{\color{black}{12}}}}{5 \cdot \color{Cerulean}{\cancel{\color{black}{12}}}}\color{black}{=}\frac{1}{5}$

Ми говоримо, що дріб$\frac{12}{60}$ еквівалентний$\frac{1}{5}$. Дроби знаходяться в найпростішому вигляді, якщо чисельник і знаменник не мають спільного множника, крім$1$. Аналогічно при роботі з раціональними виразами шукайте фактори для скасування. Наприклад,

$\frac{x+4}{(x-3)(x+4)}=\frac{1 \cdot\color{Cerulean}{\cancel{\color{black}{(x+4)}}}}{(x-3)\color{Cerulean}{\cancel{\color{black}{(x+4)}}}}=\frac{1}{x-3}$

Отриманий раціональний вираз еквівалентний, якщо він має один і той же домен. Тому ми повинні записати обмеження і написати

$\frac{x+4}{(x-3)(x+4)}=\frac{1}{x-3}, \text { where } x \neq 3 \text { and } x \neq-4$

У словах,$\frac{x+4}{(x-3)(x+4)}$ еквівалентно$\frac{1}{x-3}$, якщо$x≠3$ і$x≠−4$. Ми можемо перевірити це, вибравши кілька значень, за допомогою яких можна оцінити обидва вирази, щоб побачити, чи однакові результати. Тут вибираємо$x=7$ і оцінюємо наступним чином:

$\begin{aligned} \frac{x+4}{(x-3)(x+4)} &=\frac{1}{x-3} \\ \frac{(\color{OliveGreen}{7}\color{black}{)}+4}{(\color{OliveGreen}{7}\color{black}{-}3)(\color{OliveGreen}{7}\color{black}{+}4)} &=\frac{1}{(\color{OliveGreen}{7}\color{black}{)}-3} \\ \frac{11}{(4)(11)} &=\frac{1}{4} \\ \frac{1}{4} &=\frac{1}{4}\:\:\color{Cerulean}{\checkmark} \end{aligned}$

Важливо вказати обмеження перед спрощенням раціональних виразів, оскільки спрощений вираз може бути визначено для обмежень оригіналу. При цьому вирази не рівнозначні. Тут −4 визначено для спрощеного еквівалента, але не для оригіналу, як показано нижче:

$\begin{aligned} \frac{x+4}{(x-3)(x+4)} &=\frac{1}{x-3} \\ \frac{(\color{OliveGreen}{-4}\color{black}{)}+4}{(\color{OliveGreen}{-4}\color{black}{-}3)(\color{OliveGreen}{-4}\color{black}{+}4)} &=\frac{1}{(\color{OliveGreen}{-4}\color{black}{)}-3} \\ \frac{0}{(-7)(0)} &=\frac{1}{-7} \\ \frac{0}{0} &=-\frac{1}{7} \quad \color{red}{x} \end{aligned}$

Приклад$\PageIndex{5}$

Спростити і сформулювати обмеження:

$\frac{25 x^{2}}{15 x^{3}}$

Рішення:

У цьому прикладі вираз undefined, коли x дорівнює 0.

$\frac{25 x^{2}}{15 x^{3}}=\frac{25(\color{OliveGreen}{0}\color{black}{)}^{2}}{15(\color{OliveGreen}{0}\color{black}{)}^{3}}=\frac{0}{0}\:\:\color{Cerulean}{Undefined}$

Тому домен складається з усіх дійсних чисел x, де$x≠0$. При такому розумінні ми можемо скасувати загальні фактори.

$\begin{aligned} \frac{25 x^{2}}{15 x^{3}} &=\frac{5 \cdot \color{Cerulean}{\cancel{\color{black}{5 x^{2}}}}}{3 x \cdot \color{Cerulean}{\cancel{\color{black}{5 x^{2}}}}} \\ &=\frac{5}{3 x} \end{aligned}$

Відповідь:

$\frac{5}{3 x}$, де$x\neq 0$

Приклад$\PageIndex{6}$

Викладіть обмеження та спростіть:

$\frac{3x(x-5)}{(2x-1)(x-5)}$

Рішення:

Для визначення обмежень встановіть знаменник рівний 0 і вирішіть.

$(2 x+1)(x-5)=0$

$\begin{array}{rlrl}{2 x+1} & {=0} & {\text { or }} & {x-5=0} \\ {2 x} & {=-1} & &{x=5} \\ {x} & {=-\frac{1}{2}}\end{array}$

Домен складається з усіх дійсних чисел, крім$−\frac{1}{2}$ і$5$. Далі знаходимо еквівалентний вираз шляхом скасування загальних факторів.

$\begin{aligned} \frac{3 x(x-5)}{(2 x+1)(x-5)} &=\frac{3 x \color{Cerulean}{\cancel{\color{black}{(x-5)}}}}{(2 x+1)\color{Cerulean}{\cancel{\color{black}{(x-5)}}}} \\ &=\frac{3 x}{2 x+1} \end{aligned}$

Відповідь:

$\frac{3 x}{2 x+1}$, де$x\neq -\frac{1}{2}$ і$x\neq 5$

Як правило, раціональні вирази не даються в факторованій формі. Якщо це так, спочатку коефіцієнт, а потім скасуйте. Кроки викладені в наступному прикладі.

Приклад$\PageIndex{7}$

Викладіть обмеження та спростіть:

$\frac{3 x+6}{x^{2}+x-2}$

Рішення:

Крок 1: Повністю перерахуйте чисельник та знаменник.

$\frac{3 x+6}{x^{2}+x-2}=\frac{3(x+2)}{(x-1)(x+2)}$

Крок 2: Визначте обмеження для домену. Для цього встановлюємо знаменник рівним 0 і вирішуємо.

$(x-1)(x+2)=0$

$\begin{array}{rlrl}{x-1} & {=0} & {\text { or }} & {x+2=0} \\ {x} & {=1} && {x=-2}\end{array}$

Домен складається з усіх дійсних чисел, крім$−2$ і$1$.

Крок 3: Скасуйте загальні фактори, якщо такі є.

$\begin{aligned} \frac{3 x+6}{x^{2}+x-2} &=\frac{3\color{Cerulean}{\cancel{\color{black}{(x+2)}}}}{(x-1)\color{Cerulean}{\cancel{\color{black}{(x+2)}}}} \\ &=\frac{3}{x-1} \end{aligned}$

Відповідь:

$\frac{3}{x-1}$, де$x\neq 1$ і$x\neq -2$

Приклад$\PageIndex{8}$

Викладіть обмеження та спростіть:

Рішення:

Спочатку множник чисельник і знаменник.

Будь-яке значення x, що призводить до значення$0$ в знаменнику, є обмеженням. Шляхом огляду ми визначаємо, що домен складається з усіх дійсних чисел, крім$4$ і$3$. Далі скасуйте загальні фактори.

$\begin{array}{l}{=\color{black}{\frac{\color{Cerulean}{\cancel{\color{black}{(x-3)}}}\color{black}{(x+10)}}{(x-4)\color{Cerulean}{\cancel{\color{black}{(x-3)}}}}}} \\ {=\frac{x+10}{x-4}}\end{array}$

Відповідь:

$\frac{x+10}{x-4}$, де$x\neq 3$ і$x\neq 4$

Важливо пам'ятати, що ми можемо скасувати лише фактори продукту. Поширеною помилкою є скасування термінів. Наприклад,

Вправа$\PageIndex{1}$

Викладіть обмеження та спростіть:

$\frac{x^{2}-16}{5x^{2}-20x}$

Відповідь: $\frac{x+4}{5 x}$, де$x\neq 0$ і$x\neq 4$

У деяких прикладах зробимо широке припущення, що знаменник ненульовий. Коли ми робимо це припущення, нам не потрібно визначати обмеження.

Приклад$\PageIndex{9}$

Спростити:

(Припустимо, що всі знаменники ненульові.)

Рішення:

Фактор чисельника шляхом групування. Коефіцієнт знаменника за допомогою формули різниці квадратів.

Далі скасуйте загальні фактори.

$\begin{array}{l}{=\frac{\color{Cerulean}{\cancel{\color{black}{(x+y)}}}\color{black}{(y-3)}}{\color{Cerulean}{\cancel{\color{black}{(x+y)}}}\color{black}{(x-y)}}} \\ {=\frac{y-3}{x-y}}\end{array}$

Відповідь:

$\frac{y-3}{x-y}$

Протилежні біноміальні фактори

Нагадаємо, що протилежним дійсному числу a є −a. Аналогічно, ми можемо визначити протилежність многочлена P як −P. Розглянемо спочатку протилежне біноміалу$a−b$:

\[-(a-b)=-a+b=b-a\]

Це призводить нас до протилежного біноміального властивості:

\[-(a-b)=(b-a)\]

Це еквівалентно факторингу a$–1$.

\[(b-a)=-1(a-b)\]

Якщо$a≠b$, то ми можемо розділити обидві сторони на$(a−b)$ і отримати наступне:

$\frac{b-a}{a-b}=-1$

Приклад$\PageIndex{10}$

Викладіть обмеження та спростіть:

$\frac{3-x}{x-3}$

Рішення:

За допомогою огляду ми можемо побачити, що знаменником є$0$ if$x=3$. Тому$3$ є обмеження на домен. Застосуйте протилежну біноміальну властивість до чисельника, а потім скасуйте.

Відповідь:

$\frac{3-x}{x-3}$, де$x\neq 3$

Оскільки додавання є комутативним, ми маємо

\[(a+b)=(b+a)\]

або

$\frac{b+a}{a+b}=1$

Слідкуйте за тим, щоб не сплутати це з протилежним біноміальним властивістю. Також важливо нагадати, що

$\frac{-a}{b}=-\frac{a}{b}=\frac{a}{-b}$

Іншими словами, покажіть негативний дріб, помістивши негативний знак в чисельнику, перед рядком дробу, або в знаменнику. Як правило, негативних знаменників уникають.

Приклад$\PageIndex{11}$

Спростити і сформулювати обмеження:

$\frac{4-x^{2}}{x^{2}+3 x-10}$

Рішення:

Почніть з факторингу чисельника і знаменника.

$\begin{aligned} \frac{4-x^{2}}{x^{2}+3 x-10} &=\frac{(2+x)\color{Cerulean}{(2-x)}}{\color{Cerulean}{(x-2)}\color{black}{(}x+5)}\qquad\qquad\quad\color{Cerulean}{The\:restrictions\:are\:x\neq2\:and\:x\neq-5.} \\ &=\frac{(2+x) \cdot(-1)\color{Cerulean}{\cancel{\color{black}{(x-2)}}}}{\color{Cerulean}{\cancel{\color{black}{(x-2)}}}\color{black}{(x+5)}}\quad\:\color{Cerulean}{Apply\:the\:opposite\:binomial\:property,\:then\:cancel.} \\ &=\frac{(2+x) \cdot(-1)}{(x+5)} \\ &=-\frac{2+x}{x+5} \quad \text { or } \quad=-\frac{x+2}{x+5} \end{aligned}$

Відповідь:

$-\frac{x+2}{x+5}$, де$x\neq 2$ і$x\neq -5$

Вправа$\PageIndex{2}$

Спростити і сформулювати обмеження:

Відповідь: $\frac{-2x+3}{x+5}$, де$x\neq\pm 5$

Раціональні функції

Раціональні функції мають вигляд

\[r(x)=\frac{p(x)}{q(x)}\],

де p (x) і q (x) - многочлени і q (x) 0. Домен раціональної функції складається з усіх дійсних чисел x таких, що знаменник q (x) 0.

Приклад$\PageIndex{12}$

Спростити:$r(x)=\frac{2 x^{2}+5 x-3}{6 x^{2}+18 x}$.
Вказати домен.
Розрахувати$r(-2)$.

Рішення:

а. щоб спростити раціональну функцію, спочатку коефіцієнт, а потім скасувати.

$\begin{aligned} r(x) &=\frac{2 x^{2}+5 x-3}{6 x^{2}+18 x} \\ &=\frac{(2 x-1)\color{Cerulean}{\cancel{\color{black}{(x+3)}}}}{6 x\color{Cerulean}{\cancel{\color{black}{(x+3)}}}} \\ &=\frac{2 x-1}{6 x} \end{aligned}$

б. для визначення обмежень встановіть знаменник вихідної функції рівним 0 і вирішіть.

$\begin{array}{l}{6 x^{2}+18 x=0} \\ {6 x(x+3)=0}\end{array}$

$\begin{array}{cc}{6 x=0} & {\text { or } \quad x+3=0} \\ {x=0} & {x=-3}\end{array}$

Домен складається з усіх дійсних чисел x, де$x≠0$ і$x≠−3$.

c Оскільки не$−2$ є обмеженням, підставляємо його змінною x за допомогою спрощеної форми.

$\begin{aligned} r(x) &=\frac{2 x-1}{6 x} \\ r(-2) &=\frac{2(\color{OliveGreen}{-2}\color{black}{)}-1}{6(\color{OliveGreen}{-2}\color{black}{)}} \\ &=\frac{-4-1}{-12} \\ &=\frac{-5}{-12} \\ &=\frac{5}{12} \end{aligned}$

Відповідь:

a.$\frac{2 x-1}{6 x}$ b. Доменом є всі дійсні числа, крім$0$ і$−3$. c.$r(-2) = \frac{5}{12}$

Якщо функція витрат$C(x)$ представляє вартість виробництва х одиниць, то середня вартість$c(x)$ - це вартість, поділена на кількість вироблених одиниць.

\[\color{Cerulean}{Average\:cost}\color{black}{:} c(x)=\frac{C(x)}{x}\]

Приклад$\PageIndex{13}$

Вартість в доларах виробництва футболок з логотипом компанії задається тим$C(x)=7x+200$, де х представляє кількість вироблених сорочок. Визначаємо середню собівартість виробництва

40 футболок
250 футболок
1000 футболок

Рішення:

Налаштуйте функцію, що представляє середню вартість.

$c(x)=\frac{C(x)}{x}=\frac{7 x+200}{x}$

Далі обчислюємо c (40), c (250) і c (1000).

$\begin{aligned} c(40) &=\frac{7(\color{OliveGreen}{40}\color{black}{)}+200}{\color{OliveGreen}{40}}=\frac{280+200}{40}=\frac{480}{40}=12.00 \\ c(250) &=\frac{7(\color{OliveGreen}{250}\color{black}{)}+200}{\color{OliveGreen}{250}}=\frac{1750+200}{250}=\frac{1950}{250}=7.80 \\ c(1000) &=\frac{7(\color{OliveGreen}{1000}\color{black}{)}+200}{\color{OliveGreen}{1000}}=\frac{7000+200}{1000}=\frac{7200}{1000}=7.20 \end{aligned}$

Відповідь:

Якщо випускається 40 футболок, то середня вартість однієї футболки становить $12,00.
Якщо випускається 250 футболок, то середня вартість однієї футболки становить 7,80$.
Якщо випускається 1000 футболок, то середня вартість однієї футболки становить 7,20$.

Ключові виноси

Раціональні вирази зазвичай визначаються не для всіх дійсних чисел. Дійсні числа, які дають значення 0 в знаменнику, не є частиною домену. Ці значення називаються обмеженнями.
Спрощення раціональних виразів схоже на спрощення дробів. Спочатку множник чисельник і знаменник, а потім скасуйте загальні фактори. Раціональні вирази спрощуються, якщо в чисельнику і знаменнику немає загальних факторів, відмінних від 1.
Спрощені раціональні вирази еквівалентні значенням в області вихідного виразу. Обов'язково вкажіть обмеження, якщо знаменники не приймаються ненульовими.
Використовуйте протилежну біноміальну властивість для скасування біноміальних факторів, які передбачають віднімання. Використовуйте$−(a−b)=b−a$ для заміни факторів, які потім скасують. Не плутайте це з факторами, які передбачають додавання, такими як$(a+b)=(b+a)$.

Вправа$\PageIndex{3}$ Rational Expressions

Оцінити для заданого множини x -значень.

$5x; {−1, 0, 1}$
$\frac{4x^{3}}{x^{2}}; {−1, 0, 1} $
$\frac{1}{x+9}; {−10, −9, 0} $
$\frac{x+6}{x−5}; {−6, 0, 5}$
$\frac{3x(x−2)}{2x−1}; {0, \frac{1}{2}, 2}$
$\frac{9x^{2}−1}{x−7}; {0, \frac{1}{3}, 7} $
$5x^{2}−9; {−3, 0, 3}$
$\frac{x^{2}−2}{5x^{2}−3x−10}; {−5, −4, 5}$
Заповніть наступну діаграму:
$Скріншот (308) .png$
Малюнок$\PageIndex{1}$
Заповніть наступну діаграму:
$Скріншот (309) .png$
Малюнок$\PageIndex{2}$
Заповніть наступну діаграму:
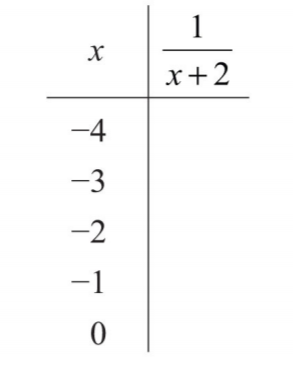$Скріншот (310) .png$
Малюнок$\PageIndex{3}$
Заповніть наступну діаграму:
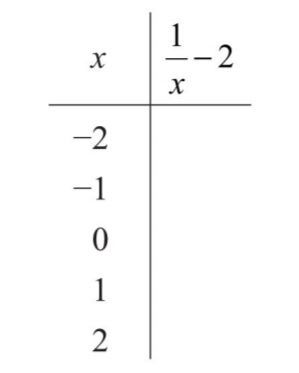$Знімок екрана (311) .png$
Малюнок$\PageIndex{4}$

Відповідь

1. $−5$, невизначений,$5$

3. $−1$, невизначений,$\frac{1}{9}$

5. $0$, невизначений,$0$

7. Невизначено,$−\frac{5}{9}$, невизначено

Знімок екрана (312) .png — Малюнок$\PageIndex{5}$

11.

Знімок екрана (313) .png — Малюнок$\PageIndex{6}$

Вправа$\PageIndex{4}$ Rational Expressions

Вага об'єкта залежить від його висоти над поверхнею землі. Якщо об'єкт важить 120 фунтів на поверхні землі, то його вага в фунтах, Ш, х милі над поверхнею наближається за формулою

$W=\frac{120\cdot 4000^{2}}{(4000+x)^{2}}$

Для кожної задачі нижче, приблизний вага 120-фунтового об'єкта на заданій висоті над поверхнею землі. (1 миля = 5280 футів)

100 миль
1000 миль
44 350 фут (ів)
90 000 футів

Відповідь

1. 114 фунтів

3. 119,5 фунтів

Вправа$\PageIndex{5}$ Rational Expressions

Співвідношення ціни та прибутку (P/E) - це показник, який використовується для порівняння оцінок аналогічних публічно торгуваних компаній. Коефіцієнт P/E розраховується з використанням ціни акцій та прибутку на акцію (EPS) за попередній 12-місячний період наступним чином:

P/E = Ціна за акцію прибуток на акцію

Якщо кожна акція акцій компанії оцінюється в $22.40, то розрахуйте коефіцієнт P/E, враховуючи наступні значення прибутку на акцію.

$1.40
$1.21
Що відбувається зі співвідношенням P/E, коли заробіток зменшується?
Що відбувається зі співвідношенням P/E при збільшенні прибутку?

Відповідь

1. 16

3. Збільшується коефіцієнт P/E.

Вправа$\PageIndex{6}$ Rational Expressions

Вкажіть обмеження для домену.

$\frac{1}{3x}$
$\frac{3x^{2}}{7x^{5}}$
$\frac{3x(x+1)}{x+4}$
$\frac{2x^{2}(x−3)}{x−1}$
$\frac{1}{5x−1}$
$\frac{x−2}{3x−2}$
$\frac{x−9}{5x(x−2)}$
$\frac{1}{(x−3)(x+6)}$
$\frac{x}{1−x^{2}}$
$\frac{x^{2}−9}{x^{2}−36}$
$\frac{1}{2x(x+3)(2x−1)}$
$\frac{x−3}{(3x−1)(2x+3)}$
$\frac{4x(2x+1)}{12x^{2}+x−1}$
$\frac{x−5}{3x^{2}−15x}$

Відповідь

1. $x≠0$

3. $x≠−4$

5. $x≠\frac{1}{5}$

7. $x≠0$і$x≠2$

9. $x≠±1$

11. $x≠0$,$x≠−3$, і$x≠\frac{1}{2}$

13. $x≠−\frac{1}{3}$і$x≠\frac{1}{4}$

Вправа$\PageIndex{7}$ Simplifying Rational Expressions

Зазначте обмеження, а потім спростіть.

$\frac{5x^{2}}{20x^{3}}$
$\frac{12x^{6}}{60x}$
$\frac{3x^{2}(x−2)}{9x(x−2)}$
$\frac{20(x−3)(x−5)}{6(x−3)(x+1)}$
$\frac{6x^{2}(x−8)}{36x(x+9)(x−8)}$
$\frac{16x^{2}−1}{(4x+1)^{2}}$
$\frac{9x^{2}−6x+1}{(3x−1)^{2}}$
$\frac{x−7}{x^{2}−49}$
$\frac{x^{2}−64}{x^{2}+8x}$
$\frac{x+10}{x^{2}−100}$
$\frac{2x^{3}−12x^{2}}{5x^{2}−30x}$
$\frac{30x^{5}+60x^{4}}{2x^{3}−8x}$
$\frac{2x−12}{x^{2}+x−6}$
$\frac{x^{2}−x−6}{3x^{2}−8x−3}$
$\frac{6x^{2}−25x+25}{3x^{2}+16x−35}$
$\frac{3x^{2}+4x−1}{5x^{2}−9}$
$\frac{x^{2}−10x+21}{x^{2}−4x−21}$
$\frac{x^{3}−1}{x^{2}−1}$
$\frac{x^{3}+8}{x^{2}−4}$
$\frac{x^{4}−1}{6x^{2}−4}$

Відповідь

1. $\frac{1}{4x}; x≠0$

3. $\frac{x}{3}; x≠0, 2$

5. $\frac{x}{6(x+9)}; x≠0,−9, 8$

7. $1; x≠\frac{1}{3}$

9. $\frac{x−8}{x}; x≠0,−8$

11. $\frac{2x}{5}; x≠0, 6$

13. $\frac{2x−12}{x^{2}+x−6}\; x≠−2, \frac{3}{2}$

15. $\frac{2x−5}{x+7}; x≠−7, \frac{5}{3}$

17. $\frac{x−3}{x+3}; x≠−3, 7$

19. $\frac{x^{2}-2 x+4}{x-2} ; x≠±2$

Вправа$\PageIndex{8}$ Simplifying Rational Expressions with Opposite Binomial Factors

Зазначте обмеження, а потім спростіть.

$\frac{x−9}{9−x}$
$\frac{3x−2}{2−3x}$
$\frac{x+6}{6+x}$
$\frac{3x+1}{1+3x}$
$\frac{(2x−5)(x−7)}{(7−x)(2x−1)}$
$\frac{(3x+2)(x+5)}{(x−5)(2+3x)}$
$\frac{x^{2}−4}{(2−x)^{2}}$
$\frac{16−9x^{2}}{(3x+4)^{2}}$
$\frac{4x^{2}(10−x)}{3x^{3}−300x}$
$−\frac{2x+1}{4x^{3}−49x}$
$\frac{2x^{2}−7x−4}{1−4x^{2}}$
$\frac{9x^{2}−4}{4x−6x^{2}}$
$\frac{x^{2}−5x−14}{7−15x+2x^{2}}$
$\frac{2x^{3}+x^{2}−2x−1}{1+x−2x^{2}}$
$\frac{x^{3}+2 x-3 x^{2}-6}{2+x^{2}}$
$\frac{27+x^{3}}{x^{2}+6x+9}$
$\frac{64−x^{3}}{x^{2}−8x+16}$
$\frac{x^{2}+4}{4−x^{2}}$

Відповідь

1. $−1; x≠9 $

3. $1; x≠−6 $

5. $\frac{−2x−5}{2x−1}; x≠\frac{1}{2},7$

7. $\frac{x+2}{x−2}; x≠2$

9. $−\frac{4x}{3(x+10)}; x≠±10, 0$

11. $\frac{x−4}{1−2x}; x≠±\frac{1}{2}$

13. $\frac{x+2}{2x−1}; x≠\frac{1}{2},7$

15. $x−3$; жодного

17. $\frac{−16+4x+x^{2}}{x−4}; x≠4$

Вправа$\PageIndex{9}$ Simplifying Rational Expressions with Opposite Binomial Factors

Спростити. (Припустимо, що всі знаменники ненульові.)

$−\frac{15x^{3}y^{2}}{5xy^{2}(x+y)}$
$\frac{14x^{7}y^{2}(x−2y)^{4}}{7x^{8}y(x−2y)^{2}}$
$\frac{y+x}{x^{2}−y^{2}}$
$\frac{y−x}{x^{2}−y^{2}}$
$\frac{x^{2}−y^{2}}{(x−y)^{2}}$
$\frac{a^{2}−ab−6b^{2}}{a^{2}−6ab+9b^{2}}$
$\frac{2a^{2}−11a+12}{−32+2a^{2}}$
$\frac{a^{2}b−3a^{2}}{3a^{2}−3ab}$
$\frac{x y^{2}-x+y^{3}-y}{x-x y^{2}}$
$\frac{x^{3}−xy^{2}−x^{2}y+y}{3x^{2}−2xy+y^{2}}$
$\frac{x^{3}−27}{x^{2}+3x+9}$
$\frac{x^{2}−x+1}{x^{3}+1}$

Відповідь

1. $−\frac{3x^{2}}{x+y}$

3. $\frac{1}{x−y}$

5. $\frac{x+y}{x−y}$

7. $\frac{2 a-3}{2(a+4)}$

9. $-\frac{x+y}{x}$

11. $x−3$

Вправа$\PageIndex{10}$ Rational Functions

Розрахуйте наступне.

$f(x)=\frac{5x}{x−3}; f(0), f(2), f(4)$
$f(x)=\frac{x+7}{x^{2}+1}; f(−1), f(0), f(1) $
$g(x)=\frac{x^{3}}{(x−2)^{2}}; g(0), g(2), g(−2) $
$g(x)=\frac{x^{2}−9}{9−x^{2}}; g(−2), g(0), g(2) $
$g(x)=\frac{x^{3}}{x^{2}+1}; g(−1), g(0), g(1)$
$g(x)=\frac{5x+1}{x^{2}−25}; g(−\frac{1}{5}), g(−1), g(−5)$

Відповідь

1. f (0) =0, f (2) =−10, f (4) =20

3. g (0) =0, g (2) невизначено, g (−2) =−$\frac{1}{2}$

5. g (−1) =−$\frac{1}{2}$, g (0) =0, g (1) =$\frac{1}{2}$

Вправа$\PageIndex{11}$ Rational Functions

Вкажіть обмеження для домену, а потім спростіть.

$f(x)=−\frac{3x^{2}−6x}{x^{2}+4x+4}$
$f(x)=\frac{x^{2}+6x+9}{2x^{2}+5x−3 }$
$g(x)=\frac{9−x}{x^{2}−81}$
$g(x)=\frac{x^{3}−27}{3−x}$
$g(x)=\frac{3x−15}{10−2x}$
$g(x)=\frac{25−5x}{4x−20}$
Вартість в доларах виробництва кавових кухлів з логотипом компанії задається тим$C(x)=x+40$, де х представляє кількість вироблених кухлів. Розрахуйте середню вартість виготовлення 100 кухлів і середню вартість виготовлення 500 кухлів.
Вартість в доларах оренди вантажівки, що рухається за добу, дається$C(x)=0.45x+90$, де х являє собою кількість пройдених миль. Розрахуйте середню вартість за милю, якщо вантажівка проїхала 250 миль за один день.
Вартість в доларах виробництва світшоти з нестандартним дизайном на спині дається$C(x)=1200+(12−0.05x)x$, де х представляє кількість вироблених сорочок. Розрахуйте середню вартість виготовлення 150 нестандартних сорочок.
Вартість в доларах виробництва виготовленої на замовлення литої деталі задається$C(x)=500+(3−0.001x)x$, де х являє собою кількість вироблених деталей. Розрахуйте середню вартість виготовлення 1000 нестандартних деталей.

Відповідь

1. $f(x)=−\frac{3x}{x+2}; x≠−2 $

3. $g(x)=−\frac{1}{x+9}; x≠±9 $

5. $g(x)=−\frac{3}{2}; x≠5 $

7. Середня вартість виробництва 100 кухлів становить $1,40 за кухоль. Середня вартість виробництва 500 кухлів становить $1.08 за кухоль.

9. $12.50

Вправа$\PageIndex{12}$ Discussion Board

Поясніть чому$\frac{b−a}{a−b}=−1$ і проілюструйте цей факт, підставивши деякі числа для змінних.
Поясніть чому$\frac{b+a}{a+b}=1$ і проілюструйте цей факт, підставивши деякі числа для змінних.
Поясніть, чому ми не можемо скасувати x у виразі$\frac{x}{x+1}$.

Відповідь

1. Відповіді можуть відрізнятися

3. Відповіді можуть відрізнятися