7.7: Варіація

Last updated
Save as PDF

Page ID: 58078

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Вирішуйте програми, що включають пряму зміну.
Вирішуйте програми, що включають зворотну варіацію.
Вирішити додатки, що включають спільну варіацію

Пряма варіація

Розглянемо вантажний поїзд, що рухається з постійною швидкістю 30 миль на годину. Рівняння, яке виражає відстань, пройдену з цією швидкістю за часом, задається

$D=30t$

Через$1$ годину поїзд пройшов$30$ кілометри, через$2$ години поїзд проїхав$60$ кілометри і так далі. Ми можемо побудувати діаграму і графік це відношення.

Таблиця$\PageIndex{1}$
Час$t$, в годиниках	Відстань$D=30t$
\ (t\), у годинах">0	\ (Д = 30т\) ">0
\ (t\), у годинах">1	\ (Д = 30т\) ">30
\ (t\), у годинах">2	\ (Д = 30т\) ">60
\ (t\), у годинах">3	\ (Д = 30т\) ">90
\ (t\), у годинах">4	\ (Д = 30т\) ">120

Знімок екрана (326) .png — Малюнок$\PageIndex{1}$

У цьому прикладі ми бачимо, що відстань змінюється з часом як добуток постійної швидкості,$30$ миль на годину та змінної,$t$. Цей зв'язок описується як пряма варіація і$30$ називається постійною варіації. Крім того, якщо ми розділимо обидві сторони$D=30t$ на$t$ ми маємо

$\frac{D}{t}=30$

У такому вигляді розумно сказати, що$D$ пропорційно$t$, де$30$ знаходиться константа пропорційності. Загалом, у нас

Таблиця$\PageIndex{2}$
Ключові слова	Переклад
«$y$змінюється безпосередньо як$x$»	\[y=kx\]
«$y$прямо пропорційно$x$»
«$y$пропорційно$x$»

Тут$k$ ненульова і називається константою варіації або константою пропорційності.

Приклад$\PageIndex{1}$

Окружність кола прямо пропорційна його діаметру, а константа пропорційності -$π$. Якщо окружність вимірюється$20$ дюймами, то який радіус кола?

Рішення:

$C$Дозволяти представляти окружність кола.

$d$Дозволяти представляти діаметр кола.

Використовуйте той факт, що «окружність прямо пропорційна діаметру», щоб написати рівняння, яке пов'язує дві змінні.

$C=kd$

Нам дано, що «константа пропорційності є»$π$, або$k=π$. Тому пишемо

$C=πd$

Тепер скористайтеся цією формулою, щоб знайти,$d$ коли довжина окружності дорівнює$20$ дюймам.

$\begin{aligned} 20&=\pi d \\ \frac{20}{\color{Cerulean}{\pi}}&=\frac{\pi d}{\color{Cerulean}{\pi}}\\ \frac{20}{\pi}&=d \end{aligned}$

Радіус кола,$r$, дорівнює половині його діаметра.

$\begin{aligned} r&=\frac{d}{2} \\ &=\frac{\color{OliveGreen}{\frac{20}{\pi}}}{2} \\ &=\frac{20}{\pi}\cdot \frac{1}{2} \\ &= \frac{10}{\pi} \end{aligned}$

Відповідь:

Радіус -$\frac{10}{π}$ дюйми, або приблизно$3.18$ дюйми

Як правило, нам не дадуть константу варіації. Замість цього нам буде надана інформація, з якої її можна визначити.

Приклад$\PageIndex{2}$

Вага об'єкта на землі залежить безпосередньо від його ваги на Місяці. Якщо чоловік важить$180$ кілограми на землі, то він буде важити$30$ кілограми на Місяці. Встановіть алгебраїчне рівняння, яке виражає вагу на землі з точки зору ваги на Місяці, і використовуйте його для визначення ваги жінки на Місяці, якщо вона важить$120$ кілограми на землі.

Рішення:

Нехай$y$ представляють вагу на Землі.

Нехай$x$ представляють вагу на Місяці.

Нам дано, що «вага на землі змінюється безпосередньо до ваги на Місяці».

$y=kx$

Щоб знайти константу варіації$k$, використовуйте задану інформацію. A$180$ -pound людина на землі важить$30$ фунти на Місяці, або$y=180$ коли$x=30$.

$180 = k \cdot 30$

Вирішити для$k$.

$\begin{aligned} \frac{180}{30} &=k \\ 6&=k \end{aligned}$

Далі встановіть формулу, яка моделює задану інформацію.

$y=6x$

Це означає, що вага людини на землі в$6$ рази перевищує її вагу на Місяці. Щоб відповісти на питання, використовуйте вагу жінки на землі,$y=120$ фунти, і вирішуйте для$x$.

$\begin{aligned} 120&=6x \\ \frac{120}{6} &=x \\ 20&=x \end{aligned}$

Відповідь:

Жінка важить$20$ кілограми на настрій.

Зворотна варіація

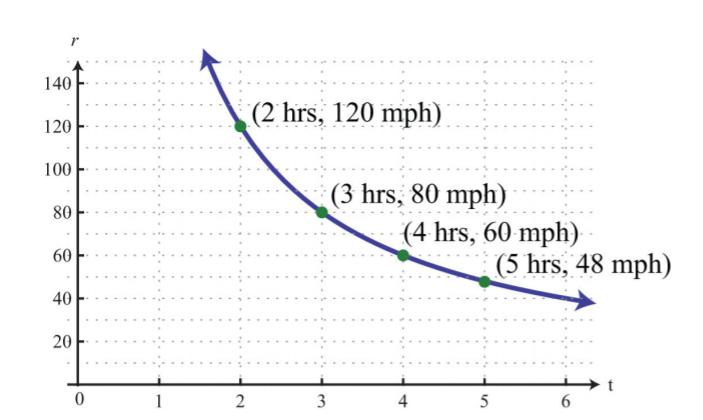
Далі розглянемо взаємозв'язок між часом і ставкою,

$r=\frac{D}{t}$

Якщо ми хочемо пройти фіксовану відстань, то ми можемо визначити середню швидкість, необхідну для проходження цієї відстані за певний проміжок часу. Наприклад, якщо ми хочемо проїхати 240 миль за 4 години, ми можемо визначити необхідну середню швидкість наступним чином:

$r=\frac{240}{4}=6$

Середня швидкість, необхідна для проїзду 240 миль за 4 години, становить 60 миль на годину. Якщо ми хочемо проїхати 240 миль за 5 годин, то визначаємо необхідну швидкість, використовуючи аналогічне рівняння:

$r=\frac{240}{5}=48$

У цьому випадку нам доведеться лише в середньому 48 миль на годину. Ми можемо скласти діаграму і переглянути цю залежність на графіку.

Таблиця$\PageIndex{3}$
Час$t$ в годинах	Швидкість$r=\frac{240}{t}$
\ (t\) в годинах">2	\ (r=\ гідророзриву {240} {t}\) ">120
\ (t\) в годинах">3	\ (r=\ гідророзриву {240} {t}\) ">80
\ (t\) в годинах">4	\ (r=\ гідророзриву {240} {t}\) ">60
\ (t\) в годинах">5	\ (r=\ frac {240} {t}\) ">48

Знімок екрана (327) .png — Малюнок$\PageIndex{2}$

Це приклад зворотного зв'язку. Ми говоримо, що$r$ обернено пропорційно часу$t$, де$240$ константа пропорційності. Загалом, у нас

Таблиця$\PageIndex{4}$
Ключові слова	Переклад
«$y$змінюється обернено, як$x$»	\[y=\frac{k}{x}\]
«$y$обернено пропорційна$x$»	\[y=\frac{k}{x}\]

Знову ж таки,$k$ ненульовий і називається константою варіації або константою пропорційності.

Приклад$\PageIndex{3}$

Якщо$y$ змінюється обернено, як$x$ і$y=5$ коли$x=2$, то знайдіть константу пропорційності та рівняння, яке пов'язує дві змінні.

Рішення:

Якщо дозволити$k$ представляти константу пропорційності, то твердження «$y$змінюється обернено як$x$» можна записати наступним чином:

$y=\frac{k}{x}$

Використовуйте наведену інформацію,$y=5$ коли$x=2$, щоб знайти$k$.

$5=\frac{k}{2}$

Вирішити для$k$.

$\begin{aligned} \color{Cerulean}{2}\color{black}{\cdot 5}&=\color{Cerulean}{2}\color{black}{\cdot\frac{k}{2}\\10&=k} \end{aligned}$

Тому формула, яка моделює проблему, є

$y=\frac{10}{x}$

Відповідь:

Константа пропорційності є$10$, а рівняння є$y=\frac{10}{x}$.

Приклад$\PageIndex{4}$

Вага об'єкта змінюється обернено, як квадрат його відстані від центру землі. Якщо предмет важить$100$ кілограми на поверхні землі (приблизно в$4,000$ милі від центру), то скільки він буде важити в$1,000$ милі над земною поверхнею?

Рішення:

$w$Дозволяти представляти вагу об'єкта.

$d$Дозволяти представляти відстань об'єкта від центру Землі.

Оскільки "$w$змінюється обернено, як квадрат»$d$, ми можемо написати

$w=\frac{k}{d^{2}}$

Використовуйте надану інформацію для пошуку$k$. Об'єкт важить$100$ фунти на поверхні землі, приблизно в$4,000$ милі від центру. Іншими словами,$w = 100$ коли$d = 4,000$:

$100=\frac{k}{(4000)^{2}}$

Вирішити для$k$:

$\begin{aligned} \color{Cerulean}{(4,000)^{2}}\color{black}{\cdot 100}&=\color{Cerulean}{(4,000)^{2}}\color{black}{\cdot\frac{k}{(4,000)^{2}}}\\ 1,600,000,000&=k \\ 1.6\times 10^{9} &=k \end{aligned}$

Тому ми можемо змоделювати проблему за допомогою наступної формули:

$w=\frac{1.6\times 10^{9}}{d^{2}}$

Щоб скористатися формулою, щоб знайти вагу, нам потрібно відстань від центру землі. Оскільки об'єкт знаходиться в$1,000$ милі над поверхнею, знайдіть відстань від центру землі, додавши$4,000$ милі:

$d=4,000+1,000=5,000$миль

Щоб відповісти на питання, скористайтеся формулою с$d = 5,000$.

$\begin{aligned} y &= \frac{1.6\times 10^{9}}{(\color{OliveGreen}{5,000}\color{black}{)^{2}}} \\ &=\frac{1.6\times 10^{9}}{25,000,000}\\ &=\frac{1.6\times 10^{9}}{2.5\times 10^{7}}\\ &=0.64\times 10^{2}\\ &=64 \end{aligned}$

Відповідь:

Об'єкт буде важити$64$ фунти на відстані$1,000$ миль над поверхнею землі.

Спільна варіація

Нарешті, ми визначаємо відносини між декількома змінними. Загалом, у нас

Таблиця$\PageIndex{5}$
Лексика	Переклад
«$y$варіюється спільно як$x$ і$z$»	\[y=kyz\]
«$y$спільно пропорційна$x$ і$z$»	\[y=kyz\]

Тут$k$ ненульова і називається константою варіації або константою пропорційності.

Приклад$\PageIndex{5}$

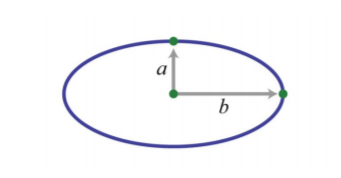
Площа еліпса змінюється разом як половина$a$ великої осі еліпса, так і$b$ половина другорядної осі еліпса. Якщо площа еліпса дорівнює$300π \text{cm}^{2}$, де$a=10$ см і$b=30$ см, то яка константа пропорційності? Дайте формулу для площі еліпса.

Знімок екрана (328) .png — Малюнок$\PageIndex{3}$

Рішення:

Якщо ми дозволимо$A$ представляти площу еліпса, то ми можемо використовувати оператор «площа змінюється спільно як$a$ і$b$», щоб написати

$A=kab$

Щоб знайти константу варіації$k$, використовуйте той факт, що площа - це$300π$ коли$a=10$ і$b=30$.

$\begin{aligned} 300\pi &=k(\color{OliveGreen}{10}\color{black}{)(}\color{OliveGreen}{30}\color{black}{)} \\ 300\pi &=300k \\ \pi&=k \end{aligned}$

Отже, формула для площі еліпса

$A=\pi ab$

Відповідь:

Константа пропорційності є$π$, а формула для площі є$A=abπ$.

Вправа$\PageIndex{1}$

Враховуючи, що$y$ змінюється безпосередньо як квадрат, так$x$ і обернено до$z$, де$y = 2$ коли$x = 3$ і$z = 27$, знайти$y$ коли$x = 2$ і$z = 16$.

Відповідь: $\frac{3}{2}$

Ключові виноси

Налаштування проблем варіації зазвичай вимагає декількох кроків. Спочатку визначте ключові слова, щоб встановити рівняння, а потім використовувати дану інформацію, щоб знайти константу варіації$k$. Визначивши константу варіації, напишіть формулу, яка моделює задачу. Як тільки формула знайдена, використовуйте її, щоб відповісти на питання.

Вправа$\PageIndex{2}$ Variation Problems

Переведіть наступні пропозиції в математичну формулу.

Відстань$D$, яку може проїхати автомобіль, прямо пропорційна часу$t$, що він подорожує з постійною швидкістю.
Розширення підвісної пружини,$d$, прямо пропорційна вазі$w$, прикріпленому до нього.
Автомобільна відстань розриву$d$, прямо пропорційна квадрату швидкості автомобіля,$v$.
$V$Обсяг сфери змінюється безпосередньо як куб її радіуса,$r$.
Обсяг$V$, заданої маси газу обернено пропорційний тиску$p$, що чиниться на нього.
Інтенсивність світла від джерела світла обернено пропорційна квадрату відстані$d$, від джерела.$I$
Кожна частинка речовини у Всесвіті притягує кожну іншу частинку з силою$F$, яка прямо пропорційна добутку мас$m_{2}$,$m_{1}$ причому, частинок і обернено пропорційна квадрату відстані$d$, між ними.
Простий$I$ відсоток,, спільно пропорційний річній процентній ставці$r$, і час$t$, в роках вкладається фіксована сума грошей.
Період$T$, маятника прямо пропорційний квадратному кореню його довжини,$L$.
Час$t$, який потрібно об'єкту, щоб впасти, прямо пропорційно квадратному кореню відстані$d$, яке воно падає.

Відповідь

1. $D=kt$

3. $d=kv^{2}$

5. $V=\frac{k}{p}$

7. $F=\frac{km_{1}⋅m_{2}}{d^{2}}$

9. $T=k\sqrt{L}$

Вправа$\PageIndex{3}$ Variation Problems

Побудувати математичну модель з урахуванням наступного.

$y$змінюється безпосередньо як$x$, так і$y = 30$ коли$x = 6$.
$y$змінюється безпосередньо як$x$, так і$y = 52$ коли$x = 4$.
$y$прямо пропорційна$x$, і$y = 12$ коли$x = 3$.
$y$прямо пропорційна$x$, і$y = 120$ коли$x = 20$.
$y$змінюється безпосередньо як$x$, так і$y = 14$ коли$x = 10$.
$y$змінюється безпосередньо як$x$, так і$y = 2$ коли$x = 8$.
$y$змінюється обернено як$x$, так і$y = 5$ коли$x = 7$.
$y$змінюється обернено як$x$, так і$y = 12$ коли$x = 2$.
$y$обернено пропорційна$x$, і$y = 3$ коли$x = 9$.
$y$обернено пропорційна$x$, і$y = 21$ коли$x = 3$.
$y$змінюється обернено як$x$, так і$y = 2$ коли$x = \frac{1}{8}$.
$y$змінюється обернено як$x$, так і$y = \frac{3}{2}$ коли$x = \frac{1}{9}$.
$y$змінюється спільно як$x$ і$z$, де$x = 4$ і$y = 8$ коли$z = \frac{1}{2}$.
$y$змінюється спільно як$x$ і$z$, де$x =\frac{1}{3}$ і$y = 24$ коли$z = 9$.
$y$спільно пропорційна$x$ і$z$, де$y = 2$ коли$x = 1$ і$z = 3$.
$y$спільно пропорційна$x$ і$z$, де$y = 15$ коли$x = 3$ і$z = 7$.
$y$змінюється спільно як$x$ і$z$, де$x = \frac{1}{2}$ і$y = \frac{2}{3}$ коли$z = 12$.
$y$змінюється спільно як$x$ і$z$, де$x = \frac{3}{2}$ і$y = 5$ коли$z = \frac{2}{9}$.
$y$змінюється безпосередньо як квадрат$x$, де$y = 45$ коли$x = 3$.
$y$змінюється безпосередньо як квадрат$x$, де$y = 3$ коли$x = \frac{1}{2}$.
$y$обернено пропорційна квадрату$x$, де$y = 27$ коли$x = \frac{1}{3}$.
$y$обернено пропорційна квадрату$x$, де$y = 9$ коли$x = \frac{2}{3}$.
$y$варіюється спільно як$x$ і квадрат$z$, де$y = 54$ коли$x = 2$ і$z = 3$.
$y$варіюється спільно як$x$ і квадрат$z$, де$y = 6$ коли$x = \frac{1}{4}$ і$z = \frac{2}{3}$.
$y$змінюється спільно як$x$$z$ і обернено, як квадрат$w$, де,$y = 30$ коли$x = 8, z = 3$, і$w = 2$
$y$варіюється спільно як$x$$z$ і обернено як квадрат$w$, де$y = 5$ коли$x= 1, z = 3$, і$w = \frac{1}{2}$.
$y$варіюється безпосередньо як квадратний корінь, так$x$ і обернено як$z$, де,$y = 12$ коли$x= 9$ і$z = 5$.
$y$змінюється безпосередньо як квадратний корінь$x$ і обернено як квадрат$z$, де$y = 15$ коли$x = 25$ і$z = 2$.
$y$змінюється безпосередньо як квадрат$x$ і обернено, як$z$ і квадрат$w$, де$y = 14$ коли$x = 4, w = 2$, і$z = 2$.
$y$варіюється безпосередньо як квадратний корінь$x$ і обернено, як$z$ і квадрат$w$, де$y = 27$ коли$x = 9, w = \frac{1}{2}$, і$z = 4$.

Відповідь

1. $y=5x$

3. $y=4x$

5. $y=\frac{7}{5}x$

7. $y=\frac{35}{x}$

9. $y=\frac{27}{x}$

11. $y=\frac{1}{4x}$

13. $y=4xz$

15. $y=\frac{2}{3}xz$

17. $y=\frac{1}{9}xz$

19. $y=5x^{2}$

21. $y=3x^{2}$

23. $y=3xz^{2}$

25. $y=\frac{5xz}{w^{2}}$

27. $y=\frac{20x}{\sqrt{z}}$

29. $y=\frac{7x^{2}}{w^{2}z}$

Вправа$\PageIndex{4}$ Variation Problems

Додатки, що включають варіацію.

Виручка в доларах прямо пропорційна кількості проданих фірмових толстовок. Якщо дохід, отриманий від продажу$25$ сорочок, становить $$318.75$, то визначте виручку, якщо$30$ продаються толстовки.
Податок з продажу при покупці нового автомобіля варіюється безпосередньо як і ціна автомобіля. Якщо купується$18,000$ новий автомобіль $, то податок з продажу становить $$1,350$. Скільки стягується податок з продажу, якщо новий автомобіль коштує в $$22,000$?
Ціна частки простих акцій в компанії прямо пропорційна прибутку на акцію (EPS) за попередні 12 місяців. Якщо ціна частки звичайних акцій в компанії дорівнює $,$22.55$ а EPS публікується як $$1.10$, то визначте вартість акцій, якщо EPS збільшується на $$0.20$.
Відстань, пройдена в дорозі, залежить безпосередньо від часу, проведеного в дорозі. Якщо$126$ -мильна поїздка може бути здійснена за$3$ годинами, то яку відстань можна проїхати в$4$ годинами?
Окружність кола прямо пропорційна його радіусу. Якщо окружність кола з радіусом$7$ сантиметрів вимірюється як$14π$ сантиметри, то знайдіть константу пропорційності.
Площа кола змінюється безпосередньо як квадрат його радіуса. Якщо площа кола з радіусом$7$ сантиметрів визначається$49π$ квадратними сантиметрами, то знайдіть константу пропорційності.
Площа поверхні сфери змінюється безпосередньо як квадрат її радіуса. Коли радіус сфери вимірює$2$ метри, площа поверхні вимірює$16π$ квадратні метри. Знайдіть площу поверхні сфери з радіусом$3$ метрів.
Обсяг сфери змінюється безпосередньо як куб її радіуса. Коли радіус сфери вимірює$3$ метри, обсяг становить$36π$ кубічні метри. Знайдіть об'єм сфери з радіусом$1$ метра.
При фіксованій висоті обсяг конуса прямо пропорційний квадрату радіуса біля основи. Коли радіус біля основи вимірює$10$ сантиметри, обсяг становить$200$ кубічні сантиметри. Визначте обсяг конуса, якщо радіус підстави зменшено вдвічі.
Відстань$d$, об'єкт у вільному падінні падає безпосередньо залежить від квадрата часу$t$, що він падав. Якщо предмет у вільному падінні опускає$36$ ноги за$1.5$ лічені секунди, то як далеко він впаде за$3$ лічені секунди?

Відповідь

1. $$382.50 $

3. $$26.65 $

5. $2π$

7. $36π$квадратних метрів

9. $50$кубічні сантиметри

Вправа$\PageIndex{5}$ Variation Problems

Закон Гука передбачає, що розширення підвісної пружини прямо пропорційно прикріпленому до неї вазі. Константа зміни називається постійною пружини.

Якщо підвісна пружина розтягується на$5$ дюйми, коли до неї прикріплений вага$20$ -фунт, то визначте її постійну пружину.
Якщо підвісна пружина розтягується$3$ сантиметрами при прикріпленні до неї$2$ -кілограмової ваги, то визначте постійну пружини.
Якщо підвісна пружина розтягується на$3$ дюйми, коли прикріплена вага$2$ -фунт, то наскільки вона розтягнеться з додаванням ваги$5$ -pound?
Якщо підвісна пружина розтягується$6$ сантиметрами, коли до неї прикріплений$4$ кілограмовий вага, то як далеко вона розтягнеться з прикріпленим$2$ -кілограмовим вагою?

Відповідь

1. $\frac{1}{4}$

3. $7.5$дюймів

Вправа$\PageIndex{6}$ Variation Problems

Відстань розриву автомобіля прямо пропорційна квадрату його швидкості.

Якщо потрібно$36$ ноги, щоб зупинити конкретний автомобіль, що рухається зі швидкістю$30$ миль на годину, то скільки відстань розриву потрібно, якщо швидкість -$35$ милі на годину?
Після аварії було визначено, що водієві потрібні$80$ ноги, щоб зупинити свій автомобіль. В експерименті в подібних умовах потрібно$45$ ноги, щоб зупинити автомобіль, що рухається зі швидкістю$30$ миль на годину. Оцініть, наскільки швидко рухався водій до аварії.

Відповідь: 1. $49$ноги

Вправа$\PageIndex{7}$ Variation Problems

Закон Бойла стверджує, що якщо температура залишається постійною, обсяг$V$,, заданої маси газу обернено пропорційний тиску$p$, що чиниться на неї.

Повітряна куля заповнюється до обсягу$216$ кубічних дюймів на водолазному човні під$1$ тиском. Якщо балон береться під водою приблизно$33$ футів, де тиск вимірює$2$ атмосфери, то який обсяг балона?
Якщо балон заповнюється до$216$ кубічних дюймів під тиском$3$ атмосфер на глибині$66$ футів, то який обсяг був би на поверхні, де тиск -$1$ атмосфера?
Щоб збалансувати гойдалки, відстань від точки опори, на якій повинен сидіти людина, обернено пропорційно його вазі. Якщо$72$ -фунт хлопчик сидить$3$ ногами від точки опори, то як далеко від точки опори повинен сидіти$54$ - фунт хлопчик, щоб збалансувати гойдалки?
Струм$I$, в електричному провіднику обернено пропорційний його опору,$R$. Якщо струм$\frac{1}{4}$ ампер при опорі$100$ Ом, то який струм при опорі$150$ Ом?
Кількість чоловіків, представлених тим$y$, що потрібно прокласти бруківку під'їзної доріжки прямо пропорційно площі$A$, проїзду і обернено пропорційно кількості часу$t$, дозволеного на виконання завдання. Як правило,$3$ чоловіки можуть укладати$1,200$ квадратні фути кругляка за$4$ годинами. Скільки чоловіків потрібно буде укладати$2,400$ квадратні фути кругляка$6$ за даними годинами?
Обсяг правого кругового циліндра змінюється спільно як квадрат його радіуса і його висоти. Правий круглий циліндр з$3$ -сантиметровим радіусом і висотою$4$ сантиметрів має обсяг$36π$ кубічних сантиметрів. Знайдіть формулу об'єму правого кругового циліндра через його радіус і висоту.
Період$T$, маятника прямо пропорційний квадратному кореню його довжини,$L$. Якщо довжина маятника$1$ метр, то період становить приблизно$2$ секунди. Приблизний період маятника, який становить$0.5$ метр в довжину.
Час$t$, який потрібно об'єкту, щоб впасти, прямо пропорційно квадратному кореню відстані$d$, яке воно падає. Об'єкт, що впав з$4$ ніг, займе$\frac{1}{2}$ друге місце, щоб вдарити об землю. Скільки часу знадобиться скинутий з$16$ ніг предмет, щоб вдаритися об землю?

Відповідь

1. $108$кубічних дюймів

3. $4$ноги

5. $4$чоловіки

7. $1.4$секунд

Вправа$\PageIndex{8}$ Variation Problems

Універсальний закон гравітації Ньютона стверджує, що кожна частинка матерії у Всесвіті притягує кожну іншу частинку силою$F$, яка прямо пропорційна добутку мас$m_{2}$,$m_{1}$ причому, частинок і обернено пропорційна квадрату відстані, $d$, Між ними. Константа пропорційності називається гравітаційної константою.

Якщо два об'єкти з масою$50$ кілограмів і$100$ кілограмів знаходяться в$\frac{1}{2}$ метрах один від одного, то вони виробляють приблизно$1.34×10^{−6}$ ньютони (N) сили. Обчисліть гравітаційну константу.
Використовуйте гравітаційну константу з попередньої вправи, щоб написати формулу, яка наближає силу$F$, в ньютонах між двома масами$m_{1}$ і$m_{2}$, виражену в кілограмах, враховуючи відстань$d$ між ними в метрах.
Обчисліть силу в ньютонах між землею і місяцем, враховуючи, що маса Місяця дорівнює приблизно$7.3×10^{22}$ кілограмам, маса землі дорівнює приблизно$6.0×10^{24}$ кілограмам, а відстань між ними - в середніх$1.5×10^{11}$ метрах.
Розрахуйте силу в ньютонах між землею і сонцем, враховуючи, що маса Сонця становить приблизно$2.0×10^{30}$ кілограми, маса землі дорівнює приблизно$6.0×10^{24}$ кілограмам, а відстань між ними - в середніх$3.85×10^{8}$ метрах.
Якщо$y$ змінюється безпосередньо як квадрат$x$, то як$y$ зміниться, якщо$x$ подвоюється?
Якщо$y$ змінюється обернено, як квадрат$t$, то як$y$ зміниться, якщо$t$ подвоюється?
Якщо$y$ змінюється безпосередньо як квадрат$x$ і обернено як квадрат$t$, то як$y$ зміниться, якщо обидва$x$ і$t$ подвоюються?

Відповідь

1. $6.7×10^{−11} \frac{N m^{2}}{kg^{2}}$

3. $1.98×10^{20}$N

5. $y$зміни за фактором$4$

7. $y$залишається незмінним

Ключові слова	Переклад
«\(y\)змінюється безпосередньо як\(x\)»	\[y=kx\]
«\(y\)прямо пропорційно\(x\)»
«\(y\)пропорційно\(x\)»

Ключові слова	Переклад
«\(y\)змінюється обернено, як\(x\)»	\[y=\frac{k}{x}\]
«\(y\)обернено пропорційна\(x\)»	\[y=\frac{k}{x}\]

Лексика	Переклад
«\(y\)варіюється спільно як\(x\) і\(z\)»	\[y=kyz\]
«\(y\)спільно пропорційна\(x\) і\(z\)»	\[y=kyz\]