3.E: Огляд вправ і зразок іспиту

Огляд вправ

Вправа\(\PageIndex{1}\) Rectangular Coordinate System

Графік заданої множини впорядкованих пар.

1. \(\{(−3, 4), (−4, 0), (0, 3), (2, 4)\}\)
2. \(\{(−5, 5), (−3, −1), (0, 0), (3, 2)\}\)
3. Графік точок\((−3, 5), (−3, −3),\) і\((3, −3)\) на прямокутній координатній площині. З'єднайте точки і обчислите площу фігури.
4. Графік точок\((−4, 1), (0, 1), (0, −2),\) і\((−4, −2)\) на прямокутній координатній площині. З'єднайте точки і обчислите площу фігури.
5. Графік точок\((1, 0), (4, 0), (1, −5),\) і\((4, −5)\) на прямокутній координатній площині. З'єднайте точки і розрахуйте периметр фігури.
6. Графік точок\((−5, 2), (−5, −3), (1, 2),\) і\((1, −3)\) на прямокутній координатній площині. З'єднайте точки і розрахуйте периметр фігури.

Відповідь

1.

Малюнок 3.E.1

3. Площа:\(24\) квадратні одиниці

Малюнок 3.E.2

5. Периметр:\(16\) одиниці

Малюнок 3.E.3

Вправа\(\PageIndex{2}\) Rectangular Coordinate System

Обчисліть відстань між заданими двома точками.

1. \((−1, −2)\)і\((5, 6)\)
2. \((2, −5)\)і\((−2, −2)\)
3. \((−9, −3)\)і\((−8, 4)\)
4. \((−1, 3)\)і\((1, −3)\)

Відповідь

1. \(10\)одиниць

3. \(5\sqrt{2}\)одиниць

Вправа\(\PageIndex{3}\) Rectangular Coordinate System

Обчисліть середину між заданими точками.

1. \((−1, 3)\)і\((5, −7)\)
2. \((6, −3)\)і\((−8, −11)\)
3. \((7, −2)\)і\((−6, −1)\)
4. \((−6, 0)\)і\((0, 0)\)
5. Показати алгебраїчно, що точки\((−1, −1), (1, −3),\) і\((2, 0)\) утворюють рівнобедрений трикутник.
6. Показати алгебраїчно, що точки\((2, −1), (6, 1),\) і\((5, 3)\) утворюють прямокутний трикутник.

Відповідь

1. \((2,-2)\)

3. \((\frac{1}{2},-\frac{3}{2})\)

5. Відповіді можуть відрізнятися

Вправа\(\PageIndex{4}\) Graph by Plotting Points

Визначте, чи є дана точка рішенням.

1. \(−5x+2y=7\);\((1, −1)\)
2. \(6x−5y=4\);\((−1, −2)\)
3. \(y=\frac{3}{4}x+1\);\((−\frac{2}{3}, \frac{1}{2})\)
4. \(y=−\frac{3}{5}x−2\);\((10, −8)\)

Відповідь

1. Ні

3. Так

Вправа\(\PageIndex{5}\) Graph by Plotting Points

Знайдіть щонайменше п'ять впорядкованих парних розв'язків і графік.

1. \(y=−x+2\)
2. \(y=2x−3\)
3. \(y=\frac{1}{2}x−2\)
4. \(y=−\frac{2}{3}x\)
5. \(y=3\)
6. \(x=−3\)
7. \(x−5y=15\)
8. \(2x−3y=12\)

Відповідь

1.

Малюнок 3.E.4

3.

Малюнок 3.E.5

5.

Малюнок 3.E.6

7.

Малюнок 3.Е.7

Вправа\(\PageIndex{6}\) Graph Using Intercepts

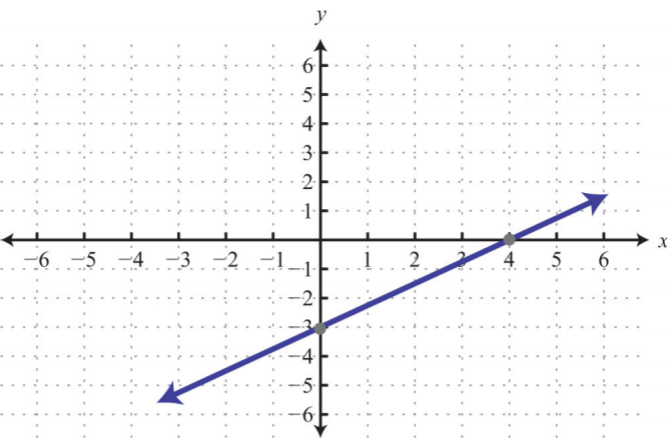
З огляду на графік, знайдіть\(x\) - і\(y\) - перехоплення.

1.

Малюнок 3.E.8

2.

Малюнок 3.E.9

3.

Малюнок 3.Е.10

4.

Малюнок 3.Е.11

Відповідь

1. \(y\)-перехоплення:\((0, −2)\);\(x\) -перехоплення:\((−4, 0)\)

3. \(y\)-перехоплення: немає;\(x\) -перехоплення:\((5, 0)\)

Вправа\(\PageIndex{7}\) Graph Using Intercepts

Знайдіть перехоплення і графуйте їх.

1. \(3x−4y=12\)
2. \(2x−y=−4\)
3. \(\frac{1}{2}x−\frac{1}{3}y=1\)
4. \(−\frac{1}{2}x+\frac{2}{3}y=2\)
5. \(y=−\frac{5}{3}x+5\)
6. \(y=−3x+4\)

Відповідь

1.

Малюнок 3.E.12

3.

Малюнок 3.E.13

5.

Малюнок 3.Е.14

Вправа\(\PageIndex{8}\) Graph Using the \(y\)-Intercept and Slope

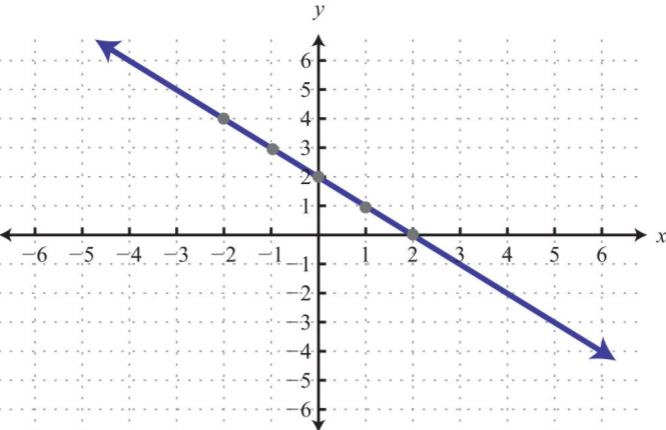
З огляду на графік, визначають ухил і\(y\) -перехоплення.

1.

Малюнок 3.Е.15

2.

Малюнок 3.E.16

Відповідь

1. \(y\)-перехоплення:\((0, 1)\); нахил:\(−2\)

Вправа\(\PageIndex{9}\) Graph Using the \(y\)-Intercept and Slope

Визначте ухил, враховуючи дві точки.

1. \((−3, 8)\)і\((5, −6)\)
2. \((0, −5)\)і\((−6, 3)\)
3. \((\frac{1}{2}, −\frac{2}{3})\)і\((\frac{1}{4}, −\frac{1}{3})\)
4. \((5, −\frac{3}{4})\)і\((2, −\frac{3}{4})\)

Відповідь

1. \(-\frac{7}{4}\)

3. \(-\frac{4}{3}\)

Вправа\(\PageIndex{10}\) Graph Using the \(y\)-Intercept and Slope

Висловіть в ухил-перехоплення формі і визначте нахил і\(y\) -перехоплення.

1. \(12x−4y=8\)
2. \(3x−6y=24\)
3. \(−\frac{1}{3}x+\frac{3}{4}y=1\)
4. \(−5x+3y=0\)

Відповідь

1. \(y=3x−2\); нахил:\(3\);\(y\) -перехоплення\((0, −2)\)

3. \(y=\frac{4}{9}x+\frac{4}{3}\); нахил:\(\frac{4}{9}\);\(y\) -перехоплення\((0, \frac{4}{3})\)

Вправа\(\PageIndex{11}\) Graph Using the \(y\)-Intercept and Slope

1. \(y=−x+3\)
2. \(y=4x−1\)
3. \(y=−2x\)
4. \(y=−\frac{5}{2}x+3\)
5. \(2x−3y=9\)
6. \(2x+\frac{3}{2}y=3\)
7. \(y=0\)
8. \(x−4y=0\)

Відповідь

1.

Малюнок 3.Е.17

3.

Малюнок 3.Е.18

5.

Малюнок 3.E.19

7.

Малюнок 3.Е.20

Вправа\(\PageIndex{12}\) Finding Linear Equations

З огляду на графік, визначте рівняння прямої.

1.

Малюнок 3.Е.21

2.

Малюнок 3.Е.22

3.

Малюнок 3.Е.23

4.

Малюнок 3.E.24

Відповідь

1. \(y=−2x+1\)

3. \(y=−5\)

Вправа\(\PageIndex{13}\) Finding Linear Equations

Знайдіть рівняння прямої, заданої нахилом і точкою на прямій.

1. \(m = \frac{1}{2}\);\((−4, 8)\)
2. \(m = −\frac{1}{5}\);\((−5, −9)\)
3. \(m = \frac{2}{3}\);\((1, −2)\)
4. \(m = −\frac{3}{4}\);\((2, −3)\)

Відповідь

1. \(y=\frac{1}{2}x+10\)

3. \(y=\frac{2}{3}x−\frac{8}{3}\)

Вправа\(\PageIndex{14}\) Finding Linear Equations

Знайдіть рівняння прямої, заданої двома точками на прямій.

1. \((−5, −5)\)і\((10, 7)\)
2. \((−6, 12)\)і\((3, −3)\)
3. \((2, −1)\)і\((−2, 2)\)
4. \((\frac{5}{2}, −2)\)і\((−5, \frac{5}{2})\)
5. \((7, −6)\)і\((3, −6)\)
6. \((10, 1)\)і\((10, −3)\)

Відповідь

1. \(y=\frac{4}{5}x−1\)

3. \(y=−\frac{3}{4}x+\frac{1}{2}\)

5. \(y=−6\)

Вправа\(\PageIndex{15}\) Parallel and Perpendicular Lines

Визначте, чи є лінії паралельними, перпендикулярними чи ні.

1. \(\left\{\begin{aligned}−3x+7y&=14\\6x−14y&=42\end{aligned}\right.\)
2. \(\left\{\begin{aligned}2x+3y&=18\\2x−3y&=36\end{aligned}\right.\)
3. \(\left\{\begin{aligned}x+4y&=2\\8x−2y=&−1\end{aligned}\right.\)
4. \(\left\{\begin{aligned}y&=2\\x&=2\end{aligned}\right.\)

Відповідь

1. Паралельний

3. Перпендикуляр

Вправа\(\PageIndex{16}\) Parallel and Perpendicular Lines

Знайти рівняння прямої у вигляді ухил-перехоплення.

1. Паралельно\(5x−y=15\) і проходячи наскрізь\((−10, −1)\).
2. Паралельно\(x−3y=1\) і проходячи наскрізь\((2, −2)\).
3. Перпендикулярно\(8x−6y=4\) і проходить наскрізь\((8, −1)\).
4. Перпендикулярно\(7x+y=14\) і проходить наскрізь\((5, 1)\).
5. Паралельно\(y=1\) і проходячи наскрізь\((4, −1)\).
6. Перпендикулярно\(y=1\) і проходить наскрізь\((4, −1)\).

Відповідь

1. \(y=5x+49\)

3. \(y=−\frac{3}{4}x+5\)

5. \(y=−1\)

Вправа\(\PageIndex{17}\) Introduction to Functions

Визначте домен і діапазон і станьте, чи є це функцією чи ні.

1. \(\{(−10, −1), (−5, 2), (5, 2)\}\)

2. \(\{(−12, 4), (−1, −3), (−1, −2)\}\)

3.

Малюнок 3.Е.25

4.

Малюнок 3.E.26

5.

Малюнок 3.Е.27

6.

Малюнок 3.Е.28

Відповідь

1. Домен:\(\{−10, −5, 5\}\); діапазон:\(\{−1, 2\}\); функція: yes

3. Домен:\(R\); діапазон:\(R\); функція: yes

5. Домен:\([−3,∞)\); діапазон:\(R\); функція: немає

Вправа\(\PageIndex{18}\) Introduction to Functions

Враховуючи наступне,

1. \(f(x)=9x−4\), знайти\(f(−1)\).
2. \(f(x)=−5x+1\), знайти\(f(−3)\).
3. \(g(x)=\frac{1}{2}x−\frac{1}{3}\), знайти\(g(−\frac{1}{3})\).
4. \(g(x)=−\frac{3}{4}x+\frac{1}{3}\), знайти\(g(\frac{2}{3})\).
5. \(f(x)=9x−4\), знайти\(x\) коли\(f(x)=0\).
6. \(f(x)=−5x+1\), знайти\(x\) коли\(f(x)=2\).
7. \(g(x)=\frac{1}{2}x−\frac{1}{3}\), знайти\(x\) коли\(g(x)=1\).
8. \(g(x)=−\frac{3}{4}x+\frac{1}{3}\), знайти\(x\) коли\(g(x)=−1\).

Відповідь

1. \(f(−1)=−13\)

3. \(g(−\frac{1}{3})=−\frac{1}{2}\)

5. \(x=\frac{4}{9}\)

7. \(x=\frac{8}{3}\)

Вправа\(\PageIndex{19}\) Introduction to Functions

З огляду на графік функції\(f(x)\), визначте наступне.

Малюнок 3.E.29

1. \(f(3)\)
2. \(x\)коли\(f(x)=4\)

Відповідь

1. \(f(3)=−2\)

Вправа\(\PageIndex{20}\) Linear Inequalities (Two Variables)

Чи є впорядкована пара розв'язком заданої нерівності?

1. \(6x−2y≤1\);\((−3, −7)\)
2. \(−3x+y>2\);\((0, 2)\)
3. \(6x−10y<-1\);\((5,-3)\)
4. \(x-\frac{1}{3}y>0\);\((1, 4)\)
5. \(y>0\);\((−3, −1)\)
6. \(x≤−5\);\((−6, 4)\)

Відповідь

1. Так

3. Ні

5. Так

Вправа\(\PageIndex{21}\) Linear Inequalities (Two Variables)

Графік набору розв'язків.

1. \(y≥−2x+1\)
2. \(y<3x−4\)
3. \(−x+y≤3\)
4. \(\frac{5}{2}x+\frac{1}{2}y≤2\)
5. \(3x−5y>0\)
6. \(y>0\)

Відповідь

1.

Малюнок 3.E.30

3.

Малюнок 3.E.31

5.

Малюнок 3.E.32

Зразок іспиту

Вправа\(\PageIndex{22}\)

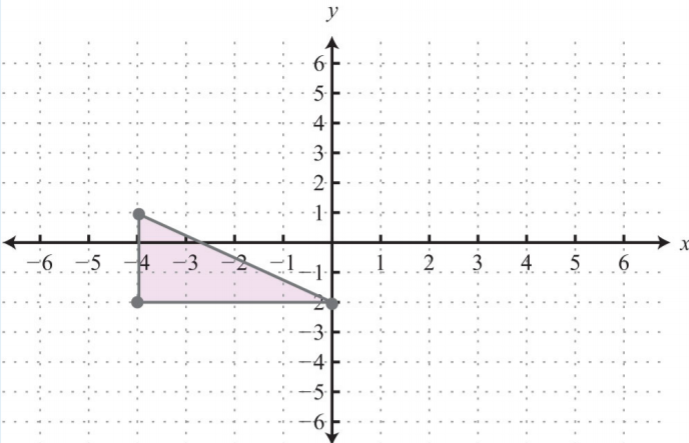
1. Графік точок\((−4, −2), (−4, 1),\) і\((0, −2)\) на прямокутній координатній площині. З'єднайте точки і обчислите площу фігури.
2. Чи\((−2, 4)\) є рішенням\(3x−4y=−10\)? Обґрунтуйте свою відповідь.

Відповідь

1. Площа:\(6\) квадратні одиниці

Малюнок 3.E.33

Вправа\(\PageIndex{23}\)

Задавши множину\(x\) -значень\(\{−2, −1, 0, 1, 2\}\), знайдіть відповідні\(y\) -значення і графуйте наступний графік.

1. \(y=x−1\)
2. \(y=−x+1\)
3. На одному і тому ж наборі осей, графік\(y=4\) і\(x=−3\). Дайте точку, де вони перетинаються.

Відповідь

1.

Малюнок 3.E.34

3. Перехрестя:\((-3,4)\)

Малюнок 3.E.35

Вправа\(\PageIndex{24}\)

Знайдіть\(x\) - і\(y\) -перехоплення і використовуйте ці точки для графіка наступного.

1. \(2x−y=8\)
2. \(12x+5y=15\)
3. Обчисліть ухил лінії, що проходить через\((−4, −5)\) і\((−3, 1)\).

Відповідь

2.

Малюнок 3.E.36

Вправа\(\PageIndex{25}\)

Визначте ухил і\(y\) -перехоплення. Використовуйте їх для побудови графіків наступного.

1. \(y=−\frac{3}{2}x+6\)
2. \(5x−2y=6\)
3. Дано\(m=−3\), визначте\(m_{⊥}\).
4. Задані лінії паралельні, перпендикулярні чи ні? \(\left\{\begin{aligned} -2x+3y&=-12\\4x-6y&=30 \end{aligned}\right.\)
5. Визначте ухил заданих ліній.
   1. \(y=−2\)
   2. \(x=\frac{1}{3}\)
   3. Ці лінії паралельні, перпендикулярні чи ні?
6. Визначте рівняння лінії з ухилом,\(m=−\frac{3}{4}\) що проходить наскрізь\((8, 1)\).
7. Знайдіть рівняння до лінії, що проходить через\((−2, 3)\) і\((4, 1)\).
8. Знайдіть рівняння прямої паралельної\(5x−y=6\) прохідній\((−1, −2)\).
9. Знайдіть рівняння прямої, перпендикулярної\(−x+2y=4\) прохідній\((\frac{1}{2}, 5)\).

Відповідь

1. Ухил:\(−\frac{3}{2}\);\(y\) -перехоплення:\((0, 6)\)

Малюнок 3.E.37

3. \(m_{⊥}=\frac{1}{3}\)

5. а.\(0\); б. Невизначено; c. перпендикулярно

6. \(y=−\frac{3}{4}x+7\)

8. \(y=5x+3\)

Вправа\(\PageIndex{26}\)

Задано лінійну функцію\(f(x)=−\frac{4}{5}x+2\), визначте наступне.

1. \(f(10)\)
2. \(x\)коли\(f(x)=0\)
3. Графік набору рішень:\(3x−4y>4\).
4. Графік набору рішень:\(y−2x≥0\).
5. Компанія з прокату автомобілів стягує $\(32.00\) плюс $\(0.52\) за милю. Напишіть рівняння, яке дає вартість оренди автомобіля в перерахунку на кількість пройдених миль. Скористайтеся формулою, щоб визначити вартість оренди автомобіля і проїзду його\(46\) миль.
6. Автомобіль був придбаний новий за $\(12,000\) і був проданий через 5 років за $\(7,000\). Напишіть лінійне рівняння, яке дає значення автомобіля з точки зору його віку в роках.
7. Площа прямокутника -\(72\) квадратні метри. Якщо ширина вимірює\(4\) метри, то визначте довжину прямокутника.

Відповідь

1. \(f(10)=−6\)

3.

Малюнок 3.Е.38

5. вартість\(=0.52x+32\); $\(55.92\)

7. \(18\)метрів