3.2: Графік за допомогою побудови точок

Last updated
Save as PDF

Page ID: 58104

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Перевірте розв'язки лінійних рівнянь з двома змінними.
Лінії графіка шляхом побудови точок.
Визначте і графік горизонтальних і вертикальних ліній.

Розв'язки рівнянь з двома змінними

Лінійне рівняння з двома змінними має стандартний вигляд$ax+by=c$, де$a,b$, і$c$ є дійсними числами і$a$ і не$b$ є обома$0$. Розв'язки рівнянь такого виду є$(x, y)$ впорядкованими парами, де координати при підстановці в рівняння виробляють істинне твердження.

Приклад$\PageIndex{1}$

Визначте, чи$(−4, 1)$ є$(1, −2)$ і є рішеннями$6x−3y=12$.

Рішення:

Підставте$y$ значення$x$ - і -у рівняння, щоб визначити, чи впорядкована пара виробляє істинний оператор.

$\begin{array}{c|c}{\underline{Check\:\:(1,-2)}}&{\underline{Check\:\:(-4,1)}}\\{6x-3y=12}&{6x-3y=12} \\{6(\color{OliveGreen}{1}\color{black}{)-3(}\color{OliveGreen}{-2}\color{black}{)=12}}&{6(\color{OliveGreen}{-4}\color{black}{)-3(}\color{OliveGreen}{1}\color{black}{)=12}}\\{6+6=12}&{-24-3=12}\\{12=12\quad\color{Cerulean}{\checkmark}}&{-27=12\quad\color{red}{x}}\end{array}$

Відповідь:

$(1,-2)$це рішення, а не$(-4,1)$ є.

Часто буває, що лінійне рівняння дається у вигляді, де одна зі змінних, як правило$y$, ізольована. Якщо це так, то ми можемо перевірити, що впорядкована пара є рішенням, підставивши значення для однієї з координат і спростивши, чи отримаємо ми іншу.

Приклад$\PageIndex{2}$

Чи є$(\frac{1}{2}, −3)$ і$(−5, 14)$ рішення$y=2x−4$?

Рішення:

Підставляємо$x$ -значення і спрощуємо, щоб побачити, чи отримані відповідні$y$ -значення.

$\begin{array}{c|c} {\underline{x=\frac{1}{2}}}&{\underline{x=-5}}\\{y=2x-4}&{y=2x-4}\\{=2\color{black}{\left(\color{OliveGreen}{\frac{1}{2}} \right)-4}}&{=2(\color{OliveGreen}{-5}\color{black}{)-4}}\\{=1-4}&{=-10-4}\\{=-3\quad\color{Cerulean}{\checkmark}}&{=-14\quad\color{red}{x}} \end{array}$

Відповідь:

$(\frac{1}{2},-3)$це рішення, а не$(-5,14)$ є.

Вправа$\PageIndex{1}$

Чи$(6, −1)$ є рішенням$y=−\frac{2}{3}x+3$?

Відповідь: Так

Коли задано лінійні рівняння з двома змінними, ми можемо вирішити для однієї зі змінних, як правило$y$, і отримати еквівалентне рівняння наступним чином:

Написано в такому вигляді, ми бачимо, що$y$ залежить від$x$. $x$Ось незалежна змінна і$y$ є залежною змінною.

$\left. \begin{aligned} 6x-3y&=12 \\ y&=2x-4\end{aligned}\right\} \color{Cerulean}{Equivalent\:equations}$

Лінійне рівняння$y=2x−4$ може бути використано для пошуку впорядкованих парних розв'язків. Якщо підставити будь-яке дійсне число для$x$, то ми можемо спростити знайти відповідне значення y. Наприклад, якщо, то$x=3$$y=2(3)−4=6−4=2$, і ми можемо сформувати впорядковане парне рішення,$(3, 2)$. Оскільки існує нескінченно багато дійсних чисел на вибір$x$, лінійне рівняння має нескінченно багато впорядкованих парних розв'язків$(x, y)$.

Приклад$\PageIndex{3}$

Знайти впорядковані парні розв'язки рівняння$5x−y=14$ з заданими$x$ -значеннями$\{−2, −1, 0, 4, 6\}$.

Рішення:

По-перше, вирішуйте для$y$.

Далі підставляємо$x$ -значення в рівняння$y=5x−14$, щоб знайти відповідні$y$ -значення.

$x-value$$y-value$$Solution$$x=-2$$(-2,-24)$$x=-1$$(-1,-19)$$x=0$$(0,-14)$$x=4$$(4,6)$$x=6$$(6,16)$ Таблиця$\PageIndex{1}$

Відповідь:

$\{(−2, −24), (−1, −19), (0, −14), (4, 6), (6, 16)\}$

У попередньому прикладі наведено певні$x$ -значення, але це не завжди буде так. Розглядаючи$x$ як незалежну змінну, ми можемо вибрати будь-які значення для,$x$ а потім підставити їх у рівняння, щоб знайти відповідні$y$ -значення. Цей метод виробляє стільки упорядкованих парних рішень, скільки ми хочемо.

Приклад$\PageIndex{4}$

Знайти п'ять упорядкованих парних рішень для$6x+2y=10$.

Рішення:

По-перше, вирішуйте для$y$.

$\begin{aligned} 6x+2y&=10 \\ 6x+2y\color{Cerulean}{-6x}&=10\color{Cerulean}{-6x} \\ 2y&=-6x+10 \\ \frac{2y}{\color{Cerulean}{2}}&=\frac{-6x+10}{\color{Cerulean}{2}} \\ y&=\frac{-6x}{2}+\frac{10}{2} \\ y&=-3x+5 \end{aligned}$

Далі вибираємо будь-який набір$x$ -values. Зазвичай ми вибираємо деякі негативні значення і деякі позитивні значення. У цьому випадку ми знайдемо відповідні$y$ -значення, коли$x$ є$\{−2, −1, 0, 1, 2\}$. Зробіть заміни, необхідні для заповнення наступної таблиці (часто називають t-chart):

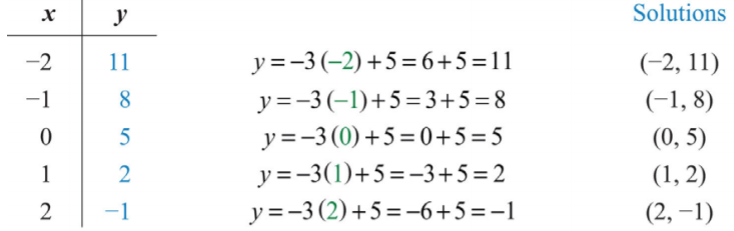Знімок екрана (489) .png — Малюнок$\PageIndex{1}$

Відповідь:

$\{(−2, 11), (−1, 8), (0, 5), (1, 2), (2, −1)\}$. Оскільки впорядкованих парних рішень нескінченно багато, відповіді можуть змінюватися в залежності від вибору значень для незалежної змінної.

Вправа$\PageIndex{2}$

Знайти п'ять упорядкованих парних рішень для$10x−2y=2$.

Відповідь: $\{(−2, −11), (−1, −6), (0, −1), (1, 4), (2, 9)\}$(відповіді можуть відрізнятися)

Графік за допомогою побудови точок

Оскільки розв'язки лінійних рівнянь є впорядкованими парами, вони можуть бути побудовані на графіку за допомогою прямокутної системи координат. Множину всіх розв'язків лінійного рівняння можна представити на прямокутній координатній площині за допомогою прямої, що з'єднує щонайменше дві точки; ця лінія називається її графом. Щоб проілюструвати це, побудуйте п'ять впорядкованих парних розв'язків до лінійного рівняння$6x+2y=10$.$\{(−2, 11), (−1, 8), (0, 5), (1, 2), (2, −1)\}$

Скріншот (490) .png — Малюнок$\PageIndex{2}$

Зверніть увагу, що точки є колінеарними; це буде так для будь-якого лінійного рівняння. Намалюйте лінію через точки з прямим краєм і додайте стрілки на обох кінцях, щоб вказати, що графік триває нескінченно довго.

Знімок екрана (491) .png — Малюнок$\PageIndex{3}$

Отримана лінія представляє всі рішення$6x+2y=10$, яких існує нескінченно багато. Етапи побудови графічних ліній шляхом побудови точок описані в наступному прикладі.

Приклад$\PageIndex{5}$

Знайдіть п'ять упорядкованих парних рішень і графік:

$10x−5y=10$.

Рішення:

Крок 1: Вирішити для$y$.

Крок 2: Виберіть принаймні два$x$ -значення та знайдіть відповідні$y$ -значення. У цьому розділі ми виберемо п'ять дійсних чисел для використання як$x$ -values. Хорошою практикою є вибір$0$ і деяких негативних чисел, а також деяких позитивних чисел.

Знімок екрана (493) .png — Малюнок$\PageIndex{4}$

Не завжди буде той випадок, який$y$ можна вирішити через$x$ цілочисельні коефіцієнти. Насправді коефіцієнти часто виявляються дробами.

Приклад$\PageIndex{6}$

Знайдіть п'ять упорядкованих парних рішень і графік:

$−5x+2y=10$.

Рішення:

$\begin{aligned} -5x+2y&=10 \\ -5x+2y\color{Cerulean}{+5x}&=10\color{Cerulean}{+5x} \\ 2y&=5x+10 \\ frac{2y}{\color{Cerulean}{2}}&=\frac{5x+10}{\color{Cerulean}{2}} \\ y&=\frac{5x}{2}+\frac{10}{2} \\ y&=\frac{5}{2}x+5 \end{aligned}$

Пам'ятайте, що ви можете вибрати будь-яке дійсне число для незалежної змінної$x$, тому вибирайте тут мудро. Так як знаменник коефіцієнта змінної$x$ є$2$, ви можете уникнути дробів, вибравши кратні$2$ для$x$ -значень. В цьому випадку вибираємо набір$x$ -значень$\{−6, −4, −2, 0, 2\}$ і знаходимо відповідні$y$ -значення.

Знімок екрана (494) .png — Малюнок$\PageIndex{6}$

П'ять рішень є$\{(−6, −10), (−4, −5), (−2, 0), (0, 5), (2, 10)\}$. Тут ми вибираємо масштабувати$x$ -вісь з кратними$2$ і$y$ -вісь з кратними$5$.

Відповідь:

Скріншот (495) .png — Малюнок$\PageIndex{7}$

Вправа$\PageIndex{3}$

Знайдіть п'ять упорядкованих парних рішень і графік:$x+2y=6$.

Відповідь: $\{(−2, 4), (0, 3), (2, 2), (4, 1), (6, 0)\}$

$Знімок екрана (496) .png$
Малюнок$\PageIndex{8}$

Горизонтальні та вертикальні лінії

Нам потрібно розпізнати шляхом огляду лінійні рівняння, які представляють собою вертикальну або горизонтальну лінію.

Приклад$\PageIndex{7}$

Графік шляхом побудови п'яти точок:$y=−2$.

Рішення:

Так як дане рівняння не має змінної$x$, ми можемо переписати його з$0$ коефіцієнтом for$x$.

$y=0x-2$

Виберіть будь-які п'ять значень для$x$ і переконайтеся, що відповідне$y$ -значення завжди$−2$.

Знімок екрана (497) .png — Малюнок$\PageIndex{9}$

Тепер у нас є п'ять замовлених парних рішень для побудови сюжету$\{(−2, −2), (−1, −2), (0, −2), (1, −2), (2, −2)\}$.

Відповідь:

Знімок екрана (498) .png — Малюнок$\PageIndex{10}$

Коли коефіцієнт для змінної$x$ дорівнює$0$, графік є горизонтальною лінією. Взагалі рівняння для горизонтальної лінії можна записати у вигляді$y=k$, де$k$ представляє будь-яке дійсне число.

Приклад$\PageIndex{8}$

Графік шляхом побудови п'яти точок:$x = 3$.

Рішення:

Так як дане рівняння не має змінної$y$, перепишіть його з$0$ коефіцієнтом for$y$.

$x=0y+3$

Виберіть будь-які п'ять значень для$y$ і переконайтеся, що відповідне$x$ -значення завжди$3$.

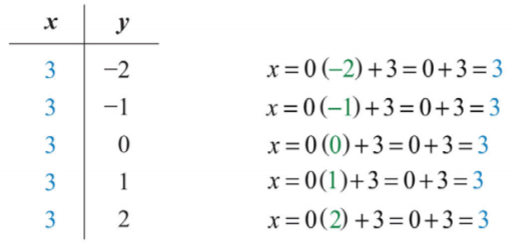Скріншот (499) .png — Малюнок$\PageIndex{11}$

Тепер у нас є п'ять упорядкованих парних рішень для побудови:$\{(3, −2), (3, −1), (3, 0), (3, 1), (3, 2)\}$.

Відповідь:

Знімок екрана (500) .png — Малюнок$\PageIndex{12}$

Коли коефіцієнт для змінної$y$ дорівнює$0$, графік являє собою вертикальну лінію. Загалом, рівняння для вертикальної лінії можна записати як$x=k$, де$k$ представляє будь-яке дійсне число.

Підводячи підсумок, якщо$k$ це дійсне число.

\[y=k\quad\color{Cerulean}{Horizontal\:line}\]

\[x=k\quad\color{Cerulean}{Vertical\:line}\]

Вправа$\PageIndex{4}$

Графік$y=5$ і$x=−2$ на одному і тому ж наборі осей і визначають, де вони перетинаються.

Відповідь: $(-2,5)$

Ключові винос

Розв'язки лінійних рівнянь з двома змінними$ax+by=c$ є впорядкованими парами$(x, y)$, де координати при підстановці в рівняння призводять до істинного твердження.
Лінійні рівняння з двома змінними мають нескінченно багато впорядкованих парних рішень. Коли розв'язки графуються, вони є колінеарними.
Щоб знайти впорядковані парні розв'язки, вибирають значення для незалежної змінної$x$, як правило, і підставляють їх у рівняння, щоб знайти відповідні$y$ -значення.
Для побудови графіків лінійних рівнянь визначте щонайменше два впорядкованих парних розв'язку і проведіть через них лінію з прямолінійним краєм.
Горизонтальні лінії описуються тим$y = k$, де$k$ знаходиться будь-яке дійсне число.
Вертикальні лінії описуються тим$x = k$, де$k$ є будь-яке дійсне число.

Вправа$\PageIndex{5}$ Solutions to Linear Systems

Визначте, чи є дана точка рішенням.

$5x−2y=4; (−1, 1)$
$3x−4y=10; (2, −1)$
$−3x+y=−6; (4, 6)$
$−8x−y=24; (−2, −3)$
$−x+y=−7; (5, −2)$
$9x−3y=6; (0, −2)$
$\frac{1}{2}x+\frac{1}{3}y=−\frac{1}{6}; (1, −2)$
$\frac{3}{4}x−\frac{1}{2}y=−1; (2, 1)$
$4x−3y=1; (\frac{1}{2}, \frac{1}{3})$
$−10x+2y=−\frac{9}{5}; (\frac{1}{5}, \frac{1}{10})$
$y=\frac{1}{3}x+3; (6, 3)$
$y=−4x+1; (−2, 9)$
$y=\frac{2}{3}x−3; (0, −3)$
$y=−\frac{5}{8}x+1; (8, −5)$
$y=−\frac{1}{2}x+\frac{3}{4}; (−\frac{1}{2}, 1)$
$y=−\frac{1}{3}x−\frac{1}{2}; (\frac{1}{2}, −\frac{2}{3})$
$y=2; (−3, 2)$
$y=4; (4, −4)$
$x=3; (3, −3)$
$x=0; (1, 0)$

Відповідь

1. Ні

3. Так

5. Так

7. Так

9. Так

11. Ні

13. Так

15. Так

17. Так

19. Так

Вправа$\PageIndex{6}$ Solutions to Linear Systems

Знайти впорядковані парні розв'язки, задані множиною$x$ -values.

$y=−2x+4; \{−2, 0, 2\}$
$y=12x−3; \{−4, 0, 4\}$
$y=−\frac{3}{4}x+\frac{1}{2}; \{−2, 0, 2\}$
$y=−3x+1; \{−\frac{1}{2}, 0, \frac{1}{2}\}$
$y=−4; \{−3, 0, 3\}$
$y=\frac{1}{2}x+\frac{3}{4}; \{−\frac{1}{4}, 0, \frac{1}{4}\}$
$2x−3y=1; \{0, 1, 2\}$
$3x−5y=−15; \{−5, 0, 5\}$
$–x+y=3; \{−5, −1, 0\}$
$\frac{1}{2}x−\frac{1}{3}y=−4; \{−4, −2, 0\}$
$\frac{3}{5}x+\frac{1}{10}y=2; \{−15, −10, −5\}$
$x−y=0; \{10, 20, 30\}$

Відповідь

1. $\{(−2, 8), (0, 4), (2, 0)\}$

3. $\{(−2, 2), (0, 1/2), (2, −1)\}$

5. $\{(−3, −4), (0, −4), (3, −4)\}$

7. $\{(0, −\frac{1}{3}), (1, \frac{1}{3}), (2, 1)\}$

9. $\{(−5, −2), (−1, 2), (0, 3)\}$

11. $\{(−15, 110), (−10, 80), (−5, 50)\}$

Вправа$\PageIndex{7}$ Solutions to Linear Systems

Знайти впорядковані парні розв'язки, задані множиною$y$ -значень.

$y=\frac{1}{2}x−1; \{−5, 0, 5\}$
$y=−\frac{3}{4}x+2; \{0, 2, 4\}$
$3x−2y=6; \{−3, −1, 0\}$
$−x+3y=4; \{−4, −2, 0\}$
$\frac{1}{3}x−\frac{1}{2}y=−4; \{−1, 0, 1\}$
$\frac{3}{5}x+\frac{1}{10}y=2; \{−20, −10, −5\}$

Відповідь

1. $\{(−8, −5), (2, 0), (12, 5)\}$

3. $\{(0, −3), (\frac{4}{3}, −1), (2, 0)\}$

5. $\{(−\frac{27}{2}, −1), (−12, 0), (−\frac{21}{2}, 1)\}$

Вправа$\PageIndex{8}$ Graphing Lines

Задано множини$x$ -значень$\{−2, −1, 0, 1, 2\}$, знайдіть відповідні$y$ -значення і графуйте їх.

$y=x+1$
$y=−x+1$
$y=2x−1$
$y=−3x+2$
$y=5x−10$
$5x+y=15$
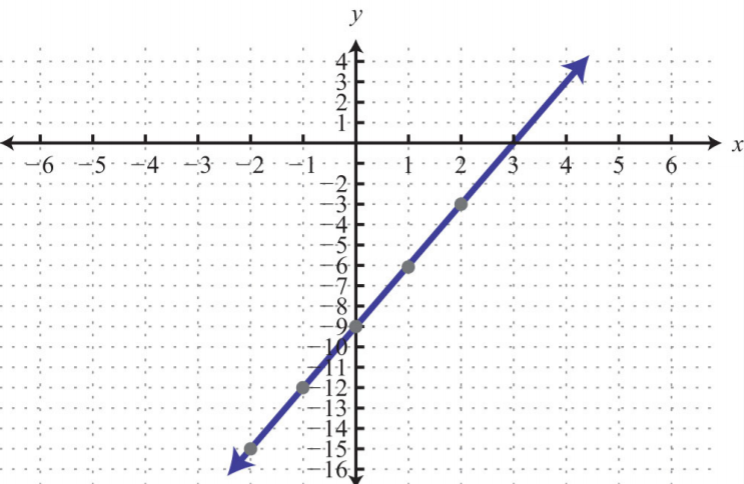
$3x−y=9$
$6x−3y=9$
$y=−5$
$y=3$

Відповідь

Скріншот (501) .png — Малюнок$\PageIndex{13}$

Знімок екрана (502) .png — Малюнок$\PageIndex{14}$

Знімок екрана (503) .png — Малюнок$\PageIndex{15}$

Знімок екрана (504) .png — Малюнок$\PageIndex{16}$

Знімок екрана (506) .png — Малюнок$\PageIndex{17}$

Вправа$\PageIndex{9}$ Graphing Lines

Знайдіть щонайменше п'ять впорядкованих парних розв'язків і графік.

$y=2x−1$
$y=−5x+3$
$y=−4x+2$
$y=10x−20$
$y=−\frac{1}{2}x+2$
$y=\frac{1}{3}x−1$
$y=\frac{2}{3}x−6$
$y=−\frac{2}{3}x+2$
$y=x$
$y=−x$
$−2x+5y=−15$
$x+5y=5$
$6x−y=2$
$4x+y=12$
$−x+5y=0$
$x+2y=0$
$\frac{1}{10}x−y=3$
$\frac{3}{2}x+5y=30$

Відповідь

Знімок екрана (507) .png — Малюнок$\PageIndex{18}$

Знімок екрана (508) .png — Малюнок$\PageIndex{19}$

Знімок екрана (509) .png — Малюнок$\PageIndex{20}$

Скріншот (510) .png — Малюнок$\PageIndex{21}$

Знімок екрана (511) .png — Малюнок$\PageIndex{22}$

11.

Скріншот (512) .png — Малюнок$\PageIndex{23}$

13.

Знімок екрана (513) .png — Малюнок$\PageIndex{24}$

15.

Знімок екрана (514) .png — Малюнок$\PageIndex{25}$

17.

Знімок екрана (515) .png — Малюнок$\PageIndex{26}$

Вправа$\PageIndex{10}$ Horizontal and Vertical Lines

Знайдіть щонайменше п'ять впорядкованих парних розв'язків і наведіть графік їх.

$y=4$
$y=−10$
$x=4$
$x=−1$
$y=0$
$x=0$
$y=\frac{3}{4}$
$x=−\frac{5}{4}$
Графік ліній$y=−4$ і$x=2$ на одному і тому ж наборі осей. Де вони перетинаються?
Графік ліній$y=5$ і$x=−5$ на одному і тому ж наборі осей. Де вони перетинаються?
Що таке рівняння, яке описує$x$ -вісь?
Що таке рівняння, яке описує$y$ -вісь?