3.1: Прямокутна система координат
- Page ID
- 58098
Цілі навчання
- Покладіть точки за допомогою прямокутної системи координат.
- Обчисліть відстань між будь-якими двома точками в прямокутній координатній площині.
- Визначте середину між будь-якими двома точками.
Прямокутна система координат
Прямокутна система координат складається з двох дійсних числових ліній, які перетинаються під прямим кутом. Горизонтальна числова лінія називається\(x\) -віссю, а вертикальна числова лінія називається\(y\) -віссю. Ці дві числові лінії визначають плоску поверхню, яка називається площиною, і кожна точка на цій площині пов'язана з впорядкованою парою дійсних чисел\((x, y)\). Перше число називається \(x\)-координатою, а друге \(y\)- координатою. Перетин двох осей відомий як початок, яке відповідає точці\((0, 0)\).
.png)
Впорядкована пара\((x, y)\) представляє позицію точки відносно початку. \(x\)-coordinate представляє позицію праворуч від початку, якщо вона позитивна, і ліворуч від початку, якщо вона негативна. \(y\)-coordinate представляє позицію над початком, якщо вона позитивна, і нижче початку, якщо вона негативна. Використовуючи цю систему, кожна позиція (точка) на площині однозначно ідентифікується. Наприклад, пара\((2, 3)\) позначає положення щодо початку, як показано на малюнку:
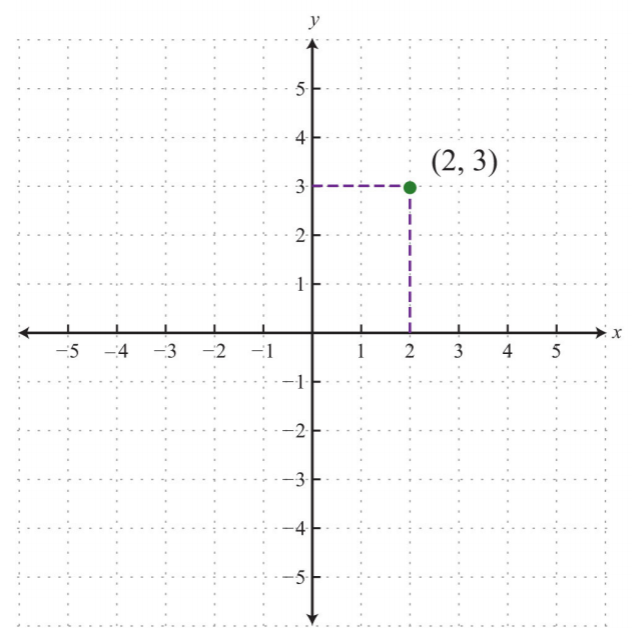.png)
Цю систему часто називають декартовою системою координат, названою на честь французького математика Рене Декарта (1596— 1650).
\(x\)- і\(y\) -осі розбивають площину на чотири області, які називаються квадрантами, названі римськими цифрами I, II, III та IV, як показано на малюнку. У квадранті I обидві координати позитивні. У квадранті II\(x\) -координата від'ємна, а\(y\) -координата - додатна. У третьому квадранті обидві координати є негативними. У квадранті IV\(x\) -координата позитивна, а\(y\) -координата - негативна.
.png)
Приклад\(\PageIndex{1}\)
Побудуйте\((−3, 5)\) впорядковану пару і визначте квадрант, в якому вона лежить.
Рішення:
Координати\(x=−3\) та\(y=5\) вказують\(3\) одиниці точки ліворуч від та\(5\) одиниць вище початку.
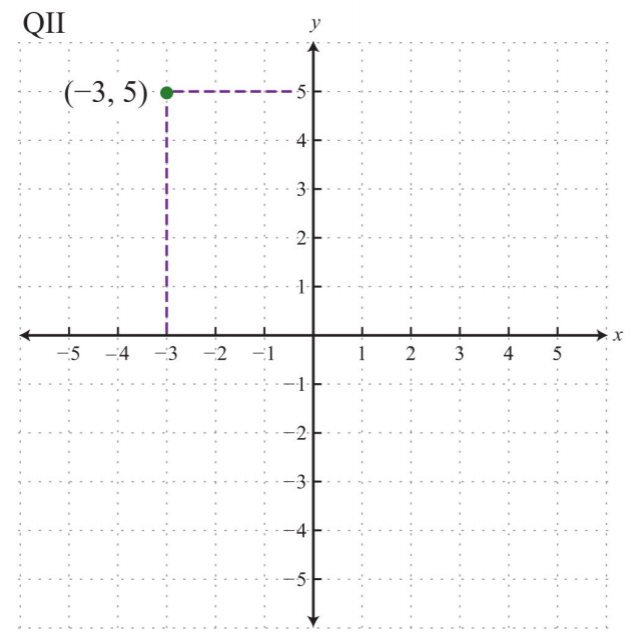.png)
Відповідь:
Точка побудована у квадранті II (QII), оскільки\(x\) координата -від'ємна, а\(y\) координата - додатна.
Впорядковані пари з\(0\) однією з координат не лежать у квадранті; ці точки знаходяться на одній або іншій осі (або точка є початком, якщо обидві координати\(0\)). Також масштаб, зазначений на\(x\) -осі, може відрізнятися від шкали, зазначеної на\(y\) -осі. Вибирайте масштаб, зручний для даної ситуації.
Приклад\(\PageIndex{2}\)
Покладемо цей набір впорядкованих пар:
\(\{(4, 0), (−6, 0), (0, 3), (−2, 6), (−4, −6)\}\).
Рішення:
Кожна позначка на\(x\) -осі представляє\(2\) одиниці, а кожна позначка на\(y\) -осі -\(3\) одиниці.
.png)
Приклад\(\PageIndex{3}\)
Покладемо цей набір впорядкованих пар:
\(\{(−6, −5), (−3, −3), (0, −1), (3, 1), (6, 3)\}\).
Рішення:
.png)
У цьому прикладі точки здаються колінеарними або лежать на одній лінії. Вся глава зосереджена на пошуку та вираженні точок з цією властивістю.
Вправа\(\PageIndex{1}\)
Побудуйте множину точок\(\{(5, 3), (−3, 2), (−2, −4), (4, −3)\}\) і вкажіть, в якому квадранті вони лежать.
- Відповідь
-
.png)
Малюнок\(\PageIndex{7}\)
Графіки використовуються в повсякденному житті для візуального відображення даних. Лінійний графік складається з набору пов'язаних значень даних, розміщених на координатній площині і з'єднаних відрізками лінії. Як правило, незалежна величина, така як час, відображається на\(x\) -осі, а залежна величина, така як пройдена відстань, на\(y\) -осі.
Приклад\(\PageIndex{4}\)
Наступний графік показує кількість математичних та статистичних ступенів бакалавра, присуджених у Сполучених Штатах щороку з 1970 року.
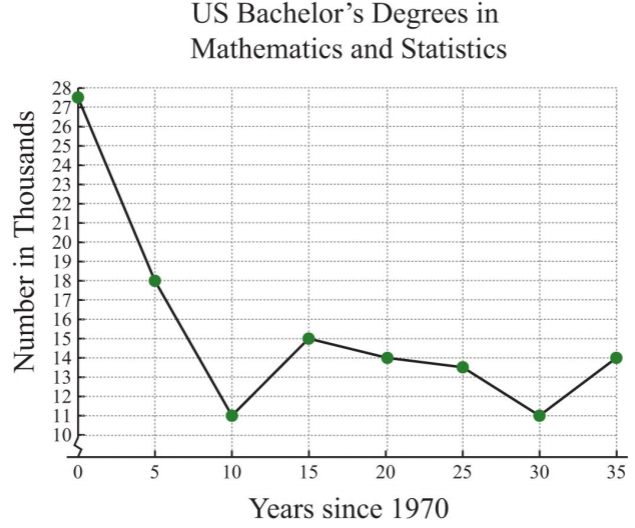.png)
- Скільки ступенів бакалавра математики та статистики було присвоєно в 1975 році?
- У які роки кількість математичних та статистичних ступенів присуджувалася на низькому рівні\(11,000\)?
Рішення:
a Шкала на\(x\) -осі представляє час з 1970 року, тому для визначення кількості градусів, присуджених в 1975 році, прочитайте\(y\) -значення графіка в\(x = 5\).
.png)
\(y\)Значення\(x = 5\) -відповідне є\(18\). Графік вказує, що це тисячі; в 1975 році були\(18,000\) математичні та статистичні ступені.
б Щоб знайти рік, яку було присуджено певну кількість ступенів, спочатку подивіться на\(y\) -вісь. У цьому випадку\(11,000\) градуси зображуються\(11\) на\(y\) -осі; подивіться вправо, щоб побачити, в які роки це сталося.
.png)
\(y\)-value\(11\) відбувається в двох точках даних, одна де\(x = 10\) і інша де\(x = 30\). Ці значення відповідають 1980 і 2000 рокам відповідно.
Відповіді:
- У 1975 році були присуджені ступені\(18,000\) математики та статистики.
- У 1980 і 2000 роках були присуджені мінімуми\(11,000\) математики та статистики.
Формула відстані
Часто потрібно обчислити відстань між двома точками в площині. Для цього сформуйте прямокутний трикутник, використовуючи дві точки як вершини трикутника, а потім застосуйте теорему Піфагора. Нагадаємо, що теорема Піфагора стверджує, що якщо задано будь-який прямокутний трикутник з катетами вимірювання\(a\) і\(b\) одиницями, то квадрат міри гіпотенузи\(c\) дорівнює сумі квадратів катетів:\(a^{2}+b^{2}=c^{2}\). Іншими словами, гіпотенуза будь-якого прямокутного трикутника дорівнює квадратному кореню суми квадратів його катетів.
.png)
Приклад\(\PageIndex{5}\)
Знайти відстань між\((−1, 2)\) і\((3, 5)\).
Рішення:
Сформуйте прямокутний трикутник, провівши горизонтальні та вертикальні лінії через дві точки. Це створює прямокутний трикутник, як показано нижче:
.png)
Довжина катета\(b\) обчислюється шляхом знаходження відстані між\(x\) -значеннями заданих точок, а довжина катета\(a\) обчислюється шляхом знаходження відстані між заданими\(y\) -значеннями.
\(\begin{aligned} a&=5-2=3\text{units} \\ b&=3-(-1)=3+1=4\text{units} \end{aligned}\)
Далі використовуйте теорему Піфагора, щоб знайти довжину гіпотенузи.
\(\begin{aligned} c&=\sqrt{3^{2}+4^{2}} \\ &=\sqrt{9+16} \\ &=\sqrt{25} \\ &=5\:\text{units} \end{aligned}\)
Відповідь:
Відстань між двома точками дорівнює\(5\) одиницям.
Узагальніть цей процес, щоб отримати формулу, яка може бути використана для алгебраїчного обчислення відстані між будь-якими двома заданими точками.
.png)
З огляду на дві точки\((x_{2}, y_{2})\),\((x_{1}, y_{1})\) а, потім відстань\(d\), між ними задається за формулою відстані:
\[\sqrt{(x_{2}+x_{1})^{2}+(y_{2}+y_{1})^{2}}\]
Приклад\(\PageIndex{6}\)
Обчисліть відстань між\((−3, −1)\) і\((−2, 4)\).
Рішення:
Скористайтеся формулою відстані.
\(\begin{array}{cc} {x_{1},y_{1}}&{x_{2},y_{2}}\\{(\color{Cerulean}{-3}\color{black}{,}\color{OliveGreen}{-1}\color{black}{)}}&{(\color{Cerulean}{-2}\color{black}{,}\color{OliveGreen}{4}\color{black}{)}} \end{array}\)
Хорошою практикою є включення формули в загальному вигляді як частину письмового рішення перед підстановкою значень для змінних. Це покращує читабельність і зменшує ймовірність помилок.
\(\begin{aligned} d&=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} \\ &=\sqrt{(\color{Cerulean}{-2}\color{black}{-(}\color{Cerulean}{-3}\color{black}{))^{2}+(}\color{OliveGreen}{4}\color{black}{-(}\color{OliveGreen}{-1}\color{black}{))^{2}}} \\ &=\sqrt{(-2+3)^{2}+(4+1)^{2}} \\ &=\sqrt{(1)^{2}+(5)^{2}} \\ &=\sqrt{1+25} \\ &=\sqrt{26} \end{aligned}\)
Відповідь:
\(\sqrt{26}\)одиниць
Вправа\(\PageIndex{2}\)
Обчисліть відстань між\((−7, 5)\) і\((−1, 13)\).
- Відповідь
-
\(10\)одиниць
Приклад\(\PageIndex{7}\)
Чи три точки\((1, −1), (3, −3)\), і\((3, 1)\) утворюють прямокутний трикутник?
Рішення:
Теорема Піфагора стверджує, що наявність довжин сторін, які задовольняють властивість,\(a^{2}+b^{2}=c^{2}\) є необхідною і достатньою умовою прямих трикутників. Іншими словами, якщо можна показати, що сума квадратів довжин катетів трикутника дорівнює квадрату довжини гіпотенузи, то фігура повинна бути прямокутним трикутником. Спочатку обчисліть довжину кожної сторони, використовуючи формулу відстані.
| Геометрія | Розрахунок |
|---|---|
.png) |
Окуляри:\((1,-1)\) і\((3,-3)\) \(\begin{aligned} a&=\sqrt{(3-1)^{2}+(-3-(-1))^{2}} \\ &=\sqrt{(a)^{2}+(-3+1)^{2}} \\ &=\sqrt{4+(-2)^{2}} \\ &=\sqrt{4+4} \\ &=\sqrt{8} \end{aligned}\) |
.png) |
Окуляри:\((1,-1)\) і\((3,1)\) \(\begin{aligned} b&=\sqrt{(3-1)^{2}+(1-(-1))^{2}} \\ &=\sqrt{2^{2}+(1+1)^{2}} \\ &=\sqrt{4+(2)^{2}} \\ &=\sqrt{4+4} \\ &=\sqrt{8} \end{aligned}\) |
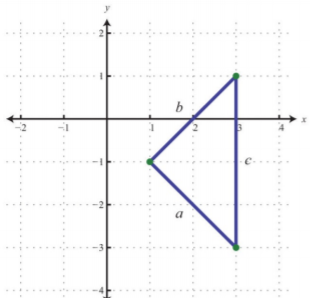.png) |
Окуляри:\((3,-3)\) і\((3,1)\) \(\begin{aligned} c&=\sqrt{(3-3)^{2}+(1-(-3))^{2}} \\ &=\sqrt{(0)^{2}+(1+3)^{2}} \\ &=\sqrt{0+(4)^{2}} \\ &=\sqrt{16} \\ &=4 \end{aligned}\) |
Тепер перевіряємо, чи є\(a^{2}+b^{2}=c^{2}\).
\(a^{2}+b^{2}=c^{2}\)
\(\begin{aligned} (\sqrt{8})^{2}+(\sqrt{8})^{2}&=(4)^{2} \\ \sqrt{64}+\sqrt{64}&=16 \\ 8+8&=16\\16&=16\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Відповідь:
Так, три точки утворюють прямокутний трикутник. Насправді, оскільки дві ноги рівні по довжині, точки утворюють рівнобедрений прямокутний трикутник.
Формула середньої точки
Точка, яка перетинає відрізок лінії, утворений двома точками\((x_{2}, y_{2})\),\((x_{1}, y_{1})\) і, називається середньою точкою і задається за такою формулою:
\[ \left( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right) \]
Середина - це впорядкована пара, утворена шляхом знаходження середнього\(x\) значення\(y\) -значень та середнього значення заданих точок.
Приклад\(\PageIndex{8}\)
Обчисліть середню точку між\((−1, −2)\) і\((7, 4)\).
Рішення:
Спочатку обчислити середнє значення\(x\) - і\(y\) -значень заданих балів.
\(\begin{array}{cc} {(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-1,-2)}&{(7,4)} \end{array}\)
\(\begin{aligned} \frac{x_{1}+x_{2}}{2}&=\frac{-1+7}{2}&=\frac{6}{2}&=3 \\ \frac{y_{1}+y_{2}}{2}&=\frac{-2+4}{2}&=\frac{2}{2}&=1 \end{aligned}\)
Далі сформуйте середню точку як впорядковану пару, використовуючи усереднені координати.
\(\left( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right)\)
\((3,1)\)
Відповідь:
\((3,1)\)
Щоб переконатися, що це дійсно середина, обчисліть відстань між двома заданими точками і переконайтеся, що результат дорівнює сумі двох рівних відстаней від кінцевих точок до цієї середньої точки. Ця перевірка залишається читачеві як вправу.
.png)
Вправа\(\PageIndex{3}\)
Знайдіть середину між\((−6, 5)\) і\((6, −11)\).
- Відповідь
-
\((0,-3)\)
Ключові винос
- Використовуйте прямокутну систему координат, щоб однозначно ідентифікувати точки на площині за допомогою впорядкованих пар\((x, y)\). Впорядковані пари вказують положення щодо походження. \(x\)-coordinate вказує положення ліворуч і праворуч від початку. \(y\)-coordinate вказує на позицію вище або нижче початку.
- Шкали на\(x\) -осі і\(y\) -осі можуть бути різними. Виберіть масштаб для кожної осі, який підходить для даної задачі.
- Графіки використовуються для візуалізації реальних даних. Зазвичай незалежні дані пов'язані з\(x\) -віссю, а залежні дані пов'язані з\(y\) -віссю.
- Теорема Піфагора дає нам необхідну і достатню умову прямих трикутників. Дано прямокутний трикутник, то міри сторін задовольняють\(a^{2}+b^{2}=c^{2}\). І навпаки, якщо сторони задовольняють\(a^{2}+b^{2}=c^{2}\), то трикутник повинен бути прямокутним трикутником.
- Формула відстані\(d=\sqrt{(x_{2}−x_{1})^{2}+(y_{2}−y_{1})^{2}}\), походить від теореми Піфагора і дає нам відстань між будь-якими двома точками,\((x_{1}, y_{1})\) причому\((x_{2}, y_{2})\), в прямокутній координатній площині.
- Формула середньої точки виводиться шляхом взяття середнього значення кожної координати та формування впорядкованої пари.\(\left( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right)\)
Вправа\(\PageIndex{4}\) Ordered Pairs
Дайте координати точок\(A, B, C, D,\) і\(E\).
1.
.png)
2.
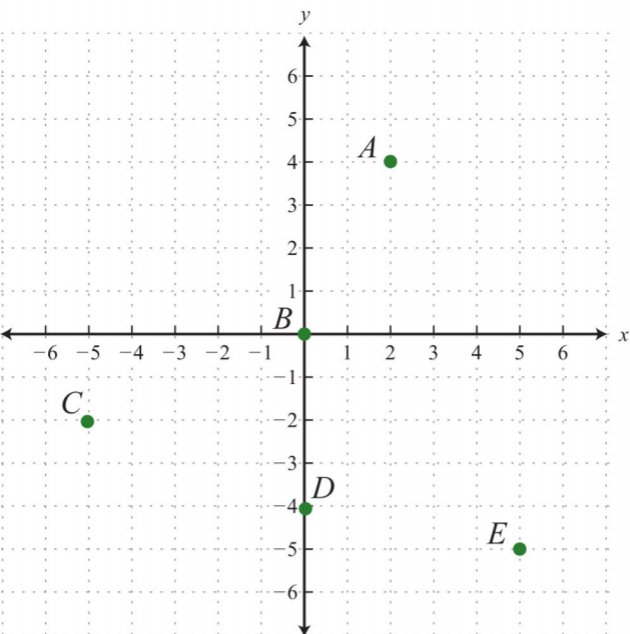.png)
3.
.png)
4.
.png)
5.
.png)
6.
.png)
- Відповідь
-
1. \(A: (3, 5); B: (−2, 3); C: (−5, 0); D: (1, −3); E: (−3, −4)\)
3. \(A: (0, 6); B: (−4, 3); C: (−8, 0); D: (−6, −6); E: (8, −9)\)
5. \(A: (−10, 25); B: (30, 20); C: (0, 10); D: (15, 0); E: (25, −10)\)
Вправа\(\PageIndex{5}\) Ordered Pairs
Графік заданої множини впорядкованих пар.
- \(\{(−4, 5), (−1, 1), (−3, −2), (5, −1)\}\)
- \(\{(−15, −10), (−5, 10), (15, 10), (5, −10)\}\)
- \(\{(−2, 5), (10, 0), (2, −5), (6, −10)\}\)
- \(\{(−8, 3), (−4, 6), (0, −6), (6, 9)\}\)
- \(\{(−10, 5), (20, −10), (30, 15), (50, 0)\}\)
- \(\{(−\frac{5}{3}, −\frac{1}{2}),(−\frac{1}{3}, \frac{1}{2}),(\frac{2}{3}, −1),(\frac{5}{3}, 1)\}\)
- \(\{(−\frac{3}{5}, −\frac{4}{3}),(\frac{2}{5}, \frac{4}{3}),(1, −\frac{2}{3}),(0, 1)\}\)
- \(\{(−3.5, 0), (−1.5, 2), (0, 1.5), (2.5, −1.5)\}\)
- \(\{(−0.8, 0.2), (−0.2, −0.4), (0, −1), (0.6, −0.4)\}\)
- \(\{(−1.2, −1.2), (−0.3, −0.3), (0, 0), (0.6, 0.6), (1.2, 1.2)\}\)
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{24}\) 3.
.png)
Малюнок\(\PageIndex{25}\) 5.
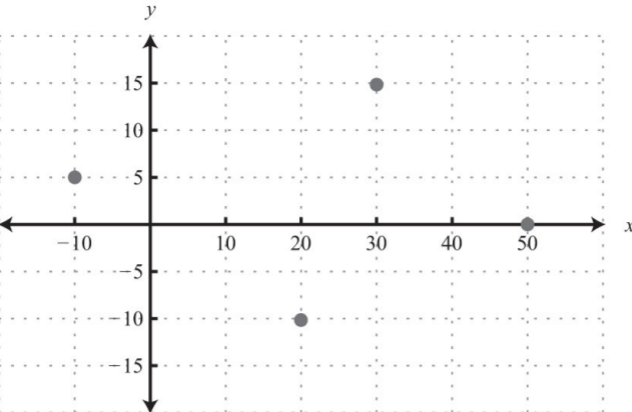.png)
Малюнок\(\PageIndex{26}\) 7.
.png)
Малюнок\(\PageIndex{27}\) 9.
.png)
Малюнок\(\PageIndex{28}\)
Вправа\(\PageIndex{6}\) Ordered Pairs
Створіть квадрант, в якому лежить дана точка.
- \((−3, 2)\)
- \((5, 7)\)
- \((−12, −15)\)
- \((7, −8)\)
- \((−3.8, 4.6)\)
- \((17.3, 1.9)\)
- \((−\frac{1}{8}, −\frac{5}{8})\)
- \((\frac{3}{4}, −\frac{1}{4})\)
- \(x>0\)і\(y<0\)
- \(x<0\)і\(y<0\)
- \(x<0\)і\(y>0\)
- \(x>0\)і\(y>0\)
- Відповідь
-
1. QII
3. QIII
5. QII
7. QIII
9. QIV
11. QII
Вправа\(\PageIndex{7}\) Ordered Pairs
Середня ціна галона звичайного неетилованого бензину в містах США наведена на наступному графіку рядків. Використовуйте графік, щоб відповісти на наступні питання.
.png)
- Якою була середня ціна галона неетилованого бензину в 2004 році?
- Якою була середня ціна галона неетилованого бензину в 1976 році?
- В які роки склалися середні ціни на галон неетилованого бензину $\(1.20\)?
- Яке зростання цін на галон бензину з 1980 по 2008 рік?
- Яким було процентне зростання ціни на галон неетилованого бензину з 1976 по 1980 рік?
- Яким було процентне зростання ціни на галон неетилованого бензину з 2000 по 2008 рік?
- Відповідь
-
1. $\(1.80\)
3. 1980 по 1984, 1996
3. \(100\)%
Вправа\(\PageIndex{8}\) Ordered Pairs
Середня ціна білої муки універсального призначення в містах США з 1980 по 2008 рік наведена в наступному рядковому графіку. Використовуйте графік, щоб відповісти на наступні питання.
.png)
- Якою була середня ціна за фунт універсального білого борошна в 2000 році?
- Якою була середня ціна за фунт універсального білого борошна в 2008 році?
- В якому році ціна на борошно зросла в середньому $\(0.25\) за фунт?
- В які роки зросла ціна на борошно в середньому $\(0.20\) за фунт?
- Яким був процентний приріст борошна з 2000 по 2008 рік?
- Яким був процентний приріст борошна з 1992 по 2000 рік?
- Відповідь
-
1. $\(0.30\)
3. 1992
5. \(67\)%
Вправа\(\PageIndex{9}\) Ordered Pairs
З огляду на наступні дані, створіть лінійний графік.
1. Відсоток від загальної кількості випускників середньої школи, які вступили до коледжу.
| Рік | Відсоток |
|---|---|
| 1969 | \(36\)% |
| 1979 | \(40\)% |
| 1989 | \(47\)% |
| 1999 | \(42\)% |
2. Середньодобова температура вказана в градусах Фаренгейта в травні.
| іспит | Температура |
|---|---|
| 8:00 ранку | \(60\) |
| 12:00 вечора | \(72\) |
| 16:00 вечора | \(75\) |
| 8:00 вечора | \(67\) |
| 12:00 ранку | \(60\) |
| 4:00 ранку | \(55\) |
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{31}\)
Вправа\(\PageIndex{10}\) Ordered Pairs
Обчисліть площу форми, утвореної шляхом з'єднання наступного набору вершин.
- \(\{(0, 0), (0, 3), (5, 0), (5, 3)\}\)
- \(\{(−1, −1), (−1, 1), (1, −1), (1, 1)\}\)
- \(\{(−2, −1), (−2, 3), (5, 3), (5, −1)\}\)
- \(\{(−5, −4), (−5, 5), (3, 5), (3, −4)\}\)
- \(\{(0, 0), (4, 0), (2, 2)\}\)
- \(\{(−2, −2), (2, −2), (0, 2)\}\)
- \(\{(0, 0), (0, 6), (3, 4)\}\)
- \(\{(−2, 0), (5, 0), (3, −3)\}\)
- Відповідь
-
1. \(15\)квадратні одиниці
3. \(28\)квадратні одиниці
5. \(4\)квадратні одиниці
7. \(9\)квадратні одиниці
Вправа\(\PageIndex{11}\) Distance Formula
Обчисліть відстань між заданими двома точками.
- \((−5, 3)\)і\((−1, 6)\)
- \((6, −2)\)і\((−2, 4)\)
- \((0, 0)\)і\((5, 12)\)
- \((−6, −8)\)і\((0, 0)\)
- \((−7, 8)\)і\((5, −1)\)
- \((−1, −2)\)і\((9, 22)\)
- \((−1, 2)\)і\((−\frac{7}{2}, −4)\)
- \((−\frac{1}{2}, \frac{1}{3})\)і\((\frac{5}{2}, −\frac{11}{3})\)
- \((−\frac{1}{3}, \frac{2}{3})\)і\((1, −\frac{1}{3})\)
- \((\frac{1}{2}, −\frac{3}{4})\)і\((\frac{3}{2}, \frac{1}{4})\)
- \((1, 2)\)і\((4, 3)\)
- \((2, −4)\)і\((−3, −2)\)
- \((−1, 5)\)і\((1, −3)\)
- \((1, −7)\)і\((5, −1)\)
- \((−7, −3)\)і\((−1, 6)\)
- \((0, 1)\)і\((1, 0)\)
- \((−0.2, −0.2)\)і\((1.8, 1.8)\)
- \((1.2, −3.3)\)і\((2.2, −1.7)\)
- Відповідь
-
1. \(5\)одиниць
3. \(13\)одиниць
5. \(15\)одиниць
7. \(\frac{13}{2}\)одиниць
9. \(\frac{5}{3}\)одиниць
11. \(\sqrt{10}\)одиниць
13. \(2\sqrt{17}\)одиниць
15. \(3\sqrt{13}\)одиниць
17. \(2.8\)одиниць
Вправа\(\PageIndex{12}\) Distance Formula
Для кожної задачі покажіть, що три точки утворюють прямокутний трикутник.
- \((−3, −2), (0, −2),\)і\((0, 4)\)
- \((7, 12), (7, −13),\)і\((−5, −4)\)
- \((−1.4, 0.2), (1, 2),\)і\((1, −3)\)
- \((2, −1), (−1, 2),\)і\((6, 3)\)
- \((−5, 2), (−1, −2),\)і\((−2, 5)\)
- \((1, −2), (2, 3),\)і\((−3, 4)\)
- Відповідь
-
1. Доказ
3. Доказ
5. Доказ
Вправа\(\PageIndex{13}\) Distance Formula
Рівнобедрені трикутники мають дві ніжки однакової довжини. Для кожної задачі покажіть, що наступні точки утворюють рівнобедрений трикутник.
- \((1, 6), (−1, 1),\)і\((3, 1)\)
- \((−6, −2), (−3, −5),\)і\((−9, −5)\)
- \((−3, 0), (0, 3),\)і\((3, 0)\)
- \((0, −1), (0, 1),\)і\((1, 0)\)
- Відповідь
-
1. Доказ
3. Доказ
Вправа\(\PageIndex{14}\) Distance Formula
Обчисліть площу і периметр трикутників, утворених наступним набором вершин.
- \(\{(−4, −5), (−4, 3), (2, 3)\}\)
- \(\{(−1, 1), (3, 1), (3, −2)\}\)
- \(\{(−3, 1), (−3, 5), (1, 5)\}\)
- \(\{(−3, −1), (−3, 7), (1, −1)\}\)
- Відповідь
-
1. Периметр:\(24\) одиниці виміру; площа:\(24\) квадратні одиниці
3. Периметр:\(8+4\sqrt{2}\) одиниці виміру; площа:\(8\) квадратні одиниці
Вправа\(\PageIndex{15}\) Midpoint Formula
Знайдіть середину між заданими двома точками.
- \((−1, 6)\)і\((−7, −2) \)
- \((8, 0)\)і\((4, −3) \)
- \((−10, 0)\)і\((10, 0) \)
- \((−3, −6)\)і\((−3, 6) \)
- \((−10, 5)\)і\((14, −5) \)
- \((0, 1)\)і\((2, 2) \)
- \((5, −3)\)і\((4, −5) \)
- \((0, 0)\)і\((1, 1) \)
- \((−1, −1)\)і\((4, 4) \)
- \((3, −5)\)і\((3, 5) \)
- \((−\frac{1}{2}, −\frac{1}{3})\)і\((\frac{3}{2}, \frac{7}{3})\)
- \((\frac{3}{4}, −\frac{2}{3})\)і\((\frac{1}{8}, −\frac{1}{2})\)
- \((\frac{5}{3}, \frac{1}{4})\)і\((−\frac{1}{6}, −\frac{3}{2})\)
- \((−\frac{1}{5}, −\frac{5}{2})\)і\((\frac{7}{10}, −\frac{1}{4})\)
- Дано прямокутний трикутник, утворений вершинами\((0, 0), (6, 0),\) і\((6, 8)\), показують, що середні точки сторін утворюють прямокутний трикутник.
- З огляду на рівнобедрений трикутник, утворений вершинами\((−10, −12), (0, 12),\) і\((10, −12)\), показують, що середні точки сторін також утворюють рівнобедрений трикутник.
- Обчисліть площу трикутника, утвореного вершинами\((−4, −3), (−1, 1),\) і\((2, −3)\). (Підказка: Вершини утворюють рівнобедрений трикутник.)
- Обчисліть площу трикутника, утвореного вершинами\((−2, 1), (4, 1),\) і\((1, −5)\).
- Відповідь
-
1. \((−4, 2)\)
3. \((0, 0)\)
5. \((2, 0)\)
7. \((\frac{9}{2}, −4)\)
9. \((\frac{3}{2}, \frac{3}{2})\)
11. \((\frac{1}{2}, 1)\)
13. \((\frac{3}{4}, −\frac{5}{8})\)
15. \(12\)квадратні одиниці
Вправа\(\PageIndex{16}\) Discussion Board Topics
- Досліджуйте та обговоріть життя та внесок у математику Рене Декарта.
- Досліджуйте та обговоріть історію прямокутного трикутника та теорему Піфагора.
- Що таке піфагорійська трійка? Наведіть кілька прикладів.
- Поясніть, чому не можна використовувати лінійку для обчислення відстані на графіку.
- Як розділити відрізок лінії лише циркулем та прямим краєм?
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
5. Відповіді можуть відрізнятися
