3.3: Графік за допомогою перехоплення
- Page ID
- 58112
Цілі навчання
- Визначте і знайдіть\(x\) - і\(y\) -перехоплення графа.
- Графік лінії з використанням\(x\) - і\(y\) -перехоплює
Визначення\(x\) - і\(y\) -перехоплення
\(x\)-intercept - це точка, де графік прямої перетинає\(x\) вісь -.
\(y\)-intercept - це точка, де графік прямої перетинає\(y\) вісь -.
Ці точки мають форму\((x,0)\) і\((0,y)\), відповідно.
.png)
Малюнок\(\PageIndex{1}\)
Щоб знайти\(x\) - і\(y\) -перехоплення алгебраїчно, використовуйте той факт, що всі\(x\) -перехоплення мають\(y\) -значення нуля, а всі\(y\) -перехоплення мають\(x\) -значення нуля. Щоб знайти\(y\) -intercept, встановити\(x=0\) і визначити відповідне\(y\) -значення. Аналогічно знайти\(x\) -intercept, встановити\(y=0\) і визначити відповідне\(x\) -значення.
Приклад\(\PageIndex{1}\)
Знайдіть\(x\) - і\(y\) -перехоплює:
\(−3x+2y=12\).
Рішення:
Щоб знайти\(x\) -перехоплення, встановлюємо\(y = 0\).
Тому\(x\) -перехоплення є\((−4, 0)\). Щоб знайти\(y\) -перехоплення, встановлюємо\(x = 0\).
\(\begin{aligned} -3x+2y&=12 &\color{Cerulean}{To\:find\:the\:y-intercept,} \\ \color{Cerulean}{\downarrow}\qquad &&\color{Cerulean}{set\:x=0.} \\ -3(\color{OliveGreen}{0}\color{black}{)+2y}&=12 \\ 2y&=12\\y&=6 \end{aligned}\)
Звідси\(y\) -перехоплення є\((0, 6)\). Зверніть увагу, що це лінійне рівняння наведено на графіку вище.
Відповідь:
\(x\)-перехоплення:\((−4, 0)\);\(y\) -перехоплення:\((0, 6)\)
Приклад\(\PageIndex{2}\)
Знайдіть\(x\) - і\(y\) -перехоплює:
\(y=−3x+9\)
Рішення:
Почніть з пошуку\(x\) -перехоплення.
\(\begin{aligned} y&=-3x+9 &\color{Cerulean}{Set\:y=0.} \\ \color{Cerulean}{\downarrow}&& \\ \color{OliveGreen}{0}&=-3x+9&\color{Cerulean}{Solve\:for\:x.} \\ 3x&=9 \\ x&=3 \end{aligned}\)
\(x\)-Перехоплення є\((3, 0)\). Далі визначте\(y\) -перехоплення.
\(\begin{aligned} y&=-3x+9 &\color{Cerulean}{Set\:x=0.}\end{aligned}\)
\( \color{Cerulean}{\downarrow}\qquad\qquad\:\:\:\)
\(\begin{aligned} y&=-3(\color{OliveGreen}{0}\color{black}{)+9} & \color{Cerulean}{Solve\:for\:y.} \\ y&=9 \end{aligned}\)
\(y\)-Перехоплення є\((0, 9)\).
Відповідь:
\(x\)-перехоплення:\((3, 0)\);\(y\) -перехоплення:\((0, 9)\)
Майте на увазі, що перехоплення - це впорядковані пари, а не цифри. Іншими словами,\(x\) -перехоплення - це\(x=2\) не скоріше\((2, 0)\). Крім того, не всі графіки обов'язково мають обидва перехоплення: наприклад,
.png)
Малюнок\(\PageIndex{2}\)
Горизонтальна лінія, зображена вище, має\(y\) -перехоплення\((0, −2)\) і не\(x\) -перехоплення.
.png)
Малюнок\(\PageIndex{3}\)
Вертикальна лінія, зображена вище, має\(x\) -перехоплення\((3, 0)\) і не\(y\) -перехоплення.
Вправа\(\PageIndex{1}\)
Знайдіть\(x\) - і\(y\) -перехоплює:
\(4x−y=2\).
- Відповідь
-
\(x\)-перехоплення:\((\frac{1}{2}, 0)\);\(y\) -перехоплення:\((0, −2)\)
Графічні лінії за допомогою перехоплення
Оскільки дві точки визначають лінію, ми можемо використовувати\(x\) - і\(y\) -перехоплення для графіка лінійних рівнянь. Ми щойно окреслили простий метод пошуку перехоплень; тепер ми окреслимо кроки для графічних ліній за допомогою перехоплень.
Приклад\(\PageIndex{3}\)
Графік з використанням перехоплень:
\(2x−3y=12\).
Рішення:
Крок 1: Знайдіть\(x\) - і\(y\) -перехоплює.
\(\begin{array}{c|c}{\underline{\color{Cerulean}{To\:find\:the\:x-intercept,\:set\:y=0.}}}&{\underline{\color{Cerulean}{To\:find\:the\:y-intercept,\:set\:x=0.}}}\\{2x-3y=12}&{2x-3y=12}\\{2x-3(\color{OliveGreen}{0}\color{black}{)=12}}&{2(\color{OliveGreen}{0}\color{black}{)-3y=12}}\\{2x=12}&{-3y=12}\\{x=6}&{y=-4}\\{x-intercept:\:(6,0)}&{y-intercept:\:(0,-4)} \end{array}\)
Крок 2: Побудуйте перехоплення і проведіть через них лінію. Використовуйте straightedge, щоб створити красиву пряму лінію. Додайте стрілку на будь-якому кінці, щоб вказати, що лінія триває нескінченно довго в будь-якому напрямку.
Відповідь:
.png)
Малюнок\(\PageIndex{4}\)
Приклад\(\PageIndex{4}\)
Графік з використанням перехоплень:
\(y=−\frac{1}{5}x+3\).
Рішення:
Почніть з визначення\(x\) - і\ (y\ -перехоплення.
\(\begin{array}{c|c}{\underline{\color{Cerulean}{x-intercept}}}&{\underline{\color{Cerulean}{y-intercept}}}\\{y=-\frac{1}{5}x+3}&{y=-\frac{1}{5}x+3}\\{\color{OliveGreen}{0}\color{black}{=-\frac{1}{5}x+3}}&{y=-\frac{1}{5}(\color{OliveGreen}{0}\color{black}{)+3}}\\{\frac{1}{5}x=3}&{y=3}\\{\color{Cerulean}{5\cdot}\color{black}{\frac{1}{5}x=}\color{Cerulean}{5\cdot}\color{black}{3}}&{y-intercept:\:(0,3)}\\{x=15}&{}\\{x-intercept:\:(15,0)}&{} \end{array}\)
Далі намалюйте дві точки і проведіть через них лінію з прямим краєм.
Відповідь:
.png)
Малюнок\(\PageIndex{5}\)
Приклад\(\PageIndex{5}\)
Графік з використанням перехоплень:
\(y=−2x\).
Рішення:
\(\begin{array}{c|c}{\underline{\color{Cerulean}{x-intercept}}}&{\underline{\color{Cerulean}{y-intercept}}}\\{y=-2x}&{y=-2x}\\{\color{OliveGreen}{0}\color{black}{=-2x}}&{y=-2(\color{OliveGreen}{0}\color{black}{)}}\\{\frac{0}{\color{Cerulean}{-2}}=\frac{-2x}{\color{Cerulean}{-2}}}&{y=0}\\{0=x}&{y-intercept:\:(0,0)}\\{x-intercept:\:(0,0)}&{}\end{array}\)
Тут\(x\) - і\(y\) -перехоплення насправді одна і та ж точка, походження. Нам знадобиться ще хоча б одна точка, щоб ми могли навести графік лінії. Виберіть будь-яке значення для\(x\) і визначте відповідне значення для\(y\).
.png)
Малюнок\(\PageIndex{6}\)
Скористайтеся впорядкованими\((0, 0), (−1, 2)\) парними\((1, −2)\) розв'язками і графуйте лінію.
Відповідь:
.png)
Малюнок\(\PageIndex{7}\)
Підводячи підсумок, будь-яке лінійне рівняння може бути побудовано на графіку, знайшовши дві точки і з'єднавши їх лінією, проведеною прямолінійним краєм. Два важливих і корисних моменти\(x\) - і\(y\) -перехоплення; знайти ці точки шляхом підстановки\(y = 0\) і\(x = 0\), відповідно. Цей метод знаходження перехоплень буде використовуватися протягом усього нашого вивчення алгебри.
Вправа\(\PageIndex{2}\)
Графік з використанням перехоплень:
\(3x−5y=15\).
- Відповідь
-
\(x\)-перехоплення:\((5, 0)\);\(y\) -перехоплення:\((0, −3)\)
Пошук перехоплень з урахуванням графіка
The\(x\) - і\(y\) -перехоплення є важливими пунктами на будь-якому графіку. У цій главі мова піде про графіки лінійних рівнянь. Однак на даний момент ми можемо використовувати ці ідеї для визначення перехоплень нелінійних графів. Пам'ятайте, що перехоплення - це впорядковані пари, які вказують, де графік перетинає осі.
Приклад\(\PageIndex{6}\)
Знайти\(x\) - і\(y\) -перехоплення задано на наступному графіку:
.png)
Малюнок\(\PageIndex{8}\)
Рішення:
Бачимо, що графік перетинає\(x\) -вісь у двох місцях. Цей графік має два\(x\) -перехоплення, а саме,\((−4, 0)\) і\((2, 0)\). Крім того, графік перетинає\(y\) вісь -в одному місці. Єдине\(y\) -перехоплення є\((0, −3)\).
Відповідь:
\(x\)-перехоплює:\((−4, 0), (2, 0)\);\(y\) -перехоплення:\((0, −3)\)
У нашому вивченні алгебри ми побачимо, що деякі графіки мають багато перехоплень. Також ми побачимо, що деякі графіки не мають жодних.
Приклад\(\PageIndex{7}\)
З огляду на наступний графік, знайдіть\(x\) - і\(y\) -перехоплення:
.png)
Малюнок\(\PageIndex{9}\)
Рішення:
Це графік кола; ми бачимо, що він не перетинається жодної осі. Тому цей графік не має ніяких перехоплень.
Відповідь:
Жоден
Ключові винос
- Оскільки дві точки визначають будь-яку лінію, ми можемо графувати лінії, використовуючи\(x\) - і\(y\) -перехоплення.
- Знайти\(x\) -перехоплення, встановити\(y = 0\) і вирішити для\(x\).
- Знайти\(y\) -перехоплення, встановити\(x = 0\) і вирішити для\(y\).
- Цей метод знаходження\(x\) - і\(y\) -перехоплення буде використовуватися протягом усього нашого вивчення алгебри, оскільки він працює для будь-якого рівняння.
- Щоб намалювати лінію, знайдіть перехоплення, якщо вони існують, і проведіть пряму лінію через них. Використовуйте straightedge, щоб створити лінію і включити стрілки на обох кінцях, щоб вказати, що лінія простягається нескінченно в будь-якому напрямку.
- Горизонтальні і вертикальні лінії не завжди мають обидва\(x\) - і\(y\) -перехоплення.
Вправа\(\PageIndex{3}\) Intercepts
З огляду на графік, знайдіть\(x\) - і\(y\) -перехоплення.
1.
.png)
Малюнок\(\PageIndex{10}\)
2.
.png)
Малюнок\(\PageIndex{11}\)
3.
.png)
Малюнок\(\PageIndex{12}\)
4.
.png)
Малюнок\(\PageIndex{13}\)
5.
.png)
Малюнок\(\PageIndex{14}\)
6.
.png)
Малюнок\(\PageIndex{15}\)
- Відповідь
-
1. \(y\)-перехоплення:\((0, −3)\);\(x\) -перехоплення:\((4, 0)\)
3. \(y\)-перехоплення:\((0, −3)\);\(x\) -перехоплення: немає
5. \(y\)-перехоплення:\((0, 0)\);\(x\) -перехоплення:\((0, 0)\)
Вправа\(\PageIndex{4}\) Intercepts
Знайдіть\(x\) - і\(y\) -перехоплює.
- \(5x−4y=20 \)
- \(−2x+7y=−28 \)
- \(x−y=3 \)
- \(−x+y=0 \)
- \(3x−4y=1 \)
- \(−2x+5y=3 \)
- \(\frac{1}{4}x−\frac{1}{3}y=1\)
- \(−\frac{2}{5}x+\frac{3}{4}y=2\)
- \(y=6\)
- \(y=−3\)
- \(x=2\)
- \(x=−1\)
- \(y=mx+b \)
- \(ax+by=c\)
- Відповідь
-
1. \(x\)-перехоплення:\((4, 0)\);\(y\) -перехоплення:\((0, −5) \)
3. \(x\)-перехоплення:\((3, 0)\);\(y\) -перехоплення:\((0, −3) \)
5. \(x\)-перехоплення:\((\frac{1}{3}, 0)\);\(y\) -перехоплення:\((0, −\frac{1}{4})\)
7. \(x\)-перехоплення:\((4, 0)\);\(y\) -перехоплення:\((0, −3) \)
9. \(x\)-перехоплення: немає;\(y\) -перехоплення:\((0, 6) \)
11. \(x\)-перехоплення:\((2, 0)\);\(y\) -перехоплення: немає
13. \(x\)-перехоплення:\((−\frac{b}{m}, 0)\);\(y\) -перехоплення:\((0, b)\)
Вправа\(\PageIndex{5}\) Graph Using Intercepts
Знайдіть перехоплення і графуйте їх.
- \(3x+4y=12\)
- \(−2x+3y=6\)
- \(5x−2y=10\)
- \(−4x−8y=16\)
- \(−\frac{1}{2}x+\frac{1}{3}y=1\)
- \(\frac{3}{4}x−\frac{1}{2}y=−3\)
- \(2x−\frac{5}{2}y=10\)
- \(2x−\frac{7}{3}y=−14\)
- \(4x−y=−8\)
- \(6x−y=6\)
- \(–x+2y=1\)
- \(3x+4y=6\)
- \(2x+y=−1\)
- \(−2x+6y=3\)
- \(15x+4y=−60\)
- \(−25x+3y=75\)
- \(4x+2y=0\)
- \(3x−y=0\)
- \(−12x+6y=−4\)
- \(3x+12y=−4\)
- \(y=2x+4\)
- \(y=−x+3\)
- \(y=\frac{1}{2}x+1\)
- \(y=\frac{2}{3}x−3\)
- \(y=−\frac{2}{5}x+1\)
- \(y=−\frac{5}{8}x−\frac{5}{4}\)
- \(y=−\frac{7}{8}x−\frac{7}{2}\)
- \(y=−x+\frac{3}{2}\)
- \(y=3\)
- \(y=\frac{3}{2}\)
- \(x=5\)
- \(x=−2\)
- \(y=5x\)
- \(y=−x\)
- Відповідь
-
1.
.png)
Малюнок\(\PageIndex{16}\)
3.
.png)
Малюнок\(\PageIndex{17}\)
5.
.png)
Малюнок\(\PageIndex{18}\)
7.
.png)
Малюнок\(\PageIndex{19}\)
9.
.png)
Малюнок\(\PageIndex{20}\)
11.
.png)
Малюнок\(\PageIndex{21}\)
13.
.png)
Малюнок\(\PageIndex{22}\)
15.
.png)
Малюнок\(\PageIndex{23}\)
17.
.png)
Малюнок\(\PageIndex{24}\)
19.
.png)
Малюнок\(\PageIndex{25}\)
21.
.png)
Малюнок\(\PageIndex{26}\)
23.
.png)
Малюнок\(\PageIndex{27}\)
25.
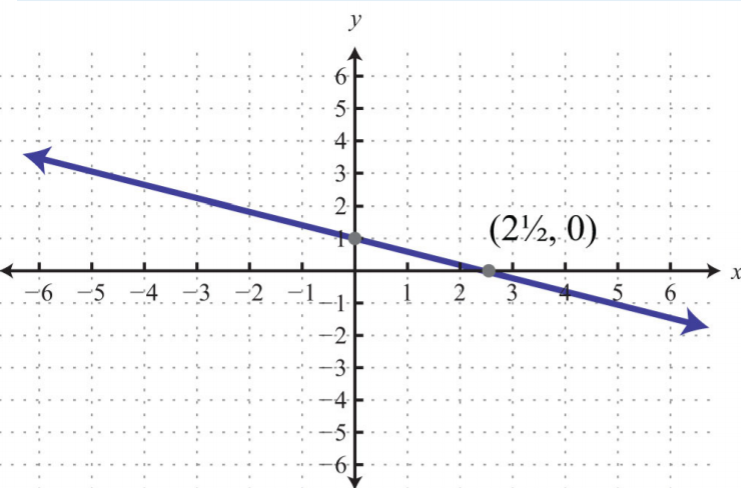.png)
Малюнок\(\PageIndex{28}\)
27.
.png)
Малюнок\(\PageIndex{29}\)
29.
.png)
Малюнок\(\PageIndex{30}\)
31.
.png)
Малюнок\(\PageIndex{31}\)
33.
.png)
Малюнок\(\PageIndex{32}\)
Вправа\(\PageIndex{6}\) Intercepts of Nonlinear Graphs
За заданим графіком знаходимо\(x\) - і\(y\) -перехоплення.
1.
.png)
Малюнок\(\PageIndex{33}\)
2.
.png)
Малюнок\(\PageIndex{34}\)
3.
.png)
Малюнок\(\PageIndex{35}\)
4.
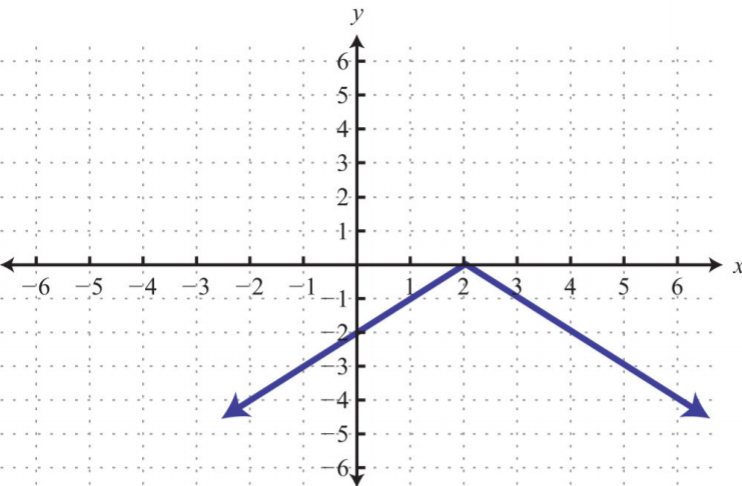.png)
Малюнок\(\PageIndex{36}\)
5.
.png)
Малюнок\(\PageIndex{37}\)
6.
.png)
Малюнок\(\PageIndex{38}\)
7.
.png)
Малюнок\(\PageIndex{39}\)
8.
.png)
Малюнок\(\PageIndex{40}\)
9.
.png)
Малюнок\(\PageIndex{41}\)
10.
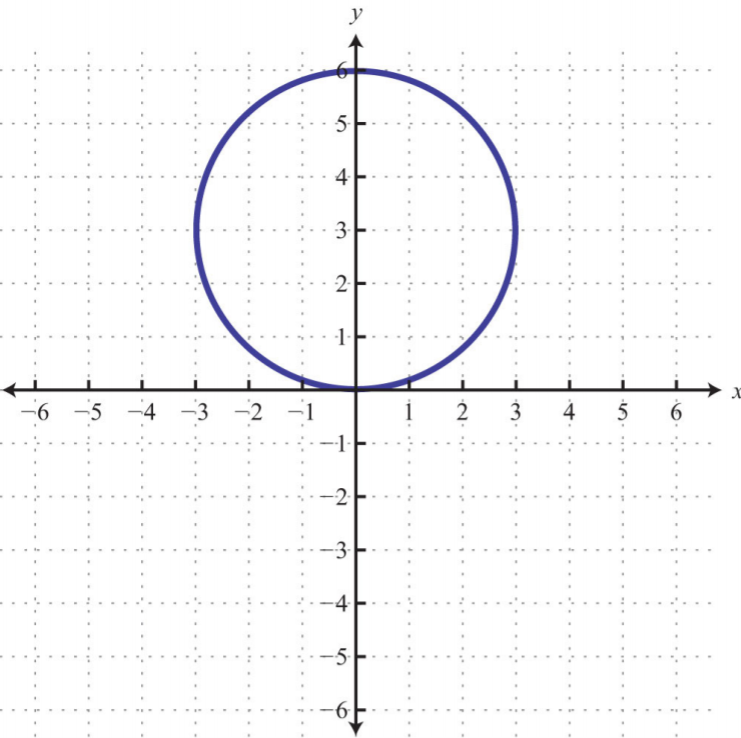.png)
Малюнок\(\PageIndex{42}\)
- Відповідь
-
1. \(x\)-перехоплює:\((−3, 0), (3, 0)\);\(y\) -перехоплення:\((0, −3)\)
3. \(x\)-перехоплює:\((−4, 0), (0, 0)\);\(y\) -перехоплення:\((0, 0) \)
5. \(x\)-перехоплює:\((−2, 0), (2, 0)\);\(y\) -перехоплення:\((0, −1) \)
7. \(x\)-перехоплює:\((−3, 0), (0, 0), (2, 0)\);\(y\) -перехоплення:\((0, 0) \)
9. \(x\)-перехоплює:\((−4, 0), (4, 0)\);\(y\) -перехоплює:\((0, −4), (0, 4)\)
Вправа\(\PageIndex{7}\) Discussion Board Topics
- Що таке\(x\) -перехоплення лінії\(y = 0\)?
- Що таке\(y\) -перехоплення лінії\(x = 0\)?
- Чи всі лінії мають перехоплення?
- Скільки перехоплень може мати коло? Намалюйте кола, показуючи всі можливі номери перехоплень.
- Досліджуйте та розміщуйте визначення сегмента лінії, променя та лінії. Чому стрілки важливі?
- Відповідь
-
1. Відповіді можуть відрізнятися
3. Відповіді можуть відрізнятися
5. Відповіді можуть відрізнятися
