7.2: Кола

Коло - одна з найбільш часто зустрічаються геометричних фігур. Колеса, кільця, записи фонографа, годинник, монети - це лише кілька прикладів поширених предметів з круглою формою. Коло має безліч застосувань у будівництві машин та в архітектурному та декоративному дизайні.

Для малювання кола використовуємо інструмент, який називається циркулем (рис.$\PageIndex{1}$). Компас складається з двох рук, одна закінчується гострою металевою точкою, а інша прикріплена до олівця. Малюємо коло, обертаючи олівець, поки металева точка тримається так, щоб вона не рухалася, Положення металевої точки називається центром кола. Відстань між центром і кінчиком олівця називається радіусом кола, радіус залишається таким же, як і коло малюється.

Малюнок$\PageIndex{1}$: За допомогою циркуля намалюйте коло.

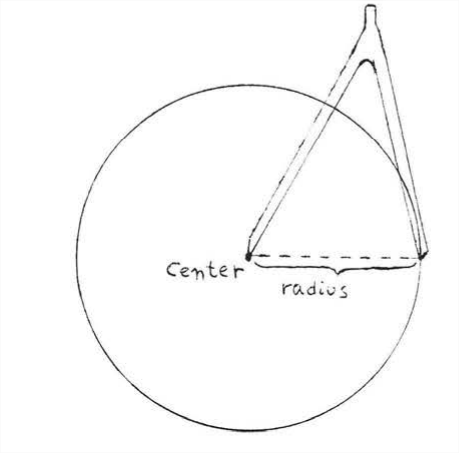
Метод побудови кола передбачає наступне визначення:

Визначення: Коло

Коло - це фігура, що складається з усіх точок, які є заданою відстанню від фіксованої точки, яка називається центром. Наприклад, коло на малюнку 2 складається з усіх точок, які знаходяться на відстані 3 від центру 0. Радіус - це відстань будь-якої точки на колі від центру.

Коло на малюнку$\PageIndex{2}$ має радіус 2. Термін радіус також використовується для позначення будь-якого з відрізків лінії від точки на колі до центру. На$\PageIndex{2}$ малюнку кожна з відрізків$OA, OB$ лінії і$OC$ є радіусом. З визначення кола випливає, що всі радіуси кола рівні. Так$\PageIndex{2}$ на малюнку три радіуси$OA, OB$, і$OC$ всі рівні 3.

Малюнок$\PageIndex{2}$: Коло з радіусом 3. (Авторське право; автор через джерело)

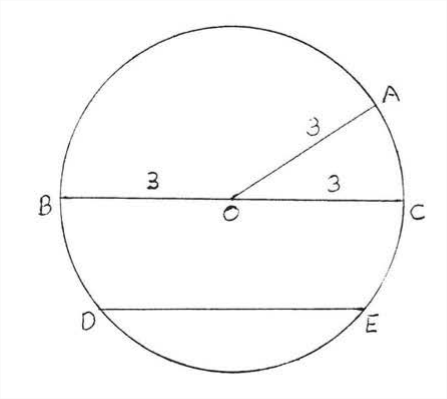
Коло зазвичай називають по його центру. Коло на малюнку$\PageIndex{2}$ називається колом$O$.

Хорда - це відрізок лінії, що з'єднує дві точки на колі. На малюнку$\PageIndex{2}$,$DE$ це акорд. Діаметр - це хорда, яка проходить через центр. \ (BC - діаметр. Діаметр завжди вдвічі перевищує довжину радіуса, оскільки він складається з двох радіусів. Будь-який діаметр кола 0 дорівнює 6. Всі діаметри кола рівні.

Приклад$\PageIndex{1}$

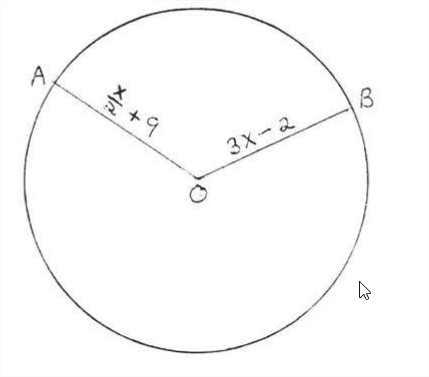
Знайти радіус і діаметр і діаметр.

Рішення

Всі радіуси рівні так

\ [\ begin {вирівняний}

О А &=О Б\\

\ гідророзриву {x} {2} +9 &=3 х-2\\

(2)\ ліворуч (\ розриву {x} {2} +9\ праворуч) &= (3 x-2) (2)\\

х+18 &=6 х-4\\

22 &=5 х\\

x &=\ гідророзриву {22} {5} =4.4

\ end {вирівняний}\]

Перевірка:

$OA = OB$

\ [\ begin {масив} {r|l}

\ гідророзриву {x} {2} +9 & 3 х-2\\

\ гідророзриву {4.4} {2} +9 & 3 (4.4) -2\\

2,2+9 & 13,2-2\\

11.2 & 11.2

\ end {масив}\]

Тому радіус$OA = OB$ = 11,2, а діаметр = 2 (11,2) =22,4.

Відповідь: радіус =11,2, діаметр =22,4.

Наступні три теореми показують, що діаметр кола і перпендикулярна бісектриса хорди в колі насправді одне і те ж.

Теорема$\PageIndex{1}$

Діаметр, перпендикулярний хорді, бісекції хорди.

На малюнку$\PageIndex{3}$, якщо$AB \perp CD$ тоді$AE = EB$.

Малюнок$\PageIndex{3}$: Діаметр$CD$ перпендикулярний хорді$AB$.

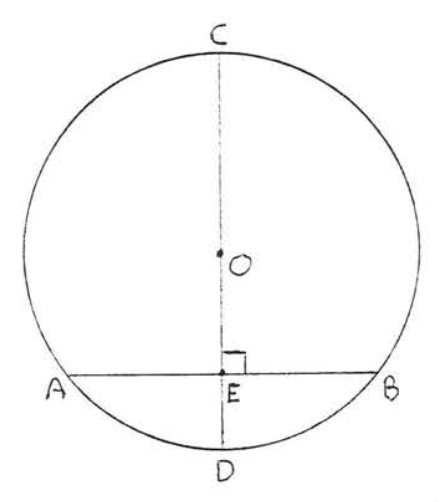
Доказ

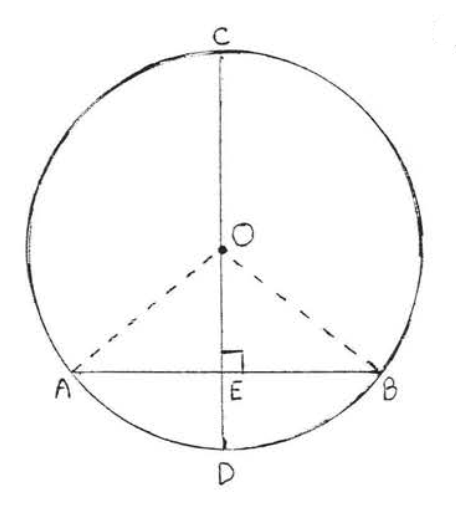
Малюнок$\PageIndex{4}$: Малюємо$OA$ і$OB$.

Малюємо$OA$ і$OB$ (Малюнок$\PageIndex{4}$). $OA = OB$тому що всі радіуси кола рівні. $OE = OE$через ідентичність. Тому$\triangle ACE \cong \triangle BOE$ гіп-нога = гіп-нога. Звідси$AE = BE$ тому, що вони є відповідними сторонами конгруентних трикутників.

Приклад$\PageIndex{2}$

Знайти$AB$:

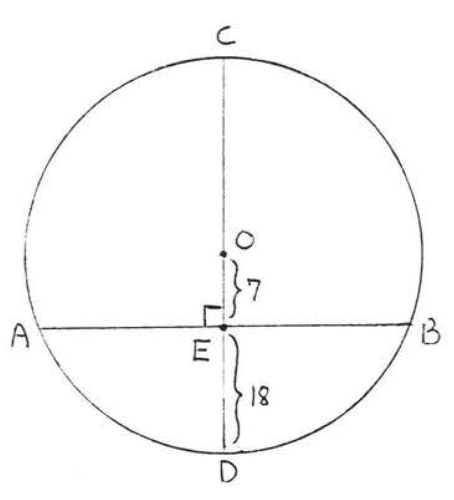
Рішення

Малюнок$\PageIndex{5}$: Малювати$OA$.

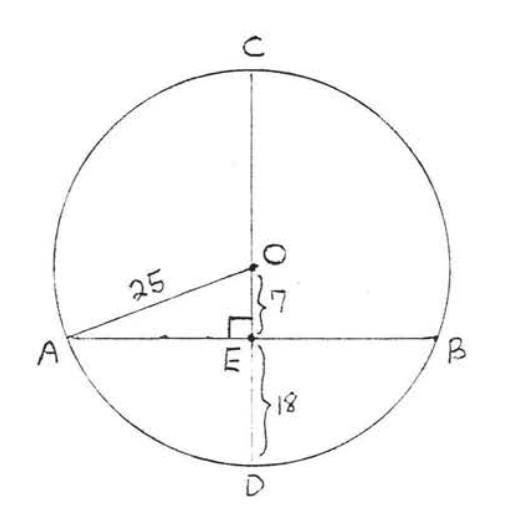
Малювати$OA$ (малюнок$\PageIndex{5}$). $OA = \text{radius} = OD = 18 + 7 = 25$. $\triangle AOE$це прямокутний трикутник, і тому ми можемо використовувати теорему Піфагора, щоб знайти$AE$:

$\begin{array} {rcl} {\text{AE}^2+\text{CE}^2} & = & {\text{CA}^2} \\ {\text{AE}^2 + 7^2} & = & {25^2} \\ {\text{AE}^2 + 49} & = & {625} \\ {\text{AE}^2} & = & {576} \\ {\text{AE}} & = & {24} \end{array}$

За теоремою$\PageIndex{1}$,$EB = AE = 24$ так$AB = AE + EB = 24 + 24 = 48$.

Відповідь:$AB = 48$.

Теорема$\PageIndex{2}$

Діаметр, який перетинає хорду, яка не є діаметром, перпендикулярна їй.

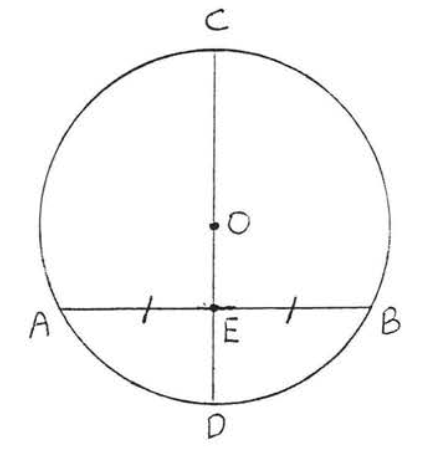
На малюнку$\PageIndex{6}$, якщо$AE = EB$ тоді$AB \perp CD$.

Малюнок$\PageIndex{6}$: Діаметр$CD$ бісекційної хорди$AB$.

Доказ

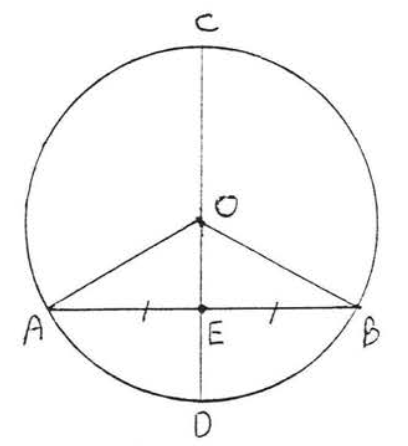
Малюнок$\PageIndex{7}$: Малюємо$OA$ і$OB$.

Малюємо$OA$ і$OB$ (Малюнок$\PageIndex{7}$). $OA = OB$тому що всі радіуси рівні,$OE = OE$ (ідентичність) і$AE = EB$ (дано). Тому$\triangle AOE \cong \triangle BOE$ по$SSS = SSS$. Тому$\triangle AEO = \triangle BEO$. Оскільки$\angle AEO$ і$\angle BEO$ є додатковими, ми також повинні мати$\angle AEO = \angle BEO = 90^{\circ}$, що ми повинні були довести.

Приклад$\PageIndex{3}$

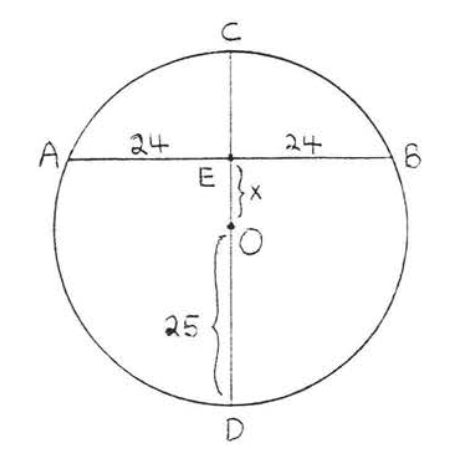
Знайти$x$:

Рішення

Малюнок$\PageIndex{8}$: Малювати$OA$.

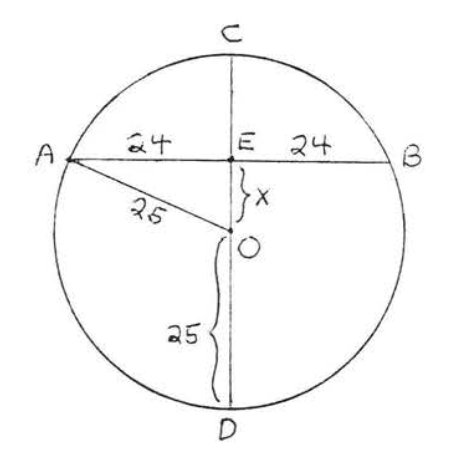
Малювати$OA$ (малюнок$PageIndex{8}$). $OA = \text{radius} = OD = 25$. Згідно з теоремою$\PageIndex{2}$,$AB \perp CD$. Тому$\triangle AOE$ прямокутний трикутник, і ми можемо використовувати теорему Піфагора, щоб знайти$x$:

$$\begin{array} {rcl} {\text{OE}^2 + \text{AE}^2} & = & {\text{OA}^2} \\ {x^2 + 24^2} & = & {25^2} \\ {x^2 + 576} & = & {625} \\ {x^2} & = & {49} \\ {x} & = & {7} \end{array}$$

Відповідь:$x = 7$.

Теорема$\PageIndex{3}$

Перпендикулярна бісектриса хорди повинна проходити через центр кола (тобто це діаметр).

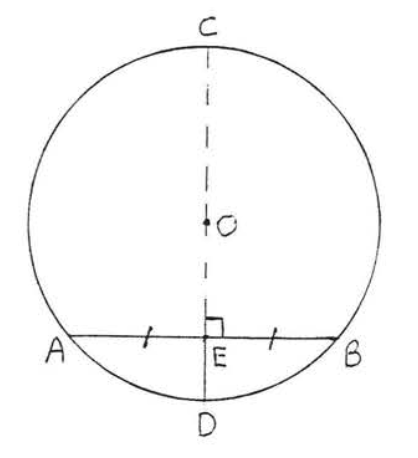
На малюнку$\PageIndex{9}$, якщо$CD \perp AB$ і$AE = EB$ то$O$ треба лежати далі$CD$.

Малюнок$\PageIndex{9}$: Якщо$CD$ це перпендикулярна бісектриса,$AB$ то$CD$ повинна проходити крізь$O$.

Доказ

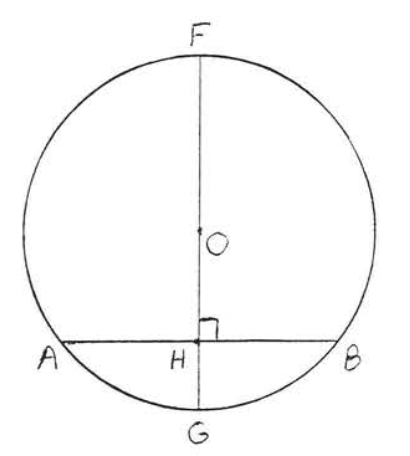
Малюнок$\PageIndex{10}$: Провести$FG$ через$O$ перпендикулярно до$AB$.

Намалюйте діаметр$FG$ через$O$ перпендикулярно$AB$ в$H$ (рис.$\PageIndex{10}$). Тоді відповідно до Теореми$\PageIndex{1}$$H$ необхідно розділити бісекцію$AB$. Звідси$H$ і$E$ знаходяться одна і та ж точка$FG$ і і$CD$ одна і та ж лінія. Так$O$ лежить далі$CD$. На цьому доказ завершено.

Приклад$\PageIndex{4}$

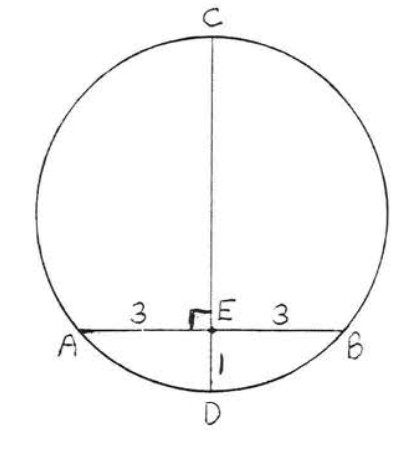
Знайдіть радіус кола:

Рішення

Малюнок$\PageIndex{11}$: Намалюйте$OA$ і нехай$r$ буде радіус.

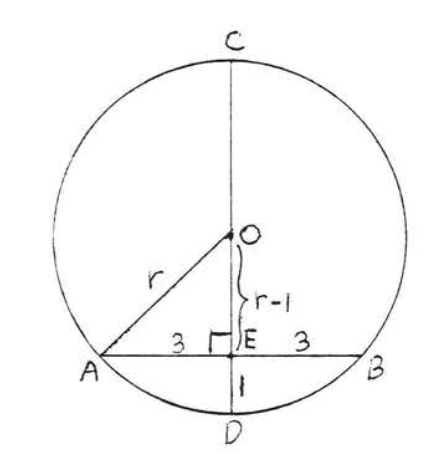
Згідно теоремі$\PageIndex{3}$,$O$ повинен лежати далі$CD$. Малювати$OA$ (малюнок$\PageIndex{11}$). $r$Дозволяти радіус. Потім$OA = OD = r$ і$OE = r - 1$. Щоб знайти,$r$ застосуємо теорему Піфагора до прямокутного трикутника$AOE$:

$$\begin{array} {rcl} {\text{AE}^2 + \text{OE}^2} & = & {\text{OA}^2} \\ {3^2 + (r - 1)^2} & = & {r^2} \\ {9 + r^2 - 2r + 1} & = & {r^2} \\ {10} & = & {2r} \\ {5} & = & {r} \end{array}$$

Відповідь:$r = 5$.

Приклад$\PageIndex{5}$

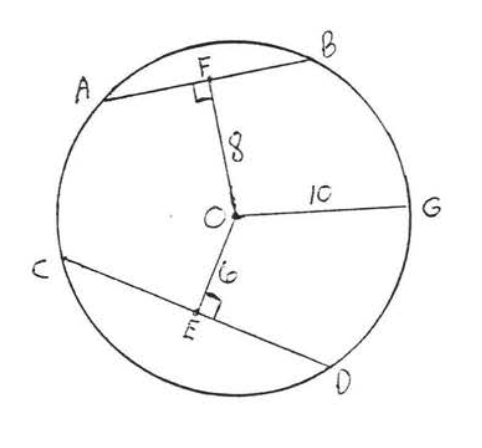
Знайдіть, яка хорда$CD$,$AB$ або, більше, якщо радіус кола дорівнює 25:

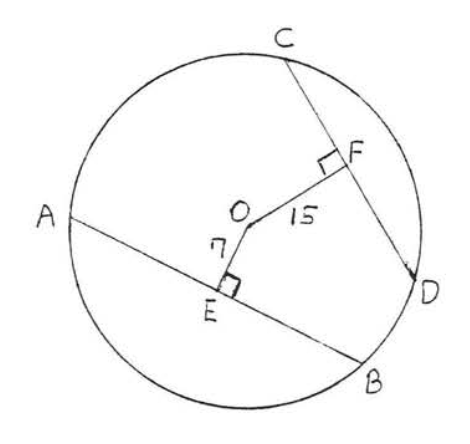
Рішення

Малюнок$\PageIndex{12}$: Малюємо$OA, OB, OC$ і$OD$.

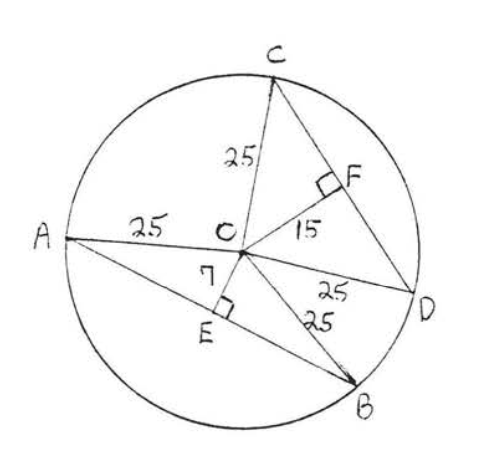
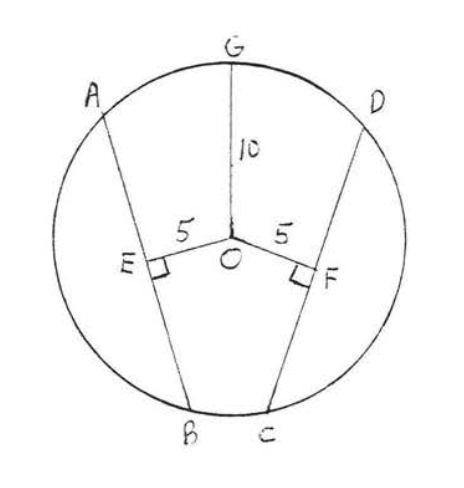
Малюємо$OA, OB, OC$ і$OD$ (Малюнок$\PageIndex{12}$). Кожен є радіусом і дорівнює 25. Використовуємо теорему Піфагора, застосовану до прямокутного трикутника$AOE$, щоб знайти$AE$:

$$\begin{array} {rcl} {\text{AE}^2 + \text{OE}^2} & = & {\text{OA}^2} \\ {\text{AE}^2 + 7^2} & = & {25^2} \\ {\text{AE}^2 + 49} & = & {625} \\ {\text{AE}^2} & = & {576} \\ {\text{AE}} & = & {24} \end{array}$$

Так як$OE$ перпендикулярні бісекти$AB$ (теорема$\PageIndex{1}$)$BE = AE = 24$ і так$AB = AE + BE = 24 + 24 = 48$.

Аналогічно, щоб знайти$CF$, застосуємо теорему Піфагора до прямокутного трикутника$COF$:

$$\begin{array} {rcl} {\text{CF}^2 + \text{OF}^2} & = & {\text{OC}^2} \\ {\text{CF}^2 + 15^2} & = & {25^2} \\ {\text{CF}^2 + 225} & = & {625} \\ {\text{CF}^2} & = & {400} \\ {\text{CF}} & = & {20} \end{array}$$

Знову ж таки, з$\PageIndex{1}$ теореми ми знаємо$OF$ бісекти$CD$, отже$DF = CF = 20$ і$CD = 40$.

Відповідь:$AB = 48$$CD = 40$,$AB$, більше ніж$CD$.

Приклад$\PageIndex{5}$ пропонує наступну теорему (яку ми стверджуємо без доказів):

Теорема$\PageIndex{4}$

Довжина хорди визначається її відстанню від центру кола; чим ближче до центру, тим більше хорда.

Історична записка

Визначення кола і по суті всіх теорем цього і наступних двох розділів можна знайти в Книзі III Стихій Евкліда.

Проблеми

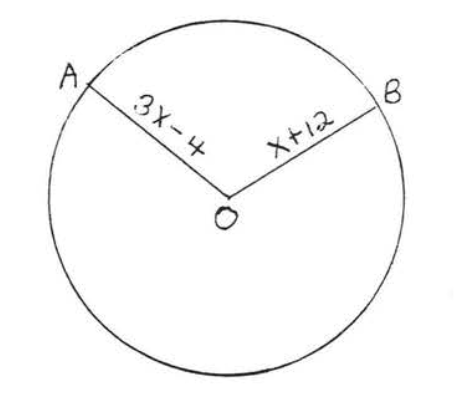
1 - 2. Знайдіть радіус і діаметр:

1.

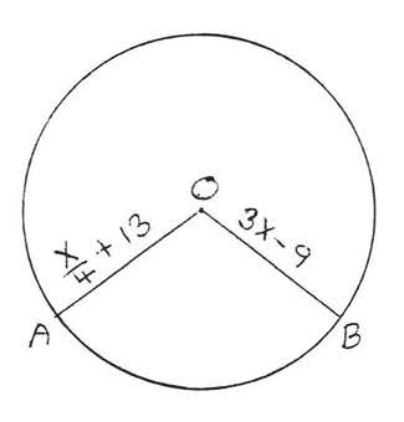
2.

3 - 4. Знайти$AB$:

3.

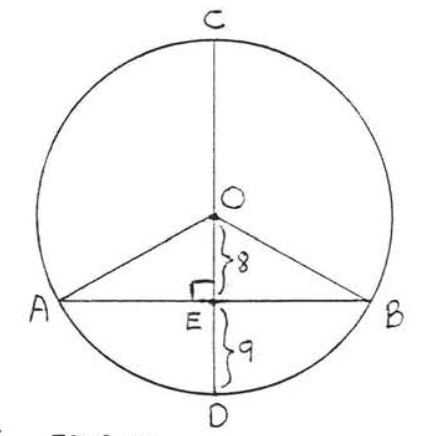
4.

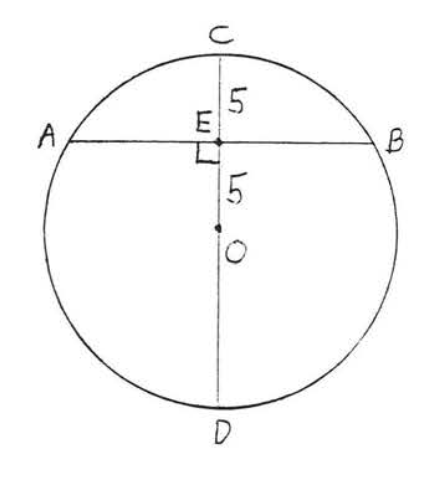
5 - 6. Знайти$x$:

5.

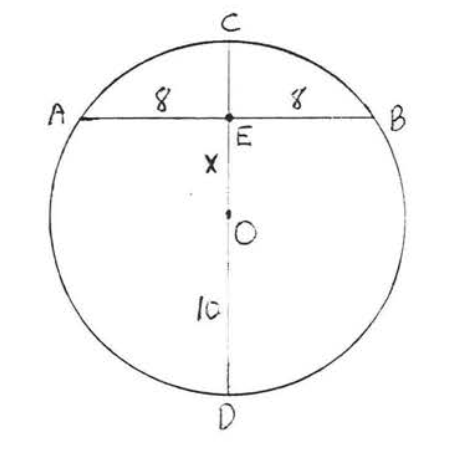
6.

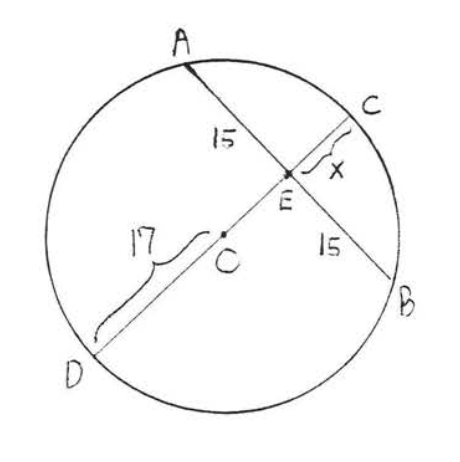
7 - 10. Знайдіть радіус і діаметр:

7.

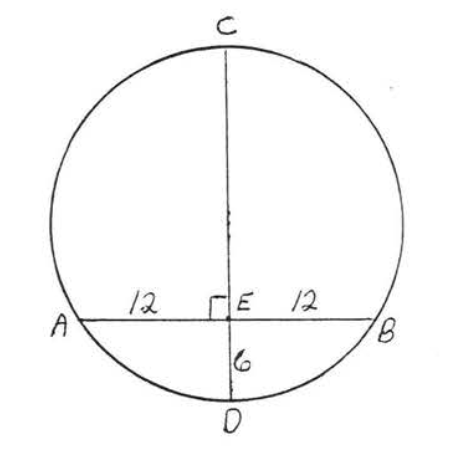
8.

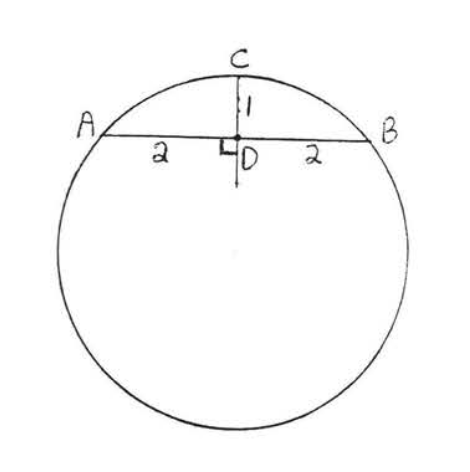
9.

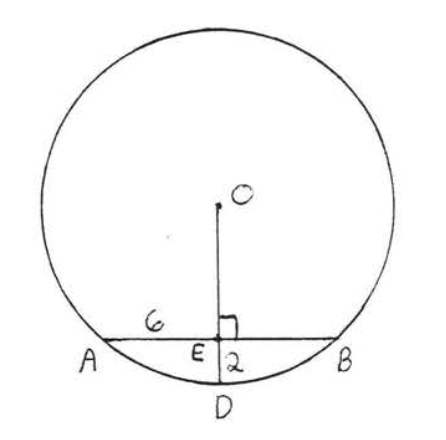
10.

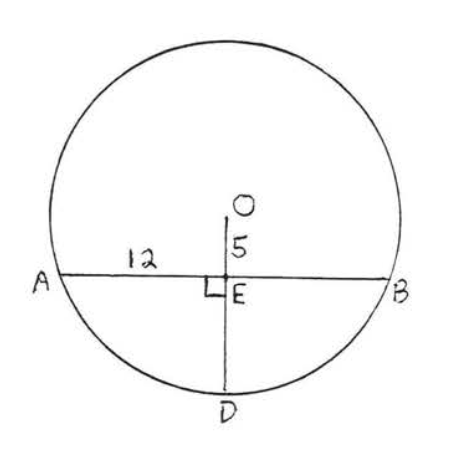
11 - 12. Знайдіть довжини$AB$ і$CD$:

11.

12.