12.3: Парабола

Цілі навчання

• Графові параболи з вершинами на початку.
• Напишіть рівняння парабол в стандартному вигляді.
• Графові параболи з вершинами, які не знаходяться на початку.
• Вирішити прикладні завдання, пов'язані з параболами.

Чи знали ви, що олімпійський факел запалюється за кілька місяців до початку ігор? Обрядовий спосіб розпалювання полум'я такий же, як і в давнину. Церемонія відбувається в храмі Гери в Олімпії, Греція, і корениться в грецькій міфології, віддаючи данину Прометею, який вкрав вогонь у Зевса, щоб дати всім людям. Одна з одинадцяти діючих жриць поміщає факел у фокус параболічного дзеркала (рис.$\PageIndex{1}$), яке фокусує світлові промені від сонця, щоб розпалити полум'я.

Малюнок$\PageIndex{1}$: Олімпійський факел завершує свою подорож по світу, коли він використовується для запалювання олімпійського котла під час церемонії відкриття. (кредит: Кен Хакман, ВПС США)

Параболічні дзеркала (або відбивачі) здатні захоплювати енергію і фокусувати її в одній точці. Про переваги цієї властивості свідчить величезний перелік параболічних об'єктів, які ми використовуємо щодня: супутникові антени, підвісні мости, телескопи, мікрофони, прожектори та автомобільні фари, щоб назвати декілька. Параболічні відбивачі також використовуються в пристроях альтернативної енергетики, таких як сонячні плити та водонагрівачі, оскільки вони недорогі у виробництві і потребують невеликого обслуговування. У цьому розділі ми розглянемо параболу та її використання, включаючи недорогі, енергоефективні сонячні конструкції.

Графік парабол з вершинами на початку

Раніше ми бачили, що еліпс утворюється, коли площину прорізає правий круглий конус. Якщо площина паралельна краю конуса, утворюється необмежена крива. Ця крива є параболою (рис.$\PageIndex{2}$).

Малюнок$\PageIndex{2}$: Парабола

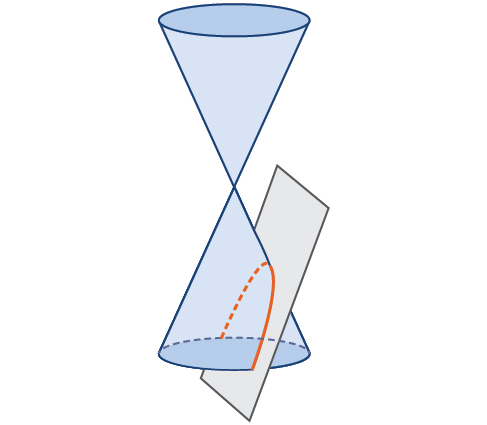
Як і еліпс і гіпербола, парабола також може бути визначена набором точок в координатній площині. Парабола - це сукупність всіх точок$(x,y)$ на площині, які знаходяться на однаковій відстані від фіксованої лінії, званої директрисою, і фіксованою точкою (фокусом) не на директрисі.

Раніше ми дізналися про вершину параболи і осі симетрії. Тепер розширимо дискусію, включивши інші ключові особливості параболи (рис.$\PageIndex{3}$). Зверніть увагу, що вісь симетрії проходить через фокус і вершину і перпендикулярна директрисі. Вершина є середньою точкою між директрисою і фокусом. Відрізок лінії, який проходить через вогнище і паралельний директрисі, називається латус прямою кишкою. Кінцеві точки прямої кишки лоток лежать на кривій. За визначенням, віддалене d від фокуса до будь-якої точки$P$ на параболі дорівнює відстані від$P$ до директриси.

Малюнок$\PageIndex{3}$: Основні особливості параболи

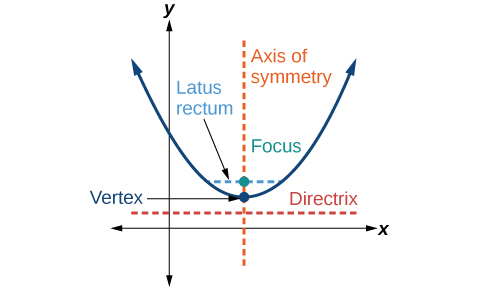
Для роботи з параболами в координатній площині ми розглянемо два випадки: ті, у яких вершина біля початку та ті, що мають вершину в точці, відмінній від початку. Починаємо з першого.

Малюнок$\PageIndex{4}$

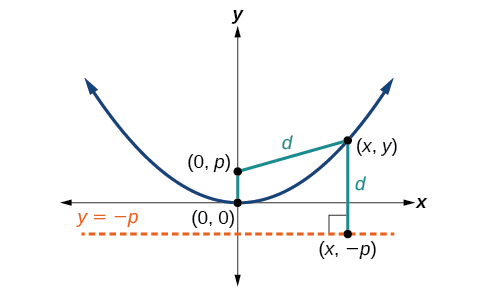
$(x,y)$Дозволяти точка на параболі з вершиною$(0,0)$, фокусом і директрисою$(0,p)$,$y=−p$ як показано на малюнку$\PageIndex{4}$. Віддалене d від точки$(x,y)$ до точки$(x,−p)$ на директрисі - це різниця y -значень:$d=y+p$. Відстань від фокуса$(0,p)$ до точки також$(x,y)$ дорівнює$d$ і може бути виражено за допомогою формули відстані.

$$\begin{align*} d &=\sqrt{{(x−0)}^2+{(y−p)}^2} \\[4pt] &=\sqrt{x^2+{(y−p)}^2} \end{align*}$$

Встановіть два вирази для$d$ рівних один одному і вирішіть for,$y$ щоб вивести рівняння параболи. Ми робимо це тому, що відстань від$(x,y)$ до$(0,p)$ дорівнює відстані від$(x,y)$ до$(x,−p)$.

$$\sqrt{x^2+{(y−p)}^2}=y+p$$

Потім ми квадрат обидві сторони рівняння, розширюємо квадрат члени, і спростити, об'єднавши подібні терміни.

$$\begin{align*} x^2+{(y−p)}^2 &={(y+p)}^2 \\[4pt] x^2+y^2−2py+p^2 &=y^2+2py+p^2 \\[4pt] x^2−2py &=2py \\[4pt] x^2 &=4py \end{align*}$$

Рівняння парабол з вершиною -$(0,0)$ це$y^2=4px$ коли вісь x - вісь симетрії і$x^2=4py$ коли y -вісь - вісь симетрії. Ці стандартні форми наведені нижче, разом з їх загальними графіками і ключовими особливостями.

СТАНДАРТНІ ФОРМИ ПАРАБОЛ З ВЕРШИНОЮ$(0,0)$

Таблиця$\PageIndex{1}$ та рисунок$\PageIndex{5}$ узагальнюють стандартні риси парабол з вершиною біля початку.

Таблиця$\PageIndex{1}$

Вісь симетрії	Рівняння	Фокус	Директриса	Кінцеві точки прямої кишки
x -вісь	$y^2=4px$	$(p, 0)$	$x=−p$	$(p, \pm 2p)$
Y -вісь	$x^2=4py$	$(0, p)$	$y=−p$	$(\pm 2p, p)$

Малюнок$\PageIndex{5}$: ($p>0$а) Коли вісь симетрії є віссю x, парабола відкривається праворуч. (b) Коли$p<0$ і вісь симетрії є віссю х, парабола відкривається ліворуч. (c) Коли$p<0$ і вісь симетрії є віссю y, парабола відкривається. (d) Коли$p<0$ і вісь симетрії є віссю y, парабола відкривається вниз.

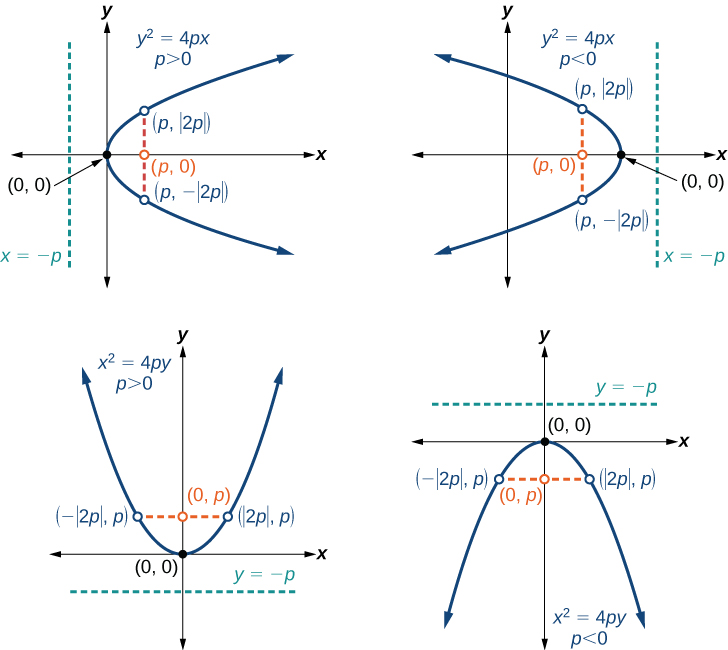
Ключовими особливостями параболи є її вершина, вісь симетрії, фокус, директриса і пряма кишка (рис.$\PageIndex{5}$). Коли дано стандартне рівняння для параболи, орієнтованої на початок, ми можемо легко визначити ключові особливості для графіка параболи. Лінія вважається дотичною до кривої, якщо вона перетинає криву рівно в одній точці. Якщо накреслити лінії, дотичні до параболи в кінцевих точках прямої кишки латуса, то ці лінії перетинаються на осі симетрії, як показано на малюнку$\PageIndex{6}$.

Малюнок$\PageIndex{6}$

Як: Задано рівняння стандартної форми для параболи з центром$(0,0)$, sketch the graph

1. Визначте, яка з стандартних форм застосовується до даного рівняння:$y^2=4px$ або$x^2=4py$.
2. Використовуйте стандартну форму, визначену на кроці 1, для визначення осі симетрії, фокусу, рівняння прямої кишки та кінцевих точок прямої кишки.
   • Якщо рівняння у вигляді$y^2=4px$, то
     • віссю симетрії є$x$ -вісь,$y=0$
     • $4p$множина дорівнює коефіцієнту$x$ в заданому рівнянні для розв'язання$p$. Якщо$p>0$, парабола відкривається вправо. Якщо$p<0$, парабола відкривається зліва.
     • використовувати$p$ для пошуку координат фокусу,$(p,0)$
     • використовувати$p$ для пошуку рівняння директриси,$x=−p$
     • використовувати$p$ для пошуку кінцевих точок прямої кишки латуса,$(p,\pm 2p)$. По черзі$x=p$ підставляємо в вихідне рівняння.
   • Якщо рівняння у вигляді$x^2=4py$, то
     • віссю симетрії є$y$ -вісь,$x=0$
     • $4p$множина дорівнює коефіцієнту$y$ в заданому рівнянні для розв'язання$p$. Якщо$p>0$, парабола розкривається. Якщо$p<0$, парабола відкривається вниз.
     • використовувати$p$ для пошуку координат фокусу,$(0,p)$
     • використовувати$p$ для пошуку рівняння директриси,$y=−p$
     • використовувати$p$ для пошуку кінцевих точок прямої кишки латуса,$(\pm 2p,p)$
3. Помістіть фокус, директрису та пряму кишку, і намалюйте плавну криву, щоб сформувати параболу.

-вісь як вісь симетрії

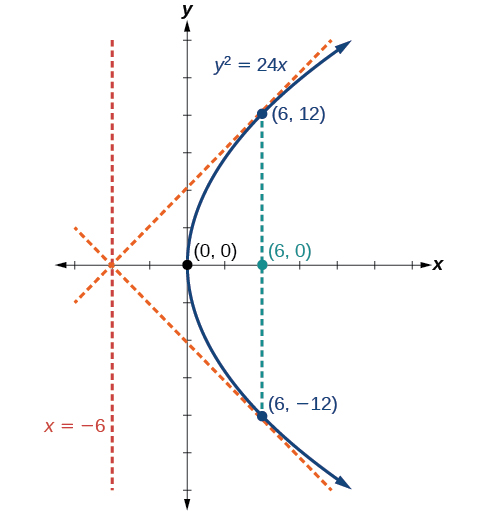
Графік$y^2=24x$. Визначте та позначте фокус, директрису та кінцеві точки прямої кишки.

Рішення

Стандартна форма, яка застосовується до даного рівняння, є$y^2=4px$. Таким чином, віссю симетрії є х -вісь. Звідси випливає, що:

• $24=4p$, Отже$p=6$. З тих пір$p>0$ парабола відкривається вправо
• координати фокусу$(p,0)=(6,0)$
• рівняння директриси дорівнює$x=−p=−6$
• кінцеві точки прямої кишки латуса мають однакову x -координату у фокусі. Щоб знайти кінцеві точки,$x=6$ підставляємо в вихідне рівняння:$(6,\pm 12)$

Далі ми будуємо фокус, директрису та пряму кишку, і малюємо плавну криву, щоб сформувати параболу (рис.$\PageIndex{7}$).

Малюнок$\PageIndex{7}$

Вправа$\PageIndex{1}$

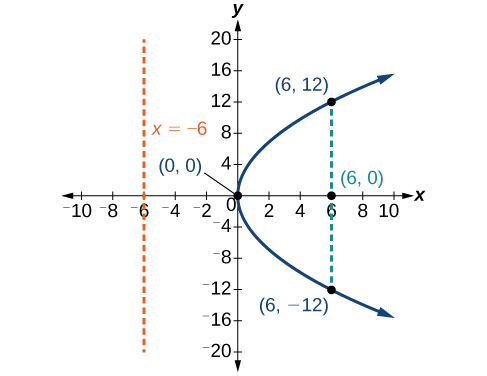
Графік$y^2=−16x$. Визначте та позначте фокус, директрису та кінцеві точки прямої кишки.

Відповідь

• Фокус:$(−4,0)$
• Директриса:$x=4$
• Кінцеві точки прямої прямої кишки:$(−4,\pm 8)$

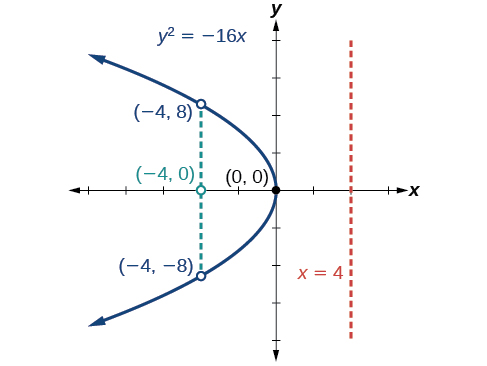
Малюнок$\PageIndex{8}$

-вісь як вісь симетрії

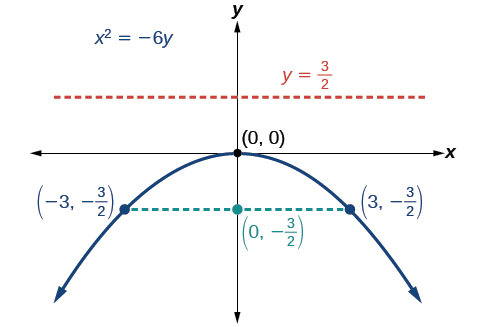
Графік$x^2=−6y$. Визначте та позначте фокус, директрису та кінцеві точки прямої кишки.

Рішення

Стандартна форма, яка застосовується до даного рівняння, є$x^2=4py$. Таким чином, віссю симетрії є$y$ -вісь. Звідси випливає, що:

• $−6=4p$, Отже$p=−\dfrac{3}{2}$. З тих пір$p<0$, парабола відкривається вниз.
• координати фокусу$(0,p)=(0,−\dfrac{3}{2})$
• рівняння директриси дорівнює$y=−p=\dfrac{3}{2}$
• кінцеві точки прямої кишки латуса можна знайти шляхом підстановки$y=\dfrac{3}{2}$ в вихідне рівняння,$(\pm 3,−\dfrac{3}{2})$

Далі ми розміщуємо фокус, директрису та пряму кишку, і намалюємо плавну криву, щоб сформувати параболу.

Малюнок$\PageIndex{9}$

Вправа$\PageIndex{2}$

Графік$x^2=8y$. Визначте та позначте фокус, директрису та кінцеві точки прямої кишки.

Відповідь

• Фокус:$(0,2)$
• Директриса:$y=−2$
• Кінцеві точки прямої прямої кишки:$(\pm 4,2)$.

Малюнок$\PageIndex{10}$

Написання рівнянь парабол у стандартній формі

У попередніх прикладах ми використовували стандартне рівняння параболи для обчислення місць її ключових ознак. Ми також можемо використовувати обчислення у зворотному напрямку, щоб написати рівняння для параболи, якщо задано її ключові особливості.

Як: З огляду на його фокус і директрису, запишіть рівняння для параболи в стандартному вигляді

1. Визначте, чи є віссю симетрії$x$ - або$y$ -віссю.
   1. Якщо задані координати фокуса мають вигляд$(p,0)$, то віссю симетрії є$x$ -вісь. Використовуйте стандартну форму$y^2=4px$.
   2. Якщо задані координати фокуса мають вигляд$(0,p)$, то віссю симетрії є$y$ -вісь. Використовуйте стандартну форму$x^2=4py$.
2. Помножити$4p$.
3. Підставте значення з кроку 2 у рівняння, визначене в кроці 1.

Приклад$\PageIndex{3}$: Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix

Що таке рівняння для параболи з фокусом$(−\dfrac{1}{2},0)$ і директрисою$x=\dfrac{1}{2}$?

Рішення

Фокус має вигляд$(p,0)$, тому рівняння матиме вигляд$y^2=4px$.

• Помножуючи$4p$, ми маємо$4p=4(−\dfrac{1}{2})=−2$.
• Підставляючи$4p$, у нас є$y^2=4px=−2x$. =

Тому рівняння для параболи є$y^2=−2x$.

Вправа$\PageIndex{3}$

Що таке рівняння для параболи з фокусом$\left(0,\dfrac{7}{2}\right)$ і директрисою$y=−\dfrac{7}{2}$?

Відповідь

$x^2=14y$.

Графік парабол з вершинами, які не біля початку

Як і інші графіки, з якими ми працювали, графік параболи можна перекласти. Якщо парабола перекладається$h$ одиницями горизонтально, а$k$ одиниці вертикально, вершина буде$(h,k)$. Цей переклад призводить до стандартної форми рівняння, яке ми бачили раніше,$x$ замінене$(x−h)$ і$y$ замінене на$(y−k)$.

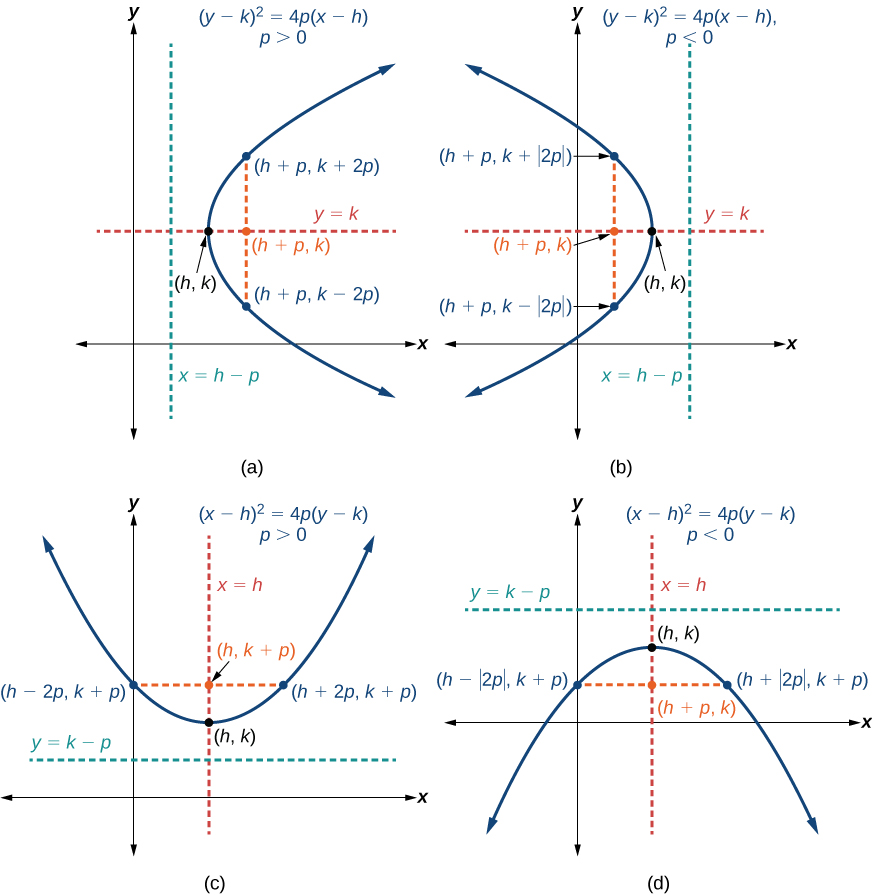
Для графування парабол з вершиною,$(h,k)$ відмінною від початку, ми використовуємо стандартну форму${(y−k)}^2=4p(x−h)$ для парабол, які мають вісь симетрії паралельну$x$ -осі, і${(x−h)}^2=4p(y−k)$ для парабол, що мають вісь симетрії, паралельну$y$ -осі. Ці стандартні форми наведені нижче, разом з їх загальними графіками і ключовими особливостями.

СТАНДАРТНІ ФОРМИ ПАРАБОЛ З ВЕРШИНОЮ$(H, K)$

Таблиця$\PageIndex{2}$ та рисунок$\PageIndex{11}$ підсумовують стандартні риси парабол з вершиною в точці$(h,k)$.

Таблиця$\PageIndex{2}$

Вісь симетрії	Рівняння	Фокус	Директриса	Кінцеві точки прямої кишки
$y=k$	${(y−k)}^2=4p(x−h)$	$(h+p, k)$	$x=h−p$	$(h+p, k\pm 2p)$
$x=h$	${(x−h)}^2=4p(y−k)$	$(h, k+p)$	$y=k−p$	$(h\pm 2p, k+p)$

Малюнок$\PageIndex{11}$: (а) Коли$p>0$ парабола відкривається праворуч. (б) Коли$p<0$ парабола відкривається вліво. (c) Коли$p>0$, парабола відкривається. (d) Коли$p<0$, парабола відкривається вниз.

Як: Задано рівняння стандартної форми для параболи з центром$(h,k)$, sketch the graph

1. Визначте, яка з стандартних форм застосовується до даного рівняння:${(y−k)}^2=4p(x−h)$ або${(x−h)}^2=4p(y−k)$.
2. Використовуйте стандартну форму, визначену на кроці 1, для визначення вершини, осі симетрії, фокусу, рівняння прямої кишки та кінцевих точок прямої кишки латуса.
   • Якщо рівняння має вигляд${(y−k)}^2=4p(x−h)$, то:
     • використовувати дане рівняння для ідентифікації$h$ та$k$ для вершини,$(h,k)$
     • використовувати значення$k$ для визначення осі симетрії,$y=k$
     • $4p$множина дорівнює коефіцієнту$(x−h)$ в заданому рівнянні для розв'язання$p$. Якщо$p>0$, парабола відкривається вправо. Якщо$p<0$, парабола відкривається зліва.
     • використовувати$h$$k$, і$p$ знайти координати фокусу,$(h+p, k)$
     • використовувати$h$ andp p, щоб знайти рівняння директриси,$x=h−p$
     • використовувати$h$$k$, і$p$ знайти кінцеві точки прямої кишки,$(h+p,k\pm 2p)$
   • Якщо рівняння має вигляд${(x−h)}^2=4p(y−k)$, то:
     • використовувати дане рівняння для ідентифікації$h$ та$k$ для вершини,$(h,k)$
     • використовувати значення$h$ для визначення осі симетрії,$x=h$
     • $4p$множина дорівнює коефіцієнту$(y−k)$ в заданому рівнянні для розв'язання$p$. Якщо$p>0$, парабола розкривається. Якщо$p<0$, парабола відкривається вниз.
     • використовувати$h$$k$, і$p$ знайти координати фокусу,$(h, k+p)$
     • використовувати$k$ і$p$ знайти рівняння директриси,$y=k−p$
     • використовувати$h$$k$, і$p$ знайти кінцеві точки прямої кишки,$(h\pm 2p, k+p)$
3. Покладіть вершину, вісь симетрії, фокус, директрису та пряму кишку, і намалюйте плавну криву, щоб сформувати параболу.

Приклад$\PageIndex{4}$: Graphing a Parabola with Vertex $(h, k)$ and Axis of Symmetry Parallel to the $x$-axis

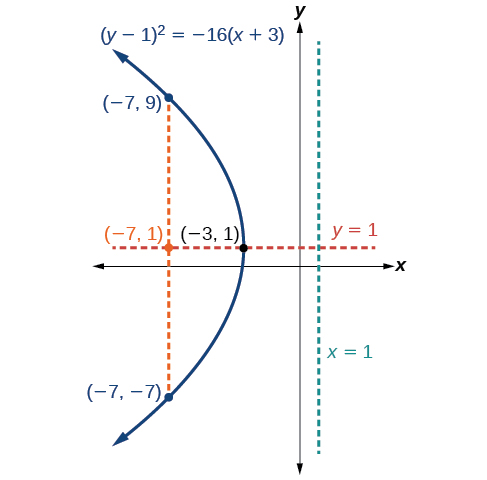
Графік${(y−1)}^2=−16(x+3)$. Визначте та позначте вершину, вісь симетрії, фокус, директрису та кінцеві точки прямої кишки.

Рішення

Стандартна форма, яка застосовується до даного рівняння, є${(y−k)}^2=4p(x−h)$. Таким чином, вісь симетрії паралельна$x$ -осі. Звідси випливає, що:

• вершина$(h,k)=(−3,1)$
• вісь симетрії$y=k=1$
• $−16=4p$, Отже$p=−4$. З тих пір$p<0$, парабола відкривається зліва.
• координати фокусу$(h+p,k)=(−3+(−4),1)=(−7,1)$
• рівняння директриси дорівнює$x=h−p=−3−(−4)=1$
• кінцеві точки прямої кишки прямої кишки є$(h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))$, або$(−7,−7)$ і$(−7,9)$

Далі ми розміщуємо вершину, вісь симетрії, фокус, директрису та пряму кишку, і намалюємо плавну криву, щоб сформувати параболу (рис.$\PageIndex{10}$).

Малюнок$\PageIndex{12}$

Вправа$\PageIndex{4}$

Графік${(y+1)}^2=4(x−8)$. Визначте та позначте вершину, вісь симетрії, фокус, директрису та кінцеві точки прямої кишки.

Відповідь

• Вершина:$(8,−1)$
• Вісь симетрії:$y=−1$
• Фокус:$(9,−1)$
• Директриса:$x=7$
• Кінцеві точки прямої прямої кишки:$(9,−3)$ і$(9,1)$.

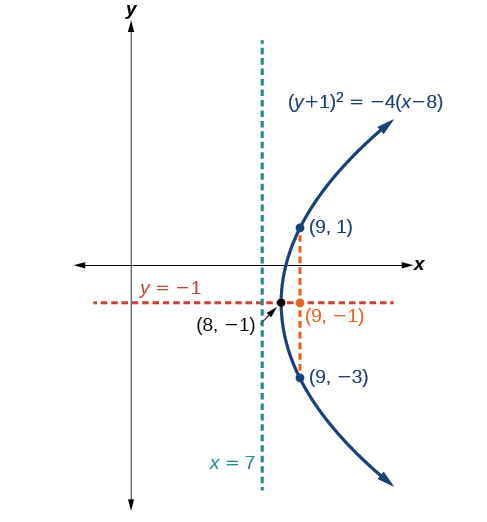
Малюнок$\PageIndex{13}$

Приклад$\PageIndex{5}$: Graphing a Parabola from an Equation Given in General Form

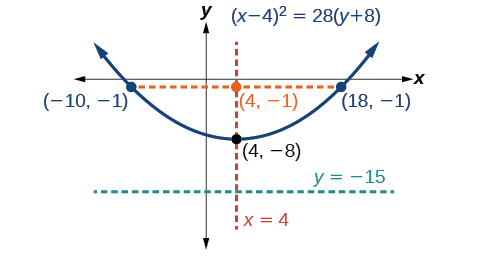
Графік$x^2−8x−28y−208=0$. Визначте та позначте вершину, вісь симетрії, фокус, директрису та кінцеві точки прямої кишки.

Рішення

Почніть з написання рівняння параболи в стандартній формі. Стандартна форма, яка застосовується до даного рівняння, є${(x−h)}^2=4p(y−k)$. Таким чином, вісь симетрії паралельна$y$ -осі. Щоб висловити рівняння параболи в такому вигляді, почнемо з виділення членів, які містять змінну,$x$ щоб завершити квадрат.

$$\begin{align*} x^2−8x−28y−208&=0 \\[4pt] x^2−8x &=28y+208 \\[4pt] x^2−8x+16 &=28y+208+16 \\[4pt] (x−4)^2 &=28y+224 \\[4pt] (x−4)^2 &=28(y+8) \\[4pt] (x−4)^2&= 4⋅7⋅(y+8) \end{align*}$$

Звідси випливає, що:

• вершина$(h,k)=(4,−8)$
• вісь симетрії$x=h=4$
• з тих пір$p=7$,$p>0$ і так парабола відкривається
• координати фокусу$(h,k+p)=(4,−8+7)=(4,−1)$
• рівняння директриси дорівнює$y=k−p=−8−7=−15$
• кінцеві точки прямої кишки прямої кишки є$(h\pm 2p,k+p)=(4\pm 2(7),−8+7)$, або$(−10,−1)$ і$(18,−1)$

Далі ми розміщуємо вершину, вісь симетрії, фокус, директрису та пряму кишку, і намалюємо плавну криву, щоб сформувати параболу (рис.$\PageIndex{14}$).

Малюнок$\PageIndex{14}$

Вправа$\PageIndex{5}$

Графік${(x+2)}^2=−20(y−3)$. Визначте та позначте вершину, вісь симетрії, фокус, директрису та кінцеві точки прямої кишки.

Відповідь

• Вершина:$(−2,3)$
• Вісь симетрії:$x=−2$
• Фокус:$(−2,−2)$
• Директриса:$y=8$
• Кінцеві точки прямої прямої кишки:$(−12,−2)$ і$(8,−2)$.

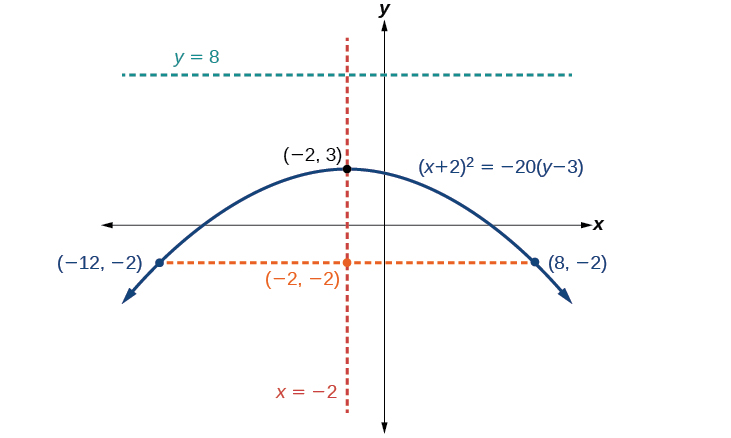
Малюнок$\PageIndex{15}$

Рішення прикладних проблем за участю парабол

Як ми згадували на початку розділу, параболи використовуються для проектування багатьох об'єктів, які ми використовуємо щодня, таких як телескопи, підвісні мости, мікрофони та радіолокаційне обладнання. Параболічні дзеркала, такі як той, який використовувався для освітлення олімпійського факела, мають дуже унікальну відбиваючу властивість. Коли промені світла, паралельні осі симетрії параболи, спрямовані в бік будь-якої поверхні дзеркала, світло відбивається безпосередньо до вогнища (рис.$\PageIndex{16}$). Ось чому олімпійський факел запалюється, коли він утримується у фокусі параболічного дзеркала.

Малюнок$\PageIndex{16}$: Відображає властивість парабол

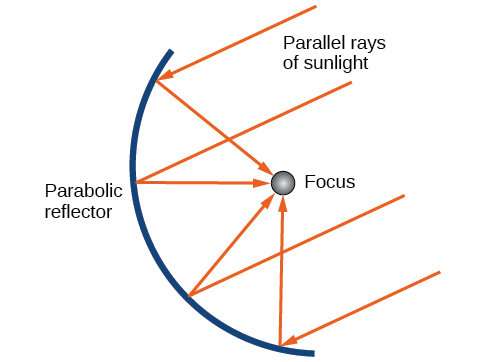
Параболічні дзеркала мають здатність фокусувати енергію сонця в одній точці, піднімаючи температуру на сотні градусів за лічені секунди. Таким чином, параболічні дзеркала представлені у багатьох недорогих, енергоефективних сонячних продуктах, таких як сонячні плити, сонячні нагрівачі та навіть пожежні стартери.

Приклад$\PageIndex{6}$: Solving Applied Problems Involving Parabolas

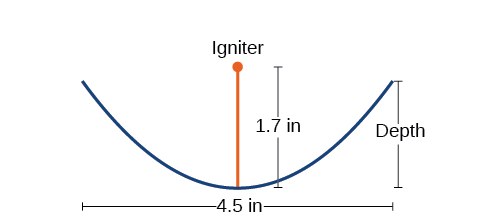
Перетин конструкції для дорожнього сонячного пожежного стартера показано на малюнку$\PageIndex{17}$. Сонячні промені відбиваються від параболічного дзеркала до об'єкта, прикріпленого до запальника. Оскільки запальник розташований у вогнищі параболи, відбиті промені змушують об'єкт згоряти всього за лічені секунди.

1. Знайдіть рівняння параболи, яка моделює пожежний стартер. Припустимо, що вершина параболічного дзеркала є початком координатної площини.
2. Використовуйте рівняння, знайдене в частині (а), щоб знайти глибину пожежного стартера.

Малюнок$\PageIndex{17}$ Перетин дорожнього сонячного пожежного стартера

Рішення

1. Вершина страви є початком координатної площини, тому парабола прийме стандартну форму$x^2=4py$, де$p>0$. Запальник, який є фокусом, знаходиться на$1.7$ дюймах вище вершини страви. Таким чином ми маємо$p=1.7$.

$$\begin{align*} x^2&=4py\qquad \text{Standard form of upward-facing parabola with vertex } (0,0)\\ x^2&=4(1.7)y\qquad \text{Substitute } 1.7 \text{ for } p\\ x^2&=6.8y\qquad \text{Multiply.} \end{align*}$$

2. Блюдо розширюється$\dfrac{4.5}{2}=2.25$ дюйми по обидва боки від походження. Ми можемо замінити$2.25$$x$ в рівнянні з частини (а), щоб знайти глибину страви.

$$\begin{align*} x^2&=6.8y\qquad \text{ Equation found in part } (a)\\ {(2.25)}^2&=6.8y\qquad \text{Substitute } 2.25 \text{ for } x\\ y&\approx 0.74\qquad \text{Solve for } y \end{align*}$$

Блюдо глибиною близько$0.74$ дюймів.

Вправа$\PageIndex{6}$

Сонячні плити розміром з балкон були розроблені для сімей, які проживають в Індії. Верх тарілки має діаметр$1600$ мм. Сонячні промені відбиваються від параболічного дзеркала в сторону «плити», яка розміщена в$320$ мм від основи.

1. Знайдіть рівняння, яке моделює перетин сонячної плити. Припустимо, що вершина параболічного дзеркала є початком координатної площини, і що парабола відкривається праворуч (тобто має вісь x - як вісь симетрії).
2. Використовуйте рівняння, знайдене в частині (а), щоб знайти глибину плити.

Відповідь на

$y^2=1280x$

Відповідь б

Глибина плити -$500$ мм

Ключові рівняння

Парабола, вершина на початку, вісь симетрії на осі x	$y^2=4px$
Парабола, вершина на початку, вісь симетрії на осі y	$x^2=4py$
Парабола, вершина at$(h,k)$, вісь симетрії на осі x	${(y−k)}^2=4p(x−h)$
Парабола, вершина at$(h,k)$, вісь симетрії на осі y	${(x−h)}^2=4p(y−k)$

Ключові концепції

• Парабола - це сукупність всіх точок$(x,y)$ на площині, які знаходяться на однаковій відстані від фіксованої лінії, званої директрисою, і фіксованою точкою (фокусом) не на директрисі.
• Стандартна форма параболи з вершиною$(0,0)$ та віссю x як її віссю симетрії може бути використана для графування параболи. Якщо$p>0$, парабола відкривається вправо. Якщо$p<0$, парабола відкривається зліва. Див$\PageIndex{1}$. Приклад.
• Стандартна форма параболи з вершиною$(0,0)$ та віссю y як її віссю симетрії може бути використана для графування параболи. Якщо$p>0$, парабола розкривається. Якщо$p<0$, парабола відкривається вниз. Див$\PageIndex{2}$. Приклад.
• Коли задано фокус і директрису параболи, ми можемо записати її рівняння в стандартній формі. Див$\PageIndex{3}$. Приклад.
• Стандартна форма параболи з вершиною$(h,k)$ і віссю симетрії, паралельною$x$ -осі, може бути використана для графування параболи. Якщо$p>0$, парабола відкривається вправо. Якщо$p<0$, парабола відкривається зліва. Див$\PageIndex{4}$. Приклад.
• Стандартна форма параболи з вершиною$(h,k)$ і віссю симетрії, паралельною$y$ -осі, може бути використана для графування параболи. Якщо$p>0$, парабола розкривається. Якщо$p<0$, парабола відкривається вниз. Див$\PageIndex{5}$. Приклад.
• Реальні ситуації можуть бути змодельовані за допомогою стандартних рівнянь парабол. Наприклад, враховуючи діаметр і фокус поперечного перерізу параболічного відбивача, ми можемо знайти рівняння, яке моделює його сторони. Див$\PageIndex{6}$. Приклад.