5.2: Спрощення радикальних виразів

Цілі навчання

• Спростіть радикальні вирази, використовуючи добуток і часткове правило для радикалів.
• Використовуйте формули за участю радикалів.

Спрощення радикальних виразів

Алгебраїчний вираз, що містить радикали, називається радикальним виразом ¹⁴. Ми використовуємо продукт і правила коефіцієнта, щоб спростити їх.

Приклад\(\PageIndex{1}\):

Спростити:\(\sqrt [ 3 ] { 27 x ^ { 3 } }\).

Рішення

Використовуйте той факт, що\(\sqrt [ n ] { a ^ { n } } = a\) коли\(n\) непарний.

\(\begin{aligned} \sqrt [ 3 ] { 27 x ^ { 3 } } & = \sqrt [ 3 ] { 3 ^ { 3 } \cdot x ^ { 3 } }\quad\quad \color{Cerulean} { Apply \:the\: product \:rule\: for\: radicals.} \\ & = \sqrt [ 3 ] { 3 ^ { 3 } } \cdot \sqrt [ 3 ] { x ^ { 3 } }\quad \color{Cerulean} { Simplify. } \\ & = 3 \cdot x \\ & = 3 x \end{aligned}\)

Відповідь:

\(3x\)

Приклад\(\PageIndex{2}\):

Спростити:\(\sqrt [ 4 ] { 16 y ^ { 4 } }\).

Рішення

Використовуйте той факт, що\(\sqrt [ n ] { a ^ { n } } = | a |\) коли\(n\) рівний.

\(\begin{aligned} \sqrt [ 4 ] { 16 y ^ { 4 } } & = \sqrt [ 4 ] { 2 ^ { 4 } y ^ { 4 } }\quad\quad\:\:\: \color{Cerulean} { Apply\: the\: product\: rule\: for\: radicals.} \\ & = \sqrt [ 4 ] { 2 ^ { 4 } } \cdot \sqrt [ 4 ] { y ^ { 4 } }\:\:\:\: \color{Cerulean} { Simplify. } \\ & = 2 \cdot | y | \\ & = 2 | y | \end{aligned}\)

Оскільки\(y\) є змінною, вона може представляти собою від'ємне число. Таким чином, нам потрібно переконатися, що результат був позитивним, включивши абсолютне значення.

Відповідь:

\(2 | y |\)

Примітка

Як правило, в цей момент в алгебрі ми відзначаємо, що всі змінні приймаються позитивними. Якщо це так, то\(y\) в попередньому прикладі позитивний і оператор абсолютного значення не потрібен. Приклад можна спростити наступним чином.

\(\begin{aligned} \sqrt [ 4 ] { 16 y ^ { 4 } } & = \sqrt [ 4 ] { 2 ^ { 4 } y ^ { 4 } } \\ & = \sqrt [ 4 ] { 2 ^ { 4 } } \cdot \sqrt [ 4 ] { y ^ { 4 } } \\ & = 2 y \end{aligned}\)

У цьому розділі ми будемо вважати, що всі змінні позитивні. Це дозволяє зосередитися на обчисленні\(n\) коренів без технічних аспектів, пов'язаних з\(n\) основною проблемою кореня. З цієї причини ми будемо використовувати наступну властивість для решти розділу,

\(\sqrt [ n ] { a ^ { n } } = a , \quad \text { if } a \geq 0 \quad \color{Cerulean}{nth \:root}\)

При спрощенні радикальних виразів шукайте фактори з повноваженнями, які відповідають індексу.

Приклад\(\PageIndex{3}\):

Спростити:\(\sqrt { 12 x ^ { 6 } y ^ { 3 } }\).

Рішення

Почніть з визначення квадратних коефіцієнтів\(12, x^{ 6}\), і\(y^{ 3}\).

\(\left. \begin{array} { l } { 12 = \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 } \\ { x ^ { 6 } = \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 } }} \\ { y ^ { 3 } = \color{Cerulean}{y ^ { 2} }\color{black}{ \cdot} y } \end{array} \right\} \quad\color{Cerulean}{Square\:factors}\)

Зробіть ці заміни, а потім застосуйте правило продукту для радикалів і спростіть.

\(\begin{aligned} \sqrt { 12 x ^ { 6 } y ^ { 3 } } & = \sqrt { \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 \cdot \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 }}\color{black}{ \cdot}\color{Cerulean}{ y ^ { 2} }\color{black}{ \cdot} y } \quad\quad\quad\quad\:\color{Cerulean} { Apply\:the\: product \:rule\: for\: radicals. } \\ & = \sqrt { 2 ^ { 2 } } \cdot \sqrt { \left( x ^ { 3 } \right) ^ { 2 } } \cdot \sqrt { y ^ { 2 } } \cdot \sqrt { 3 y } \quad\color{Cerulean} { Simplify. } \\ & = 2 \cdot x ^ { 3 } \cdot y \cdot \sqrt { 3 y } \\ & = 2 x ^ { 3 } y \sqrt { 3 y } \end{aligned}\)

Відповідь:

\(2 x ^ { 3 } y \sqrt { 3 y }\)

Приклад\(\PageIndex{4}\):

Спростити:\(\sqrt { \frac { 18 a ^ { 5 } } { b ^ { 8 } } }\).

Рішення

Почніть з визначення квадратних\(18\) коефіцієнтів\(a^{5}\), і\(b^{8}\).

\(\left. \begin{array} { l } { 18 = 2 \cdot \color{Cerulean}{3 ^ { 2} } } \\ { a ^ { 5 } = a ^ { 2 } \cdot a ^ { 2 } \cdot a = \color{Cerulean}{\left( a ^ { 2 } \right) ^ { 2 }}\color{black}{ \cdot} a } \\ { b ^ { 8 } = b ^ { 4 } \cdot b ^ { 4 } \quad\:\:= \color{Cerulean}{\left( b ^ { 4 } \right) ^ { 2 }} } \end{array}\quad \right\}\quad\color{Cerulean}{Square\:factors}\)

Зробіть ці заміни, застосуйте продукт і правила частки для радикалів, а потім спростіть.

\(\begin{aligned} \sqrt { \frac { 18 a ^ { 5 } } { b ^ { 8 } } } & = \sqrt { \frac { 2 \cdot \color{Cerulean}{3 ^ { 2} }\color{black}{ \cdot}\color{Cerulean}{ \left( a ^ { 2 } \right) ^ { 2 }}\color{black}{ \cdot} a } { \color{Cerulean}{\left( b ^ { 4 } \right) ^ { 2 } } }}\quad\quad\color{Cerulean}{Apply\:the\:product\:and\:quotient\:rule\:for\:radicals.} \\ & = \frac { \sqrt { 3 ^ { 2 } } \cdot \sqrt { \left( a ^ { 2 } \right) ^ { 2 } } \cdot \sqrt { 2 a } } { \sqrt { \left( b ^ { 4 } \right) ^ { 2 } } }\quad \color{Cerulean}{Simplify.} \\ & = \frac { 3 a ^ { 2 } \sqrt { 2 a } } { b ^ { 4 } } \end{aligned}\)

Відповідь:

\(\frac { 3 a ^ { 2 } \sqrt { 2 a } } { b ^ { 4 } }\)

Приклад\(\PageIndex{5}\):

Спростити:\(\sqrt [ 3 ] { 80 x ^ { 5 } y ^ { 7 } }\).

Рішення

Почніть з визначення кубічних факторів\(80 , x ^ { 5 }\), і\(y^{7}\).

\(\left. \begin{array} { l } { 80 = 2 ^ { 4 } \cdot 5 = \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 \cdot 5 } \\ { x ^ { 5 } = \color{Cerulean}{x ^ { 3 }}\color{black}{ \cdot} x ^ { 2 } } \\ { y ^ { 7 } = y ^ { 6 } \cdot y =\color{Cerulean}{ \left( y ^ { 2 } \right) ^ { 3 } }\color{black}{\cdot} y } \end{array} \quad\right\}\quad\color{Cerulean}{Cubic\:factors}\)

Зробіть ці заміни, а потім застосуйте правило продукту для радикалів і спростіть.

\(\begin{aligned} \sqrt [ 3 ] { 80 x ^ { 5 } y ^ { 7 } } & = \sqrt [ 3 ] { \color{Cerulean}{2 ^ { 3} }\color{black}{ \cdot} 2 \cdot 5 \cdot \color{Cerulean}{x ^ { 3 }}\color{black}{ \cdot} x ^ { 2 } \cdot \color{Cerulean}{\left( y ^ { 2 } \right) ^ { 3 }}\color{black}{ \cdot} y } \\ & = \sqrt [ 3 ] { \color{Cerulean}{2 ^ { 3} } } \color{black}{\cdot} \sqrt [ 3 ] { \color{Cerulean}{x ^ { 3 }} }\color{black}{ \cdot} \sqrt [ 3 ] { \color{Cerulean}{\left( y ^ { 2 } \right) ^ { 3 } } }\color{black}{\cdot} \sqrt [ 3 ] { 2 \cdot 5 \cdot x ^ { 2 } \cdot y } \\ & = 2 \cdot x y ^ { 2 } \cdot \sqrt [ 3 ] { 10 x ^ { 2 } y } \\ & = 2 x y ^ { 2 } \sqrt [ 3 ] { 10 x ^ { 2 } y } \end{aligned}\)

Відповідь:

\(2 x y ^ { 2 } \sqrt [ 3 ] { 10 x ^ { 2 } y }\)

Приклад\(\PageIndex{6}\):

Спростити:\(\sqrt [ 3 ] { \frac { 9 x ^ { 6 } } { y ^ { 3 } z ^ { 9 } } }\).

Рішення

Коефіцієнт\(9 = 3^{2}\), а значить, не має досконалих кубових факторів. Він залишиться єдиним радикалом, оскільки всі інші фактори є кубами, як показано нижче:

\(\left. \begin{array} { l } { x ^ { 6 } = \left( x ^ { 2 } \right) ^ { 3 } } \\ { y ^ { 3 } = ( y ) ^ { 3 } } \\ { z ^ { 9 } = \left( z ^ { 3 } \right) ^ { 3 } } \end{array} \quad\right\}\quad\color{Cerulean}{Cubic\:factors}\)

Замініть змінні цими еквівалентами, застосуйте правила продукту та коефіцієнта для радикалів, а потім спростіть.

\(\begin{aligned} \sqrt [ 3 ] { \frac { 9 x ^ { 6 } } { y ^ { 3 } z ^ { 9 } } } & = \sqrt [ 3 ] { \frac { 9 \cdot \left( x ^ { 2 } \right) ^ { 3 } } { y ^ { 3 } \cdot \left( z ^ { 3 } \right) ^ { 3 } } } \\ & = \frac { \sqrt [ 3 ] { 9 } \cdot \sqrt [ 3 ] { \left( x ^ { 2 } \right) ^ { 3 } } } { \sqrt [ 3 ] { y ^ { 3 } } \cdot \sqrt [ 3 ] { \left( z ^ { 3 } \right) ^ { 3 } } } \\ & = \frac{\sqrt[3]{9} \:\cdot\:x^{2} }{y\:\cdot\:z^{3}}\\&= \frac{x^{2}\:\sqrt[3]{9}}{yz^{3}}\end{aligned}\)

Відповідь:

\(\frac { x ^ { 2 } \sqrt [ 3 ] { 9 } } { y z ^ { 3 } }\)

Приклад\(\PageIndex{7}\):

Спростити:\(\sqrt [ 4 ] { 81 a ^ { 4 } b ^ { 5 } }\).

Рішення

Визначте всі фактори, які можуть бути записані як досконалі сили\(4\). Тут важливо це побачити\(b^{5} = b^{4} ⋅ b\). Звідси фактор\(b\) залишиться всередині радикала.

\(\begin{aligned} \sqrt [ 4 ] { 81 a ^ { 4 } b ^ { 5 } } & = \sqrt [ 4 ] { 3 ^ { 4 } \cdot a ^ { 4 } \cdot b ^ { 4 } \cdot b } \\ & = \sqrt [ 4 ] { 3 ^ { 4 } } \cdot \sqrt [ 4 ] { a ^ { 4 } } \cdot \sqrt [ 4 ] { b ^ { 4 } } \cdot \sqrt [ 4 ] { b } \\ & = 3 \cdot a \cdot b \cdot \sqrt [ 4 ] { b } \\ & = 3 a b \sqrt [ 4 ] { b } \end{aligned}\)

Відповідь:

\(3 a b \sqrt [ 4 ] { b }\)

Приклад\(\PageIndex{8}\):

Спростити:\(\sqrt [ 5 ] { - 32 x ^ { 3 } y ^ { 6 } z ^ { 5 } }\).

Рішення

Зверніть увагу, що змінний коефіцієнт\(x\) не може бути записаний як сила\(5\) і, таким чином, залишиться всередині радикала. Крім того,\(y^{6} = y^{5} ⋅ y\); фактор\(y\) залишиться всередині радикалу, а також.

\(\begin{aligned} \sqrt [ 3 ] { - 32 x ^ { 3 } y ^ { 6 } z ^ { 5 } } & = \sqrt [ 5 ] { \color{Cerulean}{( - 2 ) ^ { 5 } }\color{black}{\cdot} x ^ { 3 } \cdot\color{Cerulean}{ y ^ { 5} }\color{black}{ \cdot} y \cdot \color{Cerulean}{z ^ { 5} } } \\ & = \sqrt [ 5 ] {\color{Cerulean}{ ( - 2 ) ^ { 5 } }} \color{black}{\cdot} \sqrt [ 5 ] { \color{Cerulean}{y ^ { 5 }} }\color{black}{ \cdot} \sqrt [ 5 ] { \color{Cerulean}{z ^ { 5} } }\color{black}{ \cdot} \sqrt [ 5 ] { x ^ { 3 } \cdot y } \\ & = - 2 \cdot y \cdot z \cdot \sqrt [ 5 ] { x ^ { 3 } \cdot y } \\ & = - 2 y z \sqrt [ 5 ] { x ^ { 3 } y } \end{aligned}\)

Відповідь:

\(- 2 y z \sqrt [ 5 ] { x ^ { 3 } y }\)

Порада: Щоб спростити пошук кореня, розділіть повноваження на індекс.\(n\)

\(\begin{aligned} \sqrt { a ^ { 6 } } = a ^ { 3 } , & \text { which is } a ^ { 6 \div 2 } = a ^ { 3 } \\ \sqrt [ 3 ] { b ^ { 6 } } = b ^ { 2 } , & \text { which is } b ^ { 6 \div 3 } = b ^ { 2 } \\ \sqrt[6]{c^{6}} = c\:\:, &\: \text{which is} \:{c^{6\div 6} = c^{1}} \end{aligned}\)

Якщо індекс не ділиться на потужність рівномірно, то ми можемо використовувати частку і залишок для спрощення. Наприклад,

\(\begin{aligned} \sqrt { a ^ { 5 } }& = a ^ { 2 } \cdot \sqrt { a } , \text { which is } a ^ { 5 \div 2 } = a ^ { 2 r 1 } \\ \sqrt [ 3 ] { b ^ { 5 } }& = b \cdot \sqrt [ 3 ] { b ^ { 2 } } , \text { which is } b ^ { 5 \div 3 } = b ^ { 1 r 2 } \\ \sqrt[5]{c^{14}} &= c^{2} \cdot\sqrt[5]{c^{4}}, \text{which is} \:c^{14\div 5} = c^{2r4} \end{aligned}\)

Коефіцієнт є показником фактора поза радикалом, а залишок - показник фактора, що залишився всередині радикала.

Вправа\(\PageIndex{1}\)

Спростити:\(\sqrt [ 3 ] { 162 a ^ { 7 } b ^ { 5 } c ^ { 4 } }\).

Відповідь

\(3 a ^ { 2 } b c \sqrt [ 3 ] { 6 a b ^ { 2 } c }\)

www.youtube.com/В/КТ9КА1НФМЛК

Формули за участю радикалів

Формули часто складаються з радикальних виразів. Наприклад, період маятника, або час, який потрібен маятнику для розгойдування з одного боку в інший і назад, залежить від його довжини за наступною формулою.

\(T = 2 \pi \sqrt { \frac { L } { 32 } }\)

Тут\(T\) представлений період в секундах і\(L\) представляє довжину в футах маятника.

Приклад\(\PageIndex{9}\):

Якщо довжина маятника вимірює\(1 \frac{1}{2}\) фути, то обчисліть період, округлений до найближчої десятої частки секунди.

Рішення

\(1 \frac{1}{2} = \frac{3}{2}\)Замінюємо,\(L\) а потім спрощуємо.

\(\begin{aligned} T & = 2 \pi \sqrt { \frac { L } { 32 } } \\ & = 2 \pi \sqrt { \frac { \frac{3}{2} } { 32 } } \\ & = 2 \pi \sqrt { \frac { 3 } { 2 } \cdot \frac { 1 } { 32 } } \quad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals.} \\ & = 2 \pi \frac { \sqrt { 3 } } { \sqrt { 64 } }\quad\quad\:\:\:\color{Cerulean}{Simplify.} \\ & = \frac { \pi \sqrt { 3 } } { 4 } \approx 1.36 \end{aligned}\)

Відповідь:

Період становить приблизно\(1.36\) секунди.

Часто потрібно обчислити відстань між двома точками в площині. Для цього сформуйте прямокутний трикутник, використовуючи дві точки як вершини трикутника, а потім застосуйте теорему Піфагора. Нагадаємо, що теорема Піфагора стверджує, що якщо задано будь-який прямокутний трикутник з катетами вимірювання\(a\) і\(b\) одиницями, то квадрат міри гіпотенузи\(c\) дорівнює сумі квадратів катетів:\(a^{2} + b^{2} = c^{2}\). Іншими словами, гіпотенуза будь-якого прямокутного трикутника дорівнює квадратному кореню суми квадратів його катетів.

Малюнок\(\PageIndex{1}\)

Приклад\(\PageIndex{10}\):

Знайти відстань між\((-5,3)\) і\((1,1)\).

Рішення

Сформуйте прямокутний трикутник, намалювавши горизонтальні та вертикальні лінії через дві точки. Це створює прямокутний трикутник, як показано нижче:

Малюнок\(\PageIndex{2}\)

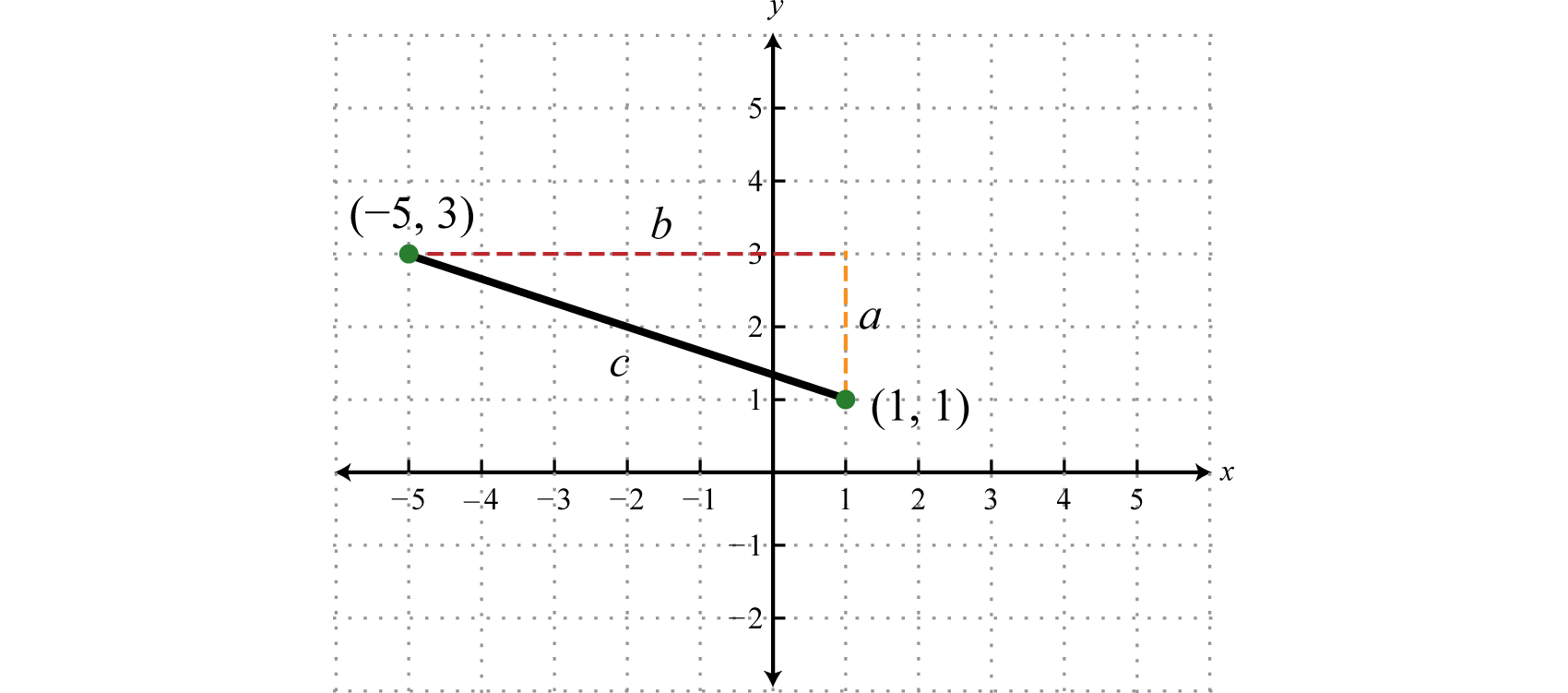
Довжина катета\(b\) обчислюється шляхом знаходження відстані між\(x\) -значеннями заданих точок, а довжина катета\(a\) обчислюється шляхом знаходження відстані між заданими\(y\) -значеннями.

\(\begin{array} { l } { a = 3 - 1 = 2 \text { units } } \\ { b = 1 - ( - 5 ) = 1 + 5 = 6 \text { units } } \end{array}\)

Далі використовуйте теорему Піфагора, щоб знайти довжину гіпотенузи.

\(\begin{aligned} c & = \sqrt { 2 ^ { 2 } + 6 ^ { 2 } } \\ & = \sqrt { 4 + 36 } \\ & = \sqrt { 40 } \\ & = \sqrt { 4 \cdot 10 } \\ & = 2 \sqrt { 10 } \text { units } \end{aligned}\)

Відповідь:

Відстань між двома точками дорівнює\(2 \sqrt{10}\) одиницям.

Узагальніть цей процес, щоб отримати формулу, яка може бути використана для алгебраїчного обчислення відстані між будь-якими двома заданими точками.

Малюнок\(\PageIndex{3}\)

З огляду на дві точки,\(\left( x _ { 1 } , y _ { 1 } \right)\) і\(\left( x _ { 2 } , y _ { 2 } \right)\) відстань,\(d|), between them is given by the distance formula¹⁵, \(d = \sqrt { \left( x _ { 2 } - x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } - y _ { 1 } \right) ^ { 2 } }\).

Приклад\(\PageIndex{11}\):

Обчисліть відстань між\((-4,7)\) і\((2,1)\).

Рішення

Використовуйте формулу відстані з наступними пунктами.

\(\begin{array} { l } { \left( x _ { 1 } , y _ { 1 } \right) \left( x _ { 2 } , y _ { 2 } \right) } \\ { (\color{Cerulean}{ - 4}\color{black}{,}\color{OliveGreen}{7}\color{black}{ )} \quad ( \color{Cerulean}{2}\color{black}{,}\color{OliveGreen}{1}\color{black}{ )} } \end{array}\)

Хорошою практикою є включення формули в загальному вигляді перед підстановкою значень для змінних; це покращує читабельність і зменшує ймовірність помилок.

\(\begin{aligned} d & = \sqrt { \left( x _ { 2 } - x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } - y _ { 1 } \right) ^ { 2 } } \\ & = \sqrt { ( \color{Cerulean}{2}\color{black}{ -} ( \color{Cerulean}{- 4}\color{black}{ )} ) ^ { 2 } + ( \color{OliveGreen}{1}\color{black}{ -}\color{OliveGreen}{ 7}\color{black}{ )} ^ { 2 } } \\ & = \sqrt { ( 2 + 4 ) ^ { 2 } + ( 1 - 7 ) ^ { 2 } } \\ & = \sqrt { ( 6 ) ^ { 2 } + ( - 6 ) ^ { 2 } } \\ & = \sqrt { 72 }\\ & = \sqrt{36\cdot2} \\ & = 6 \sqrt { 2 } \end{aligned}\)

Відповідь:

Відстань між двома точками дорівнює\(6\sqrt{2}\) одиницям.

Приклад\(\PageIndex{12}\):

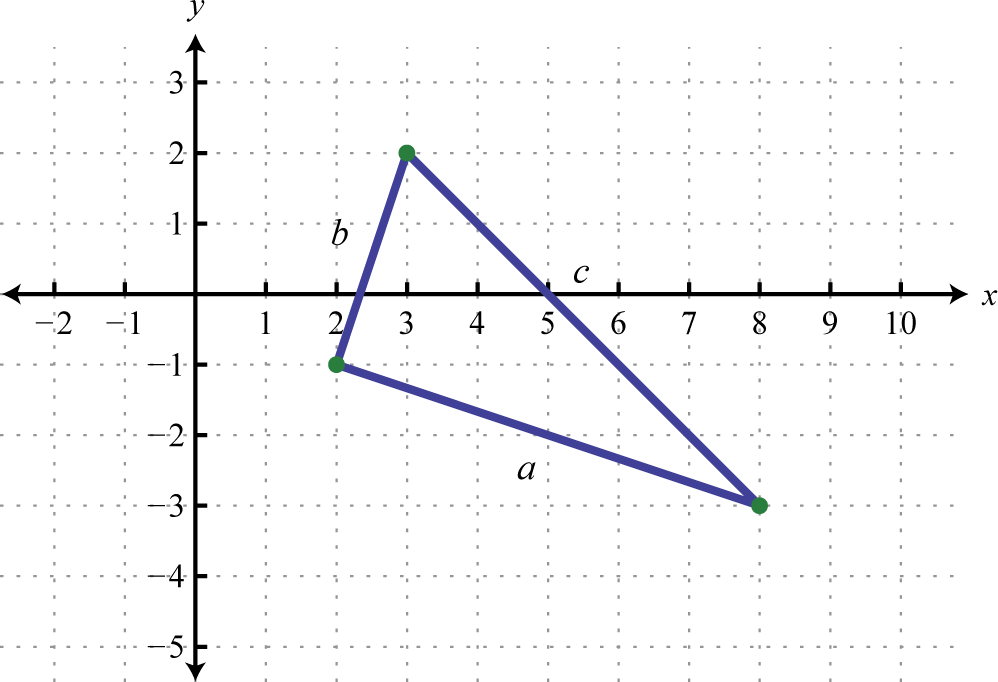
Чи три точки\(( 2 , - 1 ) , ( 3,2 )\), і\((8,-3)\) утворюють прямокутний трикутник?

Рішення

Теорема Піфагора стверджує, що наявність довжин сторін, які задовольняють властивість,\(a^{2} + b^{2}= c^{2}\) є необхідною і достатньою умовою прямих трикутників. Іншими словами, якщо можна показати, що сума квадратів довжин катетів трикутника дорівнює квадрату довжини гіпотенузи, то трикутник повинен бути прямокутним трикутником. Спочатку обчисліть довжину кожної сторони, використовуючи формулу відстані.

Таблиця\(\PageIndex{1}\)

Геометрія	Розрахунок
Малюнок\(\PageIndex{4}\)	Окуляри:\((2,-1)\) і\((8,-3)\) \(\begin{array} { l } { a = \sqrt { ( 8 - 2 ) ^ { 2 } + [ - 3 - ( - 1 ) ] ^ { 2 } } } \\ { = \sqrt { ( 6 ) ^ { 2 } + ( - 3 + 1 ) ^ { 2 } } } \\ { = \sqrt { 36 + ( - 2 ) ^ { 2 } } } \\ { = \sqrt { 36 + 4 } } \\ { = \sqrt{40} } \\ { = 2 \sqrt { 10 } } \end{array}\)
Малюнок\(\PageIndex{5}\)	Окуляри:\((2,-1)\) і\((3,2)\) \(\begin{array} { l } { b = \sqrt { ( 3 - 2 ) ^ { 2 } + [ 2 - ( - 1 ) ] ^ { 2 } } } \\ { = \sqrt { ( 1 ) ^ { 2 } + ( 2 + 1 ) ^ { 2 } } } \\ = \sqrt{1+ (3)^{2}}\\{ = \sqrt { 1 + 9 } } \\ { = \sqrt { 10 } } \end{array}\)
Малюнок\(\PageIndex{6}\)	Окуляри:\((3,2)\) і\((8,-3)\) \(\begin{array} { l } { c = \sqrt { ( 8 - 3 ) ^ { 2 } + ( - 3 - 2 ) ^ { 2 } } } \\ { = \sqrt { ( 5 ) ^ { 2 } + ( - 5 ) ^ { 2 } } } \\ { = \sqrt { 25 + 25 } } \\ { = \sqrt { 50 } } \\ { = 5 \sqrt { 2 } } \end{array}\)

Тепер перевіряємо, чи є\(a ^ { 2 } + b ^ { 2 } = c ^ { 2 }\).

\(\begin{aligned} a ^ { 2 } + b ^ { 2 } & = c ^ { 2 } \\ ( 2 \sqrt { 10 } ) ^ { 2 } + ( \sqrt { 10 } ) ^ { 2 } &= ( 5 \sqrt { 2 } ) ^ { 2 } \\ 4 ( \sqrt { 10 } ) ^ { 2 } + ( \sqrt { 10 } ) ^ { 2 } & = 25 ( \sqrt { 2 } ) ^ { 2 } \\ 4 \cdot 10 + 10 &= 25 \cdot 2 \\ 50 &= 50 \:\:\color{Cerulean}{✓}\end{aligned}\)

Відповідь:

Так, три точки утворюють прямокутний трикутник.

Вправа\(\PageIndex{2}\)

Швидкість транспортного засобу до того, як були застосовані гальма, можна оцінити по довжині слідів занесення, залишених на дорозі. На мокрому бетоні швидкість\(v\) в милі на годину можна оцінити за формулою\(v = 2 \sqrt { 3 d }\), де\(d\) представлена довжина слідів занесення в футах. Оцініть швидкість транспортного засобу перед застосуванням гальм, якщо сліди ковзання залишили позаду вимірюють\(27\) ноги. Округлення до найближчої милі на годину.

Відповідь

\(18\)миль на годину

www.youtube.com/В/8ISCYU3YWQW

Ключові винос

• Щоб спростити радикальний вираз, шукайте фактори радикаі з повноваженнями, які відповідають індексу. Якщо вони виявлені, їх можна спростити, застосувавши продукт і правила частки для радикалів, а також властивість\(\sqrt [ n ] { a ^ { n } } = a\), де\(a\) ненегативне.
• Радикальний вираз спрощується, якщо його радикаі не містить ніяких факторів, які можна записати як досконалі сили індексу.
• Зазвичай ми припускаємо, що всі змінні вирази в межах радикала є невід'ємними. Це дозволяє зосередитися на спрощенні радикалів без технічних проблем, пов'язаних з основним\(n\) коренем. Якщо цього припущення не зробити, ми забезпечимо позитивний результат, використовуючи абсолютні значення при спрощенні радикалів з рівними показниками.

Вправа\(\PageIndex{3}\)

Припустимо, що змінна може представляти будь-яке дійсне число, а потім спростити.

1. \(\sqrt { 9 x ^ { 2 } }\)
2. \(\sqrt { 16 y ^ { 2 } }\)
3. \(\sqrt [ 3 ] { 8 y ^ { 3 } }\)
4. \(\sqrt [ 3 ] { 125 a ^ { 3 } }\)
5. \(\sqrt [ 4 ] { 64 x ^ { 4 } }\)
6. \(\sqrt [ 4 ] { 81 y ^ { 4 } }\)
7. \(\sqrt { 36 a ^ { 4 } }\)
8. \(\sqrt { 100 a ^ { 8 } }\)
9. \(\sqrt { 4 a ^ { 6 } }\)
10. \(\sqrt { a ^ { 10 } }\)
11. \(\sqrt { 18 a ^ { 4 } b ^ { 5 } }\)
12. \(\sqrt { 48 a ^ { 5 } b ^ { 3 } }\)
13. \(\sqrt [ 6 ] { 128 x ^ { 6 } y ^ { 8 } }\)
14. \(\sqrt [ 6 ] { a ^ { 6 } b ^ { 7 } c ^ { 8 } }\)
15. \(\sqrt { ( 5 x - 4 ) ^ { 2 } }\)
16. \(\sqrt { ( 3 x - 5 ) ^ { 4 } }\)
17. \(\sqrt { x ^ { 2 } - 6 x + 9 }\)
18. \(\sqrt { x ^ { 2 } - 10 x + 25 }\)
19. \(\sqrt { 4 x ^ { 2 } + 12 x + 9 }\)
20. \(\sqrt { 9 x ^ { 2 } + 6 x + 1 }\)

Відповідь

1. \(3 | x |\)

3. \(2y\)

5. \(2 | x |\)

7. \(6 a ^ { 2 }\)

9. \(2 \left| a ^ { 3 } \right|\)

11. \(3 a ^ { 2 } b ^ { 2 } \sqrt { 2 b }\)

13. \(2 | x y | \sqrt [ 6 ] { 2 y ^ { 2 } }\)

15. \(| 5 x - 4 |\)

17. \(| x - 3 |\)

19. \(| 2x + 3 |\)

Вправа\(\PageIndex{4}\)

Спростити. (Припустимо, що всі змінні вирази представляють собою позитивні числа.)

1. \(\sqrt { 49 a ^ { 2 } }\)
2. \(\sqrt { 64 b ^ { 2 } }\)
3. \(\sqrt { x ^ { 2 } y ^ { 2 } }\)
4. \(\sqrt { 25 x ^ { 2 } y ^ { 2 } z ^ { 2 } }\)
5. \(\sqrt { 180 x ^ { 3 } }\)
6. \(\sqrt { 150 y ^ { 3 } }\)
7. \(\sqrt { 49 a ^ { 3 } b ^ { 2 } }\)
8. \(\sqrt { 4 a ^ { 4 } b ^ { 3 } c }\)
9. \(\sqrt { 45 x ^ { 5 } y ^ { 3 } }\)
10. \(\sqrt { 50 x ^ { 6 } y ^ { 4 } }\)
11. \(\sqrt { 64 r ^ { 2 } s ^ { 6 } t ^ { 5 } }\)
12. \(\sqrt { 144 r ^ { 8 } s ^ { 6 } t ^ { 2 } }\)
13. \(\sqrt { ( x + 1 ) ^ { 2 } }\)
14. \(\sqrt { ( 2 x + 3 ) ^ { 2 } }\)
15. \(\sqrt { 4 ( 3 x - 1 ) ^ { 2 } }\)
16. \(\sqrt { 9 ( 2 x + 3 ) ^ { 2 } }\)
17. \(\sqrt { \frac { 9 x ^ { 3 } } { 25 y ^ { 2 } } }\)
18. \(\sqrt { \frac { 4 x ^ { 5 } } { 9 y ^ { 4 } } }\)
19. \(\sqrt { \frac { m ^ { 7 } } { 36 n ^ { 4 } } }\)
20. \(\sqrt { \frac { 147 m ^ { 9 } } { n ^ { 6 } } }\)
21. \(\sqrt { \frac { 2 r ^ { 2 } s ^ { 5 } } { 25 t ^ { 4 } } }\)
22. \(\sqrt { \frac { 36 r ^ { 5 } } { s ^ { 2 } t ^ { 6 } } }\)
23. \(\sqrt [ 3 ] { 27 a ^ { 3 } }\)
24. \(\sqrt [ 3 ] { 125 b ^ { 3 } }\)
25. \(\sqrt [ 3 ] { 250 x ^ { 4 } y ^ { 3 } }\)
26. \(\sqrt [ 3 ] { 162 a ^ { 3 } b ^ { 5 } }\)
27. \(\sqrt [ 3 ] { 64 x ^ { 3 } y ^ { 6 } z ^ { 9 } }\)
28. \(\sqrt [ 3 ] { 216 x ^ { 12 } y ^ { 3 } }\)
29. \(\sqrt [ 3 ] { 8 x ^ { 3 } y ^ { 4 } }\)
30. \(\sqrt [ 3 ] { 27 x ^ { 5 } y ^ { 3 } }\)
31. \(\sqrt [ 3 ] { a ^ { 4 } b ^ { 5 } c ^ { 6 } }\)
32. \(\sqrt [ 3 ] { a ^ { 7 } b ^ { 5 } c ^ { 3 } }\)
33. \(\sqrt [ 3 ] { \frac { 8 x ^ { 4 } } { 27 y ^ { 3 } } }\)
34. \(\sqrt [ 3 ] { \frac { x ^ { 5 } } { 125 y ^ { 6 } } }\)
35. \(\sqrt [ 3 ] { 360 r ^ { 5 } s ^ { 12 } t ^ { 13 } }\)
36. \(\sqrt [ 3 ] { 540 r ^ { 3 } s ^ { 2 } t ^ { 9 } }\)
37. \(\sqrt [ 4 ] { 81 x ^ { 4 } }\)
38. \(\sqrt [ 4 ] { x ^ { 4 } y ^ { 4 } }\)
39. \(\sqrt [ 4 ] { 16 x ^ { 4 } y ^ { 8 } }\)
40. \(\sqrt [ 4 ] { 81 x ^ { 12 } y ^ { 4 } }\)
41. \(\sqrt [ 4 ] { a ^ { 4 } b ^ { 5 } c ^ { 6 } }\)
42. \(\sqrt [ 4 ] { 5 ^ { 4 } a ^ { 6 } c ^ { 8 } }\)
43. \(\sqrt [ 4 ] { 128 x ^ { 6 } }\)
44. \(\sqrt [ 4 ] { 243 y ^ { 7 } }\)
45. \(\sqrt [ 5 ] { \frac { 32 m ^ { 10 } } { n ^ { 5 } } }\)
46. \(\sqrt [ 5 ] { \frac { 3 ^ { 7 } m ^ { 9 } } { n ^ { 10 } } }\)
47. \(- 3 \sqrt { 4 x ^ { 2 } }\)
48. \(7 \sqrt { 9 y ^ { 2 } }\)
49. \(- 5 x \sqrt { 4 x ^ { 2 } y }\)
50. \(- 3 y \sqrt { 16 x ^ { 3 } y ^ { 2 } }\)
51. \(12 a b \sqrt { a ^ { 5 } b ^ { 3 } }\)
52. \(6 a ^ { 2 } b \sqrt { 9 a ^ { 7 } b ^ { 2 } }\)
53. \(2 x \sqrt [ 3 ] { 8 x ^ { 6 } }\)
54. \(- 5 x ^ { 2 } \sqrt [ 3 ] { 27 x ^ { 3 } }\)
55. \(2 a b \sqrt [ 3 ] { - 8 a ^ { 4 } b ^ { 5 } }\)
56. \(5 a ^ { 2 } b \sqrt [ 3 ] { - 27 a ^ { 3 } b ^ { 3 } }\)

Відповідь

1. \(7a\)

3. \(xy\)

5. \(6 x \sqrt { 5 x }\)

7. \(7 a b \sqrt { a }\)

9. \(3 x ^ { 2 } y \sqrt { 5 x y }\)

11. \(8 r s ^ { 3 } t ^ { 2 } \sqrt { t }\)

13. \(x + 1\)

15. \(2 ( 3 x - 1 )\)

17. \(\frac { 3 x \sqrt { x } } { 5 y }\)

19. \(\frac { m ^ { 3 } \sqrt { m } } { 6 n ^ { 2 } }\)

21. \(\frac { r s ^ { 2 } \sqrt { 2 s } } { 5 t ^ { 2 } }\)

23. \(3 a\)

25. \(5 x y \sqrt [ 3 ] { 2 x }\)

27. \(4 x y ^ { 2 } z ^ { 3 }\)

29. \(2 x y \sqrt [ 3 ] { y }\)

31. \(a b c ^ { 2 } \sqrt [ 3 ] { a b ^ { 2 } }\)

33. \(\frac { 2 x \sqrt [ 3 ] { x } } { 3 y }\)

35. \(2 r s ^ { 4 } t ^ { 4 } \sqrt [ 3 ] { 45 r ^ { 2 } t }\)

37. \(3 x\)

39. \(2xy^{2}\)

41. \(a b c \sqrt [ 4 ] { b c ^ { 2 } }\)

43. \(2 x \sqrt [ 4 ] { 8 x ^ { 2 } }\)

45. \(\frac { 2 m ^ { 2 } } { n }\)

47. \(-6x\)

49. \(- 10 x ^ { 2 } \sqrt { y }\)

51. \(12 a ^ { 3 } b ^ { 2 } \sqrt { a b }\)

53. \(4 x ^ { 3 }\)

55. \(- 4 a ^ { 2 } b ^ { 2 } \sqrt [ 3 ] { a b ^ { 2 } }\)

Вправа\(\PageIndex{5}\)

Перепишіть наступне як радикальний вираз з коефіцієнтом\(1\).

1. \(3 x \sqrt { 6 x }\)
2. \(5 y \sqrt { 5 y }\)
3. \(a b \sqrt { 10 a }\)
4. \(2 a b ^ { 2 } \sqrt { a }\)
5. \(m ^ { 2 } n \sqrt { m n }\)
6. \(2 m ^ { 2 } n ^ { 3 } \sqrt { 3 n }\)
7. \(2 x \sqrt [ 3 ] { 3 x }\)
8. \(3 y \sqrt [ 3 ] { y ^ { 2 } }\)
9. \(2 y ^ { 2 } \sqrt [ 4 ] { 4 y }\)
10. \(x ^ { 2 } y \sqrt [ 5 ] { 9 x y ^ { 2 } }\)

Відповідь

1. \(\sqrt { 54 x ^ { 3 } }\)

3. \(\sqrt { 10 a ^ { 3 } b ^ { 2 } }\)

5. \(\sqrt { m ^ { 5 } n ^ { 3 } }\)

7. \(\sqrt [ 3 ] { 24 x ^ { 4 } }\)

9. \(\sqrt [ 4 ] { 64 y ^ { 9 } }\)

Вправа\(\PageIndex{6}\)

Період\(T\) в секундах маятника задається за формулою

\(T = 2 \pi \sqrt { \frac { L } { 32 } }\)

де\(L\) являє собою довжину в футах маятника. Обчисліть період, враховуючи кожну з наступних довжин. Дайте точне значення і приблизне значення, округлене до найближчої десятої частки секунди.

1. \(8\)стопи
2. \(32\)стопи
3. \(\frac{1}{2}\)стопа
4. \(\frac{1}{8}\)стопа

Відповідь

1. \(π\)секунди;\(3.1\) секунди

3. \(\frac { \pi } { 4 }\)секунди;\(0.8\) секунди

Вправа\(\PageIndex{7}\)

Час\(t\) у секундах, на який об'єкт знаходиться у вільному падінні, задається формулою

\(t = \frac { \sqrt { s } } { 4 }\)

де\(s\) позначає відстань у футах, на яку впав об'єкт. Обчисліть час, який потрібно об'єкту для падіння, враховуючи кожне з наступних відстаней. Дайте точне значення і приблизне значення, округлене до найближчої десятої частки секунди.

1. \(48\)стопи
2. \(80\)стопи
3. \(192\)стопи
4. \(288\)стопи
5. Швидкість транспортного засобу до того, як були застосовані гальма, можна оцінити по довжині слідів занесення, залишених на дорозі. На сухому тротуарі швидкість\(v\) в милі на годину можна оцінити за формулою\(v = 2 \sqrt { 6 d }\), де\(d\) представлена довжина слідів занесення в футах. Оцініть швидкість транспортного засобу перед застосуванням гальм на сухому тротуарі, якщо сліди ковзання залишили позаду вимірювати\(27\) ноги. Округлення до найближчої милі на годину.
6. \(r\)Радіус сфери можна обчислити за формулою\(r = \frac { \sqrt [ 3 ] { 6 \pi ^ { 2 } V } } { 2 \pi }\), де\(V\) представлений об'єм сфери. Який радіус сфери, якщо обсяг дорівнює\(36π\) кубічним сантиметрам?

Відповідь

1. \(\sqrt{3}\)секунди;\(1.7\) секунди

3. \(2\sqrt{3}\)секунди;\(3.5\) секунди

5. \(25\)миль на годину

Вправа\(\PageIndex{8}\)

Задано функцію знайти\(y\) -intercept

1. \(f ( x ) = \sqrt { x + 12 }\)
2. \(f ( x ) = \sqrt { x + 8 } - 3\)
3. \(f ( x ) = \sqrt [ 3 ] { x - 8 }\)
4. \(f ( x ) = \sqrt [ 3 ] { x + 27 }\)
5. \(f ( x ) = \sqrt [ 3 ] { x + 16 }\)
6. \(f ( x ) = \sqrt [ 3 ] { x + 3 } - 1\)

Відповідь

1. \(( 0,2 \sqrt { 3 } )\)

3. \((0,-2)\)

5. \(( 0,2 \sqrt [ 3 ] { 2 } )\)

Вправа\(\PageIndex{9}\)

Використовуйте формулу відстані, щоб обчислити відстань між заданими двома точками.

1. \((5,-7)\)і\((3,-8)\)
2. \((-9,7)\)і\((-8,4)\)
3. \((-3,-4)\)і\((3,-6)\)
4. \((-5,-2)\)і\((1,-6)\)
5. \((-1,1)\)і\((-4,10)\)
6. \((8,-3)\)і\((2,-12)\)
7. \((0,-6)\)і\((-3,0)\)
8. \((0,0)\)і\((8,-4)\)
9. \(\left( \frac { 1 } { 2 } , - \frac { 1 } { 2 } \right)\)і\(\left( - 1 , \frac { 3 } { 2 } \right)\)
10. \(\left( - \frac { 1 } { 3 } , 2 \right) \)і\(\left( \frac { 5 } { 3 } , - \frac { 2 } { 3 } \right)\)

Відповідь

1. \(\sqrt{5}\)одиниць

3. \(2\sqrt{10}\)одиниць

5. \(3\sqrt{10}\)одиниць

7. \(3\sqrt{5}\)одиниць

9. \(\frac{5}{2}\)одиниць

Вправа\(\PageIndex{10}\)

Визначте, чи три точки утворюють прямокутний трикутник. Використовуйте теорему Піфагора, щоб обґрунтувати свою відповідь.

1. \(( 2 , - 1 ) , ( - 1,2 ) , \text { and } ( 6,3 )\)
2. \(( - 5,2 ) , ( - 1 , - 2 ) , \text { and } ( - 2,5 )\)
3. \(( - 5,0 ) , ( 0,3 ) , \text { and } ( 6 , - 1 )\)
4. \(( - 4 , - 1 ) , ( - 2,5 ) , \text { and } ( 7,2 )\)
5. \(( 1 , - 2 ) , ( 2,3 ) , \text { and } ( - 3,4 )\)
6. \(( - 2,1 ) , ( - 1 , - 1 ) , \text { and } ( 1,3 )\)
7. \(( - 4,0 ) , ( - 2 , - 10 ) , \text { and } ( 3 , - 9 )\)
8. \(( 0,0 ) , ( 2,4 ) , \text { and } ( - 2,6 )\)

Відповідь

1. прямокутний трикутник

3. Чи не прямокутний трикутник

5. прямокутний трикутник

7. прямокутний трикутник

Вправа\(\PageIndex{11}\)

1. Дайте значення для\(x\) такого, що\(\sqrt { x ^ { 2 } } \neq x\). Поясніть, чому важливо припустити, що змінні являють собою невід'ємні числа.
2. Досліджуйте та обговоріть досягнення Крістофа Рудольфа. За що йому зараховують?
3. Що таке сурд, і звідки береться слово?
4. Дослідження способів, за допомогою яких слідчі поліції можуть визначити швидкість руху транспортного засобу після аварії. Поділіться своїми висновками на дошці обговорень.

Відповідь

1. Відповідь може відрізнятися

3. Відповідь може відрізнятися

Виноски

¹⁴ Алгебраїчний вираз, який містить радикали.

¹⁵ Дано дві точки\((x_{1} , y_{1} )\) і\((x_{2}, y_{2})\), обчислити відстань\(d\) між ними за формулою\(d=\sqrt { \left( x _ { 2 } - x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } - y _ { 1 } \right) ^ { 2 } }\).