4.3: Терміни факторингу

Цілі навчання

• Факторні триноміали форми\(x^{2}+bx+c\).
• Факторні триноміали вищого ступеня.
• Факторні триноміали форми\(ax^{2}+bx+c\).
• Факторні триноми за допомогою методу змінного струму.

Факторинг триноміалів, провідний коефіцієнт яких один

(Факторинг Тримінал форми\(x^{2}+bx+c\))

Деякі триноми форми\(x^{2}+bx+c\) можуть враховуватися як добуток біноміалів. Якщо триноміал такого типу факторів, то у нас є:

\(\begin{aligned} x ^ { 2 } + b x + c & = ( x + m ) ( x + n ) \\ & = x ^ { 2 } + n x + m x + m n \\ & = x ^ { 2 } + ( n + m ) x + m n \end{aligned}\)

Це дає нам

\(b=n+m\)і\(c=mn\)

Коротше кажучи, якщо провідним коефіцієнтом факторного триноміала є\(1\), то коефіцієнти останнього члена повинні складати до коефіцієнта середньострокового. Це спостереження є ключем до факторингу триномів за допомогою методики, відомої як метод проб і помилок (або здогадки та перевірки) ¹⁸.

Приклад\(\PageIndex{1}\):

Фактор\(x^{2}+12x+20\).

Рішення

Починаємо з написання двох наборів порожніх дужок. Якщо триноміал цього форм-фактора, то він буде множиться на два лінійних біноміальних множника.

\(x ^ { 2 } + 12 x + 20 = ( \quad ) ( \quad)\)

Запишіть множники першого члена в першому просторі кожного набору дужок. В даному випадку фактор\(x^{2}=x⋅x\).

\(x ^ { 2 } + 12 x + 20 = ( x \quad ) ( x\quad )\)

Визначте фактори останнього члена, сума яких дорівнює коефіцієнту середньострокового. Для цього перерахуйте всі множники\(20\) і знайдіть фактори, сума яких дорівнює\(12\).

\(\begin{aligned} 20 & = 1 \cdot 20 \:\:\rightarrow\:\: 1 + 20 = 21 \\ & =\color{OliveGreen}{ 2 \cdot 10 \:\:\rightarrow\:\: 2 + 10}\color{black}{ =}\color{OliveGreen}{ 12} \\ & = 4 \cdot 5 \:\:\:\:\rightarrow\:\: 4 + 5 = 9 \end{aligned}\)

Вибирайте\(20 = 2 ⋅ 10\) тому, що\(2 + 10 = 12\). Напишіть в останньому семестрі кожного біноміала, використовуючи фактори, визначені на попередньому кроці.

\(x ^ { 2 } + 12 x + 20 = ( x + 2 ) ( x + 10 )\)

Це можна візуально інтерпретувати наступним чином:

Малюнок\(\PageIndex{1}\)

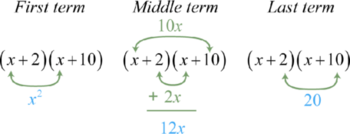
Перевірте, множивши два біноміали.

\(\begin{aligned} ( x + 2 ) ( x + 10 ) & = x ^ { 2 } + 10 x + 2 x + 20 \\ & = x ^ { 2 } + 12 x + 20 \:\:\color{Cerulean}{✓} \end{aligned}\)

Відповідь

\[(x+2)(x+10) \nonumber\]

Оскільки множення є комутативним, порядок факторів не має значення.

\(\begin{aligned} x ^ { 2 } + 12 x + 20 & = ( x + 2 ) ( x + 10 ) \\ & = ( x + 10 ) ( x + 2 ) \end{aligned}\)

Якщо останній член триноміала позитивний, то або обидва постійні фактори повинні бути негативними, або обидва повинні бути позитивними.

Приклад\(\PageIndex{2}\):

Фактор\(x ^ { 2 } y ^ { 2 } - 7 x y + 12\).

Рішення

По-перше, фактор\(x^{2}y^{2}=xy⋅xy\).

\(x ^ { 2 } y ^ { 2 } - 7 x y + 12 = ( x y \quad \color{Cerulean}{?}\color{black}{ )} ( x y \quad\color{Cerulean}{?}\color{black}{ )}\)

Далі шукаємо фактори, сума\(12\) яких дорівнює\(−7\).

\(\begin{aligned} 12 & = 1 \cdot 12 \:\:\rightarrow\:\: - 1 + ( - 12 ) = - 13 \\ & = 2 \cdot 6 \:\:\:\:\rightarrow\:\: - 2 + ( - 6 ) = - 8 \\ & = \color{OliveGreen}{3 \cdot 4\:\:\:\: \rightarrow\:\: - 3 + ( - 4 ) = - 7} \end{aligned}\)

В цьому випадку вибирають\(−3\) і\(−4\) тому, що\((−3)(−4)=+12\) і\(−3+(−4)=−7\).

\(\begin{aligned} x ^ { 2 } y ^ { 2 } - 7 x y + 12 & = ( x y\quad \color{Cerulean}{?}\color{black}{ )} ( x y\quad\color{Cerulean}{ ?}\color{black}{ )} \\ & = ( x y - 3 ) ( x y - 4 ) \end{aligned}\)

Перевірити

\(\begin{aligned} ( x y - 3 ) ( x y - 4 ) & = x ^ { 2 } y ^ { 2 } - 4 x y - 3 x y + 12 \\ & = x ^ { 2 } y ^ { 2 } - 7 x y + 12 \:\:\color{Cerulean}{✓} \end{aligned}\)

Відповідь

\(( x y - 3 ) ( x y - 4 )\)

Якщо останній термін триноміала негативний, то один з його факторів повинен бути негативним.

Приклад\(\PageIndex{3}\):

Фактор:\(x ^ { 2 } - 4 x y - 12 y ^ { 2 }\).

Рішення

Почніть з факторингу першого терміну\(x ^ { 2 } = x \cdot x\).

\(x ^ { 2 } - 4 x y - 12 y ^ { 2 } = \left( \begin{array} { l l } { x } & { \color{Cerulean}{?} } \end{array} \right) \left( \begin{array} { l l } { x } & { \color{Cerulean}{?} } \end{array} \right)\)

Фактори розвитку\(12\) наведені нижче. У цьому прикладі ми шукаємо фактори, сума яких дорівнює\(−4\).

\(\begin{aligned} 12 & = 1 \cdot 12 \:\:\rightarrow\:\: 1 + ( - 12 ) = - 11 \\ & =\color{OliveGreen}{ 2 \cdot 6\:\:\:\: \rightarrow\:\: 2 + ( - 6 ) = - 4} \\ & = 3 \cdot 4\:\:\:\: \rightarrow\:\: 3 + ( - 4 ) = - 1 \end{aligned}\)

Тому коефіцієнт останнього терміну може враховуватися як\(−12=2(−6)\), де\(2+(−6)=−4\). Оскільки останній термін має змінний коефіцієнт\(y^{2}\), використання\(−12y^{2}=2y(−6y)\) та множник триноміального наступним чином:

\(\begin{aligned} x ^ { 2 } - 4 x y - 12 y ^ { 2 } & = ( x \quad \color{Cerulean}{?}\color{black}{ )} ( x \quad \color{Cerulean}{?}\color{black}{ )} \\ & = ( x + 2 y ) ( x - 6 y ) \end{aligned}\)

Помножте, щоб перевірити.

\(\begin{aligned} ( x + 2 y ) ( x - 6 y ) & = x ^ { 2 } - 6 x y + 2 y x - 12 y ^ { 2 } \\ & = x ^ { 2 } - 6 x y + 2 x y - 12 y ^ { 2 } \\ & = x ^ { 2 } - 4 x y - 12 y ^ { 2 } \:\:\color{Cerulean}{✓}\end{aligned}\)

Відповідь

\(( x + 2 y ) ( x - 6 y )\)

Часто наше перше припущення не дасть правильної факторизації. Цей процес може зажадати повторних випробувань. З цієї причини перевірка дуже важлива і не є необов'язковою.

Приклад\(\PageIndex{4}\):

Фактор\(a ^ { 2 } + 10 a - 24\).

Рішення

Перший термін цього триноміалу, фактори\(a^{2}\), як\(a⋅a\).

\(a ^ { 2 } + 10 a - 24 = \left( \begin{array} { l l } { a } & { ? } \end{array} \right) \left( \begin{array} { l l } { a } & { ? } \end{array} \right)\)

Розглянемо фактори\(24\):

\(\begin{aligned} 24 & = 1 \cdot 24 \\ & = \color{OliveGreen}{2 \cdot 12} \\ & = 3 \cdot 8 \\ & = \color{red}{4 \cdot 6} \end{aligned}\)

Припустимо, ми вибираємо фактори\(4\) і\(6\) тому\(4 + 6 = 10\), що коефіцієнт середньострокової. Тоді ми маємо наступну некоректну факторизацію:

\(a ^ { 2 } + 10 a - 24 \stackrel{\color{red}{?}}{\color{black}{=}} ( a + 4 ) ( a + 6 ) \:\:\color{red}{Incorrect\:Factorization}\)

Коли ми множимо, щоб перевірити, ми знаходимо помилку.

\(\begin{aligned} ( a + 4 ) ( a + 6 ) & = a ^ { 2 } + 6 a + 4 a + 24 \\ & = a ^ { 2 } + 10 a \color{red}{+ 24}\:\:\color{red}{✗} \end{aligned}\)

У цьому випадку середній термін є правильним, але останній термін - ні. Так як останній термін в вихідному вираженні негативний, потрібно вибирати фактори, протилежні за знаком. Тому треба спробувати ще раз. Цього разу ми вибираємо фактори\(−2\) і\(12\) тому\(−2+12=10\).

\(a ^ { 2 } + 10 a - 24 = ( a - 2 ) ( a + 12 )\)

Тепер перевірка показує, що ця факторизація правильна.

\(\begin{aligned} ( a - 2 ) ( a + 12 ) & = a ^ { 2 } + 12 a - 2 a - 24 \\ & = a ^ { 2 } + 10 a \color{OliveGreen}{- 24}\:\:\color{Cerulean}{✓} \end{aligned}\)

Відповідь

\(( a - 2 ) ( a + 12 )\)

Якщо ми вибираємо фактори з розумом, то зможемо скоротити значну частину здогадок в цьому процесі. Однак, якщо припущення не є правильним, не турбуйтеся; просто спробуйте інший набір факторів. Майте на увазі, що деякі многочлени є простими. Для прикладу розглянемо триноміал\(x^{2}+3x+20\) і фактори\(20\):

\(\begin{aligned} 20 & = 1 \cdot 20 \\ & = 2 \cdot 10 \\ & = 4 \cdot 5 \end{aligned}\)

Немає факторів, сума\(20\) яких є\(3\). Тому початковий триноміал не може бути врахований як добуток двох біноміалів з цілими коефіцієнтами. Триноміал є простим.

Факторингові триноми вищого ступеня

Ми можемо використовувати техніку проб і помилок для фактора триноміалів вищого ступеня.

Приклад\(\PageIndex{5}\):

Фактор\(x ^ { 4 } + 6 x ^ { 2 } + 5\).

Рішення

Почніть з факторингу першого терміну\(x ^ { 4 } = x ^ { 2 } \cdot x ^ { 2 }\).

\(x ^ { 4 } + 6 x ^ { 2 } + 5 = \left( x ^ { 2 } \quad \color{Cerulean}{?} \right) \left( x ^ { 2 } \quad \color{Cerulean}{?} \right)\)

Так як\(5\) є простим і коефіцієнт середньострокового позитивний, вибирайте\(+1\) і в\(+5\) якості чинників останнього члена.

\(\begin{aligned} x ^ { 4 } + 6 x ^ { 2 } + 5 & = \left( x ^ { 2 } \quad \color{Cerulean}{?} \right) \left( x ^ { 2 } \quad \color{Cerulean}{?} \right) \\ & = \left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } + 5 \right) \end{aligned}\)

Зверніть увагу, що змінна частина середнього терміну є\(x^{2}\) і факторизація перевіряє.

\(\begin{aligned} \left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } + 5 \right) & = x ^ { 4 } + 5 x ^ { 2 } + x ^ { 2 } + 5 \\ & = x ^ { 4 } + 6 x ^ { 2 } + 5\:\:\color{Cerulean}{✓} \end{aligned}\)

Відповідь

\(\left( x ^ { 2 } + 1 \right) \left( x ^ { 2 } + 5 \right)\)

Приклад\(\PageIndex{6}\):

Фактор:\(x ^ { 2 n } + 4 x ^ { n } - 21\) де\(n\) додатне ціле число.

Рішення

Почніть з факторингу першого терміну\(x ^ { 2 n } = x ^ { n } \cdot x ^ { n }\).

\(x ^ { 2 n } + 4 x ^ { n } - 21 = \left( \begin{array} { l l } { x ^ { n } } & { \color{Cerulean}{?} } \end{array} \right) \left( \begin{array} { l l } { x ^ { n } } & {\color{Cerulean}{ ?} } \end{array} \right)\)

Фактор\(- 21 = 7 ( - 3 )\) тому, що\(7 + ( - 3 ) = + 4\) і пишуть

\(\begin{aligned} x ^ { 2 n } + 4 x ^ { n } - 21 & = \left( x ^ { n } \quad \color{Cerulean}{?} \right) \left( x ^ { n } \quad \color{Cerulean}{?} \right) \\ & = \left( x ^ { n } + 7 \right) \left( x ^ { n } - 3 \right) \end{aligned}\)

Відповідь

\[\left( x ^ { n } + 7 \right) \left( x ^ { n } - 3 \right) \nonumber\]

Чек залишається на розгляд зчитувача.

Вправа\(\PageIndex{1}\)

Фактор\(x ^ { 6 } - x ^ { 3 } - 42\).

Відповідь

\[\left( x ^ { 3 } + 6 \right) \left( x ^ { 3 } - 7 \right) \nonumber\]

Факторинг триноміалів, провідний коефіцієнт яких не один

(Факторинг Тримінал форми\(ax^{2}+bx+c\))

Факторинг триноміалів форми\(ax^{2}+bx+c\) може бути складним завданням, оскільки на середньострокову перспективу впливають фактори обох\(a\) і\(c\). Загалом,

\(\begin{aligned} \color{Cerulean}{a}\color{black}{ x} ^ { 2 } + \color{Cerulean}{b}\color{black}{ x} + \color{Cerulean}{c} & = ( p x + m ) ( q x + n ) \\ & = p q x ^ { 2 } + p n x + q m x + m n \\ & = \color{Cerulean}{p q}\color{black}{ x} ^ { 2 } + \color{Cerulean}{( p n + q m ) }\color{black}{x} + \color{Cerulean}{m n} \end{aligned}\)

Це дає нам,

\(a=pq\)і\(b=pn+qm\), де\(c=mn\)

Коротше кажучи, коли провідний коефіцієнт триноміала є чимось іншим\(1\), буде більше уваги при визначенні факторів методом проб і помилок. Ключ полягає в розумінні того, як виходить середній термін. Розмножуємо\((5x+3)(2x+3)\) і уважно стежимо за формуванням середньоріччя.

Малюнок\(\PageIndex{2}\)

Як ми бачили раніше, добуток перших членів кожного біноміала дорівнює першому члену триноміала. Середній член триноміала - це сума добутків зовнішнього і внутрішнього членів біноміалів. Добуток останніх членів кожного біноміала дорівнює останньому члену триноміала. Візуально ми маємо наступне:

Малюнок\(\PageIndex{3}\)

З цієї причини потрібно шукати добуток факторів першого і останнього членів, сума яких дорівнює коефіцієнту середньострокового. Наприклад, щоб фактор\(6x^{2}+29x+35\), подивіться на фактори\(6\) і\(35\).

\(\begin{aligned} 6 & = 1 \cdot 635 = 1 \cdot 35 \\ & = \color{OliveGreen}{2 \cdot 3} \quad \color{black}{=}\color{OliveGreen}{ 5 \cdot 7} \end{aligned}\)

Комбінація, яка виробляє коефіцієнт середнього терміну, є\(2⋅7+3⋅5=14+15=29\). Переконайтеся, що зовнішні члени мають коефіцієнти\(2\) і\(7\), і що внутрішні члени мають коефіцієнти\(5\) і\(3\). Використовуйте цю інформацію, щоб зарахувати тріноміал.

\(\begin{aligned} 6 x ^ { 2 } + 29 x + 35 & = ( 2 x \quad \color{Cerulean}{?}\color{black}{ )} ( 3 x \quad \color{Cerulean}{?}\color{black}{ )} \\ & = ( 2 x + 5 ) ( 3 x + 7 ) \end{aligned}\)

Ми завжди можемо перевірити, множивши; це залишається читачеві.

Приклад\(\PageIndex{7}\)

Фактор\(5 x ^ { 2 } + 16 x y + 3 y ^ { 2 }\).

Рішення

Оскільки провідний коефіцієнт і останній член є простими, існує лише один спосіб коефіцієнта кожного.

\(5=1⋅5\)і\(3=1⋅3\)

Почніть з написання факторів першого члена\(5x^{2}\), наступним чином:

\(5 x ^ { 2 } + 16 x y + 3 y ^ { 2 } = ( x \quad \color{Cerulean}{?} \color{black}{)} ( 5 x \quad \color{Cerulean}{?}\color{black}{ )}\)

Середній і останній термін є позитивними; тому фактори\(3\) вибираються як позитивні числа. При цьому єдиний вибір - в яку угруповання розмістити ці фактори.

\((x+y)(5x+3y)\)або\((x+3y)(5x+y)\)

Визначте, яка групування є правильною, множивши кожен вираз.

\(\begin{aligned} ( x + y ) ( 5 x + 3 y ) & = 5 x ^ { 2 } + 3 x y + 5 x y + 3 y ^ { 2 } \\ & = 5 x ^ { 2 } + 8 x y + 3 y ^ { 2 } x \:\:\color{red}{✗} \\ ( x + 3 y ) ( 5 x + y ) & = 5 x ^ { 2 } + x y + 15 x y + 3 y ^ { 2 } \\ & = 5 x ^ { 2 } + 16 x y + 3 y ^ { 2 } \:\:\color{Cerulean}{✓}\end{aligned}\)

Відповідь

\(( x + 3 y ) ( 5 x + y )\)

Приклад\(\PageIndex{8}\)

Фактор:\(18 a ^ { 2 } b ^ { 2 } - a b - 4\).

Рішення

Спочатку розглянемо фактори коефіцієнтів першого і останнього членів.

\(\begin{aligned} 18 & = 1 \cdot 18\:\quad4 =\color{OliveGreen}{ 1 \cdot 4} \\ & =\color{OliveGreen}{ 2 \cdot 9} \:\:\:\:\:\quad\color{black}{=} 2 \cdot 2 \\ & = 3 \cdot 6 \end{aligned}\)

Ми шукаємо добуток факторів, сума яких дорівнює коефіцієнту середньострокової,\(−1\). Після деякої думки ми можемо побачити, що сума\(8\) і\(−9\) є\(−1\) і комбінація, яка дає це наступним чином:

\(2 ( 4 ) + 9 ( - 1 ) = 8 - 9 = - 1\)

Факторинг починається з цього моменту з двох наборів порожніх дужок.

\(18 a ^ { 2 } b ^ { 2 } - a b - 4 = ( \quad ) (\quad )\)

\(2ab\)Використовують і\(9ab\) як фактори\(18a^{2}b^{2}\).

\(18 a ^ { 2 } b ^ { 2 } - a b - 4 = ( 2 a b \quad \color{Cerulean}{?}\color{black}{ )} \:( 9 a b\quad\color{Cerulean}{ ?}\color{black}{ )}\)

Далі використовуйте фактори\(1\) і\(4\) в правильному порядку, щоб внутрішні і зовнішні вироби були\(−9ab\) і\(8ab\) відповідно.

\(18 a ^ { 2 } b ^ { 2 } - a b - 4 = ( 2 a b - 1 ) ( 9 a b + 4 )\)

Відповідь

\(( 2 a b - 1 ) ( 9 a b + 4 )\). Повна перевірка залишається за зчитувачем.

Це гарна практика, щоб перший фактор з GCF, якщо він є. Роблячи це, виходить триноміальний коефіцієнт з меншими коефіцієнтами. Як ми бачили, триноми з меншими коефіцієнтами вимагають набагато менше зусиль для фактора. Цей часто ігноруваний крок варто визначити рано.

Приклад\(\PageIndex{9}\):

Фактор\(12 y ^ { 3 } - 26 y ^ { 2 } - 10 y\).

Рішення

Почніть з факторингу GCF.

\(12 y ^ { 3 } - 26 y ^ { 2 } - 10 y = 2 y \left( 6 y ^ { 2 } - 13 y - 5 \right)\)

Після\(2y\) факторингу коефіцієнти отриманого триноміала менше і мають менше факторів. Ми можемо враховувати отриманий триноміал, використовуючи\(6=2(3)\) і\(5=(5)(1)\). Зверніть увагу, що ці фактори можуть виробляти двома\(−13\) способами:

\(\begin{array} { l } { 2 ( - 5 ) + 3 ( - 1 ) = - 10 - 3 = - 13 } \\ { 2 ( \color{OliveGreen}{1}\color{black}{ )} + 3 (\color{OliveGreen}{ - 5}\color{black}{ )} = 2 - 15 = - 13 } \end{array}\)

Оскільки останній термін є\(−5\), правильне поєднання вимагає факторів\(1\) і\(5\) бути протилежними ознаками. Тут ми використовуємо\(2(1) = 2\) і\(3(−5) = −15\) тому, що сума є\(−13\) і добуток\((1)(−5) = −5\).

\(\begin{aligned} 12 y ^ { 3 } - 26 y ^ { 2 } - 10 y & = 2 y \left( 6 y ^ { 2 } - 13 y - 5 \right) \\ & = 2 y ( 2 y\quad \color{Cerulean}{?}\color{black}{ )} ( 3 y\quad\color{Cerulean}{ ?}\color{black}{ )} \\ & = 2 y ( 2 y - 5 ) ( 3 y + 1 ) \end{aligned}\)

Перевірка.

\(\begin{aligned} 2 y ( 2 y - 5 ) ( 3 y + 1 ) & = 2 y \left( 6 y ^ { 2 } + 2 y - 15 y - 5 \right) \\ & = 2 y \left( 6 y ^ { 2 } - 13 y - 5 \right) \\ & = 12 y ^ { 3 } - 26 y ^ { 2 } - 10 y\color{Cerulean}{✓} \end{aligned}\)

Фактор\(2y\) є частиною факторної форми вихідного виразу; обов'язково включіть його у відповідь.

Відповідь

\(2 y ( 2 y - 5 ) ( 3 y + 1 )\)

Хорошою практикою є послідовна робота з триноми, де провідний коефіцієнт є позитивним. Якщо провідний коефіцієнт негативний, розрахуйте його разом з будь-яким GCF. Зверніть увагу, що іноді фактор буде\(−1\).

Приклад\(\PageIndex{10}\)

Фактор:\(- 18 x ^ { 6 } - 69 x ^ { 4 } + 12 x ^ { 2 }\).

Рішення

У цьому прикладі GCF є\(3x^{2}\). Оскільки провідний коефіцієнт негативний, ми починаємо з факторингу\(−3x^{2}\).

\(- 18 x ^ { 6 } - 69 x ^ { 4 } + 12 x ^ { 2 } = - 3 x ^ { 2 } \left( 6 x ^ { 4 } + 23 x ^ { 2 } - 4 \right)\)

На цьому етапі вважайте решту тріноміалу, як зазвичай, не забуваючи написати\(−3x^{2}\) як фактор остаточної відповіді. Використовувати\(6 = 1(6)\) і\(−4 = 4(−1) \) тому\(1(−1)+6(4)=23\). Тому,

\(\begin{aligned} - 18 x ^ { 6 } - 69 x ^ { 4 } + 12 x ^ { 2 } & = - 3 x ^ { 2 } \left( 6 x ^ { 4 } + 23 x ^ { 2 } - 4 \right) \\ & = - 3 x ^ { 2 } \left( x ^ { 2\quad } \right) \left( 6 x ^ { 2 }\quad \right) \\ & = - 3 x ^ { 2 } \left( x ^ { 2 } + 4 \right) \left( 6 x ^ { 2 } - 1 \right) \end{aligned}\)

Відповідь

\(- 3 x ^ { 2 } \left( x ^ { 2 } + 4 \right) \left( 6 x ^ { 2 } - 1 \right)\). Чек залишається на розгляд зчитувача.

Вправа\(\PageIndex{2}\)

Фактор:\(- 12 a ^ { 5 } b + a ^ { 3 } b ^ { 3 } + a b ^ { 5 }\).

Відповідь

\(- a b \left( 3 a ^ { 2 } - b ^ { 2 } \right) \left( 4 a ^ { 2 } + b ^ { 2 } \right)\)

www.youtube.com/В/АІГКУУТБК 4

Факторинг з використанням методу змінного струму

Альтернативний метод факторингу триномів, який називається методом AC ¹⁹, використовує метод групування для факторингу чотиричленних поліномів. Якщо триноміал у формі\(ax^{2}+bx+c\) може бути врахований, то середній член\(bx\), може бути замінений двома долями з коефіцієнтами, сума яких дорівнює\(b\) і добуток\(ac\). Ця заміна призводить до еквівалентного виразу з чотирма термінами, які можуть бути враховані шляхом групування.

Приклад\(\PageIndex{11}\):

Фактор за допомогою методу змінного струму:\(18 x ^ { 2 } - 31 x + 6\).

Рішення

Ось\(a=18, b=-31\), і\(c=6\).

\(\begin{aligned} a c & = 18 ( 6 ) \\ & = 108 \end{aligned}\)

Фактор\(108\), і пошук факторів, сума яких є\(−31\).

\ почати {вирівняний} 108 & = - 1 (- 108)\\ & = - 2 (- 54)\\ & = - 3 (- 36)\\ & =\ колір {оливково-зелений} {- 4 (- 27)}\ колір {✓}\\ &\ колір {чорний} {=} - 6 (- 18)\\ & = - 9 (- 12)\\\\ колір {чорний} {=} - 6 (- 18)\ & = - 9 (- 12)\\\\ кінець}

При цьому сума коефіцієнтів\(−27\) і\(−4\) дорівнює середньому коефіцієнту,\(−31\). Тому\(−31x=−27x−4x\), і ми можемо написати

\(18 x ^ { 2 } \color{OliveGreen}{- 31 x}\color{black}{ +} 6 = 18 x ^ { 2 } \color{OliveGreen}{- 27 x - 4 x}\color{black}{ +} 6\)

Фактор еквівалентного виразу за групуванням.

\(\begin{aligned} 18 x ^ { 2 } - 31 x + 6 & = 18 x ^ { 2 } - 27 x - 4 x + 6 \\ & = 9 x ( 2 x - 3 ) - 2 ( 2 x - 3 ) \\ & = ( 2 x - 3 ) ( 9 x - 2 ) \end{aligned}\)

Відповідь

\(( 2 x - 3 ) ( 9 x - 2 )\)

Приклад\(\PageIndex{12}\):

Фактор за допомогою методу змінного струму:\(4 x ^ { 2 } y ^ { 2 } - 7 x y - 15\).

Рішення

Ось\(a=4, b= -7\), і\(c=-15\).

\(\begin{aligned} a c & = 4 ( - 15 ) \\ & = - 60 \end{aligned}\)

Фактор\(−60\) і пошук факторів, сума яких є\(−7\).

\(\begin{aligned} - 60 & = 1 ( - 60 ) \\ & = 2 ( - 30 ) \\ & = 3 ( - 20 ) \\ & = 4 ( - 15 ) \\ & = \color{OliveGreen}{5 ( - 12 )}\:\:\color{Cerulean}{✓} \\ & = 6 ( - 10 ) \end{aligned}\)

Сума множників\(5\) і\(−12\) дорівнює середньому коефіцієнту,\(−7\). \(−7xy\)Замінити на\(5xy−12xy\).

\(\begin{aligned} 4 x ^ { 2 } y ^ { 2 } - 7 x y - 15 & = 4 x ^ { 2 } y ^ { 2 } + 5 x y - 12 x y - 15\quad\color{Cerulean}{Factor\:by\:grouping.} \\ & = x y ( 4 x y + 5 ) - 3 ( 4 x y + 5 ) \\ & = ( 4 x y + 5 ) ( x y - 3 ) \end{aligned}\)

Відповідь

\[( 4 x y + 5 ) ( x y - 3 ).\]

Чек залишається на розгляд зчитувача.

Якщо фактори\(ac\) не можуть бути знайдені для додавання,\(b\) то триноміал є простим.

Ключові винос

• Якщо триноміал\(x^{2}+bx+c\) форм-факторів у добуток двох біноміалів, то коефіцієнт середнього члена - це сума множників останнього члена.
• Якщо триноміал\(ax^{2}+bx+c\) форм-факторів в добуток двох біноміалів, то коефіцієнт середньострокового буде сумою певних добутків факторів першого і останнього членів.
• Якщо триноміал має найбільший загальний фактор, то це найкраща практика, щоб спочатку вивести GCF, перш ніж намагатися перерахувати його в добуток біноміалів.
• Якщо провідний коефіцієнт триноміала є негативним, то це найкраща практика спочатку фактор, що негативний фактор, перш ніж намагатися фактор триноміалу.
• Факторинг є одним з найбільш важливих навичок, необхідних в алгебрі. З цієї причини ви повинні практикувати роботу стільки проблем, скільки потрібно, щоб стати досвідченим.

Вправа\(\PageIndex{3}\)

Фактор.

1. \(x ^ { 2 } + 5 x - 6\)
2. \(x ^ { 2 } + 5 x + 6\)
3. \(x ^ { 2 } + 4 x - 12\)
4. \(x ^ { 2 } + 3 x - 18\)
5. \(x ^ { 2 } - 14 x + 48\)
6. \(x ^ { 2 } - 15 x + 54\)
7. \(x ^ { 2 } + 11 x - 30\)
8. \(x ^ { 2 } - 2 x + 24\)
9. \(x ^ { 2 } - 18 x + 81\)
10. \(x ^ { 2 } - 22 x + 121\)
11. \(x ^ { 2 } - x y - 20 y ^ { 2 }\)
12. \(x ^ { 2 } + 10 x y + 9 y ^ { 2 }\)
13. \(x ^ { 2 } y ^ { 2 } + 5 x y - 50\)
14. \(x ^ { 2 } y ^ { 2 } - 16 x y + 48\)
15. \(a ^ { 2 } - 6 a b - 72 b ^ { 2 }\)
16. \(a ^ { 2 } - 21 a b + 80 b ^ { 2 }\)
17. \(u ^ { 2 } + 14 u v - 32 v ^ { 2 }\)
18. \(m ^ { 2 } + 7 m n - 98 n ^ { 2 }\)
19. \(( x + y ) ^ { 2 } - 2 ( x + y ) - 8\)
20. \(( x - y ) ^ { 2 } - 2 ( x - y ) - 15\)
21. \(x ^ { 4 } - 7 x ^ { 2 } - 8\)
22. \(x ^ { 4 } + 13 x ^ { 2 } + 30\)
23. \(x ^ { 4 } - 8 x ^ { 2 } - 48\)
24. \(x ^ { 4 } + 25 x ^ { 2 } + 24\)
25. \(y ^ { 4 } - 20 y ^ { 2 } + 100\)
26. \(y ^ { 4 } + 14 y ^ { 2 } + 49\)
27. \(x ^ { 4 } + 3 x ^ { 2 } y ^ { 2 } + 2 y ^ { 4 }\)
28. \(x ^ { 4 } - 8 x ^ { 2 } y ^ { 2 } + 15 y ^ { 4 }\)
29. \(a ^ { 4 } b ^ { 4 } - 4 a ^ { 2 } b ^ { 2 } + 4\)
30. \(a ^ { 4 } + 6 a ^ { 2 } b ^ { 2 } + 9 b ^ { 4 }\)
31. \(x ^ { 6 } - 18 x ^ { 3 } - 40\)
32. \(x ^ { 6 } + 18 x ^ { 3 } + 45\)
33. \(x ^ { 6 } - x ^ { 3 } y ^ { 3 } - 6 y ^ { 6 }\)
34. \(x ^ { 6 } + x ^ { 3 } y ^ { 3 } - 20 y ^ { 6 }\)
35. \(x ^ { 6 } y ^ { 6 } + 2 x ^ { 3 } y ^ { 3 } - 15\)
36. \(x ^ { 6 } y ^ { 6 } + 16 x ^ { 3 } y ^ { 3 } + 48\)
37. \(x ^ { 2 n } + 12 x ^ { n } + 32\)
38. \(x ^ { 2 n } + 41 x ^ { n } + 40\)
39. \(x ^ { 2 n } + 2 a x ^ { n } + a ^ { 2 }\)
40. \(x ^ { 2 n } - 2 a x ^ { n } + a ^ { 2 }\)

Відповідь

1. \(( x - 1 ) ( x + 6 )\)

3. \(( x - 2 ) ( x + 6 )\)

5. \(( x - 6 ) ( x - 8 )\)

7. Прем'єр

9. \(( x - 9 ) ^ { 2 }\)

11. \(( x - 5 y ) ( x + 4 y )\)

13. \(( x y - 5 ) ( x y + 10 )\)

15. \(( a + 6 b ) ( a - 12 b )\)

17. \(( u - 2 v ) ( u + 16 v )\)

19. \(( x + y - 4 ) ( x + y + 2 )\)

21. \(\left( x ^ { 2 } - 8 \right) \left( x ^ { 2 } + 1 \right)\)

23. \(\left( x ^ { 2 } + 4 \right) \left( x ^ { 2 } - 12 \right)\)

25. \(\left( y ^ { 2 } - 10 \right) ^ { 2 }\)

27. \(\left( x ^ { 2 } + y ^ { 2 } \right) \left( x ^ { 2 } + 2 y ^ { 2 } \right)\)

29. \(\left( a ^ { 2 } b ^ { 2 } - 2 \right) ^ { 2 }\)

31. \(\left( x ^ { 3 } - 20 \right) \left( x ^ { 3 } + 2 \right)\)

33. \(\left( x ^ { 3 } + 2 y ^ { 3 } \right) \left( x ^ { 3 } - 3 y ^ { 3 } \right)\)

35. \(\left( x ^ { 3 } y ^ { 3 } - 3 \right) \left( x ^ { 3 } y ^ { 3 } + 5 \right)\)

37. \(\left( x ^ { n } + 4 \right) \left( x ^ { n } + 8 \right)\)

39. \(\left( x ^ { n } + a \right) ^ { 2 }\)

Вправа\(\PageIndex{4}\)

Фактор.

1. \(3 x ^ { 2 } + 20 x - 7\)
2. \(2 x ^ { 2 } - 9 x - 5\)
3. \(6 a ^ { 2 } + 13 a + 6\)
4. \(4 a ^ { 2 } + 11 a + 6\)
5. \(6 x ^ { 2 } + 7 x - 10\)
6. \(4 x ^ { 2 } - 25 x + 6\)
7. \(24 y ^ { 2 } - 35 y + 4\)
8. \(10 y ^ { 2 } - 23 y + 12\)
9. \(14 x ^ { 2 } - 11 x + 9\)
10. \(9 x ^ { 2 } + 6 x + 8\)
11. \(4 x ^ { 2 } - 28 x + 49\)
12. \(36 x ^ { 2 } - 60 x + 25\)
13. \(27 x ^ { 2 } - 6 x - 8\)
14. \(24 x ^ { 2 } + 17 x - 20\)
15. \(6 x ^ { 2 } + 23 x y - 4 y ^ { 2 }\)
16. \(10 x ^ { 2 } - 21 x y - 27 y ^ { 2 }\)
17. \(8 a ^ { 2 } b ^ { 2 } - 18 a b + 9\)
18. \(12 a ^ { 2 } b ^ { 2 } - a b - 20\)
19. \(8 u ^ { 2 } - 26 u v + 15 v ^ { 2 }\)
20. \(24 m ^ { 2 } - 26 m n + 5 n ^ { 2 }\)
21. \(4 a ^ { 2 } - 12 a b + 9 b ^ { 2 }\)
22. \(16 a ^ { 2 } + 40 a b + 25 b ^ { 2 }\)
23. \(5 ( x + y ) ^ { 2 } - 9 ( x + y ) + 4\)
24. \(7 ( x - y ) ^ { 2 } + 15 ( x - y ) - 18\)
25. \(7 x ^ { 4 } - 22 x ^ { 2 } + 3\)
26. \(5 x ^ { 4 } - 41 x ^ { 2 } + 8\)
27. \(4 y ^ { 6 } - 3 y ^ { 3 } - 10\)
28. \(12 y ^ { 6 } + 4 y ^ { 3 } - 5\)
29. \(5 a ^ { 4 } b ^ { 4 } - a ^ { 2 } b ^ { 2 } - 18\)
30. \(21 a ^ { 4 } b ^ { 4 } + 5 a ^ { 2 } b ^ { 2 } - 4\)
31. \(6 x ^ { 6 } y ^ { 6 } + 17 x ^ { 3 } y ^ { 3 } + 10\)
32. \(16 x ^ { 6 } y ^ { 6 } + 46 x ^ { 3 } y ^ { 3 } + 15\)
33. \(8 x ^ { 2 n } - 10 x ^ { n } - 25\)
34. \(30 x ^ { 2 n } - 11 x ^ { n } - 6\)
35. \(36 x ^ { 2 n } + 12 a x ^ { n } + a ^ { 2 }\)
36. \(9 x ^ { 2 n } - 12 a x ^ { n } + 4 a ^ { 2 }\)
37. \(- 3 x ^ { 2 } + 14 x + 5\)
38. \(- 2 x ^ { 2 } + 13 x - 20\)
39. \(- x ^ { 2 } - 10 x + 24\)
40. \(- x ^ { 2 } + 8 x + 48\)
41. \(54 - 12 x - 2 x ^ { 2 }\)
42. \(60 + 5 x - 5 x ^ { 2 }\)
43. \(4 x ^ { 3 } + 16 x ^ { 2 } + 20 x\)
44. \(2 x ^ { 4 } - 12 x ^ { 3 } + 14 x ^ { 2 }\)
45. \(2 x ^ { 3 } - 8 x ^ { 2 } y - 24 x y ^ { 2 }\)
46. \(6 x ^ { 3 } - 9 x ^ { 2 } y - 6 x y ^ { 2 }\)
47. \(4 a ^ { 3 } b - 4 a ^ { 2 } b ^ { 2 } - 24 a b ^ { 3 }\)
48. \(15 a ^ { 4 } b - 33 a ^ { 3 } b ^ { 2 } + 6 a ^ { 2 } b ^ { 3 }\)
49. \(3 x ^ { 5 } y + 30 x ^ { 3 } y ^ { 3 } + 75 x y ^ { 5 }\)
50. \(45 x ^ { 5 } y ^ { 2 } - 60 x ^ { 3 } y ^ { 4 } + 20 x y ^ { 6 }\)

Відповідь

1. \(( 3 x - 1 ) ( x + 7 )\)

3. \(( 2 a + 3 ) ( 3 a + 2 )\)

5. \(( 6 x - 5 ) ( x + 2 )\)

7. \(( 8 y - 1 ) ( 3 y - 4 )\)

9. Прем'єр

11. \(( 2 x - 7 ) ^ { 2 }\)

13. \(( 9 x + 4 ) ( 3 x - 2 )\)

15. \(( 6 x - y ) ( x + 4 y )\)

17. \(( 4 a b - 3 ) ( 2 a b - 3 )\)

19. \(( 2 u - 5 v ) ( 4 u - 3 v )\)

21. \(( 2 a - 3 b ) ^ { 2 }\)

23. \(( x + y - 1 ) ( 5 x + 5 y - 4 )\)

25. \(\left( x ^ { 2 } - 3 \right) \left( 7 x ^ { 2 } - 1 \right)\)

27. \(\left( y ^ { 3 } - 2 \right) \left( 4 y ^ { 3 } + 5 \right)\)

29. \(\left( a ^ { 2 } b ^ { 2 } - 2 \right) \left( 5 a ^ { 2 } b ^ { 2 } + 9 \right)\)

31. \(\left( 6 x ^ { 3 } y ^ { 3 } + 5 \right) \left( x ^ { 3 } y ^ { 3 } + 2 \right)\)

33. \(\left( 2 x ^ { n } - 5 \right) \left( 4 x ^ { n } + 5 \right)\)

35. \(\left( 6 x ^ { n } + a \right) ^ { 2 }\)

37. \(- ( x - 5 ) ( 3 x + 1 )\)

39. \(- ( x - 2 ) ( x + 12 )\)

41. \(- 2 ( x - 3 ) ( x + 9 )\)

43. \(4 x \left( x ^ { 2 } + 4 x + 5 \right)\)

45. \(2 x ( x + 2 y ) ( x - 6 y )\)

47. \(4 a b ( a - 3 b ) ( a + 2 b )\)

49. \(3 x y \left( x ^ { 2 } + 5 y ^ { 2 } \right) ^ { 2 }\)

Вправа\(\PageIndex{5}\)

Фактор.

1. \(4 - 25 x ^ { 2 }\)
2. \(8 x ^ { 3 } - y ^ { 3 }\)
3. \(9 x ^ { 2 } - 12 x y + 4 y ^ { 2 }\)
4. \(30 a ^ { 2 } - 57 a b - 6 b ^ { 2 }\)
5. \(10 a ^ { 2 } - 5 a - 6 a b + 3 b\)
6. \(3 x ^ { 3 } - 4 x ^ { 2 } + 9 x - 12\)
7. \(x ^ { 2 } + 4 y ^ { 2 }\)
8. \(x ^ { 2 } - x + 2\)
9. \(15 a ^ { 3 } b ^ { 2 } + 6 a ^ { 2 } b ^ { 3 } - 3 a b ^ { 4 }\)
10. \(54 x ^ { 2 } - 63 x\)

Відповідь

1. \(( 2 - 5 x ) ( 2 + 5 x )\)

3. \(( 3 x - 2 y ) ^ { 2 }\)

5. \(( 2 a - 1 ) ( 5 a - 3 b )\)

7. Прем'єр

9. \(3 a b ^ { 2 } \left( 5 a ^ { 2 } + 2 a b - b ^ { 2 } \right)\)

Вправа\(\PageIndex{6}\)

1. Створіть свій власний триноміал форми\(ax^{2} + bx + c\), що чинники. Поділіться ним разом з рішенням на дошці обговорень.
2. Створіть тріноміал форми\(ax^{2} + bx + c\), яка не впливає на фактор, і поділіть його разом з причиною, чому він не фактор.

Відповідь

1. Відповідь може відрізнятися

Виноски

¹⁸ Описано метод факторингу триноміала шляхом систематичної перевірки факторів, щоб побачити, чи є їх продукт вихідним триноміалом.

¹⁹ Метод, який використовується для факторингу триноміалів шляхом заміни середнього члена двома термінами, які дозволяють множити результуючий чотиричленний многочлен шляхом групування.