1.2: Факторинг

Last updated
Save as PDF

Page ID: 58885

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі будуть розглянуті три найпоширеніші види факторингу - факторинг найбільшого спільного фактора, факторинг Триноміальний та факторинг різниці квадратів.

Найбільший загальний фактор

Факторинг найбільшого загального фактора по суті скасовує розподільне множення, яке часто зустрічається в математичних виразах. Цей фактор може бути мономіальним або поліноміальним, але в цих прикладах ми розглянемо мономіальні загальні фактори.

При$3 x y^{2}(5 x-2 y)=15 x^{2} y^{2}-6 x y^{3}$ множенні мономіальний член$3 x y^{2}$ множиться або розподіляється на обидва члени всередині дужок. Процес факторизації скасовує це множення.

Приклад$\PageIndex{1}$

Фактор

\[7 x^{2}+14 x \nonumber\]

Рішення

Цей вислів має два терміни. Коефіцієнти поділяють загальний коефіцієнт 7 і єдина змінна, яка бере участь в цьому виразі, є$x$. Найвища сила змінної, яка поділяється обома термінами, полягає в$x^{1},$ тому, що це сила$x$, яка може бути врахована з обох термінів. Найбільшим поширеним фактором є$7 x$

\[7 x^{2}+14 x=7 x(x+2) \nonumber\]

Не потрібно відразу знаходити найбільший спільний фактор. У більш складних завданнях факторинг може здійснюватися шматками, подібними за модою до зменшення фракцій.

Приклад$\PageIndex{2}$

Фактор

\[42 x^{2} y^{6}+98 x y^{3}-210 x^{3} y^{2} \nonumber\]

Рішення

Цей вислів має три терміни. Не відразу зрозуміло, що найбільший загальний коефіцієнт коефіцієнтів, але всі вони парні числа, так що ми могли б принаймні розділити їх усіх$2 .$ на$98 x y^{3}$ Термін має$x^{1},$ що означає, що це найвища сила$x$, що ми могли б фактор з усіх термінів. The$210 x^{3} y^{2}$ має,$y^{2},$ яка є найвищою силою$y$, що може бути врахована з усіх термінів. Таким чином, ми можемо принаймні приступити до цих факторів:

\ [\ почати {вирівняний}
42 x^ {2} y^ {6} +98 x y^ {3} -210 x^ {3} y^ {2} &=2 x y^ {2} * 21 x y^ {4} +2 х y^ {2} * 49 y-2 x y^ {2} * 105 x^ {2}\ &=2 x y^ {
2}\ &=2 x y^ {2} x y^ {4} +49 y-105 x^ {2}\ праворуч)
\ кінець {вирівняний}\]

Зараз ми не дуже намагалися знайти найбільший спільний фактор на початку цієї проблеми, тому важливо продовжувати ставити під сумнів, чи є якісь інші загальні фактори. 21 і 49 чітко поділяють загальний фактор,$7,$ тому було б сенс побачити, чи$105$ ділиться на$7$ також. Якщо ми$7,$ ділимо$105$ на ми бачимо, що$105=7^{*} 15 .$ Таким чином, ми можемо також перерахувати загальний фактор$7$ з інших членів в дужках.

\ [\ почати {вирівняний}
2 х y^ {2}\ ліворуч (21 x y^ {4} +49 y-105 x^ {2}\ праворуч) &= 2 x y^ {2}\ ліворуч (7* 3 x y^ {4} +7 y-7* 15 x^ {2}\ праворуч)\\
&=7 * 2 х y^ {2}\ ліворуч (3 x y^ {4}} +7 y-15 x^ {2}\ праворуч)\\
&=14 x y^ {2}\ ліворуч (3 x y^ {4} +7 y-15 x^ {2}\ праворуч)
\ кінець {вирівняний }\]

Триміальний факторинг$(a=1)$

Триноміальний факторинг скасовує множення двох біноміалів, і він поставляється в двох смаках - простому і складному. Найпростіша форма триноміального факторингу передбачає триноміальний вираз у вигляді,$a x^{2}+b x+c$ в якому значення$a$ дорівнює 1. Це робить задачу факторизації простішою, ніж якщо значення не$a$ дорівнює 1.

Приклад$\PageIndex{3}$

Фактор$x^{2}+7 x+10$

рішення

У цьому прикладі значення$a$ є,$1,$ що робить цей тип триноміального факторингу трохи менш складним, ніж це було б інакше. Незалежно від того, чи$a$ є значення 1 фундаментальним питанням, що регулює цей тип факторингу, є$+$ або$-$ ознакою постійного терміну. У цій задачі постійний термін позитивний. Це означає, що нам потрібно знайти фактори 10, які складаються до$7 .$ Це відносно просто:

\[ x^{2}+7 x+10=(x+2)(x+5) \nonumber \]

Проблема супутника до цього є$x^{2}-7 x+10$. Зверніть увагу, що в цьому випадку знак постійного члена все ще позитивний, а це означає, що нам все ще потрібні множники 10, які складаються до$7 .$ Це означає, що нам все ще потрібно використовувати 2 і$5 .$ Однак у цьому випадку замість +10 виробляється з множення (+2) (+5) це результат множення$(-2)(-5) .$ Це те, що робить 7 у другому прикладі негативним:

\[x^{2}-7 x+10=(x-2)(x-5) \nonumber\]

Приклад$\PageIndex{4}$

Фактор$x^{2}+3 x-10$

Рішення

В цьому випадку ознака постійного терміна негативний. Це означає, що нам потрібно знайти фактори 10, які мають різницю$3 .$ Це все ще 5 і 2.

\[x^{2}+3 x-10=(x-2)(x+5) \nonumber\]

Множення на (-2) і (+5) виробляють (-10) і той факт, що 2 і 5 мають протилежні ознаки створює різницю, яка дає нам$(+3) .$ Супутник проблеми до цього є$x^{2}-3 x-10$. У цьому випадку знак постійного члена все ще негативний, що означає, що нам все ще потрібні множники 10, які мають різницю$3 .$ Це означає, що нам все ще потрібно використовувати 2 і$5 .$ Однак в цьому випадку замість (+3) як коефіцієнт середнього члена, нам знадобиться (-3). Для цього ми просто скасовуємо знаки 2 і 5 від попередньої проблеми:

\[x^{2}-3 x-10=(x+2)(x-5) \nonumber\]

Тепер (+2) (-5) дає нам,$(-10),$ але$+2 x-5 x$ дає нам$(-3 x)$ замість$(+3 x)$.

Приклад$\PageIndex{5}$

Фактор$x^{2}+11 x-42$

Рішення

У цій задачі ознака постійного терміна негативний. Це означає, що нам потрібні фактори 42, які мають різницю Систематичне дослідження всіх пар факторів 42 може допомогти нам знайти правильну пару:
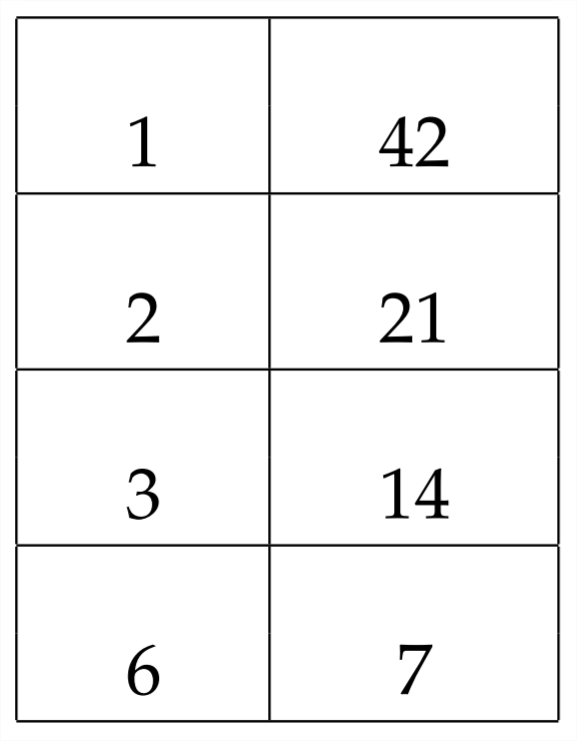
$clipboard_e7b7dee5ac08dff1325ea6137d420e944.png$
Тут ми бачимо, що фактори 3 і 14 мають різницю$11 .$ Це означає, що ми будемо використовувати$11 .$ ці фактори в нашій відповіді:$(x \quad 3)(x$
14). Визначаючи, як розмістити$-$ знаки$+$ і в дужках, ми можемо повернутися до початкової проблеми:$x^{2}+11 x-42 .$ Якщо ми хочемо різниці,$(+11 x),$ то нам потрібно буде мати$a(+14)$ і$a(-3)$

\[x^{2}+11 x-42=(x-3)(x+14) \nonumber\]

Приклад$\PageIndex{6}$

Фактор$x^{2}+28 x+96$

Рішення

У цій задачі знак постійного терміна позитивний. Це означає, що нам потрібні фактори 96, які складаються до$28 .$ Систематичне дослідження всіх пар факторів 96 може допомогти нам знайти правильну пару:
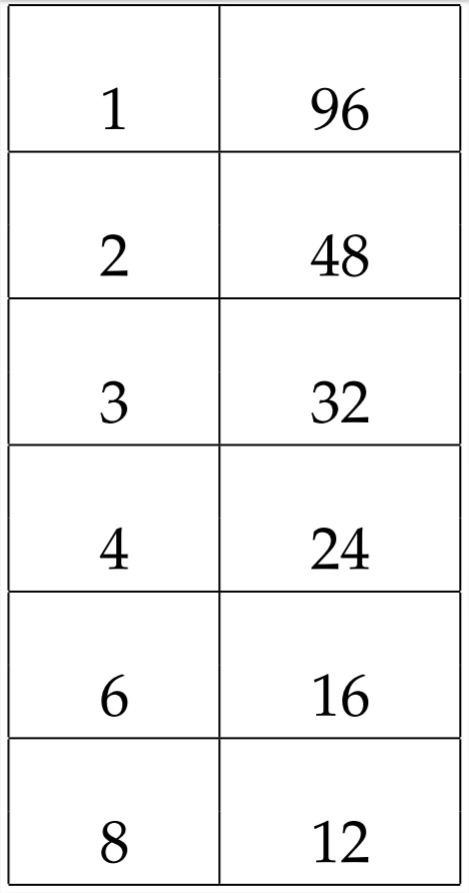
$clipboard_eb08a7c15defb2eafbec448582cd21da7.png$
Тут ми бачимо, що фактори 4 і 24 складаються до$28 .$ Це означає, що ми будемо використовувати ці фактори в нашому відповідь:$(x \quad 4)(x \quad 24) .$ Визначаючи, як розмістити$-$ знаки$+$ та в дужках, ми можемо повернутися до початкової проблеми:

$x^{2}+28 x+96 .$Якщо ми хочемо, щоб 4 і 24 додавалися,$(+28),$ то вони обидва повинні бути позитивними:

\[x^{2}+28 x+96=(x+4)(x+24) \nonumber\]

При побудові графіків пар факторів у попередніх двох задачах нічого складнішого, ніж поділ постійного члена на числа$1,2,3,4,5,6, \dots$ і так далі, може допомогти вам знайти повний список пар множників. Якщо ви не отримуєте ціле число при діленні - наприклад$96 \div 5=19.2,$, це число не входить до списку пар множників.

Триміальний факторинг$(a \neq 1)$

Якщо значення не$a$ є,$1,$ це означає, що, якщо триноміал є факторним, принаймні один з його біноміальних факторів також має коефіцієнт, відмінний від$1 .$ Наприклад:

\[(2 x+7)(x-3)=2 x^{2}+1 x-21 \nonumber\]

Якби ми спробували скасувати це множення через процес триноміального факторингу, ми повинні дивитися на знак постійного члена. В даному прикладі знак негативний. Це все ще означає, що нам потрібно буде знайти пари факторів, які виробляють різницю$(+1 x)$ як середнього терміну. Однак у цьому сценарії не просто фактори 21 беруть участь у виробництві,$(+1 x),$ а поєднання факторів 21 та факторів провідного коефіцієнта$2 .$ Середній термін$(+1 x)$ походить від множення$(2 x)(-3)$ та множення (+7) $(+1 x)$

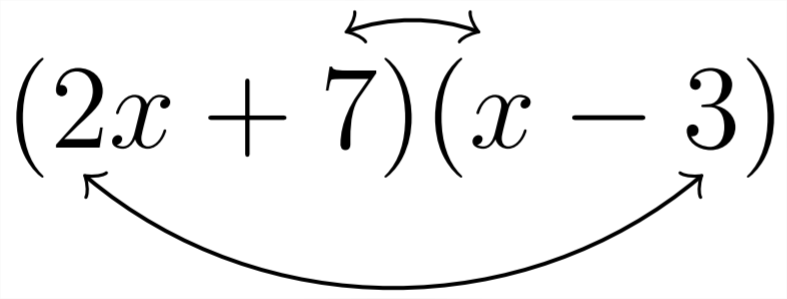
$clipboard_eb1f844b6aa6087ff8d767d80ec92e070.png$

\ [
\ почати {вирівняний}
(2 x+7) (x-3) &=2 x^ {2} -6 x+7 x-21\
&=2 x^ {2} +x-21
\ кінець {вирівняний}
\]

Намагаючись фактор триноміального подібного$2 x^{2}+x-21$, ми повинні взяти це до уваги. Наприклад, якби ми мали фактор$3 x^{2}-10 x+8$, ми повинні спочатку все ж подивитися на знак постійного терміна, який, в даному випадку, є позитивним. Це означає, що ми хочемо факторні пари, які будуть складатися до$10 .$ Але ми повинні враховувати взаємодію факторів 3 з факторами 3 є простим числом, а це означає, що у нас немає вибору - його можна розділити лише на$3 * 1,$ так що ми можемо почати:$8 .$

\[\text { Factor } 3 x^{2}+10 x+8\]

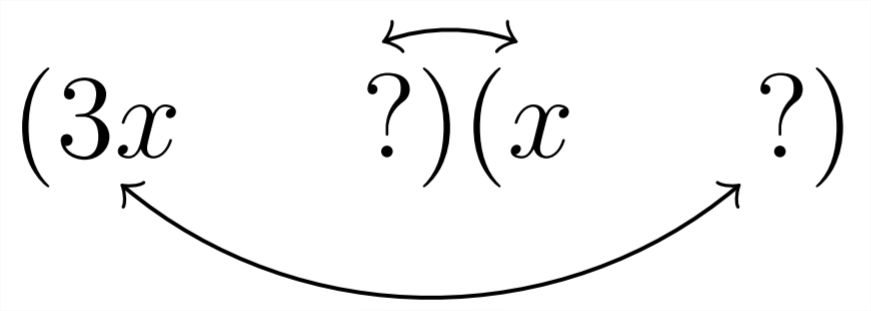
$clipboard_eaaf5bf5e8c72fb3fa21e5c9fcfe12b32.png$
Наші варіанти заповнення знаків питання будуть виходити з факторів 8,$8 * 1$ або$4 * 2 .$ Процес методом проб і помилок:

$clipboard_eeecd7bde9383df2bcfde3a051b3639f0.png$
Ми бачимо, що вибір вище:

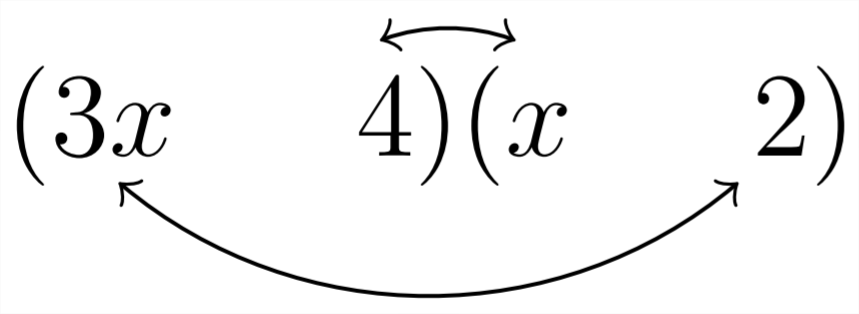
$clipboard_e77c59eccb7da45484e18ecae4cf6c759.png$

дає нам необхідний$10 x$ як середній термін. оскільки початкова проблема полягала в тому, що$3 x^{2}+10 x+8$ ми хочемо заповнити знаки як позитивні:

\[3 x^{2}+10 x+8=(3 x+4)(x+2)\]

Другий метод обробки цього виду факторингу залежить від того, як фактори провідного коефіцієнта та постійного терміну взаємодіють один з одним для отримання середньострокової перспективи. У цьому процесі, з огляду на задачу$3 x^{2}+10+8$, ми можемо помножити перший і останній коефіцієнт, а потім подивитися на пари коефіцієнтів добутку:

\[3 * 8=24\]

1	24
2	12
3	8
4	6

Ми бачимо, що пара факторів 24, яка додає до 10 є$6 * 4 .$ Ми продовжуємо, розділяючи на,$10 x$$6 x+4 x$ а потім фактор шляхом групування. Якщо вам незручно з факторингом шляхом групування, то це, ймовірно, не є хорошим методом, щоб спробувати. Однак, якщо вам зручно факторинг шляхом групування, решта процесу є відносно простим:

\[3 x^{2}+10 x+8=3 x^{2}+6 x+4 x+8\]

Потім ми враховуємо загальний коефіцієнт з перших двох членів і останніх двох членів окремо, а потім перерахуємо загальний біноміальний коефіцієнт$(x+2)$

\ [\ почати {вирівняний}
3 x^ {2} +10 x+8 &=3 x^ {2} +6 x+4 x+8\\
&=3 x (x+2) +4 (x+2)\
& =( x+2) (x+2) (3 x+4)
\ кінець {вирівняний}\]

Приклад$\PageIndex{7}$

Фактор$7 x^{2}-5 x-18$

Рішення

У цьому прикладі знак постійного члена є негативним, що означає, що нам знадобиться множник пари, які виробляють різницю провідний коефіцієнт,$7,$ який є простим, так що, знову ж таки, єдиний спосіб розділити 7 є$5 .$$7 * 1$

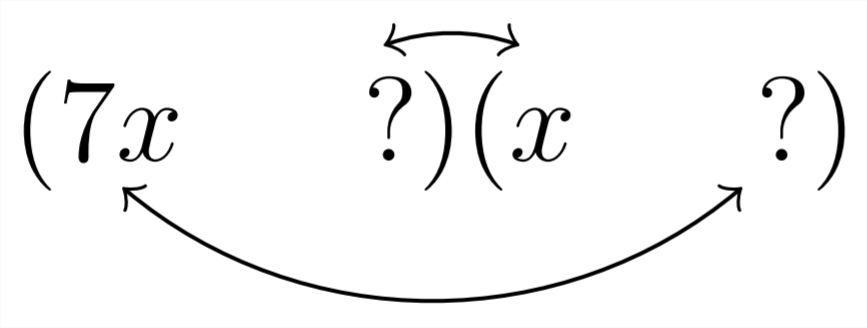
$clipboard_eb65b0a0664368b2609ae0a4b731ad68b.png$

Варіанти заповнення знаків питання походять від факторів,$18,$ для яких існує три можливості:$18 * 1,9 * 2,$ або$6 * 3 .$ Ми спробуємо кожну з цих пар факторів замість знаків питання:
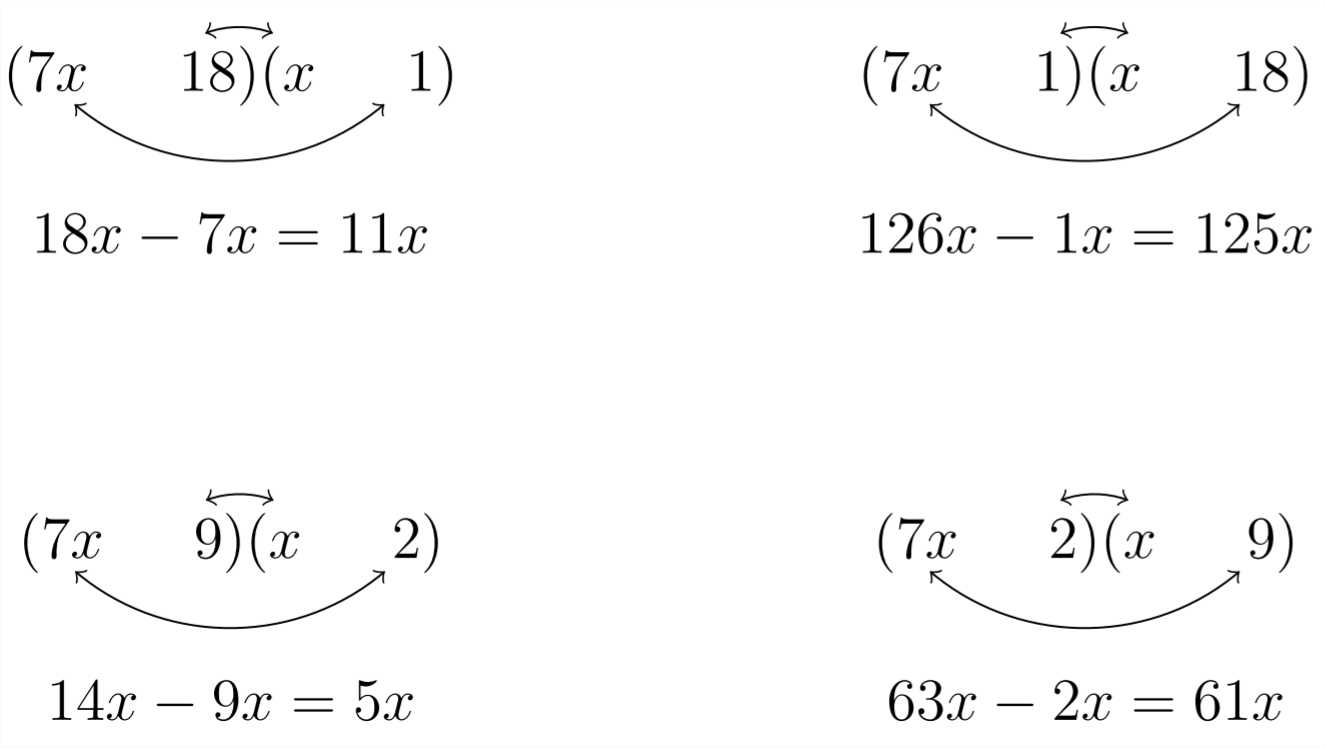
$clipboard_ee05f338aa4050dd3aa060f8809412d2f.png$
$clipboard_e2345e6121ef2d5212d15e5993322a930.png$
Вибір вище:

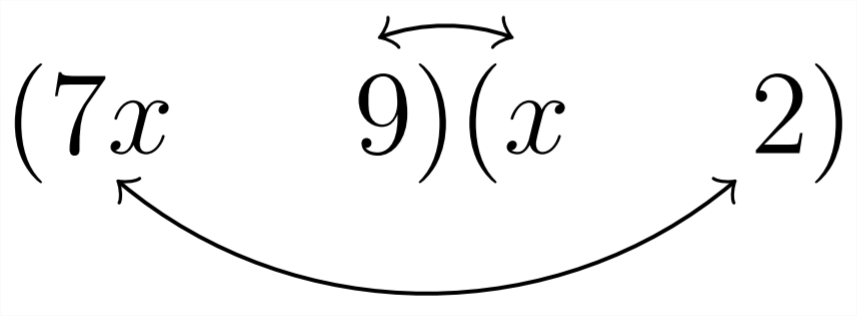
$clipboard_ec9241af7d614e7f353f271dfd1a3c4bd.png$
дає нам необхідний$5 x$ як середній термін. оскільки ми шукаємо а$(-5 x),$ ми зробимо 14 негативних і 9 позитивних:$-14 x+9 x=-5 x$

\[7 x^{2}-5 x-18=(7 x+9)(x-2) \nonumber\]

Якщо ми хочемо спробувати інший метод для факторингу$7 x^{2}-5 x-18$, ми б помножити,$7 * 18=126,$ а потім працювати, щоб знайти множник пари 126, які мають різницю 5
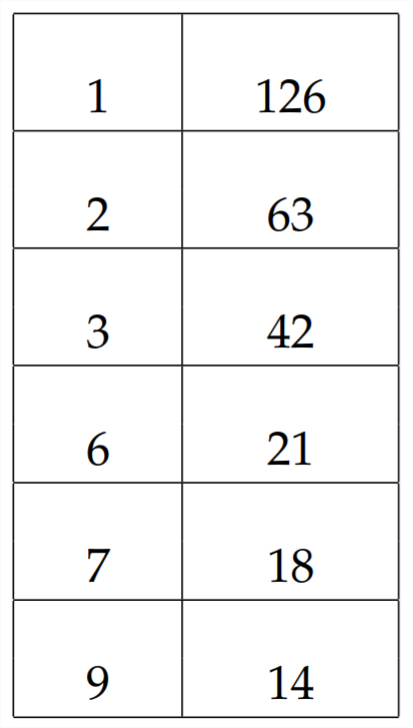
$clipboard_eb0c4a2b5788adc18823f7c0a289ab55d.png$

Тут, остання пара множника$9 * 14$, має різницю$5 .$ Отже, ми переходимо до коефіцієнт за групуванням:

\ [\ begin {вирівняний}
7 x^ {2} -5 x-18 &=7 x^ {2} +9 x-14 x-18\
&= x (7 x+9) -2 (7 x+9)\
& =( 7 x+9) (x-2)
\ end {вирівняний}
\]
Зверніть увагу, що коли -2 було враховано з останніх двох термінів$-14 x-18$, ми закінчилися$-2(7 x+9)$, тому що$(-2) *(+9)=-18 .$ це також важливо, тому що для того, щоб врахувати загальний біноміальний фактор$(7 x+9),$ цього біноміального, повинен бути точно однаковим в обох термінів.

Різниця квадратів

Факторинг різниці квадратів насправді є особливою формою триноміального факторингу. Якщо розглядати триноміал форми,$a x^{2}+b x+c,$ де$c$ є досконалим квадратом та негативом, ми знайдемо щось цікаве про можливі значення$b$, які роблять триноміальний факторним.
Приклад
\ [
\ text {Розглянемо} x^ {2} +b x-36
\]
Щоб цей вираз був факторним, середній$b$ коефіцієнт повинен дорівнювати різниці будь-якої з пар множників$36 .$ Якщо ми подивимось на можливий коефіцієнт пар, ми бачимо наступне:
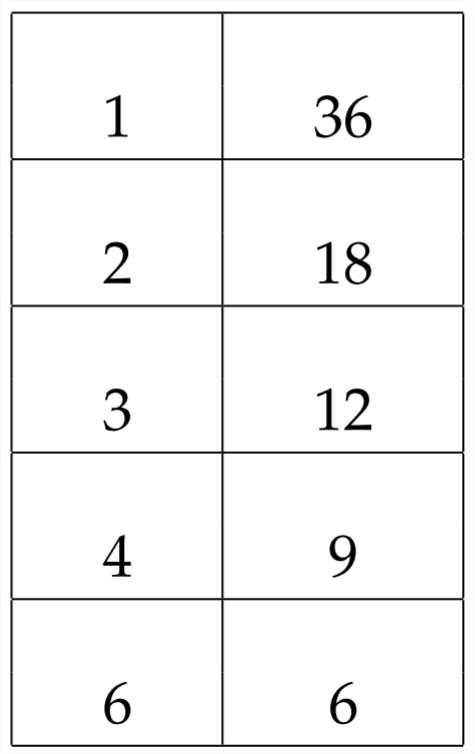
$clipboard_e1dbc0bd1112b4f1d6a532744d7790654.png$

Це означає, що можливі значення для$b$ того, щоб зробити цей вираз факторним, є:

\ [\ begin {масив} {c}
36-1=35\ rightarrow x^ {2} +35 x-36 =( x+36) (x-1)\\
18-2=16\ rightarrow x^ {2} +16 x-36 =( x+18) (x-2)\\
12-3=9\ rightarrow ^ {2} +9 x-36= (x+12) (x-3)\\
9-4=5\ стрілка вправо x^ {2} +5 x-36 =( x+9) (х-4)\
6-6=0\ стрілка вправо x ^ {2} +0 x-36=x^ {2} -36 =( x+6) (x-6)
\ кінець {масив}
\]

Як ми бачимо, факторинг$x^{2}-36$ означає, що фактори ідеального квадрата$36=6 * 6$ скасують один одного, залишаючи$0 x$ посередині. Якщо в якості провідного коефіцієнта є досконалий квадрат, то це число має бути також квадратним корінням:
\ [
16 x^ {2} -25 =( 4 x+5) (4 x-5)
\]
У наведеному вище прикладі,$+20 x$ і$-20 x$ як середні члени скасовують один одного, залишаючи просто $16 x^{2}-25$

Ці три типи факторингу також можна поєднувати між собою, як ми бачимо на наступних прикладах.

Приклад$\PageIndex{6}$

Фактор$2 x^{2}-50$

Рішення

Це не триноміал, тому що він не має трьох термінів. Це також не різниця квадратів, оскільки 2 та 50 не є ідеальними квадратами. Однак існує загальний множник 2, який ми можемо перерахувати:
\ [
2 x^ {2} -50=2\ left (x^ {2} -25\ right)
\]
Вираз всередині дужок є різницею квадратів і має бути враховано:
\ [
2 x^ {2} -50=2\ left (x^ {2} -25\ праворуч) =2 (x+5) (x-5)
\]

Приклад$\PageIndex{7}$

Фактор$24-2 x-x^{2}$

Рішення

Тут ознака$x^{2}$ терміна негативний. Для цієї задачі ми можемо перерахувати$a-1$ і діяти так, як ми робили з попередніми задачами, в яких провідний коефіцієнт був позитивним, або ми можемо перерахувати його таким, яким він є:
\ [
24-2 x-x^ {2} =-\ left (x^ {2} +2 x-24\ right) =- (x+6) (x-4)
\]

Якщо ми хочемо розрахувати його таким, яким він є, ми повинні знати, що постійний термін позитивний, а квадратичний термін негативний, що означає, що ми хочемо, щоб множники 24 мали різницю 2
\ [
24-2 x-x^ {2} =( 6+x) (4-x)
\]

Приклад$\PageIndex{8}$

Фактор$6 x^{2}+12 x+6$

Рішення

По-перше, ми помічаємо, що цей вираз має загальний коефіцієнт$6 .$ Якщо ми перерахуємо,
$6,$ то ми повинні залишитися з простішою задачею:
\ [
6 x^ {2} +12 x+6=6\ left (x^ {2} +2 x+1\ right) =6 (x+1) (x+1) =6 (x+1) =6 (x+1) ^ {2}
\]

Вправи$\PageIndex{1}$

Фактор кожного виразу повністю.
1)$\quad 8 a^{2} b^{3}+24 a^{2} b^{2}$
2)$\quad 19 x^{2} y-38 x^{2} y^{3}$
3)$\quad 13 t^{8}+26 t^{4}-39 t^{2}$
4)$\quad 5 y^{5}+25 y^{4}-20 y^{3}$
5)$\quad 45 m^{4} n^{5}+36 m n^{6}+81 m^{2} n^{3}$
6)$\quad125 x^{3} y^{5}+60 x^{4} y^{4}-85 x^{5} y^{2}$

Фактор кожного триноміала на добуток двох біноміалів.
7)$\quad a^{2}+3 a+2$
8)$\quad y^{2}-8 y-48$
9)$\quad x^{2}-6 x-27$
10)$\quad t^{2}-13 t+42$
11)$\quad m^{2}+3 m-54$
12)$\quad x^{2}+11 x+24$

Фактор повністю. Не забудьте спочатку шукати загальний фактор. Якщо многочлен є простим, вкажіть це.
13)$\quad a^{2}-9$
14)$\quad y^{2}-121$
15)$\quad -49+k^{2}$
16)$\quad -64+t^{2}$
17)$\quad 6 x^{2}-54$
18)$\quad 25 y^{2}-4$
19)$\quad 200-2 a^{2}$
20)$\quad 3 m^{2}-12$
21)$\quad 98-8 k^{2}$
22) $\quad -80 w^{2}+45$
23)$\quad 5 y^{2}-80$
24)$\quad -4 a^{2}+64$
25)$\quad 8 y^{2}-98$
26)$\quad 24 a^{2}-54$
27)$\quad 36 k-49 k^{3}$
28)$\quad 16 y-81 y^{3}$

Фактор кожного триноміалу повністю. Не забудьте спочатку шукати загальний фактор. Якщо многочлен є простим, вкажіть це.
29)$\quad 3 y^{2}-15 y+16$
30)$\quad 8 a^{2}-14 a+3$
31)$\quad 9 x^{2}-18 x+8$
32)$\quad 6 a^{2}-17 a+12$
33)$\quad 2 x^{2}+7 x+6$
34)$\quad 2 m^{2}+13 m-18$
35)$\quad 20 y^{2}+22 y+6$
36)$\quad 36 x^{2}+81 x+45$
37)$\quad 24 a^{2}-42 a+9$
38)$\quad 48 x^{2}-74 x-10$

Фактор кожного виразу повністю.
39)$\quad 30+7 y-y^{2}$
40)$\quad 45+4 a-a^{2}$
41)$\quad 24-10 x-x^{2}$
42)$\quad 36-9 x-x^{2}$
43)$\quad 84-8 x-x^{2}$
44)$\quad 72-6 a-a^{2}$
45)$\quad 6 y^{2}+24 y+15$
46)$\quad 10 y^{2}-75 y+35$
47)$\quad 20 a x^{2}-36 a x-8 a$

Відповідь: 1)$\quad 8 a^{2} b^{2}(b+3)$
3)$\quad 13 t^{2}\left(t^{6}+2 t^{2}-3\right)$
5)$\quad 9 m n^{3}\left(5 m^{3} n^{2}+4 n^{3}+9 m\right)$
7)$\quad (a+2)(a+1)$
9)$\quad (x-9)(x+3)$
11)$\quad (m+9)(m-6)$
13)$\quad (a+3)(a-3)$
15)$\quad (k+7)(k-7)$
17)$\quad 6(x+3)(x-3)$
19)$\quad 2(10+a)(10-a)$
21)$\quad 2(7+2 k)(7-2 k)$
23)$\quad 5(y+4)(y-4)$
25)$\quad 2(2 y+7)(2 y-7)$
27)$\quad k(6+7 k)(6-7 k)$
29)$\quad$ ПРАЙМ
31)$\quad(3 x-4)(3 x-2)$
33)$\quad(2 x+3)(x+2)$
35) $\quad 2(5 y+3)(2 y+1)$
37)$\quad 3(2 a-3)(4 a-1)$
39)$\quad(10-y)(3+y)$
41)$\quad(12+x)(2-x)$
43)$\quad(14+x)(6-x)$
45)$\quad 3\left(2 y^{2}+8 y+5\right)$
47)$\quad 4 a(5 x+1)(x-2)$

Найбільший загальний фактор

Триміальний факторинг\((a=1)\)

Триміальний факторинг\((a \neq 1)\)

Різниця квадратів