Глава 9 Огляд вправ
- Page ID
- 58695
Глава 9 Огляд вправ
Спрощення та використання квадратних коренів
Спрощення виразів за допомогою квадратних коренів
У наступних вправах спростити.
\(\sqrt{64}\)
\(\sqrt{144}\)
- Відповідь
-
12
\(−\sqrt{25}\)
\(−\sqrt{81}\)
- Відповідь
-
−9
\(\sqrt{−9}\)
\(\sqrt{−36}\)
- Відповідь
-
не дійсне число
\(\sqrt{64}+\sqrt{225}\)
\(\sqrt{64+225}\)
- Відповідь
-
17
У наступних вправах оцініть кожен квадратний корінь між двома послідовними цілими числами.
\(\sqrt{28}\)
\(\sqrt{155}\)
- Відповідь
-
\(12<\sqrt{155}<13\)
Приблизні квадратні корені
У наступних вправах наблизити кожен квадратний корінь і округлити до двох знаків після коми.
\(\sqrt{15}\)
\(\sqrt{57}\)
- Відповідь
-
7.55
Спрощення змінних виразів з квадратними коренями
У наступних вправах спростити.
\(\sqrt{q^2}\)
\(\sqrt{64b^2}\)
- Відповідь
-
8б
\(−\sqrt{121a^2}\)
\(\sqrt{225m^{2}n^{2}}\)
- Відповідь
-
15 млн
\(−\sqrt{100q^2}\)
\(\sqrt{49y^2}\)
- Відповідь
-
7й
\(\sqrt{4a^{2}b^{2}}\)
\(\sqrt{121c^{2}d^{2}}\)
- Відповідь
-
11кд
Спрощення квадратних коренів
Використовуйте властивість продукту для спрощення квадратних коренів
У наступних вправах спростити.
\(\sqrt{300}\)
\(\sqrt{98}\)
- Відповідь
-
\(7\sqrt{2}\)
\(\sqrt{x^{13}}\)
\(\sqrt{y^{19}}\)
- Відповідь
-
\(y^{9}\sqrt{y}\)
\(\sqrt{16m^4}\)
\(\sqrt{36n^{13}}\)
- Відповідь
-
\(6n^{6}\sqrt{n}\)
\(\sqrt{288m^{21}}\)
\(\sqrt{150n^7}\)
- Відповідь
-
\(5n^3\sqrt{6n}\)
\(\sqrt{48r^{5}s^{4}}\)
\(\sqrt{108r^{5}s^{3}}\)
- Відповідь
-
\(6r^{2}s\sqrt{3rs}\)
\(\frac{10−\sqrt{50}}{5}\)
\(\frac{6+\sqrt{72}}{6}\)
- Відповідь
-
\(1+\sqrt{2}\)
У наступних вправах спростити.
\(\sqrt{\frac{16}{25}}\)
\(\sqrt{\frac{81}{36}}\)
- Відповідь
-
\(\frac{3}{2}\)
\(\sqrt{\frac{x^8}{x^4}}\)
\(\sqrt{\frac{y^6}{y^2}}\)
- Відповідь
-
\(y^2\)
\(\sqrt{\frac{98p^6}{2p^2}}\)
\(\sqrt{\frac{72q^8}{2q^4}}\)
- Відповідь
-
\(6q^2\)
\(\sqrt{\frac{65}{121}}\)
\(\sqrt{\frac{26}{169}}\)
- Відповідь
-
\(\frac{\sqrt{26}}{13}\)
\(\sqrt{\frac{64x^4}{25x^2}}\)
\(\sqrt{\frac{36r^{10}}{16r^5}}\)
- Відповідь
-
\(\frac{3r^2\sqrt{r}}{2}\)
\(\sqrt{\frac{48p^{3}q^{5}}{27pq}}\)
\(\sqrt{\frac{12r^{5}s^{7}}{75r^{2}s}}\)
- Відповідь
-
\(\frac{2rs^3\sqrt{r}}{5}\)
Додавання та віднімання квадратних коренів
Додавання та віднімання, як квадратні корені
У наступних вправах спростити.
\(3\sqrt{2}+\sqrt{2}\)
\(5\sqrt{5}+7\sqrt{5}\)
- Відповідь
-
\(12\sqrt{5}\)
\(4\sqrt{y}+4\sqrt{y}\)
\(6\sqrt{m}−2\sqrt{m}\)
- Відповідь
-
\(4\sqrt{m}\)
\(−3\sqrt{7}+2\sqrt{7}−\sqrt{7}\)
\(8\sqrt{13}+2\sqrt{3}+3\sqrt{13}\)
- Відповідь
-
\(11\sqrt{13}+2\sqrt{3}\)
\(3\sqrt{5xy}−\sqrt{5xy}+3\sqrt{5xy}\)
\(2\sqrt{3rs}+\sqrt{3rs}−5\sqrt{rs}\)
- Відповідь
-
\(3\sqrt{3rs}−5\sqrt{rs}\)
Додавання та віднімання квадратних коренів, які потребують спрощення
У наступних вправах спростити.
\(\sqrt{32}+3\sqrt{2}\)
\(\sqrt{8}+\sqrt{32}\)
- Відповідь
-
\(5\sqrt{2}\)
\(\sqrt{72}+\sqrt{50}\)
\(\sqrt{48}+\sqrt{75}\)
- Відповідь
-
\(9\sqrt{3}\)
\(3\sqrt{32}+\sqrt{98}\)
\(\frac{1}{3}\sqrt{27}−\frac{1}{8}\sqrt{192}\)
- Відповідь
-
0
\(\sqrt{50y^5}−\sqrt{72y^5}\)
Додайте сюди текст вправ.
- Відповідь
-
\(17n^2\sqrt{2}\)
Помножте квадратні коріння
У наступних вправах спростити.
\(\sqrt{2}·\sqrt{20}\)
\(2\sqrt{2}·6\sqrt{14}\)
- Відповідь
-
\(24\sqrt{7}\)
\(\sqrt{2m^2}·\sqrt{20m^4}\)
\((\sqrt{62y})(\sqrt{350y^3})\)
- Відповідь
-
\(180y^2\)
\((6\sqrt{3v^4})(5\sqrt{30v})\)
\((\sqrt{8})^2\)
- Відповідь
-
8
\((−\sqrt{10})^2\)
\((2\sqrt{5})(5\sqrt{5})\)
- Відповідь
-
50
\((−3\sqrt{3})(5\sqrt{18})\)
У наступних вправах спростити.
\(10(2−\sqrt{7})\)
- Відповідь
-
\(20−10\sqrt{7}\)
\(\sqrt{3}(4+\sqrt{12})\)
\((5+\sqrt{2})(3−\sqrt{2})\)
- Відповідь
-
\(13−2\sqrt{2}\)
\((5−3\sqrt{7})(1−2\sqrt{7})\)
\((1−3\sqrt{x})(5+2\sqrt{x})\)
- Відповідь
-
\(5−13\sqrt{x}−6x\)
\((3+4\sqrt{y})(10−\sqrt{y})\)
\((1+6\sqrt{p})^2\)
- Відповідь
-
\(1+12\sqrt{p}+36p\)
\((2−6\sqrt{5})^2\)
\((3+2\sqrt{7})(3−2\sqrt{7})\)
- Відповідь
-
−19
\((6−\sqrt{11})(6+\sqrt{11})\)
Розділіть квадратні коріння
Розділіть квадратні коріння
У наступних вправах спростити.
\(\frac{\sqrt{75}}{10}\)
- Відповідь
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{2−\sqrt{12}}{6}\)
\(\frac{\sqrt{48}}{\sqrt{27}}\)
- Відповідь
-
\(\frac{4}{3}\)
\(\frac{\sqrt{75x^7}}{\sqrt{3x^3}}\)
\(\frac{\sqrt{20y^5}}{\sqrt{2y}}\)
- Відповідь
-
\(y^2\sqrt{10}\)
\(\frac{\sqrt{98p^{6}q^{4}}}{\sqrt{2p^{4}q^{8}}}\)
У наступних вправах раціоналізуйте знаменник.
\(\frac{10}{\sqrt{15}}\)
- Відповідь
-
\(\frac{2\sqrt{15}}{3}\)
\(\frac{6}{\sqrt{6}}\)
\(\frac{5}{3\sqrt{5}}\)
- Відповідь
-
\(\frac{\sqrt{5}}{3}\)
\(\frac{10}{2\sqrt{6}}\)
\(\sqrt{\frac{3}{28}}\)
- Відповідь
-
\(\frac{\sqrt{21}}{14}\)
\(\sqrt{\frac{9}{75}}\)
У наступних вправах раціоналізуйте знаменник.
\(\frac{4}{4+\sqrt{27}}\)
- Відповідь
-
\(\frac{16−12\sqrt{3}}{−11}\)
\(\frac{5}{2−\sqrt{10}}\)
\(\frac{4}{2−\sqrt{5}}\)
- Відповідь
-
\(−8−4\sqrt{5}\)
\(\frac{5}{4−\sqrt{8}}\)
\(\frac{\sqrt{2}}{\sqrt{p}+\sqrt{3}}\)
- Відповідь
-
\(\frac{\sqrt{2p}−\sqrt{6}}{p−3}\)
\(\frac{\sqrt{x}−\sqrt{2}}{\sqrt{x}+\sqrt{2}}\)
Вирішити рівняння з квадратними коренями
Розв'язувати радикальні рівнян
У наступних вправах розв'яжіть рівняння.
\(\sqrt{7z+1}=6\)
- Відповідь
-
5
\(\sqrt{4u−2}−4=0\)
\(\sqrt{6m+4}−5=0\)
- Відповідь
-
\(\frac{7}{2}\)
\(\sqrt{2u−3}+2=0\)
\(\sqrt{u−4}+4=u\)
- Відповідь
-
немає рішення
\(\sqrt{v−9}+9=0\)
\(\sqrt{r−4}−r=−10\)
- Відповідь
-
13
\(\sqrt{s−9}−s=−9\)
\(2\sqrt{2x−7}−4=8\)
- Відповідь
-
\(\frac{43}{2}\)
\(\sqrt{2−x}=\sqrt{2x−7}\)
\(\sqrt{a}+3=\sqrt{a+9}\)
- Відповідь
-
0
\(\sqrt{r}+3=\sqrt{r+4}\)
\(\sqrt{u}+2=\sqrt{u+5}\)
- Відповідь
-
\(\frac{11}{6}\)
\(\sqrt{n+11}−1=\sqrt{n+4}\)
\(\sqrt{y+5}+1=\sqrt{2y+3}\)
- Відповідь
-
11
У наступних вправах вирішуйте. Округлені наближення до одного знака після коми.
Піддон дернової покриє площу близько 600 квадратних футів. Trinh хоче замовити піддон з дерну, щоб зробити квадратний газон у себе на задньому дворі. Скористайтеся формулою,\(s=\sqrt{A}\) щоб знайти довжину кожної сторони свого газону.
Вертоліт скинув пакет з висоти 900 футів над мілиною мандрівного туриста. Скористайтеся формулою\(t=\frac{\sqrt{h}}{4}\), щоб знайти, скільки секунд знадобилося, щоб посилка дісталася до мандрівного.
- Відповідь
-
7,5 секунд
Офіцер Моралес заміряв сліди занесення одного з автомобілів, що потрапили в ДТП. Довжина слідів заносу становила 245 футів. Використовуйте формулу,\(s=\sqrt{24d}\) щоб знайти швидкість автомобіля до того, як були застосовані гальма.
Вищі коріння
Спрощення виразів з вищими коренями
У наступних вправах спростити.
- \(\sqrt[6]{64}\)
- \(\sqrt[3]{64}\)
- Відповідь
-
- 2
- 4
- \(\sqrt[3]{−27}\)
- \(\sqrt[4]{−64}\)
- \(\sqrt[9]{d^9}\)
- \(\sqrt[8]{v^8}\)
- Відповідь
-
- d
- |в|
- \(\sqrt[5]{a^{10}}\)
- \(\sqrt[3]{b^{27}}\)
- \(\sqrt[4]{16x^8}\)
- \(\sqrt[6]{64y^{12}}\)
- Відповідь
-
- \(2x^2\)
- \(2y^2\)
- \(\sqrt[7]{128r^{14}}\)
- \(\sqrt[4]{81s^{24}}\)
Використовуйте властивість продукту для спрощення виразів з вищими коренями
У наступних вправах спростити.
- \(\sqrt[9]{d^9}\)
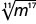
- Відповідь
-
- d
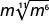
- \(\sqrt[3]{54}\)
- \(\sqrt[4]{128}\)
- \(\sqrt[5]{64c^8}\)
- \(\sqrt[4]{48d^7}\)
- Відповідь
-
- \(2c\sqrt[5]{2c^3}\)
- \(2d\sqrt[4]{3d^3}\)
- \(\sqrt[3]{343q^7}\)
- \(\sqrt[6]{192r^9}\)
- \(\sqrt[3]{−500}\)
- \(\sqrt[4]{−16}\)
- Відповідь
-
- \(−5\sqrt[3]{4}\)
- не дійсне число
У наступних вправах спростити.
\(\sqrt[5]{\frac{r^{10}}{r^5}}\)
\(\sqrt[3]{\frac{w^{12}}{w^2}}\)
- Відповідь
-
\(w^3\sqrt[3]{w}\)
\(\sqrt[4]{\frac{64y^8}{4y^5}}\)
\(\sqrt[3]{\frac{54z^9}{2z^3}}\)
- Відповідь
-
\(3z^2\)
\(\sqrt[6]{\frac{64a^7}{b^2}}\)
У наступних вправах спростити.
\(4\sqrt[5]{20}−2\sqrt[5]{20}\)
- Відповідь
-
\(2\sqrt[5]{20}\)
\(4\sqrt[3]{18}+3\sqrt[3]{18}\)
\(\sqrt[4]{1250}−\sqrt[4]{162}\)
- Відповідь
-
\(2\sqrt[4]{2}\)
\(\sqrt[3]{640c^5}−\sqrt[3]{−80c^3}\)
\(\sqrt[5]{96t^8}+\sqrt[5]{486t^4}\)
- Відповідь
-
\(2t^\sqrt[5]{3t^3}+3\sqrt[5]{2t^4}\)
Раціональні показники
Спрощення виразів за допомогою\(a^{\frac{1}{n}}\)
У наступних вправах пишіть як радикальний вираз.
\(r^{\frac{1}{8}}\)
\(s^{\frac{1}{10}}\)
- Відповідь
-
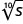
У наступних вправах пишіть з раціональним показником.
\(\sqrt[5]{u}\)
\(\sqrt[6]{v}\)
- Відповідь
-
\(v^{\frac{1}{6}}\)
\(\sqrt[3]{9m}\)
\(\sqrt[6]{10z}\)
- Відповідь
-
\((10z)^{\frac{1}{6}}\)
У наступних вправах спростити.
\(16^{\frac{1}{4}}\)
\(32^{\frac{1}{5}}\)
- Відповідь
-
2
\((−125)^{\frac{1}{3}}\)
\((125)^{−\frac{1}{3}}\)
- Відповідь
-
\(\frac{1}{5}\)
\((−9)^{\frac{1}{2}}\)
\((36)^{−\frac{1}{2}}\)
- Відповідь
-
\(\frac{1}{6}\)
У наступних вправах пишіть з раціональним показником.
\(\sqrt[3]{q^5}\)
\(\sqrt[5]{n^8}\)
- Відповідь
-
\(n^{\frac{8}{5}}\)
У наступних вправах спростити.
\(27^{−\frac{2}{3}}\)
\(64^{\frac{5}{2}}\)
- Відповідь
-
32 768
\(36^{\frac{3}{2}}\)
\(81^{−\frac{5}{2}}\)
- Відповідь
-
\(\frac{1}{59,049}\)
Використовуйте закони експонентів для спрощення виразів з раціональними показниками
У наступних вправах спростити.
\(3^{\frac{4}{5}}·3^{\frac{6}{5}}\)
\((x^6)^{\frac{4}{3}}\)
- Відповідь
-
\(x^8\)
\(\frac{z^{\frac{5}{2}}}{z^{\frac{7}{5}}}\)
\((16s^{\frac{9}{4}})^{\frac{1}{4}}\)
- Відповідь
-
\(2s^{\frac{9}{16}}\)
\((m^{8}n^{12})^{\frac{1}{4}}\)
\(\frac{z^{\frac{2}{3}}·z^{−\frac{1}{3}}}{z^{−\frac{5}{3}}}\)
- Відповідь
-
\(z^2\)
Практика Тест
У наступних вправах спростити.
\(\sqrt{81+144}\)
\(\sqrt{169m^{4}n^{2}}\)
- Відповідь
-
\(13m^{2}|n|\)
\(\sqrt{36n^{13}}\)
\(3\sqrt{13}+5\sqrt{2}+\sqrt{13}\)
- Відповідь
-
\(4\sqrt{13}+5\sqrt{2}\)
\(5\sqrt{20}+2\sqrt{125}\)
\((3\sqrt{6y})(\sqrt{250y^3})\)
- Відповідь
-
\(180y^2\sqrt{3}\)
\((2−5\sqrt{x})(3+\sqrt{x})\)
\((1−2\sqrt{q})^2\)
- Відповідь
-
\(1−4\sqrt{q}+4q\)
- \(\sqrt{a^{12}}\)
- \(\sqrt[3]{b^{21}}\)
- \(\sqrt[4]{81x^{12}}\)
- \(\sqrt[6]{64y^{18}}\)
- Відповідь
-
- \(3x^3\)
- \(2y^3\)
\(\sqrt[6]{\frac{64r^{12}}{25r^6}}\)
\(\sqrt{\frac{14y^3}{7y}}\)
- Відповідь
-
\(y\sqrt{2}\)
\(\frac{\sqrt{256x^7}}{\sqrt{54x^2}}\)
\(\sqrt[4]{512}−2\sqrt[4]{32}\)
- Відповідь
-
0
- \(256^{\frac{1}{4}}\)
- \(243^{\frac{1}{5}}\)
\(49^{\frac{3}{2}}\)
- Відповідь
-
343
\(25^{−\frac{5}{2}}\)
\(\frac{w^{\frac{3}{4}}}{w^{\frac{7}{4}}}\)
- Відповідь
-
\(\frac{1}{w}\)
\((27s^{\frac{3}{5}})^{\frac{1}{3}}\)
У наступних вправах раціоналізуйте знаменник.
\(\frac{3}{2\sqrt{6}}\)
- Відповідь
-
\(\frac{\sqrt{6}}{4}\)
\(\frac{\sqrt{3}}{\sqrt{x}+\sqrt{5}}\)
У наступних вправах вирішуйте.
\(3\sqrt{2x−3}−20=7\)
- Відповідь
-
42
\(\sqrt{3u−2}=\sqrt{5u+1}\)
У наступній вправі вирішуйте.
Вертоліт, що летів на висоті 600 футів, скинув пакет на рятувальну шлюпку. Скористайтеся формулою\(t=\frac{\sqrt{h}}{4}\), щоб знайти, скільки секунд знадобилося, щоб посилка дісталася до мандрівного. Округліть відповідь до найближчої десятої частки секунди.
- Відповідь
-
6.1 секунди
