9.4: Помножте квадратні корені

Last updated
Save as PDF

Page ID: 58701

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

Розмножуємо квадратні коріння
Використовуйте множення поліномів для множення квадратних коренів

Примітка

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Спрощення: (3u) (8v).
Якщо ви пропустили цю проблему, перегляньте приклад 6.2.31.
Спрощення: 6 (12−7n).
Якщо ви пропустили цю проблему, перегляньте приклад 6.3.1.
Спростити: (2+a) (4−a).
Якщо ви пропустили цю проблему, перегляньте приклад 6.3.34.

Помножте квадратні коріння

Ми використали Product Property of Square Roots для спрощення квадратних коренів шляхом видалення ідеальних квадратних факторів. Властивість продукту квадратних коренів говорить

\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]

Ми можемо використовувати властивість продукту квадратних коренів «навпаки» для розмноження квадратних коренів.

\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]

Пам'ятайте, ми припускаємо, що всі змінні більше або рівні нулю.

Ми перепишемо властивість продукту квадратних коренів, щоб ми побачили обидва способи разом.

Визначення: ВЛАСТИВІСТЬ ПРОДУКТУ КВАДРАТНИХ КОРЕНІВ

Якщо a, b є невід'ємними дійсними числами, то

$\sqrt{ab}=\sqrt{a}·\sqrt{b}$і$\sqrt{a}·\sqrt{b}=\sqrt{ab}$.

Так ми можемо помножити$\sqrt{3}·\sqrt{5}$ in this way:

\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]

Іноді виріб дає нам ідеальний квадрат:

\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]

Навіть коли виріб не є ідеальним квадратом, ми повинні шукати ідеальні квадратні фактори та спрощувати радикал, коли це можливо.

Множення радикалів з коефіцієнтами багато в чому схоже на множення змінних з коефіцієнтами. Для множення 4x·3y ми множимо коефіцієнти разом, а потім змінні. Результат - 12xy. Майте це на увазі, як ви робите ці приклади.

Приклад$\PageIndex{1}$

Спростити:

$\sqrt{2}·\sqrt{6}$
$(4\sqrt{3})(2\sqrt{12})$.

Відповідь

1.	$\sqrt{2}·\sqrt{6}$
Множення за допомогою властивості продукту.	$\sqrt{12}$
Спростити радикал.	$\sqrt{4}·\sqrt{3}$
Спростити.	$2\sqrt{3}$
2.	$(4\sqrt{3})(2\sqrt{12})$
Множення за допомогою властивості продукту.	$8\sqrt{36}$
Спростити радикал.	$8·6$
Спростити.	$48$

Приклад$\PageIndex{2}$

Спростити:

$\sqrt{3}·\sqrt{6}$
$(2\sqrt{6})(3\sqrt{12})$.

Відповідь

$3\sqrt{2}$
$36\sqrt{2}$

Приклад$\PageIndex{3}$

Спростити:

$\sqrt{5}·\sqrt{10}$
$(6\sqrt{3})(5\sqrt{6})$

Відповідь

$5\sqrt{2}$
$90\sqrt{2}$

Приклад$\PageIndex{4}$

Спростити:$(6\sqrt{2})(3\sqrt{10})$

Відповідь

	$(6\sqrt{2})(3\sqrt{10})$
Множення за допомогою властивості продукту.	$18\sqrt{20}$
Спростити радикал.	$18\sqrt{4}·\sqrt{5}$
Спростити.	$18·2·\sqrt{5}$
	$36\sqrt{5}$

Приклад$\PageIndex{5}$

Спростити:$(3\sqrt{2})(2\sqrt{30})$

Відповідь: $12\sqrt{15}$

Приклад$\PageIndex{6}$

Спростити:$(3\sqrt{3})(3\sqrt{6})$.

Відповідь: $27\sqrt{2}$

Коли нам доводиться множити квадратні корені, ми спочатку знаходимо продукт, а потім видаляємо будь-які ідеальні квадратні фактори.

Приклад$\PageIndex{7}$

Спростити:

$(\sqrt{8x^3})(\sqrt{3x})$
$(\sqrt{20y^2})(\sqrt{5y^3})$

Відповідь

1.	$(\sqrt{8x^3})(\sqrt{3x})$
Множення за допомогою властивості продукту.	$\sqrt{24x^4}$
Спростити радикал.	$\sqrt{4x^4}·\sqrt{6}$
Спростити.	$2x^2\sqrt{6}$
2.	$(\sqrt{20y^2})(\sqrt{5y^3})$
Множення за допомогою властивості продукту.	$\sqrt{100y^5}$
Спростити радикал.	$10y^2\sqrt{y}$

Приклад$\PageIndex{8}$

Спростити:

$(\sqrt{6x^3})(\sqrt{3x})$
$(\sqrt{2y^3})(\sqrt{50y^2})$.

Відповідь

$3x^2\sqrt{2}$
$10y^2\sqrt{y}$

Приклад$\PageIndex{9}$

Спростити:

$(\sqrt{6x^5})(\sqrt{2x})$
$(\sqrt{12y^2})(\sqrt{3y^5})$

Відповідь

$2x^3\sqrt{3}$
$6y^2\sqrt{y}$

Приклад$\PageIndex{10}$

Спростити:$(10\sqrt{6p^3})(3\sqrt{18p})$

Відповідь

	$(10\sqrt{6p^3})(3\sqrt{18p})$
Помножити.	$30\sqrt{108p^4}$
Спростити радикал.	$30\sqrt{36p^4}·\sqrt{3}$
	$30·6p^2·\sqrt{3}$
	$180p^2\sqrt{3}$

Приклад$\PageIndex{11}$

Спростити:$(\sqrt{62x^2})(8\sqrt{45x^4})$

Відповідь: $144x^3\sqrt{10}$

Приклад$\PageIndex{12}$

Спростити:$(2\sqrt{6y^4})(12\sqrt{30y})$.

Відповідь: $144y^2\sqrt{5y}$

Приклад$\PageIndex{13}$

Спростити:

$(\sqrt{2})^2$
$(−\sqrt{11})^2$.

Відповідь

1.	$(\sqrt{2})^2$
Рерайт як продукт.	$(\sqrt{2})(\sqrt{2})$
Помножити.	$\sqrt{4}$
Спростити.	2
2.	$(−\sqrt{11})^2$
Рерайт як продукт.	$(−\sqrt{11})(−\sqrt{11})$
Помножити.	$\sqrt{121}$
Спростити.	11

Приклад$\PageIndex{14}$

Спростити:

$(\sqrt{12})^2$
$(−\sqrt{15})^2$.

Відповідь

Приклад$\PageIndex{15}$

Спростити:

$(\sqrt{16})^2$
$(−\sqrt{20})^2$.

Відповідь

Результати попереднього прикладу призводять нас до цієї властивості.

Визначення: КВАДРАТНИЙ КОРІНЬ

Якщо a - невід'ємне дійсне число, то

$(\sqrt{a})^2=a$

Розуміючи, що квадрат і взяття квадратного кореня є «протилежними» операціями, ми можемо спростити$(\sqrt{2})^2$ і отримати 2 відразу. Коли ми множимо два як квадратні корені в частині (а) наступного прикладу, це те саме, що і квадрат.

Приклад$\PageIndex{16}$

Спростити:

$(2\sqrt{3})(8\sqrt{3})$
$(3\sqrt{6})^2$.

Відповідь

1.	$(2\sqrt{3})(8\sqrt{3})$
Помножити. Запам'ятайте,$(\sqrt{3}^2)$	16·3
Спростити.	48
2.	$(3\sqrt{6})^2$
Помножити.	9·6
Спростити.	54

Приклад$\PageIndex{17}$

Спростити:

$(6\sqrt{11})(5\sqrt{11})$
$(5\sqrt{8})^2$.

Відповідь

Приклад$\PageIndex{18}$

Спростити:

$(3\sqrt{7})(10\sqrt{7})$
$(−4\sqrt{6})^2$.

Відповідь

Використовуйте множення поліномів для множення квадратних коренів

У наступних кількох прикладах ми будемо використовувати властивість Distributive для множення виразів з квадратними коренями.

Спочатку розподілимо, а потім спростимо квадратні коріння, коли це можливо.

Приклад$\PageIndex{19}$

Спростити:

$3(5−\sqrt{2})$
$\sqrt{2}(4−\sqrt{10})$.

Відповідь

1.	$3(5−\sqrt{2})$
Розподілити.	$15−3\sqrt{2})$
2.	$\sqrt{2}(4−\sqrt{10})$
Розподілити.	$4\sqrt{2}−\sqrt{20}$
Спростити.	$4\sqrt{2}−2\sqrt{5}$

Приклад$\PageIndex{20}$

Спростити:

$2(3−\sqrt{5})$
$\sqrt{3}(2−\sqrt{18})$.

Відповідь

$6−2\sqrt{5}$
$2\sqrt{3}−3\sqrt{6}$

Приклад$\PageIndex{21}$

Спростити:

$6(2+\sqrt{6})$
$\sqrt{7}(1+\sqrt{14})$.

Відповідь

$12+\sqrt{6}$
$\sqrt{7}+7\sqrt{2}$

Приклад$\PageIndex{22}$

Спростити:

$\sqrt{5}(7+2\sqrt{5})$
$\sqrt{6}(\sqrt{2}+\sqrt{18})$.

Відповідь

1.	$\sqrt{5}(7+2\sqrt{5})$
Розподілити.	$7\sqrt{5}+2·5$
Спростити.	$7\sqrt{5}+10$
	$10+7\sqrt{5}$
2.	$\sqrt{6}(\sqrt{2}+\sqrt{18})$
Помножити.	$\sqrt{12}+\sqrt{108}$
Спростити.	$(\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})$
	$2\sqrt{3}+6\sqrt{3}$
Поєднуються як радикали.	$8\sqrt{3}$

Приклад$\PageIndex{23}$

Спростити:

$\sqrt{6}(1+3\sqrt{6})$
$\sqrt{12}(\sqrt{3}+\sqrt{24})$

Відповідь

$18+\sqrt{6}$
$6+12\sqrt{2}$

Приклад$\PageIndex{24}$

Спростити:

$\sqrt{8}(2−5\sqrt{8})$
$\sqrt{14}(\sqrt{2}+\sqrt{42})$

Відповідь

$−40+4\sqrt{2}$
$2\sqrt{7}+14\sqrt{3}$

Коли ми працювали з многочленами, ми множили біноми на біноміали. Пам'ятайте, це дало нам чотири продукти, перш ніж ми поєднали будь-які подібні терміни. Щоб отримати всі чотири продукти, ми організували нашу роботу, як правило, методом FOIL.

Приклад$\PageIndex{25}$

Спростити:$(2+\sqrt{3})(4−\sqrt{3})$

Відповідь

	$(2+\sqrt{3})(4−\sqrt{3})$
Помножити.	$8−2\sqrt{3}+4\sqrt{3}−3$
Поєднуйте подібні терміни.	$5+2\sqrt{3}$

Приклад$\PageIndex{26}$

Спростити:$(1+\sqrt{6})(3−\sqrt{6})$.

Відповідь: $−3+2\sqrt{6}$

Приклад$\PageIndex{27}$

Спростити:$(4−\sqrt{10})(2+\sqrt{10})$.

Відповідь: $−2+2\sqrt{10}$

Приклад$\PageIndex{28}$

Спростити:$(3−2\sqrt{7})(4−2\sqrt{7})$.

Відповідь

	$(3−2\sqrt{7})(4−2\sqrt{7})$
Помножити.	$12−6\sqrt{7}−8\sqrt{7}+4·7$
Спростити.	$12−6\sqrt{7}−8\sqrt{7}+28$
Поєднуйте подібні терміни.	$40−14\sqrt{7}$

Приклад$\PageIndex{29}$

Спростити:$(6−3\sqrt{7})(3+4\sqrt{7})$.

Відповідь: $−66+15\sqrt{7}$

Приклад$\PageIndex{30}$

Спростити:$(2−3\sqrt{11})(4−\sqrt{11})$

Відповідь: $41+14\sqrt{11}$

Приклад$\PageIndex{31}$

Спростити:$(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})$.

Відповідь

	$3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})$
Помножити.	$3·2+12\sqrt{10}−\sqrt{10}−4·5$
Спростити.	$6+12\sqrt{10}−\sqrt{10}−20$
Поєднуйте подібні терміни.	$−14+11\sqrt{10}$

Приклад$\PageIndex{32}$

Спростити:$(5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})$

Відповідь: $1+9\sqrt{21}$

Приклад$\PageIndex{33}$

Спростити:$(\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})$

Відповідь: $−12−20\sqrt{3}$

Приклад$\PageIndex{34}$

Спростити:$(4−2\sqrt{x})(1+3\sqrt{x})$.

Відповідь

	$(4−2\sqrt{x})(1+3\sqrt{x})$.
Помножити.	$4+12\sqrt{x}−2\sqrt{x}−6x$
Поєднуйте подібні терміни.	$4+10\sqrt{x}−6x$

Приклад$\PageIndex{35}$

Спростити:$(6−5\sqrt{m})(2+3\sqrt{m})$.

Відповідь: $12+8\sqrt{m}−15m$

Приклад$\PageIndex{36}$

Спростити:$(10+3\sqrt{n})(1−5\sqrt{n})$

Відповідь: $10−47\sqrt{n}−15n$

Зверніть увагу, що деякі спеціальні продукти полегшили нашу роботу, коли ми раніше множили біноми. Це вірно, коли ми також розмножуємо квадратні корені. Спеціальні формули продуктів, які ми використовували, наведені нижче.

Визначення: СПЕЦІАЛЬНІ ФОРМУЛИ ПРОДУКТУ

\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]

Ми будемо використовувати спеціальні формули продукту в наступних кількох прикладах. Почнемо з формули Біноміальні квадрати.

Приклад$\PageIndex{37}$

Спростити:

$(2+\sqrt{3})^2$
$(4−2\sqrt{5})^2$.

Відповідь

Обов'язково включайте термін 2ab при квадраті біном.

	$.$
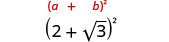
Множте, використовуючи біноміальний квадратний візерунок.	$.$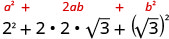
Спростити.	$.$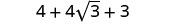
Поєднуйте подібні терміни.	$.$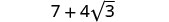

	$.$
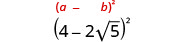
Множте, використовуючи біноміальний квадратний візерунок.	$.$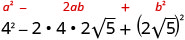
Спростити.	$.$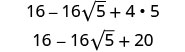
Поєднуйте подібні терміни.	$.$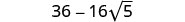

Приклад$\PageIndex{38}$

Спростити:

$(10+\sqrt{2})^2$
$(1+3\sqrt{6})^2$.

Відповідь

$102+20\sqrt{2}$
$55+6\sqrt{6}$

Вправа$\PageIndex{39}$

Спростити:

$(6-\sqrt{5})^2$
$(9-2\sqrt{10})^2$.

Відповідь

$41-12\sqrt{5}$
$121-36\sqrt{10}$

Приклад$\PageIndex{40}$

Спростити:$(1+3\sqrt{x})^2$.

Відповідь

	$.$
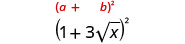
Множте, використовуючи біноміальний квадратний візерунок.	$.$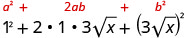
Спростити.	$.$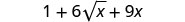

Приклад$\PageIndex{41}$

Спростити:$(2+5\sqrt{m})^2$.

Відповідь: $4+20\sqrt{m}+25m$

Приклад$\PageIndex{42}$

Спростити:$(3−4\sqrt{n})^2$.

Відповідь: $9−24\sqrt{n}+16n$

У наступних двох прикладах ми знайдемо твір кон'югатів.

Приклад$\PageIndex{43}$

Спростити:$(4−\sqrt{2})(4+\sqrt{2})$.

Відповідь

	$.$
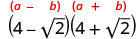
Множте, використовуючи біноміальний квадратний візерунок.	$.$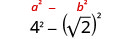
Спростити.	$.$

Приклад$\PageIndex{44}$

Спростити:$(2−\sqrt{3})(2+\sqrt{3})$

Відповідь: 1

Приклад$\PageIndex{45}$

Спростити:$(1+\sqrt{5})(1−\sqrt{5})$

Відповідь: −4

Приклад$\PageIndex{46}$

Спростити:$(5−2\sqrt{3})(5+2\sqrt{3})$

Відповідь

	$.$
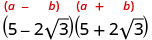
Множте, використовуючи біноміальний квадратний візерунок.	$.$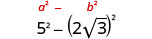
Спростити.	$.$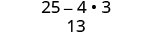

Приклад$\PageIndex{47}$

Спростити:$(3−2\sqrt{5})(3+2\sqrt{5})$.

Відповідь: −11

Приклад$\PageIndex{48}$

Спростити:$(4+5\sqrt{7})(4−5\sqrt{7})$.

Відповідь: −159

Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з розмноженням квадратних коренів.

Властивість продукту
Помножте біноміали квадратними коренями

Ключові поняття

Властивість добутку квадратних коренів Якщо a, b є невід'ємними дійсними числами, то
$\sqrt{ab}=\sqrt{a·b}$і$\sqrt{a}·\sqrt{b}=\sqrt{ab}$
Спеціальні формули множення бічленів і кон'югатів:
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
Метод FOIL може бути використаний для множення біноміалів, що містять радикали.

	\((6\sqrt{2})(3\sqrt{10})\)
Множення за допомогою властивості продукту.	\(18\sqrt{20}\)
Спростити радикал.	\(18\sqrt{4}·\sqrt{5}\)
Спростити.	\(18·2·\sqrt{5}\)
	\(36\sqrt{5}\)

	\((10\sqrt{6p^3})(3\sqrt{18p})\)
Помножити.	\(30\sqrt{108p^4}\)
Спростити радикал.	\(30\sqrt{36p^4}·\sqrt{3}\)
	\(30·6p^2·\sqrt{3}\)
	\(180p^2\sqrt{3}\)

1.	\(\sqrt{5}(7+2\sqrt{5})\)
Розподілити.	\(7\sqrt{5}+2·5\)
Спростити.	\(7\sqrt{5}+10\)
	\(10+7\sqrt{5}\)
2.	\(\sqrt{6}(\sqrt{2}+\sqrt{18})\)
Помножити.	\(\sqrt{12}+\sqrt{108}\)
Спростити.	\((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\)
	\(2\sqrt{3}+6\sqrt{3}\)
Поєднуються як радикали.	\(8\sqrt{3}\)

	\((2+\sqrt{3})(4−\sqrt{3})\)
Помножити.	\(8−2\sqrt{3}+4\sqrt{3}−3\)
Поєднуйте подібні терміни.	\(5+2\sqrt{3}\)

	\((3−2\sqrt{7})(4−2\sqrt{7})\)
Помножити.	\(12−6\sqrt{7}−8\sqrt{7}+4·7\)
Спростити.	\(12−6\sqrt{7}−8\sqrt{7}+28\)
Поєднуйте подібні терміни.	\(40−14\sqrt{7}\)

1.	\(\sqrt{2}·\sqrt{6}\)
Множення за допомогою властивості продукту.	\(\sqrt{12}\)
Спростити радикал.	\(\sqrt{4}·\sqrt{3}\)
Спростити.	\(2\sqrt{3}\)
2.	\((4\sqrt{3})(2\sqrt{12})\)
Множення за допомогою властивості продукту.	\(8\sqrt{36}\)
Спростити радикал.	\(8·6\)
Спростити.	\(48\)

1.	\((\sqrt{8x^3})(\sqrt{3x})\)
Множення за допомогою властивості продукту.	\(\sqrt{24x^4}\)
Спростити радикал.	\(\sqrt{4x^4}·\sqrt{6}\)
Спростити.	\(2x^2\sqrt{6}\)
2.	\((\sqrt{20y^2})(\sqrt{5y^3})\)
Множення за допомогою властивості продукту.	\(\sqrt{100y^5}\)
Спростити радикал.	\(10y^2\sqrt{y}\)

1.	\((\sqrt{2})^2\)
Рерайт як продукт.	\((\sqrt{2})(\sqrt{2})\)
Помножити.	\(\sqrt{4}\)
Спростити.	2
2.	\((−\sqrt{11})^2\)
Рерайт як продукт.	\((−\sqrt{11})(−\sqrt{11})\)
Помножити.	\(\sqrt{121}\)
Спростити.	11

1.	\((2\sqrt{3})(8\sqrt{3})\)
Помножити. Запам'ятайте,\((\sqrt{3}^2)\)	16·3
Спростити.	48
2.	\((3\sqrt{6})^2\)
Помножити.	9·6
Спростити.	54

1.	\(3(5−\sqrt{2})\)
Розподілити.	\(15−3\sqrt{2})\)
2.	\(\sqrt{2}(4−\sqrt{10})\)
Розподілити.	\(4\sqrt{2}−\sqrt{20}\)
Спростити.	\(4\sqrt{2}−2\sqrt{5}\)

	\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\)
Помножити.	\(3·2+12\sqrt{10}−\sqrt{10}−4·5\)
Спростити.	\(6+12\sqrt{10}−\sqrt{10}−20\)
Поєднуйте подібні терміни.	\(−14+11\sqrt{10}\)

	\((4−2\sqrt{x})(1+3\sqrt{x})\).
Помножити.	\(4+12\sqrt{x}−2\sqrt{x}−6x\)
Поєднуйте подібні терміни.	\(4+10\sqrt{x}−6x\)

Цілі навчання

Примітка

Помножте квадратні коріння

Визначення: ВЛАСТИВІСТЬ ПРОДУКТУ КВАДРАТНИХ КОРЕНІВ

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\)

Приклад\(\PageIndex{7}\)

Приклад\(\PageIndex{8}\)

Приклад\(\PageIndex{9}\)

Приклад\(\PageIndex{10}\)

Приклад\(\PageIndex{11}\)

Приклад\(\PageIndex{12}\)

Приклад\(\PageIndex{13}\)

Приклад\(\PageIndex{14}\)

Приклад\(\PageIndex{15}\)

Визначення: КВАДРАТНИЙ КОРІНЬ

Приклад\(\PageIndex{16}\)

Приклад\(\PageIndex{17}\)

Приклад\(\PageIndex{18}\)

Використовуйте множення поліномів для множення квадратних коренів

Приклад\(\PageIndex{19}\)

Приклад\(\PageIndex{20}\)

Приклад\(\PageIndex{21}\)

Приклад\(\PageIndex{22}\)

Приклад\(\PageIndex{23}\)

Приклад\(\PageIndex{24}\)

Приклад\(\PageIndex{25}\)

Приклад\(\PageIndex{26}\)

Приклад\(\PageIndex{27}\)

Приклад\(\PageIndex{28}\)

Приклад\(\PageIndex{29}\)

Приклад\(\PageIndex{30}\)

Приклад\(\PageIndex{31}\)

Приклад\(\PageIndex{32}\)

Приклад\(\PageIndex{33}\)

Приклад\(\PageIndex{34}\)

Приклад\(\PageIndex{35}\)

Приклад\(\PageIndex{36}\)

Визначення: СПЕЦІАЛЬНІ ФОРМУЛИ ПРОДУКТУ

Приклад\(\PageIndex{37}\)

Приклад\(\PageIndex{38}\)

Вправа\(\PageIndex{39}\)

Приклад\(\PageIndex{40}\)

Приклад\(\PageIndex{41}\)

Приклад\(\PageIndex{42}\)

Приклад\(\PageIndex{43}\)

Приклад\(\PageIndex{44}\)

Приклад\(\PageIndex{45}\)

Приклад\(\PageIndex{46}\)

Приклад\(\PageIndex{47}\)

Приклад\(\PageIndex{48}\)

Ключові поняття