9.5: Розділіть квадратні корені
- Page ID
- 58699
До кінця цього розділу ви зможете:
- Розділіть квадратні коріння
- Раціоналізувати одночленний знаменник
- Раціоналізувати двочленний знаменник
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Знайдіть дріб,\(\frac{5}{8}\) еквівалентний знаменнику 48.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.6.1. - Спростити:\((\sqrt{5})^2\).
Якщо ви пропустили цю проблему, перегляньте приклад 9.4.13. - Помножте: (7+3x) (7−3x).
Якщо ви пропустили цю проблему, перегляньте Вправа 6.4.22.
Розділіть квадратні коріння
Ми знаємо, що ми спрощуємо дроби, видаляючи множники, спільні для чисельника та знаменника. Коли у нас в чисельнику є дріб з квадратним коренем, ми спочатку спрощуємо квадратний корінь. Тоді ми можемо шукати загальні фактори.
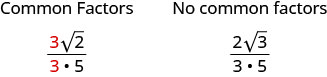
Спростити:\(\frac{\sqrt{54}}{6}\)
- Відповідь
-
\(\frac{\sqrt{54}}{6}\) Спростити радикал. \(\frac{\sqrt{9}·\sqrt{6}}{6}\) Спростити. \(\frac{3\sqrt{6}}{6}\) Прибрати загальні фактори. \(\frac{3\sqrt{6}}{3·2}\) Спростити. \(\frac{\sqrt{6}}{2}\)
Спростити:\(\frac{\sqrt{32}}{8}\).
- Відповідь
-
\(\frac{\sqrt{2}}{2}\)
Спростити:\(\frac{\sqrt{75}}{15}\).
- Відповідь
-
\(\frac{\sqrt{3}}{3}\)
Спростити:\(\frac{6−\sqrt{24}}{12}\).
- Відповідь
-
\(\frac{6−\sqrt{24}}{12}\) Спростити радикал. \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\) Спростити. \(\frac{6−2\sqrt{6}}{12}\) Фактор загального множника з чисельника. \(\frac{2(3−\sqrt{6})}{12}\) Прибрати загальні фактори. \(\frac{2(3−\sqrt{6})}{2·6}\) Спростити. \(\frac{3−\sqrt{6}}{6}\)
Спростити:\(\frac{8−\sqrt{40}}{10}\).
- Відповідь
-
\(\frac{4−\sqrt{10}}{5}\)
Спростити:\(\frac{10−\sqrt{75}}{20}\).
- Відповідь
-
\(\frac{5−\sqrt{3}}{4}\)
Ми використали частку властивості квадратних коренів для спрощення квадратних коренів дробів. Коефіцієнтна властивість квадратних коренів говорить
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\),\(b \ne 0\).
Іноді нам потрібно буде використовувати частку властивість квадратних коренів «навпаки», щоб спростити дріб з квадратними коренями.
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\),\(b \ne 0\).
Ми перепишемо часткове властивість квадратних коренів, щоб ми побачили обидва способи разом. Пам'ятайте: ми припускаємо, що всі змінні більше або рівні нулю, так що їх квадратні корені є дійсними числами.
Якщо a, b є невід'ємними дійсними числами і\(b \ne 0\), то
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)і\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
Ми будемо використовувати частку властивість квадратних коренів «навпаки», коли дріб, з якого ми починаємо, є часткою двох квадратних коренів, і жоден радиканд не є ідеальним квадратом. Коли ми записуємо дріб в одному квадратному корені, ми можемо знайти спільні множники в чисельнику та знаменнику.
Спростити:\(\frac{\sqrt{27}}{\sqrt{75}}\)
- Відповідь
-
\(\frac{\sqrt{27}}{\sqrt{75}}\) Жоден радиканд не є ідеальним квадратом, тому перепишіть, використовуючи часткову властивість квадратного кореня. \(\sqrt{\frac{27}{75}}\) Видаліть загальні множники в чисельнику і знаменнику. \(\sqrt{\frac{9}{25}}\) Спростити. \(\frac{3}{5}\)
Спростити:\(\frac{\sqrt{48}}{\sqrt{108}}\)
- Відповідь
-
\(\frac{2}{3}\)
Спростити:\(\frac{\sqrt{96}}{\sqrt{54}}\)
- Відповідь
-
\(\frac{4}{3}\)
Ми будемо використовувати Quotient властивість для експонентів\(\frac{a^m}{a^n}=a^{m−n}\), коли у нас є змінні з показниками в радикандах.
Спростити:\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
- Відповідь
-
\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\) Жоден радиканд не є ідеальним квадратом, тому перепишіть, використовуючи часткову властивість квадратного кореня. \(\sqrt{\frac{6y^5}{2y}}\) Видаліть загальні множники в чисельнику і знаменнику. \(\sqrt{3y^4}\) Спростити. \(y^2\sqrt{3}\)
Спростити:\(\frac{\sqrt{12r^3}}{\sqrt{6r}}\).
- Відповідь
-
\(r\sqrt{2}\)
Спростити:\(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)
- Відповідь
-
\(p^2\sqrt{7}\)
Спростити:\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
- Відповідь
-
\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\) Перепишіть, використовуючи коефіцієнтну властивість квадратних коренів. \(\sqrt{\frac{72x^3}{162x}}\) Видаліть загальні фактори. \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\) Спростити. \(\sqrt{\frac{4x^2}{9}}\) Спростити радикал. \(\frac{2x}{3}\)
Спростити:\(\frac{\sqrt{50s^3}}{\sqrt{128s}}\).
- Відповідь
-
\(\frac{5s}{8}\)
Спростити:\(\frac{\sqrt{75q^5}}{\sqrt{108q}}\).
- Відповідь
-
\(\frac{5q^2}{6}\)
Спростити:\(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\).
- Відповідь
-
\(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\) Перепишіть, використовуючи коефіцієнтну властивість квадратних коренів. \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\) Видаліть загальні фактори. \ (\ sqrt {\ frac {49b^4} {a^2}}\ Спростити радикал. \(\frac{7b^2}{a}\)
Спростити:\(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\).
- Відповідь
-
\(\frac{9x^2}{y^2}\)
Спростити:\(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\).
- Відповідь
-
\(\frac{10n^3}{m}\)
Раціоналізувати знаменник з одним терміном
До того, як калькулятор став інструментом повсякденного життя, для пошуку приблизних значень квадратних коренів використовувалися таблиці квадратних коренів. На малюнку зображена частина таблиці з квадратів і квадратних коренів. Квадратні корені наближені до п'яти знаків після коми в цій таблиці.
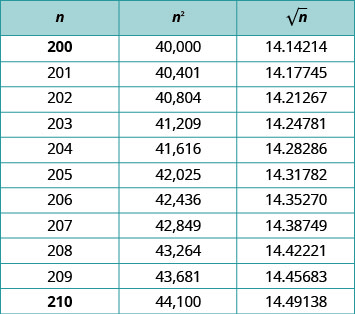
Якщо комусь потрібно було наблизити дріб з квадратним коренем у знаменнику, це означало робити довге ділення з п'ятьма десятковими місцями. Це був дуже громіздкий процес.
З цієї причини був розроблений процес, який отримав назву раціоналізація знаменника. Дріб з радикалом в знаменнику перетворюється в еквівалентний дріб, знаменником якого є ціле число. Цей процес використовується і сьогодні і корисний і в інших областях математики теж.
Процес перетворення дробу з радикалом в знаменнику в еквівалентний дріб, знаменником якого є ціле число, називається раціоналізацією знаменника.
Квадратні корені чисел, які не є ідеальними квадратами, є ірраціональними числами. Коли ми раціоналізуємо знаменник, пишемо еквівалентний дріб з раціональним числом в знаменнику.
Давайте розглянемо числовий приклад.
\[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]
Але ми можемо знайти дріб еквівалентний\(\frac{1}{\sqrt{2}}\) шляхом множення чисельника і знаменника на\(\sqrt{2}\).
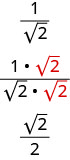
Тепер, якщо нам потрібно приблизне значення, ділимо\(2) \overline{1.41421}\). Це набагато простіше.
Незважаючи на те, що у нас є калькулятори, доступні майже скрізь, фракція з радикалом у знаменнику все одно повинна бути раціоналізована. Не вважається спрощеним, якщо знаменник містить квадратний корінь.
Аналогічно квадратний корінь не вважається спрощеним, якщо радикаі містить дріб.
Квадратний корінь вважається спрощеним, якщо є
- відсутність ідеально-квадратних факторів у радиканді
- немає дробів в радиканді
- немає квадратних коренів у знаменнику дробу
Щоб раціоналізувати знаменник, використовуємо властивість, яка\((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.
Ми будемо використовувати цю властивість для раціоналізації знаменника в наступному прикладі.
Спростити:\(\frac{4}{\sqrt{3}}\).
- Відповідь
-
Щоб прибрати квадратний корінь від знаменника, множимо його на себе. Щоб дроби були еквівалентними, множимо і чисельник, і знаменник на один і той же коефіцієнт.
\(\frac{4}{\sqrt{3}}\)
Помножте чисельник і знаменник на\(\sqrt{3}\)\(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\) Спростити. \(\frac{4\sqrt{3}}{3}\)
Спростити:\(\frac{5}{\sqrt{3}}\).
- Відповідь
-
\(\frac{5\sqrt{3}}{3}\)
Спростити:\(\frac{6}{\sqrt{5}}\).
- Відповідь
-
\(\frac{6\sqrt{5}}{5}\)
Спростити:\(−\frac{8}{3\sqrt{6}}\)
- Відповідь
-
Щоб прибрати квадратний корінь від знаменника, множимо його на себе. Щоб дроби були еквівалентними, множимо і чисельник, і знаменник на\(\sqrt{6}\).
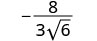
Помножте і чисельник, і знаменник на\(\sqrt{6}\). 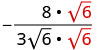
Спростити. 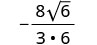
Видаліть загальні фактори. 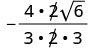
Спростити. 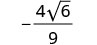
Спростити:\(\frac{5}{2\sqrt{5}}\).
- Відповідь
-
\(\frac{\sqrt{5}}{2}\)
Спростити:\(−\frac{9}{4\sqrt{3}}\).
- Відповідь
-
\(−\frac{3\sqrt{3}}{4}\)
Завжди спочатку спрощуйте радикал у знаменнику, перш ніж раціоналізувати його. Таким чином, цифри залишаються меншими і з ними легше працювати.
Спростити:\(\sqrt{\frac{5}{12}}\).
- Відповідь
-
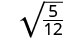
Дріб не є ідеальним квадратом, тому перепишіть, використовуючи
властивість частки.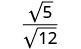
Спростити знаменник. 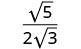
Раціоналізувати знаменник. 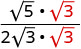
Спростити. 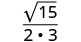
Спростити. 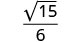
Спростити:\(\sqrt{\frac{7}{18}}\).
- Відповідь
-
\(\frac{\sqrt{14}}{6}\)
Спростити:\(\sqrt{\frac{3}{32}}\).
- Відповідь
-
\(\frac{\sqrt{6}}{8}\)
Спростити:\(\sqrt{\frac{11}{28}}\)
- Відповідь
-
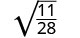
Перепишіть, використовуючи властивість Коефіцієнт. 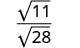
Спростити знаменник. 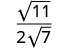
Раціоналізувати знаменник. 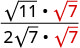
Спростити. 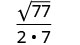
Спростити. 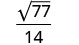
Спростити:\(\sqrt{\frac{3}{27}}\).
- Відповідь
-
\(\frac{1}{3}\)
Спростити:\(\sqrt{\frac{10}{50}}\)
- Відповідь
-
\(\frac{\sqrt{5}}{5}\)
Раціоналізувати двочленний знаменник
Коли знаменником дробу є сума або різниця з квадратними коренями, для раціоналізації знаменника ми використовуємо візерунок «Добуток сполучених».
\[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]
Коли ми множимо біном, який включає квадратний корінь за його сполученим, продукт не має квадратних коренів.
Спростити:\(\frac{4}{4+\sqrt{2}}\).
- Відповідь
-
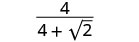
Помножте чисельник і знаменник на сполучений знаменник. 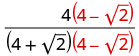
Помножте відмінювання в знаменнику. 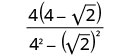
Спростити знаменник. 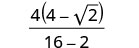
Спростити знаменник. 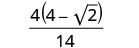
Видаліть загальні множники з чисельника і знаменника. 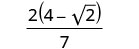
Ми залишаємо чисельник у факторованому вигляді, щоб полегшити пошук загальних факторів після спрощення знаменника.
Спростити:\(\frac{2}{2+\sqrt{3}}\).
- Відповідь
-
\(\frac{2(2−\sqrt{3})}{1}\)
Спростити:\(\frac{5}{5+\sqrt{3}}\).
- Відповідь
-
\(\frac{5(5−\sqrt{3})}{22}\)
Спростити:\(\frac{5}{2−\sqrt{3}}\).
- Відповідь
-
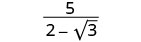
Помножте чисельник і знаменник на сполучений знаменник. 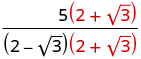
Помножте відмінювання в знаменнику. 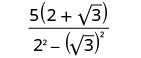
Спростити знаменник. 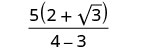
Спростити знаменник. 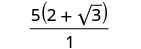
Спростити. 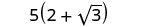
Спростити:\(\frac{3}{1−\sqrt{5}}\).
- Відповідь
-
\(−\frac{3(1+\sqrt{5})}{4}\)
Спростити:\(\frac{2}{4−\sqrt{6}}\).
- Відповідь
-
\(\frac{4+\sqrt{6}}{5}\)
Спростити:\(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\).
- Відповідь
-
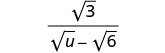
Помножте чисельник і знаменник на сполучений знаменник. 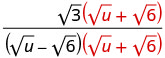
Помножте відмінювання в знаменнику. 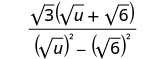
Спростити знаменник. 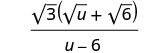
Спростити:\(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- Відповідь
-
\(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)
Спростити:\(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\).
- Відповідь
-
\(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)
Спростити:\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\).
- Відповідь
-
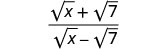
Помножте чисельник і знаменник на сполучений знаменник. 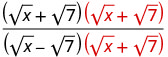
Помножте відмінювання в знаменнику. 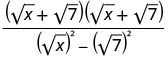
Спростити знаменник. 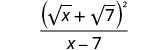
Ми не ставимо в квадрат чисельник. У факторованій формі ми бачимо, що немає загальних факторів, які слід видалити з чисельника та знаменника.
Спростити:\(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).
- Відповідь
-
\(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)
Спростити:\(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\).
- Відповідь
-
\(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)
Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з розділенням та раціоналізацією.
- Розподіл і раціоналізація
Ключові поняття
- Коефіцієнтна властивість квадратних коренів
- Якщо a, b є невід'ємними дійсними числами і\(b \ne 0\), то
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)і\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
- Якщо a, b є невід'ємними дійсними числами і\(b \ne 0\), то
- Спрощені квадратні коріння
Квадратний корінь вважається спрощеним, якщо є- немає ідеальних квадратних факторів у радиканді
- немає дробів в радиканді
- немає квадратних коренів у знаменнику дробу
Глосарій
- раціоналізація знаменника
- Процес перетворення дробу з радикалом в знаменнику в еквівалентний дріб, знаменником якого є ціле число, називається раціоналізацією знаменника.
