Skip to main content
LibreTexts - Ukrayinska

6.3: Множення многочленів

  1. Last updated
  2. Save as PDF
  • Page ID
    58991

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Помножити многочлен на мономіал
    • Помножити біноміал на біноміал
    • Помножте триноміал на біноміал
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Розподілити:\(2(x+3)\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 1.10.31.
    2. Поєднуйте подібні терміни:\(x^{2}+9x+7x+63\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 1.3.37.

    Помножити многочлен на мономіал

    Ми використали властивість Distributive для спрощення виразів на кшталт\(2(x−3)\). Ви помножили обидва члени в дужках,\(x\) і\(3\), на\(2\), щоб отримати\(2x−6\). З новою лексикою цієї глави ви можете сказати, що ви множили біном\(x−3\), на мономіал,\(2\).

    Множення біноміала на мономіал для вас не є новим! Ось приклад:

    Вправа\(\PageIndex{1}\)

    Помножити:\(4(x+3)\).

    Відповідь
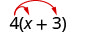
      4 рази х плюс 3. Дві стрілки простягаються від 4, закінчуючись на х і 3.
    Розподілити. \(4 \cdot x+4 \cdot 3\)
    Спростити. \(4 x+12\)
    Вправа\(\PageIndex{2}\)

    Помножити:\(5(x+7)\).

    Відповідь

    5х+35

    Вправа\(\PageIndex{3}\)

    Помножити:\(3(y+13)\).

    Відповідь

    3 роки +39

    Вправа\(\PageIndex{4}\)

    Помножити: y (y−2).

    Відповідь
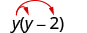
      y раз у мінус 2. Дві стрілки відходять від коефіцієнта y, що закінчуються на y і мінус 2 в дужках.
    Розподілити. \(y \cdot y-y \cdot 2\)
    Спростити. \(y^{2}-2 y\)
    Вправа\(\PageIndex{5}\)

    Помножити:\(x(x−7)\).

    Відповідь

    \(x^{2}-7 x\)

    Вправа\(\PageIndex{6}\)

    Помножити:\(d(d−11)\).

    Відповідь

    \(d^{2}-11d\)

    Вправа\(\PageIndex{7}\)

    Помножити:\(7x(2 x+y)\)

    Відповідь
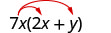
      7 х разів 2 х плюс y. дві стрілки простягаються від 7х, закінчуючись на 2x і y.
    Розподілити. 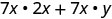7 х разів 2 х плюс 7 х разів у.
    Спростити. 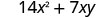14 х в квадраті плюс 7 х у.
    Вправа\(\PageIndex{8}\)

    Помножити:\(5x(x+4 y)\)

    Відповідь

    \(5 x^{2}+20 x y\)

    Вправа\(\PageIndex{9}\)

    Помножити:\(2p(6 p+r)\)

    Відповідь

    \(12 p^{2}+2 p r\)

    Вправа\(\PageIndex{10}\)

    Помножити:\(-2 y\left(4 y^{2}+3 y-5\right)\)

    Відповідь
      Негативний 2 у разів 4 y в квадраті плюс 3 у мінус 5. Три стрілки простягаються від негативних 2 y, закінчуючись на 4 y в квадраті, 3 y, і мінус 5.
    Розподілити. 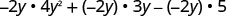Негативний 2 у разів 4 y в квадраті плюс негативний 2 y разів 3 y мінус негативний 2 y разів 5.
    Спростити. 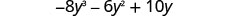Негативні 8 y в кубі мінус 6 у квадраті плюс 10 у.
    Вправа\(\PageIndex{11}\)

    Помножити:\(-3 y\left(5 y^{2}+8 y-7\right)\)

    Відповідь

    \(-15 y^{3}-24 y^{2}+21 y\)

    Вправа\(\PageIndex{12}\)

    Помножити:\(4x^{2}\left(2 x^{2}-3 x+5\right)\)

    Відповідь

    \(8 x^{4}-24 x^{3}+20 x^{2}\)

    Вправа\(\PageIndex{13}\)

    Помножити:\(2x^{3}\left(x^{2}-8 x+1\right)\)

    Відповідь
      2 х куб разів х квадрат мінус 8 х плюс 1. Три стрілки простягаються від 2 х в кубі, закінчуючись на х квадрат, мінус 8 х, і 1.
    Розподілити. \(2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1\)
    Спростити. \(2 x^{5}-16 x^{4}+2 x^{3}\)
    Вправа\(\PageIndex{14}\)

    Множення: 4\(x\left(3 x^{2}-5 x+3\right)\)

    Відповідь

    \(12 x^{3}-20 x^{2}+12 x\)

    Вправа\(\PageIndex{15}\)

    Помножити:\(-6 a^{3}\left(3 a^{2}-2 a+6\right)\)

    Відповідь

    \(-18 a^{5}+12 a^{4}-36 a^{3}\)

    Вправа\(\PageIndex{16}\)

    Помножити:\((x+3) p\)

    Відповідь
    Мономіал - другий фактор. x плюс 3, в дужках, раз p. дві стрілки простягаються від p, що закінчуються на х і 3.
    Розподілити. \(x \cdot p+3 \cdot p\)
    Спростити. \ (\ х р+3 р)
    Вправа\(\PageIndex{17}\)

    Помножити:\((x+8) p\)

    Відповідь

    \(x p+8 p\)

    Вправа\(\PageIndex{18}\)

    Помножити:\((a+4) p\)

    Відповідь

    \(a p+4 p\)

    Помножте біноміал на біноміал

    Подібно до того, як існують різні способи представлення множення чисел, існує кілька методів, які можуть бути використані для множення біноміального на біноміальне число. Ми почнемо з використання розподільної властивості.

    Помножити біноміал на біноміал за допомогою розподільної властивості

    Подивіться на Вправу\(\PageIndex{16}\), де ми помножили біном на мономіал.

    Інструкції Вираз
    Початкові вирази x плюс 3, в дужках, раз p. дві стрілки простягаються від p, що закінчуються на х і 3.
    Ми розподілили їх\(p\), щоб отримати: 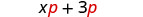х р плюс 3 п.
    Що робити, якщо у нас\((x + 7)\) замість\(p\)? х плюс 3 помножити на х плюс 7. Дві стрілки простягаються від x плюс 7, закінчуючись на x і 3 в першому біном.
    Розподілити\((x + 7)\). 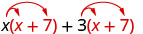Сума двох добутків. Твір х і х плюс 7, плюс твір 3 і х плюс 7.
    Розподіліть ще раз. \(x^{2}+7 x+3 x+21\)
    Поєднуйте подібні терміни. \(x^{2}+10 x+21\)

    Зверніть увагу, що перед об'єднанням подібних термінів у вас було чотири терміни. Ви помножили два члени першого біноміала на два члени другого двочлена - чотири множення.

    Вправа\(\PageIndex{19}\)

    Помножити:\((y+5)(y+8)\)

    Відповідь
      Добуток двох біноміалів, у плюс 5 і у плюс 8. Дві стрілки простягаються від y плюс 8, закінчуючись на y і 5 в першому біном.
    Розподілити (у + 8). 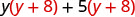Сума двох добутків, добуток y і y плюс 8, плюс добуток 5 і y плюс 8.
    Розподілити ще раз \(y^{2}+8 y+5 y+40\)
    Поєднуйте подібні терміни. \ (\ y^ {2} +13 й+40)
    Вправа\(\PageIndex{20}\)

    Помножити:\((x+8)(x+9)\)

    Відповідь

    \(x^{2}+17 x+72\)

    Вправа\(\PageIndex{21}\)

    Помножити:\((5 x+9)(4 x+3)\)

    Відповідь

    \(20 x^{2}+51 x+27\)

    Вправа\(\PageIndex{22}\)

    Помножити:\((2 y+5)(3 y+4)\)

    Відповідь
      Добуток двох біноміалів, 2 у плюс 5 і 3 у плюс 4. Дві стрілки простягаються від 3y плюс 4, закінчуючись на 2y і 5 в першому біном.
    Розподілити (3 у + 4). 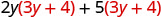Сума двох добутків, добуток 2 у і 3 у плюс 4, плюс добуток 5 і 3 у плюс 4.
    Розподілити ще раз \(6 y^{2}+8 y+15 y+20\)
    Поєднуйте подібні терміни. \(6 y^{2}+23 y+20\)
    Вправа\(\PageIndex{23}\)

    Помножити:\((3 b+5)(4 b+6)\)

    Відповідь

    \(12 b^{2}+38 b+30\)

    Вправа\(\PageIndex{24}\)

    Помножити:\((a+10)(a+7)\)

    Відповідь

    \(a^{2}+17 a+70\)

    Вправа\(\PageIndex{25}\)

    Помножити:\((4 y+3)(2 y-5)\)

    Відповідь
      Приклад 6.36.jpg
    Розподілити. 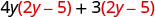Сума двох добутків, добуток 4у і 2у мінус 5, плюс добуток 3 і 2у мінус 5.
    Розподіліть ще раз. \(8 y^{2}-20 y+6 y-15\)
    Поєднуйте подібні терміни. \(8 y^{2}-14 y-15\)
    Вправа\(\PageIndex{26}\)

    Помножити:\((5 y+2)(6 y-3)\)

    Відповідь

    \(30 y^{2}-3 y-6\)

    Вправа\(\PageIndex{27}\)

    Помножити:\((3 c+4)(5 c-2)\)

    Відповідь

    \(15 c^{2}+14 c-8\)

    Вправа\(\PageIndex{28}\)

    Помножити:\((x-2)(x-y)\)

    Відповідь
      Добуток двох двочленів, x мінус 2 і x мінус y. Дві стрілки простягаються від x мінус y, що закінчуються на x і 2 у першому біном.
    Розподілити. Різниця двох продуктів. Твір х і х мінус 7, мінус добуток 2 і х мінус у.
    Розподіліть ще раз. \(x^{2}-x y-2 x+2 y\)
    Немає подібних термінів для комбінування.  
    Вправа\(\PageIndex{29}\)

    Помножити:\((a+7)(a-b)\)

    Відповідь

    \(a^{2}-a b+7 a-7 b\)

    Вправа\(\PageIndex{30}\)

    Помножити:\((x+5)(x-y)\)

    Відповідь

    \(x^{2}-x y+5 x-5 y\)

    Помножити біноміал на біноміал за допомогою методу FOIL

    Пам'ятайте, що коли ви множите біном на біном, ви отримуєте чотири члени. Іноді ви можете комбінувати подібні терміни, щоб отримати триноміал, але іноді, як у Вправи\(\PageIndex{28}\), немає подібних термінів для поєднання.

    Давайте ще раз розглянемо останній приклад і звернемо особливу увагу на те, як ми отримали чотири терміни.

    \[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y}\end{array} \nonumber\]

    Звідки взявся перший термін?\(x^{2}\)

    Ця цифра пояснює, як помножити біноміал за допомогою методу FOIL. Він має дві колонки, з письмовими інструкціями зліва та математикою праворуч. У верхній частині малюнка текст в лівій колонці говорить «Це добуток х і х, перші члени в х мінус 2 і х мінус у». У правій колонці показано добуток x мінус 2 і x мінус y. Стрілка простягається від x в x мінус 2 і закінчується на x мінус y. Нижче наведено слово «Перший». Один рядок вниз, текст у лівій колонці говорить: «Наступні терміни, негативні xy, є добутком x і негативного y, двох зовнішніх членів». У правій колонці - добуток x мінус 2 і x мінус y, з іншою стрілкою, що тягнеться від x в x мінус 2 до y в x мінус y. Один рядок вниз, текст у лівій колонці говорить: «Третій термін, негативний 2 х, є добутком негативних 2 і х, двох внутрішніх термінів». У правій колонці знаходиться добуток x мінус 2 і x мінус y з третьою стрілкою, що тягнеться від мінус 2 в x мінус 2 і закінчується на x в x мінус y. В останньому рядку текст у лівій колонці говорить: «І останній термін, плюс 2y, походить від множення двох останніх членів, негативних 2 та негативних y». У правій колонці - добуток х мінус 2 і х мінус у, з четвертою стрілкою, що тягнеться від мінус 2 в х мінус 2 до мінус у х мінус у.

    Ми скорочуємо «Перший, Зовнішній, Внутрішній, Останній» як FOIL. Букви позначають 'F перший, O Outer, I внутрішній, L ast'. Слово FOIL легко запам'ятати і гарантує, що ми знаходимо всі чотири продукти.

    \[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y} \\ {F \qquad O\qquad I\qquad L}\end{array}\]

    Давайте розглянемо (х+3) (х+7).

    Розподільна власність ФОЛЬГА
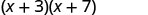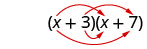    Твір х плюс 3 і х плюс 7. Добуток х плюс 3 і х плюс у Стрілка простягається від х в х плюс 3 до х в х плюс 7. Друга стрілка простягається від х в х плюс 3 до 7 в х плюс 7. Третя стрілка простягається від 3 в х плюс 3 до х х плюс 7. Четверта стрілка простягається від 3 в х плюс 3 до 7 в х плюс 7.
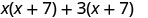    Сума двох добутків, добутку х і х плюс 7, і добутку 3 і х плюс 7.  
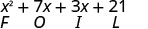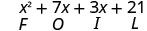    х в квадраті плюс 7 х плюс 3 х плюс 21. Нижче х квадрат - буква F, нижче 7 х - буква O, нижче 3 х - буква I, а нижче 21 - буква L, написання FOIL. х в квадраті плюс 7 х плюс 3 х плюс 21. Нижче х квадрат - буква F, нижче 7 х - буква O, нижче 3 х - буква I, а нижче 21 - буква L, написання FOIL.
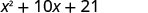    х в квадраті плюс 10 х плюс 21. \(x^{2}+10 x+21\)

    Зверніть увагу, як терміни в третьому рядку відповідають шаблону FOIL.

    Тепер ми зробимо приклад, де ми використовуємо шаблон FOIL для множення двох біноміалів.

    Вправа\(\PageIndex{31}\): How to Multiply a Binomial by a Binomial using the FOIL Method

    Множення за допомогою методу FOIL:\((x+5)(x+9)\)

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і п'ять рядків. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Другий і третій стовпці містять математику. У верхньому рядку таблиці в першій клітинці зліва написано «Крок 1. Перші ряди помножте». Другий стовпець містить добуток бічленів х плюс 5 і х плюс 9. Нижче наведено добуток х плюс 5 і х плюс 9 знову, зі стрілкою, що простягається від x у першому біноміальному до x у другому біном. Третій стовпець містить x у квадраті плюс порожній плюс порожній плюс порожній. Нижче х в квадраті знаходиться буква F, а під кожною з трьох заготовок - букви O, I і L відповідно.
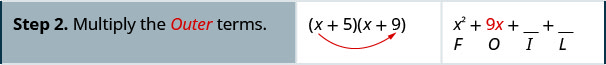
    У другому рядку в першій клітинці написано «Крок 2. Помножте зовнішні долі». У другій клітинці є добуток х плюс 5 і х плюс 9 знову, зі стрілкою, що простягається від x у першому біном до 9 у другому біноміальному. Третя комірка містить x у квадраті плюс 9x плюс порожній плюс порожній, з літерою F під x квадратом, O під 9x, а I та L під двома пробілами.
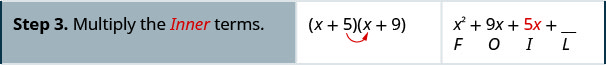
    У третьому ряду в першій клітинці написано «Крок 3. Помножте внутрішні терміни». Друга клітинка містить добуток х плюс 5 і х плюс 9 знову, зі стрілкою, що простягається від 5 у першому біноміале до x у другому біном. Третя комірка містить х у квадраті плюс 9x плюс 5x плюс порожній, з F під x в квадраті, O під 9x, I під 5x, і L під порожнім.
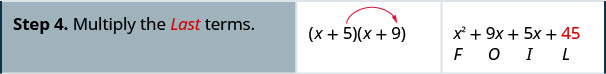
    У четвертому ряду в першій клітинці написано «Крок 4. Помножте останні терміни». У другій клітинці - добуток х плюс 5 і х плюс 9 знову, зі стрілкою, що тягнеться від 5 в першому біном до 9 у другому біном. Третя комірка містить х у квадраті плюс 9x плюс 6x плюс 45, з F під x в квадраті, O під 9x, I під 6x, а L під 45.
    У заключному рядку перша клітинка читає «Крок 5. Поєднуйте подібні терміни, коли це можливо». Друга клітинка порожня. Третя комірка містить остаточний вираз: x у квадраті плюс 15x плюс 45.

    Вправа\(\PageIndex{32}\)

    Множення за допомогою методу FOIL:\((x+6)(x+8)\)

    Відповідь

    \(x^{2}+14 x+48\)

    Вправа\(\PageIndex{33}\)

    Множення за допомогою методу FOIL:\((y+17)(y+3)\)

    Відповідь

    \(y^{2}+20 y+51\)

    Нижче ми підсумуємо кроки методу FOIL. Метод FOIL застосовується лише до множення бічленів, а не інших поліномів!

    МНОЖТЕ ДВА БІНОМІАЛИ МЕТОДОМ ФОЛЬГИ
    .

    Коли ви множите методом FOIL, малювання ліній допоможе вашому мозку зосередитися на візерунку і полегшить його нанесення.

    Вправа\(\PageIndex{34}\)

    Помножити:\((y−7)(y+4)\).

    Відповідь

    Ця цифра має три стовпці, з написаними інструкціями в першому стовпці і математикою у другому і третьому стовпцях. У верхній частині малюнка текст в першому стовпці говорить «Помножте перші члени». Другий стовпець містить добуток двох бічленів, y мінус 7 і y плюс 4, зі стрілкою, що простягається від y в першому біном до y у другому біном. Третій стовпець містить y в квадраті плюс порожній плюс порожній плюс порожній. Під y квадратом знаходиться буква F, а під кожним порожнім - літери O, I та L відповідно. Один рядок вниз, текст у першому стовпці говорить «Помножте зовнішні члени». Другий стовпець містить добуток y мінус 7 і y плюс 4 знову, з другою стрілкою, що простягається від y в першому біном до 4 у другому біном. Третій стовпець містить y в квадраті плюс 4y плюс порожній плюс порожній. Нижче y в квадраті F, нижче 4y - O, а під пробілами I і L. Один рядок вниз, текст у першому стовпці говорить «Помножте внутрішні члени». Середній стовпець містить добуток y мінус 7 і y плюс 4 знову, з третьою стрілкою, що йде від мінуса 7 в першому біноміале до y у другому біном. Третій стовпець містить y в квадраті плюс 4y мінус 7y плюс порожній. Один рядок вниз, текст у першому стовпці говорить «Помножте останні члени». Другий стовпець містить добуток y мінус 7 і y плюс 4 знову, з четвертою стрілкою, що простягається від мінус 7 в першому біноміале до 4 у другому біном. У третьому стовпці є повний вираз, y в квадраті плюс 4y мінус 7y мінус 28, з кожною буквою FOIL під кожним з термінів. У нижній частині зображення текст у першому стовпці говорить «Об'єднати як терміни». У правій колонці знаходиться y в квадраті мінус 3y мінус 28.

    Вправа\(\PageIndex{35}\)

    Помножити:\((x−7)(x+5)\).

    Відповідь

    \(x^{2}-2 x-35\)

    Вправа\(\PageIndex{36}\)

    Помножити: (b−3) (b+6).

    Відповідь

    \(b^{2}+3 b-18\)

    Вправа\(\PageIndex{37}\)

    Помножити:\((4x+3)(2x−5)\).

    Відповідь

    Ця цифра має три стовпчики. У верхній частині малюнка другий стовпець містить добуток двох біноміалів, 4х плюс 3 і 2х мінус 5. Один рядок вниз, текст у першому стовпці говорить: «Помножте перші члени. 4x на 2 рази». Другий стовпець містить 8x квадрат плюс порожній плюс порожній плюс порожній. Під 8x квадратом знаходиться буква F, а під кожним порожнім - літери O, I та L відповідно. Один рядок вниз, текст у першому стовпці говорить: «Помножте зовнішні члени. 4x на негативні 5». Другий стовпець містить 8x в квадраті мінус 20x плюс порожній плюс порожній. Нижче 8x квадрат F, нижче 20x - O, а під пробілами I і L. Один рядок вниз, текст у першому стовпці говорить: «Помножте внутрішні члени. 3 рази 2x». Другий стовпець містить 8x в квадраті мінус 20x плюс 6x плюс порожній. Один рядок вниз, текст у першому стовпці говорить: «Помножте останні члени. 3 рази негативні 5». Другий стовпець містить повний вираз, 8x у квадраті мінус 20x плюс 6x мінус 15, з кожною буквою FOIL під кожним з термінів. У нижній частині зображення текст у першому стовпці говорить «Об'єднати як терміни». У правій колонці знаходиться 8х в квадраті мінус 14х мінус 15. У третьому стовпці знову добуток двох бічленів, 4x плюс 3 рази 2x мінус 5. Стрілка простягається від 4x у першому біноміальному до 2x у другому біном. Друга стрілка простягається від 4x у першому біноміальному до мінус 5 у другому біном. Третя стрілка простягається від 3 у першому біном до 2x у другому біном. Четверта стрілка простягається від 3 у першому біном до мінус 5 у другому біном.

    Вправа\(\PageIndex{38}\)

    Помножити:\((3x+7)(5x−2)\).

    Відповідь

    \(15 x^{2}+29 x-14\)

    Вправа\(\PageIndex{39}\)

    Помножити:\((4y+5)(4y−10)\).

    Відповідь

    \(16 y^{2}-20 y-50\)

    Кінцевими продуктами в останніх чотирьох прикладах були тріноміали, оскільки ми могли поєднати два середні терміни. Це не завжди так.

    Вправа\(\PageIndex{40}\)

    Помножити:\((3x−y)(2x−5)\).

    Відповідь
      \((3 x-y)(2 x-5)\)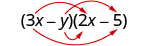
      Стрілка простягається від 3 х у першому біном до 2 х у другому біном. Друга стрілка простягається від 3 х у першому біном до мінус 5 у другому біном. Третя стрілка простягається від y в першому біном до 2 x у другому біном. Четверта стрілка простягається від y в першому біном до мінус 5 у другому біном.
    Помножте Першу. 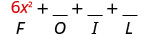6 х в квадраті плюс порожній плюс порожній плюс порожній. Під квадратом 6 х знаходиться буква F.
    Помножте Зовнішнє. 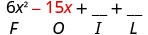6 х в квадраті мінус 15 х плюс порожній плюс порожній. Під 15 х знаходиться буква О.
    Помножте Внутрішнє. 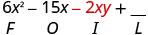6x в квадраті мінус 15x мінус 2xy плюс порожній. Під мінус 2 х у знаходиться буква I.
    Помножте Останній. 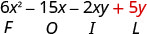6 х в квадраті мінус 15 х мінус 2 х у плюс 5 у, під 5 y - буква L.
    Поєднуйте як терміни - їх немає. \(6 x^{2}-15 x-2 x y+5 y\)
    Вправа\(\PageIndex{41}\)

    Помножити: (10c−d) (c−6).

    Відповідь

    \(10 c^{2}-60 c-c d+6 d\)

    Вправа\(\PageIndex{42}\)

    Помножити: (7x−y) (2x−5).

    Відповідь

    \(14 x^{2}-35 x-2 x y+10 y\)

    Будьте обережні з показниками в наступному прикладі.

    Вправа\(\PageIndex{43}\)

    Помножити:\(\left(n^{2}+4\right)(n-1)\)

    Відповідь
      \(\left(n^{2}+4\right)(n-1)\)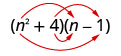
      Добуток двох двочленів, n в квадраті плюс 4 і n мінус 1. Стрілка простягається від n квадратів у першому біноміале до n у другому біном. Друга стрілка простягається від n квадратів у першому біноміале до мінус 1 у другому біном. Третя стрілка простягається від 4 у першому біноміальному до n у другому біном. Четверта стрілка простягається від 4 у першому біном до мінус 1 у другому біном.
    Помножте Першу. 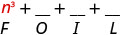N куб плюс порожній плюс порожній плюс порожній. Під n кубами знаходиться буква F.
    Помножте Зовнішнє. 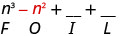N куб мінус п в квадраті плюс порожній плюс порожній. Під мінусом n в квадраті знаходиться буква O.
    Помножте Внутрішнє. 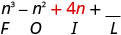n куб мінус п в квадраті плюс 4 п плюс порожній. Під 4 п - буква I.
    Помножте Останній. 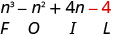n куб мінус п в квадраті плюс 4 п мінус 4. Під мінус 4 - буква L.
    Поєднуйте як терміни - їх немає. \ (\ n^ {3} -n^ {2} +4 n-4)
    Вправа\(\PageIndex{44}\)

    Помножити:\(\left(x^{2}+6\right)(x-8)\)

    Відповідь

    \(x^{3}-8 x^{2}+6 x-48\)

    Вправа\(\PageIndex{45}\)

    Помножити:\(\left(y^{2}+7\right)(y-9)\)

    Відповідь

    \(y^{3}-9 y^{2}+7 y-63\)

    Вправа\(\PageIndex{46}\)

    Помножити:\((3 p q+5)(6 p q-11)\)

    Відповідь
      \((3 p q+5)(6 p q-11)\)  
    Помножте Першу. 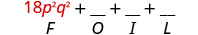18 р в квадраті q в квадраті плюс порожній плюс порожній плюс порожній. Під 18 p квадратом q в квадраті знаходиться буква F. Твір двох бічленів, 3 р q плюс 5 і 6 р q мінус 11. Стрілка простягається від 3 p q в першому біноміале до 6 p q у другому біном. Друга стрілка простягається від 3 p q в першому біном до мінус 11 у другому біном. Третя стрілка простягається від 5 в першому біном до 6 p q у другому біном. Четверта стрілка простягається від 5 у першому біном до мінус 11 у другому біном.
    Помножте Зовнішнє. 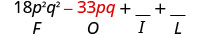18 р в квадраті q в квадраті мінус 33 р q плюс порожній плюс порожній. Під мінус 33 р q - буква О.
    Помножте Внутрішнє. 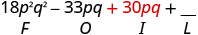18 р в квадраті q в квадраті мінус 33 р q плюс 30 р q плюс порожній. Під 30 р q - буква I.  
    Помножте Останній. 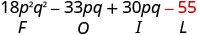18 р в квадраті q в квадраті мінус 33 р q плюс 30 р q мінус 55. Під мінус 55 - буква L.  
    Поєднуйте як терміни - їх немає. \(18 p^{2} q^{2}-3 p q-55\)
    Вправа\(\PageIndex{47}\)

    Помножити:\((2 a b+5)(4 a b-4)\)

    Відповідь

    \(8 a^{2} b^{2}+12 a b-20\)

    Вправа\(\PageIndex{48}\)

    Помножити:\((2 x y+3)(4 x y-5)\)

    Відповідь

    \(8 x^{2} y^{2}+2 x y-15\)

    Помножити біноміал на біноміал вертикальним методом

    Метод FOIL, як правило, є найшвидшим методом множення двох біноміалів, але він працює лише для біноміалів. Ви можете використовувати розподільну властивість, щоб знайти добуток будь-яких двох поліномів. Ще один метод, який працює для всіх поліномів, - це Вертикальний метод. Це дуже схоже на метод, який ви використовуєте для множення цілих чисел. Подивіться уважно на цей приклад множення двозначних чисел.

    На цій цифрі показано вертикальне множення 23 і 46. Число 23 вище числа 46. Нижче цього є частковий твір 138 над частковим твором 92. Кінцевий продукт знаходиться внизу і становить 1058. Текст на правій стороні зображення говорить: «Почніть з множення 23 на 6, щоб отримати 138. Далі множимо 23 на 4, вибудовуючи частковий твір в правильні стовпці. Останній ви додаєте часткові продукти».

    Тепер ми застосуємо цей же метод, щоб помножити два біноміали.

    Вправа\(\PageIndex{49}\)

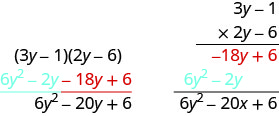
    Множення за допомогою вертикального методу:\((3 y-1)(2 y-6)\)

    Відповідь

    Неважливо, який біноміал йде на верхівці.

    \[\begin{array}{lll}{\text { Multiply } 3 y-1 \text { by }-6 \text { . }}&& \\ {\text { Multiply } 3 y-1 \text { by } 2 y \text { . }}& &\\ \\ &{\qquad\space3 y-1} & \\& {\dfrac{ \space\space\times 2 y-6}{\quad-18 y+6}} & \text{partial product} & \\ &

    ParseError: EOF expected (click for details)
    Callstack:
    at (Математика/Алгебра/Книга:_Елементарна_алгебра_(OpenStax)/06:_Поліноми/6.03:_Множення_многочленів), /content/body/div[4]/div[3]/div[1]/div/dl/dd/p[2]/span/span, line 1, column 3
    & \text{partial product} & \\ \text{Add like terms.} &&\text{product} \end{array}\]

    Зверніть увагу, що часткові продукти такі ж, як терміни в методі FOIL.

    Ця цифра має два стовпчики. У лівій колонці - добуток двох бічленів, 3й мінус 1 і 2й мінус 6. Нижче це 6y в квадраті мінус 2y мінус 18y плюс 6. Нижче це 6y в квадраті мінус 20y плюс 6. У правій колонці вертикальне множення 3y мінус 1 і 2y мінус 6. Нижче це частковий добуток негативний 18y плюс 6. Нижче це частковий твір 6y в квадраті мінус 2y. Нижче це 6y в квадраті мінус 20y плюс 6.

    Вправа\(\PageIndex{50}\)

    Множення за допомогою вертикального методу:\((5 m-7)(3 m-6)\)

    Відповідь

    \(15 m^{2}-51 m+42\)

    Вправа\(\PageIndex{51}\)

    Множення за допомогою вертикального методу:\((6 b-5)(7 b-3)\)

    Відповідь

    \(42 b^{2}-53 b+15\)

    Зараз ми використали три методи множення біноміалів. Обов'язково практикуйте кожен метод, і спробуйте вирішити, який з них ви віддаєте перевагу. Методи перераховані тут всі разом, щоб допомогти вам їх запам'ятати.

    МНОЖЕННЯ ДВОХ БІНОМІАЛІВ

    Щоб помножити біноміали, використовуйте:

    • Розподільна власність
    • Фольга метод
    • вертикальний метод

    Пам'ятайте, що FOIL працює лише при множенні двох біноміалів.

    Помножте триноміал на біноміал

    Ми помножили мономи на мономи, мономи на многочлени та біноми на біноми. Тепер ми готові помножити тріноміал на біноміал. Пам'ятайте, що FOIL не буде працювати в цьому випадку, але ми можемо використовувати або властивість Distributive, або вертикальний метод. Спочатку ми розглянемо приклад з використанням Дистрибутивне властивість.

    Вправа\(\PageIndex{52}\)

    Множення за допомогою розподільної властивості:\((b+3)\left(2 b^{2}-5 b+8\right)\)

    Відповідь
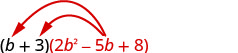
      Добуток двочлена, b плюс 3, і триноміала, 2 b в квадраті мінус 5 b плюс 8. Дві стрілки простягаються від тріноміала, що закінчуються на b і 3 в біном.
    Розподілити. 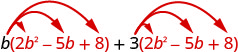Сума двох добутків, добуток b і 2 b в квадраті мінус 5 б плюс 8, і добуток 3 і 2 b в квадраті мінус 5 б плюс 8.
    Помножити. \(2 b^{3}-5 b^{2}+8 b+6 b^{2}-15 b+24\)
    Поєднуйте подібні терміни. \(2 b^{3}+b^{2}-7 b+24\)
    Вправа\(\PageIndex{53}\)

    Множення за допомогою розподільної властивості:\((y-3)\left(y^{2}-5 y+2\right)\)

    Відповідь

    \(y^{3}-8 y^{2}+17 y-6\)

    Вправа\(\PageIndex{54}\)

    Множення за допомогою розподільної властивості:\((x+4)\left(2 x^{2}-3 x+5\right)\)

    Відповідь

    \(2 x^{3}+5 x^{2}-7 x+20\)

    Тепер давайте зробимо це ж множення за допомогою вертикального методу.

    Вправа\(\PageIndex{55}\)

    Множення за допомогою вертикального методу:\((b+3)\left(2 b^{2}-5 b+8\right)\)

    Відповідь

    Простіше поставити многочлен з меншою кількістю членів на дно, оскільки таким чином ми отримуємо менше часткових продуктів.

    \((2b^2 − 5b + 8)\)Помножте на 3. .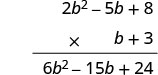
      .
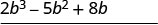
    Помножити\((2b^2 − 5b + 8)\) на\(b\). \(2 b^{3}+b^{2}-7 b+24\)
    Додайте подібні терміни.
    Вправа\(\PageIndex{56}\)

    Множення за допомогою вертикального методу:\((y-3)\left(y^{2}-5 y+2\right)\)

    Відповідь

    \(y^{3}-8 y^{2}+17 y-6\)

    Вправа\(\PageIndex{57}\)

    Множення за допомогою вертикального методу:\((x+4)\left(2 x^{2}-3 x+5\right)\)

    Відповідь

    \(2 x^{3}+5 x^{2}-7 x+20\)

    Зараз ми побачили два методи, які можна використовувати для множення тріноміала на біноміал. Після того, як ви практикуєте кожен метод, ви, ймовірно, знайдете, що ви віддаєте перевагу одному шляху над іншим. Ми перерахуємо обидва методи, перераховані тут, для зручності довідки.

    МНОЖЕННЯ ТРІНОМІАЛУ НА БІНОМІАЛ

    Щоб помножити триноміал на біноміал, використовуйте:

    • Розподільна власність
    • вертикальний метод
    Примітка

    Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з множенням поліномів:

    • Множення показників 1
    • Множення показників 2
    • Множення показників 3

    Ключові концепції

    • Метод FOIL для множення двох біноміалів —Помножити два біноміали:
      1. Помножте Перші члени.
      2. Помножте Зовнішні члени.
      3. Помножте Внутрішні члени.
      4. Помножте Останні члени.
    • Множення двох біноміалів —Щоб помножити біноміали, використовуйте:
    • Множення триноміала на біноміал —Щоб помножити триноміал на біноміал, використовуйте: