Skip to main content
LibreTexts - Ukrayinska

4.4E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    58824

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Використовуйте геоборди для моделювання схилу

    У наступних вправах знайдіть нахил, змодельований на кожній геобарді.

    Вправа\(\PageIndex{1}\)

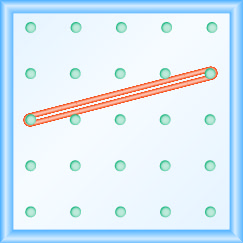
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 3 і кілочком в стовпчику 5, ряду 2 натягується гумка, утворюючи лінію.

    Відповідь

    \(\frac{1}{4}\)

    Вправа\(\PageIndex{2}\)

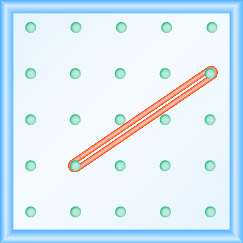
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 2, ряду 4 і кілочком в стовпчику 5, ряду 2 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{3}\)

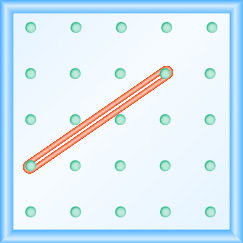
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 4 і кілочком в стовпчику 4, ряду 2 натягується гумка, утворюючи лінію.

    Відповідь

    \(\frac{2}{3}\)

    Вправа\(\PageIndex{4}\)

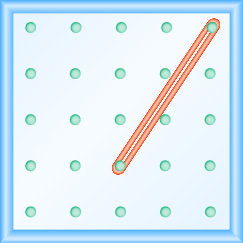
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 3, ряду 4 і кілочком в стовпчику 5, ряду 1 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{5}\)

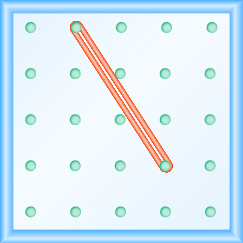
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 2, ряду 1 і кілочком в стовпчику 4, ряду 4 натягується гумка, утворюючи лінію.

    Відповідь

    \(\frac{-3}{2}=-\frac{3}{2}\)

    Вправа\(\PageIndex{6}\)

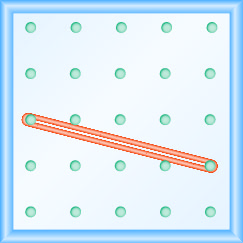
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 3 і кілочком в стовпчику 5, ряду 4 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{7}\)

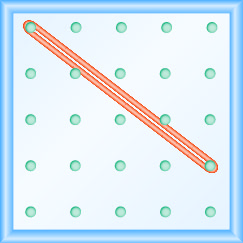
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 1 і кілочком в стовпчику 5, ряду 4 натягується гумка, утворюючи лінію.

    Відповідь

    \(-\frac{2}{3}\)

    Вправа\(\PageIndex{8}\)

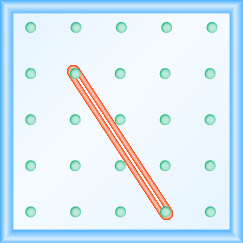
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 2, ряду 2 і кілочком в стовпчику 4, ряду 5 натягується гумка, утворюючи лінію.

    У наступних вправах моделюйте кожен нахил. Намалюйте картинку, щоб показати свої результати.

    Вправа\(\PageIndex{9}\)

    \(\frac{2}{3}\)

    Відповідь

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 2, ряду 5 і кілочком в стовпчику 5, ряду 3 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{10}\)

    \(\frac{3}{4}\)

    Вправа\(\PageIndex{11}\)

    \(\frac{1}{4}\)

    Відповідь

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 4 і кілочком в стовпці 5, ряду 3 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{12}\)

    \(\frac{4}{3}\)

    Вправа\(\PageIndex{13}\)

    \(-\frac{1}{2}\)

    Відповідь

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 4 і кілочком в стовпчику 3, ряду 5 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{14}\)

    \(-\frac{3}{4}\)

    Вправа\(\PageIndex{15}\)

    \(-\frac{2}{3}\)

    Відповідь

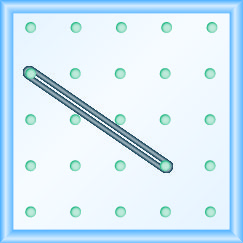
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 2 і кілочком в стовпчику 4, ряду 4 натягується гумка, утворюючи лінію.

    Вправа\(\PageIndex{16}\)

    \(-\frac{3}{2}\)

    \(m=\frac{rise}{run}\)Використовується для пошуку нахилу прямої з її графіка

    У наступних вправах знайдіть нахил кожної показаної лінії.

    Вправа\(\PageIndex{17}\)

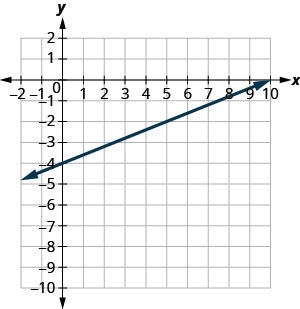
    Графік показує координатну площину x y. Осі x та y проходять від негативних 10 до 10. Через точки (від'ємний 10, від'ємний 8), (0, від'ємний 4), і (10, 0).

    Відповідь

    \(\frac{2}{5}\)

    Вправа\(\PageIndex{18}\)

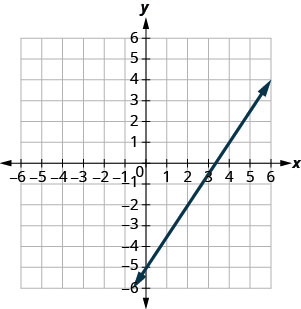
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємний 2, від'ємний 8) і (2, від'ємний 2) проходить лінія.

    Вправа\(\PageIndex{19}\)

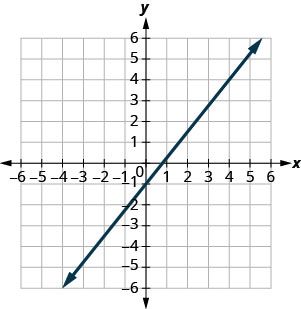
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємний 4, негативний 6) і (4, 4) проходить лінія.

    Відповідь

    \(\frac{5}{4}\)

    Вправа\(\PageIndex{20}\)

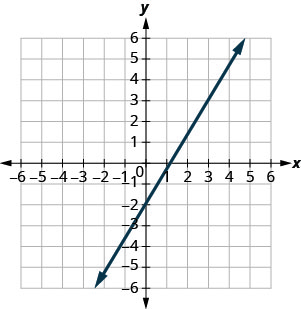
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Лінія перехоплює вісь y в (0, від'ємний 2) і проходить через точку (3, 3).

    Вправа\(\PageIndex{21}\)

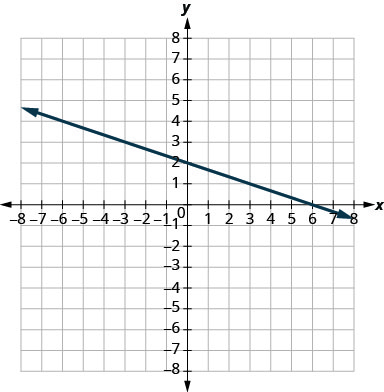
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 3, 3) і (3, 1) проходить лінія.

    Відповідь

    \(-\frac{1}{3}\)

    Вправа\(\PageIndex{22}\)

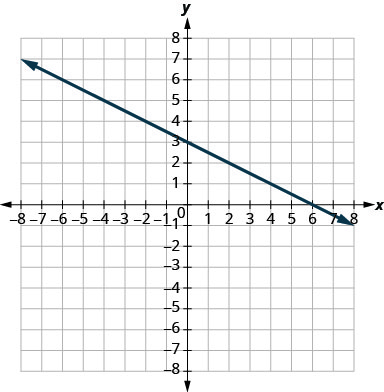
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 2, 4) і (2, 2) проходить лінія.

    Вправа\(\PageIndex{23}\)

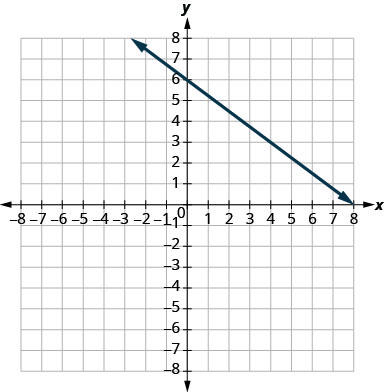
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Лінія перехоплює вісь y в (0, 6) і проходить через точку (4, 3).

    Відповідь

    \(-\frac{3}{4}\)

    Вправа\(\PageIndex{24}\)

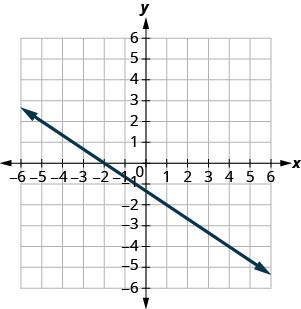
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точку проходить лінія (від'ємна 3, 1) і перехоплює вісь y в (0, негативний 1).

    Вправа\(\PageIndex{25}\)

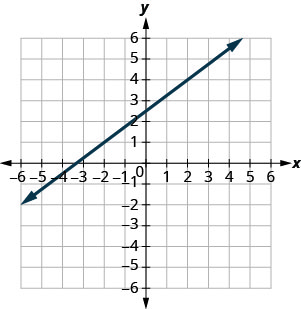
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 2, 1) і (2, 4) проходить лінія.

    Відповідь

    \(\frac{3}{4}\)

    Вправа\(\PageIndex{26}\)

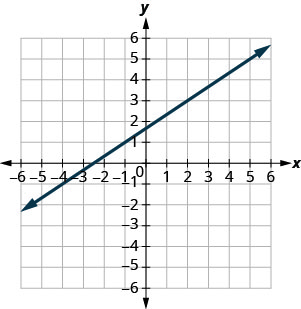
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 1, 1) і (2, 3) проходить лінія.

    Вправа\(\PageIndex{27}\)

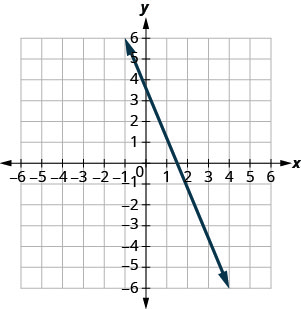
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 1, 6) і (1, 1) проходить лінія.

    Відповідь

    \(-\frac{5}{2}\)

    Вправа\(\PageIndex{28}\)

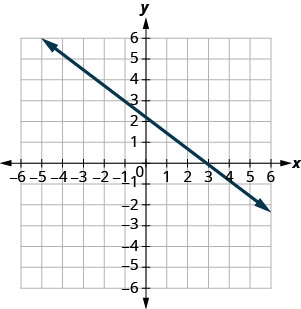
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точку проходить лінія (від'ємна 1, 3) і перехоплює вісь x в (3, 0).

    Вправа\(\PageIndex{29}\)

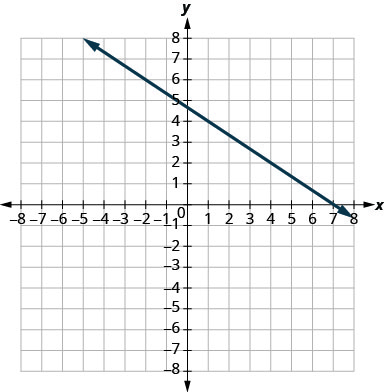
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 2, 6) і (1, 4) проходить лінія.

    Відповідь

    \(-\frac{2}{3}\)

    Вправа\(\PageIndex{30}\)

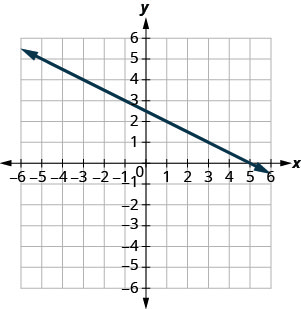
    Графік показує координатну площину x y. Осі x та y проходять від негативних 10 до 10. Через точки (від'ємні 1, 3) і (1, 2) проходить лінія.

    Вправа\(\PageIndex{31}\)

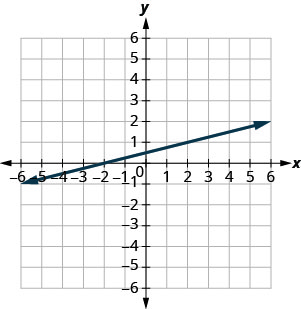
    Графік показує координатну площину x y. Осі x та y проходять від негативних 10 до 10. Лінія перехоплює вісь x в (від'ємний 2, 0) і проходить через точку (2, 1).

    Відповідь

    \(\frac{1}{4}\)

    Вправа\(\PageIndex{32}\)

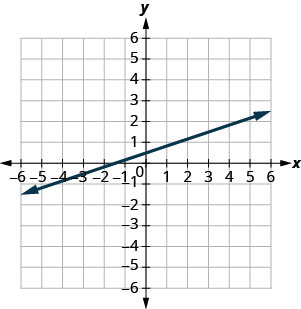
    Графік показує координатну площину x y. Осі x та y проходять від негативних 10 до 10. Через точки (4, 2) і (7, 3) проходить лінія.

    Знайти нахил горизонтальних і вертикальних ліній

    У наступних вправах знайдіть нахил кожної лінії.

    Вправа\(\PageIndex{33}\)

    y=3

    Відповідь

    0

    Вправа\(\PageIndex{34}\)

    y=1

    Вправа\(\PageIndex{35}\)

    х=4

    Відповідь

    невизначений

    Вправа\(\PageIndex{36}\)

    х=2

    Вправа\(\PageIndex{37}\)

    y=−2

    Відповідь

    0

    Вправа\(\PageIndex{38}\)

    y=−3

    Вправа\(\PageIndex{39}\)

    x=−5

    Відповідь

    невизначений

    Вправа\(\PageIndex{40}\)

    x=−4

    Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

    У наступних вправах використовуйте формулу нахилу, щоб знайти нахил лінії між кожною парою точок.

    Вправа\(\PageIndex{41}\)

    (1,4), (3,9)

    Відповідь

    \(\frac{5}{2}\)

    Вправа\(\PageIndex{42}\)

    (2,3), (5,7)

    Вправа\(\PageIndex{43}\)

    (0,3), (4,6)

    Відповідь

    \(\frac{3}{4}\)

    Вправа\(\PageIndex{44}\)

    (0,1), (5,4)

    Вправа\(\PageIndex{45}\)

    (2,5), (4,0)

    Відповідь

    \(-\frac{5}{2}\)

    Вправа\(\PageIndex{46}\)

    (3,6), (8,0)

    Вправа\(\PageIndex{47}\)

    (−3,3), (4, −5)

    Відповідь

    \(-\frac{8}{7}\)

    Вправа\(\PageIndex{48}\)

    (−2,4), (3, −1)

    Вправа\(\PageIndex{49}\)

    (−1, −2), (2,5)

    Відповідь

    \(\frac{7}{3}\)

    Вправа\(\PageIndex{50}\)

    (−2, −1), (6,5)

    Вправа\(\PageIndex{51}\)

    (4, −5), (1, −2)

    Відповідь

    −1

    Вправа\(\PageIndex{52}\)

    (3, −6), (2, −2)

    Графік лінії з заданою точкою та нахилом

    У наступних вправах графік кожної лінії з заданою точкою і нахилом.

    Вправа\(\PageIndex{53}\)

    \((1,-2) ; m=\frac{3}{4}\)

    Відповідь

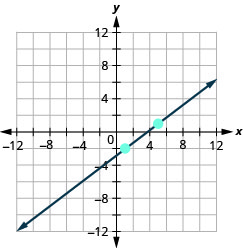
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (1, від'ємний 2) і (5, 1) проходить лінія.

    Вправа\(\PageIndex{54}\)

    \((1,-1) ; m=\frac{2}{3}\)

    Вправа\(\PageIndex{55}\)

    \((2,5) ; m=-\frac{1}{3}\)

    Відповідь

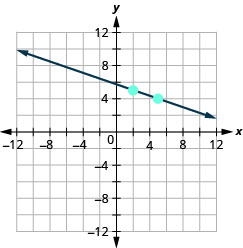
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (2, 5) і (5, 4) проходить лінія.

    Вправа\(\PageIndex{56}\)

    \((1,4) ; m=-\frac{1}{2}\)

    Вправа\(\PageIndex{57}\)

    \((-3,4) ; m=-\frac{3}{2}\)

    Відповідь

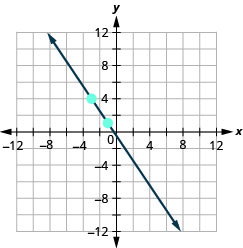
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (від'ємні 3, 4) і (від'ємні 1, 1) проходить лінія.

    Вправа\(\PageIndex{58}\)

    \((-2,5) ; m=-\frac{5}{4}\)

    Вправа\(\PageIndex{59}\)

    \((-1,-4) ; m=\frac{4}{3}\)

    Відповідь

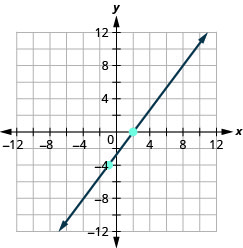
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки проходить лінія (від'ємна 1, негативна 4) і перехоплює вісь x в (2, 0).

    Вправа\(\PageIndex{60}\)

    \((-3,-5) ; m=\frac{3}{2}\)

    Вправа\(\PageIndex{61}\)

    \(y\)-перехопити\(3 ; m=-\frac{2}{5}\)

    Відповідь

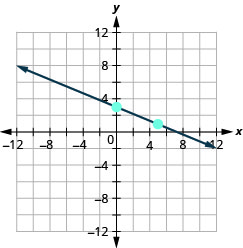
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Лінія перехоплює вісь y в (0, 3) і проходить через точку (5, 1).

    Вправа\(\PageIndex{62}\)

    \(y\)-перехопити\(5 ; m=-\frac{4}{3}\)

    Вправа\(\PageIndex{63}\)

    \(x\)-перехопити\(-2 ; m=\frac{3}{4}\)

    Відповідь

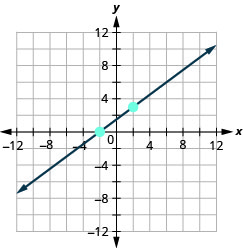
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Лінія перехоплює вісь x в (від'ємний 2, 0) і проходить через точку (2, 3).

    Вправа\(\PageIndex{64}\)

    \(x\)-перехопити\(-1 ; m=\frac{1}{5}\)

    Вправа\(\PageIndex{65}\)

    \((-3,3) ; m=2\)

    Відповідь

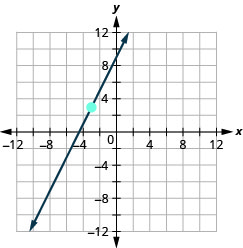
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (від'ємні 3, 3) і (від'ємні 2, 5) проходить лінія.

    Вправа\(\PageIndex{66}\)

    \((-4,2) ; m=4\)

    Вправа\(\PageIndex{67}\)

    \((1,5) ; m=-3\)

    Відповідь

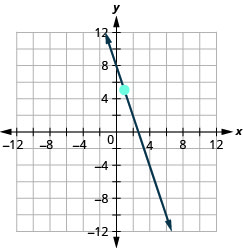
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (1, 5) і (2, 2) проходить лінія.

    Вправа\(\PageIndex{68}\)

    \((2,3) ; m=-1\)

    Щоденна математика

    Вправа\(\PageIndex{69}\)

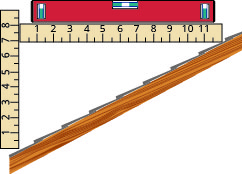
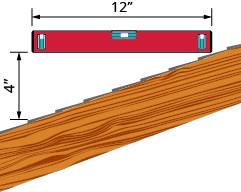
    Ухил покрівлі. Простий спосіб визначити нахил даху - встановити один кінець 12-дюймового рівня на поверхні даху і тримати його на рівні. Потім візьміть рулетку або лінійку і відміряйте від іншого кінця рівня вниз до поверхні даху. Це дасть вам ухил покрівлі. Будівельники іноді називають це кроком і стверджують його як «крок x 12», що означає\(\frac{x}{12}\), де x - вимірювання від даху до рівня - підйом. Це також іноді заявляється як «крок x-in-12».

    1. Який ухил покрівлі на цій картині?
    2. Що таке крок в будівельному плані?
      На цьому малюнку показана одна сторона похилого даху будинку. Підйом покрівлі має маркування «4 дюйми», а прогін покрівлі маркується «12 дюймів».
    Відповідь
    1. \(\frac{1}{3}\)
    2. Крок 4 12 або крок 4 в 12
    Вправа\(\PageIndex{70}\)

    Нахил покрівлі, показаний тут, вимірюється за допомогою 12-дюймового рівня і лінійки. Який ухил у цієї покрівлі?

    На цьому малюнку показана одна сторона похилого даху будинку. Підйом даху вимірюється лінійкою і показаний на 7 дюймів. Прогін даху вимірюється дванадцятьма дюймовим рівнем і показаний як 12 дюймів.

    Вправа\(\PageIndex{71}\)

    Дорожній клас. Місцева дорога має клас 6%. Клас дороги - це її ухил, виражений у відсотках. Знайдіть ухил дороги як частку, а потім спростіть. Який підйом і біг відображали б цей схил або ухил?

    Відповідь

    \(\frac{3}{50} ;\)підйом\(=3,\) бігти\(=50\)

    Вправа\(\PageIndex{72}\)

    Шосе класу. Місцева дорога піднімається на 2 фути на кожні 50 футів шосе.

    1. Що таке ухил магістралі?
    2. Клас магістралі - це його ухил, виражений у відсотках. Який сорт цієї магістралі?
    Вправа\(\PageIndex{73}\)

    Пандус для колясок. Правила для пандусів для інвалідних колясок вимагають максимального підйому на 1 дюйм для 12-дюймового пробігу.

    1. Скільки повинен бути пандус, щоб вмістити 24-дюймовий підйом до дверей?
    2. Створіть модель цього пандуса.
    Відповідь
    1. 288 дюймів (24 фути)
    2. Моделі будуть відрізнятися.
    Вправа\(\PageIndex{74}\)

    Пандус для колясок. Підйом на 1 дюйм для 16-дюймового пробігу полегшує вершнику інвалідного візка піднятися на рампу.

    1. Скільки повинен бути пандус, щоб легко вмістити 24-дюймовий підйом до дверей?
    2. Створіть модель цього пандуса.

    Письмові вправи

    Вправа\(\PageIndex{75}\)

    Про що говорить знак схилу про лінію?

    Відповідь

    Коли нахил є додатним числом, лінія піднімається зліва направо. Коли нахил є від'ємним числом, лінія спускається зліва направо.

    Вправа\(\PageIndex{76}\)

    Чим графік прямої з нахилом\(m=\frac{1}{2}\) відрізняється від графіка прямої з нахилом\(m=2 ?\)

    Вправа\(\PageIndex{77}\)

    Чому нахил вертикальної лінії «невизначений»?

    Відповідь

    Вертикальна лінія має 0 прогонів, а оскільки поділ на 0 не визначено, нахил не визначено.

    Самостійна перевірка

    ⓐ Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

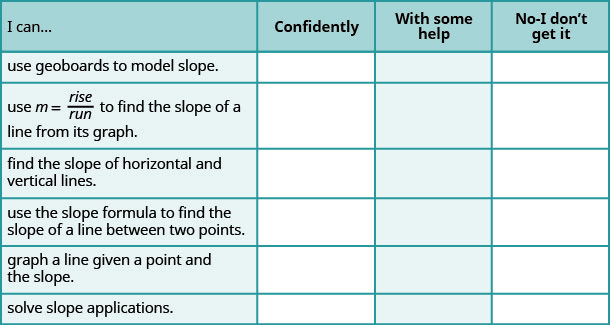
    Ця таблиця складається з семи рядків і чотирьох стовпців. Перший рядок є рядком заголовка, і він позначає кожен стовпець. Перша колонка позначена «Я можу...», друга «Впевнено», третя «З деякою допомогою» і остання «Ні—не отримую». У стовпці «Я можу...» наступний рядок читає «використовувати геоботи для моделювання нахилу». У третьому рядку написано: «Використовуйте m дорівнює зростанню, розділеному на пробіг, щоб знайти нахил прямої з її графіка». Четвертий ряд говорить «знайти нахил горизонтальних і вертикальних ліній». П'ятий ряд говорить «використовуйте формулу нахилу, щоб знайти нахил прямої між двома точками». Шостий рядок читає «графік лінії з заданою точкою і нахилом». В останньому рядку написано «вирішити програми нахилу». Решта стовпці порожні.

    ⓑ За шкалою 1—10, як би ви оцінили своє володіння цим розділом у світлі ваших відповідей на контрольний список? Як ви можете це покращити?

    Глосарій

    геобад
    Геобард - це дошка з сіткою з кілочків на ній.
    негативний ухил
    Негативний нахил рядка йде вниз, коли ви читаєте зліва направо.
    позитивний ухил
    Позитивний нахил рядка піднімається вгору, коли ви читаєте зліва направо.
    підйом
    Підйом лінії - це її вертикальна зміна.
    бігти
    Прогін лінії - це її горизонтальна зміна.
    формула нахилу
    Нахил лінії між двома точками\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\) є\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\).
    нахил лінії
    Нахил лінії є\(m=\frac{\text { rise }}{\text { run }}\). Підйом вимірює вертикальну зміну, а пробіг вимірює зміну горизонталі.