4.1: Використовуйте прямокутну систему координат
- Page ID
- 58836
До кінця цього розділу ви зможете:
- Графік точок у прямокутній системі координат
- Перевірка розв'язків рівняння у двох змінних
- Заповніть таблицю розв'язків лінійного рівняння
- Знайти розв'язки лінійного рівняння у двох змінних
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Оцініть\(x+3\), коли\(x=−1\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.5.25. - Оцінити,\(2x−5y\) коли\(x=3\) і y=−2.
Якщо ви пропустили цю проблему, перегляньте Вправа 1.5.28. - Вирішити для y:\(40−4y=20\)
Якщо ви пропустили цю проблему, перегляньте Вправу 2.3.1.
Графік точок на прямокутній системі координат
Подібно до того, як карти використовують систему сітки для ідентифікації місць, система сітки використовується в алгебрі, щоб показати зв'язок між двома змінними в прямокутній системі координат. Прямокутна система координат також називається xy -площиною або «координатною площиною».
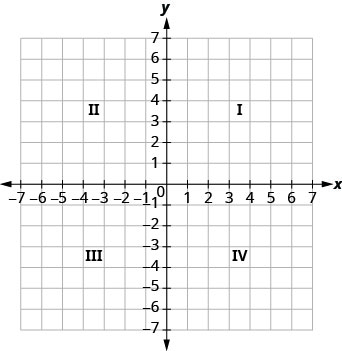
Горизонтальна числова лінія називається віссю х. Вертикальна числова лінія називається віссю y. Вісь x та вісь y разом утворюють прямокутну систему координат. Ці осі ділять площину на чотири області, звані квадрантами. Квадранти ідентифікуються римськими цифрами, що починаються справа вгорі і йдуть проти годинникової стрілки. Див\(\PageIndex{1}\). Малюнок.
У прямокутній системі координат кожна точка представлена впорядкованою парою. Перше число в впорядкованій парі - координата x точки, а друге число - y -координата точки.
Впорядкована пара (x, y) (x, y) дає координати точки в прямокутній системі координат.
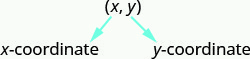
Перше число - координата x.
Друге число - координата y.
Фраза «замовлена пара» означає, що порядок важливий. Що таке впорядкована пара точки, де осі перетинаються? У цей момент обидві координати дорівнюють нулю, тому її впорядкована пара є\((0,0)\). Точка\((0,0)\) має особливу назву. Його називають походженням.
Точка\((0,0)\) називається початком. Це точка, де перетинаються вісь x і y -вісь.
Ми використовуємо координати, щоб знайти точку на xy -площині. Давайте побудуємо крапку\((1,3)\) як приклад. Спочатку знайдіть 1 на осі x і злегка намалюйте вертикальну лінію через x = 1x=1. Потім знайдіть 3 на осі y і намалюйте горизонтальну лінію через y = 3y = 3. Тепер знайдіть точку, де ці дві лінії зустрічаються - це точка з координатами\((1,3)\).
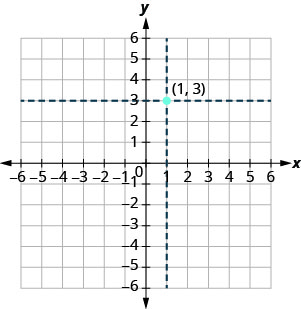
Зверніть увагу, що вертикальна лінія\(x=1\) і горизонтальна лінія наскрізь не\(y=3\) є частиною графіка. Ми просто використовували їх, щоб допомогти нам знайти точку\((1,3)\).
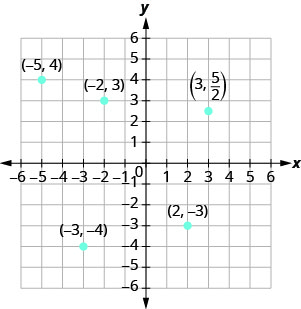
Побудуйте кожну точку в прямокутній системі координат і визначте квадрант, в якому знаходиться точка:
- (−5,4)
- (−3, −4)
- (2, −3)
- (−2,3)
- \((3, \frac{5}{2})\)
- Відповідь
-
Перше число координатної пари - координата x, а друге число - координата y.
- Починаючи з x=−5, точка знаходиться ліворуч від осі y. Крім того, починаючи з y = 4, точка знаходиться вище осі x. Точка (−5,4) знаходиться у II квадранті.
- Починаючи з x=−3, точка знаходиться ліворуч від осі y. Крім того, починаючи з y=−4, точка знаходиться нижче осі x. Точка (−3, −4) знаходиться в третьому квадранті.
- Починаючи з x = 2, точка знаходиться праворуч від осі y. Починаючи з y=−3, точка знаходиться нижче осі x. Точка (2, −3) знаходиться в квадранті lV.
- Починаючи з x=−2, точка знаходиться ліворуч від осі y. Починаючи з y=3, точка знаходиться вище осі x. Точка (−2,3) знаходиться у II квадранті.
- Починаючи з x = 3, точка знаходиться праворуч від осі y. Так як\(y = \frac{5}{2}\), точка знаходиться вище осі х. (Може бути корисно писати\(\frac{5}{2}\) як змішане число або десяткове число.) \((3, \frac{5}{2})\)Справа в квадранті I.
Малюнок\(\PageIndex{4}\)
Побудуйте кожну точку в прямокутній системі координат і визначте квадрант, в якому знаходиться точка:
- (−2,1)
- (−3, −1)
- (4, −4)
- (−4,4)
- \((-4, \frac{3}{2})\)
- Відповідь
-
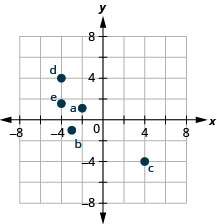
Побудуйте кожну точку в прямокутній системі координат і визначте квадрант, в якому знаходиться точка:
- (−4,1)
- (−2,3)
- (2, −5)
- (−2,5)
- \((-3, \frac{5}{2})\)
- Відповідь
-
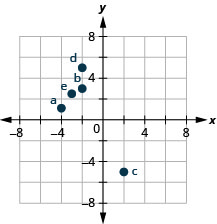
Як знаки впливають на розташування точок? Можливо, ви помітили деякі закономірності, коли ви намалювали точки в попередньому прикладі.
Що стосується точки на малюнку\(\PageIndex{4}\) в квадранті IV, що ви помічаєте про знаки координат? А як щодо знаків координат точок у третьому квадранті? Другий квадрант? Перший квадрант?
Чи можете ви сказати, просто подивившись на координати, в якому квадранті знаходиться точка (−2,5)? У якому квадранті знаходиться (2, −5)?
Таким чином ми можемо узагальнити шаблони знаків квадрантів.
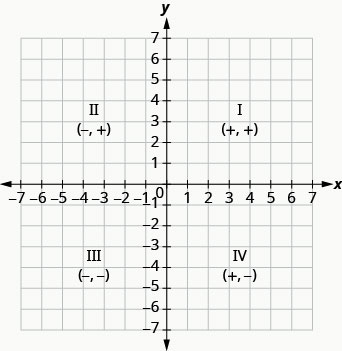
\[\begin{array}{ccc}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\]
Що робити, якщо одна координата дорівнює нулю, як показано на малюнку\(\PageIndex{6}\)? Де знаходиться точка (0,4)? Де знаходиться точка (−2,0)?
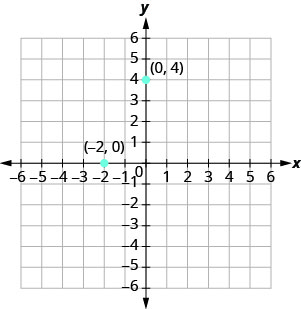
Точка (0,4) знаходиться на осі y, а точка (−2,0) - на осі x.
Точки з y -координатою, рівною 0, знаходяться на осі x і мають координати (a,0).
Точки з координатою x, рівною 0, знаходяться на осі y і мають координати (0, b).
Ділянка кожної точки:
- (0,5)
- (4,0)
- (−3,0)
- (0,0)
- (0, −1)
- Відповідь
-
- Починаючи з x=0, точка, координати якої (0,5), знаходиться на осі y.
- Починаючи з y=0, точка, координати якої (4,0), знаходиться на осі x.
- Починаючи з y=0, точка, координати якої (−3,0), знаходиться на осі x.
- Оскільки x = 0 і y=0, точка, координати якої (0,0), є початком.
- Починаючи з x=0, точка, координати якої (0, −1), знаходиться на осі y.
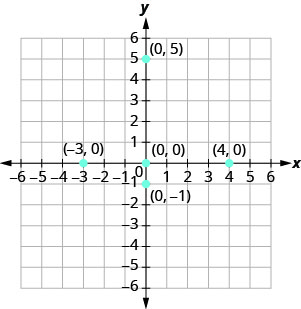
Малюнок\(\PageIndex{7}\)
Ділянка кожної точки:
- (4,0)
- (−2,0)
- (0,0)
- (0,2)
- (0, −3).
- Відповідь
-
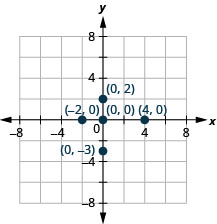
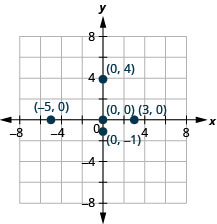
Ділянка кожної точки:
- (−5,0)
- (3,0)
- (0,0)
- (0, −1)
- (0,4).
- Відповідь
-
В алгебрі можливість ідентифікувати координати точки, показаної на графіку, так само важлива, як і можливість будувати точки. Щоб визначити координату x точки на графіку, прочитайте число на осі x безпосередньо над точкою або під нею. Щоб визначити y -координату точки, прочитайте число на осі y безпосередньо ліворуч або праворуч від точки. Пам'ятайте, коли ви пишете впорядковану пару, використовуйте правильний порядок, (x, y).
Назвіть впорядковану пару кожної точки, показаної в прямокутній системі координат.
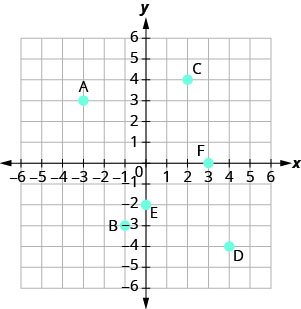
- Відповідь
-
Точка A знаходиться вище −3 на осі x, тому координата x точки дорівнює −3.
Точка знаходиться зліва від 3 на осі y, тому y -координата точки дорівнює 3. - Координати точки є (−3,3).
-
Точка B знаходиться нижче −1 на осі x, тому координата x точки дорівнює −1.
Точка знаходиться ліворуч від −3 на осі y, тому координата y точки дорівнює −3. - Координати точки є (−1, −3).
Точка C знаходиться вище 2 на осі x, тому координата x точки дорівнює 2.
Точка знаходиться праворуч від 4 на осі y, тому y -координата точки дорівнює 4. - Координати точки становлять (2,4).
- Точка D знаходиться нижче 4 на осі x, тому координата x точки дорівнює 4.
- Точка знаходиться праворуч від −4 на осі y, тому координата y точки дорівнює −4.
- Координати точки є (4, −4).
-
Точка E знаходиться на осі y при y = −2. Координати точки E є (0, −2).
Точка F знаходиться на осі x = 3. Координати точки F є (3,0).
Назвіть впорядковану пару кожної точки, показаної в прямокутній системі координат.
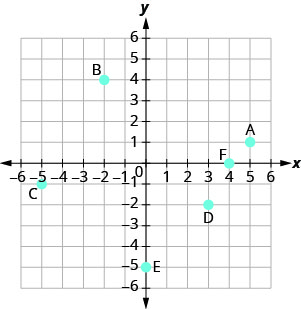
- Відповідь
-
A: (5,1) B: (−2,4) C: (−5, −1) D: (3, −2) E: (0, −5) F: (4,0)
Назвіть впорядковану пару кожної точки, показаної в прямокутній системі координат.
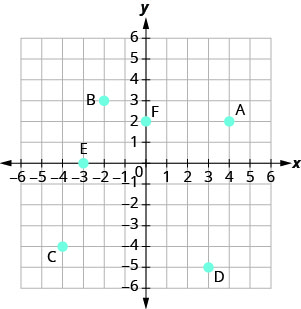
- Відповідь
-
A: (4,2) B: (−2,3) C: (−4, −4) D: (3, −5) E: (−3,0) F: (0,2)
Перевірка розв'язків рівняння у двох змінних
До теперішнього часу всі рівняння, які ви розв'язали, були рівняннями лише з однією змінною. Майже в кожному випадку, коли ви вирішували рівняння, ви отримали рівно одне рішення. Процес розв'язання рівняння закінчився твердженням типу x=4. (Потім ви перевірили рішення, підставивши назад у рівняння.)
Ось приклад рівняння в одній змінній, і його одне рішення.
\[\begin{aligned} 3 x+5 &=17 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
Але рівняння можуть мати більше однієї змінної. Рівняння з двома змінними можуть мати вигляд Ax+By=C. рівняння такого виду називаються лінійними рівняннями в двох змінних.
Рівняння виду Ax+By=C, де A і B не обидва нуль, називається лінійним рівнянням в двох змінних.
Зверніть увагу на рядок слова в лінійному. Ось приклад лінійного рівняння в двох змінних, x і y.
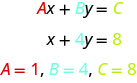
Рівняння y=−3x+5 також є лінійним рівнянням. Але, здається, це не у формі Ax+By=C. ми можемо використовувати властивість додавання рівності та переписати його у формі Ax+By=C.
\(\begin{array}{llll} {} &{y} &{=} &{-3x + 5} \\ {\text{Add to both sides.}} &{y + 3x } &{=} &{-3x + 5 + 3x} \\{\text{Simplify.}} &{y + 3x} &{=} &{5} \\{\text{Use the Commutative Property to put it in}} &{3x + y} &{=} &{5} \\{Ax+By = C\text{ form.}} &{} &{} &{} \end{array}\)
Переписуючи y=−3x+5 як 3x+y = 5, ми можемо легко побачити, що це лінійне рівняння у двох змінних, оскільки воно має вигляд Ax+By=C Коли рівняння має форму Ax+By=C, ми говоримо, що воно в стандартній формі.
Лінійне рівняння знаходиться в стандартній формі, коли записано Ax+By=C.
Більшість людей вважають за краще, щоб A, B і C були цілими числами і\(A\geq 0\) при написанні лінійного рівняння в стандартній формі, хоча це не є строго необхідним.
Лінійні рівняння мають нескінченно багато розв'язків. Для кожного числа, яке підставляється на x, є відповідне значення y. Ця пара значень є розв'язком лінійного рівняння і представлена впорядкованою парою (x, y). Коли ми підставляємо ці значення x і y в рівняння, результат є істинним твердженням, тому що значення на лівій стороні дорівнює значенню з правого боку.
Впорядкована пара (x, y) - це рішення лінійного рівняння Ax+By=C, якщо рівняння є істинним твердженням, коли в рівняння підставляються x - і y -значення впорядкованої пари.
Визначте, які впорядковані пари є розв'язками рівняння x+4y=8.
(а) (0,2)
(б) (2, −4)
(c) (−4,3)
- Відповідь
-
Підставити x - і y -значення з кожної впорядкованої пари в рівняння і визначити, чи є результат істинним твердженням.
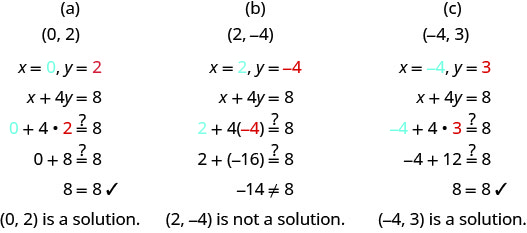
Які з наступних впорядкованих пар є розв'язками 2x+3y=6?
- (3,0)
- (2,0)
- (6, −2)
- Відповідь
-
1, 3
Які з наступних впорядкованих пар є розв'язками рівняння 4x−y=8?
- (0,8)
- (2,0)
- (1, −4)
- Відповідь
-
2, 3
Які з наступних впорядкованих пар є розв'язками рівняння y=5x−1?
(а) (0, −1)
(б) (1,4)
(c) (−2, −7)
- Відповідь
-
Підставити x - і y -значення з кожної впорядкованої пари в рівняння і визначити, чи призводить воно до істинного твердження.
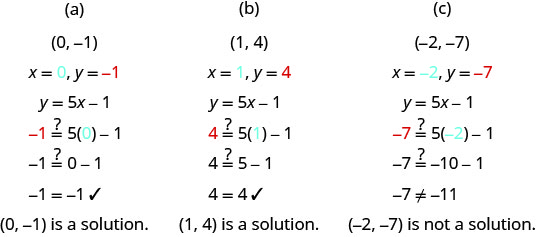
Які з наступних впорядкованих пар є розв'язками рівняння y=4x−3?
- (0,3)
- (1,1)
- (−1, −1)
- Відповідь
-
2
Які з наступних впорядкованих пар є розв'язками рівняння y=−2x+6?
- (0,6)
- (1,4)
- (−2, −2)
- Відповідь
-
1, 2
Заповніть таблицю розв'язків лінійного рівняння у двох змінних
У наведених вище прикладах ми підставили x - і y -значення заданої впорядкованої пари, щоб визначити, чи є це рішення лінійного рівняння. Але як знайти впорядковані пари, якщо їх не дано? Це простіше, ніж ви думаєте - ви можете просто вибрати значення для xx, а потім вирішити рівняння для yy. Або виберіть значення для yy, а потім вирішіть для xx.
Ми почнемо з розв'язків рівняння y = 5x−1, які ми знайшли у Вправі\(\PageIndex{13}\). Ми можемо узагальнити цю інформацію в таблиці рішень, як показано в табл\(\PageIndex{1}\).
| y=5x−1 | ||
| х | у | (х, у) |
| 0 | −1 | (0, −1) |
| 1 | 4 | (1,4) |
Щоб знайти третє рішення, ми дозволимо x=2 і вирішимо для y.
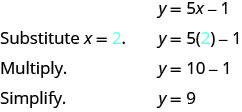
Впорядкована пара (2,9) є розв'язком y=5x−1. Ми додамо його в табл\(\PageIndex{2}\).
| y=5x−1 | ||
| х | у | (х, у) |
| 0 | −1 | (0, −1) |
| 1 | 4 | (1,4) |
| 2 | 9 | (2,9) |
Ми можемо знайти більше розв'язків рівняння, підставивши будь-яке значення x або будь-яке значення y та вирішивши отримане рівняння, щоб отримати іншу впорядковану пару, яка є розв'язком. Розв'язків цього рівняння нескінченно багато.
Заповніть таблицю, щоб знайти три розв'язки рівняння y=4x−2.
| y=4x−2 | ||
| х | у | (х, у) |
| 0 | ||
| −1 | ||
| 2 | ||
- Відповідь
-
Замініть x=0, x = −1 та x=2 на y=4x−2.
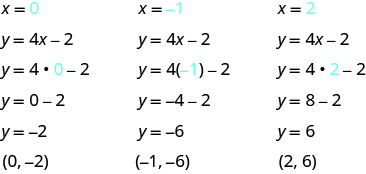
-
Результати наведені в табл\(\PageIndex{4}\).
y=4x−2 х у (х, у) 0 −2 (0, −2) −1 −6 (−1, −6) 2 6 (2,6) Таблиця\(\PageIndex{4}\)
Заповніть таблицю, щоб знайти три розв'язки цього рівняння: y=3x−1.
| y=3x−1 | ||
| х | у | (х, у) |
| 0 | ||
| −1 | ||
| 2 | ||
- Відповідь
-
y=3x−1 х у (х, у) 0 -1 (0, -1) −1 -4 (-1, -4) 2 5 (2, 5) Таблиця\(\PageIndex{6}\)
Заповніть таблицю, щоб знайти три розв'язки цього рівняння: y=6x+1.
| y=6х+1 | ||
| х | у | (х, у) |
| -2 | ||
- Відповідь
-
y=6х+1 х у (х, у) 0 1 (0,1) 1 7 (1,7) −2 −11 (−2, −11) Таблиця\(\PageIndex{8}\)
Заповніть таблицю,\(\PageIndex{9}\) щоб знайти три розв'язки рівняння 5x−4y=20.
| 5х−4р=20 | ||
| х | у | (х, у) |
| 0 | ||
| 5 | ||
- Відповідь
-
Підставляємо задане значення у рівняння 5x−4y=20 і вирішуємо для іншої змінної. Потім заповніть значення в таблиці.
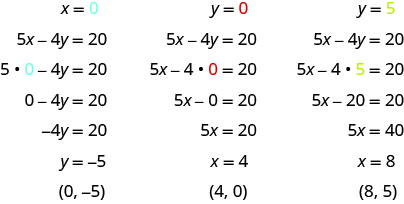
-
Результати наведені в табл\(\PageIndex{10}\).
5х−4р=20 х у (х, у) 0 −5 (0, −5) 4 0 (4,0) 8 5 (8,5) Таблиця\(\PageIndex{10}\)
Заповніть таблицю, щоб знайти три розв'язки цього рівняння: 2x−5y=20.
| 2х−5р=20 | ||
| х | у | (х, у) |
| -5 | ||
- Відповідь
-
2х−5р=20 х у (х, у) 0 −4 (0, −4) 10 0 (10,0) −5 −6 (−5, −6) Таблиця\(\PageIndex{12}\)
Заповніть таблицю, щоб знайти три розв'язки цього рівняння: 3x−4y=12.
| 3х−4р=12 | ||
| х | у | (х, у) |
| -4 | ||
- Відповідь
-
3х−4р=12 х у (х, у) 0 −3 (0, −3) 4 0 (4,0) −4 −6 (−4, −6) Таблиця\(\PageIndex{14}\)
Пошук розв'язків лінійного рівняння
Щоб знайти рішення лінійного рівняння, ви дійсно можете вибрати будь-яке число, яке ви хочете замінити в рівняння для x або y Але оскільки вам потрібно буде використовувати це число для розв'язання для іншої змінної, це гарна ідея вибрати число, з яким легко працювати.
Коли рівняння знаходиться в y -формі, з y сам по собі на одній стороні рівняння, зазвичай легше вибрати значення x, а потім вирішити для y.
Знайдіть три розв'язки рівняння y=−3x+2.
- Відповідь
-
Ми можемо замінити будь-яке значення, яке ми хочемо, для x або будь-яке значення для y. Оскільки рівняння знаходиться у формі y, буде простіше підставити значення x. Давайте виберемо x=0, x=1 та x=−1.



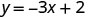
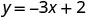
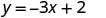
Підставляємо значення в рівняння. 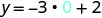
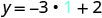
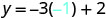
Спростити. 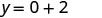
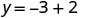
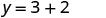
Спростити. 
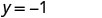

Напишіть замовлену пару. (0, 2) (1, -1) (-1, 5) Перевірте. y=−3x+2 y=−3x+2 y=−3x+2 \(2 \stackrel{?}{=} -3 \cdot 0 + 2\) \(-1 \stackrel{?}{=} -3 \cdot 1 + 2\) \(5 \stackrel{?}{=} -3 (-1) + 2\) \(2 \stackrel{?}{=} 0 + 2\) \(-1 \stackrel{?}{=} -3 + 2\) \(5 \stackrel{?}{=} -3 + 2\) \(2 = 2\checkmark\) \(-1 = -1\checkmark\) \(5 = 5\checkmark\) - Таблиця\(\PageIndex{15}\)
-
Отже, (0,2), (1, −1) та (−1,5) є розв'язками y=−3x+2. Ми показуємо їх в табл\(\PageIndex{16}\).
y=−3x+2 х у (х, у) 0 2 (0,2) 1 −1 (1, −1) −1 5 (−1,5) Таблиця\(\PageIndex{16}\)
Знайдіть три розв'язки цього рівняння: y=−2x+3.
- Відповідь
-
Відповіді будуть відрізнятися.
Знайдіть три розв'язки цього рівняння: y=−4x+1.
- Відповідь
-
Відповіді будуть відрізнятися.
Ми бачили, як використання нуля як одного значення x робить пошук значення y легко. Коли рівняння має стандартну форму, і x і y знаходяться на одній стороні рівняння, зазвичай простіше спочатку знайти одне рішення, коли x = 0 знайти друге рішення, коли y=0, а потім знайти третє рішення.
Знайдіть три розв'язки рівняння 3х+2y=6.
- Відповідь
-
Ми можемо замінити будь-яке значення, яке ми хочемо для x або будь-яке значення для y Оскільки рівняння в стандартній формі, давайте виберемо спочатку x = 0, потім y=0, а потім знайдемо третю точку.

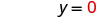

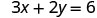
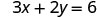
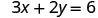
Підставляємо значення в рівняння. 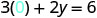
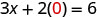
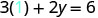
Спростити. 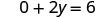
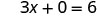
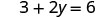
Вирішити. 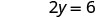
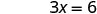
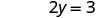
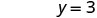

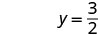
Напишіть замовлену пару. (0, 3) (2, 0) \((1,\frac{3}{2})\) Перевірте. 3х+2р=6 3х+2р=6 3х+2р=6 \(3\cdot 0 + 2\cdot 3 \stackrel{?}{=} 6\) \(3\cdot 2 + 2\cdot 0 \stackrel{?}{=} 6\) \(3\cdot 1 + 2\cdot \frac{3}{2} \stackrel{?}{=} 6\) \(0 + 6 \stackrel{?}{=} 6\) \(6 + 0 \stackrel{?}{=} 6\) \(3 + 3 \stackrel{?}{=} 6\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) Таблиця\(\PageIndex{17}\) Отже (0,3), (2,0), і всі\((1,\frac{3}{2})\) розв'язки рівняння 3х+2y=6. Ми можемо перерахувати ці три рішення в табл\(\PageIndex{18}\).
3х+2р=63х+2р=6 х у (х, у) 0 3 (0,3) 2 0 (2,0) 1 \(\frac{3}{2}\) \((1, \frac{3}{2})\) Таблиця\(\PageIndex{18}\)
Знайдіть три розв'язки рівняння 2x+3y=6.
- Відповідь
-
Відповіді будуть відрізнятися.
Знайдіть три розв'язки рівняння 4х+2y=8.
- Відповідь
-
Відповіді будуть відрізнятися.
Ключові концепції
- Знакові візерунки квадрантів
\(\begin{array}{ll}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\) - Точки на осях
- На осі x - y=0. Точки з y -координатою, рівною 0, знаходяться на осі x і мають координати (a,0).
- На осі y, x = 0. Точки з координатою x, рівною 0, знаходяться на осі y і мають координати (0, b).
- Розв'язок лінійного рівняння
- Впорядкована пара (x, y) - це рішення лінійного рівняння Ax+By=C, якщо рівняння є істинним твердженням, коли в рівняння підставляються значення x - і y - впорядкованої пари.
Глосарій
- лінійне рівняння
- Лінійне рівняння має вигляд Ax+By=C, де A і B не обидва нуль, називається лінійним рівнянням у двох змінних.
- впорядкована пара
- Впорядкована пара (x, y) дає координати точки в прямокутній системі координат.
- походження
- Точка (0,0) (0,0) називається початком. Це точка, де перетинаються вісь x і y -вісь.
- квадрант
- Вісь x та вісь y ділять площину на чотири області, які називаються квадрантами.
- прямокутна система координат
- Система сітки використовується в алгебрі, щоб показати зв'язок між двома змінними; також називається xy -plane або «координатна площина».
- x -координата
- Перше число в впорядкованій парі (x, y).
- y -координата
- Друге число в впорядкованій парі (x, y).
