3.1: Графічні рівняння вручну

Починаємо з визначення впорядкованої пари.

Замовлена пара

Конструкція$(x,y)$, де$x$ і$y$ є будь-якими дійсними числами, називається впорядкованою парою дійсних чисел.

$(4,3)$,$(−3,4)$,$(−2,−3)$, і$(3,−1)$ є прикладами впорядкованих пар.

Порядок питань

Особливу увагу зверніть на словосполучення «впорядковані пари». Порядок має значення. Отже,$(x,y)$ впорядкована пара не є такою ж$(y,x)$, як впорядкована пара, оскільки числа представлені в іншому порядку.

Декартова система координат

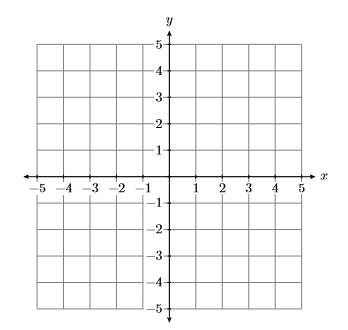
На малюнку зображена$\PageIndex{1}$ декартова система координат. На сітці ми створили дві реальні лінії, одну горизонтальну мітку$x$ (ми будемо називати цю$x$ вісь -axis), а іншу вертикальну мітку$y$ (ми будемо називати цю як$y$ -вісь).

Малюнок$\PageIndex{1}$: Декартова система координат.

Два важливих моменти:

Ось два важливих моменти, які слід зробити щодо горизонтальної та вертикальної осей на малюнку$\PageIndex{1}$.

1. Коли ви рухаєтеся зліва направо вздовж горизонтальної осі ($x$-вісь на малюнку$\PageIndex{1}$), числа збільшуються. Позитивний напрямок - вправо, негативний - вліво.
2. Коли ви рухаєтеся знизу вгору вздовж вертикальної осі ($y$-вісь на малюнку$\PageIndex{1}$), числа збільшуються. Позитивний напрямок - вгору, негативний - вниз.

Додаткові коментарі:

Малюнок$\PageIndex{2}$: Нумерація квадрантів і вказівка координат початку.

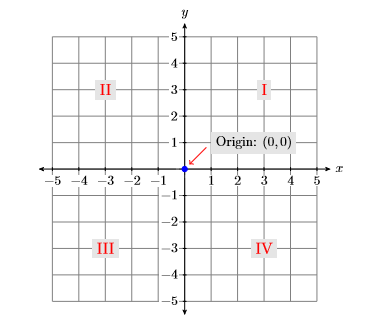
Два додаткових зауваження по порядку:

3. Точка, де горизонтальна і вертикальна осі перетинаються на малюнку,$\PageIndex{2}$ називається початком системи координат. Походження має координати$(0,0)$.
4. Горизонтальна і вертикальна осі ділять площину на чотири$\mathrm{I}, \mathrm{II}, \mathrm{MI},$ квадранта, пронумеровані і$\mathrm{IV}$ (римські цифри для одного, двох, трьох і чотирьох), як показано на малюнку$\PageIndex{2}$. Зверніть увагу, що квадранти нумеруються в порядку проти годинникової стрілки.

Примітка

Рене Декарт (1596-1650) був французьким філософом і математиком, який добре відомий відомою фразою «cogito ergo sum» (я думаю, тому я є), яка з'являється в його Discours de la methode pour bien coduire sa raison, et chercher la verite dans les sciences (Дискурс про метод правильного ведення розуму та пошуку істини в науках). У тому ж трактаті Декарт вводить свою систему координат, метод представлення точок на площині за допомогою пар дійсних чисел. Дійсно, декартова площина сучасності так названа на честь Рене Декарта, якого деякі називають «батьком сучасної математики»

Побудова впорядкованих пар

Перш ніж ми зможемо побудувати будь-які точки або намалювати будь-які графіки, нам спочатку потрібно встановити декартову систему координат на аркуші графічного паперу? Як нам це зробити? Що потрібно?

як налаштувати декартову систему координат

Намалюйте і позначте кожну вісь.

Якщо ми збираємося побудувати точки (x, y), то на аркуші графського паперу виконуємо кожне з наступних початкових завдань.

1. Використовуйте лінійку, щоб намалювати горизонтальну і вертикальну осі.
2. Позначте горизонтальну вісь як$x$ -вісь, а вертикальну вісь$y$ - вісь.

Ми не завжди позначаємо горизонтальну вісь як$x$-axis and the vertical axis as the $y$-axis. For example, if we want to plot the velocity of an object as a function of time, then we would be plotting points $(t,v)$. In that case, we would label the horizontal axis as the $t$-axis and the vertical axis as the $v$-axis.

Вкажіть шкалу на кожній осі.

3. Позначте принаймні одну вертикальну лінію сітки її числовим значенням.
4. Позначте принаймні одну горизонтальну лінію сітки з її числовим значенням.

Ваги на горизонтальній і вертикальній осях можуть відрізнятися. Однак на кожній осі шкала повинна залишатися послідовною. Тобто, як ви вважаєте праворуч від походження на$x$-axis, if each gridline represents one unit, then as you count to the left from the origin on the $x$-axis, each gridline must also represent one unit. Similar comments are in order for the $y$-axis, where the scale must also be consistent, whether you are counting up or down.

Результат цього першого кроку показаний на рисунку$\PageIndex{3}$.

Малюнок$\PageIndex{3}$ : Намалюйте та позначте кожну вісь.

Приклад наведено на рис$\PageIndex{4}$. Зауважте, що масштаб, вказаний на$x$ -осі, вказує на те, що кожна сітка вважається$1$ -одиницею, оскільки ми рахуємо зліва направо. Шкала на$y$ -осі вказує на те, що кожна лінія сітки рахується як$2$ -units, як ми рахуємо від низу до верху.

Малюнок$\PageIndex{4}$ : Вкажіть масштаб на кожній осі.

Тепер, коли ми знаємо, як налаштувати декартову систему координат на аркуші графічного паперу, ось два приклади того, як ми будуємо точки на нашій системі координат.

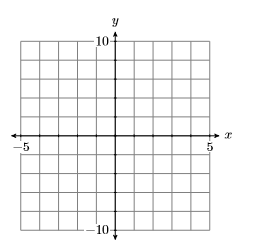
Для побудови$(4,3)$ впорядкованої пари почніть з початку і перемістіть$4$ одиниці вправо вздовж горизонтальної осі, потім$3$ одиниці вгору у напрямку вертикальної осі.

Малюнок$\PageIndex{5}$ : Сюжет о$(4,3)$.

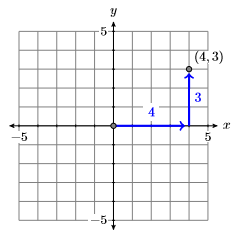
Для побудови$(−2,−3)$ впорядкованої пари почніть з початку і перемістіть$2$ одиниці вліво вздовж горизонтальної осі, потім$3$ одиниці вниз у напрямку вертикальної осі.

Малюнок$\PageIndex{6}$ : Сюжет$(-2,-3)$

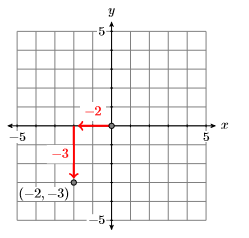
Продовжуючи таким чином, кожна впорядкована пара$(x,y)$ дійсних чисел пов'язана з унікальною точкою в декартовій площині. Навпаки, кожна точка в декартовій точці пов'язана з унікальною впорядкованою парою дійсних чисел. Через цю асоціацію ми починаємо використовувати слова «точка» і «впорядкована пара» як еквівалентні вирази, іноді посилаючись на «точку»,$(x,y)$ а інший раз до «впорядкованої пари»$(x,y)$.

Приклад$\PageIndex{1}$

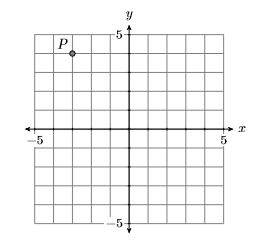
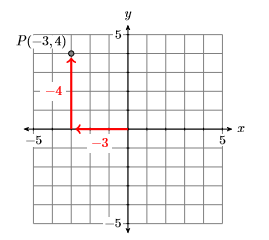
Визначте координати точки$P$ на рис$\PageIndex{7}$.

Малюнок$\PageIndex{7}$ : Визначте координати точки$P$.

Рішення

На малюнку$\PageIndex{8}$ почніть з початку, перемістіть$3$ одиниці вліво і$4$ одиниці вгору, щоб досягти точки$P$. Це говорить про те, що координати точки$P$ є$(−3,4)$.

Малюнок$\PageIndex{8}$ : Почніть з початку, перемістіть$3$ одиниці вліво і$4$ одиниці вгору.

Вправа$\PageIndex{1}$

Визначте координати$P$ точки на графіку нижче.

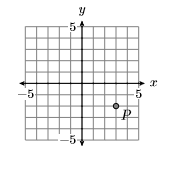
Відповідь

$(3,-2)$

Рівняння у двох змінних

Примітка

Змінні не повинні завжди бути$x$ and $y$. For example, the equati на$v =2+3 .2t$ рівняння в двох змінних,$v$ and $t$.

Рівняння$y = x + 1$ являє собою рівняння в двох змінних, в даному випадку$x$ і$y$. Розглянемо суть$(x,y) = (2 ,3)$. Якщо підставити$2$ for$x$ і$3$ for$y$ в рівнянні$y = x + 1$, то отримаємо наступний результат:

$$\begin{aligned} y &= x+1 \quad \color {Red} \text { Original equation. } \\ 3 &= 2+1 \quad \color {Red} \text { Substitute: } 2 \text { for } x, 3 \text { for } y \\ 3 &= 3 \quad \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Оскільки останній рядок є істинним твердженням, ми говоримо, що$(2,3)$ це рішення рівняння$y = x + 1$. По черзі ми говоримо, що$(2,3)$ задовольняє рівняння$y = x + 1$. З іншого боку, розглянемо суть$(x,y)=(−3,1)$. Якщо підставити$x$ і$−3$$1$ для$y$ в рівнянні$y = x + 1$, то отримаємо наступний результат.

$$\begin{aligned} y &= x+1 \quad \color {Red} \text { Original equation. } \\ 1 &= -3+1 \quad \color {Red} \text { Substitute: } -3 \text { for } x, 1 \text { for } y \\ 1 &= -2 \quad \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber$$

Оскільки останній рядок є помилковим твердженням, точка не$(−3,1)$ є рішенням рівняння$y = x+1$; тобто точка$(−3,1)$ не задовольняє рівнянню$y = x + 1$.

Розв'язки рівняння у двох змінних

Задано рівняння в змінних$x$$y$ і і точка$(x,y)=(a,b)$, якщо при$x$ заміні$a$$b$$y$ на істинне твердження результатів, то точка$(x,y)=(a,b)$ вважається розв'язком даного рівняння. По черзі скажемо, що точка$(x,y)=(a,b)$ задовольняє заданому рівнянню.

Приклад$\PageIndex{2}$

Яку з впорядкованих пар$(0,−3)$$(1,1)$ задовольняють рівняння$y =3x−2$?

Рішення

Підставляючи впорядковані пари$(0,−3)$ і$(1,1)$ в рівняння$y =3x−2$ призводять до наступних результатів:

Розглянемо$(x,y) = (0 ,−3)$. Замінник$x$ і$0$$−3$ для$y$:

$$\begin{aligned} y &=3 x-2 \\-3 &=3(0)-2 \\-3 &=-2 \end{aligned} \nonumber$$

Отримане твердження є помилковим.

Розглянемо$(x,y) = (1 ,1)$. Замінник$x$ і$1$$1$ для$y$:

$$\begin{aligned} y &=3x-2 \\ 1 &=3(1)-2 \\ 1 &=1 \end{aligned} \nonumber$$

Отримане твердження вірно.

Таким чином, впорядкована пара$(0,−3)$ не задовольняє рівнянню$y =3 x−2$, але впорядкована пара$(1 ,1)$ дійсно задовольняє рівнянню$y =3x−2$.

Вправа$\PageIndex{2}$

Яка з впорядкованих пар$(−1,3)$ and $(2,1)$ satisfy the equation $y =2x + 5$?

Відповідь

$(-1,3)$

Графічні рівняння у двох змінних

Давайте спочатку визначимо, що мається на увазі під графом рівняння у двох змінних.

Графік рівняння

Графік рівняння - це множина всіх точок, які задовольняють заданому рівнянню.

Приклад$\PageIndex{3}$

Намалюйте графік рівняння$y = x + 1$.

Рішення

Визначення вимагає побудови всіх точок у декартовій системі координат, які задовольняють рівнянню$y = x + 1$. Давайте спочатку створимо таблицю точок, які задовольняють рівнянню. Почніть зі створення трьох стовпців із заголовками$x$$y$$(x,y)$, а потім виберіть деякі значення$x$ та помістіть їх у перший стовпець.

Візьміть перше значення$x$, а саме$x = −3$, і підставляйте його в рівняння$y = x + 1$.

$$\begin{aligned}y &=x+1 \\ y &=-3+1 \\ y &=-2\end{aligned} \nonumber$$

$$\begin{array}{|c|c|c|c|}\hline x & {y=x+1} & {(x, y)} \\ \hline-3 & {-2} & {(-3,-2)} \\ -2 & {} & {} \\ {-1} & {} & {} \\ { 0} & {} & {}\\ {1} & {} & {}\\ {2} & {} & {}\\ {3} & {} &{} \\ \hline\end{array} \nonumber$$

Таким чином, коли$x = −3$, ми маємо$y = −2$. Введіть це значення в таблицю.

Продовжуйте підставляти кожне$x$ табличне значення в рівняння$y = x + 1$ і використовуйте кожен результат для заповнення відповідних записів у таблиці.

$$\begin{array}{l}{y=-3+1=-2} \\ {y=-2+1=-1} \\ {y=-1+1=0} \\ {y=0+1=1} \\ {y=1+1=2} \\ {y=2+1=3} \\ {y=3+1=4}\end{array} \nonumber$$

$$\begin{array}{|c|c|c|c|}\hline x & {y=x+1} & {(x, y)} \\ \hline-3 & {-2} & {(-3,-2)} \\ -2 & {-1} & {(-2,-1)} \\ {-1} & {0} & {(-1,0)} \\ { 0} & {1} & {(0,1)}\\ {1} & {2} & {(1,2)}\\ {2} & {3} & {(2,3)}\\ {3} & {4} &{(3,4)} \\ \hline\end{array} \nonumber$$

Останній стовпець таблиці тепер містить сім пунктів, які задовольняють рівнянню$y = x+1$. Покладіть ці точки на декартовій системі координат (див. Рис.\(\PageIndex{9}\)).

Малюнок$\PageIndex{9}$ : Сім точок, які задовольняють рівнянню$y = x + 1$.

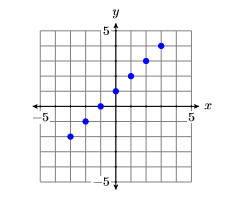
На малюнку$\PageIndex{9}$ ми намітили сім точок, які задовольняють заданому рівнянню$y = x+1$. Однак визначення вимагає побудови всіх точок, які задовольняють рівнянню. Виявляється, що візерунок розвивається на малюнку$\PageIndex{9}$, але давайте розрахуємо і побудуємо ще кілька пунктів, щоб бути впевненим. Додайте$x$ значення$−2.5$$−1.5$$−0.5$ -values$0.5$,$1.5$,,, і$2.5$ до x-стовпця таблиці, а потім використовуйте рівняння$y = x + 1$ для оцінки y на кожному з цих$x$ -значень.

$$\begin{array}{l}{y=-2.5+1=-1.5} \\ {y=-1.5+1=-0.5} \\ {y=-0.5+1=0.5} \\ {y=0.5+1=1.5} \\ {y=1.5+1=2.5} \\ {y=2.5+1=3.5}\end{array} \nonumber$$

$$\begin{array}{|c|c|c|c|}\hline x & {y=x+1} & {(x, y)} \\ \hline-2.5 & {-1.5} & {(-2.5,-1.5)} \\ -1.5 & {-0.5} & {(-1.5,-0.5)} \\ {-0.5} & {0.5} & {(-0.5,0.5)} \\ { 0.5} & {1.5} & {(0.5,1.5)}\\ {1.5} & {2.5} & {(1.5,2.5)}\\ {2.5} & {3.5} & {(2.5,3.5)}\\ \hline\end{array} \nonumber$$

Додайте ці додаткові точки до графіка на малюнку,$\PageIndex{9}$ щоб отримати зображення, показане на малюнку$\PageIndex{10}$.

Малюнок$\PageIndex{10}$ : Додавання додаткових точок до графіка$y = x + 1$.

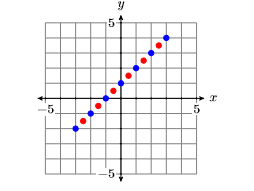
Існує нескінченна кількість точок, які задовольняють рівнянню$y = x + 1$. На малюнку$\PageIndex{10}$ ми намалювали лише$13$ точки, які задовольняють рівнянню. Однак колекція точок, побудованих на малюнку,$\PageIndex{10}$ припускає, що якби ми мали намітити залишок точок, які задовольняють рівнянню$y = x + 1$, ми отримали б графік лінії, показаної на малюнку$\PageIndex{11}$.

Малюнок$\PageIndex{11}$ : Графік$y = x + 1$ є лінією.

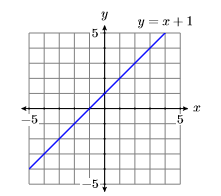
Вправа$\PageIndex{3}$

Намалюйте графік рівняння$y = −x + 2$.

Відповідь

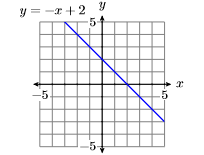
Рекомендації та вимоги

Приклад$\PageIndex{3}$ передбачає, що ми повинні використовувати наступні вказівки під час ескізу графіка рівняння.

Методичні вказівки щодо складання графіка рівняння

Коли вас попросять намалювати графік рівняння, виконайте кожен з наступних кроків:

1. Налаштуйте і обчисліть таблицю точок, які задовольняють заданому рівнянню.
2. Налаштуйте декартову систему координат на графічному папері та побудуйте точки у вашій таблиці на системі. Позначте кожну вісь (зазвичай$x$ і$y$) і вкажіть масштаб на кожній осі.
3. Якщо кількості нанесених точок достатньо, щоб уявити, якою буде форма кінцевої кривої, то намалюйте інші точки, які задовольняють рівнянню, як уявляли. Використовуйте лінійку, якщо вважаєте, що графік є лінією. Якщо графік виглядає кривою, від руки графік без використання лінійки.
4. Якщо кількість побудованих точок не дає достатньої кількості доказів, щоб уявити остаточну форму графіка, додайте більше точок до вашої таблиці, побудуйте їх і спробуйте ще раз уявити остаточну форму графіка. Якщо ви все ще не можете передбачити можливу форму графіка, продовжуйте додавати точки до вашої таблиці та будувати їх, поки не переконаєтесь у кінцевій формі графіка.

Ось деякі додаткові вимоги, яких необхідно дотримуватися при ескізному графіку рівняння.

Графічний папір, лінії, криві та лінійки.

Нижче наведені вимоги до цього класу:

5. Всі графіки повинні бути намальовані на графічному папері.
6. Всі лінії повинні бути намальовані за допомогою лінійки. Сюди можна віднести горизонтальну і вертикальну осі.
7. Якщо граф рівняння є кривою замість прямої, то графік слід малювати від руки, без допомоги лінійки.

Використання функції TABLE графічного калькулятора

Оскільки рівняння ускладнюються, створювати таблиці точок, які задовольняють рівнянню, може стати досить нудним. На щастя, графічний калькулятор має функцію TABLE, яка дозволяє легко будувати таблиці точок, які задовольняють заданому рівнянню.

Приклад$\PageIndex{4}$

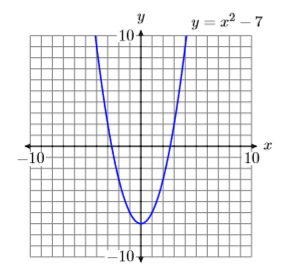
Використовуйте графічний калькулятор, щоб допомогти створити таблицю точок, які задовольняють рівнянню$y = x^2−7$. Побудуйте точки в своїй таблиці. Якщо ви не відчуваєте, що є достатньо доказів, щоб уявити, якою буде остаточна форма графіка, скористайтеся калькулятором, щоб додати більше очок до вашої таблиці та побудувати їх. Продовжуйте цей процес, поки ви не переконаєтеся в остаточній формі графіка.

Рішення

Малюнок$\PageIndex{12}$ : Графічний калькулятор.

Першим кроком є завантаження рівняння$y = x^2−7$ i в меню Y = графічного калькулятора. Самий верхній ряд кнопок на калькуляторі (див. Рис.$\PageIndex{12}$) має такий вигляд:

Малюнок$\PageIndex{13}$. Використовуйте клавіші зі стрілками вгору-вниз (див. Рис.$\PageIndex{15}$), щоб перемістити курсор після Y1 = в меню Y =, потім використовуйте наступні натискання клавіш для введення рівняння$y = x^2 −7$. Результат показаний на малюнку$\PageIndex{14}$.

Малюнок$\PageIndex{13}$ : Відкриття меню Y =. Малюнок $\PageIndex{14}$: Введення рівняння$y = x^2 −7$.

Малюнок$\PageIndex{15}$ : Клавіші зі стрілками переміщують курсор.

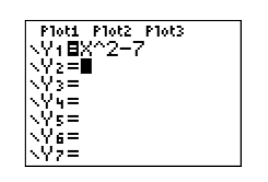
Наступний крок - «налаштувати» стіл. По-перше, зауважте, що калькулятор має символіку, надруковану на корпусі над кожною з його кнопок. Над кнопкою WINDOW ви помітите фразу TBLSET. Зверніть увагу, що він в тому ж кольорі, що і 2-я кнопка. Таким чином, щоб відкрити вікно настройки таблиці, введіть наступні натискання клавіш.

Рисунок$\PageIndex{16}$) дорівнює першому значенню x, яке ви хочете бачити у вашій таблиці. В цьому випадку введіть$−4$ після TBLStart. SettBL на приріст, який ви хочете для ваших$x$ -значень. У цьому випадку ставимо Tbl рівним$1$. Нарешті, встановіть як незалежні, так і залежні змінні на «automatic». У кожному конкретному випадку за допомогою клавіш зі стрілками виділіть слово AUTO і натисніть ENTER. Результат показаний на малюнку$\PageIndex{16}$.

Далі зверніть увагу на слово TABLE над кнопкою GRAPH в тому ж кольорі, що і 2-а клавіша. Щоб відкрити ТАБЛИЦЮ, введіть наступні натискання клавіш.

Малюнок$\PageIndex{17}$. Зверніть увагу, що ви можете використовувати клавіші зі стрілками вгору-вниз для прокрутки таблиці.

Малюнок$\PageIndex{16}$ : Відкриття меню TBLSET. Малюнок$\PageIndex{17}$ : Таблиця задовольняють балів$y = x^2 −7$.

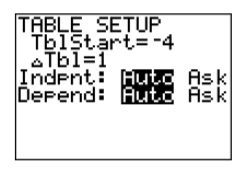
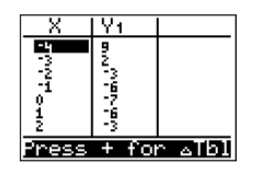
Далі введіть результати з таблиці вашого калькулятора в таблицю на аркуші графічного паперу, а потім побудуйте точки в таблиці. Результати наведені на рис$\PageIndex{18}$.

Малюнок$\PageIndex{18}$ : Побудова дев'яти точок, які задовольняють рівнянню$y = x^2 −7$.

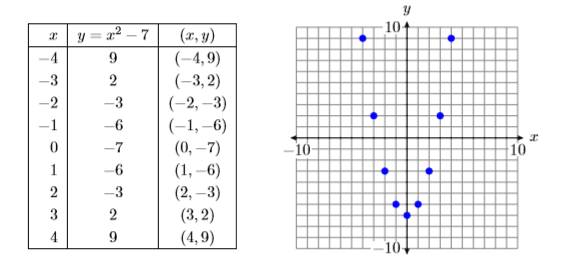
На малюнку$\PageIndex{18}$ можлива форма графіка$y = x^2 −7$ може бути очевидною вже, але давайте додамо ще кілька пунктів до нашої таблиці та побудуємо їх. Знову відкрийте вікно «налаштування» таблиці, натиснувши 2ND WINDOW. $−4$Знову встановіть TBLStart, а потім встановіть приріст Tbl на$0.5$. Результат показаний на малюнку$\PageIndex{19}$.

Малюнок$\PageIndex{19}$ : SetBL дорівнює 0,5. Малюнок$\PageIndex{20}$: Більше балів задовольняють$y = x^2 −7$.

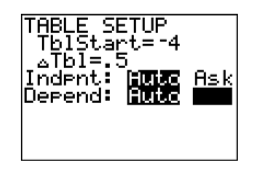
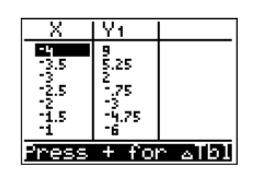
Додайте ці нові точки в таблицю на графічному папері і намалюйте їх (див. Рис.$\PageIndex{21}$).

Малюнок$\PageIndex{21}$ : Додавання додаткових точок до графіка$y = x^2 −7$.

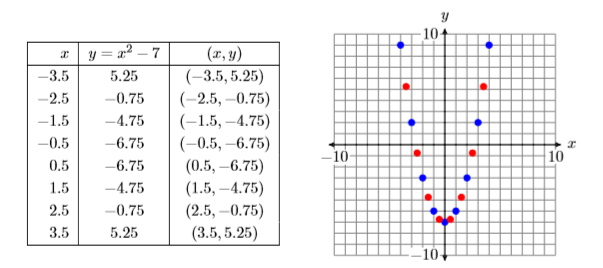
Існує нескінченна кількість точок, які задовольняють рівнянню$y = x^2−7$. На малюнку$\PageIndex{21}$ ми намалювали лише$17$ точки, які задовольняють рівнянню$y = x^2 −7$. Однак колекція точок на малюнку$\PageIndex{21}$ припускає, що якби ми мали намітити залишок точок, які задовольняють рівнянню$y = x^2 −7$, результатом буде крива (називається параболою), показана на малюнку$\PageIndex{22}$.

Малюнок$\PageIndex{22}$: Графік$y = x^2 −7$ - це крива, яка називається параболою.