1.3E: Вправи

Практика робить досконалим

Використання змінних та алгебраїчних символів

У наступних вправах перекладіть з алгебри на англійську мову.

Вправа$\PageIndex{55}$

$16−9$

Відповідь

$16$мінус$9$, різниця шістнадцять і дев'ять

Вправа$\PageIndex{56}$

$3\cdot 9$

Вправа$\PageIndex{57}$

$28\div 4$

Відповідь

$28$ділиться на$4$, частка двадцяти восьми і чотирьох

Вправа$\PageIndex{58}$

$x+11$

Вправа$\PageIndex{59}$

$(2)(7)$

Відповідь

$2$раз$7$, добуток двох і семи

Вправа$\PageIndex{60}$

$(4)(8)$

Вправа$\PageIndex{61}$

$14<21$

Відповідь

чотирнадцять менше двадцяти одного

Вправа$\PageIndex{62}$

$17<35$

Вправа$\PageIndex{63}$

$36\geq 19$

Відповідь

тридцять шість більше або дорівнює дев'ятнадцяти

Вправа$\PageIndex{64}$

$6n=36$

Вправа$\PageIndex{65}$

$y−1>6$

Відповідь

$y$$1$мінус більше$6$, різниця$y$ і одиниця більше шести

Вправа$\PageIndex{66}$

$y−4>8$

Вправа$\PageIndex{67}$

$2\leq 18\div 6$

Відповідь

$2$менше або дорівнює$18$ ділиться на$6$;$2$ менше або дорівнює частці вісімнадцяти і шести

Вправа$\PageIndex{68}$

$a\neq 1\cdot12$

У наступних вправах визначте, чи є кожне виразом чи рівнянням.

Вправа$\PageIndex{69}$

$9\cdot 6=54$

Відповідь

рівняння

Вправа$\PageIndex{70}$

$7\cdot 9=63$

Вправа$\PageIndex{71}$

$5\cdot 4+3$

Відповідь

вираз

Вправа$\PageIndex{72}$

$x+7$

Вправа$\PageIndex{73}$

$x + 9$

Відповідь

вираз

Вправа$\PageIndex{74}$

$y−5=25$

Спрощення виразів за допомогою порядку операцій

У наступних вправах спрощуйте кожен вираз.

Вправа$\PageIndex{75}$

$5^{3}$

Відповідь

$125$

Вправа$\PageIndex{76}$

$8^{3}$

Вправа$\PageIndex{77}$

$2^{8}$

Відповідь

$256$

Вправа$\PageIndex{78}$

$10^{5}$

У наступних вправах спростіть, використовуючи порядок операцій.

Вправа$\PageIndex{79}$

1. $3+8\cdot 5$
2. $(3+8)\cdot 5$

Відповідь

1. $43$
2. $55$

Вправа$\PageIndex{80}$

1. $2+6\cdot 3$
2. $(2+6)\cdot 3$

Вправа$\PageIndex{81}$

$2^{3}−12\div (9−5)$

Відповідь

$5$

Вправа$\PageIndex{82}$

$3^{2}−18\div(11−5)$

Вправа$\PageIndex{83}$

$3\cdot 8+5\cdot 2$

Відповідь

$34$

Вправа$\PageIndex{84}$

$4\cdot 7+3\cdot 5$

Вправа$\PageIndex{85}$

$2+8(6+1)$

Відповідь

$58$

Вправа$\PageIndex{86}$

$4+6(3+6)$

Вправа$\PageIndex{87}$

$4\cdot 12/8$

Відповідь

$6$

Вправа$\PageIndex{88}$

$2\cdot 36/6$

Вправа$\PageIndex{89}$

$(6+10)\div(2+2)$

Відповідь

$4$

Вправа$\PageIndex{90}$

$(9+12)\div(3+4)$

Вправа$\PageIndex{91}$

$20\div4+6\cdot5$

Відповідь

$35$

Вправа$\PageIndex{92}$

$33\div3+8\cdot2$

Вправа$\PageIndex{93}$

$3^{2}+7^{2}$

Відповідь

$58$

Вправа$\PageIndex{94}$

$(3+7)^{2}$

Вправа$\PageIndex{95}$

$3(1+9\cdot6)−4^{2}$

Відповідь

$149$

Вправа$\PageIndex{96}$

$5(2+8\cdot4)−7^{2}$

Вправа$\PageIndex{97}$

$2[1+3(10−2)]$

Відповідь

$50$

Вправа$\PageIndex{98}$

$5[2+4(3−2)]$

Оцінити вираз

У наступних вправах оцініть наступні вирази.

Вправа$\PageIndex{99}$

$7x+8$коли$x=2$

Відповідь

$22$

Вправа$\PageIndex{100}$

$8x−6$коли$x=7$

Вправа$\PageIndex{101}$

$x^{2}$коли$x = 12$

Відповідь

$144$

Вправа$\PageIndex{102}$

$x^{3}$коли$x = 5$

Вправа$\PageIndex{103}$

$x^{5}$коли$x = 2$

Відповідь

$32$

Вправа$\PageIndex{104}$

$4^{x}$коли$x = 2$

Вправа$\PageIndex{105}$

$x^{2}+3x−7$коли$x = 4$

Відповідь

$21$

Вправа$\PageIndex{106}$

$6x + 3y - 9$коли$x = 10, y = 7$

Відповідь

$9$

Вправа$\PageIndex{107}$

$(x + y)^{2}$коли$x = 6, y = 9$

Вправа$\PageIndex{108}$

$a^{2} + b^{2}$коли$a = 3, b = 8$

Відповідь

$73$

Вправа$\PageIndex{109}$

$r^{2} - s^{2}$коли$r = 12, s = 5$

Вправа$\PageIndex{110}$

$2l + 2w$коли$l = 15, w = 12$

Відповідь

$54$

Вправа$\PageIndex{111}$

$2l + 2w$коли$l = 18, w = 14$

Спростіть вирази, поєднуючи подібні терміни

У наступних вправах визначте коефіцієнт кожного члена.

Вправа$\PageIndex{112}$

$8a$

Відповідь

$8$

Вправа$\PageIndex{113}$

$13m$

Вправа$\PageIndex{114}$

$5r^{2}$

Відповідь

$5$

Вправа$\PageIndex{115}$

$6x^{3}$

У наступних вправах виділіть подібні терміни.

Вправа$\PageIndex{116}$

$x^{3}, 8x, 14, 8y, 5, 8x^{3}$

Відповідь

$x^{3}$і$8x^{3}$,$14$ і$5$

Вправа$\PageIndex{117}$

$6z, 3w^{2}, 1, 6z^{2}, 4z, w^{2}$

Вправа$\PageIndex{118}$

$9a, a^{2}, 16, 16b^{2}, 4, 9b^{2}$

Відповідь

$16$і$4$,$16b^{2}$ і$9b^{2}$

Вправа$\PageIndex{119}$

$3, 25r^{2}, 10s, 10r, 4r^{2}, 3s$

У наступних вправах визначте терміни в кожному виразі.

Вправа$\PageIndex{120}$

$15x^{2} + 6x + 2$

Відповідь

$15x^{2}, 6x, 2$

Вправа$\PageIndex{121}$

$11x^{2} + 8x + 5$

Вправа$\PageIndex{122}$

$10y^{3} + y + 2$

Відповідь

$10y^{3}, y, 2$

Вправа$\PageIndex{123}$

$9y^{3} + y + 5$

У наступних вправах спростіть наступні вирази, комбінуючи подібні терміни.

Вправа$\PageIndex{124}$

$10x+3x$

Відповідь

$13x$

Вправа$\PageIndex{125}$

$15x+4x$

Вправа$\PageIndex{126}$

$4c + 2c + c$

Відповідь

$7c$

Вправа$\PageIndex{127}$

$6y + 4y + y$

Вправа$\PageIndex{128}$

$7u + 2 + 3u + 1$

Відповідь

$10u + 3$

Вправа$\PageIndex{129}$

$8d + 6 + 2d + 5$

Вправа$\PageIndex{130}$

$10a + 7 + 5a - 2 + 7a - 4$

Відповідь

$22a + 1$

Вправа$\PageIndex{131}$

$7c + 4 + 6c - 3 + 9c - 1$

Вправа$\PageIndex{132}$

$3x^{2} + 12x + 11 + 14x^{2} + 8x + 5$

Відповідь

$17x^{2} + 20x + 16$

Вправа$\PageIndex{133}$

$5b^{2} + 9b + 10 + 2b^{2} + 3b - 4$

Перекласти англійську фразу на алгебраїчний вираз

У наступних вправах переводите фрази в алгебраїчні вирази.

Вправа$\PageIndex{134}$

різниця$14$ і$9$

Відповідь

$14−9$

Вправа$\PageIndex{135}$

різниця$19$ і$8$

Вправа$\PageIndex{136}$

продукт$9$ і$7$

Відповідь

$9\cdot 7$

Вправа$\PageIndex{137}$

продукт$8$ і$7$

Вправа$\PageIndex{138}$

частка$36$ і$9$

Відповідь

$36\div 9$

Вправа$\PageIndex{139}$

частка$42$ і$7$

Вправа$\PageIndex{140}$

сума$8x$ і$3x$

Відповідь

$8x+3x$

Вправа$\PageIndex{141}$

сума$13x$ і$3x$

Вправа$\PageIndex{142}$

частка$y$ і$3$

Відповідь

$\frac{y}{3}$

Вправа$\PageIndex{143}$

частка$y$ і$8$

Вправа$\PageIndex{144}$

вісім разів різниця$y$ і дев'ять

Відповідь

$8(y−9)$

Вправа$\PageIndex{145}$

сім разів різниця$y$ і один

Вправа$\PageIndex{146}$

Ерік має рок і класичні компакт-диски в своєму автомобілі. Кількість рок-компакт-дисків$3$ більше, ніж кількість класичних компакт-дисків. $c$Дозволяти представляти кількість класичних компакт-дисків. Напишіть вираз для кількості рок-компакт-дисків.

Відповідь

$c+3$

Вправа$\PageIndex{147}$

Кількість дівчаток у другому класі$4$ менше, ніж кількість хлопчиків. Дозвольте$b$ уявити кількість хлопчиків. Напишіть вираз для кількості дівчат.

Вправа$\PageIndex{148}$

У Грега в кишені нікельси і копійки. Кількість копійок на сім менше, ніж в два рази перевищує кількість нікелів. $n$Дозволяти представляти кількість нікелів. Напишіть вираз на кількість копійок.

Відповідь

$2n - 7$

Вправа$\PageIndex{149}$

Жаннет має купюри в розмірі 5 доларів та 10 доларів у гаманці. Кількість п'ятірок в три більше, ніж в шість разів перевищує кількість десятків. $t$Дозволяти представляти кількість десятків. Напишіть вираз для числа п'ятірок.

Щоденна математика

Вправа$\PageIndex{150}$

Автострахування автострахування Джастіна має франшизу 750 доларів за інцидент. Це означає, що він платить 750 доларів, і його страхова компанія буде платити всі витрати понад 750 доларів. Якщо Джастін подає претензію на $2,100.

1. скільки він заплатить?
2. скільки заплатить його страхова компанія?

Відповідь

1. $750
2. 1 350$

Вправа$\PageIndex{151}$

Страхування будинку Armando в будинку страхування має $2,500 франшиза за інцидент. Це означає, що він платить $2500 і страхова компанія буде платити всі витрати понад $2500. Якщо Армандо подає позов на $19,400.

1. скільки він заплатить?
2. скільки заплатить страхова компанія?

Письмові вправи

Вправа$\PageIndex{152}$

Поясніть різницю між виразом і рівнянням.

Відповідь

Відповіді можуть відрізнятися

Вправа$\PageIndex{153}$

Чому важливо використовувати порядок операцій для спрощення виразу?

Вправа$\PageIndex{154}$

Поясніть, як ви ідентифікуєте подібні терміни у виразі$8a^{2} + 4a + 9 - a^{2} - 1$

Відповідь

Відповіді можуть відрізнятися

Вправа$\PageIndex{155}$

Поясніть різницю між фразами «$4$раз сума$x$ і$y$» і «сума$4$ разів$x$ і»$y$.

Самостійна перевірка

ⓐ Використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

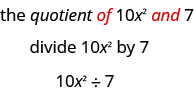
ⓑ Ознайомившись з цим контрольним списком, що ви робите, щоб стати впевненими у всіх цілях?