1.4: Додавання та віднімання цілих чисел
- Page ID
- 59102
- Використовуйте негативи і протилежності
- Спрощення: вирази з абсолютним значенням
- Додавання цілих чисел
- Віднімання цілих чисел
Більш ретельний вступ до тем, розглянутих у цьому розділі, можна знайти в розділі Преалгебра, Цілі числа.
Використовуйте негативи та протилежності
Наша робота поки що включала лише підрахунок чисел і цілих чисел. Але якщо ви коли-небудь відчували температуру нижче нуля або випадково перекреслили розрахунковий рахунок, ви вже знайомі з негативними числами. Негативні числа - це числа менше\(0\). Від'ємні числа ліворуч від нуля на числовому рядку. Див\(\PageIndex{1}\). Малюнок.
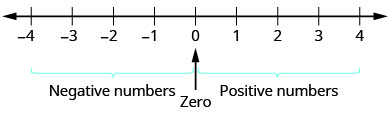
Стрілки на кінцях числового рядка вказують на те, що цифри продовжують йти вічно. Немає найбільшого позитивного числа, і немає найменшого негативного числа.
Нуль - це додатне або від'ємне число? Числа, більші за нуль, є додатними, а числа менше нуля - від'ємними. Нуль не є ні позитивним, ні негативним.
Розглянемо, як впорядковуються числа на числовому рядку. Йдучи зліва направо, цифри збільшуються в ціні. Йдучи справа наліво, цифри зменшуються в ціні. Див\(\PageIndex{2}\). Малюнок.
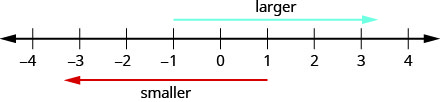
Виконання діяльності з маніпулятивної математики «Число рядка-частина 2» допоможе вам розвинути краще розуміння цілих чисел.
Пам'ятайте, що ми використовуємо позначення:
\(a \lt b\)(читати «\(a\)менше, ніж\(b\)»), коли\(a\) знаходиться\(b\) ліворуч від номера рядка.
\(a \gt b\)(читати «\(a\)більше, ніж\(b\)»), коли\(a\) знаходиться\(b\) праворуч від числового рядка.
Тепер нам потрібно розширити числовий рядок, який показав цілі числа, щоб включити негативні числа, теж. Числа, позначені точками на рис\(\PageIndex{3}\)., називаються цілими числами. Цілі числа - це числа\(...−3, −2, −1, 0, 1, 2, 3…\)

Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):
- \(14 \; \_\_\_\; 6\)
- \(-1\; \_\_\_ \;9\)
- \(-1\; \_\_\_ -4\)
- \(\;\; 2 \;\_\_\_ -20\)
Рішення:
Можливо, буде корисно звернутися до показаного номера рядка.

Малюнок\(\PageIndex{4}\)
\ (\ begin {вирівнювати*} 1. \ quad & 14\;\ _\ _\ _\; 6\\ [4pt]
& 14 > 6 &&\ text {\(14\)знаходиться\(6\) праворуч від номера рядка.}\\ [8pt]
2. \ quad & -1\;\ _\ _\ _\; 9\ [4pt]
& -1 < 9 &&\ text {\(-1\)знаходиться\(9\) ліворуч від числового рядка.}\\ [8pt]
3. \ quad & -1\;\ _\ _\ _-4\\ [4pt]
& -1 > -4 &&\ text {\(-1\)знаходиться\(-4\) праворуч від номера рядка.}\\ [8pt]
4. \ quad & 2\;\ _\ _\ _-20\\ [4pt]
& 2 > -20 &&\ text {\(2\)знаходиться\(-20\) праворуч від номера рядка.} \
\ end {вирівнювати*}\)
Замовте кожну з наступних пар чисел, використовуючи\(<\) or \(>\):
- \(15 \; \_\_\_\; 7\)
- \(-2 \; \_\_\_\; 5\)
- \(-3 \; \_\_\_\; -7\)
- \(5 \; \_\_\_\; -17\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):
- \(8 \; \_\_\_\; 13\)
- \(3 \; \_\_\_\; -4\)
- \(-5 \; \_\_\_\; -2\)
- \(9 \; \_\_\_\; -21\)
- Відповідь
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Можливо, ви помітили, що на числовому рядку негативні числа є дзеркальним відображенням позитивних чисел, з нулем посередині. Оскільки числа\(2\) і\(−2\) знаходяться на однаковій відстані від нуля, вони називаються навпроти s. \(2\)Протилежне є\(−2\), а\(−2\) протилежне є\(2\).
Протилежність числу - це число, яке знаходиться на тій же відстані від нуля на числовій лінії, але на протилежній стороні нуля.
Малюнок\(\PageIndex{5}\) ілюструє визначення.

Іноді в алгебрі один і той же символ має різні значення. Так само, як і деякі слова англійською мовою, конкретне значення стає зрозумілим, дивлячись на те, як воно використовується. Ви бачили символ «\(−\)», який використовується трьома різними способами.
\ [\ begin {align*} &10 − 4\ quad\ text {Між двома числами він вказує на операцію}\ textit {віднімання}.\\ &\ qquad\ qquad\ text {Читаємо} 10 - 4\,\ text {як «} 10\,\ text {мінус}\, 4. \ text {»}\\ [5pt]
&-8\ quad\ text {Перед числом він вказує}\ textit {негативний}\ текст {число.}\\ &\ qquad\ text {Ми читаємо} -8\ текст {як «негативна вісімка»}\\ [5pt]
&-x\ quad\ text {Перед змінною вказує}\ text це {навпроти.}\\ &\ qquad\ qquad\ text {Ми читаємо} -x\ text {як «протилежність} x\ text {»}\\ [5pt]
&- (-2)\ quad\ text {Тут є два знаки «−».} \\
&\ qquad\ qquad\ text {Той, що в дужках говорить нам, що число є від'ємним} 2. \\
&\ qquad\ qquad\ text {Той, що знаходиться поза дужками, говорить нам взяти}\ textit {протилежний}\ text {of} −2. \\
&\ qquad\ qquad\ text {Читаємо} − (−2)\ text {як «протилежність негативним двом.»} \ end {вирівнювати*}\]
\(−a\)означає протилежне числу\(a\).
Позначення\(−a\) читається як «протилежне»\(a\).
Знайти:
- протилежність\(7\)
- протилежність\(−10\)
- протилежність\(−(−6)\)
Рішення:
1. \( \quad −7\)таке ж відстань від\(0\) як\(7\), але на протилежному боці\(0\). Протилежність\(7\) є\(-7\).

2. \( \quad 10\)таке ж відстань від\(0\) як\(−10\), але на протилежному боці\(0\). Протилежність\(-10\) є\(10\).

3. \(\quad\)Протилежність\(-(-6)\) є\(-6\).

Знайти:
- протилежність\(4\)
- the opposite of \(−3\)
- \(−(−1)\)
- Answer
-
- \(-4\)
- \(3\)
- \(1\)
Знайти:
- протилежність\(8\)
- протилежність\(−5\)
- \(−(−5)\)
- Відповідь
-
- \(-8\)
- \(5\)
- \(5\)
Наша робота з протилежностями дає нам спосіб визначити цілі числа. Цілі числа і їх протилежності називаються цілими числами. Цілі числа - це числа\(…−3,−2,−1,0,1,2,3…\)
Цілі числа і їх протилежності називаються цілими числами.
Цілі числа - це числа
\[…−3,−2,−1,0,1,2,3… \nonumber \]
Оцінюючи протилежність змінної, ми повинні бути дуже обережними. Не знаючи, чи є змінна додатним чи від'ємним числом, ми не знаємо, чи є −x−x позитивним чи від'ємним. Ми можемо бачити це в прикладі\(\PageIndex{1}\).
Оцінити
- \(-x\), коли\(x = 8\)
- \(-x\), коли\(x = -8\)
Рішення:
-

-х 
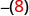
Напишіть протилежне 8. -8 -

-х 
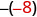
Напишіть протилежне -8. 8
Оцінити\(-n\), when
- \(n = 4\)
- \(n = -4\)
- Answer
-
- \(-4\)
- \(4\)
Оцініть\(-m\), коли
- \(m = 11\)
- \(m = -11\)
- Відповідь
-
- \(-11\)
- \(11\)
Спрощення: вирази з абсолютним значенням
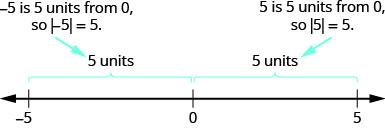
Ми побачили, що числа, такі як\(2\) і\(−2\) є протилежними, тому що вони однакові відстані від\(0\) на числовій лінії. Вони обидва дві одиниці від\(0\). Відстань між\(0\) і будь-яким числом на числовому рядку називається абсолютним значенням цього числа.
Абсолютне значення числа - це його відстань від\(0\) на числовому рядку.
Абсолютне значення числа\(n\) записується як\(|n|\).
Наприклад,
- \(−5\)це\(5\) одиниці далеко від\(0\), так\(|−5|=5\).
- \(5\)це\(5\) одиниці далеко від\(0\), так\(|5|=5\).
Малюнок\(\PageIndex{6}\) ілюструє цю ідею.
Абсолютне значення числа ніколи не є від'ємним (оскільки відстань не може бути від'ємною). Єдине число з абсолютним значенням, рівним нулю, - це саме число нуль, тому що відстань від\(0\) до\(0\) на числовому рядку дорівнює нулю одиниць.
\(|n| \geq 0\)для всіх номерів
Абсолютні значення завжди більше або рівні нулю!
Математики говорять точніше: «абсолютні значення завжди невід'ємні». Невід'ємний означає більше або дорівнює нулю.
Спростити:
- \(|3|\)
- \(|-44|\)
- \(|0|\)
Рішення:
Абсолютне значення числа - це відстань між числом і нулем. Відстань ніколи не буває від'ємною, тому абсолютне значення ніколи не буває від'ємним.
- \( |3| = 3\)
- \(|-44| = 44\)
- \( |0| = 0\)
Спростити:
- \(|4|\)
- \(|-28|\)
- \(|0|\)
- Answer
-
- \(4\)
- \(28\)
- \(0\)
Спростити:
- \(|-13|\)
- \(|47|\)
- Відповідь
-
- \(13\)
- \(47\)
У наступному прикладі ми впорядкуємо вирази з абсолютними значеннями. Пам'ятайте, позитивних чисел завжди більше, ніж від'ємні числа!
Заповніть\(<, >, \text{or} =\) для кожної з наступних пар чисел:
- \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
- \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
- \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
- \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)
Рішення:
\(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)
Заповніть\(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
- \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
- \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
- \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(>\)
Заповніть\(<, >, \text{or} =\) для кожної з наступних пар чисел:
- \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
- \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
- \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
- \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)
- Відповідь
-
- \(>\)
- \(>\)
- \(>\)
- \(<\)
Тепер ми додаємо абсолютні стовпчики значень до нашого списку символів групування. Коли ми використовуємо порядок операцій, спочатку максимально спрощуємо всередині барів абсолютного значення, потім приймаємо абсолютне значення отриманого числа.
\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]
У наступному прикладі ми спочатку спрощуємо вирази всередині барів абсолютних значень, як це робимо з дужками.
Спростити:\(24 - |19 - 3(6 - 2)|\)
Рішення:
\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]
Спростити:\(19 - |11 - 4(3 - 1)|\)
- Answer
-
\(16\)
Спростити:\(9 - |8 - 4(7 - 5)|\)
- Відповідь
-
\(9\)
Оцініть:
- \(|x|\)коли\(x = -35\)
- \(|y|\)коли\(y = -20\)
- \(-|u|\)коли\(u = 12\)
- \(-|p|\)коли\(p = -14\)
Рішення:
1. \(|x|\)коли\(x = -35\)
\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)
2. \(|y|\)коли\(y = -20\)
\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)
3. \(-|u|\)коли\(u = 12\)
\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)
4. \(-|p|\)коли\(p = -14\)
\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)
Оцініть:
- \(|x|\) when \(x = -17\)
- \(|y|\) when \(y = -39\)
- \(-|m|\) when \(m = 22\)
- \(-|p|\) when \(p = -11\)
- Answer
-
- \(17\)
- \(39\)
- \(-22\)
- \(-11\)
Оцініть:
- \(|y|\)коли\(y = -23\)
- \(|-y|\)коли\(y = -21\)
- \(-|n|\)коли\(n = 37\)
- \(-|q|\)коли\(q = -49\)
- Відповідь
-
- \(23\)
- \(21\)
- \(-37\)
- \(-49\)
Додати цілі числа
Більшість учнів влаштовують додавання і віднімання фактів для позитивних чисел. Але робити додавання або віднімання як з позитивними, так і з негативними числами може бути більш складним завданням.
Виконання діяльності з маніпулятивної математики «Додавання знакових чисел» допоможе вам краще зрозуміти додавання цілих чисел».
Ми будемо використовувати два лічильники кольорів для моделювання додавання та віднімання негативів, щоб ви могли візуалізувати процедури замість запам'ятовування правил.
Ми дозволяємо одному кольору (синій) представляти позитив. Інший колір (червоний) буде представляти негативи. Якщо у нас один позитивний лічильник і один негативний лічильник, значення пари дорівнює нулю. Вони утворюють нейтральну пару. Значення цієї нейтральної пари дорівнює нулю.
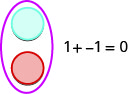
Ми будемо використовувати лічильники, щоб показати, як додати чотири факти додавання, використовуючи цифри\(5, −5\) і\(3,−3\).
\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]
Щоб додати\(5+3\), ми розуміємо, що\(5+3\) означає суму\(5\) і\(3\).
| Почнемо з\(5\) позитивів. |  |
| А потім ми додаємо\(3\) позитиви. |  |
| Тепер у нас є\(8\) позитиви. Сума\(5\) і\(3\) є\(8\). |  |
Тепер додамо\(−5 + (−3)\). Слідкуйте за схожістю з останнім прикладом\(5 + 3 = 8\).
Щоб додати\(−5 + (−3)\), ми розуміємо, що це означає суму\(−5\) і\(−3\).
| Почнемо з\(5\) негативів. |  |
| А потім додаємо\(3\) негативи. |  |
| У нас зараз\(8\) негатив. Сума\(-5\) і\(-3\) є\(-8\). |  |
Яким чином ці перші два приклади були схожі?
- Перший приклад додає\(5\) позитиви та\(3\) позитиви - обидва позитиви.
- Другий приклад додає\(5\) негативи та\(3\) негативи - обидва негативи.
У кожному випадку ми отримали\(8\) — або\(8\) позитивні, або\(8\) негативи.
Коли вивіски були однаковими, лічильники були все одного кольору, і тому ми їх додали.

Додати:
- \(1 + 4\)
- \(-1 + (-4)\)
Рішення:
1. 
\(1\)позитивний плюс\(4\) позитиви - це\(5\) позитиви.
2. 
\(1\)негативний плюс\(4\) негативи -\(5\) негативи.
Додати:
- \(2 + 4\)
- \(-2 + (-4)\)
- Answer
-
- \(6\)
- \(-6\)
Додати:
- \(2 + 5\)
- \(-2 + (-5)\)
- Відповідь
-
- \(7\)
- \(-7\)
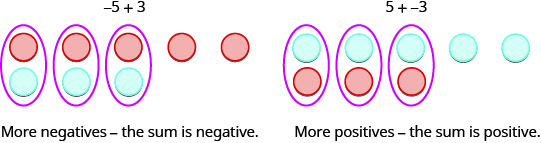
Так що ж відбувається, коли ознаки різні? Давайте додамо\(−5+3\). Ми розуміємо, що це означає суму\(−5\) і\(3\). Коли лічильники були одного кольору, ставимо їх в ряд. Коли лічильники будуть іншого кольору, вишикуємо їх один під одним.
| \(-5 + 3\)означає суму\(-5\) і\(3\). | |
| Почнемо з\(5\) негативів. |  |
| А потім ми додаємо\(3\) позитиви. | 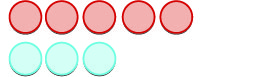 |
| Прибираємо будь-які нейтральні пари. | 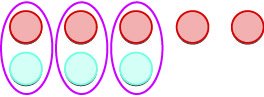 |
| У нас залишилися\(2\) негативи. |  |
| Сума\(-5\) і\(3\) є\(-2\). | \(-5 + 3 = 2\) |
Зверніть увагу, що негативів було більше, ніж позитивів, тому результат був негативним.
Давайте тепер додамо останню комбінацію,\(5+(−3)\).
| \(5 + (-3)\)означає суму\(-5\) і\(-3\). | |
| Почнемо з\(5\) позитивів. |  |
| А потім додаємо\(3\) негативи. |  |
| Прибираємо будь-які нейтральні пари. |  |
| У нас залишилися\(2\) позитиви. |  |
| Сума\(5\) і\(-3\) є\(2\). | \(5 + (-3) = 2\) |
Коли ми використовуємо лічильники для моделювання додавання позитивних і негативних цілих чисел, легко побачити, чи є більше позитивних або більше негативних лічильників. Таким чином, ми знаємо, буде сума позитивною чи негативною.
Додати:
- \(-1 + 5\)
- \(1 + (-5)\)
Рішення:
1. \(-1 + 5\)

Позитивів більше, тому сума позитивна.
Отже,\(-1 + 5 = 4\).
2. \(1 + (-5)\)

Негативів більше, тому сума негативна.
Отже,\(1 + (-5) = -4\)
Додати:
- \(-2 + 4\)
- \(2 + (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Додати:
- \(-2 + 5\)
- \(2 + (-5)\)
- Відповідь
-
- \(3\)
- \(-3\)
Тепер, коли ми додали невеликі позитивні та негативні цілі числа з моделлю, ми можемо візуалізувати модель в нашій свідомості, щоб спростити проблеми з будь-якими числами.
Коли вам потрібно додати такі цифри\(37+(−53)\), як, ви дійсно не хочете, щоб мати, щоб рахувати\(37\) сині лічильники і\(53\) червоні лічильники. Маючи модель у вашому розумі, чи можете ви візуалізувати, що б ви зробили для вирішення проблеми?
Малюнок\(37\) синій лічильники з\(53\) червоними лічильниками вишикувалися під. Оскільки червоних (негативних) лічильників буде більше, ніж синіх (позитивних) лічильників, сума буде негативною. Скільки більше червоних лічильників було б? Тому що\(53−37=16\), червоних лічильників\(16\) більше.
Тому сума\(37+(−53)\) дорівнює\(−16\).
\[37+(−53)=−16\nonumber\]
Спробуємо ще один. Ми додамо\(−74+(−27)\). Знову ж таки, уявіть\(74\) червоні лічильники і\(27\) більше червоних лічильників, так що у нас були б\(101\) червоні лічильники. Це означає, що сума є\(−101\).
\[−74+(−27)=−101\nonumber\]
Давайте ще раз подивимося на результати додавання різних комбінацій\(5,−5\) і\(3, -3\).
\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both positive, sum positive}} \end{array}\nonumber\]
Коли знаки однакові, лічильники будуть все одного кольору, тому додайте їх.
\[\begin{array} {ll} {5 + 3=-2} &{-5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]
Коли знаки різні, деякі лічильники роблять нейтральні пари, тому відніміть, щоб побачити, скільки залишилося.
Візуалізуйте модель, спрощуючи вирази в наступних прикладах.
Спростити:
- \(19 + (-47)\)
- \(-14 + (-36)\)
Рішення:
1. Так як ознаки різні, віднімаємо\(19\) від\(47\). Відповідь буде негативною, оскільки негативів більше, ніж позитивів.
\(\text{Add.} \qquad 19 + (-47) = -28\)
2. Так як знаки однакові, додаємо. Відповідь буде негативною, оскільки негативів більше, ніж позитивів.
\(\text{Add.} \qquad-14 + (-36) = -50\)
Спростити:
- \(-31 + (-19)\)
- \(15 + (-32)\)
- Answer
-
- \(-50\)
- \(-17\)
Спростити:
- \(-42 + (-28)\)
- \(25 + (-61)\)
- Відповідь
-
- \(-70\)
- \(-36\)
Методи, що використовуються до цього часу, поширюються на більш складні проблеми, як ті, які ми бачили раніше. Не забудьте стежити за порядком операцій!
Спростити:
\(-5 + 3(-2 + 7)\)
Рішення:
\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]
Спростити:
\(-2 + 5(-4 + 7)\)
- Answer
-
\(13\)
Спростити:
\(-4 + 2(-3 + 5)\)
- Відповідь
-
\(0\)
Віднімання цілих чисел
Виконання діяльності з маніпулятивної математики «Віднімання знакових чисел» допоможе вам розвинути краще розуміння віднімання цілих чисел.
Ми продовжимо використовувати лічильники для моделювання віднімання. Пам'ятайте, що сині лічильники представляють позитивні числа, а червоні - негативні числа.
Можливо, коли ви були молодшими, ви читали «\(5−3\)» як «\(5\)забрати»\(3\). Коли ви використовуєте лічильники, ви можете думати про віднімання так само!
Ми будемо моделювати чотири факти віднімання, використовуючи цифри\(5\) і\(3\).
\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]
Щоб відняти\(5−3\), повторюємо проблему як «\(5\)забрати»\(3\).
| Почнемо з\(5\) позитивів. |  |
| Ми «забираємо»\(3\) позитиви. |  |
| У нас залишилися\(2\) позитиви. | |
| Різниця\(5\) і\(3\) є\(2\). | \(2\) |
Тепер віднімемо\(−5−(−3)\). Слідкуйте за схожістю з останнім прикладом\(5−3=2\).
Щоб відняти\(−5−(−3)\), ми повторюємо це як «\(–5\)забрати\(–3\)»
| Почнемо з\(5\) негативів. |  |
|
Ми «забираємо»\(3\) негативи. |
 |
| У нас залишилися\(2\) негативи. | |
| Різниця\(-5\) і\(-3\) є\(-2\). |
\(-2\) |
Зверніть увагу, що ці два приклади дуже схожі: У першому прикладі ми віднімаємо 3 позитиви з 5 позитивів і в кінцевому підсумку з 2 позитивами.
У другому прикладі ми віднімаємо 3 негативу з 5 негативів і в кінцевому підсумку з 2 негативами.
У кожному прикладі використовувалися лічильники тільки одного кольору, а «відняти» модель віднімання було легко застосувати.
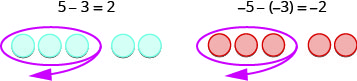
Відніміть:
- \(7 - 5\)
- \(-7 - (-5)\)
Рішення:
- \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
- \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]
Відніміть:
- \(6 - 4\)
- \(-6 - (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Відніміть:
- \(7 - 4\)
- \(-7 - (-4)\)
- Відповідь
-
- \(3\)
- \(-3\)
Що відбувається, коли нам доводиться відняти одне позитивне і одне негативне число? Нам потрібно буде використовувати як білі, так і червоні лічильники, а також деякі нейтральні пари. Додавання нейтральної пари не змінює значення. Це як зміна кварталів на нікель-значення однакове, але виглядає інакше.
- Щоб відняти\(−5−3\), ми повторюємо його як\(−5\) забираємо\(3\).
Почнемо з\(5\) негативів. Нам потрібно забрати\(3\) позитиви, але у нас немає ніяких позитивів, щоб забрати.
Пам'ятайте, нейтральна пара має значення нуль. Якщо додати\(0\) до\(5\) його вартості все одно\(5\). Ми додаємо нейтральні пари до\(5\) негативів, поки не отримаємо\(3\) позитивів, які потрібно забрати.
| \(-5 -3\)засіб\(-5\) забрати\(3\) | |
| Почнемо з\(5\) негативів. |  |
| Тепер ми додаємо нейтрали, необхідні для отримання\(3\) позитивів. |  |
| Прибираємо\(3\) позитиви. | 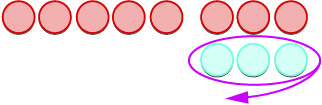 |
| Ми залишилися з\(8\) негативами. |  |
| Різниця\(-5\) і\(3\) є\(-8\). | \(-5 - 3 = -8\) |
А тепер четвертий випадок,\(5−(−3)\). Почнемо з\(5\) позитивів. Потрібно забирати\(3\) негативи, але негативів забирати немає. Таким чином, ми додаємо нейтральні пари, поки у нас не буде\(3\) негативу, щоб забрати.
| \(5 -(-3)\)засіб\(5\) забрати\(-3\) | |
| Почнемо з\(5\) позитивів. |  |
| Тепер додаємо потрібні нейтральні пари. |  |
| Прибираємо\(3\) негативи. | 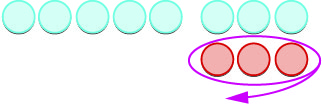 |
| Ми залишилися з\(8\) позитивами. |  |
| Різниця\(5\) і\(-3\) є\(8\). | \(5 - (-3) = 8\) |
Відніміть:
- \(-3 -1\)
- \(3 - (-1)\)
Рішення:
1.
|
Візьміть 1 позитив з доданої нейтральної пари. |
  |
\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\) |
|
Візьміть 1 негатив з доданої нейтральної пари. |
  |
\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\) |
Відніміть:
- \(-6 -4\)
- \(6 - (-4)\)
- Answer
-
- \(-10\)
- \(10\)
Відніміть:
- \(-7-4\)
- \(7 - (-4)\)
- Відповідь
-
- \(-11\)
- \(11\)
Ви помітили, що віднімання знакових чисел можна зробити шляхом додавання протилежного? У Вправи\(\PageIndex{33}\),\(−3−1\) це те ж саме,\(3−(−1)\) що\(−3+(−1)\) і таке ж, як\(3+1\). Ви часто побачите цю ідею, властивість віднімання, написане наступним чином:
\[a−b=a+(−b) \nonumber\]
Віднімання числа - це те саме, що і додавання його протилежності.
Подивіться на ці два приклади.
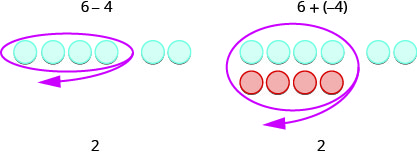
Звичайно, коли у вас є проблема віднімання, яка має лише позитивні числа, наприклад\(6−4\), ви просто робите віднімання. Ви вже\(6−4\) давно знали, як відняти. Але знання, що\(6−4\) дає таку ж відповідь, як\(6+(−4)\) допомагає, коли ви віднімаєте негативні числа. Переконайтеся, що ви розумієте, як\(6−4\) і\(6+(−4)\) даєте однакові результати!
Спростити:
- \(13 - 8 \space \text{and } 13 + (-8)\)
- \(-17 - 9 \space \text{and } -17 + (-9)\)
Рішення:
- \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
- \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)
Спростити:
- \(21 - 13 \space \text{and } 21 + (-13)\)
- \(-11 - 7 \space \text{and } -11 + (-7)\)
- Answer
-
- \(8\)
- \(-18\)
Спростити:
- \(15 - 7 \space \text{and } 15 + (-7)\)
- \(-14 - 8 \space \text{and } -14 + (-8)\)
- Відповідь
-
- \(8\)
- \(-22\)
Подивіться, що відбувається, коли ми віднімаємо негатив.

Віднімання від'ємного числа - це як додавання позитивного!
Ви часто побачите це написано як\(a−(−b)=a+b\).
Чи працює це і для інших номерів? Давайте зробимо наступний приклад і подивимося.
Спростити:
- \(9 - (-15) \space \text{and } 9 + 15\)
- \(-7 - (-4) \space \text{and } -7 + 4\)
Рішення:
- \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
- \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)
Спростити:
- \(6 - (-13) \space \text{and } 6 + 13\)
- \(-5 - (-1) \space \text{and } -5 + 1\)
- Answer
-
- \(19\)
- \(-4\)
Спростити:
- \(4 - (-19) \space \text{and } 4 + 19\)
- \(-4 - (-7) \space \text{and } -4 + 7\)
- Відповідь
-
- \(23\)
- \(3\)
Давайте ще раз подивимося на результати віднімання різних комбінацій\(5,−5\) і\(3,−3\).
\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]
Коли буде достатньо лічильників кольору відняти, віднімаємо.
\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]
Коли не вистачило б лічильників кольору забрати, додаємо.
Що відбувається, коли є більше трьох цілих чисел? Ми просто використовуємо порядок операцій як зазвичай.
Спростити:
\(7 - (-4 -3) - 9\)
Рішення:
\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]
Спростити:
\(8−(−3−1)−9\)
- Answer
-
\(3\)
Спростити:
\(12−(−9−6)−14\)
- Відповідь
-
\(12\)
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики зі складанням та відніманням цілих чисел. Вам потрібно буде включити Java у вашому веб-браузері, щоб використовувати програми.
Ключові концепції
- Додавання позитивних і від'ємних цілих чисел
\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]
- Властивість абсолютного значення:
\(|n| \geq 0\)для всіх чисел. Абсолютні значення завжди більше або рівні нулю!
- Віднімання цілих чисел
\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]
- Властивість віднімання: Віднімання числа є таким же, як додавання його протилежності.
Глосарій
- абсолютна величина
- Абсолютне значення числа - це його відстань від 0 на числовому рядку. Абсолютне значення числа nn записується як |n|.
- цілих чисел
- Цілі числа і їх протилежності називаються цілими числами:\(...−3, −2, −1, 0, 1, 2, 3...\)
- протилежний
- Протилежним числу є число, яке на тій же відстані від нуля на числовому рядку, але на протилежній стороні нуля: −\(a\) означає протилежність числу. Позначення −\(a\) читається «протилежне»\(a\).
