8.3: Завершення площі

Last updated
Save as PDF

Page ID: 58271

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У Вступі до радикальних позначень ми показали, як розв'язувати рівняння, такі$x^2 = 9$ як алгебраїчно, так і графічно.

\[\begin{aligned} x^{2} &=9 \\ x &=\pm 3 \end{aligned} \nonumber \]

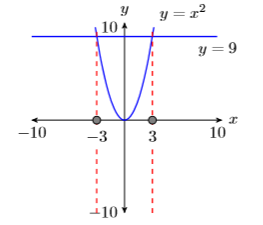
Зверніть увагу, що коли ми беремо квадратний корінь обох сторін цього рівняння, є дві відповіді, один негативний і один позитивний.

Ідеальний квадрат - це приємно, але не обов'язково. Дійсно, нам навіть доведеться врахувати ідеальний квадрат, щоб поставити нашу остаточну відповідь у простій формі.

\[\begin{aligned} x^{2} &=8 \\ x &=\pm \sqrt{8} \\ x &=\pm \sqrt{4} \sqrt{2} \\ x &=\pm 2 \sqrt{2} \end{aligned} \nonumber \]

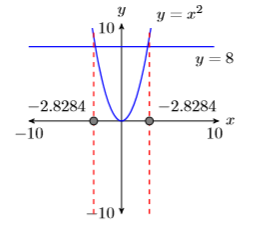
Читачі повинні використовувати свої калькулятори, щоб перевірити, що$-2 \sqrt{2} \approx -2.8284$ і$2 \sqrt{2} \approx 2.8284$.

Тепер давайте розширимо цю техніку рішення на більш широкий клас рівнянь.

Приклад$\PageIndex{1}$

Вирішити для$x : (x-4)^{2}=9$

Рішення

Подібно до рішень$x^2 = 9$ є$x = ±3$, ми використовуємо подібний підхід$(x−4)^2 = 9$ для отримання:

\[\begin{array}{rlrl}{(x-4)^{2}} & {=9} & {} & \color {Red} {\text { Original equation. }} \\ {x-4} & {=\pm 3} & {} & \color {Red} {\text { There are two square roots. }}\end{array} \nonumber \]

Щоб завершити рішення, додайте$4$ до обох сторін рівняння.

\[x=4 \pm 3 \quad \color {Red} \text { Add } 3 \text { to both sides. } \nonumber \]

Зверніть увагу, що це означає, що є дві відповіді, а саме:

\[\begin{array}{l}{x=4-3} \\ {x=1}\end{array} \nonumber \]

або

\[\begin{array}{l}{x=4+3} \\ {x=7}\end{array} \nonumber \]

Перевірка: Перевірте кожне рішення, підставивши його до вихідного рівняння.

Замінник$1$ для$x$:

\[\begin{aligned}(x-4)^{2} &=9 \\(1-4)^{2} &=9 \\(-3)^{2} &=9 \end{aligned} \nonumber \]

Замінник$7$ для$x$:

\[\begin{aligned}(x-4)^{2} &=9 \\(7-4)^{2} &=9 \\(3)^{2} &=9 \end{aligned} \nonumber \]

Оскільки останній оператор у кожній перевірці є істинним твердженням, обидва$x = 1$ і$x = 7$ є дійсними рішеннями$(x−4)^2 = 9$.

Вправа$\PageIndex{1}$

Вирішити для$x :(x+6)^{2}=10$

Відповідь: $-2$,$-10$

У$\PageIndex{1}$ прикладі права частина рівняння$(x−4)^2 = 9$ була ідеальним квадратом. Однак цього не потрібно, як покаже наступний приклад.

Приклад$\PageIndex{2}$

Вирішити для$x :(x+5)^{2}=7$

Рішення

Використовуючи ту ж методику, що і в$\PageIndex{1}$ прикладі, отримуємо:

\[\begin{array}{rlrl}{(x+5)^{2}} & {=7} & {} & \color {Red} {\text { Original equation. }} \\ {x+5} & {=\pm \sqrt{7}} & {} & \color {Red} {\text { There are two square roots. }}\end{array} \nonumber \]

Для завершення розв'язку відніміть 5 з обох сторін рівняння.

\[x=-5 \pm \sqrt{7} \quad \color {Red} \text { Subtract } 5 \text { from both sides.} \nonumber \]

Зверніть увагу, що це означає, що є дві відповіді, а саме:

\[x=-5-\sqrt{7} \quad \text { or } \quad x=-5+\sqrt{7} \nonumber \]

Перевірка: Перевірте кожне рішення, підставивши його до вихідного рівняння.

Замінник$-5-\sqrt{7}$ для$x$:

\[\begin{aligned}(x+5)^{2} &=7 \\((-5-\sqrt{7})+5)^{2} &=7 \\(-\sqrt{7})^{2} &=7 \end{aligned} \nonumber \]

Замінник$-5+\sqrt{7}$ для$x$:

\[\begin{aligned}(x+5)^{2} &=7 \\((-5+\sqrt{7})+5)^{2} &=7 \\(\sqrt{7})^{2} &=7 \end{aligned} \nonumber \]

Оскільки останній оператор у кожній перевірці є істинним твердженням, обидва$x=-5-\sqrt{7}$ і$x=-5+\sqrt{7}$ є дійсними рішеннями$(x+5)^{2}=7$.

Вправа$\PageIndex{2}$

Вирішити для$x :(x-4)^{2}=5$

Відповідь: $4+\sqrt{5}, 4-\sqrt{5}$

Іноді вам доведеться враховувати ідеальний квадрат, щоб поставити свою відповідь у простій формі.

Приклад$\PageIndex{3}$

Вирішити для$x :(x+4)^{2}=20$

Рішення

Використовуючи ту ж методику, що і в$\PageIndex{1}$ прикладі, отримуємо:

\[\begin{array}{rlrl}{(x+4)^{2}} & {=20} & {} & \color {Red} {\text { Original equation. }} \\ {x+4} & {=\pm \sqrt{20}} & {} & \color {Red} {\text { There are two square roots. }} \\ {x+4} & {=\pm \sqrt{4} \sqrt{5}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {x+4} & {=\pm 2 \sqrt{5}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2}\end{array} \nonumber \]

Для завершення розв'язку відніміть$4$ з обох сторін рівняння.

\[x=-4 \pm 2 \sqrt{5} \quad \color {Red} \text { Subtract } 4 \text { from both sides. } \nonumber \]

Зверніть увагу, що це означає, що є дві відповіді, а саме:

\[x=-4-2 \sqrt{5} \quad \text { or } \quad x=-4+2 \sqrt{5} \nonumber \]

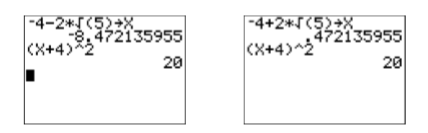
Перевірка: Хоча можна перевірити точні відповіді, давайте замість цього скористаємося нашим калькулятором. По-перше, зберігайте$-4-2 \sqrt{5}$ в$\mathbf{X}$. Далі введіть ліву частину рівняння$(x + 4)^2 = 20$ (див. Зображення зліва на малюнку$\PageIndex{3}$). Зверніть увагу, що (x+4) 2 спрощується до 20, показуючи, що$-4-2 \sqrt{5}$ це рішення$(x+4)^2 = 20$.

Подібним чином рішення$-4+2 \sqrt{5}$ також перевіряється$(x + 4)^2 = 20$ (див. Зображення праворуч на малюнку$\PageIndex{3}$).

рис. 8.3.3.png — Малюнок$\PageIndex{3}$: Перевірка$-4-2 \sqrt{5}$ і$-4+2 \sqrt{5}$ в рівнянні$(x+4)^2 = 20$.

Вправа$\PageIndex{3}$

Вирішити для$x :(x+7)^{2}=18$

Відповідь: $-7+3 \sqrt{2},-7-3 \sqrt{2}$

Ідеальні квадратні триноми переглянуті

Згадаймо квадрат біноміального ярлика.

Квадратування біноміального

Якщо$a$ і$b$ є будь-якими дійсними числами, то:\[(a±b)^2 = a^2 ±2ab + b^2 \nonumber \] Тобто ви квадратуєте перший член, берете добуток першого і другого членів і подвоюєте результат, а потім квадратично третій член.

Приклади нагадування:

\[\begin{aligned}(x+3)^{2} &=x^{2}+2(x)(3)+3^{2} \\ &=x^{2}+6 x+9 \end{aligned} \nonumber \]

\[\begin{aligned}(x-8)^{2} &=x^{2}-2(x)(8)+8^{2} \\ &=x^{2}-16 x+64 \end{aligned} \nonumber \]

Оскільки факторинг - це «немноження», це проста справа, щоб змінити процес множення та коефіцієнт цих ідеальних квадратних триноміалів.

\[x^{2}+6 x+9=(x+3)^{2} \nonumber \]

\[x^{2}-16 x+64=(x-8)^{2} \nonumber \]

Зверніть увагу, як у кожному випадку ми просто беремо квадратний корінь першого та останнього термінів.

Приклад$\PageIndex{4}$

Фактор кожного з наступних триноміалів:

$x^{2}-12 x+36$
$x^{2}+10 x+25$
$x^{2}-34 x+289$

Рішення

Всякий раз, коли перший і останній терміни триноміалу є ідеальними квадратами, ми повинні підозрювати, що у нас є ідеальний квадратний триноміал.

Перший і третій члени$x^{2}-12 x+36$ - ідеальні квадрати. Отже, ми беремо їх квадратні коріння і намагаємося:\[x^{2}-12 x+36=(x-6)^{2} \nonumber \] Зверніть увагу на те$2(x)(6)=12 x$, що є середнім терміном зліва. Рішення перевіряє.
Перший і третій члени$x^{2}+10 x+25$ - ідеальні квадрати. Отже, ми беремо їх квадратні коріння і намагаємося:\[x^{2}+10 x+25=(x+5)^{2} \nonumber \] Зверніть увагу на те$2(x)(5)=10 x$, що є середнім терміном зліва. Рішення перевіряє.
Перший і третій члени$x^{2}-34 x+289$ - ідеальні квадрати. Отже, ми беремо їх квадратні коріння і намагаємося:\[x^{2}-34 x+289=(x-17)^{2} \nonumber \] Зверніть увагу на те$2(x)(17)=34 x$, що є середнім терміном зліва. Рішення перевіряє.

Вправа$\PageIndex{4}$

Фактор:$x^2 + 30x + 225$

Відповідь: $(x+15)^{2}$

Завершення площі

У цьому розділі ми починаємо з біноміала$x^2 +bx$ і задаємо питання «До якої постійної величини ми повинні додати,$x^2 + bx$ щоб отриманий триноміал був досконалим квадратним триноміалом?» Відповідь криється в цій процедурі.

завершення квадрата

Для розрахунку константи потрібно зробити$x^2 +bx$ ідеальний квадратний триноміал:

Візьміть половину коефіцієнта$x : \dfrac{b}{2}$
Квадратний результат першого кроку:$\left(\dfrac{b}{2}\right)^{2}=\dfrac{b^{2}}{4}$
Додайте результат другого кроку до$x^{2}+b x : x^{2}+b x+\dfrac{b^{2}}{4}$

Якщо ви будете дотримуватися цього процесу, в результаті вийде ідеальний квадратний триноміал, який буде враховувати наступним чином:

\[x^{2}+b x+\dfrac{b^{2}}{4}=\left(x+\dfrac{b}{2}\right)^{2} \nonumber \]

Приклад$\PageIndex{5}$

З огляду на$x^2 + 12 x$, завершити квадрат, щоб створити ідеальний квадратний триноміал.

Рішення

Порівняйте$x^2 + 12x$ з$x^2 + bx$ і зауважте, що$b = 12$.

Візьміть половину$12: 6$
Квадратний результат першого кроку:$6^2 = 36$
Додайте результат другого кроку до$x^2 + 12x: x^2 + 12x + 36$

Перевірка: Зауважте, що перший і останній терміни$x^2 +12x+36$ є ідеальними квадратами. Візьміть квадратні корені першого та останнього термінів та фактора наступним чином:

\[x^{2}+12 x+36=(x+6)^{2} \nonumber \]

Зверніть увагу на те$2(x)(6) = 12x$, що, таким чином, середній термін перевіряє.

Вправа$\PageIndex{5}$

З огляду на$x^2 + 16x$, завершити квадрат, щоб створити ідеальний квадратний триноміал.

Відповідь: $x^{2}+16 x+64=(x+8)^{2}$

Приклад$\PageIndex{6}$

З огляду на$x^2−3x$, завершити квадрат, щоб створити ідеальний квадратний триноміал.

Рішення

Порівняйте$x^2 −3x$ з$x^2 + bx$ і зауважте, що$b =−3$.

Візьміть половину$-3 : -\dfrac{3}{2}$
Квадратний результат першого кроку:$\left(-\dfrac{3}{2}\right)^{2}=\dfrac{9}{4}$
Додайте результат другого кроку до$x^{2}-3 x : x^{2}-3 x+\dfrac{9}{4}$

Перевірка: Зауважте, що перший і останній терміни$x^{2}-3 x+\dfrac {9}{4}$ є ідеальними квадратами. Візьміть квадратні корені першого та останнього термінів та фактора наступним чином:

\[x^{2}-3 x+\dfrac{9}{4}=\left(x-\dfrac{3}{2}\right)^{2} \nonumber \]

Зверніть увагу на те$2(x)\left (\dfrac {3}{2} \right)=3 x$, що, таким чином, середній термін перевіряє.

Вправа$\PageIndex{6}$

З огляду на$x^2 −5x$, завершити квадрат, щоб створити ідеальний квадратний триноміал.

Відповідь: $x^{2}-5 x+\dfrac {10}{4}=\left(x-\dfrac {5}{2} \right)^{2}$

Розв'язування рівнянь шляхом завершення квадрата

Розглянемо наступне нелінійне рівняння.

\[x^2 =2x +2 \nonumber \]

Стандартний підхід полягає в тому, щоб зробити одну сторону нуль і коефіцієнт. \[x^2 −2x−2=0 \nonumber \]Однак швидко розуміє, що немає цілочисельної пари, добуток якої є$ac = −2$ і сума якої дорівнює$b = −2$. Отже, що ж робити в цій ситуації? Відповідь - «Завершити квадрат».

Приклад$\PageIndex{7}$

Використовуйте завершення квадрата, щоб допомогти вирішити$x^2 =2x + 2$.

Рішення

Спочатку перейдіть$2x$ до лівої частини рівняння, зберігаючи постійну$2$ в правій частині рівняння. \[x^2 −2x =2 \nonumber \]Зліва візьміть половину коефіцієнта$x: \left (\dfrac{1}{2} \right)(-2)=-1$. Квадратний результат:$(-1)^{2}=1$. Додайте цей результат до обох сторін рівняння.

\[\begin{array}{l}{x^{2}-2 x+1=2+1} \\ {x^{2}-2 x+1=3}\end{array} \nonumber \]

Тепер ми можемо врахувати ліву сторону як ідеальний квадратний триноміал.

\[(x-1)^{2}=3 \nonumber \]

Тепер, як і в прикладах$\PageIndex{1}$$\PageIndex{2}$, і$\PageIndex{3}$, ми можемо взяти квадратний корінь обох сторін рівняння. Пам'ятайте, є два квадратних кореня.

\[x-1=\pm \sqrt{3} \nonumber \]

Нарешті, додайте$1$ до обох сторін рівняння.

\[x=1 \pm \sqrt{3} \nonumber \]

Таким чином, рівняння$x^2 =2x+ 2$ має дві відповіді,$x=1-\sqrt{3}$ і$x=1+\sqrt{3}$.

Перевірка: Давайте скористаємося калькулятором для перевірки рішень. Спочатку зберігайте$1-\sqrt{3}$ в$\mathbf{X}$ (див. Зображення зліва на малюнку$\PageIndex{4}$). Потім введіть ліву і праву частини рівняння$x^2 =2 x + 2$ і порівняйте результати (див. Зображення зліва на малюнку$\PageIndex{4}$). Аналогічним чином перевірте другий відповідь$1+\sqrt{3}$ (див. Зображення праворуч на малюнку$\PageIndex{4}$).

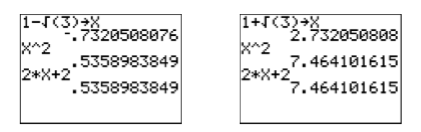
рис. 8.3.4.png — Малюнок$\PageIndex{4}$: Перевірка$1-\sqrt{3}$ і$1+\sqrt{3}$ в рівнянні$x^2 =2x + 2$.

В обох випадках зверніть увагу, що ліва і права сторони$x^2 =2x+2$ дають однаковий результат. Отже, обидва$1-\sqrt{3}$ і$1+\sqrt{3}$ є дійсними рішеннями$x^2 =2x+2$.

Вправа$\PageIndex{7}$

Використовуйте завершення квадрата, щоб допомогти вирішити$x^2 =3−6x$.

Відповідь: $-3+2 \sqrt{3},-3-2 \sqrt{3}$

Приклад$\PageIndex{8}$

Розв'яжіть рівняння$x^2 −8x−12 = 0$, як алгебраїчно, так і графічно. Порівняйте свою відповідь з кожного методу.

Рішення

Спочатку перемістіть$12$ константу в праву частину рівняння.

\[\begin{aligned} x^{2}-8 x-12=0 & \quad \color {Red} \text { Original equation. } \\ x^{2}-8 x=12 & \quad \color {Red} \text { Add } 12 \text { to both sides. } \end{aligned} \nonumber \]

Візьміть половину коефіцієнта$x :(1 / 2)(-8)=-4$. Квадрат:$(-4)^{2}=16$. Тепер додайте$16$ до обох сторін рівняння.

\[\begin{aligned} x^{2}-8 x+16 & =12+16 \quad \color {Red} \text { Add } 16 \text { to both sides. } \\ (x-4)^{2} & =28 \quad \color {Red} \text { Factor left-hand side. } \\ x-4 &=\pm \sqrt{28} \quad \color {Red} \text { There are two square roots. }\end{aligned} \nonumber \]
Відзначимо, що відповідь не в простій радикальній формі.

\[\begin{array}{rlrl}{x-4} & {=\pm \sqrt{4} \sqrt{7}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {x-4} & {=\pm 2 \sqrt{7}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2} \\ {x} & {=4 \pm 2 \sqrt{7}} & {} & \color {Red} {\text { Add } 4 \text { to both sides. }}\end{array} \nonumber \]

Графічне рішення: Введіть$\mathbf{Y1}$ рівняння$y = x^2 − 8x − 12$ в меню Y= (див. перше зображення на малюнку$\PageIndex{5}$). Після деяких експериментів ми зупинилися на параметрах WINDOW, показаних на середньому зображенні малюнка$\PageIndex{5}$. Після того, як ви ввели ці параметри ВІКНА, натисніть кнопку GRAPH, щоб створити крайнє праве зображення на малюнку$\PageIndex{5}$.

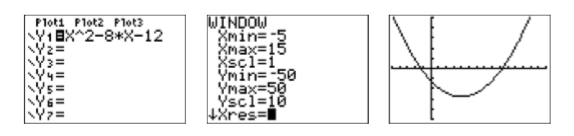
рис. 8.3.5.png — Малюнок$\PageIndex{5}$: Креслення графіка$y = x^2 −8x−12$.

Ми шукаємо рішення$x^2 −8x−12 = 0$, тому нам потрібно знайти, де графік$y = x^2 −8x−12$ перехоплює$x$ -вісь. Тобто нам потрібно знайти нулі$y = x^2 −8x−12$. Виберіть 2: нуль з меню CALC, перемістіть курсор трохи ліворуч від першого$x$ -перехоплення і натисніть ENTER у відповідь на «Ліва межа». Перемістіть курсор трохи праворуч від першого$x$ -перехоплення і натисніть ENTER у відповідь на «Right bound». Залиште курсор там, де він сидить, і натисніть ENTER у відповідь на «Вгадати». Калькулятор відповідає, знаходячи$x$ координату$x$ -перехоплення, як показано на першому зображенні на малюнку$\PageIndex{6}$.

Повторіть процес, щоб знайти другий$x$ -перехоплення$y = x^2−8x−12$ показаного на другому зображенні на малюнку$\PageIndex{6}$.

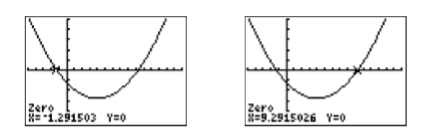
рис. 8.3.6.png — Малюнок$\PageIndex{6}$: Обчислення нулів$y = x^2 −8x−12$.

Повідомлення про рішення домашнього завдання: Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див.$\PageIndex{7}$ Рис.
Розмістіть параметри WINDOW в кінці кожної осі (див. Рис.$\PageIndex{7}$).
Позначте графік його рівнянням (див. Рис.$\PageIndex{7}$).
Пропустіть пунктирні вертикальні лінії через кожну$x$ -перехоплення. Затіньте та позначте$x$ -значення точок, де пунктирна вертикальна лінія перетинає$x$ вісь -. Це розв'язки рівняння$x^2−8x−12 = 0$ (див. Рис.$\PageIndex{7}$).

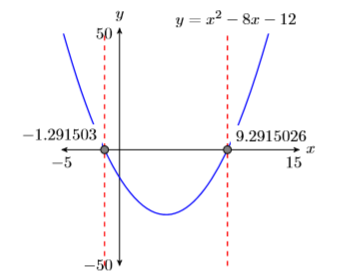
рис. 8.3.7.png — Малюнок$\PageIndex{7}$: Повідомлення про графічне рішення на домашнє завдання.

Таким чином, графічний калькулятор повідомляє, що рішення$x^2 −8x−12 = 0$ є$x \approx-1.291503$ і$x \approx 9.2915026$.

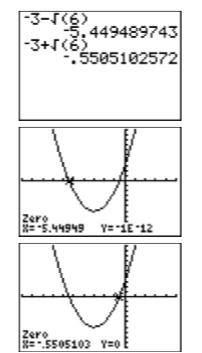
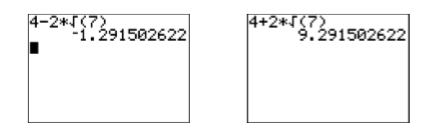
Порівняння точних та калькуляторних наближень: Наскільки добре порівнюють рішення графічного калькулятора з точними рішеннями,$x=4-2 \sqrt{7}$ і$x=4+2 \sqrt{7}$? Після введення кожного в калькулятор (див. Малюнок$\PageIndex{8}$) порівняння відмінне!

рис. 8.3.8.png — Малюнок$\PageIndex{8}$: Апроксимація точних$x=4-2 \sqrt{7}$ розв'язків і$x=4+2 \sqrt{7}$.

Вправа$\PageIndex{8}$

Вирішіть рівняння$x^2 +6x + 3 = 0$ як алгебраїчно, так і графічно, а потім порівняйте свої відповіді.

Відповідь

$-3-\sqrt{6},-3+\sqrt{6}$

$Вправа 8.3.8.png$