8.1: Вступ до радикальних позначень

Ми знаємо, як квадратувати число. Наприклад:

• $5^2 = 25$
• $(−5)^2 = 25$

Взяття квадратного кореня числа протилежно квадрату.

• Невід'ємний квадратний корінь від$25$ is$5$.
• Негативний квадратний корінь від$25$ is$−5$.

Таким чином, при пошуку квадратного кореня числа ми шукаємо число, квадрат якого дорівнює нашому числу.

Приклад$\PageIndex{1}$

Знайдіть квадратні коріння$81$.

Рішення

Шукаємо число, квадрат якого дорівнює$81$.

• Тому що$9^2 = 81$, невід'ємний квадратний корінь$81$ є$9$.
• Тому що$(−9)^2 = 81$, негативний квадратний корінь$81$ є$−9$.

Значить,$81$ має два квадратних кореня,$−9$ і$9$.

Вправа$\PageIndex{1}$

Знайдіть квадратні коріння$64$.

Відповідь

$8$і$−8$

Приклад$\PageIndex{2}$

Знайдіть квадратні коріння$0$.

Рішення

Шукаємо число, квадрат якого дорівнює$0$.

• Тому що$0^2 = 0$, невід'ємний квадратний корінь$0$ є$0$.

Жодне інше число в квадраті не буде рівним нулю. Отже, нуль має рівно один квадратний корінь, а саме нуль.

Вправа$\PageIndex{2}$

Знайдіть квадратні коріння$100$.

Відповідь

$10$і$−10$

Приклад$\PageIndex{3}$

Знайдіть квадратні коріння$−36$.

Рішення

Шукаємо число, квадрат якого дорівнює$−36$. Однак кожен раз, коли ви квадратуєте дійсне число, результат ніколи не буде негативним. Отже, не$−36$ має справжніх квадратних коренів. ¹

Вправа$\PageIndex{3}$

Знайдіть квадратні коріння$−25$.

Відповідь

немає справжніх квадратних коренів

Введення в Приклади$\PageIndex{1}$$\PageIndex{2}$, і$\PageIndex{3}$ призводять до наступного визначення.

Визначення квадратних коренів числа

Розчини$x^2 = a$ називаються квадратними коренями$a$.

Випадок:$a>0$. Рівняння$x^2 = a$ має два реальних рішення, а саме$x =\pm \sqrt{a}$.

• Позначення$\sqrt{a}$ вимагає ненегативного квадратного кореня.
• Позначення$−\sqrt{a}$ вимагає негативного квадратного кореня.

Випадок:$a = 0$. Рівняння$x^2 = 0$ має рівно одне рішення, а саме$x = 0$.

Випадок:$a<0$. Рівняння не$x^2 = a$ має реальних розв'язків.

Приклад$\PageIndex{4}$

Вирішіть$x^2 = 9$ для$x$, а потім спростіть свої відповіді.

Рішення

Оскільки права сторона позитивна$x^2 = 9$, рівняння має два рішення.

$$\begin{align*} x^2 &= 9 \quad \color {Red} \text {Original equation.}\\ x &= \pm \sqrt{9} \quad \color {Red} \text {Two answers: } -\sqrt{9} \text { and } \sqrt{9} \end{align*} \nonumber$$

Щоб спростити ці відповіді, нам потрібно розібратися в наступних фактах:

• $\sqrt{9}$викликає невід'ємний квадратний корінь$9$. Тому що$(3)^2 = 9$, невід'ємний квадратний корінь$9$ є$3$. Отже,$\sqrt{9} = 3$.
• $-\sqrt{9}$викликає негативний квадратний корінь$9$. Тому що$(−3)^2 = 9$, негативний квадратний корінь$9$ є$−3$. Отже,$-\sqrt{9}=−3$.

Таким чином, рішення$x^2 = 9$ є$x = \pm 3$, що еквівалентно вимові «$x =−3$або»$x = 3$.

Вправа$\PageIndex{4}$

Вирішіть$x^2 = 16$ для$x$, а потім спростіть свої відповіді.

Відповідь

$4$,$-4$

Приклад$\PageIndex{5}$

Вирішіть$x^2 = 0$ для$x$, а потім спростіть відповідь.

Рішення

Є тільки одне число, квадрат якого дорівнює$0$, а саме$0$.

$$\begin{align*} x^2 &= 0 \quad \color {Red} \text {Original equation.}\\ x &= 0 \quad \color {Red} \text {One answer: } (0)^2 = 0. \end{align*} \nonumber$$

Таким чином, єдиним рішенням$x^2 = 0$ є$x = 0$. Отже, невід'ємний квадратний корінь нуля дорівнює нулю. Отже,$\sqrt{0} = 0$.

Вправа$\PageIndex{5}$

Вирішіть$x^2 = 49$ для$x$, а потім спростіть відповіді.

Відповідь

$7$,$-7$

Приклад$\PageIndex{6}$

Вирішіть$x^2 =−4$ для$x$, а потім спростіть відповідь.

Рішення

Ви не можете квадратувати дійсне число і отримати негативний результат. Отже, не$x^2 = −4$ має реальних рішень. Тому не$\sqrt{-4}$ є дійсним числом.

Вправа$\PageIndex{6}$

Вирішіть$x^2 = −9$ для$x$, а потім спростіть відповіді.

Відповідь

немає реальних рішень

Приклад$\PageIndex{7}$

Спростіть кожне з наведених нижче дій:

1. $\sqrt{121}$
2. -$\sqrt{225}$
3. $\sqrt{-100}$
4. -$\sqrt{324}$

Рішення

Пам'ятайте, що позначення$\sqrt{a}$ вимагає невід'ємного квадратного кореня$a$, тоді як позначення -$\sqrt{a}$ вимагає негативного квадратного кореня$a$.

1. Тому що$11^2 = 121$, невід'ємний квадратний корінь з$225$ є$-15$. Таким чином: $$-\sqrt{225} = -15 \nonumber$$
2. Тому що$(-15)^2 = 225$, невід'ємний квадратний корінь з$121$ є$11$. Таким чином: $$\sqrt{121} = 11 \nonumber$$
3. Ви не можете квадратувати дійсне число і отримати$−100$. Тому не$\sqrt{-100}$ є дійсним числом.
4. Тому що$(-18)^2 = 324$, невід'ємний квадратний корінь з$324$ є$-18$. Таким чином: $$-\sqrt{324} = -18 \nonumber$$

Вправа$\PageIndex{7}$

Спростити:$−\sqrt{144}$

Відповідь

$-12$

Квадрат «скасовує» беручи квадратний корінь.

Квадратне квадратне коріння

Якщо$a>0$, то обидва$-\sqrt{a}$ і$\sqrt{a}$ є рішеннями$x^2 = a$. Отже, якщо підставити кожен з них в рівняння$x^2 = a$, то отримаємо:

$(-\sqrt{a})^2 = a$і$(\sqrt{a})^2 = a$

Приклад$\PageIndex{8}$

Спростіть кожне з наведених нижче виразів:

1. $(\sqrt{5})^2$
2. $(-\sqrt{7})^2$
3. $(\sqrt{-11})^2$

Рішення

Ми будемо ставитися до кожного випадку ретельно.

1. Тому що$\sqrt{5}$ це рішення$x^2 = 5$, якщо ми квадрат$\sqrt{5}$, ми повинні отримати$5$. $$(\sqrt{5})^2 =5 \nonumber$$
2. Тому що$-\sqrt{7}$ це рішення$x^2 = 7$, якщо ми квадрат$-\sqrt{7}$, ми повинні отримати$7$. $$(-\sqrt{7})^2 =7 \nonumber$$
3. Тому що не$x^2 = −11$ має реальних відповідей,$\sqrt{-11}$ це не реальне число. Поглиблені курси, такі як алгебра коледжу або тригонометрія, введуть складну систему числення та покажуть, як поводитися з цим виразом.

Вправа$\PageIndex{8}$

Спростити:$(−\sqrt{21})^2$

Відповідь

$21$

Використання графічного калькулятора

До цього моменту рівняння$x^2 = a$ задіяні ідеальні квадрати. Наприклад, якщо почати з$x^2 = 25$, то рішення є$x = \pm \sqrt {25}$. Оскільки$25$ це ідеальний квадрат, ми можемо спростити далі, приїхавши до$x =\pm 5$.

Однак права сторона$x^2 = a$ не обов'язково повинна бути ідеальним квадратом. Наприклад, рівняння$x^2 = 7$ має два реальних рішення,$x =\pm \sqrt {7}$. Оскільки$7$ це не ідеальний квадрат, ми не можемо спростити далі. У наступному прикладі ми будемо використовувати графічний калькулятор, щоб порівняти це алгебраїчне рішення з графічним рішенням і, сподіваюся, забезпечити певну впевненість, що$−\sqrt{7}$ і$\sqrt {7}$ є цілком дійсними рішеннями$x^2 = 7$.

Приклад$\PageIndex{9}$

Використовуйте графічний калькулятор для вирішення$x^2 = 7$. Потім вирішіть рівняння алгебраїчно і порівняйте відповіді.

Рішення

Введіть кожну сторону рівняння$x^2 = 7$ в меню Y= (див. Рис.$\PageIndex{1}$), а потім виберіть 6:ZStandard, щоб створити зображення на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$: Ескіз кожної сторони$x^2 = 7$.

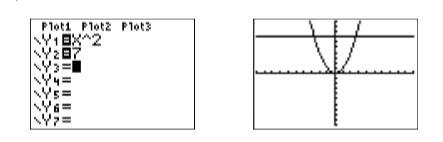
Використовуйте утиліту 5:intersect в меню CALC, щоб знайти точки перетину. Натисніть ENTER у відповідь на «Перша крива», натисніть ENTER у відповідь на «Друга крива», потім за допомогою клавіш зі стрілками перемістіть курсор ближче до точки перетину зліва, ніж той, що знаходиться праворуч. Натисніть ENTER у відповідь на «Вгадати». Це дасть точку перетину, показану на зображенні зліва на малюнку$\PageIndex{2}$. Повторіть процедуру, щоб знайти точку перетину на зображенні праворуч на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Пошук точок перетину.

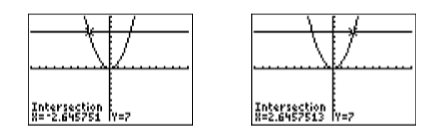
Орієнтовні рішення$x^2 = 7$ є$x≈− 2.645751$ і$x ≈2.6457513$.

Повідомлення про рішення домашнього завдання: Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

• Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див.$\PageIndex{3}$ Рис.
• Розмістіть параметри WINDOW в кінці кожної осі (див. Рисунок$\PageIndex{3}$).
• Позначте кожен граф своїм рівнянням (див. Рис.$\PageIndex{3}$).
• Пропустіть пунктирні вертикальні лінії через кожну точку перетину. Затіньте та позначте значення x точок, де пунктирна вертикальна лінія перетинає вісь x. Це розв'язки рівняння$x^2 = 7$ (див. Рис.$\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Повідомлення про графічне рішення на домашнє завдання.

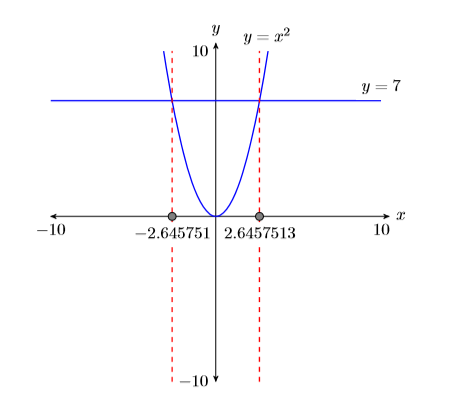
Тепер вирішуємо рівняння алгебраїчно.

$$\begin{align*} x^2 &= 7 \\ x &= \pm \sqrt{7} \end{align*} \nonumber$$

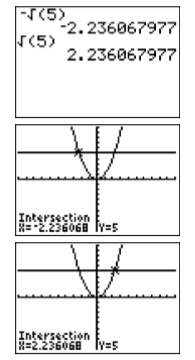
На даний момент виникає питання: «Чи відповідають ці алгебраїчні рішення графічним рішенням на малюнку$\PageIndex{3}$?» Давайте скористаємося нашим калькулятором для порівняння результатів. Знайдіть символ квадратного кореня$\sqrt{ }$ на корпусі калькулятора над$x^2$ клавішею в крайньому лівому стовпчику на клавіатурі калькулятора. Зверніть увагу, що нам доведеться використовувати$2^{nd}$ ключ для доступу до цього оператора. Введіть$-\sqrt{(7)}$ і натисніть ENTER. Потім введіть$\sqrt{(7)}$ і натисніть ENTER. Результати наведені на рис$\PageIndex{4}$.

Малюнок$\PageIndex{4}$: Обчислення$-\sqrt{7}$ і$\sqrt{7}$.

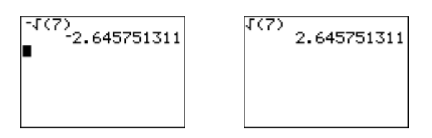
Таким чином,$-\sqrt{7} ≈− 2.645751311$ і$\sqrt{7} ≈ 2.645751311$. Зверніть увагу, як вони тісно відповідають графічним наближенням на малюнку$\PageIndex{3}$.

Вправа$\PageIndex{9}$

Вирішіть рівняння$x^2 =5$ як алгебраїчно, так і графічно, а потім порівняйте свої відповіді.

Відповідь

$-\sqrt{5}$,$\sqrt{5}$

Приклад$\PageIndex{10}$

Використовуйте графічний калькулятор для вирішення$x^2 = −5$. Потім вирішіть рівняння алгебраїчно і порівняйте відповіді.

Рішення

Введіть кожну сторону рівняння$x^2 = −5$ в меню Y= (див. Рис.$\PageIndex{5}$), а потім виберіть 6:ZStandard, щоб створити зображення на малюнку$\PageIndex{5}$.

Малюнок$\PageIndex{5}$: Ескіз кожної сторони$x^2 = −5$.

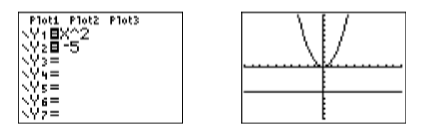
Повідомлення про рішення домашнього завдання: Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

• Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див.$\PageIndex{6}$ Рис.
• Розмістіть параметри WINDOW в кінці кожної осі (див. Рис.$\PageIndex{6}$).
• Позначте кожен граф своїм рівнянням (див. Рис.$\PageIndex{6}$).

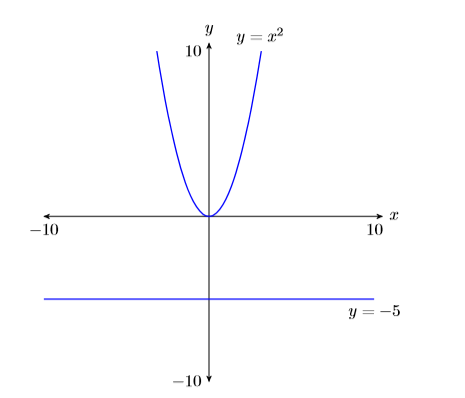
Оскільки точок перетину немає, графік на малюнку$\PageIndex{6}$ повідомляє нам, що рівняння не$x^2 = −5$ має реальних розв'язків. Тепер вирішуємо рівняння алгебраїчно. $x^2 = −5$Однак ви не можете квадратувати дійсне число і отримати негативну відповідь. Значить, рівняння не$x^2 = −5$ має реальних розв'язків. Це повністю узгоджується з графіком на малюнку$\PageIndex{6}$.

Малюнок$\PageIndex{6}$: Повідомлення про графічне рішення на домашнє завдання.

Наближення квадратних коренів

Таблиця$\PageIndex{1}$: Список квадратів

$n$	$n^2$
\ (n\) ">0	\ (n^2\) ">0
\ (n\) ">1	\ (n^2\) ">1
\ (n\) ">2	\ (n^2\) ">4
\ (n\) ">3	\ (n^2\) ">9
\ (n\) ">4	\ (n^2\) ">16
\ (n\) ">5	\ (n^2\) ">25
\ (n\) ">6	\ (n^2\) ">36
\ (n\) ">7	\ (n^2\) ">49
\ (n\) ">8	\ (n^2\) ">64
\ (n\) ">9	\ (n^2\) ">81
\ (n\) ">10	\ (n^2\) ">100
\ (n\) ">11	\ (n^2\) ">121
\ (n\) ">12	\ (n^2\) ">144
\ (n\) ">13	\ (n^2\) ">169
\ (n\) ">14	\ (n^2\) ">196
\ (n\) ">15	\ (n^2\) ">225
\ (n\) ">16	\ (n^2\) ">256
\ (n\) ">17	\ (n^2\) ">289
\ (n\) ">18	\ (n^2\) ">324
\ (n\) ">19	\ (n^2\) ">361
\ (n\) ">20	\ (n^2\) ">400
\ (n\) ">21	\ (n^2\) ">441
\ (n\) ">22	\ (n^2\) ">484
\ (n\) ">23	\ (n^2\) ">529
\ (n\) ">24	\ (n^2\) ">576
\ (n\) ">25	\ (n^2\) ">625

Квадрати в «Переліку квадратів», показані в таблиці$\PageIndex{1}$, називаються ідеальними квадратами. Кожен - квадрат цілого числа. Але не всі числа є ідеальними квадратами. Наприклад, у випадку з$\sqrt{24}$, не існує цілого числа, квадрат якого дорівнює$24$. Однак це не$\sqrt{24}$ заважає бути цілком хорошим числом.

Ми можемо використовувати «Список квадратів» для пошуку десяткових наближень, коли радиканд не є ідеальним квадратом.

Приклад$\PageIndex{11}$

Оцініть$\sqrt{24}$ за допомогою ворожіння. Використовуйте калькулятор, щоб знайти більш точний результат і порівняти цей результат зі своєю здогадкою.

Рішення

З «Переліку квадратів» зверніть увагу, що$24$ лежить між$16$ і$25$, так$\sqrt{24}$ буде лежати між$4$ і$5$, з$\sqrt{24}$ набагато ближче,$5$ ніж до$4$.

Давайте здогадаємося $$\sqrt{24}≈ 4.8\nonumber$$ . Як перевірку, давайте квадрат $$4.8. (4.8)^2 = (4 .8)(4.8) = 23.04 \nonumber$$ Не зовсім$24$! Зрозуміло, що$\sqrt{24}$ повинно бути трохи більше, ніж$4.8$.

Давайте скористаємося науковим калькулятором, щоб отримати краще наближення. З нашого калькулятора за допомогою кнопки квадратного кореня знаходимо $$\sqrt{24}≈ 4.89897948557 \nonumber$$ .

Незважаючи на те, що це краще, ніж наша оцінка$4.8$, це все одно лише наближення. Наш калькулятор був здатний надавати лише$11$ десяткові розряди. Однак точне десяткове подання$\sqrt{24}$ - це нескінченне десяткове число, яке ніколи не закінчується і ніколи не встановлює закономірність повторення.

Просто для задоволення, ось десяткове наближення,$\sqrt{24}$ що є точним до$1000$ місць, люб'язно надано www.wolframalpha.com

Якби ви помножили це число саме по собі (квадрат числа), ви б отримали число, яке є надзвичайно близьким до$24$, але це не було б точно$24$. Було б ще невелике розбіжність.

Вправа$\PageIndex{11}$

кошторис:$\sqrt{83}$

Відповідь

$9.1$

Довідка

1 Коли ми говоримо, що не$−36$ має реальних квадратних коренів, ми маємо на увазі, що немає дійсних чисел, які є квадратними коренями$−36$. Причина, по якій ми підкреслюємо слово$−36$ реальне в цій ситуації, полягає в тому, що має два квадратних кореня, які є елементами комплексних чисел, набір чисел, які зазвичай вводяться в просунутих курсах, таких як алгебра коледжу або тригонометрія.