3.6: Стандартна форма лінії

Last updated
Save as PDF

Page ID: 58129

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми розберемо стандартну форму лінії. Почнемо з простого прикладу.

Приклад$\PageIndex{1}$

Розв'яжіть рівняння$2x +3y = 6$ для$y$ і побудуйте результат.

Рішення

Спочатку вирішимо рівняння$2x +3y = 6$ для$y$. Почніть з виділення всіх членів, що містять y на одній стороні рівняння, переміщення або збереження всіх інших членів на іншій стороні рівняння.

\[\begin{aligned} 2x+3y &= 6 \quad \color{Red} \text { Original equation. } \\ 2x+3y-2x &= 6-2x \quad \color{Red} \text { Subtract } 2x \text { from both sides. } \\ 3y &= 6-2x \quad \color{Red} \text { Simplify. } \\ \dfrac{3y}{3} &= \dfrac{6-2x}{3} \quad \color{Red} \text { Divide both sides by } 3 \end{aligned} \nonumber \]

Примітка

Подібно до того, як множення є розподільним щодо додавання,\[a(b + c)=ab + ac \nonumber \] так і ділення розподільне щодо додавання. \[\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c} \nonumber \]

При діленні суми або різниці на число ми використовуємо розподільну властивість і ділимо обидва члени на це число.

\[\begin{aligned} y &= \dfrac{6}{3}-\dfrac{2x}{3} \quad \color{Red} \text { On the left, simplify. On the right, divide both terms by } 3 \\ y &= 2-\dfrac{2 x}{3} \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Нарешті, використовуйте комутативну властивість для перемикання порядку термінів праворуч від останнього результату.

\[\begin{aligned} y &= 2+\left(-\dfrac{2 x}{3}\right) \quad \color{Red} \text { Add the opposite. } \\ y &= -\dfrac{2}{3} x+2 \quad \color{Red} \text { Use the commutative property to switch the order. } \end{aligned} \nonumber \]

Оскільки рівняння$2x +3y = 6$ еквівалентно рівнянню$y=-\dfrac{2}{3} x+2$, графік$2x +3 y = 6$ є лінією, що має нахил$m = −2/3$ і$y$ -перехоплення$(0 ,2)$. Тому, щоб намалювати графік$2x+3y = 6$, графік їх перехоплюють$(0,2)$, рухаються вниз$2$ і$3$ вправо, потім малюють лінію (див. Малюнок$\PageIndex{1}$).

рис 3.6.1.png — Малюнок$\PageIndex{1}$: Графік$2x +3y = 6$, або еквівалентно,$y=-\dfrac{2}{3} x+2$

Вправа$\PageIndex{1}$

Додайте сюди текст вправ.

Відповідь: $Вправа 3.6.1.png$

Загалом, хіба що$B = 0$, ми завжди можемо вирішити рівняння$Ax + By = C$ для y:

\ [\ почати {вирівняний}
Ax+By &= C\ quad\ color {Червоний}\ текст {Оригінальне рівняння.}\\
Ax+By-Ax &= C-Ax\ quad\ color {Червоний}\ текст {Відняти} Ax\ текст {з обох сторін.}\\
За &= C-Ax\ quad\ колір {Червоний}\ текст {Спростити.}
\\ dfrac {By} {B} &= dfrac {C-Ax} {B}\ квадратний\ колір {червоний}\ текст {Розділити обидві сторони на} B\\
y &=\ dfrac {C} {B} -\ dfrac {Ax} {B}\ квадратний\ колір {червоний}\ текст {розподілити} B\
y &= -\ dfrac {A} {B} x+\ dfrac {C} {B}\ quad\ color {Red}\ text {Комутативна властивість}
\ end {вирівняний}\ nonumber\]

Зверніть увагу, що останній результат знаходиться у вигляді нахилу перехоплення$y = mx+b$, граф якого є лінією. Ми встановили наступний результат.

Факт

Графік рівняння$Ax + By = C$, являє собою лінію.

Важливі моменти: Пара важливих зауважень по порядку.

Форма$Ax + By = C$ вимагає, щоб коефіцієнти$A$$B$, і були$C$ цілими числами. Так, наприклад, ми б очистили дроби від форми,\[\dfrac{1}{2} x+\dfrac{2}{3} y=\dfrac{1}{4} \nonumber \] множивши обидві сторони на найменш спільний знаменник. \[\begin{aligned} 12\left(\dfrac{1}{2} x+\dfrac{2}{3} y\right) &=\left(\dfrac{1}{4}\right) 12 \\ 6 x+8 y &=3 \end{aligned}\nonumber \]Зверніть увагу, що коефіцієнти тепер цілі числа.
Форма$Ax + By = C$ також вимагає, щоб перший коефіцієнт був$A$ ненегативним; тобто$A ≥0$. Таким чином, якщо ми маємо,\[-5 x+2 y=6 \nonumber \] то ми б помножити обидві сторони на$−1$, приходячи до:\[\begin{aligned}-1(-5 x+2 y) &=(6)(-1) \\ 5 x-2 y &=-6 \end{aligned} \nonumber \] Зверніть увагу, що$A = 5$ тепер більше або дорівнює нулю.
Якщо$A$$B$, і$C$ мають загальний дільник більше$1$, рекомендується розділити обидві сторони на загальний дільник, таким чином «зменшуючи» коефіцієнти. Наприклад, якщо ми\[3x + 12y =−24 \nonumber \] ділимо обидві сторони на$3$ «зменшує» розмір коефіцієнтів. \[\begin{aligned} \dfrac{3 x+12 y}{3} &=\dfrac{-24}{3} \\ x+4 y &=-8 \end{aligned} \nonumber \]

Стандартна форма

Форма$Ax + By = C$, де$A$$B$, і$C$ є цілими числами$A ≥ 0$, а, називається стандартною формою рядка.

Перехоплення нахилу до стандартної форми

Ми вже перетворили пару рівнянь у стандартній формі у форму slopeintercept. Давайте повернемо процес і помістимо рівняння у формі перехоплення нахилу в стандартну форму.

Приклад$\PageIndex{2}$

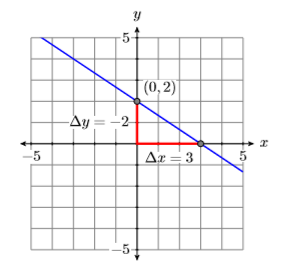
Враховуючи графік прямої на малюнку$\PageIndex{2}$, знайдіть рівняння За допомогою графіка прямої нижче, знайдіть рівняння прямої у стандартному вигляді.

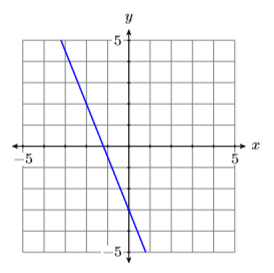
рис. 3.6.2.png — Малюнок$\PageIndex{2}$: Визначте рівняння прямої.

Рішення

Лінія перехоплює$y$ -вісь в$(0,−3)$. Від$(0,−3)$, рухайтеся вгору$5$ юнітами, потім лівими$2$ юнітами. Таким чином, лінія має нахил$\Delta y / \Delta x=-5 / 2$ (див. Малюнок$\PageIndex{3}$). Підставляємо$−5/2$ форму і$−3$ для$b$ в ухилі-перехоплення формі лінії.

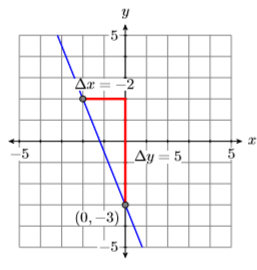
рис. 3.6.3.png — Малюнок$\PageIndex{3}$: Лінія має$y$ -перехоплення$(0,−3)$ і нахил$−5/2$.

\[\begin{aligned} y &= mx+b \quad \color{Red} \text { Slope-intercept form. } \\ y &= -\dfrac{5}{2} x-3 \quad \color{Red} \text { Substitute: }-5 / 2 \text { for } m,-3 \text { for } b \end{aligned} \nonumber \]

Щоб поставити цей результат у стандартному вигляді$Ax + By = C$, спочатку очистіть дроби, помноживши обидві сторони на спільний знаменник.

\[\begin{aligned} 2y &= 2\left[-\dfrac{5}{2} x-3\right] \quad \color{Red} \text { Multiply both sides by } 2 \\ 2y &= 2\left[-\dfrac{5}{2} x\right]-2[3] \quad \color{Red} \text { Distribute the } 2 \\ 2y &= -5x-6 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Це очищає фракції. Щоб поставити цей останній результат у вигляді$Ax+By = C$, нам потрібно$−5x$ перенести термін на іншу сторону рівняння.

\[\begin{aligned} 5x+2y &= -5x-6+5x \quad \color{Red} \text { Add } 5x \text { to both sides. } \\ 5x+2y &= -6 \quad \color{Red}\text { Simplify. } \end{aligned} \nonumber \]

Таким чином, стандартна форма лінії є$5x +2y = −6$. Зверніть увагу, що всі коефіцієнти є цілими числами, а члени розташовані в порядку$Ax+By = C$, з$A ≥0$.

Вправа$\PageIndex{2}$

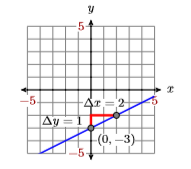
З огляду на графік лінії нижче, знайдіть рівняння прямої в стандартному вигляді.

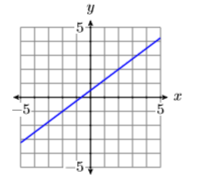
$Вправа 3.6.2.png$

Відповідь: $3 x−4y = −2$

Точка-нахил до стандартної форми

Давайте зробимо приклад, де ми повинні поставити точку-нахил форми лінії в стандартній формі.

Приклад$\PageIndex{3}$

Намалюйте лінію, що проходить через точки$(1,2)$,$(−3,−4)$ а потім знайдіть рівняння прямої в стандартному вигляді.

Рішення

Покладіть точки (−3, −4) і (1,2), потім проведіть через них лінію (див. Рис.$\PageIndex{4}$).

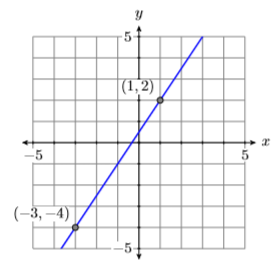
рис 3.6.4.png — Малюнок$\PageIndex{4}$: Лінія через$(−3,−4)$ і$(1,2)$.

Використовуйте точки$(−3,−4)$ і$(1,2)$ для розрахунку ухилу.

\[\begin{aligned} \text { Slope } &= \dfrac{\Delta y}{\Delta x} \quad \color{Red} \text { Slope formula. } \\ &= \dfrac{2-(-4)}{1-(-3)} \quad \color{Red} \text { Subtract coordinates of }(-3,-4) \\ &= \dfrac{6}{4} \quad \text { Simplify. } \\ &= \dfrac{3}{2} \quad \text { Reduce. } \end{aligned} \nonumber \]

Давайте підставимо$\left(x_{0}, y_{0}\right)=(1,2)$ і$m =3 /2$ в точку-нахил формі лінії. (Примітка:$\left(x_{0}, y_{0}\right)=(-3,-4)$ Заміна і$m =3 /2$ дасть ту саму відповідь. )

\[\begin{aligned} y-y_{0} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-2 &= \dfrac{3}{2}(x-1) \quad \color{Red} \text { Substitute: } 3 / 2 \text { for } m, 1 \text { for } x_{0} \end{aligned} \nonumber \]

Питання вимагає, щоб наша остаточна відповідь була представлена в стандартній формі. Спочатку очищаємо від дробів.

\[\begin{aligned} y-2 &= \dfrac{3}{2} x-\dfrac{3}{2} \quad \color{Red} \text { Distribute the } 3 / 2 \\ 2[y-2] &= 2\left[\dfrac{3}{2} x-\dfrac{3}{2}\right] \quad \color{Red} \text { Multiply both sides by } 2 \\ 2y-2[2] &= 2\left[\dfrac{3}{2} x\right]-2\left[\dfrac{3}{2}\right] \quad \color{Red} \text { Distribute the } 2 \\ 2y-4 &= 3 x-3 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Тепер, коли ми очистили дроби, ми повинні впорядкувати терміни у формі$Ax+By = C$. Нам потрібно перенести термін$3x$ на іншу сторону рівняння.

\[\begin{aligned} 2y-4-3x &= 3x-3-3x \quad \color{Red} \text { Subtract } 3 x \text { from both sides. } \\ -3x+2y-4 &= -3 \quad \color{Red} \text { Simplify, changing the order on the left-hand side. } \end{aligned} \nonumber \]

Щоб поставити це в форму$Ax + By = C$, нам потрібно$−4$ перенести термін на іншу сторону рівняння.

\[\begin{aligned} -3x+2y-4+4 &= -3+4 \quad \color{Red} \text { Add } 4 \text { to both sides. } \\ -3x+2y &= 1 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Виявляється, що$−3x+2y = 1$ знаходиться в формі$Ax +By = C$. Однак стандартна форма цього вимагає$A ≥ 0$. У нас є$A = −3$. Щоб виправити це, множимо обидві сторони на$−1$.

\[\begin{aligned} -1[-3x+2y] &= -1[1] \quad \color{Red} \text { Multiply both sides by }-1 \\ 3x-2y &= -1 \quad \color{Red} \text { Distribute the }-1 \end{aligned} \nonumber \]

Таким чином, рівняння прямої в стандартному вигляді є$3x−2y =−1$.

Примітка

Якщо ми не зможемо зменшити нахил до найнижчих членів, то рівняння прямої буде таким:\[y-2=\dfrac{6}{4}(x-1) \nonumber \]

Множення обох сторін на$4$ дасть нам результат\[4y−8=6x−6 \nonumber \] або еквівалентно:\[−6x +4y =2 \nonumber \]

Це не схоже на ту ж відповідь, але якщо ми розділимо обидві сторони на$−2$, ми отримаємо той самий результат. \[3x−2y = −1 \nonumber \]

Це показує важливість вимагати$A ≥ 0$ і «зменшення» коефіцієнтів$A$$B$, і$C$. Це дозволяє нам порівняти нашу відповідь з колегами або відповіді, представлені в цьому підручнику.

Вправа$\PageIndex{3}$

Знайти стандартну форму рівняння прямої, яка проходить через точки$(−2,4)$ and $(3,−3)$.

Відповідь: $7x +5y =6$

Перехоплює

Ми вивчили$y$ -intercept, точку, де графік перетинає$y$ -вісь, але не менш важливими є$x$ -перехоплення, точки, де графік перетинає$x$ -вісь.

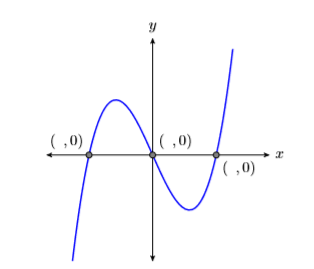
рис 3.6.5.png — Малюнок$\PageIndex{5}$: Кожен$x$ -перехоплення має$y$ -координату рівну нулю.

На$\PageIndex{5}$ малюнку графік тричі перетинає$x$ -вісь. Кожен з цих пунктів перетину називається$x$ -перехопленням. Зверніть увагу, що кожен з цих$x$ -перехоплень має$y$ -координату рівну нулю. Це призводить до наступного правила.

$x$Перехоплює: Щоб знайти$x$ -перехоплення графа рівняння,$y = 0$ підставити в рівняння і вирішити для$x$.

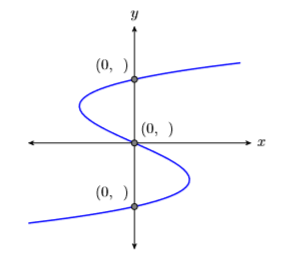
рис 3.6.6.png — Малюнок$\PageIndex{6}$: Кожен$y$ -перехоплення має$x$ -координату рівну нулю.

Аналогічно графік на малюнку тричі$\PageIndex{6}$ перетинає$y$ -вісь. Кожен з цих пунктів перетину називається a$y$ -перехоплення. Зверніть увагу, що кожен з цих$y$ -перехоплень має$x$ -координату рівну нулю. Це призводить до наступного правила.

$y$Перехоплює: Щоб знайти$y$ -перехоплення графа рівняння,$x = 0$ підставити в рівняння і вирішити для$y$.

Давайте поставимо ці правила для пошуку перехоплень для роботи.

Приклад$\PageIndex{4}$

Знайти$x$ - і$y$ -перехоплення лінії, що має рівняння$2x−3y = 6$. Побудуйте перехоплення і проведіть лінію.

Рішення

Ми знаємо, що графік$2x−3y = 6$ є лінією. Крім того, дві точки повністю визначають лінію. Це означає, що нам потрібно тільки побудувати сюжет$x$ - і$y$ -перехоплення, а потім провести лінію через них.

Знайти$x$ -перехоплення$2x−3y = 6$, замінити$0$$y$ і вирішити для$x$.

\[\begin{aligned} 2 x-3 y &=6 \\ 2 x-3(0) &=6 \\ 2 x &=6 \\ \dfrac{2 x}{2} &=\dfrac{6}{2} \\ x &=3 \end{aligned} \nonumber \]

Таким чином,$x$ -перехоплення лінії є$(3,0)$.

Знайти$y$ -перехоплення$2x−3y = 6$, замінити$0$$x$ і вирішити для$y$.

\[\begin{aligned} 2 x-3 y &=6 \\ 2(0)-3 y &=6 \\-3 y &=6 \\ \frac{-3 y}{-3} &=\frac{6}{-3} \\ y &=-2 \end{aligned} \nonumber \]

Таким чином,$y$ -перехоплення лінії є$(0,−2)$.

Побудуйте$x$ -перехоплення$(3,0)$ і$y$ -перехоплення$(0,−2)$ і проведіть через них лінію (див. Малюнок$\PageIndex{7}$).

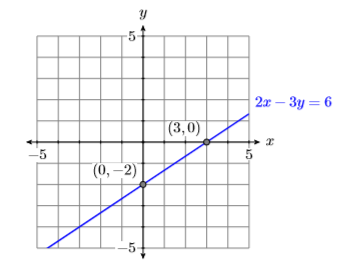
рис 3.6.7.png — Малюнок$\PageIndex{7}$: Графік$2x−3y = 6$ має перехоплює$(3,0)$ і$(0,−2)$.

Вправа$\PageIndex{4}$

Знайти$x$- і$y$ -перехоплення лінії, що має рівняння$3x +4y = −12$. Plot the intercepts and draw the line.

Відповідь

$x$-перехоплення:$(−4,0)$

$y$-перехоплення:$(0,−3)$

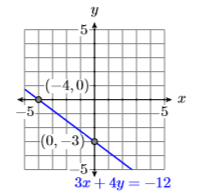
$Вправа 3.6.4.png$

Приклад$\PageIndex{5}$

Намалюйте лінію$4x +3 y = 12$, потім проведіть лінію через точку$(−2,−2)$, яка перпендикулярна лінії$4x +3 y = 12$. Знайдіть рівняння цієї перпендикулярної прямої.

Рішення

Давайте спочатку знайдемо$x$ - і$y$ -перехоплення лінії$4x +3y = 12$.

Щоб знайти$x$ -перехоплення лінії$4x+3y = 12$, замінити$0$$y$ і вирішити для$x$.

\[\begin{aligned} 4 x+3 y &=12 \\ 4 x+3(0) &=12 \\ 4 x &=12 \\ \dfrac{4 x}{4} &=\dfrac{12}{4} \\ x &=3 \end{aligned} \nonumber \]

Таким чином,$x$ -перехоплення лінії є$(3,0)$.

Щоб знайти$y$ -перехоплення лінії$4x+3y = 12$, замінити$0$$x$ і вирішити для$y$.

\[\begin{aligned} 4 x+3 y &=12 \\ 4(0)+3 y &=12 \\ 3 y &=12 \\ \dfrac{3 y}{3} &=\dfrac{12}{3} \\ y &=4 \end{aligned} \nonumber \]

Таким чином,$y$ -перехоплення лінії є$(0,4)$.

Побудуйте перехоплення і проведіть через них лінію. Зверніть увагу, що з графіка зрозуміло, що нахил прямої$3x +4y = 12$ дорівнює$−4/3$ (див. Рис.$\PageIndex{8}$).

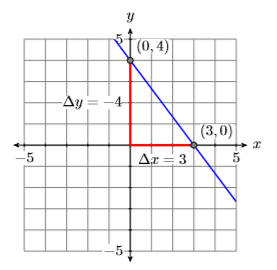
рис 3.6.8.png — Малюнок$\PageIndex{8}$: Графік$4x+3y = 12$ має перехоплення$(3,0)$$(0,4)$ та нахил$−4/3$.

Ви також можете вирішити для$y$ to put $3x +4 y = 12$ in схилу перехоплення форми для того, щоб визначити схил.

Оскільки нахил$3x+4y = 12$ є$−4/3$, нахил лінії перпендикулярно$3x +4y = 12$ буде негативним зворотним$−4/3$, а саме$3/4$. Наша перпендикулярна лінія повинна пройти через точку$(−2,−2)$. Почніть з$(−2,−2)$, перемістіть$3$ одиниці вгору, потім$4$ одиниці вправо, потім проведіть лінію. Вона повинна здаватися перпендикулярною лінії$3x +4y = 12$ (див. Малюнок$\PageIndex{9}$).

рис 3.6.9.png — Малюнок$\PageIndex{9}$: Нахил перпендикулярної лінії є негативним зворотним$−4/3$, а саме$3/4$.

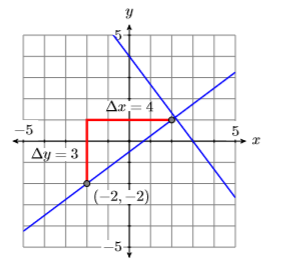
Нарешті, використовуйте точку-нахил форми$m =3 /4$, і$\left(x_{0}, y_{0}\right)=(-2,-2)$ для визначення рівняння перпендикулярної лінії.

\[\begin{aligned} y-y_{0} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-(-2) &= \dfrac{3}{4}(x-(-2)) \quad \color{Red} \text { Substitute: } 3 / 4 \text { for } m,-2 \text { for } x_{0} \text { and }-2 \text { for } y_{0} \\ y+2 &= \dfrac{3}{4}(x+2) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Розмістимо нашу відповідь в стандартній формі. Очистіть дроби.

\[\begin{aligned} y+2 &= \dfrac{3}{4} x+\dfrac{6}{4} \quad \color{Red} \text { Distribute } 3 / 4 \\ 4[y+2] &= 4\left[\dfrac{3}{4} x+\dfrac{6}{4}\right] \quad \color{Red} \text { Multiply both sides by } 4 \\ 4y+4[2] &= 4\left[\dfrac{3}{4} x\right]+4\left[\dfrac{6}{4}\right] \quad \color{Red} \text { Distribute the } 4 \\ 4y+8 &= 3x+6 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber \]

Переставляйте терміни, щоб привести їх в порядок$Ax + By = C$.

\[\begin{aligned} 4y+8-3x &= 3x+6-3x \quad \color{Red} \text { Subtract } 3x \text { from both sides. } \\ -3x+4y+8 &= 6 \quad \color{Red} \text { Simplify. Rearrange on the left. } \\ -3x+4y+8-8 &= 6-8 \quad \color{Red} \text { Subtract } 8 \text { from both sides. } \\ -3x+4y &= -2 \quad \color{Red} \text { Simplify. } \\ -1(-3x+4y) &= -1(-2) \quad \color{Red} \text { Multiply both sides by }-1 \\ 3x-4y &= 2 \quad \color{Red} \text { Distribute the }-1 \end{aligned} \nonumber \]

Значить, рівняння перпендикулярної лінії є$3x−4y = 2$.

Вправа$\PageIndex{5}$

Знайти рівняння прямої, яка проходить через точку$(3,2)$ and is perpendicular to the line $6x−5y = 15$.

Відповідь: $5x +6y = 27$

Горизонтальні та вертикальні лінії

Тут ми зберігаємо попередню обіцянку звернутися до того, що відбувається зі стандартною формою,$Ax + By = C$ коли$A = 0$ або$B = 0$. Наприклад, форма$3x = 6$, якщо порівнювати зі стандартною формою$Ax + By = C$, має$B = 0$. Аналогічно форма$2y = −12$, якщо порівнювати зі стандартною формою$Ax + By = C$, має$A = 0$. Звичайно,$3 x = 6$ може бути спрощений$x = 2$ і$2 y = −12$ може бути спрощений$y = −6$. Таким чином, якщо або$A = 0$ або$B = 0$, то стандартна форма Ax + By = C приймає форму$x = a$ і$y = b$, відповідно.

Як ми побачимо в наступному прикладі, форма$x = a$ створює вертикальну лінію, тоді як форма$y = b$ виробляє горизонтальну лінію.

Приклад$\PageIndex{6}$

Намалюйте графіки$x = 3$ і$y = −3$.

Рішення

Щоб намалювати графік$x = 3$, нагадаємо, що граф рівняння - це сукупність всіх точок, які задовольняють рівнянню. Отже, щоб намалювати графік$x = 3$, ми повинні побудувати всі точки, які задовольняють рівнянню$x = 3$; тобто ми повинні побудувати всі точки, які мають$x$ координату рівну$3$. Результат показаний на малюнку$\PageIndex{10}$.

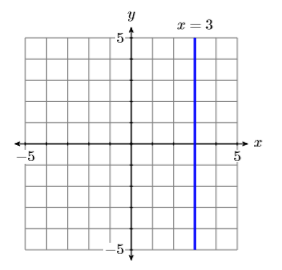
рис 3.6.10.png — Малюнок$\PageIndex{10}$: Графік$x = 3$ являє собою вертикальну лінію.

По-друге, щоб накидати графік$y = −3$, ми будуємо всі точки, що мають$y$ -координату рівну$−3$. Результат показаний на малюнку$\PageIndex{11}$.

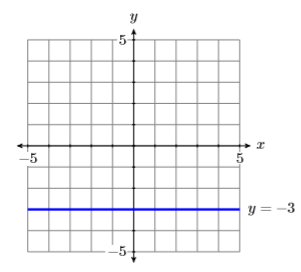
рис 3.6.11.png — Малюнок$\PageIndex{11}$: Графік$y =−3$ являє собою горизонтальну лінію.

Речі, на які слід звернути увагу:

Пара коментарів по порядку щодо рядків в рисунках$\PageIndex{10}$ і$\PageIndex{11}$.

Графік на$x = 3$ малюнку$\PageIndex{10}$, будучи вертикальною лінією, має недозначений нахил. Тому ми не можемо використовувати жодну з формул$y = mx + b$ або$y−y_0 = m(x−x_0)$ отримати рівняння прямої. Єдиний спосіб, яким ми можемо отримати рівняння, - це відзначити, що лінія - це множина всіх точок$(x,y)$,$x$ координата яких дорівнює$3$.
Однак графік, будучи горизонтальною лінією, має нульовий нахил, тому ми можемо використовувати форму перехоплення нахилу, щоб знайти рівняння прямої.$y = −3$ Зверніть увагу, що$y$ -перехоплення цього графіка є$(0,−3)$. Якщо підставити ці числа в$y = mx + b$, то отримаємо:\[\begin{aligned} y &= mx+b \quad \color{Red} \text { Slope-intercept form. } \\ y &= 0x+(-3) \quad \color{Red} \text { Substitute: } 0 \text { for } m,-3 \text { for } b \\ y &= -3 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Однак набагато простіше просто подивитися на лінію в малюнках$\PageIndex{11}$ і відзначити, що це збір всіх точок$(x,y)$ с$y = 3$.

Вправа$\PageIndex{6}$

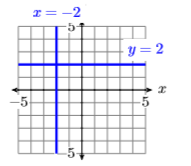
Намалюйте графіки$x = −2$ і$y = 2$.

Відповідь: $Вправа 3.6.6.png$