3.5: Точка-нахил форми лінії

У попередньому розділі ми дізналися, що якщо нам забезпечений нахил лінії та її$y$ -перехоплення, то рівняння прямої$m$ є$y = mx + b$, де нахил прямої і$b$$y$ -координата$y$ -перехоплення лінії.

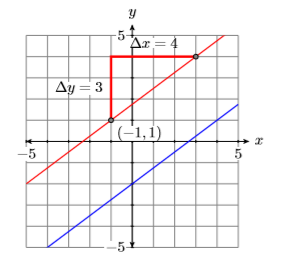
Однак припустимо, що$y$ -перехоплення невідомо? Замість цього, припустимо, що нам дано точку$(x_0,y_0)$ на лінії, і нам також кажуть, що нахил лінії дорівнює m (див. Рис.$\PageIndex{1}$).

Малюнок$\PageIndex{1}$: Лінія через точку$(x_0,y_0)$ з нахилом$m$.

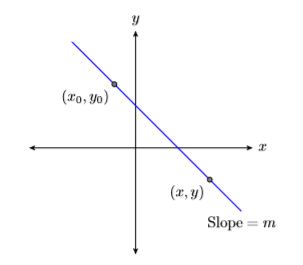
$(x,y)$Дозволяти довільна точка на прямій, потім використовувати точки$(x_0,y_0)$ і$(x,y)$ обчислити нахил лінії.

$$\begin{aligned} \text { Slope }&= \dfrac{\Delta y}{\Delta x} \quad \color{Red} \text { The slope formula. } \\ m&= \dfrac{y-y_{0}}{x-x_{0}} \quad \color{Red} \text { Substitute } m \text { for the slope. Use }(x, y) \text { and }\left(x_{0}, y_{0}\right) \text { to calculate the difference in } y \text { and the difference in } x \end{aligned} \nonumber$$

Очистити дроби з рівняння, помноживши обидві сторони на загальний знаменник.

$$\begin{aligned} m\left(x-x_{0}\right)&= \left[\dfrac{y-y_{0}}{x-x_{0}}\right]x-x_{0} \quad \color{Red} \text { Multiply both sides by } x-x_{0} \\ m\left(x-x_{0}\right)&= y-y_{0} \qquad \qquad \color{Red} \text { Cancel. } \end{aligned} \nonumber$$

Таким чином, рівняння прямої є$y−y_0 = m(x−x-0)$.

Точка-нахил форми прямої

Рівняння лінії з ухилом m, що проходить через точку,$\left(x_{0}, y_{0}\right)$ дорівнює:

$$y-y_{0}=m\left(x-x_{0}\right) \nonumber$$

Приклад$\PageIndex{1}$

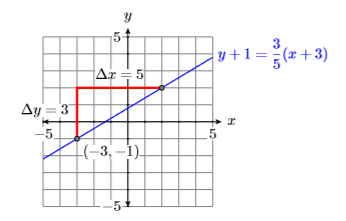
Намалюйте лінію, що проходить через точку,$(−3,−1)$ яка має нахил$3/5$, потім позначте її рівнянням.

Рішення

Покладіть точку$(−3,−1)$, потім перемістіть$3$ одиниці вгору і$5$ одиниці вправо (див. Рис.$\PageIndex{2}$). Щоб знайти рівняння, замініть$(x_0,y_0)$ і$(−3,−1)$$3/5$ для m у точково-нахиленій формі прямої.

$$\begin{aligned} {y-y_{0}} &= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-(-1) &= \dfrac{3}{5}(x-(-3)) \quad \color{Red} \text { Substitute: } 3 / 5 \text { for } m,-3 \text { for } x_{0}, \text { and }-1 \text { for } y_{0} \end{aligned} \nonumber$$

Спрощуючи, рівняння прямої є$y+1=\dfrac{3}{5}(x+3)$.

Малюнок$\PageIndex{2}$: Лінія, що проходить$(−3,−1)$ з нахилом$3/5$.

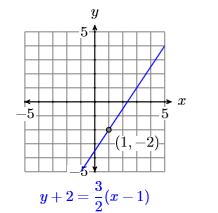
Вправа$\PageIndex{1}$

Намалюйте лінію, що проходить через точку$(1,−2)$ that has slope $3/2$, then label it with its equation.

Відповідь

У цей момент ви можете запитати: «Коли слід використовувати форму перехоплення нахилу і коли слід використовувати форму точки-нахилу?» Ось хороша порада.

Порада: Яку форму слід використовувати

Форма, яку ви повинні вибрати, залежить від наданої інформації.

1. Якщо вам дано$y$ -перехоплення і нахил, використовуйте$y = mx + b$.
2. Якщо вам дана точка і ухил, використовуйте$y−y_0 = m(x−x_0)$.

Приклад$\PageIndex{2}$

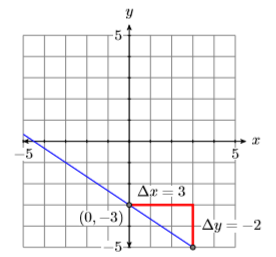
Знайдіть рівняння прямої, що проходить через точки$P(−1,2)$ і$Q(3,−4)$.

Рішення

Спочатку намалюйте точки$P(−1,2)$ і$Q(3,−4)$ і проведіть через них лінію (див. Малюнок$\PageIndex{3}$).

Малюнок$\PageIndex{3}$: Лінія, що проходить через$P(−1,2)$ і$Q(3,−4)$.

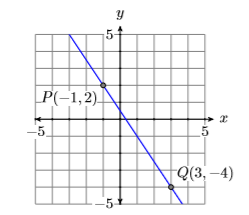
Далі обчислимо нахил лінії, віднімаючи координати точки$P(−1,2)$ з координат точки$Q(3,−4)$.

$$\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-4-2}{3-(-1)} \\ &=\dfrac{-6}{4} \\ &=-\dfrac{3}{2} \end{aligned} \nonumber$$

Таким чином, ухил є$−3/2$.

Далі скористайтеся формою точка-нахил$y−y_0 = m(x−x_0)$ для визначення рівняння прямої. Зрозуміло, що ми повинні замінити$−3/2$ форму. Але який з двох пунктів ми повинні використовувати? Якщо ми використовуємо точку$P(−1,2)$ для$(x_0,y_0)$, ми отримаємо відповідь зліва, але якщо ми використовуємо точку$Q(3,−4)$ для$(x_0,y_0)$, ми отримаємо відповідь праворуч.

$y-2=-\dfrac{3}{2}(x-(-1)) \qquad$або$\qquad y-(-4)=-\dfrac{3}{2}(x-3)$

На перший погляд, ці відповіді не виглядають однаково, але давайте розглянемо їх трохи уважніше, вирішивши$y$ поставити кожен у формі перехоплення нахилу. Почнемо з рівняння зліва.

\ [\ почати {вирівняний}
y-2 &= -\ dfrac {3} {2} (x- (-1))\ квадратний\ колір {Червоний}\ текст {Використання} м = -3/2\ текст {і}\ ліворуч (x_ {0}, y_ {0}\ праворуч) = (-1,2)\\ y-2 &= -\ dfrac {3} {2} {
2} (x+1) = (-1,2)\ y-2 &= -\ dfrac {3} {2} (x+1})\ квадратний\ колір {червоний}\ текст {Спрощення.}\\
y-2 &= -\ dfrac {3} {2} x-\ dfrac {3} {2} {2}\ квадратний\ колір { Червоний}\ текст {Розподілити} -3/2\
y-2+2 &= -\ dfrac {3} {2} x-\ dfrac {3} {2} +2\ квадратний\ колір {Червоний}\ текст {Додати} 2\ текст {на обидві сторони.}\\
y &= -\ dfrac {3} {2} x-\ dfrac {3} {3} c {4} {2}\ quad\ color {Червоний}\ текст {Ліворуч, спростити. Праворуч зробіть еквівалентні дроби із загальним знаменником.}\\
y &= -\ dfrac {3} {2} x+\ dfrac {1} {2}\ quad\ color {Red}\ text {Simplify.}
\ end {вирівняний}\ nonumber\]

Поставимо друге рівняння у вигляді нахилу-перехоплення.

Примітка

Зверніть увагу, що форма$y=-\dfrac{3}{2} x+\dfrac{1}{2}$, якщо порівнювати із загальною формою ухил-перехоплення$y = mx + b$, вказує на те, що$y$ -перехоплення є$(0,1/2)$. Вивчіть малюнок$\PageIndex{3}$. Чи здається, що$y$ -перехоплення є$(0,1/2)$?

\ [\ почати {вирівняний}
y- (-4) &= -\ dfrac {3} {2} (x-3)\ квадратний\ колір {Червоний}\ текст {Використання} м = -3/2\ текст {і}\ ліворуч (x_ {0}, y_ {0}\ праворуч) = (3, -4)\ y+4 &= -\ dfrac {3} {2} (x-3) = (3, -4)\
y+4 &= -\ dfrac {3} {2} (x-3})\ квадратний\ колір {червоний}\ текст {Спрощення.}\\
y+4 &= -\ dfrac {3} {2} x+\ dfrac {9} {2}\ квадратний\ колір { Червоний}\ текст {Розподілити} -3/2\\
y+4-4 &= -\ dfrac {3} {2} x+\ dfrac {9} {2} -4\ квадратний\ колір {Червоний}\ текст {Відніміть} 4\ текст {з обох сторін.}\
y &= -\ dfrac {3} {2} x +\ dfrac {9} {2} {2} x {9} {2} {2} dfrac {9} {2} dfrac {8} {2}\ quad\ color {Червоний}\ текст {Ліворуч, спростити. Праворуч зробіть еквівалентні дроби із загальним знаменником.}\\
y &= -\ dfrac {3} {2} x+\ dfrac {1} {2}
\ end {aligned}\ nonumber\]

Таким чином, обидва рівняння спрощують до однієї і тієї ж відповіді,$y=-\dfrac{3}{2} x+\dfrac{1}{2}$. Це означає, що рівняння$y-2=-\dfrac{3}{2}(x-(-1))$ і$y-(-4)=-\dfrac{3}{2}(x-3)$, хоча вони виглядають по-різному, однакові.

Вправа$\PageIndex{2}$

Знайти рівняння прямої, що проходить через точки$P(−2,1)$ and $Q(4,−1)$.

Відповідь

$y=-\dfrac{1}{3} x+\dfrac{1}{3}$

Приклад$\PageIndex{2}$ породжує наступну пораду.

чайові

При знаходженні рівняння прямої через дві точки$P$ і$Q$, ви можете замінити або точку,$P$ або$Q$ для$(x_0,y_0)$ у формі точки-нахилу$y−y_0 = m(x−x_0)$. Результати виглядають по-різному, але обидва вони є рівняннями однієї лінії.

Паралельні лінії

Нагадаємо, що ухил - це число, яке вимірює крутизну лінії. Якщо дві лінії паралельні (ніколи не перетинаються), вони мають однакову крутизну.

Паралельні лінії

Якщо дві лінії паралельні, вони мають однаковий нахил.

Приклад$\PageIndex{3}$

Намалюйте лінію$y=\dfrac{3}{4} x-2$, потім намалюйте лінію, що проходить через точку$(−1,1)$ that is parallel to the line $y=\dfrac{3}{4} x-2$. Знайдіть рівняння цієї паралельної прямої.

Рішення

Зверніть увагу, що$y=\dfrac{3}{4} x-2$ знаходиться в ухилі-перехоплення формі$y = mx+b$. Значить, його нахил є$3/4$ і його$y$ -перехоплення є$(0,−2)$. Побудуйте$y$ -перехоплення$(0,−2)$, перемістіть вгору$3$ одиниць, вправо$4$ одиниць, потім проведіть лінію (див. Рис.$\PageIndex{4}$).

Малюнок$\PageIndex{4}$: Лінія$y=\dfrac{3}{4} x-2$.

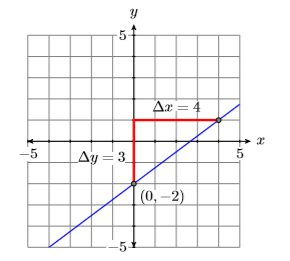
Друга лінія повинна бути паралельна першій, тому вона повинна мати однаковий нахил$3/4$. Намалюйте точку$(−1,1)$, перемістіть вгору$3$ одиниці, вправо$4$ одиниць, потім намалюйте лінію (див. Червону лінію на малюнку$\PageIndex{5}$).

Малюнок$\PageIndex{5}$: Додавання лінії, паралельної$y=\dfrac{3}{4} x-2$.

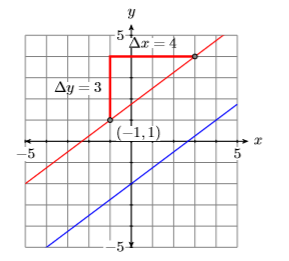
Щоб знайти рівняння паралельної червоної лінії на малюнку$\PageIndex{5}$, використовуйте форму нахилу точки,$3/4$ замініть$m$, потім$(−1,1)$ для$(x_0,y_0)$. Тобто,$−1$ замінюємо$x_0$ і$1$ для$y_0$.

$$\begin{aligned} y-y_{0}&= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-1&= \dfrac{3}{4}(x-(-1)) \quad \color{Red} \text { Substitute: } 3 / 4 \text { for } m,-1 \text { for } x_{0} \text { and } 1 \text { for } y_{0} \\ y-1&= \dfrac{3}{4}(x+1) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber$$

Перевірка: У цьому прикладі нам не потрібно було вирішувати для$y$, тому ми можемо заощадити деякі перевірочні роботи, написавши рівняння

$y-1=\dfrac{3}{4}(x+1) \qquad$у формі$\qquad y=\dfrac{3}{4}(x+1)+1$

шляхом додавання$1$ до обох сторін першого рівняння.

Далі введіть кожне рівняння, як показано на малюнку$\PageIndex{6}$, а потім змініть параметр WINDOW, як показано на малюнку$\PageIndex{7}$.

Малюнок$\PageIndex{6}$: Введіть рівняння паралельних ліній.

Малюнок$\PageIndex{7}$: Налаштуйте параметри WINDOW, як показано на малюнку.

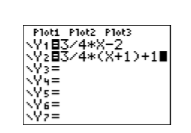
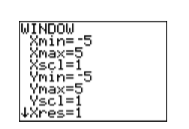
Далі натисніть кнопку GRAPH, виберіть 5:zSquare, щоб створити зображення на малюнку$\PageIndex{9}$.

Малюнок$\PageIndex{8}$: Намальовані від руки паралельні лінії.

Малюнок$\PageIndex{9}$: Натисніть кнопку GRAPH, а потім виберіть 5:zSquare, щоб створити це зображення.

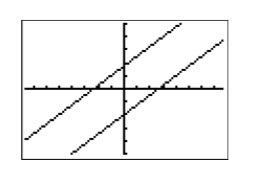
Зверніть увагу на тісну кореляцію ліній калькулятора на малюнку$\PageIndex{9}$ до намальованих від руки ліній на малюнку$\PageIndex{8}$. Це дає нам впевненість у тому, що ми взяли правильну відповідь.

Вправа$\PageIndex{3}$

Знайдіть рівняння прямої, яка проходить через точку$(2,−3)$ and is parallel to the line$y=\dfrac{3}{4} x+2$.

Відповідь

$y=\dfrac{3}{2} x-6$

Перпендикулярні лінії

Дві лінії перпендикулярні, якщо вони зустрічаються і утворюють прямий кут ($90$градуси). Наприклад, лінії$\mathcal{L}_{1}$ і на$\mathcal{L}_{2}$ малюнку$\PageIndex{10}$ перпендикулярні, а ось лінії$\mathcal{L}_{1}$ і на$\mathcal{L}_{2}$ малюнку не$\PageIndex{11}$ перпендикулярні.

Малюнок$\PageIndex{10}$: Лінії$\mathcal{L}_{1}$ і$\mathcal{L}_{2}$ розташовані перпендикулярно. Вони зустрічаються і утворюють прямий кут ($90$градуси).

Малюнок$\PageIndex{11}$: Лінії$\mathcal{L}_{1}$ і не$\mathcal{L}_{2}$ перпендикулярні. Вони не утворюють прямого кута ($90$градуси).

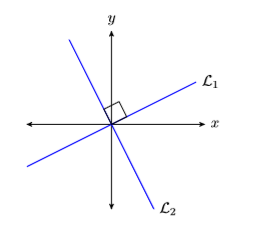
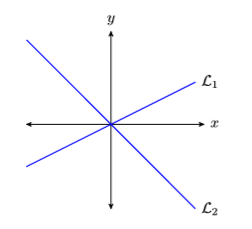
Перш ніж продовжити, нам потрібно встановити співвідношення між нахилами двох перпендикулярних ліній. Отже, розглянемо перпендикулярні лінії$\mathcal{L}_{1}$ і$\mathcal{L}_{2}$ на малюнку$\PageIndex{12}$.

Малюнок$\PageIndex{12}$: Перпендикулярні лінії$\mathcal{L}_{1}$ і$\mathcal{L}_{2}$.

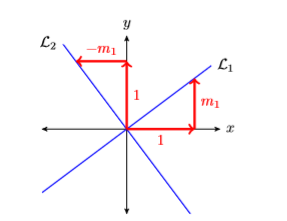
Примітка

1. Якби ми повернули лінію на$\mathcal{L}_{1}$ дев'яносто градусів проти годинникової стрілки, то вирівняли$\mathcal{L}_{1}$ б з лінією$\mathcal{L}_{2}$, як і правильні трикутники, що розкривають їх нахили.
2. $\mathcal{L}_{1}$має ухил$\dfrac{\Delta y}{\Delta x}=\dfrac{m_{1}}{1}=m_{1}$.
3. $\mathcal{L}_{2}$має ухил$\dfrac{\Delta y}{\Delta x}=\dfrac{1}{-m_{1}}=-\dfrac{1}{m_{1}}$

Нахили перпендикулярних ліній

Якщо$\mathcal{L}_{1}$ і$\mathcal{L}_{2}$ є перпендикулярними лініями і$\mathcal{L}_{1}$ має нахил$m_1$, то$\mathcal{L}_{2}$ має нахил$−1/m_1$. Тобто нахил$\mathcal{L}_{2}$ є негативним зворотним нахилу$\mathcal{L}_{1}$.

Приклади:

Щоб знайти нахил перпендикулярної лінії, інвертуйте нахил першої лінії і від'єднайте.

• Якщо нахил$\mathcal{L}_{1}$ є$2$, то нахил перпендикулярної лінії$\mathcal{L}_{2}$ дорівнює$−1/2$.
• Якщо нахил$\mathcal{L}_{1}$ є$−3/4$, то нахил перпендикулярної лінії$\mathcal{L}_{2}$ дорівнює$4/3$.

Приклад$\PageIndex{4}$

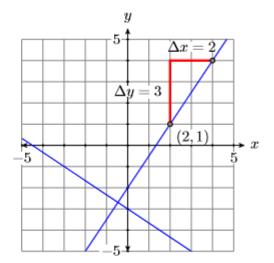
Намалюйте лінію$y=-\dfrac{2}{3} x-3$, потім намалюйте лінію$(2,1)$, через яку перпендикулярно лінії$y=-\dfrac{2}{3} x-3$. Знайдіть рівняння цієї перпендикулярної прямої.

Рішення

Зверніть увагу, що$y=-\dfrac{2}{3} x-3$ знаходиться в ухилі-перехоплення формі$y = mx+b$. Значить, його нахил є$−2/3$ і його$y$ -перехоплення є$(0,−3)$. Побудуйте$y$ -перехоплення$(0,−3)$, перемістіть праві$3$ одиниці, вниз на дві одиниці, потім проведіть лінію (див. Рис.$\PageIndex{13}$).

Малюнок$\PageIndex{13}$: Лінія$y=-\dfrac{2}{3} x-3$.

Оскільки лінія$y=-\dfrac{2}{3} x-3$ має нахил$−2/3$, нахил лінії перпендикулярно цій лінії буде негативним зворотним$−2/3$, а саме$3/2$. Таким чином, щоб провести перпендикулярну лінію, почніть в заданій точці$(2 ,1)$, перемістіть вгору$3$ одиниці, вправо$2$ одиниці, потім проведіть лінію (див. Рис.$\PageIndex{14}$).

Малюнок$\PageIndex{14}$: Додавання лінії перпендикулярно$y=-\dfrac{2}{3} x-3$.

Щоб знайти рівняння перпендикулярної лінії на малюнку$\PageIndex{14}$, використовуйте форму нахилу точки,$3/2$ замінюйте$m$, потім$(2 ,1)$ для$(x_0,y_0)$. Тобто,$2$ замінюємо$x_0$, то$1$ для$y_0$.

$$\begin{aligned} y-y_{0}&= m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-1&= \dfrac{3}{2}(x-2) \quad \color{Red} \text { Substitute: } 3 / 2 \text { for } m, 2 \text { for } x_{0} \text { and } 1 \text { for } y_{0} \end{aligned} \nonumber$$

Перевірка: У цьому прикладі нам не потрібно було вирішувати для$y$, тому ми можемо заощадити деякі перевірочні роботи, написавши рівняння

$y-1=\dfrac{3}{2}(x-2) \qquad$у формі$\quad y=\dfrac{3}{2}(x-2)+1$

шляхом додавання$1$ до обох сторін першого рівняння. Далі введіть кожне рівняння, як показано на малюнку$\PageIndex{15}$, а потім виберіть 6:zStandard, щоб створити зображення на малюнку$\PageIndex{16}$.

Малюнок$\PageIndex{15}$: Введіть рівняння перпендикулярних ліній.

Малюнок$\PageIndex{16}$: 6:zStandard виробляє дві лінії, які не виглядають перпендикулярно.

Зверніть увагу, що лінії на малюнку$\PageIndex{16}$ не здаються перпендикулярними. Ми зробили щось не так? Відповідь - ні! Той факт, що екран перегляду калькулятора ширше, ніж високий, спотворює кут, під яким зустрічаються лінії.

Щоб результат калькулятора відповідав результату на малюнку$\PageIndex{14}$, змініть параметри вікна, як показано на малюнку$\PageIndex{17}$, а потім виберіть 5:zSquare з меню ZOOM, щоб створити зображення на малюнку$\PageIndex{18}$. Зверніть увагу на тісне співвідношення ліній калькулятора на малюнку$\PageIndex{18}$ до намальованих від руки ліній на малюнку$\PageIndex{14}$. Це дає нам впевненість у тому, що ми взяли правильну відповідь.

Малюнок$\PageIndex{17}$: Змініть параметри WINDOW, як показано на малюнку.

Малюнок$\PageIndex{18}$: 5: zSquare створює дві лінії, які виглядають перпендикулярно.

Вправа$\PageIndex{4}$

Знайдіть рівняння прямої, яка проходить через точку$(−3,1)$ and is perpendicular to the line $y=-\dfrac{1}{2} x+1$.

Відповідь

$y=2 x+7$

Додатки

Давайте розглянемо реальне застосування ліній.

Приклад$\PageIndex{5}$

Вода замерзає при$32^{\circ} \mathrm{F}$ (Фаренгейт) і при$0^{\circ} \mathrm{C}$ (за Цельсієм). Вода кипить при$212^{\circ} \mathrm{F}$ і при$100^{\circ} \mathrm{C}$. Якщо співвідношення лінійне, знайдіть рівняння, яке виражає температуру Цельсія через температуру Фаренгейта. Використовуйте результат, щоб знайти температуру за Цельсієм, коли температура Фаренгейта є$113^{\circ} \mathrm{F}$.

Рішення

У цьому прикладі температура за Цельсієм залежить від температури Фаренгейта. Це робить температуру Цельсія залежною змінною, і вона розміщується на вертикальній осі. Ця температура Фаренгейта є незалежною змінною, тому вона розміщується на горизонтальній осі (див. Рис.$\PageIndex{19}$).

Далі вода замерзає$32^{\circ} \mathrm{F}$ і$0^{\circ} \mathrm{C}$, даючи нам крапку$(F,C) = (32,0)$. По-друге, вода закипає при$212^{\circ} \mathrm{F}$ і$100^{\circ} \mathrm{C}$, даючи нам крапку$(F,C)= (212,100)$. Зверніть увагу, як ми масштабували осі так, щоб кожна з цих точок вписувалася в систему координат. Нарешті, припускаючи лінійну залежність між температурами Цельсія і Фаренгейта, проведіть лінію через ці дві точки (див. Рис.$\PageIndex{19}$).

Малюнок$\PageIndex{19}$: Лінійна залежність між температурою Цельсія та Фаренгейта.

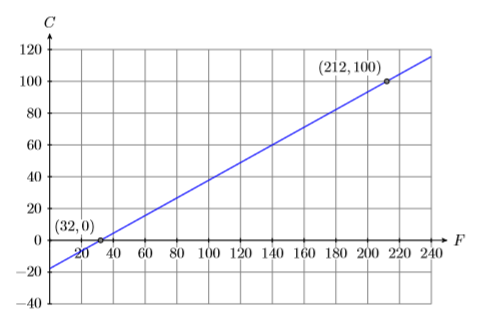
Обчисліть ухил лінії.

$$\begin{aligned} m&= \dfrac{\Delta C}{\Delta F} \quad \color{Red} \text { Slope formula. } \\ m&= \dfrac{100-0}{212-32} \quad \color{Red} \text { Use the points }(32,0) \text { and }(212,100) \text { to compute the difference in C and F}\\ m&= \dfrac{100}{180} \quad \color{Red} \text { Simplify. } \\ m&= \dfrac{5}{9} \quad \color{Red} \text { Reduce. } \end{aligned} \nonumber$$

Ви можете використовувати$(32,0)$ або$(212,100)$ у формі точкового нахилу. Точка$(32,0)$ має менші числа, тому здається легше підставити$(x_0,y_0) = (32 ,0)$ і$m =5 /9$ в точку-нахил форми$y−y_0 = m(x−x_0)$.

$$\begin{aligned} y-y_{0}=& m\left(x-x_{0}\right) \quad \color{Red} \text { Point-slope form. } \\ y-0 &=\dfrac{5}{9}(x-32) \quad \color{Red} \text { Substitute: } 5 / 9 \text { for } m, 32 \text { for } x_{0}, \text { and } 0 \text { for } y_{0} \\ y &=\dfrac{5}{9}(x-32) \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber$$

Однак наші вертикальні та горизонтальні осі$C$ позначені і$F$ (див. Рисунок\(\PageIndex{19}\)) відповідно, тому ми повинні замінити на$C$ і$y$$x$ з,$F$ щоб отримати рівняння, що виражає температуру$C$ Цельсія з точки зору Фаренгейта температура$F$.

$$C=\dfrac{5}{9}(F-32) \label{temperature}$$

Нарешті, щоб знайти температуру Цельсія, коли температура Фаренгейта є$113^{\circ} \mathrm{F}$,$113$ замініть її$F$ в Рівняння\ ref {temperature}

$$\begin{aligned} C&= \dfrac{5}{9}(F-32) \quad \color{Red} \text { Equation }(3.5.1) \\ C&= \dfrac{5}{9}(113-32) \quad \color{Red} \text { Substitute: } 113 \text { for } F \\ C&= \dfrac{5}{9}(81) \quad \color{Red} \text { Subtract. } \\ C&= 45 \quad \color{Red} \text { Multiply. } \end{aligned} \nonumber$$

Тому, якщо температура Фаренгейта є$113^{\circ} \mathrm{F}$, то температура за Цельсієм є$45^{\circ} \mathrm{C}$.

Вправа$\PageIndex{5}$

Знайдіть рівняння, яке виражає температуру Фаренгейта через температуру Цельсія. Використовуйте результат, щоб знайти температуру за Фаренгейтом, коли температура за Цельсієм є$25^{\circ} \mathrm{C}$.

Відповідь

$77^{\circ} \mathrm{F}$