4.1.6: Закон косинусів
Знайдіть невідому сторону, задану двома сторонами і включеним кутом.
Сторони косого трикутника
Ви граєте в гру під назвою «Over the Line», де ви стоїте в одному куті трикутника і б'єте м'ячем. Поле виглядає так:
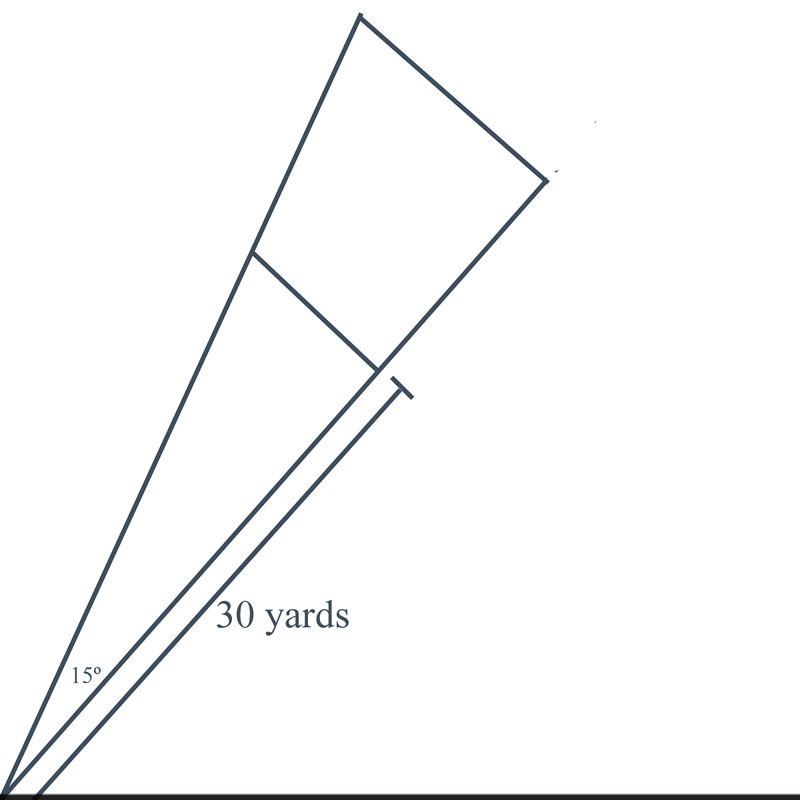
Очки набираються ударом по м'ячу так, щоб він приземлився за першу лінію в трикутнику, але перед другою лінією.
Враховуючи, що кут на лівій стороні трикутника є15∘, а довжина сторін трикутника йде до першої лінії підрахунку рахунку 30 ярдів, ви можете обчислити довжину лінії, яку ви повинні вдарити м'яч повз, щоб забити?
Пошук сторін косого трикутника
Цей урок приймає ідеї, які були застосовані лише до прямих трикутників, і інтерпретує їх так, щоб їх можна було використовувати для будь-якого типу трикутника.
По-перше, закони синусів і косинусів приймають теорему Піфагора і співвідношення і застосовують їх до будь-якого трикутника.
Закон Косинуса є узагальненням теореми Піфагора, де кут C - кут між двома заданими сторонами трикутника:
c2=a2+b2−2(a)(b)cosC
Ви помітите, що якби це був прямокутний трикутникcosC=cos90∘=0, і так третій член зникне, залишивши знайому теорему Піфагора.
Один випадок, коли ми можемо використовувати Закон Косинусів, - це коли ми знаємо дві сторони та включений кут у трикутник (SAS) і хочемо знайти третю сторону.
Розв'язування невідомих значень
1. ВикористанняΔDEF,∠E=12∘,d=18, іf=16.8. Знайтиe.
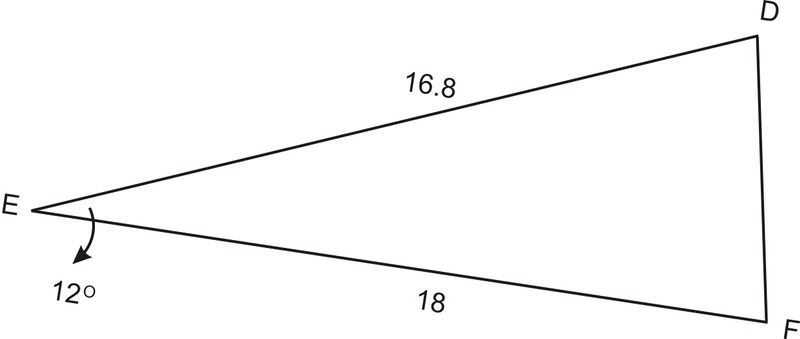
ОскількиΔDEF це не прямокутний трикутник, ми не можемо використовувати теорему Піфагора або функції тригонометрії, щоб знайти третю сторону. Однак ми можемо використовувати наш нещодавно отриманий Закон Косинусів.
e2=182+16.82−2(18)(16.8)cos12 Law of Cosinese2=324+282.24−2(18)(16.8)cos12 Simplify squarese2=324+282.24−591.5836689 Multiplye2=14.6563311 Add and subtract from left to righte≈3.8 Square root
∗ Зверніть увагу, що негативна відповідь викидається як не має геометричного значення в даному випадку.
2. Архітектор проектує кухню для клієнта. При проектуванні кухні архітектор повинен приділити особливу увагу розміщенню плити, мийки, холодильника. Для того, щоб кухня була ефективно використана, ці три зручності повинні утворювати трикутник один з одним. Це відоме як «робочий трикутник». За конструкцією три частини робочого трикутника повинні бути не менше 3 футів один від одного і не більше 7 футів один від одного. Виходячи з розмірів поточної кухні, архітектор визначив, що мийка буде знаходитися на відстані 3,6 футів від плити та на відстані 5,7 футів від холодильника. Якщо мийка утворює103∘ кут з плитою і холодильником, чи залишиться відстань між плитою і холодильником в межах робочого трикутника?
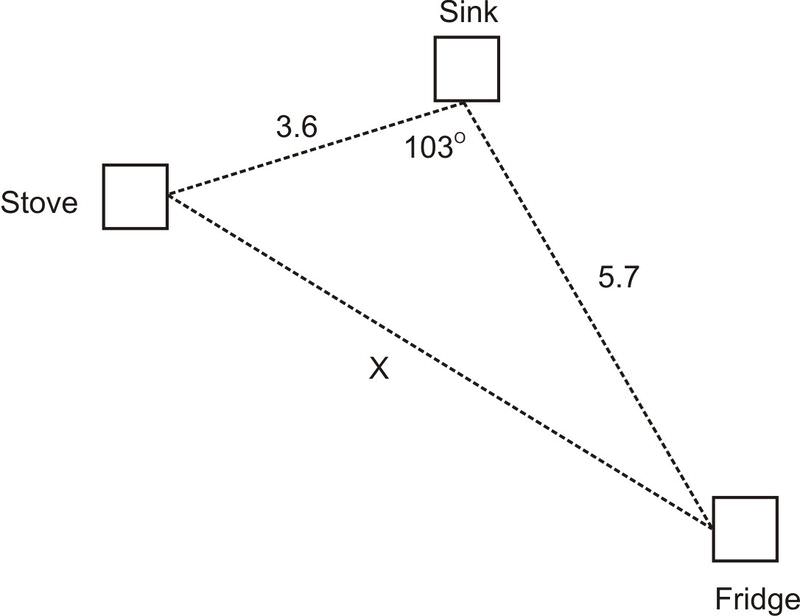
Для того щоб знайти відстань від мийки до холодильника, нам потрібно знайти сторонуx. Щоб знайти сторонуx, ми будемо використовувати Закон Косинусів, тому що ми маємо справу з тупим трикутником (і, таким чином, не маємо прямих кутів для роботи). Нам відома довжина двох сторін: раковина до плити і мийка до холодильника. Ми також знаємо, що включений кут (кут між двома відомими довжинами) є103∘. Це означає, що ми маємо справу SAS і можемо застосовувати Закон Косинусів.
x2=3.62+5.72−2(3.6)(5.7)cos103 Law of Cosinesx2=12.96+32.49−2(3.6)(5.7)cos103 Simplify squaresx2=12.96+32.49+9.23199127 Multiplyx2=54.68199127 Evaluatex≈7.4 Square root
Ні, цей трикутник не відповідає визначенню робочого трикутника. Раковина і холодильник занадто далеко один від одного на 0,4 фута.Вирішити дляj.
3. ВикористанняΔJKL,∠J=2∘,l=25, іk=27. Знайтиj.
ОскількиΔJKL це не прямокутний трикутник, ми не можемо використовувати теорему Піфагора або функції тригонометрії, щоб знайти третю сторону. Однак ми можемо використовувати наш нещодавно отриманий Закон Косинусів.
j2=252+272−2(25)(27)cos2 Law of Cosinesj2=625+729−2(25)(27)cos2 Simplify squaresj2=625+729−1349.18 Multiplyj2=4.82 Add and subtract from left to rightj≈2.20 Square root
∗ Зверніть увагу, що негативна відповідь викидається як не має геометричного значення в даному випадку.
Раніше вам було запропоновано обчислити довжину лінії, яку ви повинні вдарити м'яч повз, щоб забити.
Рішення
Оскільки ви знаєте, що довжина кожної з двох інших сторін становить 30 ярдів, а кут є15∘, ви можете скористатися Законом Косинусів, щоб знайти довжину третьої сторони.
c2=a2+b2−2abcosθc2=302+302−(2)(30)(30)cos15∘c2=900+900−1738.67c2=1800−1738.67c2=61.33c≈7.83
Знайти сторону "a" в цьому трикутнику∠A=50∘, деb=8,c=11
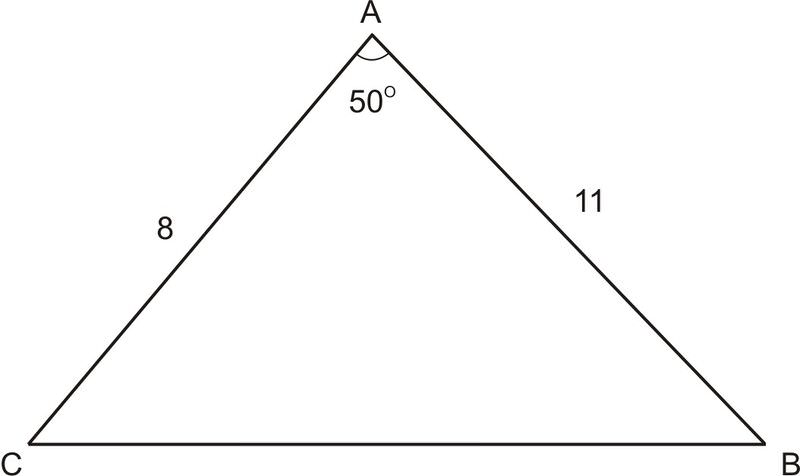
Рішення
a2=82+112−2⋅8⋅11⋅cos50∘,a≈8.5
Знайти сторону "l" в цьому трикутнику де∠L=79.5∘m=22.4,p=13.17
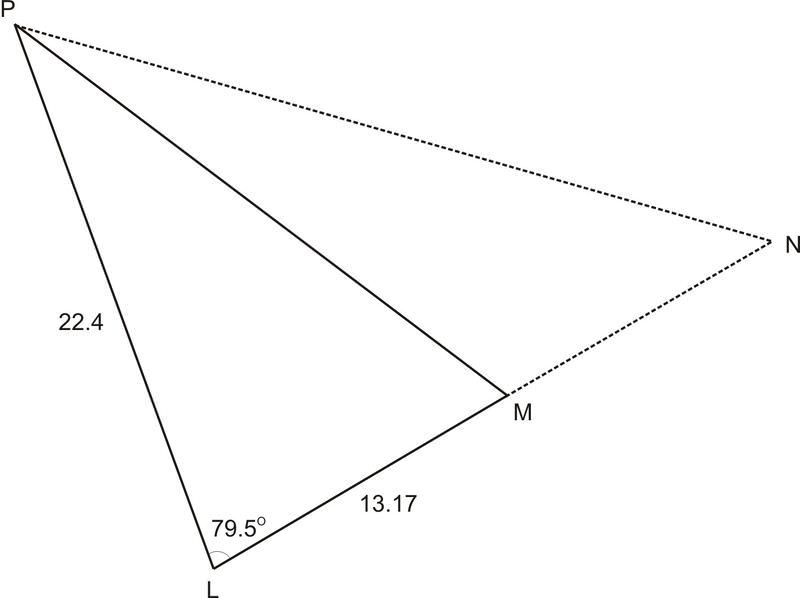
Рішення
l2=22.42+13.172−2⋅22.4⋅13.17⋅cos79.5∘,l≈23.8
Знайти сторону "b" в цьому трикутнику де∠B=67.2∘d=43,e=39
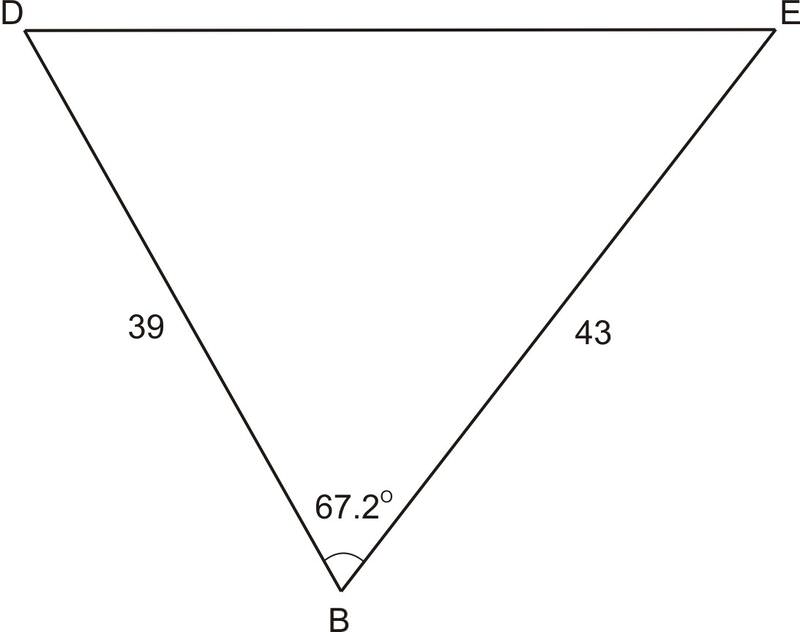
Рішення
b2=392+432−2⋅39⋅43⋅cos67.2∘,b≈45.5
Рецензія
- Законодавство Косинусів.
Для кожного трикутника нижче введіть значенняab, іc.
-
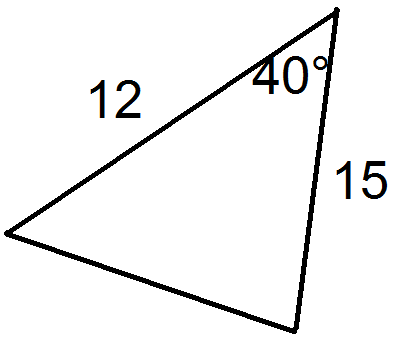
Малюнок4.1.6.7 -
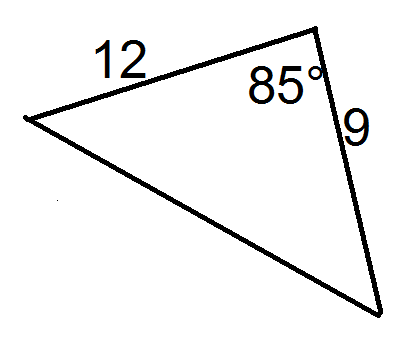
Малюнок4.1.6.8 -
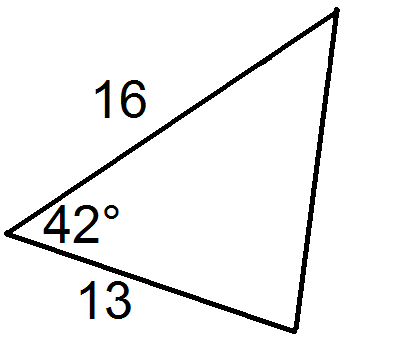
Малюнок4.1.6.9 -
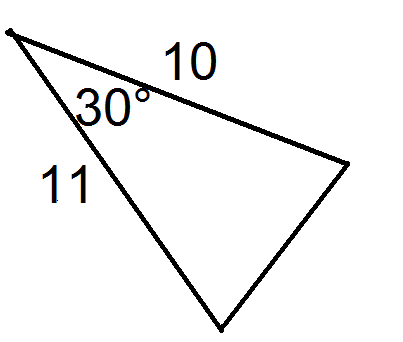
Малюнок4.1.6.10 -
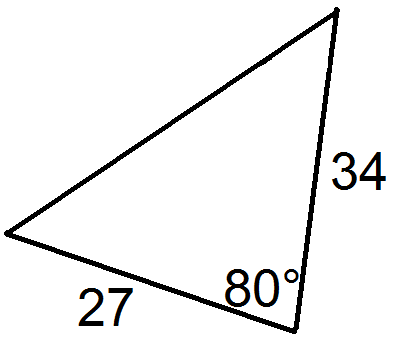
Малюнок4.1.6.11 -
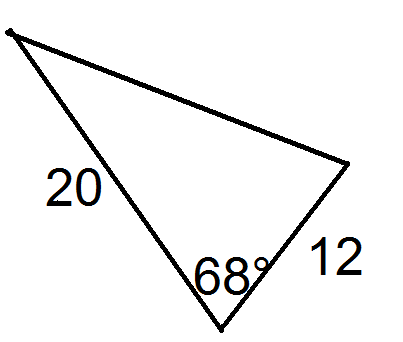
Малюнок4.1.6.12 -
Малюнок4.1.6.13
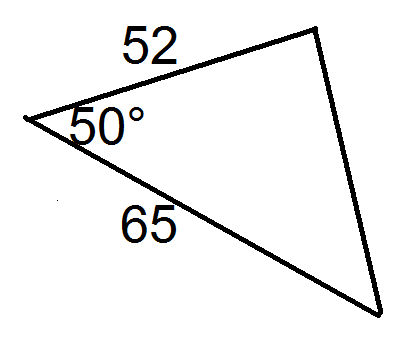
Тепер для кожного трикутника вирішуйте для відсутньої сторони, використовуючи Закон Косинусів.
-

Малюнок4.1.6.14 -

Малюнок4.1.6.15 -

Малюнок4.1.6.16 -

Малюнок4.1.6.17 -

Малюнок4.1.6.18 -

Малюнок4.1.6.19 -

Малюнок4.1.6.20 - Доведіть, що закон Косинуса еквівалентний теоремі Піфагора для всіх правильних трикутників.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.1.
Лексика
| Термін | Визначення |
|---|---|
| Включено кут | Вхідний кут в трикутник - це кут між двома відомими сторонами. |
| закон косинусів | Закон косинусів - це правило, що стосується сторін трикутника з косинусом одного з його кутів. Закон косинусів говорить про теc2=a2+b2−2abcosC,C де кут поперек з бокуc. |
| Косий трикутник | Косий трикутник - це трикутник без прямого кута в якості одного з його внутрішніх кутів. |
| Бічний кут бічного трикутника | Бічний кут бічний трикутник - це трикутник, де дві сторони і кут між ними відомі величини. |
