4.1.9: Визначте точні креслення трикутників
- Page ID
- 54639
Чи правильний трикутник на основі закону косинусів.
Ваш друг створює нову настільну гру, яка включає кілька різних фігур у формі трикутника. Однак гра вимагає точних вимірювань декількох різних фігур, які всі повинні поєднуватися один з одним. Вона приносить вам деякі частини і запитує, чи можете ви переконатися, що її вимірювання довжини сторін і кутів шматочків правильні.
Ви виймаєте перший шматок. За словами вашого друга, шматок має сторони довжиною 4 в, 5 в і 7 дюймів, а кут між стороною довжини 4 і стороною довжини 5 є\(78^{\circ} \). Вона дуже впевнена в довжині сторін, але не зовсім впевнена, чи правильно виміряла кут. Чи є спосіб визначити, чи має ігровий шматок вашого друга правильні вимірювання, або вона помилилася?
Аналіз трикутників
Наше розширення аналізу трикутників тягне нас природно до косих трикутників.
Закон Косинуса можна використовувати для перевірки точності малюнків косих трикутників. У прямокутному трикутнику ми можемо використовувати теорему Піфагора, щоб перевірити, що всі три сторони є правильною довжиною, або ми можемо використовувати тригонометричні співвідношення для перевірки вимірювання кута. Однак, маючи справу з тупим або гострим трикутником, ми повинні спиратися на Закон Косинуса.
Для наступних проблем скористаємося Законом косинусів
1. \(\Delta ABC\)В праворуч,\(a=32\),\(b=20\), І\(c=16\). Чи точний малюнок, якщо він позначає\(\angle C\) як\(35.2^{\circ} \)? Якщо ні, то що слід\(\angle C\) виміряти?
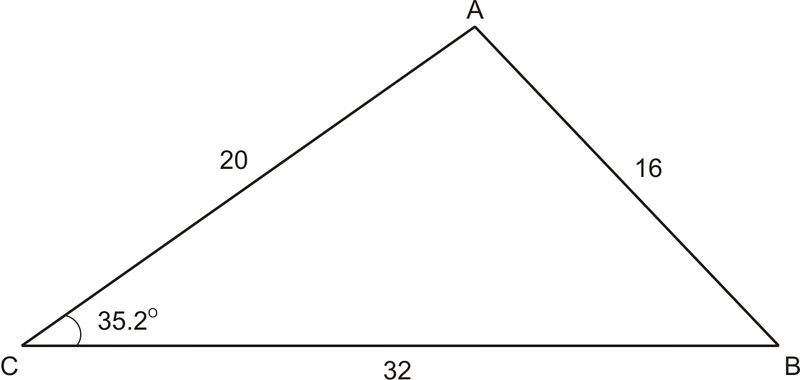
Ми будемо використовувати Закон косинусів, щоб перевірити, чи\(\angle C\) є чи ні\(35.2^{\circ} \).
\ (\ почати {вирівняний}
16^ {2} &=20^ {2} +32^ {2} -2 (20) (32)\ cos 35.2 &&\ текст {Закон косинусів}\\
256&= 400+1024-2 (20) (32)\ cos 35.2 &&\ текст {Просто квадрати}\\
256&= 400+1024-1045.94547 &&\ текст {Помножити текст {}\\
256 &\ новий 378.05453 &&\ text {Додати і відняти}
\ end {вирівняний}\)
З тих пір\(256\neq 378.05453\), ми знаємо, що\(\angle C\) це не так\(35.2^{\circ} \). Використовуючи Закон Косинусів, ми можемо розібратися в правильному вимірі\(\angle C\).
\ (\ begin {вирівняний}
16^ {2} &= 20^ {2} +32^ {2} -2 (20) (32)\ cos C &&\ текст {Закон косинусів}\\
256&=400+1024-2 (20) (32)\ cos C &\ text {Спрощення квадратів}\\
256&= 400+1024-1280\ cos C &\ текст {Множення}\
256&=1424- 1280\ cos C &&\ текст {Додати}\\
-1168&=-1280\ cos C &&\ текст {Відняти}\\
0.9125&=\ cos C &&\ текст {Розділити}
\\
24.1^ {\ circ} &\ приблизно\ кут C &\ cos^ {−1} (0.9125)
\ кінець {вирівняний}\)
Для деяких ситуацій необхідно буде використовувати не тільки Закон Косинуса, але також теорему Піфагора та тригонометричні співвідношення, щоб переконатися, що трикутник або чотирикутник були намальовані точно.
2. Будівельник отримав плани будівництва другоповерхового прибудови на будинок. На схемі показано, як архітектор хоче обрамляти дах, тоді як довжина будинку становить 20 футів. Будівельник вирішує додати перпендикулярну опорну балку від піку даху до основи. За його оцінками, нова балка повинна бути висотою 8,3 футів, але він хоче перевірити ще раз, перш ніж почати будівництво. Чи правильна оцінка будівельника 8,3 футів для нового променя? Якщо ні, то як далеко він?
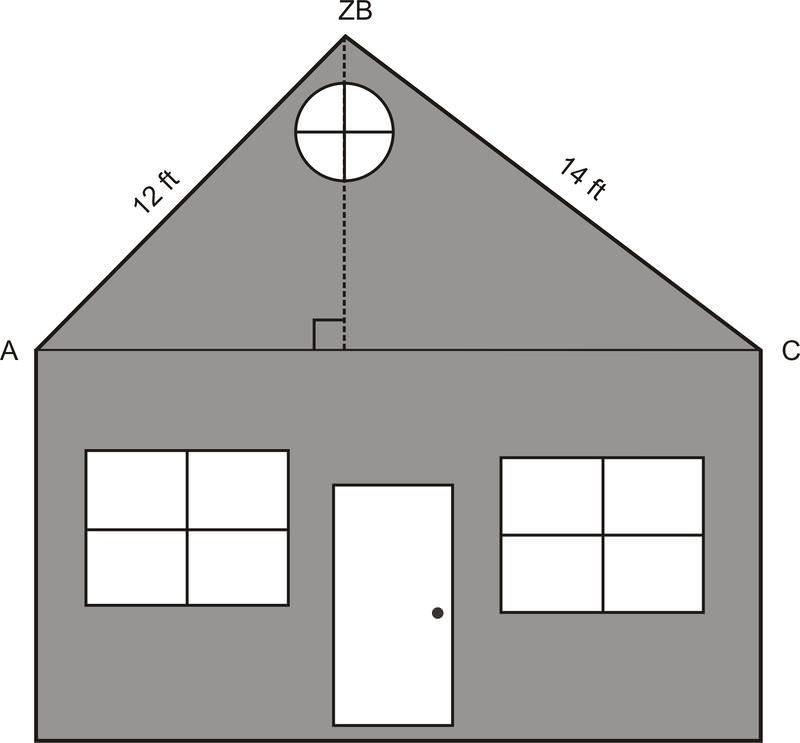
Якщо ми знали\(\angle A\) або або\(\angle C\), ми могли б використовувати тригонометричні співвідношення, щоб знайти висоту опорної балки. Однак жодна з цих кутових заходів нам не дається. Оскільки ми знаємо всі три сторони\(\Delta ABC\), ми можемо використовувати Закон Косинусів, щоб знайти один з цих кутів. Ми знайдемо\(\angle A\).
\(\begin{aligned} 14^2 &=12^2+20^2−2(12)(20)\cos A && \text{Law of Cosines}\\ 196&=144+400−480\cos A &&\text{Simplify}\\ 196& =544−480\cos A && \text{Add}\\ −348&=−480\cos A && \text{Subtract}\\ 0.725&=\cos A &&\text{Divide}\\ 43.5^{\circ}&\approx \angle A && \cos ^{−1}(0.725)\end{aligned}\)
Тепер, коли ми знаємо\(\angle A\), ми можемо використовувати його, щоб знайти довжину\(BD\).
\(\begin{aligned} \sin 43.5 &=\dfrac{x}{12}\\ 12 \sin43.5 &=x\\ 8.3&\approx x\end{aligned}\)
Так, оцінка будівельника в 8.3 футів для опорної балки є точною.
В\(\Delta CIR\),\(c=63\),,\(i=52\), і\(r=41.9\). Знайдіть міру всіх трьох кутів.
\(\begin{aligned} 63^2&=52^2+41.9^2−2\cdot 52\cdot 41.9\cdot \cos C \\ 52^2&=63^2+41.9^2−2\cdot 63\cdot 41.9\cdot \cos I \\ 180^{\circ} −83.5^{\circ} −55.1^{\circ} &=41.4^{\circ} \\ \angle C &\approx 83.5^{\circ} \\ \angle I&\approx 55.1^{\circ} \\ \angle R&\approx 41.4^{\circ} \end{aligned}\)
Раніше вас запитали, чи існує спосіб визначити, чи має ігровий шматок вашого друга правильні вимірювання.
Рішення
Оскільки ваш друг впевнений у довжині сторін трикутника, вам слід використовувати ті, як відомі величини в Законі Косинусів і вирішити для кута:
\(\begin{aligned} 7^2&=5^2+4^2+(2)(5)(4)\cos \theta \\ 49&=25+16+40\cos \theta \\ 49−25−16&=40\cos \theta \\ \dfrac{8}{40}&=\cos \theta \\ \cos ^{−1}\dfrac{8}{40}&=\theta \\ \theta &=78.46 \end{aligned}\)
Так що, як з'ясовується, ваш друг досить близький. Її вимірювання, ймовірно, були незначними неточними через її округлення від транспортира.
Знайдіть,\(AD\) використовуючи теорему Піфагора, Закон Косинуса, триг-функції або будь-яку комбінацію з трьох.
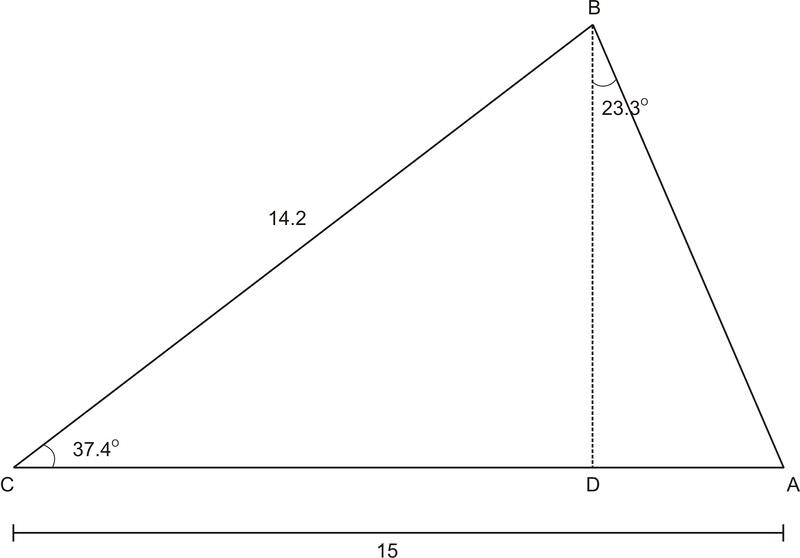
Рішення
Спочатку знайдіть\(AB\).
\(AB^2=14.2^2+15^2−2\cdot 14.2\cdot 15\cdot \cos 37.4^{\circ} \),\(AB=9.4\). \(\sin 23.3^{\circ} =\dfrac{AD}{9.4}\),\(AD=3.7\).
Знайти,\(HK\) використовуючи теорему Піфагора, Закон Косинуса, триг-функції, або будь-яку комбінацію трьох if\(JK=3.6\),\(KI=5.2\),\(JI=1.9\),\(HI=6.7\), і\(\angle KJI=96.3^{\circ} \).
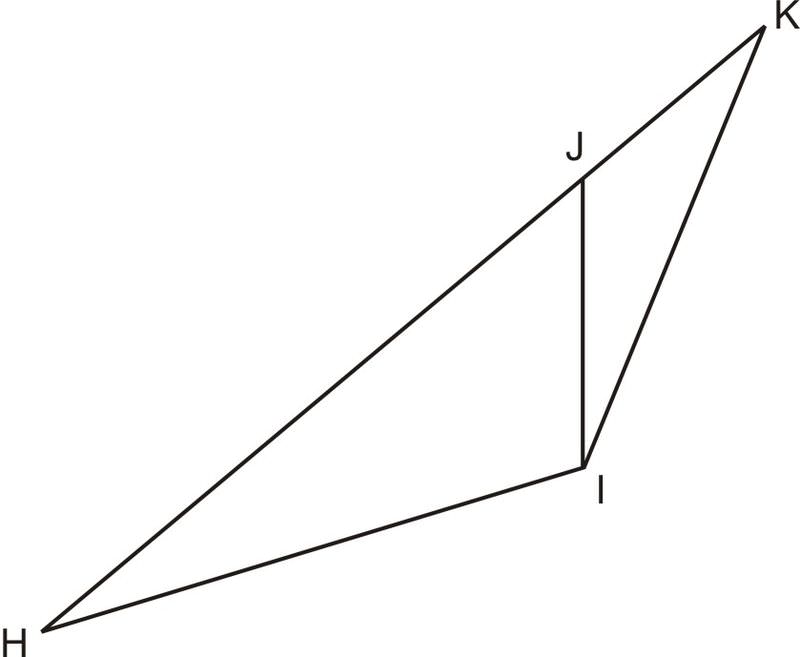
Рішення
\(\angle HJI=180^{\circ} −96.3^{\circ} =83.7^{\circ} \)(Ці два кути є лінійною парою). \(6.7^2=HJ^2+1.9^2−2\cdot HJ\cdot 1.9\cdot \cos 83.7^{\circ} \). Це спрощує до квадратного рівняння\(HJ^2−0.417HJ−41.28\). Використовуючи квадратичну формулу, ми можемо визначити це\(HJ\approx 6.64\). Отже, з тих пір\(HJ+JK=HK\),\(6.64+3.6\approx HK\approx 10.24\).
Використовуйте Закон косинусів, щоб визначити, чи правильно намальований наступний трикутник. Якщо немає, визначте, наскільки далеко вимір сторони\(d\) "" знаходиться від правильного значення.
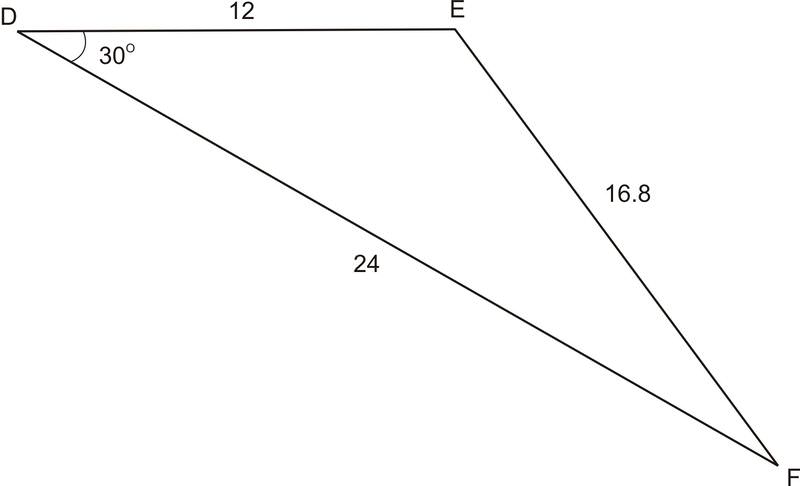
Рішення
Щоб визначити це, використовуйте Закон косинусів і вирішіть для d, щоб визначити, чи є картинка точною. \(d^2=12^2+24^2−2\cdot 12\cdot 24\cdot \cos 30^{\circ} \),\(d=14.9\), Що означає\(d\) на зображенні вимкнено на 1.9.
Рецензія
- Якщо ви знаєте довжини всіх трьох сторін трикутника і міру одного кута, як можна визначити, чи правильно намальований трикутник?
Визначте, чи правильно позначений кожен трикутник.
-
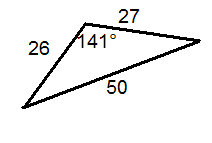
Малюнок\(\PageIndex{6}\) -
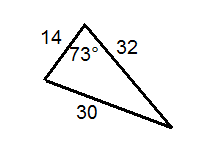
Малюнок\(\PageIndex{7}\) -
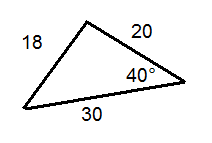
Малюнок\(\PageIndex{8}\) -
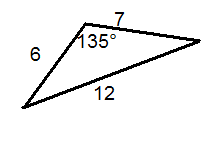
Малюнок\(\PageIndex{9}\) -
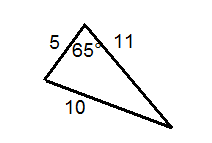
Малюнок\(\PageIndex{10}\) -
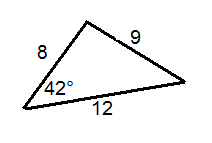
Малюнок\(\PageIndex{11}\)
Визначити, чи можна кожен описаний трикутник. Припустимо, кути були округлені до найближчого градуса.
- В\(\Delta BCD\),\(b=4\),\(c=4\),\(d=5\), і\(m\angle B=51^{\circ} \).
- В\(\Delta ABC\),\(a=7\),\(b=4\),\(c=9\), і\(m\angle B=34^{\circ} \).
- В\(\Delta BCD\),\(b=3\),\(c=2\),\(d=7\), і\(m\angle D=138^{\circ} \).
- В\(\Delta ABC\),\(a=8\),\(b=6\),\(c=13.97\), і\(m\angle C=172^{\circ} \).
- В\(\Delta ABC\),\(a=4\),\(b=4\),\(c=9\), і\(m\angle B=170^{\circ} \).
- В\(\Delta BCD\),\(b=3\),\(c=5\),\(d=4\), і\(m\angle C=90^{\circ} \).
- В\(\Delta ABC\),\(a=8\),\(b=3\),\(c=6\), і\(m\angle A=122^{\circ} \).
- Якщо ви використовуєте Закон Косинусів, щоб вирішити для\(m\angle C\) в\(\Delta ABC\) де\(a=3\)\(b=7\), і\(c=12\), ви отримаєте помилку. Поясніть чому.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.3.
Лексика
| Термін | Визначення |
|---|---|
| закон косинусів | Закон косинусів - це правило, що стосується сторін трикутника з косинусом одного з його кутів. Закон косинусів говорить про те\(c^2=a^2+b^2−2ab\cos C\),\(C\) де кут поперек з боку\(c\). |