4.1.8: Визначення невідомих кутів за законом косинусів

Last updated
Save as PDF

Page ID: 54623

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Знайти невідомий кут заданої довжини всіх 3 сторін

Саріне малює трикутник. Вона вимірює довжину сторін і записує свої виміри наступним чином. Яка міра кута\(C\) трикутника?

\(\begin{aligned} a&=3 \\ b&=4 \\ c&=5 \end{aligned}\)

Закон косинусів з SSS

Закон косинусів\(a^2+b^2−2ab\cos C\), може бути перебудований, щоб полегшити розрахунок міри кута\(a\),\(C\) коли,\(b\) і всі\(c\) відомі довжини.

\(\begin{aligned} a^2+b^2−2ab \cos C &=c^2 \\ a^2+b^2−c^2 &=2ab\cos C\\ \dfrac{a^2+b^2−c^2}{2ab} &=\cos C \end{aligned}\)

яким можна додатково маніпулювати\(C=\cos ^{−1}\left(\dfrac{a^2+b^2−c^2 }{2ab}\right)\).

Знайдемо міру найбільшого кута в трикутнику з довжинами сторін 12, 18 і 21.

Для початку треба визначити, який кут буде найбільшим. Нагадаємо з геометрії, що найдовша сторона протилежна найбільшому куту. Найдовша сторона 21, тому ми дозволимо,\(c=21\) оскільки\(C\) це кут, який ми намагаємося знайти. Дозвольте\(a=12\)\(b=18\) і використовувати формулу для вирішення,\(C\) як показано на малюнку. Не має значення, які сторони ми присвоюємо\(a\) і\(b\). Вони взаємозамінні за формулою.

\(m\angle C=\cos ^{−1}\left(\dfrac{12^2+18^2−21^2 }{2(12)(18)}\right) \approx 86^{\circ}\)

Примітка: Будьте обережні, щоб поставити круглі дужки навколо всього чисельника і всього знаменника на калькуляторі, щоб забезпечити належний порядок операцій. Екран калькулятора повинен виглядати наступним чином:

\(\cos ^{−1}((12^2+18^2−21^2)/(2(12)(18)))\)

Тепер знайдемо значення\(x\), до найближчого ступеня.

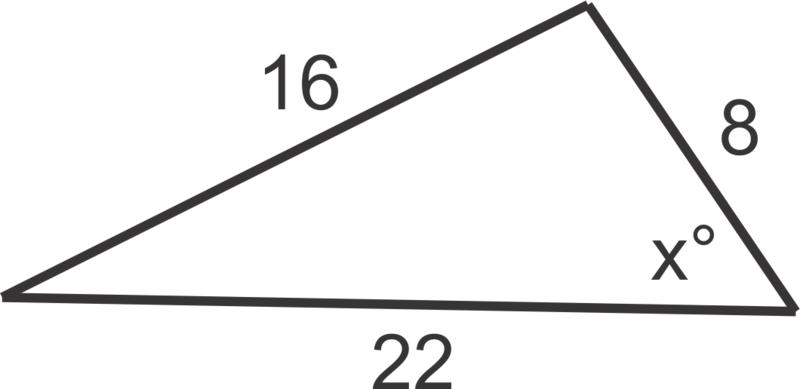
F-д_924С7ЕФ78Д4Е2Е2ЕЕ8БК5Е85Д1ДФ9ДФ5Ф4С34ДБ630Б776Б65Б91Е+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Кут з мірою\(x^{\circ} \) буде кут\(C\) так\(c=16\),\(a=22\) і\(b=8\). Пам'ятайте,\(a\) і\(b\) є взаємозамінними в формулі. Тепер ми можемо замінити змінні відомими мірами і вирішити.

\(\cos ^{−1}\left(\dfrac{22^2+8^2−16^2}{2(22)(8)}\right)\approx 34^{\circ}\)

Нарешті, давайте знайдемо\(m\angle A\), якщо\(a=10\),\(b=15\) і\(c=21\).

Спочатку давайте переставимо формулу, щоб відобразити сторони заданого та запитаного кута:

\(\cos A=\left(\dfrac{b^2+c^2−a^2}{2(b)(c)}\right)\), тепер підключіть наші цінності

\(m\angle A=\cos ^{−1}\left( \dfrac{15^2+21^2−10^2}{2(15)(21)}\right) \approx 26^{\circ}\)

Приклад\(\PageIndex{1}\)

Раніше вас попросили знайти міру кута\(C\) трикутника, який має сторони\(a = 3\)\(b = 4\), і\(c = 5\).

Рішення

Ми можемо використовувати маніпульований Закон Косинусів для вирішення\(C\).

\(\begin{aligned} C&=\cos ^{−1} \dfrac{3^2+4^2−5^2}{2(3)(4)} \\ C&=\cos ^{−1} \dfrac{9+16−25}{24} \\ C&=\cos ^{−1} \dfrac{0}{24}=\cos ^{−1} 0 \\ C&=90^{\circ} \end{aligned}\)

Тому трикутник - це прямокутний трикутник.

Приклад\(\PageIndex{2}\)

Знайдіть міру на\(x\) схемі:

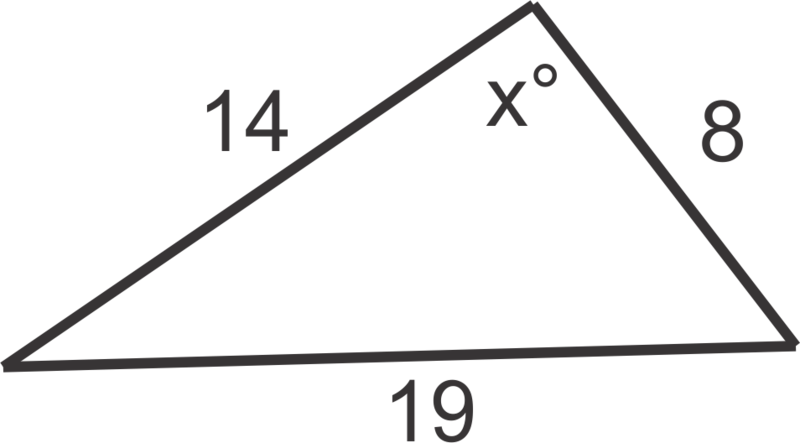
Ф-д_Е07Б58Д594Д1ФФФФ3Ф9Ф8С99789065Д7Б5Е9А9737067Е125ДБ8186Ф+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

\(\cos ^{−1}\left(\dfrac{14^2+8^2−19^2}{2(14)(8)}\right) \approx 117^{\circ}\)

Приклад\(\PageIndex{3}\)

Знайти міру найменшого кута в трикутнику з довжинами сторін 47, 54 і 72.

Рішення

Найменший кут буде протилежний стороні з довжиною 47, так що це буде наш\(c\) в рівнянні.

\(\cos ^{−1}\left(\dfrac{54^2+72^2−47^2 }{2(54)(72)}\right) \approx 41^{\circ}\)

Приклад\(\PageIndex{4}\)

Знайти\(m\angle B\), якщо\(a=68\),\(b=56\) і\(c=25\).

Рішення

Переставити формулу для розв'язання\(m\angle B\),

\(\cos B=\left(\dfrac{a^2+c^2−b^2}{2(a)(c)}\right)\);\(\cos ^{−1}\left(\dfrac{68^2+25^2−56^2}{2(68)(25)}\right)\approx 52^{\circ}\)

Рецензія

Використовуйте Закон Косинусів, щоб знайти значення\(x\), в найближчій мірі, в задачах з 1 по 6.

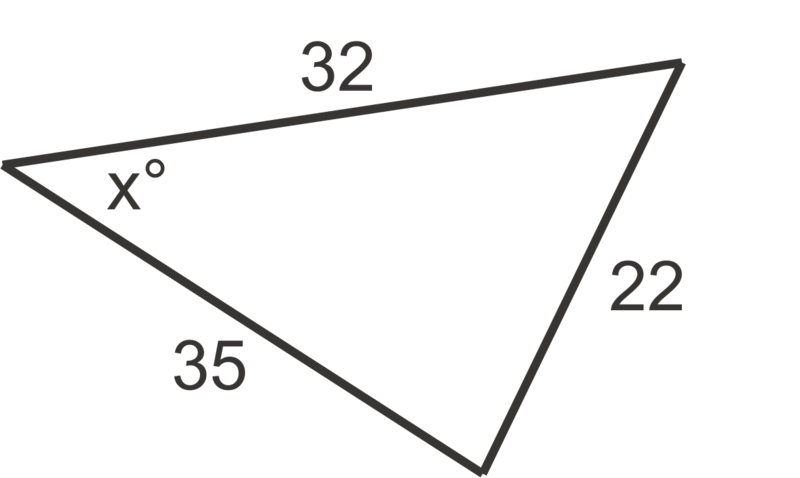
Малюнок\(\PageIndex{3}\)
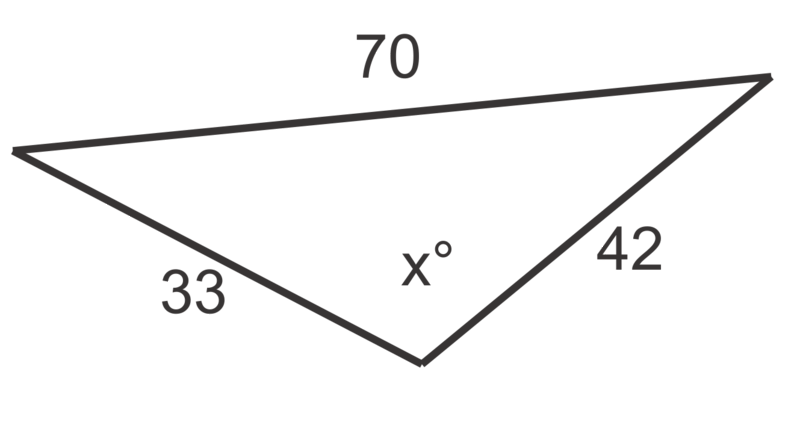
Малюнок\(\PageIndex{4}\)
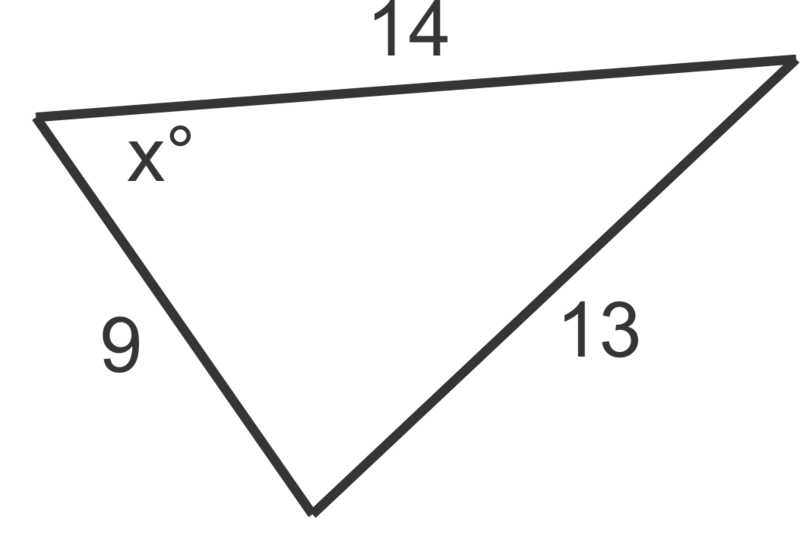
Малюнок\(\PageIndex{5}\)
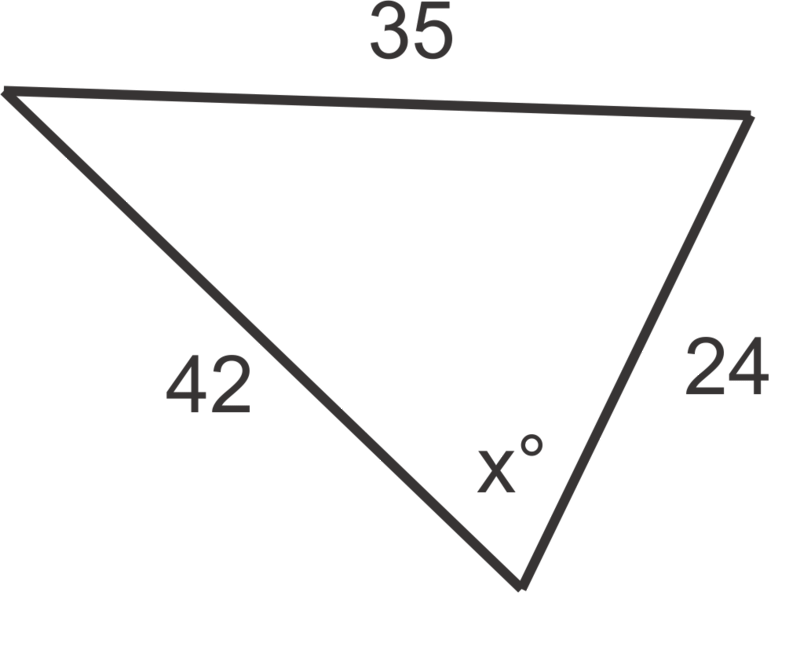
Малюнок\(\PageIndex{6}\)
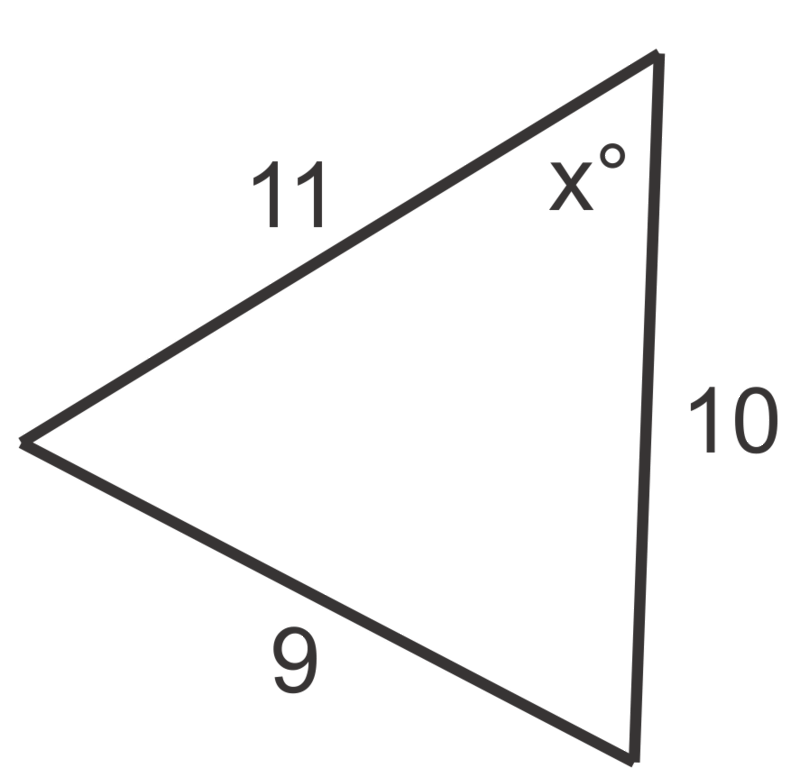
Малюнок\(\PageIndex{7}\)
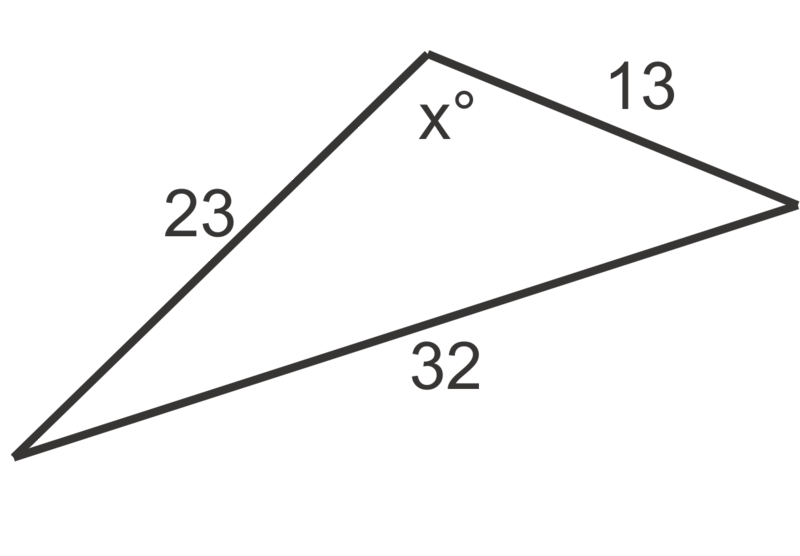
Малюнок\(\PageIndex{8}\)
Знайдіть міру найменшого кута в трикутнику з довжинами сторін 150, 165 і 200 метрів.
Знайдіть міру найбільшого кута в трикутнику з довжиною сторони 59, 83 і 100 ярдів.
Знайдіть\(m\angle C\) if\(a=6\),\(b=9\) і\(c=13\).
Знайдіть\(m\angle B\) if\(a=15\),\(b=8\) і\(c=9\).
Знайдіть\(m\angle A\) if\(a=24\),\(b=20\) і\(c=14\).
Трикутна ділянка землі межує з дорогою, парканом і струмком. Якщо ділянка уздовж дороги 100 метрів, довжина огорожі 115 метрів, а сторона уздовж струмка 90 метрів, під яким кутом зустрічаються паркан і дорога?