2.5.4: Обертання в радіанах
- Page ID
- 54765
Обертання стрілок годинника.
У вашому класі математики одного ранку ви закінчите вікторину рано. Поки ви чекаєте, ви спостерігаєте за годинником, як він відключається п'ять хвилин. Час на годиннику читається 9:00. Ваші останні уроки навчили вас, що одним із способів вимірювання положення чогось на колі є використання кута. Раптом вам приходить в голову, що це може бути застосовано до годинників. Чи можете ви визначити кут між двома стрілками годинника?
Багато цікавої інформації про обертання та про те, як їх виміряти, може надходити від погляду на годинник. Ми настільки знайомі з годинниками в нашому повсякденному житті, що не часто зупиняємося, щоб думати про ці маленькі пристрої, з постійно обертаються руками. Давайте приділимо кілька хвилин в цьому уроці для більш докладного розгляду цих прикладів обертального руху.
Для наступних проблем висловимо в радіанах
1. Стрілки годинника показують 11:20. Висловіть тупий кут, утворений годинною та хвилинною стрілками в радіанову міру.
На наступній схемі показано розташування рук в зазначений час.
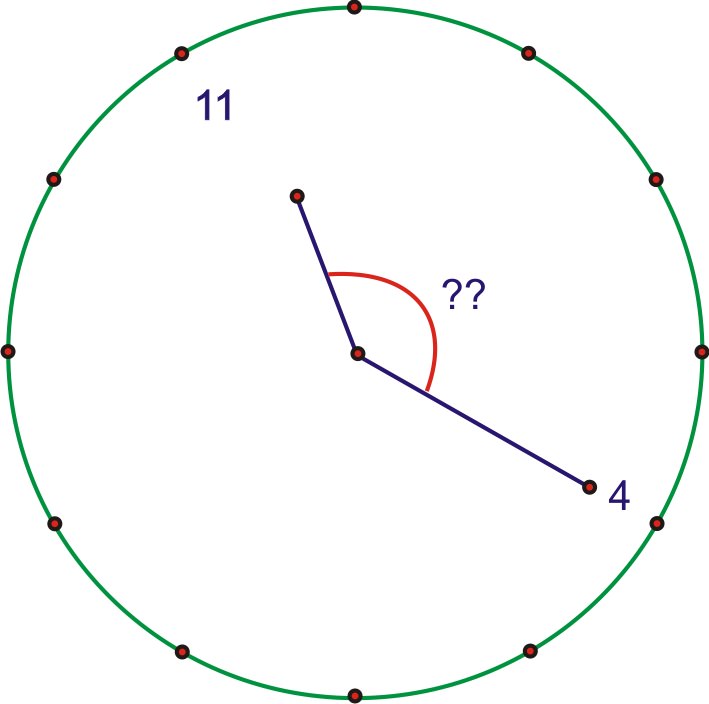
Оскільки на годиннику є 12 кроків, кут між кожною годиною маркування на годиннику є\(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (або\(30^{\circ} \)). Отже, кут між 12 і 4 дорівнює\(4\times \dfrac{\pi }{6}=\dfrac{2\pi }{3}\) (або\(120^{\circ}\)). Оскільки обертання від 12 до 4 становить одну третину повного обертання, здається розумним припустити, що годинна стрілка рухається безперервно і тому перемістилася на третину відстані між 11 і 12. Це означає, що кут між годинною стрілкою і 12 становить дві третини відстані між 11 і 12. Отже\(\dfrac{2}{3}\times \dfrac{\pi }{6}=\dfrac{2\pi }{18}=\dfrac{\pi }{9}\), і загальна міра кута тому\(\dfrac{\pi }{9}+\dfrac{2\pi }{3}=\dfrac{\pi }{9}+\dfrac{6\pi }{9}=\dfrac{7\pi }{9}\).
2. Експрес в радіанах
Стрілки годинника показують 4:15. Висловіть гострий кут, утворений годинною та хвилинною стрілками в радіанову міру.
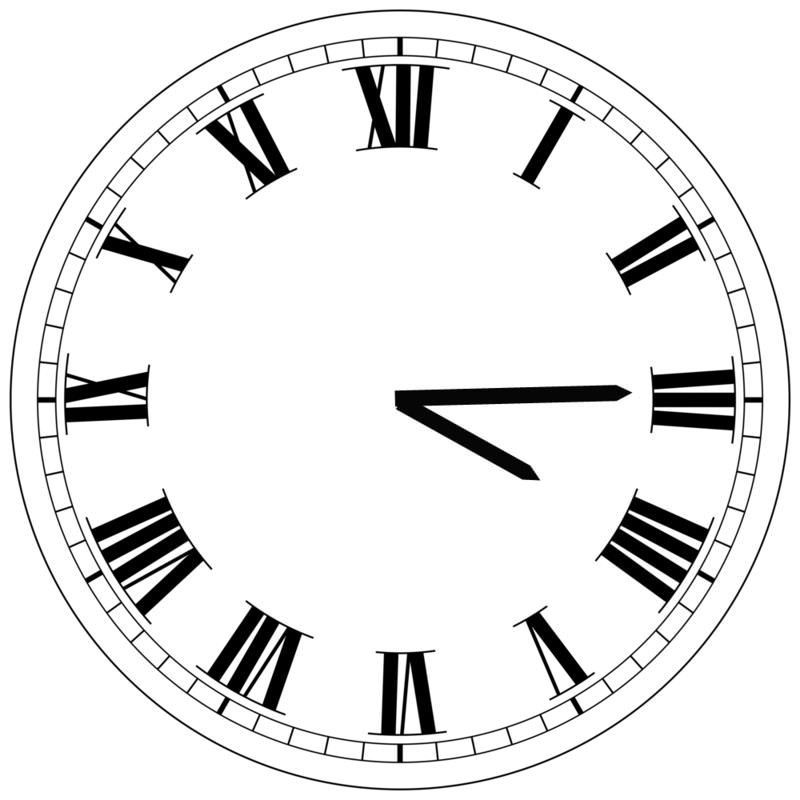
Оскільки на годиннику є 12 кроків, кут між кожною годиною маркування на годиннику є\(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (або\(30^{\circ} \)). Отже, кут між 3 (де знаходиться хвилинна стрілка, коли вона 15 хвилин після години) і 4 є\(\dfrac{\pi }{6}\) (або\(30^{\circ}\)). Далі, оскільки хвилинна стрілка перемістилася на чверть шляху навколо години, ми можемо зробити висновок, що годинна стрілка перемістилася на одну чверть шляху між чотирма і п'ятьма, тобто\(\dfrac{1}{4}\times \dfrac{\pi }{6}=\dfrac{\pi }{24}\). Додавання цих чисел дає:\(\dfrac{\pi }{6}+\dfrac{\pi }{24}=\dfrac{4\pi }{24}+\dfrac{\pi }{24}=\dfrac{5\pi }{24}\).
3. Стрілки годинника показують 2:30. Висловіть гострий кут, утворений годинною та хвилинною стрілками в радіанову міру.
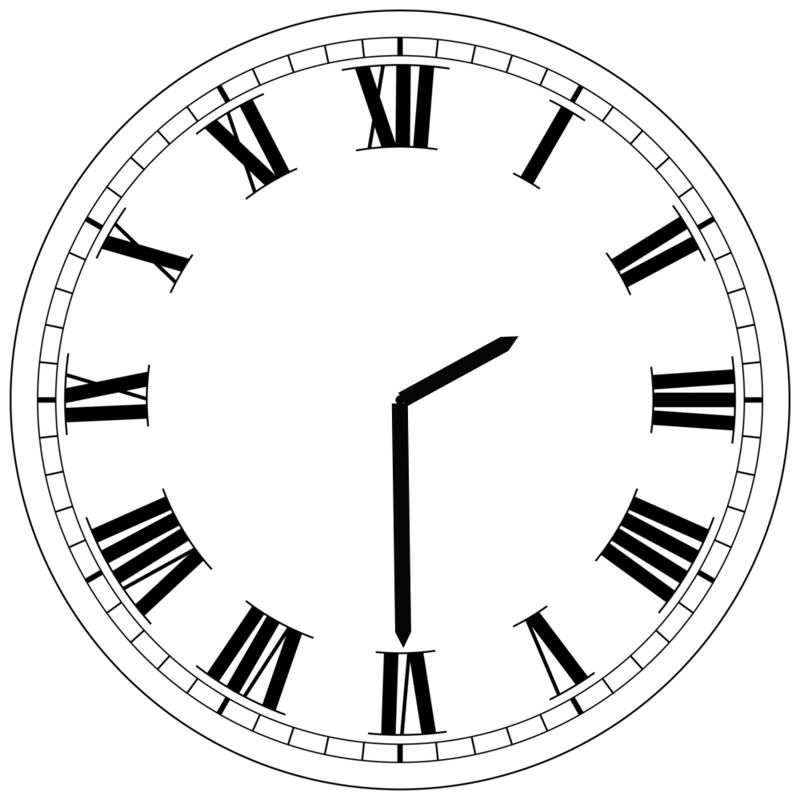
Оскільки на годиннику є 12 кроків, кут між кожною годиною маркування на годиннику є\(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (або\(30^{\circ} \)). Оскільки годинна стрілка насправді буде частиною між 2 і 3 в 2:30, почніть з визначення кутової відстані між 3 і 6, то ви можете додати додаткову частину між 2 і 3:
- Кут між 3 і 6 (де хвилинна стрілка знаходиться на 30 хвилин після години) є\(3\times \dfrac{\pi }{6}=\dfrac{3\pi }{6}=\dfrac{\pi }{2}\) (або\(90^{\circ} \)).
- Оскільки обертання від 12 до 6 становить половину повного обертання, здається розумним припустити, що годинна стрілка рухається безперервно і тому перемістилася на половину відстані між 2 і 3. Це означає, що кут між годинною стрілкою і 3 становить половину відстані між 2 і 3. Отже,\(\dfrac{1}{2}\times \dfrac{\pi }{6}=\dfrac{\pi }{12}\).
- Таким чином, загальна міра кута є\(\dfrac{\pi }{12}+\dfrac{\pi }{2}=\dfrac{\pi }{12}+\dfrac{6\pi }{12}=\dfrac{7\pi }{12}\).
Раніше вас запитали, чи можна визначити кут між двома стрілками годинника.
Рішення
Оскільки тепер ви знаєте, що кут між годинами на годиннику є\(\dfrac{\pi }{6}=30^{\circ} \), ви можете використовувати цю інформацію для побудови відповіді. Є три години між 9 і 12 на годиннику, тому відповідь:
\(3\times \dfrac{\pi }{6}=\dfrac{3\pi }{6}=\dfrac{\pi }{2}=90^{\circ}\)
Таким чином, є\(90^{\circ} \) градуси між 9 і 12 на годиннику.
На наступному зображенні показаний 24-годинний годинник.

Який кут між кожним числом годин виражений точною радіановною мірою в терміні\(\pi \)?
Рішення
Так як в колі є\(2\pi \) радіани, а є 24 окремих приросту, відповідь\(\dfrac{2\pi }{24}=\dfrac{\pi }{12}\)
Який кут між кожним числом годин виражений до найближчої десятої частини радіана? А як щодо ступеня міри?
Рішення
Так як в колі є\(2\pi \) радіани, то кількість радіанів в кожному з 24 різних поділів дорівнює\(\dfrac{2\pi }{24}\approx .3\). У градусах ми можемо зробити те ж саме, взявши кількість градусів в колі і розділивши його на 12:\(\dfrac{360}{24}=15^{\circ} \).
Оцініть міру кута між руками в показаний час до найближчого цілого градуса. А потім в радіані міра в перерахунку\(\pi \).
Рішення
\(20^{\circ} \). Відповіді можуть відрізнятися, все, що вище\(15^{\circ} \) і менше, ніж\(25^{\circ} \) є розумним. У радіанах це і є\(\dfrac{\pi }{9}\). Знову ж таки, відповіді можуть відрізнятися.
Рецензія
Використовуйте годинник нижче, щоб допомогти вам знайти кут між годинною стрілкою і хвилинною стрілкою в кожен з наступних разів. Висловіть свою відповідь в градусах менше, ніж\(180^{\circ} \). Потім висловіть свою відповідь в радіанову міру з точки зору\(\pi \).
- 3:30
- 5:15
- 4:45
- 6:30
- 6:15
- 2:30
- 12:30
- 9:30
- 10:15
- 11:30
- 3:45
- 2:15
- 7:15
- Скільки разів за 12 годин буде перекриватися годинна і хвилинна стрілки?
- Коли перший раз після 12:00 годинна і хвилинна стрілки будуть точно перекриватися?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 2.4.
Лексика
| Термін | Визначення |
|---|---|
| радіан | Радіан - це одиниця кута, яка дорівнює куту, створеному в центрі кола, дуга якого по довжині дорівнює радіусу. |