2.5.1: Радіан міра
- Page ID
- 54775
Вимірюйте кут в колі, де довжина дуги дорівнює радіусу.
Працюючи над експериментом у вашій шкільній науковій лабораторії, ваш вчитель просить вас включити детектор, обертаючи\(\dfrac{\pi}{2}\) радіани ручки. Ви відразу спантеличені, оскільки не знаєте, що таке радіанова міра або як далеко повернути ручку.
міра радіанів
До сих пір ми використовували градуси для вимірювання кутів. Але, що саме таке ступінь? \(\dfrac{1}{360^{th}}\)Ступінь - це повне обертання навколо кола. Радіани - це альтернативні одиниці, що використовуються для вимірювання кутів в тригонометрії. Так само, як це звучить, радіан заснований на радіусі кола. Один радіан (скорочено рад) - кут, створений шляхом вигину довжини радіуса навколо дуги кола. Оскільки радіан заснований на фактичній частині кола, а не довільному поділі, це набагато більш природна одиниця виміру кута для математики верхнього рівня.
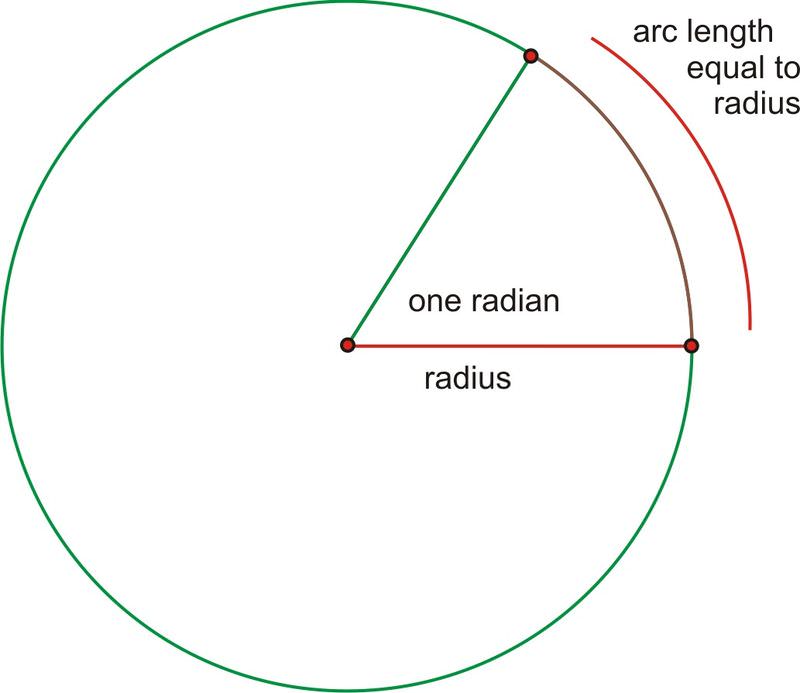
Що робити, якби ми оберталися весь шлях навколо кола? Продовжуючи додавати довжини радіуса, ми виявляємо, що для завершення обертання потрібно трохи більше 6 з них.
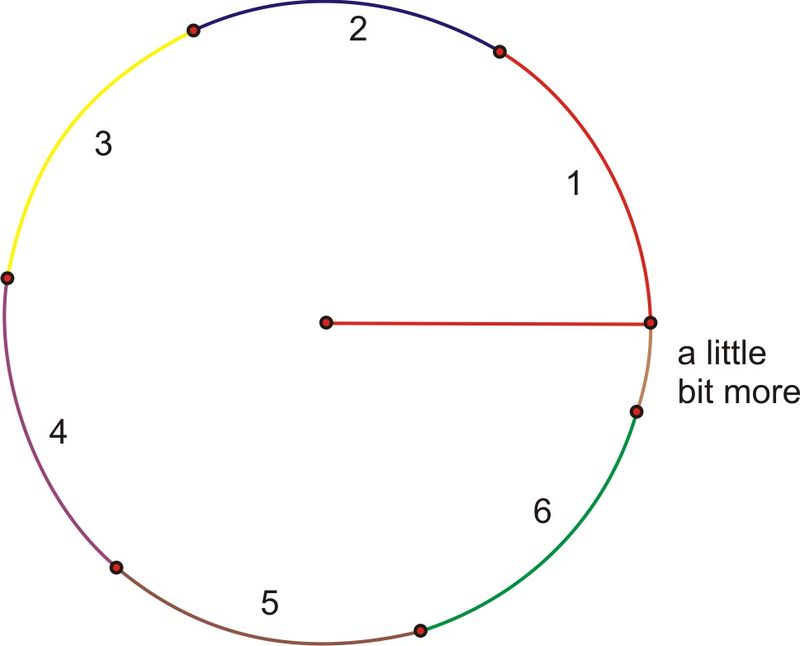
Нагадаємо з геометрії, що довжина дуги повного обертання - це окружність, де формула дорівнює довжині радіуса в\(2\pi\) рази. \(2\pi\)становить приблизно 6,28, тому довжина окружності трохи більше 6 радіусних довжин. Або, з точки зору радіанової міри, повне обертання (360 градусів) - це\(2\pi\) радіани.
\(360\text{ degrees}=2\pi \text{ radians}\)
Маючи це як відправну точку, ми можемо знайти радіанну міру інших кутів. Половина обертання, або 180 градусів, повинні бути\(\pi\) радіани, а 90 градусів повинні бути\(\dfrac{1}{2}\pi\), написані\(\dfrac{\pi}{2}\).
Продовжуючи радіанну міру повз перший квадрант, квадратні кути були визначені, крім\(270^{\circ} \). Тому що\(270^{\circ}\) знаходиться на півдорозі між\(180^{\circ} \) (\(\pi\)) і\(360^{\circ} \) (\(2\pi\)), він повинен бути\(1.5\pi\), як правило, написаний\(\dfrac{3\pi}{2}\).
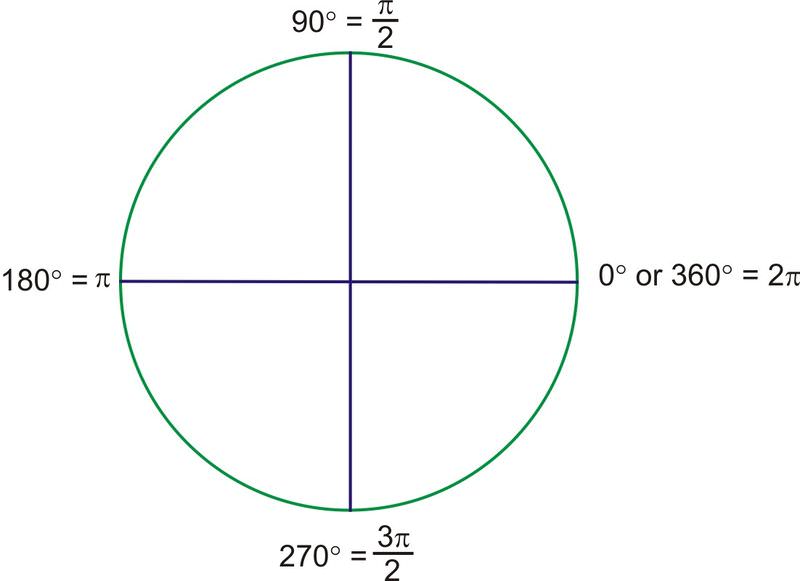
Для\(45^{\circ}\) кутів радіани всі кратні\(\dfrac{\pi}{4}\).
Наприклад,\(135^{\circ}\) є\(3\cdot 45^{\circ}\). Тому радіановна міра повинна бути\(3\cdot \dfrac{\pi}{4}\), або\(\dfrac{3\pi}{4}\). Ось решта кратних\(45^{\circ}\), в радіанах:
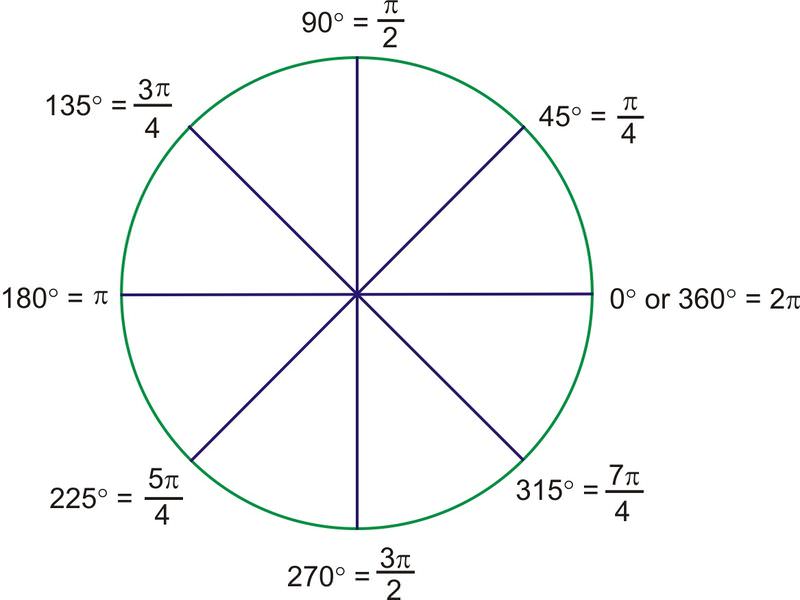
Зверніть увагу, що додаткові кути на кресленні мають опорні кути 45 градусів, а їх радіановні міри кратні\(\dfrac{\pi}{4}\). Всі парні кратні є квадратними кутами і зменшуються, як і будь-який інший дріб.
Давайте зробимо деякі проблеми, які передбачають радіановні заходи.
1. Знайдіть радіановну міру цих кутів.
| Кут в градусах | Кут в радіанах |
|---|---|
| 90 | \(\dfrac{\pi}{2}\) |
| 45 | |
| 30 |
Оскільки 45 є половиною 90, половина\(\dfrac{1}{2}\pi\) є\(\dfrac{1}{4}\pi\). 30 становить одну третину прямого кута, тому множення дає:
\(\dfrac{\pi}{2}\times \dfrac{1}{3}=\dfrac{\pi}{6}\)
і тому, що 60 в два рази більше 30:
\(2\times \dfrac{\pi}{6}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\)
Ось заповнена таблиця:
| Кут в градусах | Кут в радіанах |
|---|---|
| 90 | \(\dfrac{\pi}{2}\) |
| 45 | \(\dfrac{\pi}{4}\) |
| 30 | \(\dfrac{\pi}{6}\) |
Існує формула перетворення між радіанами та градусами, яку ви, можливо, вже виявили під час виконання цього прикладу. Однак багато кутів, які зазвичай використовуються, можна легко знайти за значеннями в цій таблиці. Наприклад, більшість студентів вважають, що легко запам'ятати 30 і 60. 30\(\pi\) старше 6, а 60\(\pi\) більше 3. Знаючи ці кути, ви можете знайти будь-який із спеціальних кутів, які мають опорні кути 30 та 60, оскільки всі вони матимуть однакові знаменники. Те ж саме стосується кратних\(\dfrac{\pi}{4}\) (45 градусів) і\(\dfrac{\pi}{2}\) (90 градусів).
2. Виконайте наступні радіанові заходи, підрахувавши в кратних\(\dfrac{\pi}{3}\) і\(\dfrac{\pi}{6}\):
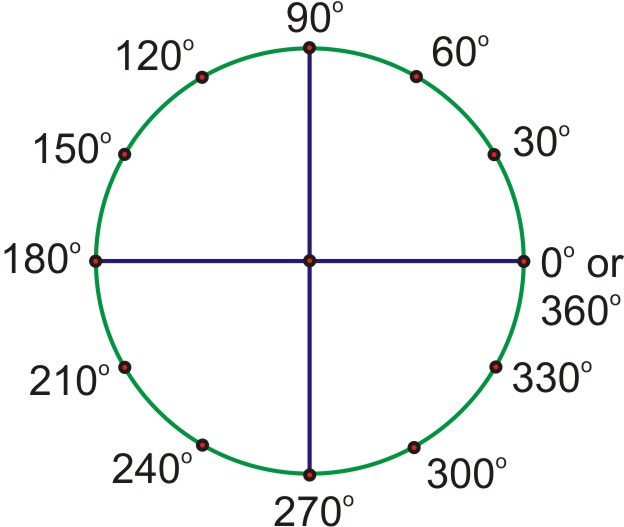
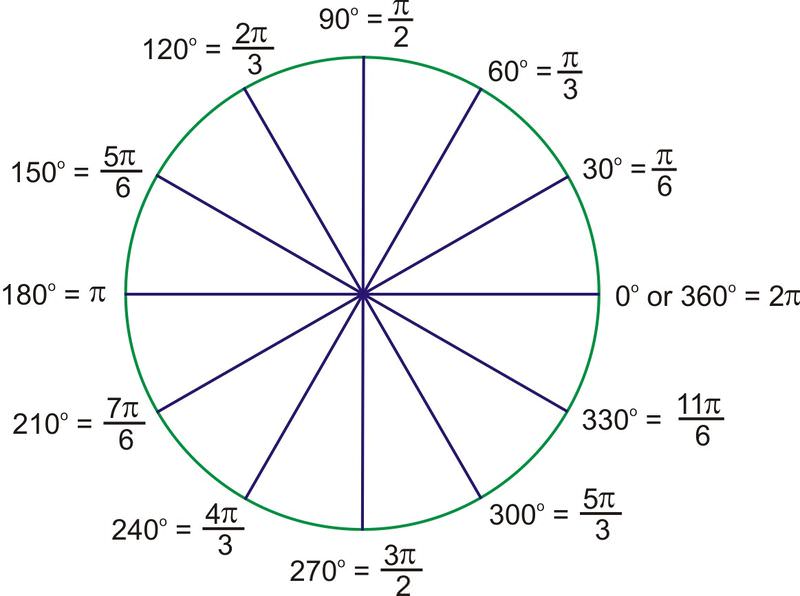
Зверніть увагу, що всі кути з 60-градусні опорні кути кратні\(\dfrac{\pi}{3}\), і всі з 30-градусних опорних кутів кратні\(\dfrac{\pi}{6}\). Підрахунок цих термінів на основі цієї моделі, а не перетворення назад в градуси, допоможе вам краще зрозуміти радіани.
3. Знайдіть радіановну міру цих кутів.
| Кут в градусах | Кут в радіанах |
|---|---|
| 120 | \(\dfrac{2 \pi}{3}\) |
| 180 | |
| 240 | |
| 270 | |
| 300 |
Оскільки 30 - це третина прямого кута, множення дає:
\(\dfrac{\pi}{2}\times 13=\dfrac{\pi}{6}\)
додавши це до відомого значення для дев'яноста градусів\(\dfrac{\pi}{2}\):
\(\dfrac{\pi}{2}+\dfrac{\pi}{6}=3\dfrac{\pi}{6}+\dfrac{\pi}{6}=4\dfrac{\pi}{6}=\dfrac{2 \pi}{3}\)
Ось заповнена таблиця:
| Кут в градусах | Кут в радіанах |
|---|---|
| 120 | \(\dfrac{2\pi}{3}\) |
| 180 | \(\pi\) |
| 240 | \(\dfrac{4\pi}{3}\) |
| 300 | \(\dfrac{5\pi}{3}\) |
Раніше вам давали проблему з приводу обертання ручки.
Рішення
З тих пір\(45^{\circ} =\dfrac{\pi}{4} \text{ rad}\)\(2\times \dfrac{\pi}{4}=\dfrac{\pi}{2}=2\times 45^{\circ}\). Тому поворот\(\dfrac{\pi}{2}\) дорівнює тому\(90^{\circ}\), який є\(\dfrac{1}{4}\) повним обертанням ручки.
Дайте радіану міру\(60^{\circ}\)
Рішення
30 - це третина прямого кута. Це означає, що з тих пір\(90^{\circ} =\dfrac{\pi}{2}\)\(30^{\circ} =\dfrac{\pi}{6}\). Тому множення дає:
\(\dfrac{\pi}{6}\times 2=\dfrac{\pi}{3}\)
Дайте радіану міру\(75^{\circ}\)
Рішення
15 - одна шоста прямокутного трикутника. Це означає, що з тих пір\(90^{\circ} =\dfrac{\pi}{2}\)\(15^{\circ} =\dfrac{\pi}{12}\). Тому множення дає:
\(\dfrac{\pi}{12}\times 5=\dfrac{5\pi}{12}\)
Дайте радіану міру\(180^{\circ}\)
Рішення
З тих пір\(90^{\circ} =\dfrac{\pi}{2}\)\(180^{\circ} =\dfrac{2\pi}{2}=\pi\)
Рецензія
Знайдіть радіановну міру кожного кута.
- \(90^{\circ}\)
- \(120^{\circ}\)
- \(300^{\circ}\)
- \(330^{\circ}\)
- \(−45^{\circ}\)
- \(135^{\circ}\)
Знайдіть градусну міру кожного кута.
- \(\dfrac{3\pi}{2}\)
- \(\dfrac{5\pi}{4}\)
- \(\dfrac{7\pi}{6}\)
- \(\dfrac{\pi}{6}\)
- \(\dfrac{5\pi}{3}\)
- \(\pi\)
- Поясніть, чому, якщо вам дано кут в градусах і ви помножите його на\(\dfrac{\pi}{180}\) ви отримаєте той же кут в радіанах.
- Поясніть, чому, якщо вам дано кут в радіанах і ви помножите його на\(\dfrac{180}{\pi}\) ви отримаєте той же кут в градусах.
- Поясніть своїми словами, чому має сенс, що в колі є\(2\pi\) радіани.
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.1.
Лексика
| Термін | Визначення |
|---|---|
| радіан | Радіан - це одиниця кута, яка дорівнює куту, створеному в центрі кола, дуга якого по довжині дорівнює радіусу. |