Skip to main content
LibreTexts - Ukrayinska

2.5.6: Довжина дуги

  1. Last updated
  2. Save as PDF
  • Page ID
    54754

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Радіус умножує кут в радіанах.

    Ви взяли свого маленького двоюрідного брата в парк розваг на день. Перебуваючи там, вона вирішує, що хотіла б покататися на каруселі. Після їзди вона схвильовано підстрибує до вас. Вона вражена тим, що вона обійшла, але певним чином «нікуди не пішла», оскільки вона опинилася там, де почала.

    «Як далеко я зайшов, коли був на півдорозі навколо повороту?» , запитує вона.

    Ви знаєте, що радіус каруселі становить 7 метрів. Чи можете ви сказати своїй маленькій двоюрідній сестрі, як далеко вона зайшла в одну половину обороту навколо їзди?

    Довжина дуги на колі залежить як від кута повороту, так і від радіусної довжини кола. Якщо згадати з минулого уроку, міра кута в радіанах визначається як довжина дуги, відрізаної на одну довжину радіуса. Що робити, якщо радіус дорівнює 4 см? Потім довжину дуги півкола\(\pi \) помножити на довжину радіуса, або\(4\pi \) см в довжину.

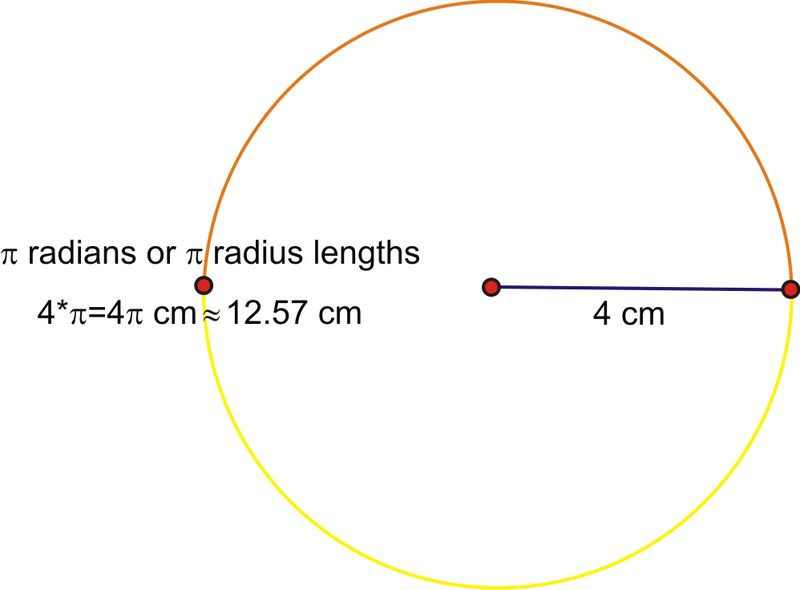
    Ф-Д_0С88Б2ДК 06Е408766С18782А7Б86ФЦК7750ААААА9А07Е71 Е6ФЕ5Ф07Е+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{1}\)

    В результаті утворюється формула, за допомогою якої можна обчислити довжину будь-якої дуги.

    \(s=r\theta \),

    де s - довжина дуги, r - радіус, а\ theta - міра кута в радіанах.

    Розв'язування цього рівняння для\(\theta \) дасть нам формулу для знаходження радіановної міри з урахуванням довжини дуги та довжини радіуса.

    Давайте розглянемо деякі проблеми, пов'язані з довжиною дуги.

    1. Знайти довжину дуг

    Лінія штрафного кидка на баскетбольному майданчику NCAA шириною 12 футів. У міжнародному змаганні це лише близько 11,81 футів. Скільки довше півкола над лінією штрафного кидка на корті NCAA?

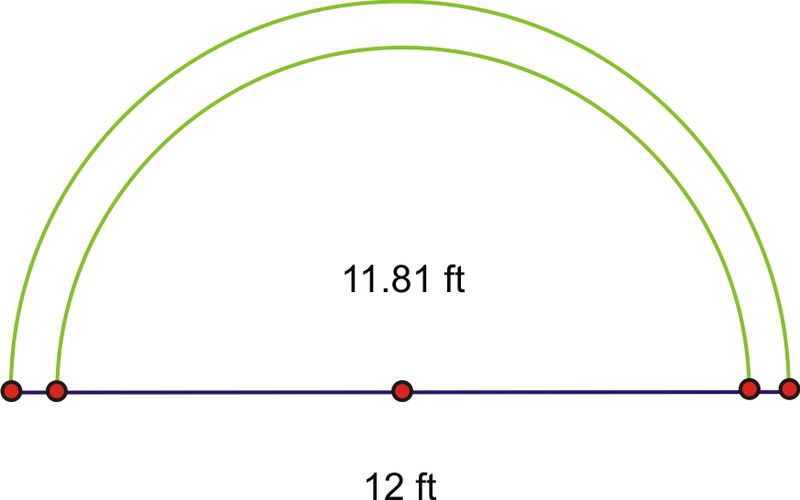
    Ф-Д_443793АААФ 61 БЕКАБ 65С243Ф0Ф1А1Д20А6Д4760 СБ6 С72333ДК4Б7CF+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{2}\)

    Знайдіть обидві довжини дуги.

    \ (\ begin {масив} {l}
    \ текст {NCAA} &\ текст {МІЖНАРОДНИЙ}\\
    s_ {1} =r\ тета & s_ {2} =r\ тета\\
    s_ {1} =\ dfrac {12} {2} (\ pi) & s_ {2}\ приблизно\ dfrac {11.81} {2} (\ пі)\\
    s_ {1} =6\ pi & s_ {2}\ приблизно 5.905\ pi
    \ end {масив}\)

    Отже, відповідь приблизно\(6\pi −5.905\pi \approx 0.095\pi\)

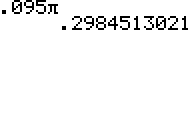
    F-D_38D39С54Б04821Б24D0CC0 КАДА7249С6АДЕ 78БА 66794933 ЕФ00Б15Ф+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Це приблизно 0.3 фута, або приблизно 3.6 дюйма довше.

    2. Дві з'єднані шестерні обертаються. Менша передача має радіус 4 дюйми, а більший радіус передачі - 7 дюймів. Який кут, через який оберталася більша шестерня, коли менша шестерня зробила одне повне обертання?

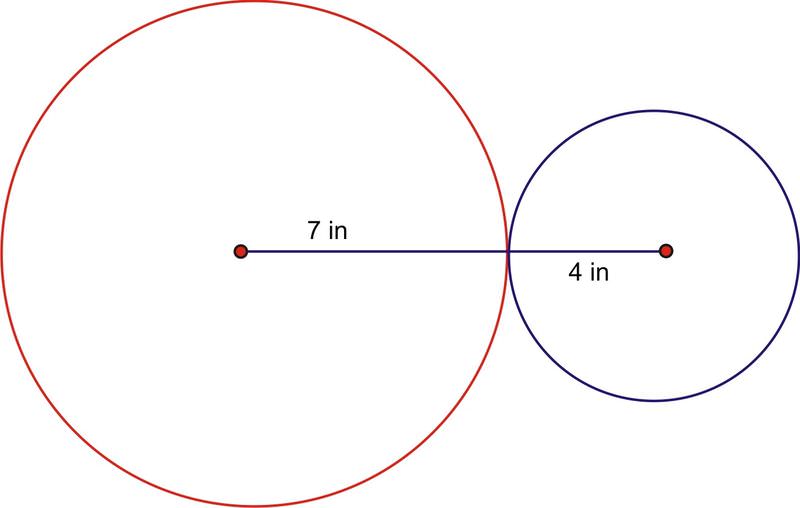
    F-д_АБА 79755Б1ЕЕ3Е296Д171С68018 ЕФ801ДА501Д791 де 69ФД9Е54+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{4}\)

    Оскільки синя шестерня виконує одне повне обертання, довжина пройденої дуги становить:

    \(\begin{aligned} s &=r\theta \\ s&=4\times 2\pi \end{aligned}\)

    Отже, довжина\(8\pi \) дуги на більшому колі утворювала б кут наступним чином:

    \(\begin{aligned} \theta &=\dfrac{s}{r} \\ \theta &=\dfrac{8\pi }{7} \\ \theta &\approx 3.6 \end{aligned}\)

    Так кут дорівнює приблизно 3,6 радіана.

    \(3.6\times 180\pi \approx 206^{\circ}\)

    3. Радіус стандартної автомобільної шини становить 27,94 см. Як далеко заходить автомобіль за один оборот шини?

    Ф-Д_10ФЦ4Д51Ф6Б0Ф7 ДеБ8278Б2174748CA42766Е7С4ДА 60442Б4647865+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{5}\)

    Оскільки відстань, пройдене шиною, дорівнює відстані навколо шини, ми можемо використовувати окружність шини, щоб відповісти на питання.

    \(\begin{aligned} s &=r\theta \\ s&=(27.94)(2\pi )\\s=175.46 \end{aligned}\)

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, чи можете ви сказати своїй маленькій двоюрідній сестрі, як далеко вона зайшла в одну половину обороту навколо їзди.

    Рішення

    Оскільки ви тепер знаєте, що ви можете виміряти довжину дуги за допомогою\(s=r\theta \), ви можете використовувати це, щоб знайти рішення питання вашого двоюрідного брата. Так як ваша двоюрідна сестра хоче знати, як далеко вона зайшла\(\dfrac{1}{2}\), коли пішла обертання, а радіус їзди становить 7 метрів, ви можете обчислити її довжину дуги:

    \(s=r\theta =7\pi \approx 21.98 \text{ meters}\)

    Приклад\(\PageIndex{2}\)

    Ви намагаєтеся підштовхнути свій автомобіль після того, як він зламався. На жаль, ви не дуже сильні, і тому машина просто гойдається вперед і назад замість того, щоб котитися, як ви натискаєте. Якщо радіус шини вашого автомобіля становить 14 дюймів, а зміна кута шини -\(\dfrac{\pi}{2}\) радіани, як далеко просунулася шина?

    Рішення

    Так як відстань, на яку переміщається шина, дорівнює довжині дуги, яку прокотила шина, можна скористатися рівнянням s=r\ theta, щоб визначити, як далеко зайшла шина:

    \(\begin{aligned} s&=r\theta \\ s&=(14)\left(\dfrac{\pi}{2}\right) \\ s&=7\pi \\ s&\approx 21.98 \text{ in}\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Якщо предмет радіусом 10 см крутиться так, що його дуга охоплює 54 см, яка зміна кута нахилу предмета?

    Рішення

    Ви знову можете використовувати рівняння\(s=r\theta \) для вирішення цієї задачі:

    \(\begin{aligned} s&=r\theta \\ \theta &=\dfrac{s}{r}=\dfrac{54}{10}=5.4 \end{aligned}\)

    Диск рухається на 5,4 радіана, що трохи менше повного обертання, так як повне обертання становить приблизно 6,28 радіана.

    Приклад\(\PageIndex{4}\)

    Якщо ваш DVD має радіус 4.5 дюймів, як далеко знаходиться точка на диску, якщо плеєр повертає його\ dfrac {\ pi} {2} радіани?

    Рішення

    Використовуючи\(s=r\theta \),

    \(\begin{aligned} s&=r\theta \\ s&=(4.5)\left(\dfrac{\pi }{2}\right) \\ s&=2.25\pi \approx 7.065\end{aligned}\)

    А точка на диску виходить 7,065 дюйма.

    Рецензія

    Радіус дії каруселі становить 8 метрів. Використовуйте цю інформацію, щоб відповісти на питання 1-3.

    1. Ви на півдорозі навколо каруселі. Як далеко ви подорожували?
    2. Ви весь шлях навколо каруселі. Як далеко ви подорожували?
    3. Тепер ви проїхали весь шлях навколо каруселі двічі. Як далеко ви подорожували?

    Піца має радіус 10 дюймів. Використовуйте цю інформацію, щоб відповісти на питання 4-6.

    1. Зріз видаляється. Довжина скоринки відсутнього скибочки становить 3 дюйма. Який центральний кут відсутнього зрізу?
    2. Ви їсте три штуки з центральним кутом\(\dfrac{4\pi }{5}\). Яку довжину скоринки ви їли?
    3. Велика піца має радіус дії 12 дюймів. Яка довжина скоринки половини великої піци?

    Діаметр шини становить 35 дюймів. Використовуйте цю інформацію, щоб відповісти на 7-10 питань.

    1. Яка довжина навколо всієї шини?
    2. Шина проїжджає одну милю (5280 футів). Скільки оборотів зробила шина?
    3. Ви котите шину, щоб вона\(7\pi \) оберталася радіани. Як далеко він рухався?
    4. Шина проїжджає півмилі. На скільки радіанів оберталася шина?

    Розглянемо стандартні годинники на 12 годин, як наведені нижче з радіусом 5 дюймів. Використовуйте це, щоб відповісти на питання 11-15.

    Ф-Д_7Б33667 КФ 316ЕБ48Ф115Е35Е29Б46Ф2ЕБА3А199АЕ 25САА 96205Д3ЕС+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{6}\)
    1. Яка довжина дуги між 3 і 7?
    2. Яка довжина дуги між 3 і 2?
    3. Це 12:30. Яка довжина дуги між хвилинною і годинною стрілками?
    4. Це 7:20. Яка довжина дуги між хвилинною і годинною стрілками?
    5. Це 1:25. Яка довжина дуги між хвилинною і годинною стрілками?

    Огляд (Відповіді)

    Щоб переглянути Рецензію, відкрийте цей PDF-файл і знайдіть розділ 2.5.

    Лексика

    Термін Визначення
    Дуга Дуга - це ділянка окружності кола.