2.5.5: Кутова швидкість

Перетворення між лінійними та кутовими швидкостями за допомогою радіуса та окружності.

Щоб знайти певну пісню на плеєрі MP3/MP4, ви можете скористатися колесом прокрутки. Це передбачає переміщення пальця навколо колеса круговими рухами. На жаль для вас, пісня, яку ви хочете, знаходиться в самому низу списку ваших пісень. Оскільки ці медіаплеєри часто можуть містити понад 1000 пісень, вам доведеться швидко прокручувати! Коли ви рухаєте пальцем по колу, ви можете задатися питанням, чи можете ви виміряти, наскільки швидко ваш палець охоплює відстань по колу.

Спостерігаючи за пальцем, розумієш, що ваш палець рухається по колу двічі кожну секунду. Якщо радіус колеса прокрутки становить 2 см, яка кутова швидкість вашого пальця під час прокручування списку пісень? Що таке лінійна швидкість?

Можливо, ви вже знайомі з вимірюванням швидкості як співвідношення відстані об'єкта, пройденого до часу, коли він перебував у русі. Однак це співвідношення стосується об'єктів, які рухаються по прямій лінії. А як щодо об'єктів, які подорожують по круговому шляху?

Ви пам'ятаєте, як грали на каруселі, коли ви були молодшими?

Малюнок$\PageIndex{1}$

Якщо по зовнішньому краю їздять дві людини, їх швидкості повинні бути однаковими. Але, що робити, якщо одна людина знаходиться близько до центру, а інша людина знаходиться на краю? Вони знаходяться на одному об'єкті, але їх швидкість насправді не однакова.

Подивіться на наступний малюнок.

Малюнок$\PageIndex{2}$

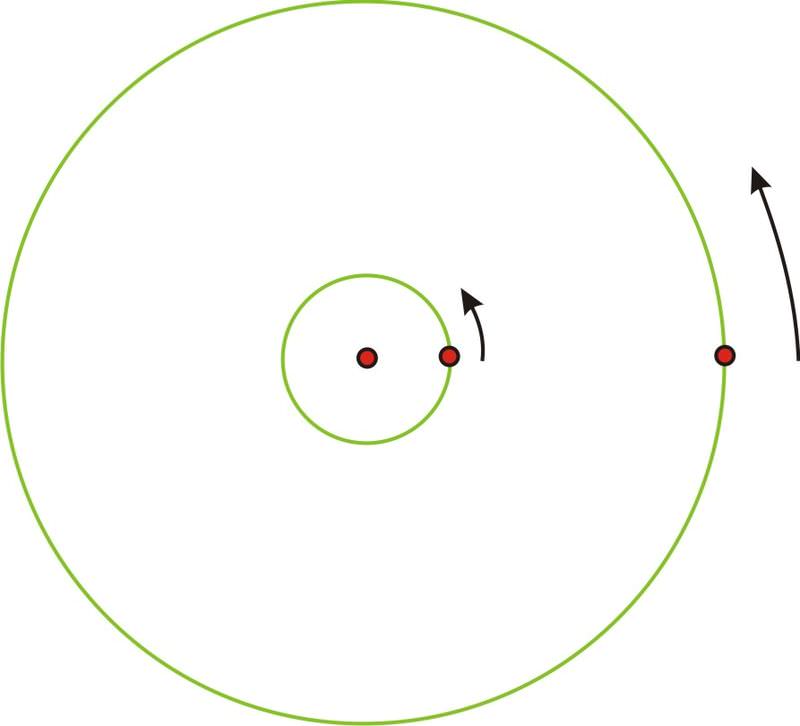
Уявіть, що точка на більшому колі - це людина на краю каруселі, а точка на меншому колі - людина до середини. Якщо карусель крутиться рівно один раз, то обидві особи також зроблять один повний оборот за однакову кількість часу.

Однак очевидно, що людина в центрі не подорожував майже так далеко. Окружність (і, звичайно, радіус) цього кола набагато менша, і тому людина, яка пройшла більшу відстань за ту ж кількість часу, насправді подорожує швидше, хоча вони знаходяться на одному об'єкті. Таким чином, людина на краю має більшу лінійну швидкість (нагадаємо, що лінійна швидкість знаходиться за допомогою distance=rate ⋅ час). Якщо ви коли-небудь насправді їздили на каруселі, ви знаєте це вже тому, що набагато веселіше бути на краю, ніж в центрі! Але є щось про двох людей, які подорожують навколо, це те ж саме. Вони обидва будуть охоплювати одне і те ж обертання за один і той же проміжок часу. Цей тип швидкості, що вимірює кут повороту за задану кількість часу, називається кутовою швидкістю.

Формула кутової швидкості така:

$\omega =\dfrac{\theta }{t}$

$\omega$є останньою буквою грецького алфавіту, омега, і зазвичай використовується як символ кутової швидкості. \ theta - кут повороту, виражений в радіановій мірі, а t - час завершення обертання.

Малюнок$\PageIndex{3}$

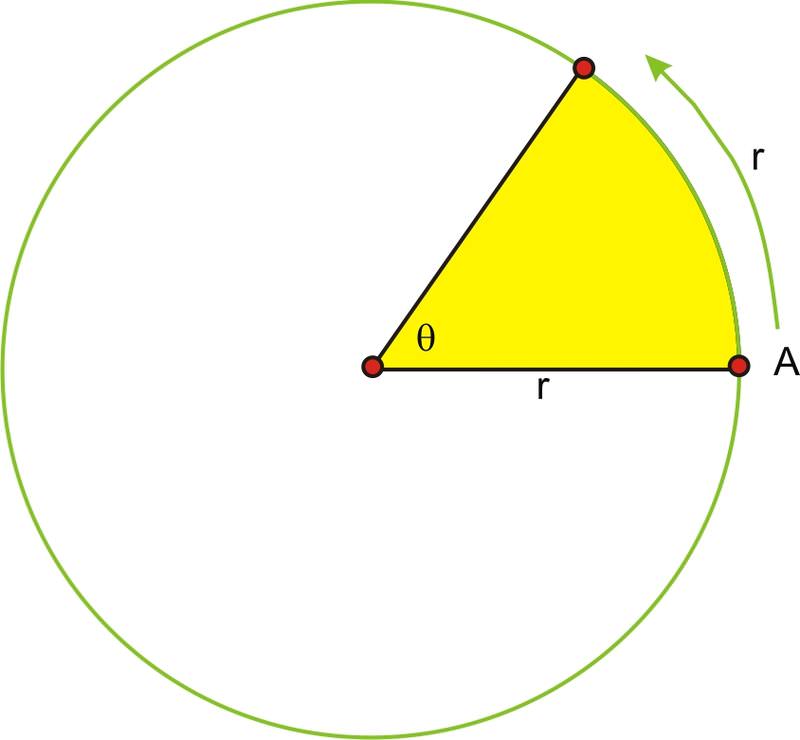
На цьому кресленні$\theta$ рівно один радіан, або довжина радіуса, зігнутого по колу. Якби точка А знадобилася рівно 2 секунди для повороту через кут, кутова швидкість А буде такою:

$\begin{aligned} \omega &=\dfrac{\theta }{t}\\ \omega &=\dfrac{1}{2} \text{ radians per second} \end{aligned}$

Для того, щоб знати лінійну швидкість частинки, нам доведеться знати фактичну відстань, тобто довжину радіуса. Припустимо, радіус дорівнює 5 см.

Якщо лінійна швидкість дорівнює v=dt, то,$v=\dfrac{5}{2}$ або$2.5 \text{ cm per second}$.

Якщо кут дорівнював рівно не 1 радіану, то відстань, пройдене точкою на колі, - це довжина дуги$s=r\theta$, або, довжина радіуса разів перевищує міру кута в радіанах.

Підстановка в формулу лінійної швидкості дає:$v=\dfrac{r\theta }{t}$ або$v=r\cdot \dfrac{\theta }{t}$.

Озирніться назад на формулу кутової швидкості. Підстановка$\omega$ дає наступну залежність між лінійною і кутовою швидкістю,$v=r\omega$. Отже, лінійна швидкість дорівнює радіусу, кратному кутовій швидкості.

Пам'ятайте, що в одиничному колі радіус дорівнює 1 одиниці, тому в цьому випадку лінійна швидкість така ж, як і кутова.

$\begin{aligned} v &=r\omega \\ v&=1\times \omega \\ v&=\omega \end{aligned}$

Тут відстань, пройдене по колу, таке ж за задану одиницю часу, що і кут повороту, виміряний в радіанах.

Обчислення лінійної та кутової швидкості

1. Ліндсей і Меган їдуть на каруселі. Меган стоїть 2,5 футів від центру, а Ліндсі їде по зовнішньому краю 7 футів від центру. Їм потрібно 6 секунд, щоб завершити обертання. Обчисліть лінійну і кутову швидкість кожної дівчини.

Малюнок$\PageIndex{4}$

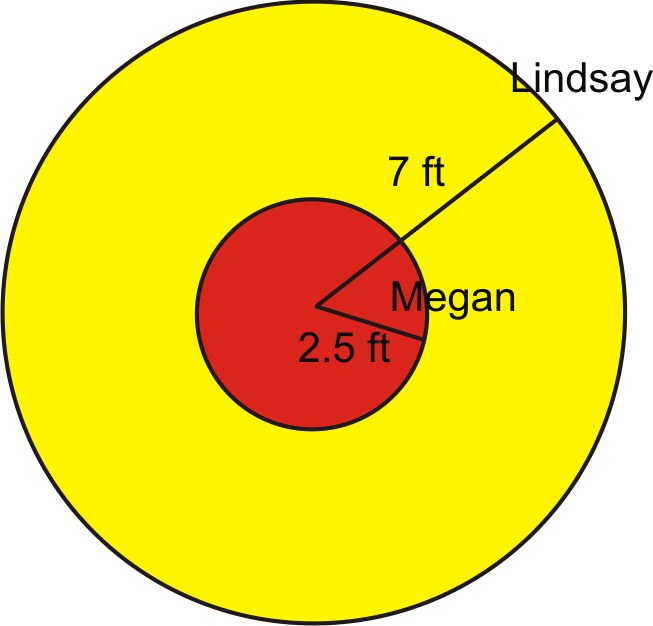
Нам кажуть, що для завершення обертання потрібно 6 секунд. Повне обертання таке ж, як і$2\pi$ радіани. Отже, кутова швидкість дорівнює:

$\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{6}=\dfrac{\pi }{3}$радіанів в секунду, що трохи більше 1 (близько 1,05), радіан в секунду. Оскільки обидві дівчата охоплюють один і той же кут повороту за однакову кількість часу, їх кутова швидкість однакова. При цьому вони обертаються приблизно на 60 градусів кола кожну секунду.

Як ми обговорювали раніше, їх лінійні швидкості різні. Використовуючи формулу, лінійна швидкість Меган дорівнює:

$v=r\omega =(2.5)\left(\dfrac{\pi }{3}\right)\approx 2.6 \text{ ft per sec}$

Ліндсей лінійна швидкість:

$v=r\omega =(7)\left(\dfrac{\pi }{3}\right)\approx 7.3 \text{ ft per sec}$

2. Клоп стоїть біля зовнішнього краю компакт-диска (так, щоб його радіус від центру диска становив 6 см), який обертається. Він помічає, що подорожував$\pi$ радіани за дві секунди. Яка у нього кутова швидкість? Яка у нього лінійна швидкість?

Малюнок$\PageIndex{5}$

Ми знаємо, що рівняння для кутової швидкості

$\omega =\dfrac{\theta }{t}=\dfrac{\pi }{2} \text{ radians per second}$.

Ми можемо використовувати дане рівняння, щоб знайти його лінійну швидкість:

$v=r\omega =(6)(\dfrac{\pi }{2})\approx 9.42 \text{ cm per sec}$

Розв'язування невідомих значень

Скільки часу потрібно помилку в попередній задачі, щоб пройти два повних ходу?

Оскільки кутова швидкість жука дорівнює$\dfrac{\pi }{2}$ радіанам в секунду, ми можемо використовувати рівняння для кутової швидкості і вирішити на час:

$\begin{aligned} \omega &=\dfrac{\theta }{t} \\ t&=\theta \omega \end{aligned}$

Оскільки в двох повних оборотах диска є$4\pi$ радіани, ми можемо використовувати це для значення\ theta:

$t=\dfrac{4\pi }{\dfrac{\pi }{2}}=4\pi \times \dfrac{2}{\pi} =8 \text{ seconds}$

Приклад$\PageIndex{1}$

Раніше вас просили знайти кутову і лінійну швидкість вашого пальця.

Рішення

Як ви з'ясували в цьому розділі, кутова швидкість - це зміна кута, поділена на зміну часу. Так як ви змітаєте по колу два рази в секунду, це стає:

$\omega =\dfrac{4\pi }{1}=4\pi \text{ rad/sec}$

Далі можна знайти лінійну швидкість за допомогою рівняння:

$v=r\omega =(2)(4\pi )=8\pi \approx 25.132 \text{ cm/s}$

Приклад$\PageIndex{2}$

Доріс і Лоїс відправляються кататися на каруселі. Доріс їде на одній із зовнішніх коней, а Лоїс їде на одній з менших коней поблизу центру. Кінь Луї знаходиться в 3 м від центру каруселі, а кінь Доріс знаходиться на 7 м далі від центру, ніж Луа. Коли карусель запускається, їм потрібно 12 секунд, щоб завершити обертання.

Обчисліть лінійну швидкість кожної дівчини. Обчисліть кутову швидкість коней на каруселі.

Рішення

Насправді простіше спочатку обчислити кутову швидкість. $\omega =\dfrac{2\pi }{12}=\dfrac{\pi }{6}$, Таким чином, кутова швидкість -$\dfrac{\pi }{6}$ рад, або$0.524$. Оскільки лінійна швидкість залежить від радіуса, у кожної дівчини своя.

Лоїс:$v=r\omega =3\cdot \dfrac{\pi }{6}=\dfrac{\pi }{2}$ або$1.57 \text{ m/sec}$

Доріс:$v=r\omega =10\cdot \dfrac{\pi }{6}=\dfrac{5 \pi }{3}$ або$5.24 \text{ m/sec}$

Приклад$\PageIndex{3}$

Великий адронний коллайдер поблизу Женеви, Швейцарія, почав експлуатацію в 2008 році і призначений для проведення експериментів, які, як сподіваються фізики, нададуть важливу інформацію про основну структуру Всесвіту. LHC кругової з окружністю приблизно 27 000 м Протони будуть прискорені до швидкості, яка дуже близька до швидкості світла ($\approx 3\times 10^8$метрів в секунду).

Скільки часу потрібно протону, щоб зробити повне обертання навколо колайдера? Яка приблизна (до найближчого метра в секунду) кутова швидкість протона, що рухається навколо коллайдера? Приблизно скільки разів протон об'їжджав би колайдер за одну повну секунду?

Рішення

$v=\dfrac{d}{t}\rightarrow 3\times 10^8=\dfrac{27,000}{t} \rightarrow t= \dfrac{2.7\times 10^4}{3\times 10^8}=0.9\times 10^{−4}=9\times 10^{−5} \text{ or } 0.00009 \text{ seconds}$

$\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{0.00009}\approx 69,813 \text{ rad/sec}$

Протон обертається навколо один раз в 0,00009 секунди. Так, за одну секунду він буде обертатися навколо LHC$1\div 0.00009=11,111.11$ разів, або трохи більше 11 111 обертань.

Приклад$\PageIndex{4}$

Тед стоїть в 2 метрах від центру веселого обходу. Якщо його лінійна швидкість становить 6 м/с, яка його кутова швидкість?

Рішення

Оскільки рівняння, що стосується лінійної та кутової швидкості, задається$v=r\omega$, ми можемо вирішити для омега:$\omega =\dfrac{v}{r}=\dfrac{6}{2}=3$

Рецензія

Бет і Стів знаходяться на каруселі. Бет знаходиться в 7 футах від центру, а Стів знаходиться прямо на краю, 7 футів далі від центру, ніж Бет. Використовуйте цю інформацію та наступну картинку, щоб відповісти на питання 1-6.

Малюнок$\PageIndex{6}$

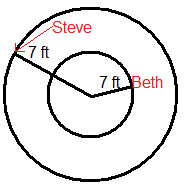
1. Карусель робить повний оборот за 12 секунд. Як далеко зайшла Бет за одну революцію? Як далеко зайшов Стів за одну революцію?
2. Якщо карусель продовжує робити обороти кожні 12 секунд, яка кутова швидкість каруселі?
3. Які лінійні швидкості Бет і Стіва?
4. Як далеко від центру повинна бути Бет, щоб мати лінійну швидкість$\pi$ футів в секунду.
5. Карусель змінюється на нову кутову швидкість$\dfrac{\pi }{3}$ радіанів в секунду. Скільки часу потрібно, щоб зробити повну революцію зараз?
6. З новою швидкістю каруселі, які нові лінійні швидкості Бет і Стіва?
7. Бет і Стів відправляються на іншу карусель, яка має кутову швидкість$\dfrac{\pi }{8}$ радіанів в секунду. Лінійна швидкість Бет -$2\pi$ фути в секунду. Як далеко вона стоїть від центру каруселі?
8. Лінійна швидкість Стіва становить лише$\dfrac{\pi }{3}$ фути в секунду. Як далеко він стоїть від центру каруселі?
9. Що таке кутова швидкість хвилинної стрілки на годиннику? (в радіанах в хвилину)
10. Що таке кутова швидкість годинної стрілки на годиннику? (в радіанах в хвилину)
11. Певний годинник має радіус 1 фут. Яка лінійна швидкість кінчика хвилинної стрілки?
12. На тому ж годиннику, яка лінійна швидкість кінчика годинної стрілки?
13. Кінчик хвилинної стрілки на іншому годиннику має лінійну швидкість 2 дюйми в хвилину. Що таке радіус годинника?
14. Що таке кутова швидкість секундної стрілки на годиннику? (в радіанах в хвилину)
15. Кінчик секундної стрілки на годиннику має лінійну швидкість 2 фути в хвилину. Що таке радіус годинника?

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.8.

Лексика

Термін	Визначення
кутова швидкість	Кутова швидкість - це відношення оборотів, які відбуваються за одиницю часу.
Кутова швидкість	Кутова швидкість обертового об'єкта - це зміна кута об'єкта, поділена на зміну часу.
розмірний аналіз	Розмірний аналіз - це процес перетворення з однієї одиниці в іншу.
лінійна швидкість	Лінійна швидкість - це відношення відстані на одиницю часу.
Лінійна швидкість	Лінійна швидкість об'єкта - це зміна положення об'єкта, поділена на зміну часу.
радіан	Радіан - це одиниця кута, яка дорівнює куту, створеному в центрі кола, дуга якого по довжині дорівнює радіусу.

Додаткові ресурси

Інтерактивний елемент

Відео: Лінійна швидкість і кутова швидкість

Практика: Кутова швидкість

Реальний світ: Побудова імпульсу