1.12:1.12 Зворотні функції
- Page ID
- 54474
Функції широко відомі як правила, які приймають входи і виробляють виходи. I обернена функція робить саме зворотне, скасовуючи те, що робить оригінальна функція. Як ви можете визначити, чи дві функції є зворотними?
Знаходження зворотних функцій
Функція записується як\(f(x)\) і її зворотна записується як\(f^{-1}(x)\). Поширена помилка полягає в тому, щоб побачити -1 і інтерпретувати його як показник і писати,\(\frac{1}{f(x)},\) але це не правильно. Замість цього\(f^{-1}(x)\) слід розглядати як нову функцію з діапазону\(f(x)\) назад до домену.
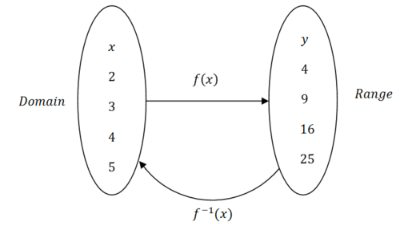
Важливо бачити цикл, який починається з\(x\), стає,\(y\) а потім повертається до\(x\). Для того, щоб дві функції дійсно були зворотними один від одного, цей цикл повинен триматися алгебраїчно.
\(f\left(f^{-1}(x)\right)=x\)і\(f^{-1}(f(x))=x\)
Коли задана функція, є два кроки, щоб знайти її зворотну. У вихідній функції спочатку перемикають змінні\(x\) і\(y\). Далі вирішуємо функцію для\(y\). Це дасть вам обернену функцію. Після знаходження зворотного важливо перевірити обидва напрямки композицій, щоб переконатися, що разом функція і її зворотна виробляють значення\(x\). Іншими словами, перевірте, що\(f\left(f^{-1}(x)\right)=x\) і\(f^{-1}(f(x))=x\).
Графічно інверси - це відображення по всій лінії\(y=x\). Нижче ви бачите зворотні\(y=e^{x}\) і\(y=\ln x .\) Зверніть увагу, як\((x, y)\) координати на одному графіку стають\((y, x)\) координатами в іншому графіку.
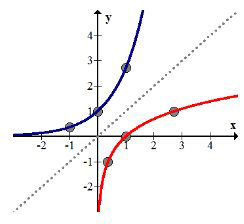
Для того, щоб вирішити, чи є зворотна функція насправді функцією, ви можете використовувати тест вертикальної лінії на зворотній функції, як зазвичай. Ви також можете використовувати тест горизонтальної лінії на вихідній функції. Тест на горизонтальну лінію точно такий же, як тест вертикальної лінії, за винятком того, що лінії просто рухаються горизонтально.
Приклади
Раніше вас запитали, як можна сказати, що дві функції є зворотними. Ви можете сказати, що дві функції є зворотними, якщо кожна скасовує іншу, завжди залишаючи оригінал\(x\).
Знайдіть зворотне, а потім перевірте зворотне алгебраїчно. \(f(x)=y=(x+1)^{2}+4\)
Щоб знайти зворотне, перемикайтеся,\(x\) а\(y\) потім вирішуйте для\(y\).
\(\begin{aligned} x &=(y+1)^{2}+4 \\ x-4 &=(y+1)^{2} \\ \pm \sqrt{x-4} &=y+1 \\-1 \pm \sqrt{x-4} &=y=f^{-1}(x) \end{aligned}\)
Щоб перевірити алгебраїчно, ви повинні показати\(x=f\left(f^{-1}(x)\right)=f^{-1}(f(x))\)
\(\begin{aligned} f\left(f^{-1}(x)\right) &=f(-1 \pm \sqrt{x-4}) \\ &=((-1 \pm \sqrt{x-4})+1)^{2}+4 \\ &=(\pm \sqrt{x-4})^{2}+4 \\ &=x-4+4=x \end{aligned}\)
\(\begin{aligned} f^{-1}(f(x)) &=f^{-1}\left((x+1)^{2}+4\right) \\ &=-1 \pm \sqrt{\left((x+1)^{2}+4\right)-4} \\ &=-1 \pm \sqrt{(x+1)^{2}} \\ &=-1+x+1=x \end{aligned}\)
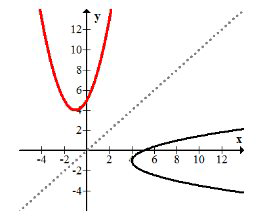
Як видно з графіка,\(\pm\) причиною зворотного є відношення замість функції. Це можна спостерігати на графіку, оскільки вихідна функція не проходить тест горизонтальної лінії, а зворотна не проходить тест вертикальної лінії.
Знайдіть зворотну функцію, а потім переконайтеся, що\(x=f\left(f^{-1}(x)\right)=f^{-1}(f(x))\).
\(f(x)=y=\frac{x+1}{x-1}\)
Іноді це досить складно переключитися,\(x\)\(y\) а потім вирішити для\(y\). Ви повинні бути обережними зі своєю алгеброю.
\(\begin{aligned} x &=\frac{y+1}{y-1} \\ x(y-1) &=y+1 \\ x y-x &=y+1 \\ x y-y &=x+1 \\ y(x-1) &=x+1 \\ y &=\frac{x+1}{x-1} \end{aligned}\)
Ця функція виявляється власною зворотною. так як вони ідентичні, потрібно лише показати, що\(x=f\left(f^{-1}(x)\right)\)
\(f\left(\frac{x+1}{x-1}\right)=\frac{\left(\frac{x+1}{x-1}\right)+1}{\left(\frac{x+1}{x-1}\right)-1}=\frac{x+1+x-1}{x+1-(x-1)}=\frac{2 x}{2}=x\)
Що таке зворотне\(f(x)=y=\sin x ?\)
Функція синуса не проходить тест горизонтальної лінії, тому її справжня зворотна функція не є функцією.
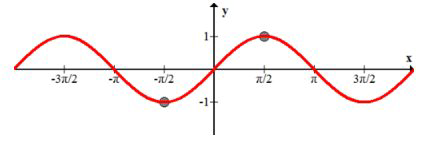
Однак, якщо ви обмежите домен лише частиною\(x\)\(-\frac{\pi}{2}\) -осі між і\(\frac{\pi}{2}\) тоді він пройде тест горизонтальної лінії, а зворотна буде функція.
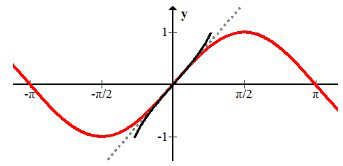
Зворотна функція синуса називається функцією дуги,\(f(x)=\sin ^{-1}(x),\) і показана чорним кольором. Він усічений так, що інвертує лише частину всієї синусоїди. Більш детально ви вивчите періодичні функції та їх інверси пізніше.
Визначте, чи\(g(x)=\frac{7}{3} x+21\) є\(f(x)=\frac{3}{7} x-21\) і є зворотними один від одного.
Незважаючи на те,\(g(x)=\frac{7}{3} x+21\) що\(f(x)=\frac{3}{7} x-21\) і мають деякі перевернуті шматки, вони не є оберненнями один одного. Для того щоб це показати, необхідно показати, що склад не спрощує\(x\).
\(\frac{3}{7}\left(\frac{7}{3} x+21\right)-21=x+9-21=x-12 \neq x\)
Рецензія
Розглянемо\(f(x)=x^{3}\)
1. Ескіз\(f(x)\) і\(f^{-1}(x)\).
2. Знайти\(f^{-1}(x)\) алгебраїчно. Це насправді функція?
3. Перевірте алгебраїчно, що\(f(x)\) і\(f^{-1}(x)\) є зворотними.
Розглянемо\(g(x)=\sqrt{x}\).
4. Ескіз\(g(x)\) і\(g^{-1}(x)\).
5. Знайти\(g^{-1}(x)\) алгебраїчно. Це насправді функція?
6. Перевірте алгебраїчно, що\(g(x)\) і\(g^{-1}(x)\) є зворотними.
Розглянемо\(h(x)=|x|\)
7. Ескіз\(h(x)\) і\(h^{-1}(x)\).
8. Знайти\(h^{-1}(x)\) алгебраїчно. Це насправді функція?
9. Перевірте графічно, що\(h(x)\) і\(h^{-1}(x)\) є зворотними.
Розглянемо\(j(x)=2 x-5\)
10. Ескіз\(j(x)\) і\(j^{-1}(x)\).
11. Знайти\(j^{-1}(x)\) алгебраїчно. Це насправді функція?
12. Перевірте алгебраїчно, що\(j(x)\) і\(j^{-1}(x)\) є зворотними.
13. Використовуйте тест горизонтальної лінії, щоб визначити, чи\(f(x)=x^{3}-2 x^{2}+1\) є зворотна функція.
14. Чи є\(g(x)=\ln (x+1)\) і\(h(x)=e^{x-1}\) обертається? Поясніть.
15. Якби вам дали таблицю значень для функції, як ви могли б створити таблицю значень для зворотної функції?
c