Skip to main content
LibreTexts - Ukrayinska

1.7:1.7 Збільшення та зменшення

  1. Last updated
  2. Save as PDF
  • Page ID
    54466

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Важливо вміти розрізняти, коли функції збільшуються і коли вони зменшуються. У бізнесі це може означати різницю між зароблянням грошей і втратою грошей. У фізиці це може означати різницю між прискоренням і уповільненням.

    Як ви вирішуєте, коли функція збільшується або зменшується?

    Збільшення та зменшення функцій

    Збільшення означає місце на графіку, де нахил позитивний.

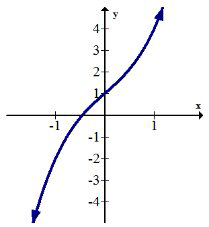
    clipboard_e34f0d7535e58d3f9490dabe743d62ea9.png

    Формальне визначення зростаючого інтервалу таке: відкритий інтервал на\(x\) осі,\((a, d)\) де кожен\(b, c \in(a, d)\) з\(b<c\) має\(f(b) \leq f(c)\)

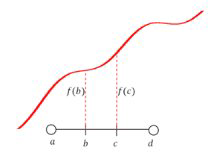
    clipboard_ea21707d4aedfd262c91fd93b267ff817.png

    Інтервал, як кажуть, строго збільшується, якщо\(f(b)<f(c)\) його підставляють у
    визначення.

    Зменшення означає місця на графіку, де нахил від'ємний. Формальне визначення спадного і строго спадного ідентичні визначенню збільшення зі зворотним знаком нерівності.

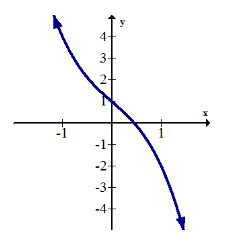
    clipboard_e5fffb9877b97f3629428aad519c8bde0.png

    Функція називається монотонною, якщо функція йде тільки в одному напрямку і ніколи не перемикається між збільшенням і зменшенням.

    З основних функцій монотонно зростаючими функціями є:

    \(f(x)=x, f(x)=x^{3}, f(x)=\sqrt{x}, f(x)=e^{x}, f(x)=\ln x, f(x)=\frac{1}{1+e^{-x}}\)

    Єдині основні функції, які не монотонно збільшуються, це:

    \(f(x)=x^{2}, f(x)=|x|, f(x)=\frac{1}{x}, f(x)=\sin x\)

    Виявлення аналітично, де функції збільшуються та зменшуються, часто вимагає обчислення. Для Precalculus буде достатньо, щоб мати можливість ідентифікувати інтервали графічно і через ваші знання про те, як виглядають батьківські функції.

    Приклади

    Приклад 1

    Раніше вас запитали, як визначити, чи збільшується чи зменшується функція. Збільшення - це де функція має позитивний нахил, а зменшення - де функція має негативний нахил. Поширена помилка полягає в тому, щоб подивитися на функцію квадратури і побачити дві криві, які симетрично збільшуються від нуля. Натомість завжди слід читати функції зліва направо і малювати лінії нахилу і вирішувати, чи є вони позитивними чи негативними.

    Приклад 2

    Оцініть, де наступна функція збільшується і зменшується.


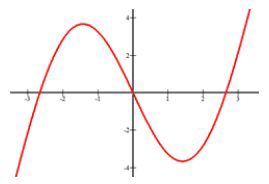
    clipboard_e1d91d5319c8f67f406f3ff101e3bf0d7.png

    Збільшення:\(x \in(-\infty,-1.5) \cup(1.5, \infty)\).
    Зниження:\(x \in(-1.5,1.5)\)

    Приклад 3

    Оцініть, де наступна функція збільшується і зменшується.

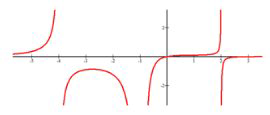
    clipboard_e68c6f0b5ae5b1bd7f0e0e187769da3dd.png

    Збільшення\(x \in(-\infty,-4) \cup(-4,-2.7) \cup(-1,2) \cup(2, \infty)\).
    Зниження\(x \in(-2.7,-1)\)

    Приклад 4

    Оцініть інтервали, де функція збільшується і зменшується.

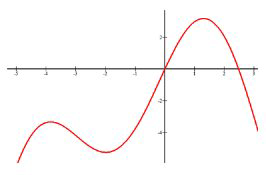
    clipboard_ecb3689630fdd2e28fddde1d96f732da4.png

    Збільшення:\(x \in(-\infty,-4) \cup(-2,1.5)\)
    Зниження:\(x \in(-4,-2) \cup(1.5, \infty)\)

    Зверніть увагу, що відкриті інтервали використовуються\(x=-4,-2,1.5\), оскільки при нахилі функції дорівнює нулю. Тут переходи нахилу від позитивного до негативного. Причина, чому використовуються відкриті дужки, полягає в тому, що функція насправді не збільшується або зменшується в цих конкретних точках.

    Приклад 5

    Неперервна функція має глобальний максимум в точці (3, 2), глобальний мінімум в (5, -12) і не має відносних екстремумів або інших місць з ухилом нуля. Які збільшуються і зменшуються інтервали для цієї функції?

    Збільшення\(x \in(-\infty, 3) \cup(5, \infty)\).
    Зниження\(x \in(3,5)\)

    Примітка:\(y\) Координати не використовуються в інтервалах. Поширеною помилкою є бажання використовувати\(y\) координати.

    Рецензія

    Використовуйте графік нижче для 1-2.

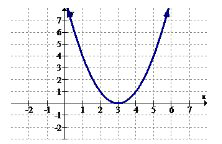
    clipboard_e0eb4499bc5048c86a3822536a0528b86.png

    1. Визначте інтервали (якщо такі є), де функція збільшується.

    2. Визначте інтервали (якщо такі є), де функція зменшується.

    Використовуйте графік нижче для 3-4.

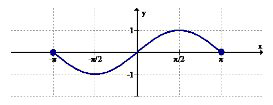
    clipboard_e0cb3d435f132bd7953a3fc9519cafabc.png

    3. Визначте інтервали (якщо такі є), де функція збільшується.

    4. Визначте інтервали (якщо такі є), де функція зменшується.

    Використовуйте графік нижче для 5-6.

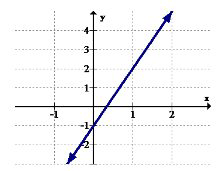
    clipboard_ea2e102851ca3669f113eb786413d59c1.png

    5. Визначте інтервали (якщо такі є), де функція збільшується.

    6. Визначте інтервали (якщо такі є), де функція зменшується.

    Використовуйте графік нижче для 7-8.

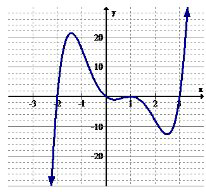
    clipboard_eb4550ac5252bda100ff36e384bb3aca9.png

    7. Визначте інтервали (якщо такі є), де функція збільшується.

    8. Визначте інтервали (якщо такі є), де функція зменшується.

    Використовуйте графік нижче для 9-10.

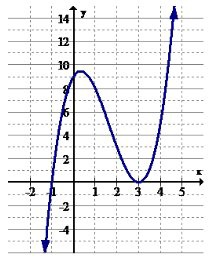
    clipboard_e38d8a6fff701f3894f15b9653e277e60.png

    9. Визначте інтервали (якщо такі є), де функція збільшується.

    10. Визначте інтервали (якщо такі є), де функція зменшується.

    11. Наведіть приклад монотонно зростаючої функції.

    12. Наведіть приклад монотонно спадаючої функції.

    13. Неперервна функція має глобальний максимум в точці (1, 4), глобальний мінімум в (3, -6) і не має відносних екстремумів або інших місць з ухилом нуля. Які збільшуються і зменшуються інтервали для цієї функції?

    14. Неперервна функція має глобальний максимум в точці (1, 1) і не має інших екстремумів або місць з ухилом нуля. Які збільшуються і зменшуються інтервали для цієї функції?

    15. Неперервна функція має глобальний мінімум в точці (5, -15) і не має інших крайнощів або місць з ухилом нуля. Які збільшуються і зменшуються інтервали для цієї функції?