1.11:1.11 Функціональний склад
- Page ID
- 54498
Функції можна додавати, віднімати, множити та ділити, створюючи нові функції та графіки, які є складними комбінаціями різних оригінальних функцій. Одним із важливих способів перетворення функцій є композиція функцій. Композиція функцій дозволяє вибудовувати дві або більше функцій, які діють на вхід в тандемі.
Чи є склад функцій по суті такий же, як множення двох функцій разом?
склад функцій
Поширеним способом опису функцій є відображення з доменного простору в простір діапазону:
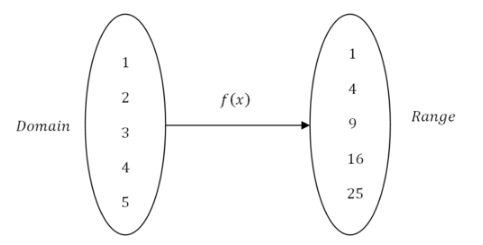
Композиція функцій означає, що у вас є дві або більше функцій і діапазон першої функції стає доменом другої функції. 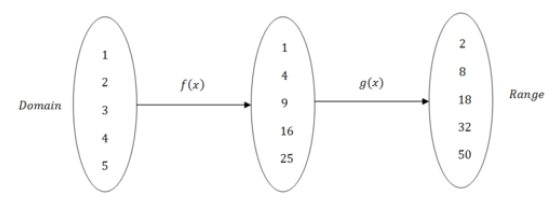
Існує два позначення, що використовуються для опису композиції функцій. У кожному випадку порядок функцій має значення, оскільки арифметично результати будуть різними. Квадратування числа, а потім подвоєння результату буде відрізнятися від подвоєння числа, а потім квадратного результату. На схемі вище,\(f(x)\) відбувається першим і\(g(x)\) відбувається другим. Це можна записати як:
\(g(f(x))\)або\((g \circ f)(x)\)
Ви повинні прочитати це "\(g\)\(f\)з»\(x\). В обох випадках зверніть увагу,\(f\) що він ближче до
\(x\) і оперує\(x\) значеннями першим.
Приклади
Раніше вас запитали, чи є склад функцій таким же, як множення двох функцій разом. Функціональний склад не такий, як множення двох функцій разом. При функціональному складі є зовнішня функція і внутрішня функція. Припустимо, дві функції були подвоєння і квадрат. Це зрозуміло, просто дивлячись на приклад введення числа 5 що 50 (квадрат потім подвоєння) відрізняється від 100 (подвоєння потім квадрат). І 50, і 100 є прикладами композиції функцій, тоді як 250 (п'ять подвоєних помножених на п'ять квадратів) є прикладом добутку двох окремих функцій, що відбуваються одночасно.
Для наступних двох прикладів скористайтеся функціями нижче:
\(f(x)=x^{2}-1\)
\(h(x)=\frac{x-1}{x+5}\)
\(g(x)=3 e^{x}-x\)
\(j(x)=\sqrt{x+1}\)
Показати\(f(h(x)) \neq h(f(x))\)
\(f(h(x))=f\left(\frac{x-1}{x+5}\right)=\left(\frac{x-1}{x+5}\right)^{2}-1\)
\(h(f(x))=h\left(x^{2}-1\right)=\frac{\left(x^{2}-1\right)-1}{\left(x^{2}-1\right)+5}=\frac{x^{2}-2}{x^{2}+4}\)
Для того, щоб по-справжньому показати, що вони не рівні, найкраще знайти конкретний лічильник приклад числа, де вони відрізняються. Іноді алгебраїчні вирази можуть виглядати по-різному, але насправді однакові. Ви повинні помітити,\(f(h(x))\) що не визначено, коли\(x=-5\) тому що тоді в знаменнику буде нуль. \(h(f(x))\)з іншого боку визначається в\(x=-5 .\) оскільки дві функціональні композиції відрізняються, можна зробити висновок:
\(f(h(x)) \neq h(f(x))\)
Що таке\(f(j(h(g(x)))) ?\)
Ці функції вкладені в аргументи інших функцій. Іноді функції значно спрощують при складанні разом, як\(f\) і\(j\) роблять в цьому випадку. Має сенс спочатку оцінити ці дві функції разом і тримати їх на зовнішній стороні аргументу.
\(f(x)=x^{2}-1 ; h(x)=\frac{x-1}{x+5} ; g(x)=3 e^{x}-x ; j(x)=\sqrt{x+1}\)
\(f(j(y))=f(\sqrt{y+1})=(\sqrt{y+1})^{2}-1=y+1-1=y\)
Зверніть увагу, як склад\(f\) і\(j\) виробляється тільки сам аргумент?
Таким чином,
\(\begin{aligned} f(j(h(g(x))))=h(g(x)) &=h\left(3 e^{x}-x\right) \\ &=\frac{\left(3 e^{x}-x\right)-1}{\left(3 e^{x}-x\right)+5} \\ &=\frac{3 e^{x}-x-1}{3 e^{x}-x+5} \end{aligned}\)
Для наступних двох прикладів скористайтеся графіками, показаними нижче:
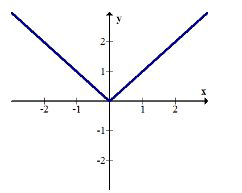
\(f(x)=|x|\)
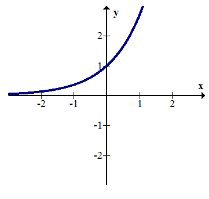
\(g(x)=e^{x}\)
\(h(x)=-x\)
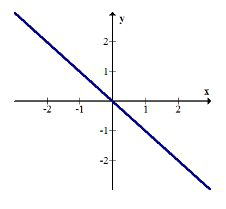
Складіть\(g(f(x))\) і графуйте результат. Опишіть трансформацію.
\(g(f(x))=g(|x|)=e^{|x|}\)
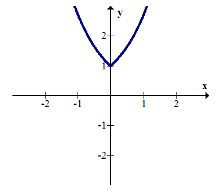
Позитивна частина експоненціального графіка була віддзеркалена над\(y\) віссю, а негативна частина експоненціального графіка була повністю обрізана.
Складіть\(h(g(x))\) і графуйте результат. Опишіть трансформацію.
\(h(g(x))=h\left(e^{x}\right)=-e^{x}\)
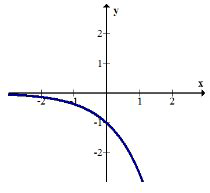
Експоненціальний графік був відображений над\(x\) -віссю.
Рецензія
Для питань 1-9 використовуйте наступні три функції:\(f(x)=|x|, h(x)=-x, g(x)=(x-2)^{2}-3\)
1. Графік\(f(x), h(x)\) і\(g(x)\).
2. Знайти\(f(g(x))\) алгебраїчно.
3. Графік\(f(g(x))\) і опишіть перетворення.
4. Знайти\(g(f(x))\) алгебраїчно.
5. Графік\(g(f(x))\) і опишіть перетворення.
6. Знайти\(h(g(x))\) алгебраїчно.
7. Графік\(h(g(x))\) і опишіть перетворення.
8. Знайти\(g(h(x))\) алгебраїчно.
9. Графік\(g(h(x))\) і опишіть перетворення.
Для 10-16 використовуйте наступні три функції:\(j(x)=x^{2}, k(x)=|x|, m(x)=\sqrt{x}\)
10. Графік\(j(x), k(x)\) і\(m(x)\).
11. Знайти\(j(k(x))\) алгебраїчно.
12. Графік\(j(k(x))\) і опишіть перетворення.
13. Знайти\(k(m(x))\) алгебраїчно.
14. Графік\(k(m(x))\) і опишіть перетворення.
15. Знайти\(m(k(x))\) алгебраїчно.
16. Графік\(m(k(x))\) і опишіть перетворення.