1.10:1.10 Безперервність і розрив

Безперервність - це властивість функцій, які можна намалювати, не піднімаючи олівець. Деякі функції, як і зворотні функції, мають дві окремі частини, які не пов'язані між собою. Функції, які не пов'язані, є переривчастими. Які три способи функції можуть бути переривчастими і як вони виникають?

Неперервність і розрив функцій

Функції, які можна намалювати, не піднімаючи олівець, називаються безперервними функціями. Ви визначите безперервний більш математично суворим способом після вивчення обмежень.

Існує три типи розривів: знімний, стрибок і нескінченний.

Знімні розриви

Знімні розриви виникають, коли раціональна функція має множник з a$x$, який існує як в чисельнику, так і в знаменнику. Знімні розриви показані на графіку порожнистим колом, який також відомий як отвір. Нижче наведено графік для$f(x)=\frac{(x+2)(x+1)}{x+1} .$ Зверніть увагу, що він виглядає так само, як$y=x+2$ за винятком отвору на$x=-1$. Під час графічної функції, ви повинні скасувати знімний коефіцієнт, графік, як зазвичай, а потім вставити отвір у відповідне місце в кінці. Є дірка в$x=-1$ тому, що коли$x=-1, f(x)=\frac{0}{0}$.

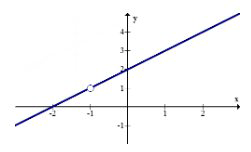
Знімні розриви можна «заповнити», якщо зробити функцію кусковою функцією і визначити частину функції в точці, де знаходиться отвір. У наведеному вище прикладі, щоб зробити$f(x)$ безперервним, ви можете перевизначити його як:

$f(x)=\left\{\begin{array}{ll}\frac{(x+2)(x+1)}{x+1}, & x \neq-1 \\ 1, & x=-1\end{array}\right.$

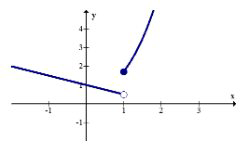
Стрибок розривів

Розриви стрибків відбуваються, коли функція має два кінці, які не зустрічаються, навіть якщо отвір заповнений. Для того, щоб задовольнити тест вертикальної лінії та переконатися, що графік справді є функцією, можна заповнити лише одну з кінцевих точок. Нижче наведено приклад функції з розривом стрибка.

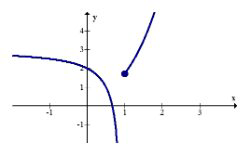
Нескінченні розриви

I нескінченні розриви виникають, коли функція має вертикальну асимптоту з однієї або обох сторін. Це показано на графіку функції нижче$x=1$.

Приклади

Приклад 1

Раніше вас запитали, як функції можуть бути переривчастими. Існує три способи, за якими функції можуть бути розривними. Коли раціональна функція має вертикальну асимптоту в результаті того, що знаменник дорівнює нулю в певній точці, вона матиме нескінченний розрив у цій точці. Коли чисельник і знаменник раціональної функції мають один або кілька однакових факторів, будуть знімні розриви, відповідні кожному з цих факторів. Нарешті, коли різні частини кускової функції не «збігаються», відбудеться стрибок розриву.

Приклад 2

Визначте розрив кускової функції графічно.

$f(x)=\left\{\begin{array}{ll}x^{2}-4 & x<1 \\ -1 & x=1 \\ -\frac{1}{2} x+1 & x>1\end{array}\right.$

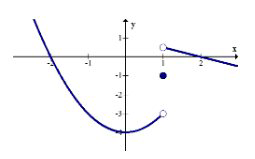
Відбувається стрибок розриву при$x=1$. Кусково функція описує функцію з трьох частин; парабола зліва, одна точка посередині та лінія праворуч.

Приклад 3

Опишіть безперервність або розрив функції$f(x)=\sin \left(\frac{1}{x}\right)$.

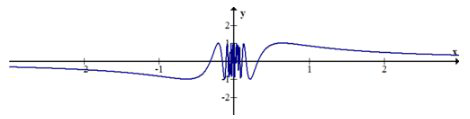
Функція, здається, коливається нескінченно, коли$x$ наближається до нуля. Одна річ, яку графік не може показати, це те, що 0 явно не в області. Графік не стріляє до нескінченності, а також не має простого отвору або розриву стрибка. Обчислення та реальний аналіз потрібні для більш точного визначення того, що відбувається.

Приклад 4

Опишіть розриви функції нижче.

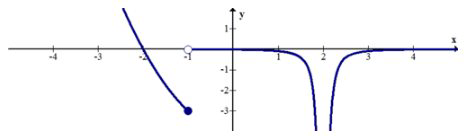
Відбувається стрибок розриву при$x=-1$ і нескінченний розрив при$x=2$.

Приклад 5

Опишіть розриви функції нижче.

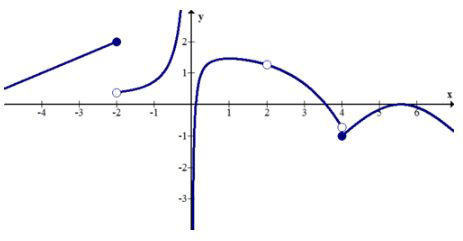
Є стрибки розривів при$x=-2$ і$x=4$. Відбувається знімний розрив при$x=2$. Відбувається нескінченний розрив при$x=0$.

Рецензія

Опишіть будь-які розриви в функціях нижче:

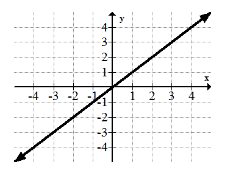
1. $y=x$

2. $y=x^{2}$

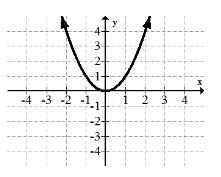
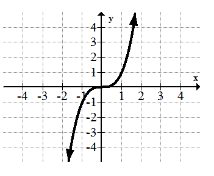
3. $y=x^{3}$

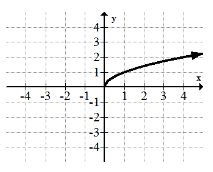
4. $y=\sqrt{x}$

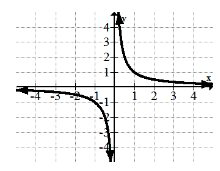
5. $y=\frac{1}{x}$

6. $y=e^{x}$

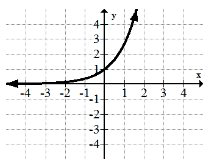
7. $y=\ln (x)$

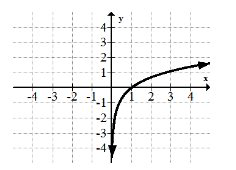
8. $y=\frac{1}{1+e^{-x}}$

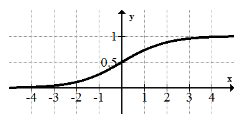
9.

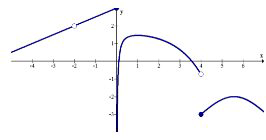
10.

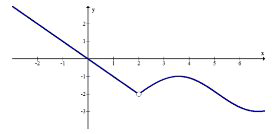
11.

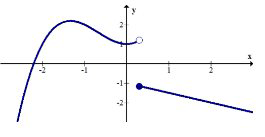
12. $f(x)$має стрибок розриву при$x=3$, знімний розрив при$x=5$, і інший стрибок розриву при$x=6$. Намалюйте малюнок графіка, який міг би бути$f(x)$.

13. $g(x)$має стрибок$x=-2,$ розриву при нескінченному розриві в$x=1,$ і інший стрибок розриву при$x=3$. Намалюйте малюнок графіка, який міг би бути$g(x)$.

14. $h(x)$має знімний розрив при$x=-4,$ стрибку розриву при$x=1$, а інший стрибок розриву при$x=7$. Намалюйте малюнок графіка, який міг би бути$h(x)$.

15. $j(x)$має нескінченний розрив при$x=0,$ знімному розриві в$x=1$, і стрибок розриву при$x=4 .$ Намалюйте малюнок графіка, який міг би бути$j(x)$.

c