Skip to main content
LibreTexts - Ukrayinska

1.5:1.5 Максимуми та Мінімуми

  1. Last updated
  2. Save as PDF
  • Page ID
    54490

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Під час їзди на американських гірках завжди є одна точка, яка є абсолютною найвищою від землі. Зазвичай є багато інших місць, які досягають досить високо, тільки не так високо, як перше. Є також місця, де американські гірки провалилися, причому один з них є абсолютним найнижчим американськими гірками. Як точно визначити та розрізнити ці різні вершини та долини?

    Пошук максимумів і мінімумів

    Глобальний максимум відноситься до точки з найбільшим\(y\) значенням, можливим для функції. Глобальний мінімум відноситься до точки з найменшим можливим\(y\) значенням. Разом ці дві цінності називаються глобальними екстремами. Там може бути тільки один глобальний максимум і тільки один глобальний мінімум. Global відноситься до всього простору, де визначена функція. Глобальні екстреми також називають абсолютними екстремами.

    Окрім глобальних максимумів та глобальних мінімумів, існують також локальні екстреми або відносні максимуми та відносні мінімуми. Слово відносне використовується, оскільки стосовно деякого сусідства ці значення виділяються як найвищі або найнижчі.

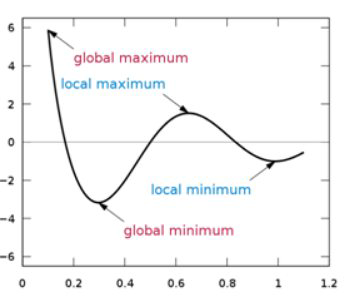
    clipboard_eeaae020fca0259f96bd43fd811716e3f.png

    Обчислення використовує передові аналітичні інструменти для обчислення екстремальних значень, але для цілей Precalculus достатньо мати можливість ідентифікувати та класифікувати екстремальні значення графічно або за допомогою технології. Наприклад, TI-84 має максимальний шукач, коли ви вибираєте <2-й > потім.

    Приклади

    Приклад 1

    Раніше вас попросили визначити та розрізнити різні піки та долини на графіку. Максимуми та мінімуми повинні бути інтуїтивно зрозумілими, оскільки вони просто визначають найвищі та найнижчі точки, або піки та долини на графіку. Існує формальна відмінність щодо того, чи є максимум найвищим на якомусь локальному відкритому інтервалі (не має значення, наскільки малий), чи це просто найвищий загальний.

    Приклад 2

    Визначте і класифікуйте всі крайності.

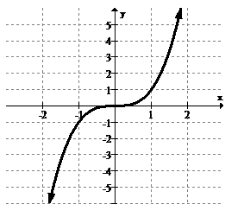
    clipboard_efc4aa2a08b741398fc10e6832d933eac.png

    Немає глобальних або локальних максимумів або мінімумів. Функція вирівнюється, але насправді не досягає піку або долини.

    Приклад 3

    Визначте та класифікуйте всі крайності на графіку нижче:

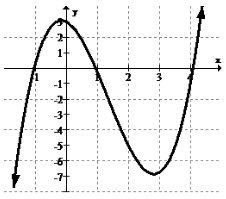
    clipboard_e16222cf60675bc9630f762d645ed858a.png

    Оскільки функція з'являється зі стрілок для збільшення і зменшення за межі дисплея, глобальних екстремумів немає. Існує локальний максимум приблизно (0, 3) і локальний мінімум приблизно (2,8, -7).

    Приклад 4

    Визначте та класифікуйте всі крайності на графіку нижче:

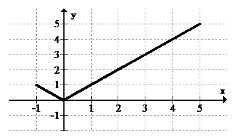
    clipboard_eb8f0a1577aab188472eace6e367e45e0.png

    Оскільки функція, здається, різко закінчується в кінцевих точках і не виходить за межі дисплея, кінцеві точки важливі.

    Існує глобальний мінімум при (0, 0). Існує локальний максимум на (-1, 1) і глобальний максимум на (5, 5).

    Приклад 5

    Визначте та класифікуйте всі крайності на графіку нижче:

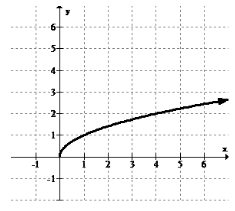
    clipboard_edea4f3a5da337b3a246a9fd4bf886bad.png

    Оскільки ця функція, здається, збільшується вправо, як зазначено стрілкою, глобального максимуму немає. Інших високих точок теж немає, тому локальних максимумів немає. Існує лише кінцева точка (0, 0), яка є глобальним мінімумом.

    Рецензія

    Використовуйте графік нижче для 1-2.


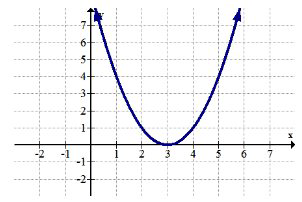
    clipboard_e2e1773ab52990f4b4dc45f22fef68772.png

    1. Визначте будь-яку глобальну крайність.

    2. Визначте будь-яку локальну крайність.

    Використовуйте графік нижче для 3-4.

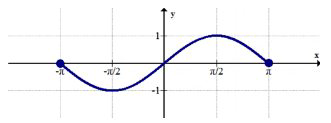
    clipboard_ea7e48b6d314a3014db1383fdc0f361d3.png

    3. Визначте будь-яку глобальну крайність.

    4. Визначте будь-яку локальну крайність.

    Використовуйте графік нижче для 5-6.

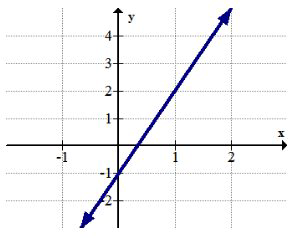
    clipboard_ea4012ddd81aca97ddf10b0e741ac0487.png

    5. Визначте будь-яку глобальну крайність.

    6. Визначте будь-яку локальну крайність.

    Використовуйте графік нижче для 7-8.

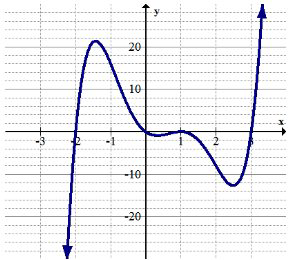
    clipboard_e1a48f11fbf727d65d8761acf83592b4d.png

    7. Визначте будь-яку глобальну крайність.

    8. Визначте будь-яку локальну крайність.

    Використовуйте графік нижче для 9-10.

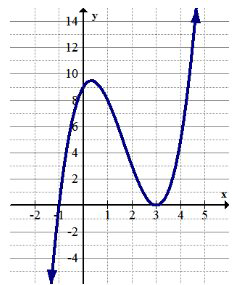
    clipboard_ee72537b886f4421cbe674fdcd6342076.png

    9. Визначте будь-яку глобальну крайність.

    10. Визначте будь-яку локальну крайність.

    11. Поясніть різницю між глобальним максимумом і локальним максимумом.

    12. Намалюйте приклад графіка з глобальним мінімумом і локальним максимумом, але не глобальним максимумом.

    13. Намалюйте приклад графіка з локальними максимумами та мінімумами, але без глобальних екстремумів.

    14. Використовуйте свій графічний калькулятор, щоб визначити та класифікувати крайності:

    \(f(x)=\frac{1}{2} x^{4}+2 x^{3}-6.5 x^{2}-20 x+24\)

    15. Використовуйте свій графічний калькулятор, щоб визначити та класифікувати крайності:

    \(g(x)=-x^{4}+2 x^{3}+4 x^{2}-2 x-3\)