Skip to main content
LibreTexts - Ukrayinska

1.4:1.4 Домен і діапазон

  1. Last updated
  2. Save as PDF
  • Page ID
    54489

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Проаналізувати засоби розглядати методично і детально. Одним із способів аналізу функцій є перегляд можливих входів (домен) та можливих виходів (діапазон). Які з основних функцій мають обмежені домени і чому?

    Домен і діапазон

    Позначення

    Домен і діапазон описуються в інтервальних позначеннях. Дужки, (), означають невключно. Дужки, [], означають включно. Наступні описи чисел в інтервальні позначення були перетворені в інтервальні позначення.

    1. Всі номери.
    \((-\infty, \infty)\)Примітка: Дужки завжди використовуються з нескінченністю.

    2. Всі від'ємні числа, не включаючи 0.

    \((-\infty, 0)\)

    3. Всі позитивні числа, включаючи 0.
    \([0, \infty)\)

    4. Кожне число від 1 до 4, включаючи 1 і 4.
    [1,4]

    5. Кожне число між 5 і 6, не включаючи 5 або 6.

    (5, 6)

    6. Цифри з 1 по 2, включаючи 1, але не включаючи 2, і цифри від
    10 до 25, включаючи як 10, так і 25

    [1,2)\(\cup[10,25]\)

    Примітка:\(\cup\) Символ означає Союз і відноситься до того, що якщо в цьому союзі\(x\) є якесь число, то воно або в першій групі, або воно знаходиться в другій групі. Цей символ асоціюється з оператором OR. Хоча це правда, що символ Союзу, здається, об'єднує одну групу та іншу групу, символ І - це\(\cap\) означає перетин. Перетин відрізняється від об'єднання тим, що перетин означає всі числа, які одночасно знаходяться як в першій групі, так і в другій групі.

    Домен і обмежений домен

    Домен - це можливі входи у функцію. Багато функцій дозволяють вводити будь-які числа. Сюди входять числа, які є додатними, негативними, нульовими, дроби або десяткові. Функція квадратування\(y=x^{2}\) - приклад, який має область всіх можливих дійсних чисел. Три функції мають дуже специфічні обмеження:

    Функція квадратного кореня: Обмеження\(y=\sqrt{x}\)
    домену:\(x \geq 0\)

    Це пов'язано з тим, що квадратний корінь від'ємного числа не є дійсним числом. Це обмеження можна спостерігати на графіку, оскільки крива закінчується в точці (0,0) і не визначається ніде, де\(x\) негативна.

    Функція журналу визначається лише для чисел, які строго більші за нуль. Це тому, що логарифмічна функція - це інший спосіб запису показників. Однією з властивостей показників є те, що будь-яке додатне число, підняте до будь-якої потужності, ніколи не призведе до негативного числа або нуля. Обмеження можна спостерігати на графіку по тому, як функція log наближається до вертикальної лінії\(x=0\) і стріляє вниз до нескінченності.

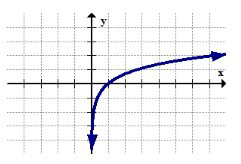
    clipboard_eaa6163d9e77aec8becd2a3a2549f8fa1.png

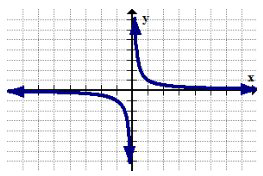
    Зворотна функція: Обмеження\(y=\frac{1}{x}\)
    домену:\(x \neq 0\)

    Зворотна функція обмежена, оскільки ви не можете розділити числа нануль. Будь-які\(x\) значення, які роблять знаменником функції нуль, знаходяться поза межами області. Це обмеження можна спостерігати на графіку тим, як зворотна функція ніколи не стосується вертикальної лінії\(x=0\).

    clipboard_ec47b44d3b519b4854111dfa6ef57b0bb.png

    Діапазон

    Діапазон - це можливі виходи функції. Практично будь-яка функція може виробляти будь-який вихід за допомогою перетворень, і тому визначення діапазону функції значно менш процедурно, ніж визначення області. Використовуйте те, що ви знаєте про форму кожної функції та їх рівняння, щоб вирішити, які\(y\) значення можна отримати, а які\(y\) значення неможливо створити.

    Пошук домену та діапазону

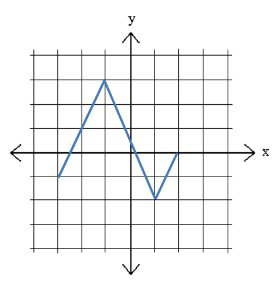
    clipboard_e7b8419b1c8e79846faa0f585f6c2daf0.png

    Домен і діапазон для графіка вище:

    Домен:\(x \in[-3,2]\)

    Діапазон:\(y \in[-2,3]\)

    Зверніть увагу, що\(\in\) символ означає «є елементом» і означає, що\(x\) або\(y\) знаходиться в цьому інтервалі, а числа в інтервалі завжди записуються в порядку збільшення. [3, -2] вважається неправильним.

    Зверніть увагу, що навіть незважаючи на те, що [-3,2] може виглядати схожим на впорядковану пару, яка представляє точку, де\(x=-3\) і\(y=2,\) це не так. І -3, і 2 є\(x\) значеннями. Це оману, чому ви завжди повинні писати,\(x \in\) тому що це нагадує вам про цей факт. Багато людей дуже плутаються, коли бачать щось подібне,\(x \in(-2,1)\) тому що бачать дужки і відразу бачать точку, коли вони повинні побачити інтервал на\(x\) осі.

    На графіку нижче є дві різні частини функції.

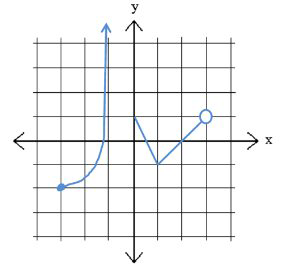
    clipboard_e5b53e02e2c6166ab6337fd267979e600.png

    Домен і діапазон для графіка вище:

    Домен:\(x \in[-3,-1) \cup[0,3)\)

    Діапазон:\(y \in[-2, \infty)\)

    Функція, здається, наближається до вертикальної лінії, фактично\(x=-1\) не досягаючи її, використовується\(s 0\) відкрита дужка. Крім того, порожня діра в точці\((3,\) 1), тому домен виключає\(x\) значення 3.

    Приклади

    Приклад 1

    Раніше вас запитали, які основні функції мають обмежені домени. Три функції, які мають обмежені домени, - це функція квадратного кореня, функція журналу та зворотна функція. Функція квадратного кореня має обмежений домен, оскільки ви не можете взяти квадратні корені від'ємних чисел і створювати дійсні числа. Функція журналу обмежена, оскільки функція журналу не визначена для роботи з недодатними числами. Реципрокна функція обмежена, оскільки числа, ділені на нуль, не визначені.

    Приклад 2

    Визначте домен і діапазон наступної функції, записаної в таблицю:

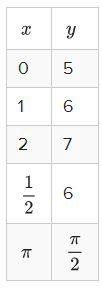
    clipboard_e094aae392df8ffa2a6e455e15e20df77.png

    Конкретне рівняння функції може бути прихованим, але з таблиці можна визначити область і діапазон безпосередньо зі\(y\) значень\(x\) і. Можливо, буде спокусливо здогадатися, що інші значення потенційно можуть працювати в таблиці, особливо якщо шаблон очевидний, але це не те питання, яке запитує, якою може бути функція. Замість цього питання просто запитує, що таке заявлений домен і діапазон.

    Домен:\(x \in\left\{0,1,2, \frac{1}{2}, \pi\right\}\)

    Діапазон:\(y \in\left\{5,6,7, \frac{\pi}{2}\right\}\)

    Зверніть увагу, що два 6, які з'являються в таблиці, не потрібно писати двічі в діапазоні.

    Приклад 3

    Визначте область наступних трьох перетворених функцій.

    1. \(y=10 \sqrt{2-x}-3\)

    Аргумент функції повинен бути більше або дорівнює 0.

    \(\begin{aligned} 2-x & \geq 0 \\-x & \geq-2 \\ x & \leq 2 \end{aligned}\)

    Домен:\(x \in(-\infty, 2]\)

    2. \(y=\frac{3 x}{x^{2}+7 x+12}\)

    Знаменник не може бути рівним\(0 .\) Спочатку знайдіть, які значення\(x\) зробили б рівним нулю, а потім ви можете виключити ці значення.

    \(\begin{aligned} x^{2}+7 x+12 &=0 \\(x+4)(x+3) &=0 \\ x &=-4,-3 \end{aligned}\)

    Домен:\(x \in(-\infty,-4) \cup(-4,-3) \cup(-3, \infty)\)

    3. \(y=-4 \ln (3 x-9)+11\)

    Аргумент повинен бути строго більше 0.

    \(3 x-9>0\)
    \(3 x>9\)
    \(x>3\)

    Домен:\(x \in(3, \infty)\)

    Приклад 4

    Що таке домен і діапазон синусоїди?

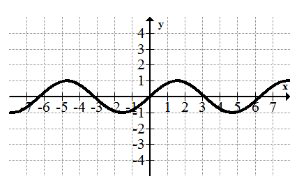
    clipboard_eeea810e2f3baf3a73ec0ccff9a01da44.png

    Домен:\(x \in(-\infty, \infty)\)

    Діапазон:\(y \in[-1,1]\)

    Рецензія

    Перетворіть наведені нижче описи чисел в інтервальні позначення.

    1. Всі позитивні числа, не включаючи 0.

    2. Кожне число між -1 і 1, включаючи -1, але не 1.

    3. Кожне число між 1 і 5, не включаючи 2 або 3, але включаючи 1 і 5.

    4. Кожне число більше 5, не включаючи 5.

    5. Всі дійсні числа, крім 1.

    Переведіть наступні нерівності в інтервальні позначення.

    6. \(-4<x \leq 5\)
    7. \(x>0\)
    8. \(-\infty<x \leq 4\)або\(5<x<\infty\)

    9.

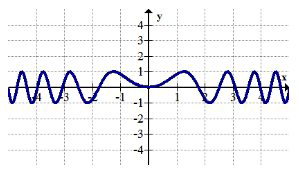
    clipboard_e40cc867a7d162e3f0ee23f90849cd4e8.png

    10.

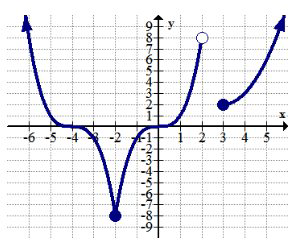
    clipboard_ebc943faf8e2d5c11ca1503ef2fccd7ad.png

    З огляду на заявлений домен і діапазон, намалюйте можливий графік.

    11. Домен:\(x \in[0, \infty)\) Діапазон:\(y \in(-2,2]\)

    12. Домен:\(x \in[-4,1) \cup(1, \infty)\) Діапазон:\(y \in(-\infty, \infty)\)

    13. З огляду на таблицю, знайдіть домен і діапазон.

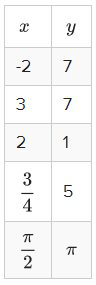
    clipboard_ef5eb6dd511ebffb7fc3fab23929415d0.png

    Знайдіть домен для наступних функцій.

    14. \(y=-3 \sqrt{x+4}-1\)
    \(y=\frac{7}{x+6}-1\)
    16. \(y=5 \ln \left(x^{2}-1\right)+4\)