9.5: Трапецієподібні та середні наближення
- Page ID
- 54344
Нагадаємо, що ми використовували різні способи наближення значення інтегралів. Сюди входили суми Рімана, що використовують ліву та праву кінцеві точки, а також середні точки для знаходження довжини кожної прямокутної плитки. У цьому уроці прямокутні плитки замінюються трапецієподібними плитками, щоб наблизити інтеграл. Думаєте, що використання трапецій дало б більш точний результат, ніж використання прямокутників? Чому? Чи можете ви придумати причину, чому увігнутість кривої функції буде мати значення в точності оцінки площі за допомогою трапецій?
Нагадаємо, що ми використовували різні способи наближення значення інтегралів. Сюди входили суми Рімана, що використовують ліву та праву кінцеві точки, а також середні точки для знаходження довжини кожної прямокутної плитки. У цьому уроці ми дізнаємося ще два методи наближення інтегралів. Перший з них, Трапецієподібний Правило, використовує ділянки трапецієподібної плитки для наближення інтеграла. Другий метод, Правило Сімпсона, використовує параболи, щоб зробити наближення.
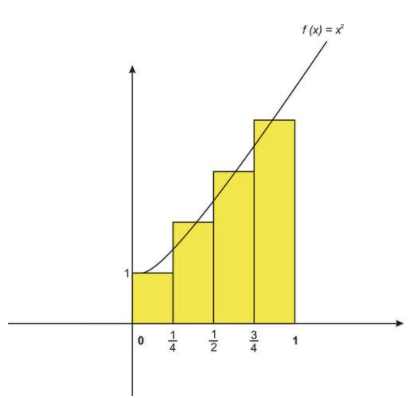
Згадаймо, як ми використовували правило середньої точки з n=4 прямокутниками для наближення площі під графіком\( f(x)=x^2+1 \nonumber\) від x=0 до x=1.
CC ЗА NC-SA
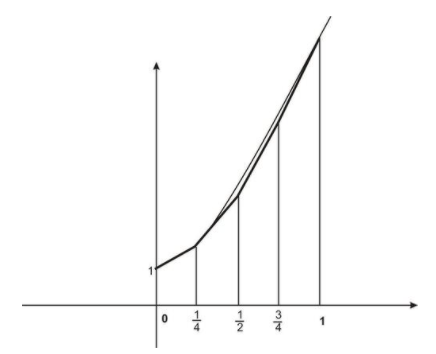
Якщо замість того, щоб використовувати значення середньої точки в кожному підінтервалі для пошуку довжини відповідного прямокутника, ми могли б замість цього сформувати трапеції, об'єднавши максимальне та мінімальне значення функції в межах кожного підінтервалу:
CC ЗА NC-SA
Площа трапеції дорівнює\( A= \frac{h(b_1+b_2)}{2} \nonumber\), де b1 і b2 - довжини паралельних сторін і h - висота. У наших трапеціях висота дорівнює △ x і b1 і b2 - значення функції. Тому при знаходженні площ трапецій ми фактично усереднюємо ліву та праву кінцеві точки кожного підінтервалу.
Тому типова трапеція мала б площу
\[ A = \frac{△x}{2} (f(x_{i−1})+f(x_i)) \nonumber\].
Щоб наблизити\ (\ int\ limits_a^b f (x) dx з n цих трапецій, ми маємо
\[ \int\limits_a^b f(x)dx ≈ \frac{1}{2} [|\sum_{i=1}^n f(x_{i−1})△x+ \sum_{i=1}^n f(x_i)△x] \nonumber\]
\[ = \frac{△x}{2} [f(x_0)+f(x_1)+f(x_1)+f(x_2)+f(x_2)+⋯+f(x_{n−1})+f(x_n)] \nonumber\]
\[ = \frac{△x}{2} [f(x_0)+2f(x_1)+2f(x_2)+⋯+2f(x_{n−1})+f(x_n)],△x= \frac{b−a}{n} \nonumber\].
Застосуйте формулу зверху і використовуйте трапецієподібне правило для\( \int\limits_0^3 x^2dx \nonumber\) наближення з n = 6.
Кожен субінтервал є\( △x= \frac{b−a}{n}= \frac{3−0}{6}= \frac{1}{2} \nonumber\).
Інтегральне наближення - це:
\[ \int\limits_0^3 x^2 dx ≈ \frac{1}{4} [f(0)+2f( \frac{1}{2})+ 2 f (1)+ 2 f ( \frac{3}{2})+2f(2)+2f( \frac{5}{2})+f(3)] \nonumber\]
\[ = \frac{1}{4} [0+(2⋅ \frac{1}{4})+(2⋅1)+(2⋅ \frac{9}{4})+(2⋅4)+(2⋅ \frac{25}{4} )+9] \nonumber\]
\[ = \frac{1}{4} [ \frac{73}{2}]= \frac{73}{8} = 9.125. \nonumber\]
Точний розв'язок можна визначити за допомогою антипохідної з фундаментальною теоремою.
\[ \int\limits_0^3 x^2 dx = \frac{x^3}{3} |_0^3 = 9 . \nonumber\]
Похибка становить близько 1,4%.
Для деяких інтегралів неможливо знайти антипохідну і числовий метод є єдиним варіантом.
Коли це так, точність наближення є проблемою. Зокрема, наскільки великим має бути n, щоб трапецієподібна оцінка була точною до заданого значення, скажімо, 0,001?
Величина похибки при використанні трапецієподібної методики при заданому значенні n може бути показана:
\[ |Error_{Trapezoidal} | ≤ \frac{k(b−a)^3}{12 n^2}, \mbox{ where } |f′′(x)|≤k \mbox{ for } a≤x≤b \nonumber\]
Це означає, що вибір\( n ≥ \sqrt{ \frac{k(b−a)^3}{12} ⋅ |Error_{Trapezoidal}| } \nonumber\) буде відповідати або перевищувати задану похибкутрапецієподібної помилки.
Знайдіть n так, щоб трапецієподібна оцінка для\( \int_0^3 x^2 dx \nonumber\) була точною до 0,001.
Нам потрібно знайти п таке, що\( |Error_{Trapezoidal}| ≤ 0.001 \nonumber\).
Спочатку зауважте, що\( |f′′(x)|=2 \mbox{ for } 0≤x≤3 \nonumber\). Отже, ми можемо взяти k = 2, щоб знайти нашу помилку пов'язану.
\[ |Error_{Trapezoidal}| ≤ \frac{2 (3−0)^3}{12 n^2} = \frac{54}{12 n^2} \nonumber\]
Нам потрібно розв'язати таку нерівність для n:
\[ \frac{54}{12n^2} < 0.001, \nonumber\]
\[ n^2 > \frac {54}{12(0.001)}, \nonumber\]
\[ n > \sqrt{ \frac{54}{12(0.001)}} ≈ 67.08 \nonumber\]
Отже, ми повинні взяти n = 68, щоб досягти бажаної точності.
Приклади
Приклад 1
Раніше вас запитали, чи вважаєте ви, що використання трапецій для наближення площі під кривою дасть більш точний результат, ніж використання прямокутників. Чи можете ви придумати причину, чому увігнутість кривої функції буде мати значення в точності оцінки площі за допомогою трапецій?
Якщо ви вважаєте, що використання трапецій дасть більш точний результат (з кількістю субінтервалів однакове), ви маєте рацію. На деяких прикладах можна візуально побачити, що трапеції краще покривають область під кривою. Зверніть увагу, однак, що якщо крива функції увігнута вгору, трапеції переоцінять площу; якщо увігнутість вниз, трапеції будуть занижувати площу.
Приклад 2
Використовуйте трапецієподібне правило, щоб наблизити 02x3dx для n = 4. Округлите відповідь до чотирьох знаків після коми і порівняйте це значення з точним значенням інтеграла. Яка очікувана помилка для n = 4?
Кожен підінтервал ми знаходимо як △ x=b−an=2−04=12.
Інтегральне наближення оцінюється наступним чином:
\[ \int\limits_0^2 x^3 dx ≈ \frac{1}{4} [f(0) + 2 f(0.5) + 2 f(1) + 2 f(1.5) + f(2) ] \nonumber\]
\[ ≈ \frac{1}{4} [0+2⋅0.125+2⋅1+2⋅3.375+8] \nonumber\]
\[ \int\limits_0^2 x^3 dx ≈ 4.25 \nonumber\]
Оцінка інтеграла дорівнює 4,25.
Точне значення інтеграла:\( \int\limits_0^2 x^3 dx = \frac{x^4}{4}|_0^2 = 4 \nonumber\).
Похибка між ними дорівнює 0,25.
Очікувана помилка з використанням n=4:
Для f′′ (x) =6x, f′′ (x) ≤6⋅2=12 в інтервалі [0,2].
Тому,\( |Error_{Trapezoidal}| ≤ \frac{k(b−a)^3}{12 n^2} = \frac{12(2)^3}{12⋅4^2}=0.5 \nonumber\).
Фактична похибка менше\( |Error_{Trapezoidal}| \nonumber\).
Приклад 3
Використовуйте трапецієподібне правило для\( \int\lim_1^2 \frac{1}{(x+1)^2} dx \nonumber\) наближення для n = 4. Округлите відповідь до чотирьох знаків після коми і порівняйте це значення з точним значенням інтеграла. Яка очікувана помилка для n = 4?
Знаходимо кожен підінтервал як\( △x = \frac{b−a}{n} = \frac{2−1}{4} = \frac{1}{4} \nonumber\).
Інтегральне наближення оцінюється наступним чином:
\[ \int\limits_1^2 \frac{1}{(x+1)^2} dx ≈ \frac{1}{8} [f(2)+2f(2.25)+2f(2.5)+2f(2.75)+f(3)] \nonumber\]
\[ ≈ \frac{1}{8} [\frac{1}{4} + 2 \frac{1}{2.25^2} + 2 \frac{1}{2.5^2} + 2 \frac{1}{2.75^2} + \frac{1}{3^2} ] \nonumber\]
\[ ≈ \frac{1}{8} [0.25+0.39506+0.32+0.26446+0.11111] \nonumber\]
\[ \int\limits_1^2 \frac{1}{(x+1)^2} dx ≈ 0.16758 ≈ 0.1676 \nonumber\]
Оцінка інтеграла дорівнює 0,1676.
Точне значення інтеграла:\[ ∫121(x+1)2dx=−1x+1∣∣∣21=16=0.16⎯⎯⎯ \nonumber\].
Помилка між ними становить 0.0009.
Очікувана помилка з використанням n=4:
Для\( f′′(x) = \frac{6}{(x+1)^4}, f′′(x) ≤ \frac{6}{(1+1)^4} = \frac{3}{8} = 0.375 \nonumber\) в інтервалі [1, 2].
Тому,\(|Error_{Tropezoidal}| ≤ \frac{k(b−a)^3}{12n^2} = \frac{0.375(1)^3}{12⋅4^2} = 0.001953 \nonumber\).
Фактична похибка менше\( |Error_{Trapeziodal}| \nonumber\).
Рецензія
Використовуйте трапецієподібне правило для наближення певних інтегралів, використовуючи задану кількість підінтервалів n.
- \( \int_1^7 (x+7)dx \mbox{ with } n=6 \nonumber\).
- \( \int_{−2}^2 (x+4)dx \mbox{ with } n=4 \nonumber\).
- \( \int_{−4}{1} (−x^2−2x+8) dx \mbox{ with } n=5 \nonumber\).
- \( \int_2^7 \frac{2}{x} dx \mbox{ with } n=5 \nonumber\).
- \( \int_0^2 x^4 dx \mbox{ with } n=4 \nonumber\).
- \( \int_0^1 sin \frac{x}{2} dx \mbox{ with } n=4 \nonumber\).
- \( \int_2^4 \sqrt{x} dx \mbox{ with } n=5 \nonumber\).
- \( \int_0^1 x^2e−xdx \mbox{ with } n=8 \nonumber\).
- \( \int_1^4 ln\sqrt{x} dx \mbox{ with } n=6 \nonumber\).
- \( \int_0^1 \sqrt{1+x^4}dx \mbox{ with } n=4 \nonumber\).
- \( \int_1^3 \frac{1}{x} dx \mbox{ with } n=8 \nonumber\).
- \( \int_0^2 x^3 dx \mbox{ for } n=8 \nonumber\).
- Знайти значення n, яке гарантує похибку не більше 10−5 у трапецієподібному наближенні\( \int_2^4 \sqrt{x} dx \nonumber\). Наскільки великим має бути n, щоб трапецієподібна оцінка\( \int_1^3 \frac{1}{x} dx \nonumber\) була точною в межах:
- 0,001?
- 0.00001?
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 5.10.
Лексика
| Термін | Визначення |
|---|---|
| трапецієподібне правило | Трапецієподібне правило являє собою метод обчислення певного інтеграла шляхом обчислення площі трапецієподібних відрізків в інтервалі інтеграції та їх підсумовування. |
Додаткові ресурси
PLIX: Грайте, вчіться, взаємодійте, досліджуйте - область спідниці
Відео: Трапецієподібне наближення площі під кривою академією Хана
Практика: трапецієподібні та середні наближення