8.18: Позначення для композитних перетворень

Інтерпретувати та використовувати позначення для комбінованих перетворень

На малюнку нижче показано складене перетворення трапеції. Напишіть правило відображення для складеного перетворення.

Малюнок\(\PageIndex{1}\)

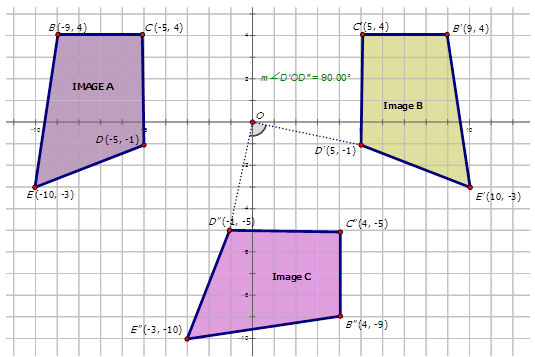
У геометрії трансформація - це операція, яка переміщує, перевертає або змінює фігуру для створення нової форми. Складене перетворення - це коли два або більше перетворень виконуються на фігурі (називається попереднім зображенням) для отримання нової фігури (званої зображенням). Має значення порядок перетворень, що виконуються в складеному перетворенні.

Щоб описати складене перетворення за допомогою нотації, вкажіть кожне з перетворень, що складають складене перетворення, і пов'яжіть їх із символом\(\circ\). Перетворення виконуються в порядку справа наліво. Згадайте наступні позначення для перекладів, роздумів та обертань:

• Переклад:\(T_{a,b}: (x,y)\rightarrow (x+a,y+b)\) це переклад\(a\) одиниць вправо і\(b\) одиниць вгору.
• Відображення:\(r_{y−axis}(x,y)\rightarrow (−x,y)\).
• Обертання:\(R_{90^{\circ}}(x,y)=(−y,x)\)

Давайте намалюємо лінію, описану нижче, і складене зображення, визначене\(r_{y−axis} \circ R_{90^{\circ}}\):

Перший переклад - це поворот\(90^{\circ}\) КНО про походження виробляти\(X′Y′\). Другий переклад є відображенням про\(y\) -осі виробляти\(X′′Y′′\).

Малюнок\(\PageIndex{2}\)

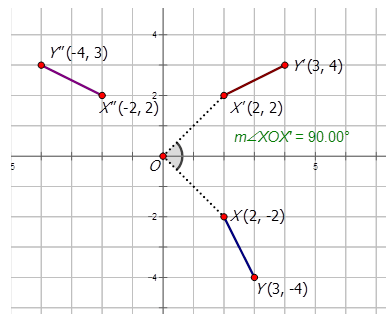
Тепер давайте намалюємо складові зображення, описані в наступних задачах:

1. Зображення A з вершинами\(A(3,5)\),\(B(4,2)\) і\(C(1,1)\) піддається складеному перетворенню з правилом відображення\(r_{x−axis} \circ r_{y−axis}\).

Малюнок\(\PageIndex{3}\)

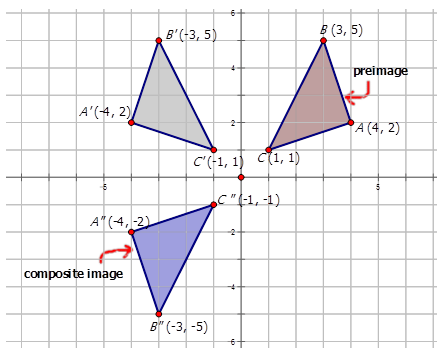
2. Зображення\(D\) з вершинами\(D(−3,7)\)\(E(−1,3)\),\(F(−7,5)\) і\(G(−5,1)\) піддається складеному перетворенню з правилом відображення\(T_{3,4} \circ r_{x−axis}\).

Малюнок\(\PageIndex{4}\)

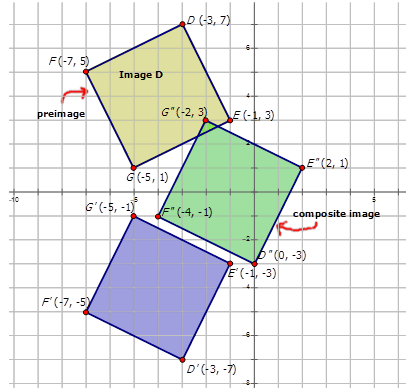
Приклад\(\PageIndex{1}\)

Раніше вам було запропоновано написати правило відображення для наступного складеного перетворення:

Малюнок\(\PageIndex{5}\)

Рішення

Трансформація з зображення\(A\) на зображення\(B\) є відображенням поперек\(y\) -осі. Позначення для цього є\(r_{y−axis}\). Трансформація для зображення B для формування зображення\(C\) є обертанням навколо походження\(90^{\circ}CW\). Позначення для цього перетворення є\(R_{270^{\circ}}\). Тому позначення для опису перетворення Image\(A\) to Image\(C\) є\(R_{270^{\circ}} \circ r_{y−axis}\)

Приклад\(\PageIndex{2}\)

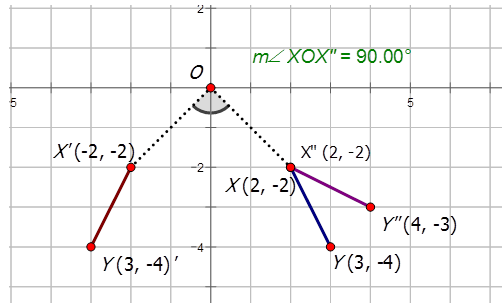
Графік лінії з\(XY\) урахуванням того, що\(X(2,−2)\) і\(Y(3,−4)\). Також графуйте складене зображення, яке задовольняє правилу\(R_{90^{\circ}} \circ r_{y−axis}\)

Рішення

Перше перетворення - це відображення про\(y\) -осі, яку потрібно виробляти\(X′Y′\). Друга трансформація - це\(90^{\circ}CCW\) поворот про походження до виробництва\(X′′Y′′\).

Малюнок\(\PageIndex{6}\)

Приклад\(\PageIndex{3}\)

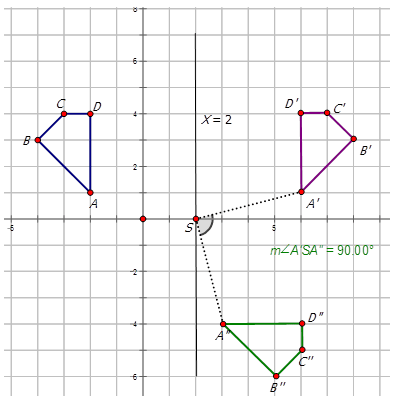
Опишіть складові перетворення на діаграмі нижче і напишіть позначення для представлення перетворення фігури\(ABCD\) в\(A′′B′′C′′D′′\).

Малюнок\(\PageIndex{7}\)

Рішення

На схемі наведено два перетворення. Перше перетворення - це відображення про лінію X = 2\), яку потрібно виробити\(A′B′C′D′\). Друге перетворення - це обертання\(90^{\circ}\) CW (або\(270^{\circ}CCW\)) навколо точки\((2, 0)\) для отримання фігури\(A′′B′′C′′D′′\). Позначення для цього складеного перетворення:

\(R_{270^{\circ}} \circ r_{x=2}\)

Приклад\(\PageIndex{4}\)

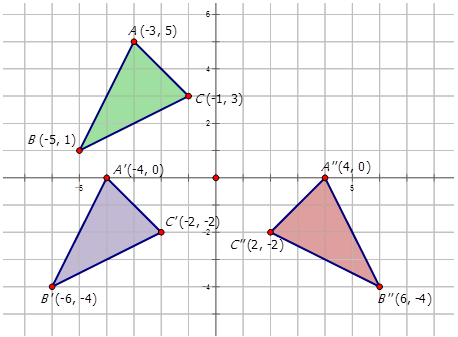
Опишіть складові перетворення на діаграмі нижче і напишіть позначення для представлення перетворення фігури\(ABC\) в\(A′′B′′C′′\).

Малюнок\(\PageIndex{8}\)

Рішення

На схемі наведено два перетворення. Перша трансформація - це переклад 1 одиниці вліво і 5 одиниць вниз, щоб виробляти\(A′B′C′\). Друге відображення в\(y\) -осі виробляємо фігуру\(A′′B′′C′′\). Позначення для цього складеного перетворення:

\(r_{y−axis} \circ T_{−1,−5}\)

Рецензія

Заповніть наступну таблицю:

Початкова точка	\(T_{3,−4} \circ R_{90^{\circ}}\)	\(r_{x−axis} \circ r_{y−axis}\)	\(T_{1,6} \circ r_{x-axis}\)	\(r_{y−axis} \circ R_{180^{\circ}}\)
1. \((1, 4)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
2. \((4, 2)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
3. \((2, 0)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
4. \((-1, 2)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
5. \((-2, -3)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
6. \((4, -1)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
7. \((3, -2)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
8. \((5, 4)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
9. \((-3, 7)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">
10. \((0, 0)\)	\ (T_ {3, −4}\ коло R_ {90^ {\ circ}\)» клас = "lt-k12-6155">	\ (r_ {x−вісь}\ коло r_ {y−вісь}\)» клас = «lt-k12-6155">	\ (T_ {1,6}\ коло r_ {вісь x}\)» клас = «lt-k12-6155">	\ (r_ {y−вісь}\ коло R_ {180^ {\ circ}\)» клас = «lt-k12-6155">

Запишіть позначення, яке представляє складене перетворення попереднього зображення\(A\) до складеного зображення на діаграмах нижче.

11. 

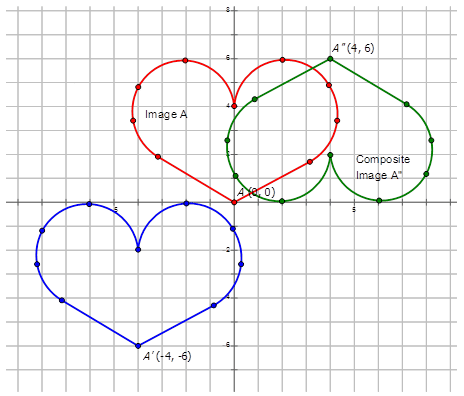
    Малюнок\(\PageIndex{9}\)

12. 

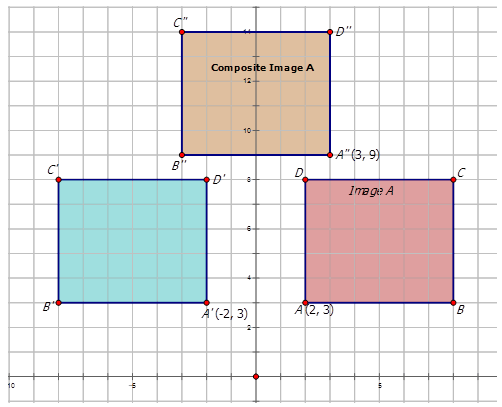
    Малюнок\(\PageIndex{10}\)

13. 

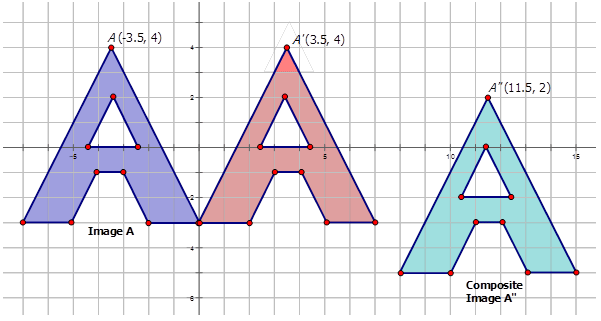
    Малюнок\(\PageIndex{11}\)

14. 

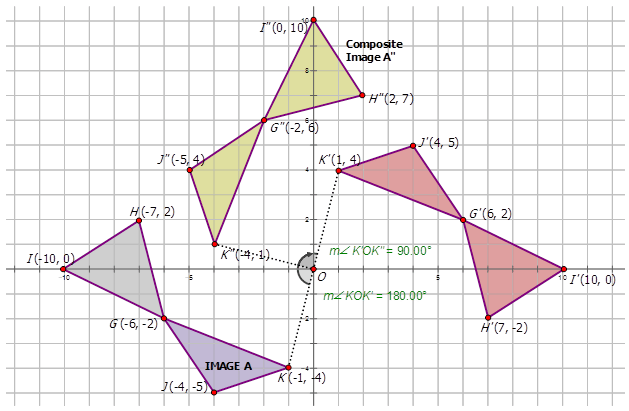
    Малюнок\(\PageIndex{12}\)

15. 

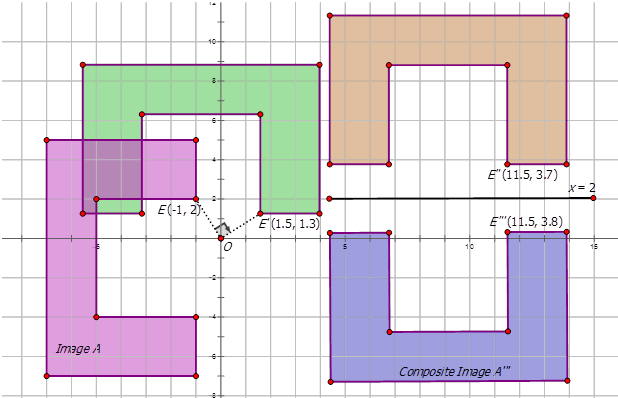
    Малюнок\(\PageIndex{13}\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.15.

Лексика

Термін	Визначення
Роздуми	Відображення - це перетворення, які призводять до «дзеркального відображення» батьківської функції. Вони викликані різними ознаками між батьківськими і дочірніми функціями.
Обертання	Обертання - це перетворення, яке перетворює фігуру на координатній площині на певну кількість градусів навколо заданої точки без зміни форми або розміру фігури.
Трансформація	Перетворення певним чином переміщує фігуру на координатну площину.

Додаткові ресурси

Практика: Позначення для композитних перетворень