8.19: Тесселяції
- Page ID
- 54911
Накладання плитки над площиною таким чином, щоб фігури заповнювали площину без нахлестів або зазорів.
Тесселяція - це плитка над площиною з однією або декількома фігурами таким чином, що фігури заповнюють площину без накладок і без зазорів. Ви, напевно, бачили тесселяції раніше. Прикладами тесселяції є: плитка для підлоги, цегляна або блокова стіна, шашка або шахова дошка, а також тканинний візерунок. Наступні малюнки також є прикладами тесселяцій.
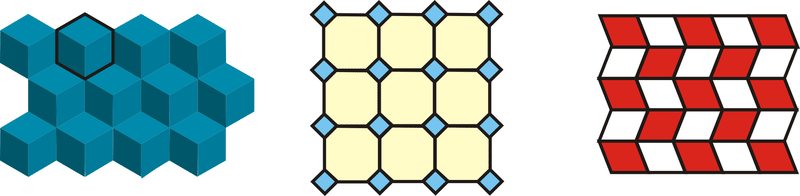
Зверніть увагу на шестикутник (кубики, перша тесселяція) і чотирикутники ідеально підходять один до одного. Якщо ми продовжуємо додавати більше, вони повністю покриють площину без зазорів або нахлестов.
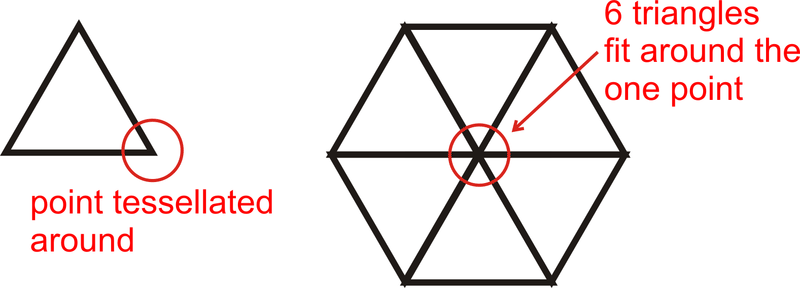
Ми будемо турбуватися лише про тесселяцію регулярних багатокутників. Щоб тесселювати фігуру, вона повинна бути в змозі точно оточувати точку, або сума кутів навколо кожної точки в тесселяції повинна бути\(360^{\circ}\). Єдині правильні багатокутники з цією ознакою - це рівносторонні трикутники, квадрати та правильні шестикутники.
Що робити, якщо вам дали шестикутник і попросили плиткою його над площиною таким чином, щоб він заповнив площину без перекриттів і без зазорів?
Приклад\(\PageIndex{1}\)
Скільки правильних шестикутників поміститься навколо однієї точки?
Рішення
Спочатку згадайте, скільки градусів знаходиться в колі, а потім з'ясуйте, скільки градусів знаходиться в кожному куті правильного шестикутника. Є\(360^{\circ}\) в колі і\(120^{\circ}\) в кожному внутрішньому куті шестикутника, тому\(\dfrac{360}{120}=3\) шестикутники будуть поміщатися навколо однієї точки.
Приклад\(\PageIndex{2}\)
Чи звичайний восьмикутник тесселює?
Рішення
Для початку нагадаємо, що є\(1080^{\circ}\) в п'ятикутнику. Кожен кут в правильному п'ятикутнику є\(1080^{\circ}\divide 8=135^{\circ}\). З цього ми знаємо, що звичайний восьмикутник не буде тесселювати сам по собі, тому що\(135^{\circ}\) не йде рівномірно\(360^{\circ}\).
Приклад\(\PageIndex{3}\)
Намалюйте тесселяцію рівносторонніх трикутників.
Рішення
У рівносторонньому трикутнику кожен кут є\(60^{\circ}\). Тому навколо кожної точки ідеально підійдуть шість трикутників.
Розширюючи викрійку, ми маємо:

Приклад\(\PageIndex{4}\)
Чи звичайний п'ятикутник тесселює?
Рішення
Для початку нагадаємо, що є\(540^{\circ}\) в п'ятикутнику. Кожен кут в правильному п'ятикутнику є\(540^{\circ}\divide 5=108^{\circ}\). З цього ми знаємо, що звичайний п'ятикутник не буде тесселювати сам по собі, оскільки\(108^{\circ}\) раз 2 або 3 не дорівнює\(360^{\circ}\).
Приклад\(\PageIndex{5}\)
Скільки квадратів поміститься навколо однієї точки?
Рішення
Спочатку згадайте, скільки градусів знаходиться в колі, а потім з'ясуйте, скільки градусів знаходиться в кожному куті квадрата. Є\(360^{\circ}\) в колі і\(90^{\circ}\) в кожному внутрішньому куті квадрата, тому\(\dfrac{360}{90}=4\) квадрати помістяться навколо однієї точки.
Рецензія
- Тесселят квадрат. Додайте кольору в свій дизайн.
- Що є прикладом тессельованого квадрата в реальному житті?
- Tessellate правильний шестикутник. Додайте кольору в свій дизайн.
- Ви також можете тесселювати два правильні багатокутники разом. Спробуйте тесселювати правильний шестикутник і рівносторонній трикутник. Спочатку визначте, скільки з кожного підходить навколо точки, а потім повторіть візерунок. Додайте кольору в свій дизайн.
- Чи тесселює звичайний додекагон (12-стороння форма)? Чому б і ні?
- Чи тесселює повітряний змій? Чому чи чому ні?
Чи тесселюють наступні цифри?
-
Малюнок\(\PageIndex{5}\) -

Малюнок\(\PageIndex{6}\) -

Малюнок\(\PageIndex{7}\) -
Малюнок\(\PageIndex{8}\) -

Малюнок\(\PageIndex{9}\)\ -

Малюнок\(\PageIndex{10}\) -

Малюнок\(\PageIndex{11}\) -

Малюнок\(\PageIndex{12}\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 12.7.
Лексика
| Термін | Визначення |
|---|---|
| тесселяція | Плитка над площиною з однією або декількома фігурами таким чином, щоб фігури заповнювали площину без нахлестів і без зазорів. |
| відрізок лінії | Відрізок лінії — це частина лінії, яка має дві кінцеві точки. |
Додаткові ресурси
Інтерактивний елемент
Відео: Принципи тесселяції - Основні
Види діяльності: Навчальний посібник з симетрії та тесселяції
Практика: Тесселяції
Реальний світ: Майстер тесселяцій