8.13: Визначення відображення

Last updated
Save as PDF

Page ID: 54897

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Трансформації, які перетворюють фігуру в її дзеркальне відображення, перевертаючи її над лінією.

Роздуми

Трансформація - це операція, яка рухає, перевертає або іншим чином змінює фігуру для створення нової фігури. Жорстке перетворення (також відоме як ізометрія або перетворення конгруентності) - це трансформація, яка не змінює розмір або форму фігури.

Жорсткі перетворення - це переклади, роздуми та обертання. Нова фігура, створена перетворенням, називається зображенням. Оригінальна фігура називається передзображенням. Якщо попередній образ - A, то зображення буде\(A′\), сказавши «простим». Якщо є зображення\(A′\), що буде позначено\(A′′\), сказав «подвійне просте».

Відображення - це перетворення, яке перетворює фігуру в її дзеркальне відображення, перевертаючи її над лінією. Лінія відображення - це лінія, над якою відбивається фігура. Якщо точка знаходиться на лінії відображення, то зображення таке ж, як і попередній образ. Зображення завжди збігаються з попередніми зображеннями.

F-д_Е8Ф5Е146ФБ3ЕФ ЕЕ17974 АБ2236509340С29АА3301497Б32ДФ0ЕА+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Хоча ви можете розмірковувати над будь-якою лінією, деякі загальні лінії роздумів мають правила, які варто запам'ятати:

Відображення над\(y\) -віссю:\((x,y)\rightarrow (−x,y)\)

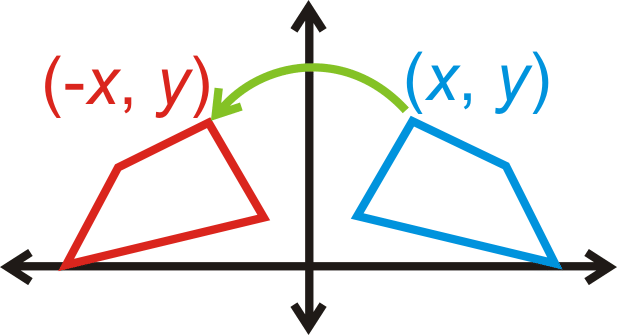
F-D_6A5265 БД2 Каб 9850 АДБ1Б8 СД 5751Ф8 ЕАААА21FF430Ф8Ф3Ф3Ф3АФ9Б6+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Відображення над\(x\) -віссю:\((x,y)\rightarrow (x,−y)\)

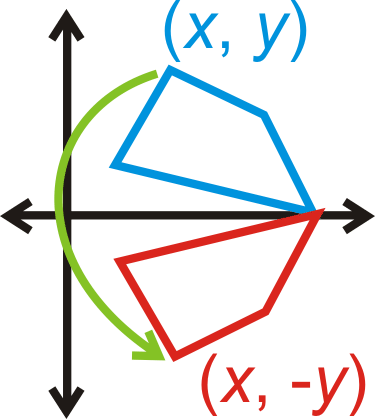
F-д_д3ФБ26Д6Б8Е8962Ф5С2147 BBC 6DA47FF86E5588F8F8A7720FF52D281+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Роздуми над\(y=x\):\((x,y)\rightarrow (y,x)\)

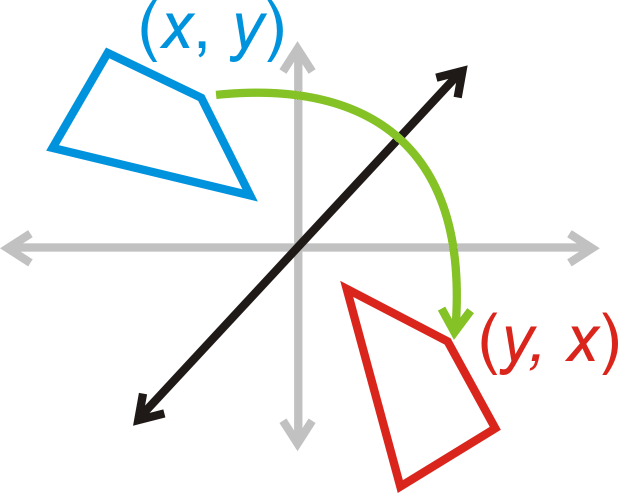
F-д_А8200 кБ8С408494Б4Б4Ф4Ф445481CD1Д70Б8Б84353285891E8774A+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Роздуми над\(y=−x\):\((x,y)\rightarrow (−y,−x)\)

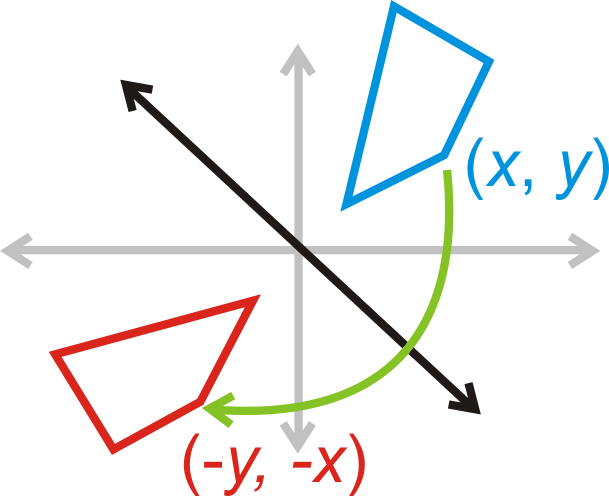
F-д_1ЕД 5С391Б0С66718С19Б2Б43Е28797118Ф2Б5Б 19904E1136C2A264E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Що робити, якщо вам дали координати чотирикутника, і вас попросили відобразити цей чотирикутник над\(y\) -віссю? Якими будуть його нові координати?

Приклад\(\PageIndex{1}\)

\(\Delta ABC\)Відображення над\(y\) -віссю. Знайдіть координати зображення.

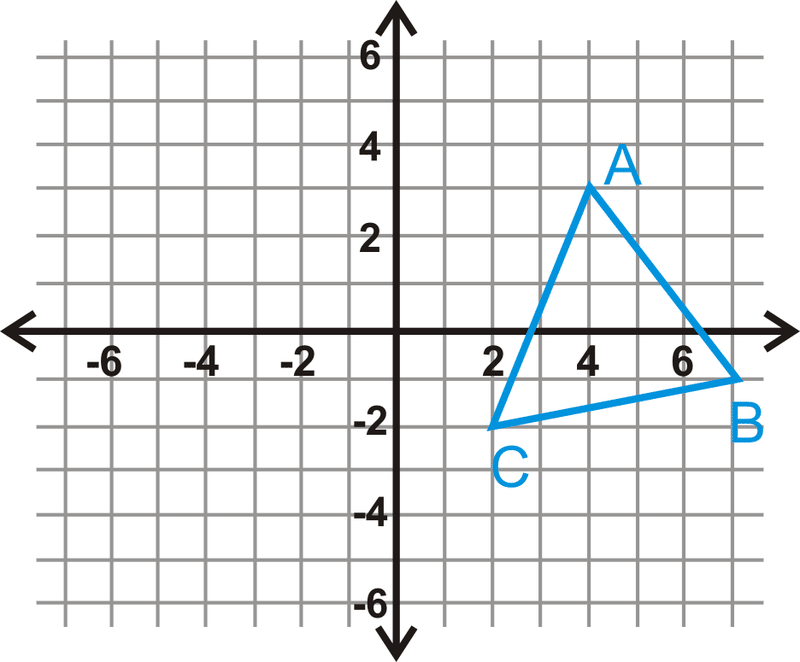
F-д_Е158 ААСА 0589Ф26993Б232С5С5С838Б4А47Е47823Д8350АФ 5С2092А5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

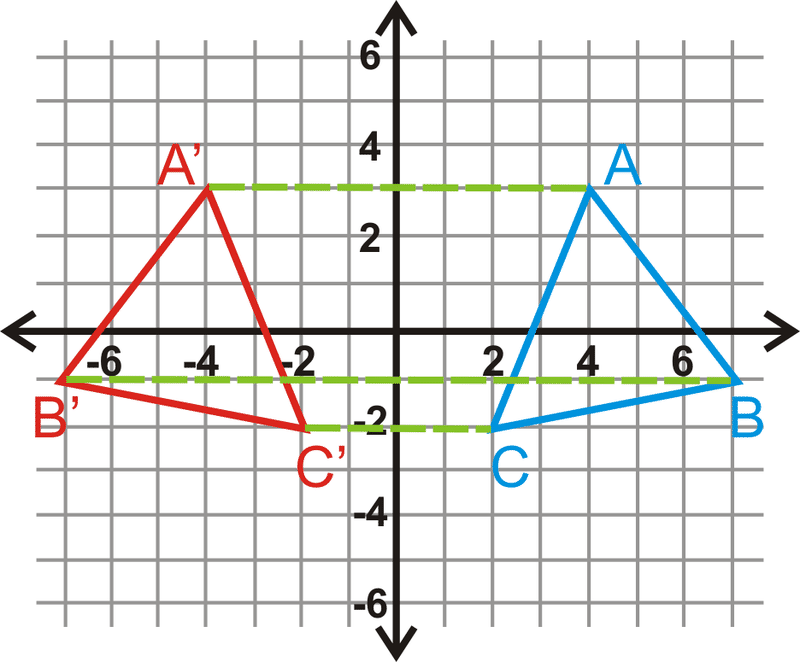
Ф-д_47Б80Б8201А5ДД2Б6Б6Е18А422А3Ф6 А6А65Б5183Е25АФ6146А8+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

\(\Delta A′B′C′\)буде на такій же відстані від\(y\) -осі як\(\Delta ABC\), але з іншого боку. Значить, їх\(x\) -координати будуть протилежними.

\(\begin{aligned} &A(4,3)\rightarrow A′(−4,3) \\ &B(7,−1)\rightarrow B′(−7,−1) \\ &C(2,−2)\rightarrow C′(−2,−2)\end{aligned}\)

Приклад\(\PageIndex{2}\)

Відобразіть букву «\(F\)′′» над\(x\) -віссю.

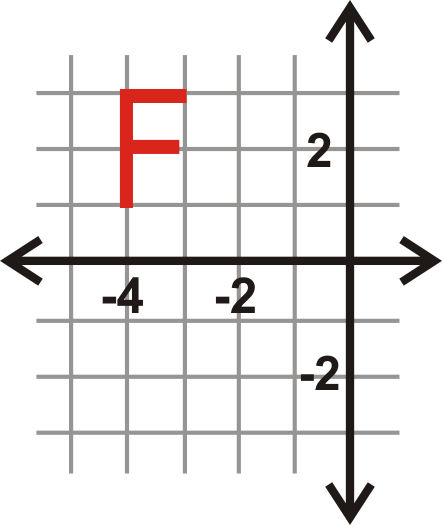
F-D_A81884E84828B8C7B9BE78Е17Ф9А706Е26 БББК0Ф496045Е0712ЕЕ+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Рішення

При відображенні літери F над\(x\) віссю\(y\) -координати матимуть однакову відстань від\(x\) осі -, але на іншій стороні від\(x\) осі -. Значить, їх\(y\) -координати будуть протилежними.

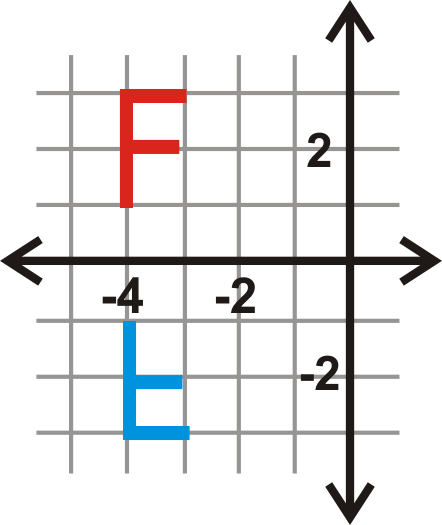
F-D_DC 1834Б Б 46Ф1Ф5110С8АФ3АЦ70Б247Е5А4655БА 8ДК6А973D66930A4+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

Приклад\(\PageIndex{3}\)

Відобразити трикутник\(\Delta ABC\) з вершинами\(A(4,5)\),\(B(7,1)\) і\(C(9,6)\) над лінією\(x=5\). Знайти координати\(A′\)\(B′\), і\(C′\).

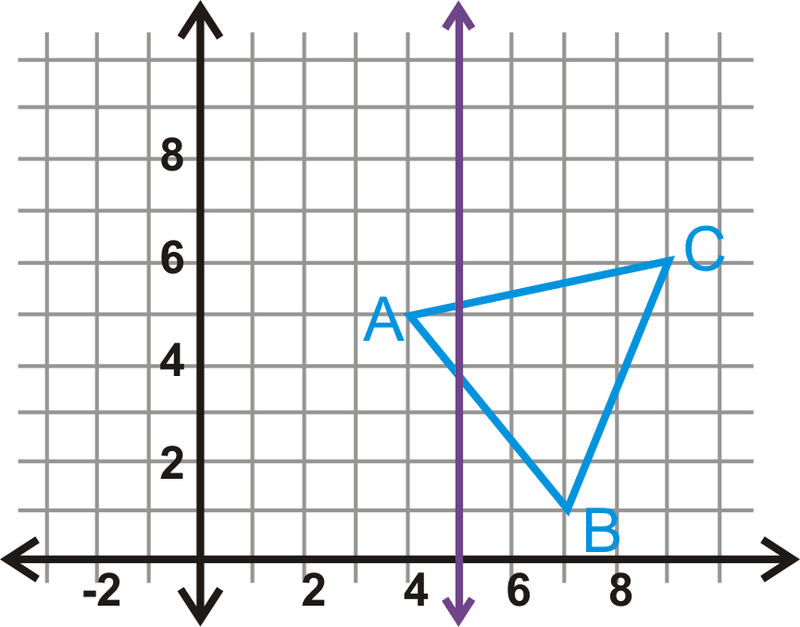
Ф-Д_5 БК ФДФ 83де31С0653843ДФ 19 ББ 89207417Б4Б4Б4Д6 CFDBD3CF6ED5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

Рішення

Вершини зображення знаходяться на тій же відстані від\(x=5\) вершин попереднього зображення.

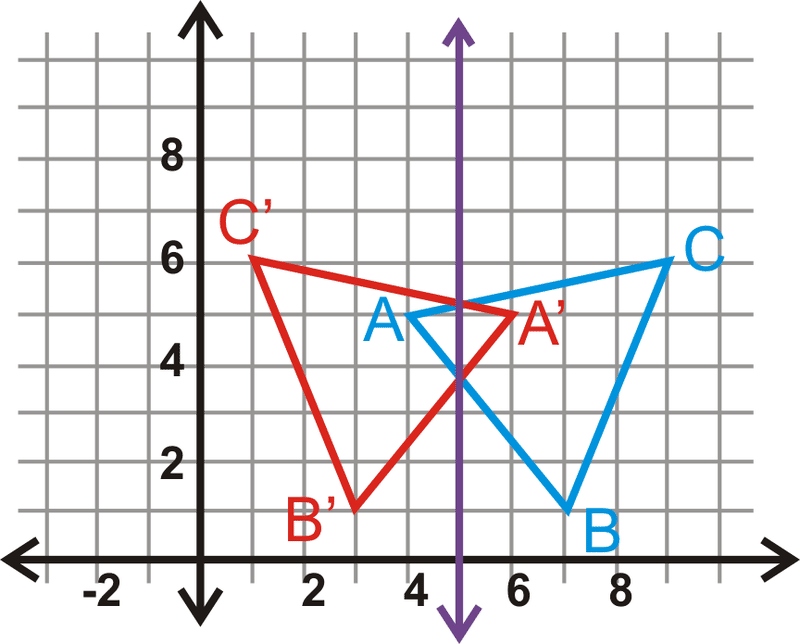
Ф-Д_ФА24А 980Д84Д5Ф2А0С93ФК 46ЕБ233262634КД5Д710ФДД701А0А+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG — Малюнок\(\PageIndex{11}\)

\(\begin{aligned} A(4,5)\rightarrow A′(6,5) \\ &B(7,1)\rightarrow B′(3,1) \\ &C(9,6)\rightarrow C′(1,6) \end{aligned}\)

Приклад\(\PageIndex{4}\)

Відобразіть відрізок лінії\(\overline{PQ}\) з кінцевими точками\(P(−1,5)\) і\(Q(7,8)\) над лінією\(y=5\).

Рішення

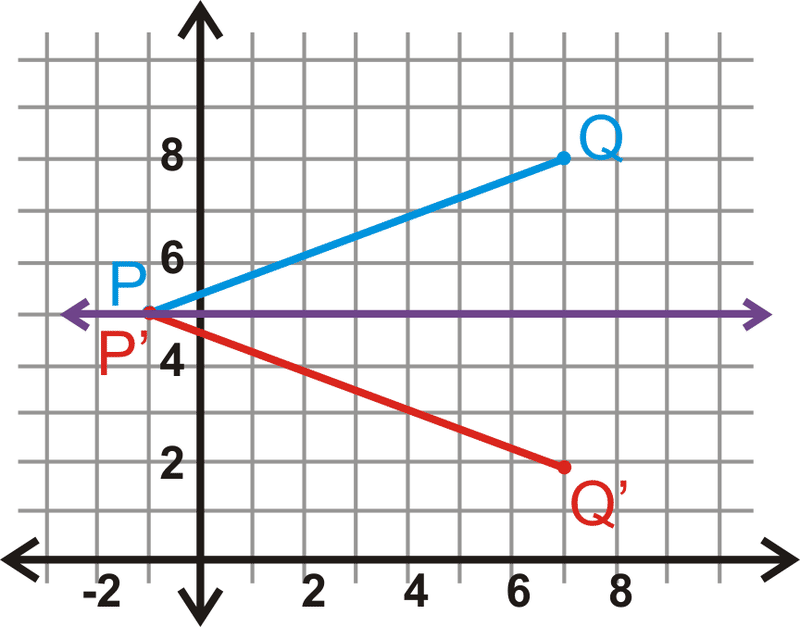
P знаходиться на лінії відображення, а значить\(P′\) має однакові координати. \(Q′\)така ж відстань від\ (y=5, але з іншого боку.

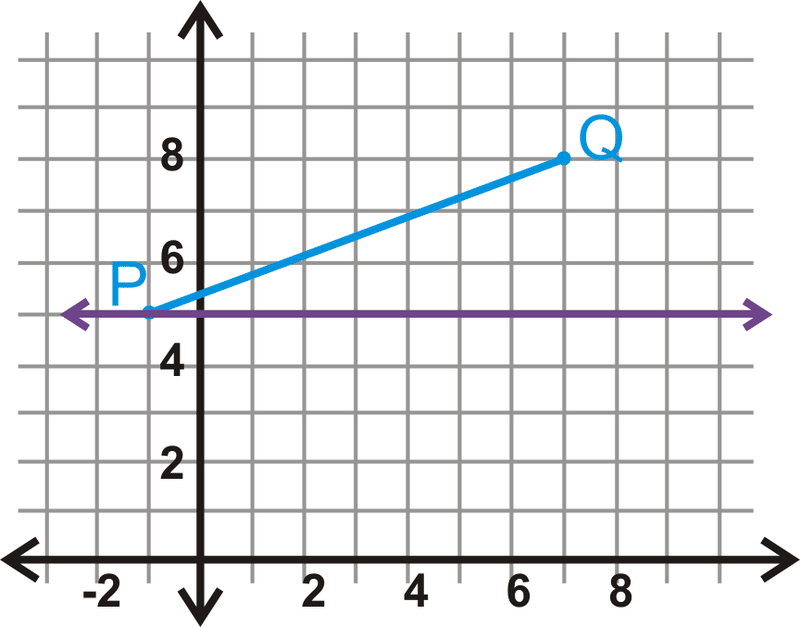
F-D_092 ФДФ CA767120408 Бад C66A1d4E92E1B9877c686E265570273BA5C5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

\(\begin{aligned}P(−1,5)&\rightarrow P′(−1,5) \\ Q(7,8)&\rightarrow Q′(7,2)\end{aligned}\)

F-D_EC26 ФДД 82415E8D3DAFF72cb683C дефаф 0449278c67689c8 деа 192+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

Приклад\(\PageIndex{5}\)

Трикутник\(\Delta LMN\) і його відображення,\(\Delta L′M′N′\) знаходяться внизу. Що таке лінія відображення?

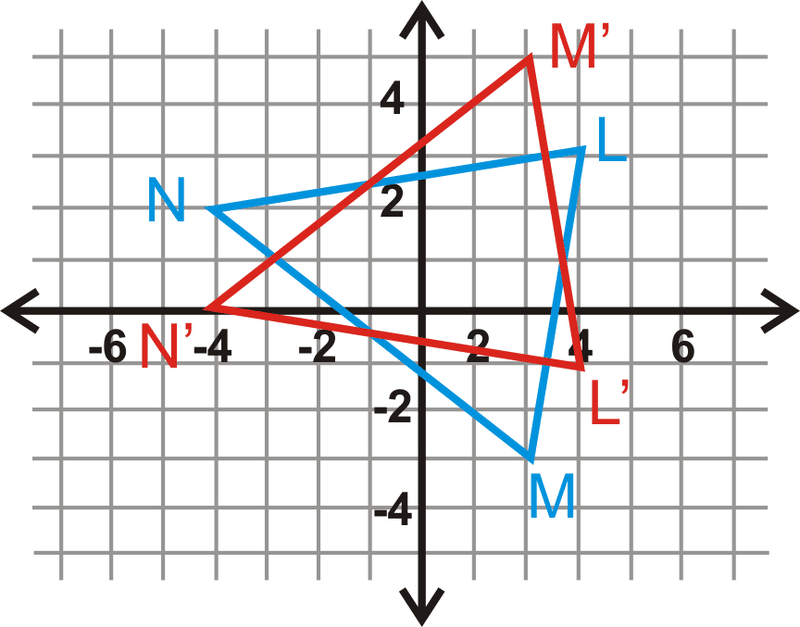
F-д_9БКС 15СБ99КФе 9А617Ф51Ф07Ф69 КБ56С3Б3Е3Е45С25Б20626Ф41+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\ (\ індекс сторінки {14})

Рішення

Дивлячись на графік, ми бачимо, що відповідні частини передзображення і зображення перетинаються при\(y=1\). Тому це лінія роздумів.

Якщо зображення не перетинає зображення, знайдіть середину між точкою попереднього зображення та його зображенням. Ця точка знаходиться на лінії відображення.

Приклад\(\PageIndex{6}\)

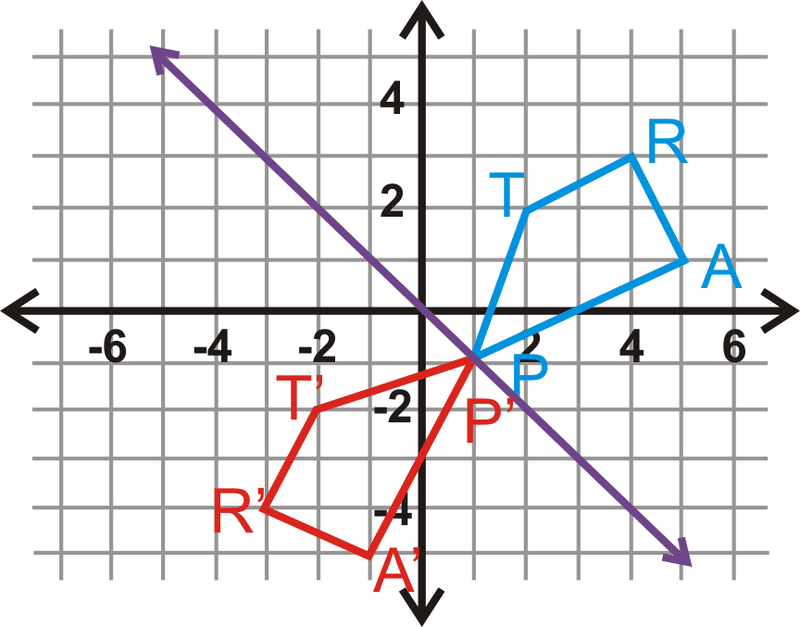
Відображати трапецію\(TRAP\) над лінією\(y=−x\).

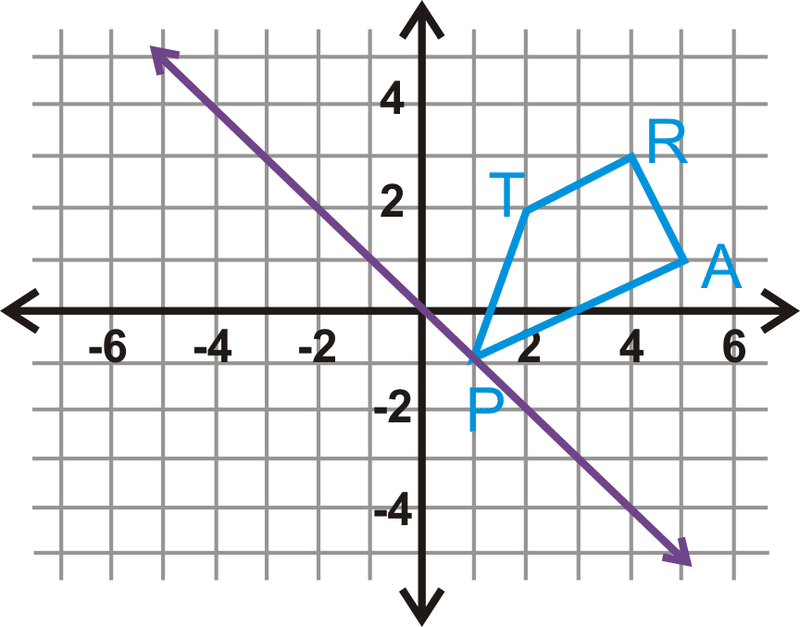
F-д_26ДАА А7Е6Ф1А045 Баб-6Е8Е1Е6440 ФЕ09696 ЕБ30ДК473406Ф10489АФА5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{15}\)

Рішення

Фіолетова лінія - це\(y=−x\). Можна відобразити трапецію над цією лінією.

\(\begin{aligned} T(2,2)\rightarrow T′(−2,−2) \\ R(4,3)\rightarrow R′(−3,−4) \\ A(5,1)&\rightarrow A′(−1,−5) \\ P(1,−1)&\rightarrow P′(1,−1) \end{aligned}\)

F-D_A484 ЕБ201C7АФ 4746Ф9А5450181 АЕ0328 БАЕ5СС74Д70Д019Ф97КБ843+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{16}\)

Рецензія

Якщо\((5,3)\) відбивається над\(y\) -віссю, що таке зображення?
Якщо\((5,3)\) відбивається над\(x\) -віссю, що таке зображення?
Якщо\((5,3)\) відбивається над\(y=x\), що таке зображення?
Якщо\((5,3)\) відбивається над\(y=−x\), що таке зображення?
Сюжетні чотири зображення. Яку форму вони роблять? Будьте конкретні.
Яка буква є відображенням над вертикальною лінією літери «\(b\)′′?
Яка буква є відображенням над горизонтальною лінією літери «\(b\)′′?

Відображати кожну фігуру над заданою лінією.

\(y\)-вісь

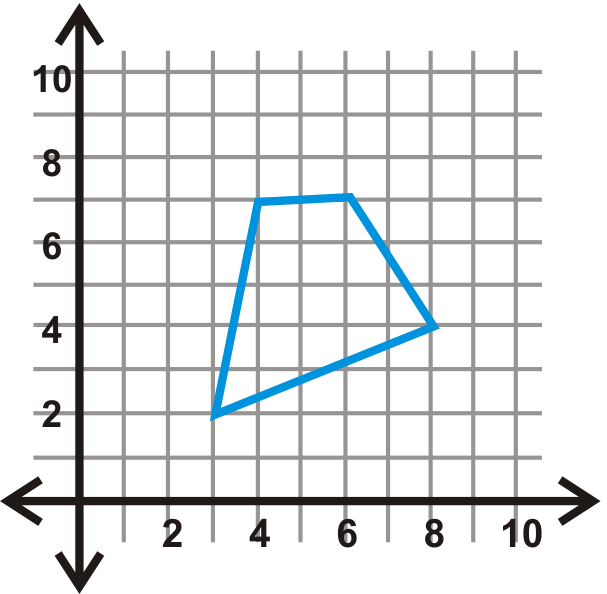
Малюнок\(\PageIndex{17}\)
\(x\)-вісь

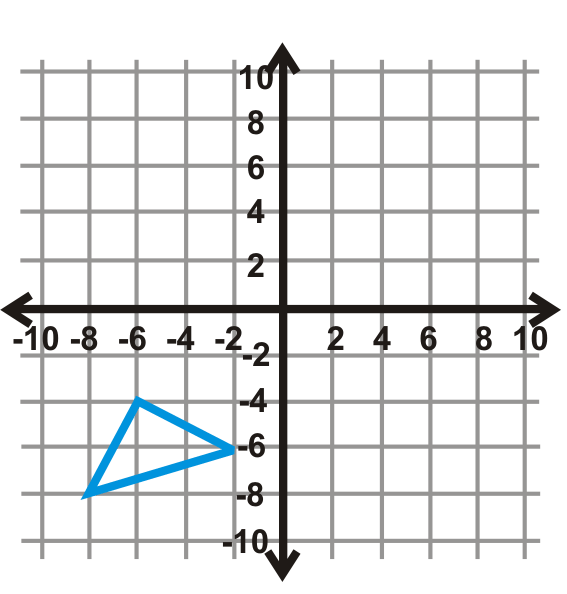
Малюнок\(\PageIndex{18}\)
\(y=3\)

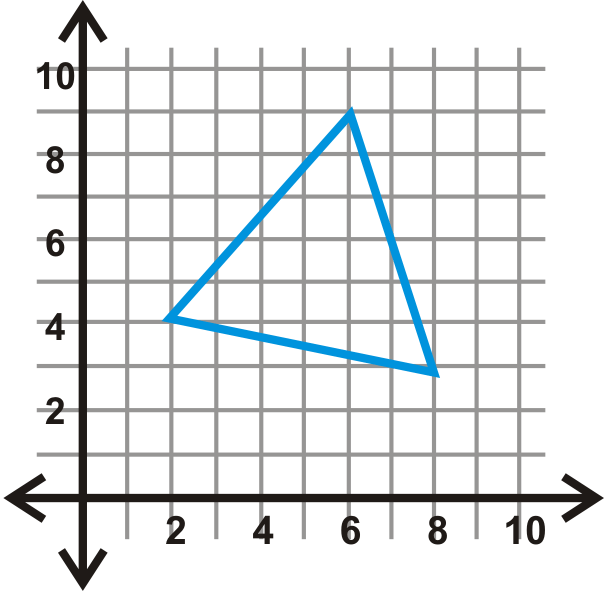
Малюнок\(\PageIndex{19}\)
\(x=−1\)

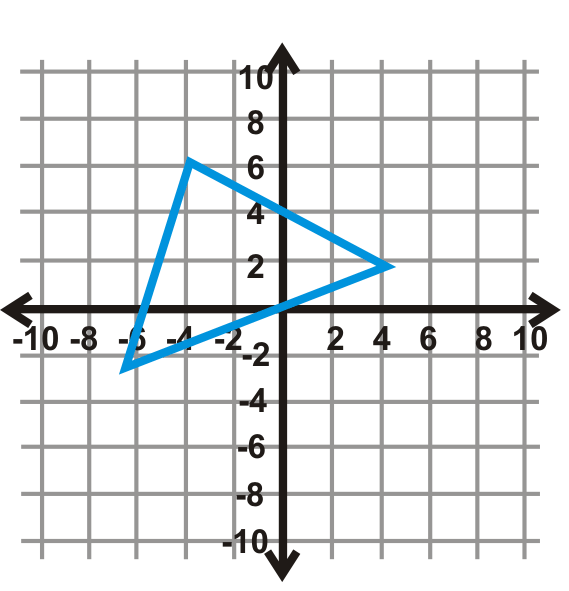
Малюнок\(\PageIndex{20}\)
\(x\)-вісь

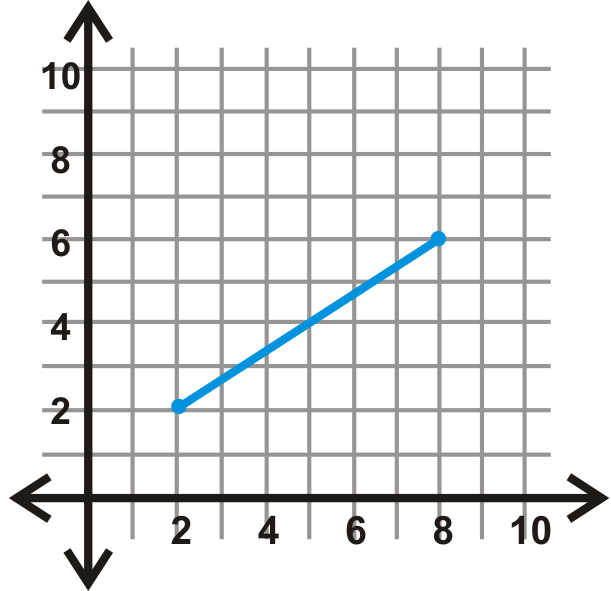
Малюнок\(\PageIndex{21}\)
\(y\)-вісь

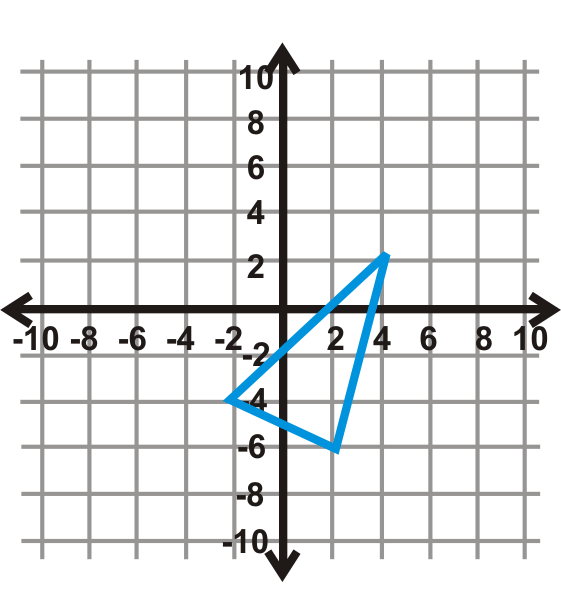
Малюнок\(\PageIndex{22}\)
\(y=x \)

Малюнок\(\PageIndex{23}\)
\(y=−x \)

Малюнок\(\PageIndex{24\)
\(x=2 \)

Малюнок\(\PageIndex{25}\)
\(y=−4 \)

Малюнок\(\PageIndex{26}\)
\(y=−x \)

Малюнок\(\PageIndex{27}\)
\(y=x \)

Малюнок\(\PageIndex{28}\)

Знайдіть лінію відображення синього трикутника (preimage) і червоного трикутника (зображення).

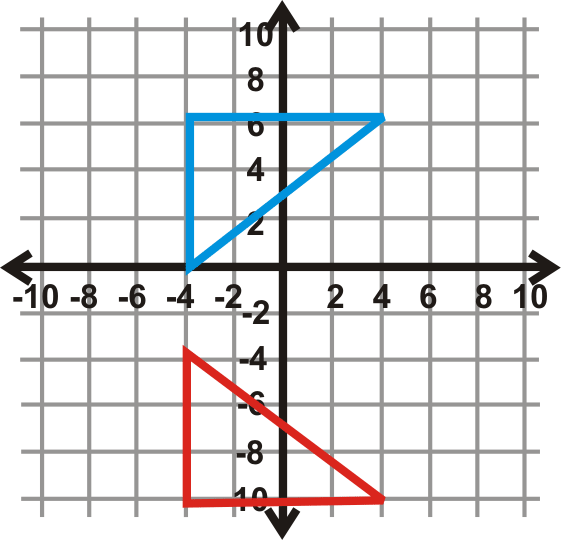
Малюнок\(\PageIndex{29}\)
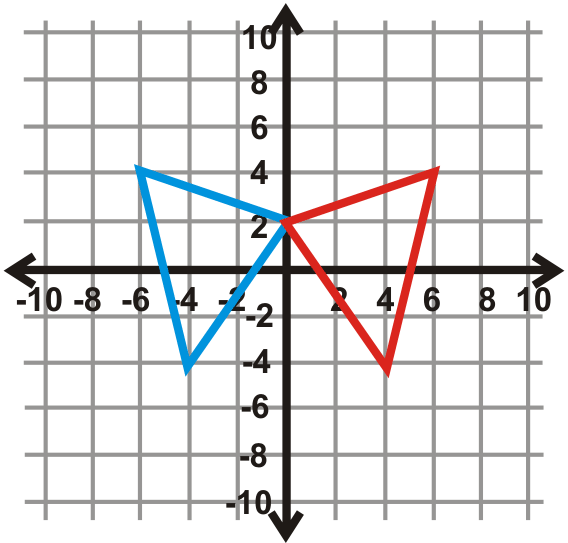
Малюнок\(\PageIndex{30}\)
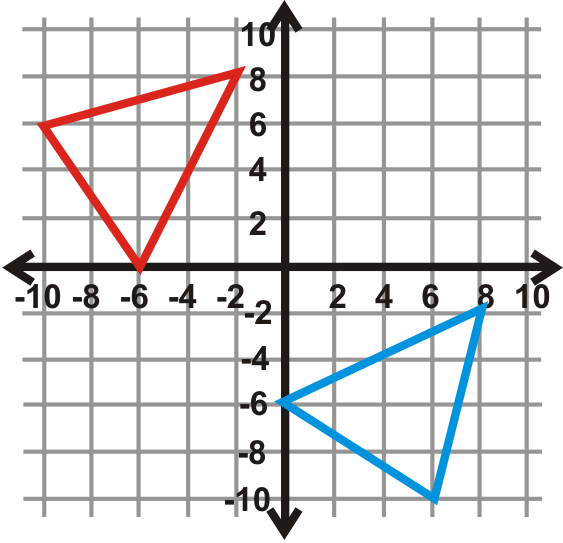
Малюнок\(\PageIndex{31}\)

Лексика

Термін	Визначення
Координатна площина	Координатна площина - це сітка, утворена горизонтальною цифровою лінією і вертикальною цифровою лінією, які перетинаються в\((0, 0)\) точці, яка називається початком. Координатна площина також називається декартовою площиною.
Геометричні візерунки	Геометричні візерунки - це візуальні візерунки геометричних фігур, які слідують правилу.
Зображення	Образ - це остаточний вигляд фігури після операції трансформації.
перпендикулярна бісектриса	Перпендикулярна бісектриса відрізка лінії проходить через середину відрізка лінії і перетинає відрізок лінії в\(90^{\circ}\).
перпендикулярні лінії	Перпендикулярні лінії - це лінії, які перетинаються під\(90^{\circ}\) кутом.
Передзображення	Попереднє зображення - це оригінальний вигляд фігури в операції трансформації.
Відображення	Відбиття - це перетворення, яке перевертає фігуру на координатній площині через задану лінію без зміни форми або розміру фігури.
Трансформація	Перетворення певним чином переміщує фігуру на координатну площину.
Жорстке перетворення	Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 12.5.

Додаткові ресурси

Інтерактивний елемент

Відео: Трансформація: Принципи рефлексії - Основні

Види діяльності: Роздуми Обговорення Питання

Навчальні посібники: Види трансформацій Навчальний посібник

Практика: Визначення рефлексії

Реальний світ: Відображення реальності